Solving Deep Reinforcement Learning Benchmarks with Linear Policy Networks
Abstract
Although Deep Reinforcement Learning (DRL) methods can learn effective policies for challenging problems such as Atari games and robotics tasks, algorithms are complex and training times are often long. This study investigates how evolution strategies (ES) perform compared to gradient-based deep reinforcement learning methods. We use ES to optimize the weights of a neural network via neuroevolution, performing direct policy search. We benchmark both regular networks and policy networks consisting of a single linear layer from observations to actions; for three classical ES methods and for three gradient-based methods such as PPO. Our results reveal that ES can find effective linear policies for many RL benchmark tasks, in contrast to DRL methods that can only find successful policies using much larger networks suggesting that current benchmarks are easier to solve than previously assumed. Interestingly, also for higher complexity tasks, ES achieves results comparable to gradient-based DRL algorithms. Furthermore, we find that by directly accessing the memory state of the game, ES are able to find successful policies in Atari, outperforming DQN. While gradient-based methods have dominated the field in recent years, ES offers an alternative that is easy to implement, parallelize, understand, and tune.
1 Introduction
Gradient-based deep reinforcement learning (DRL) has achieved remarkable success in various domains by enabling agents to learn complex behaviors in challenging environments based on their reward feedback, such as StarCraft Vinyals et al. (2019) and Go Silver et al. (2016). However, new methods are often benchmarked on simpler control tasks from OpenAI Gym, including the locomotion tasks from MuJoCo Haarnoja et al. (2018), or Atari games Mnih et al. (2015). While it simplifies the comparison between different approaches, these benchmarks may lack sufficient complexity, and performance may not always transfer to more complicated tasks. Additionally, several studies have indicated that DRL results are often hard to reproduce Islam et al. (2017), attributing these difficulties to the impact of the random seeds Henderson et al. (2018) and the choice of hyperparameters Eimer et al. (2023).
Evolution Strategies (ES) Rechenberg (1965); Bäck et al. (1991), a family of black-box optimization algorithms from the field of Evolutionary Algorithms (EAs) Bäck et al. (2023) have been studied as an alternative way to optimize neural network weights, as opposed to conventional gradient-based backpropagation Salimans et al. (2017); Such et al. (2017). An ES is used to learn a controller for an RL task by directly optimizing the neural network’s weights, which parameterize the RL policy. In this context, the ES is intrinsically an RL method that performs direct policy search, through neuroevolution Igel (2003). In supervised learning, gradient-based methods are often much more efficient than ES for training NN weights, though more likely to be trapped in local optima Mandischer (2002). For RL, the need to balance exploration with exploitation in gradient-based approaches incurs more training steps to learn an optimal policy Igel (2003), making ES an interesting alternative. While EAs are not necessarily more sample-efficient, ES can be more easily parallelized and scaled, offering the possibility for faster convergence in terms of wall-clock time, and, being a global search method, are less likely to get stuck in a local optimum Morse and Stanley (2016).
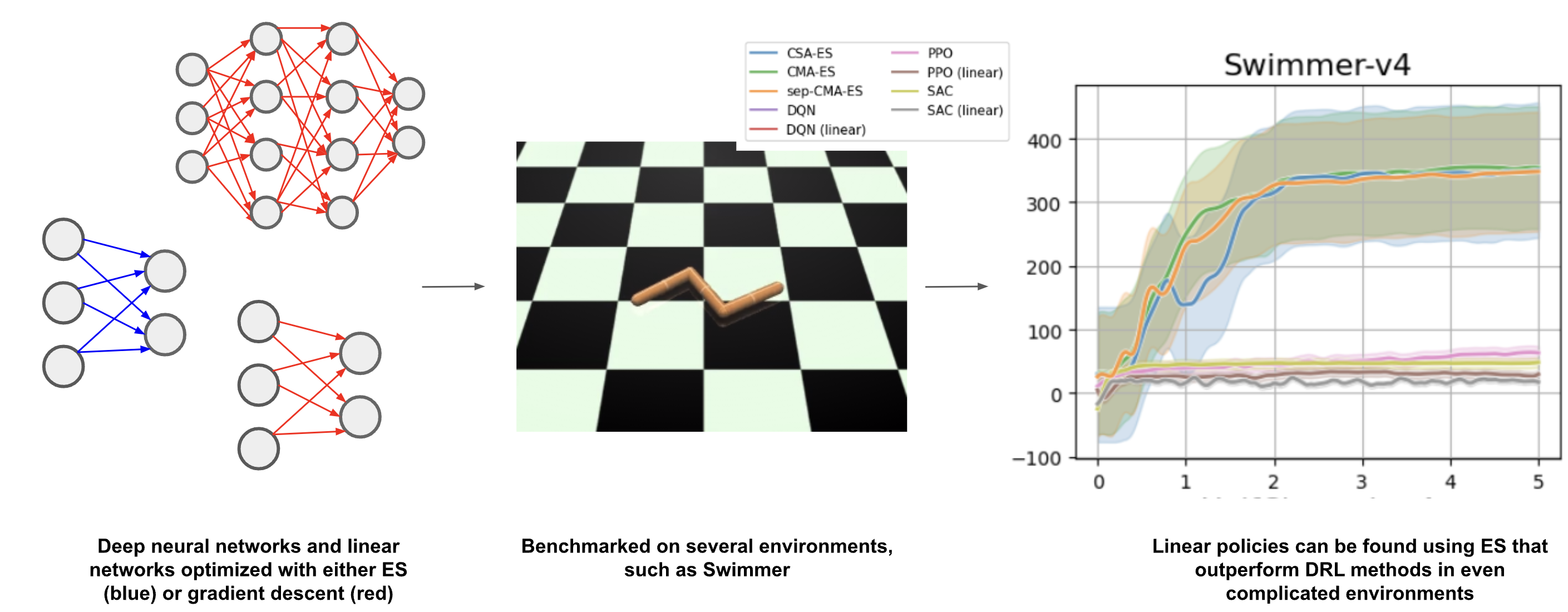
We benchmark three ES and three gradient-based RL methods on well-known RL tasks to understand the circumstances that favor ES over gradient-based methods. In particular, we study the optimization of policy networks that consist of a single linear layer, as they reduce the dimensionality of the problem Chrabąszcz et al. (2018); Rajeswaran et al. (2017). We compare these results to the larger networks that are used by common gradient-based methods. Our main contributions are as follows:
-
•
ES can find effective linear policies for many RL benchmark tasks. In contrast, methods based on gradient descent need vastly larger networks.
-
•
Contrary to the prevailing view that ES are limited to simpler tasks, they can address more complex challenges in MuJoCo. Gradient-based DRL only performs superiorly in the most challenging MuJoCo environments with more complex network architectures. This suggests that common RL benchmarks may be too simple or that conventional gradient-based solutions may be overly complicated.
-
•
Complex gradient-based approaches have dominated DRL. However, ES can be equally effective, are algorithmically simpler, allow smaller network architectures, and are thus easier to implement, understand, and tune (See Figure 1).
-
•
We find that advanced self-adaptation techniques in ES are often not required for (single-layer) neuroevolution.
The rest of the paper is organized as follows: Section 2 discusses the background and related work of ES and DRL, our algorithms are discussed in Section 3, the results are in Section 4, conclusions are in Section 5.
2 Background and Related Work
In RL, an agent learns from feedback through rewards and penalties from its environment Sutton and Barto (2018). RL problems are formulated as a Markov Decision Process , where is the set of states in the environment, the set of actions available to the agent, the probability of subsequent state transitions, the reward function, and the discount factor Bellman (1957). A policy can be computed of which action to take in each state. The policy in DRL is typically represented by a deep neural network to map states to actions (probabilities). RL aims to find the optimal policy that maximizes the expected cumulative reward of a state. RL algorithms approach this goal in different ways Plaat (2022). The most common techniques include value-function estimation Watkins and Dayan (1992); Mnih et al. (2015), policy gradient methods Williams (1992), actor-critic methods Konda and Tsitsiklis (1999); Schulman et al. (2017); Haarnoja et al. (2018), and learning a model of the environment Hafner et al. (2020); Plaat et al. (2023).
ES are a distinct class of evolutionary algorithms that are particularly suitable for optimization problems in continuous domains. ES begin with a population of randomly initialized candidate solutions in , with solutions represented as -dimensional vectors denoted by (like the policy) and a given objective function (like the reward). Via perturbations using a parameterized multivariate normal distribution, selection, and sometimes recombination, solutions evolve towards better regions in the search space Bäck et al. (1991). Evolving neural networks with EAs is called neuroevolution and can include the optimization of the network’s weights, topology, and hyperparameters Stanley et al. (2019). Using ES to evolve a neural network’s weights is similar to policy gradient methods in RL, where optimization applies to the policy’s parameter space.
Gradient-based deep RL has successfully tackled high-dimensional problems, such as playing video games with deep neural networks encompassing millions parameters Mnih et al. (2015); Vinyals et al. (2019). However, state-of-the-art ES variants are limited to smaller numbers of parameters due to the computational complexity of, for example, the adaptation of the covariance matrix of the search distribution. Covariance Matrix Adaptation Evolution Strategy (CMA-ES) is often used for dimensionality lower than Müller and Glasmachers (2018), and problems with a dimensionality become nearly impossible due to the memory requirements Loshchilov (2014). However, recent advancements have restricted the covariance matrix, in its simplest form, to its diagonal, to reduce the computational complexity Ros and Hansen (2008); Loshchilov (2014); Nomura and Ono (2022). Others sample from lower-dimensional subspaces Maheswaranathan et al. (2019); Choromanski et al. (2019).
In 2015, DRL reached a milestone by achieving superhuman performance in Atari games using raw pixel input Mnih et al. (2015). This breakthrough marked a shift in RL towards more complicated, high-dimensional problems and a shift from tabular to deep, gradient-based methods. For simpler tasks, the CMA-ES has been used to evolve neural networks for pole-balancing tasks, benefiting from covariance matrix to find parameter dependencies, enabling faster optimization Igel (2003); Heidrich-Meisner and Igel (2009). While the use of evolutionary methods for RL can be traced back to the early 90s Whitley et al. (1993); Moriarty and Mikkulainen (1996), the paper by Salimans et al. (2017) rekindled interest in ES from the field of RL as an alternative for gradient-based methods in more complicated tasks. Researchers showed that a natural evolution strategy (NES) can compete with deep RL in robot control in MuJoCo and Atari games due to its ability to scale over parallel workers. In contrast to deep methods where entire gradients are typically shared, the workers only communicate the fitness score and the random seed to generate the stochastic perturbations of the policy parameters. Studies have subsequently demonstrated that simpler methodologies can yield results comparable to NES, such as a classical ES Chrabąszcz et al. (2018) and Augmented Random Search Mania et al. (2018), which closely resembles a global search heuristic from the 1990s Salomon (1998). In addition, when separating the computer vision task from the actual policy in playing Atari, the size of the neural network can be drastically decreased Cuccu et al. (2018), and policies with a single linear layer, mapping states directly to actions, can effectively solve the continuous control tasks Chrabąszcz et al. (2018); Rajeswaran et al. (2017). The development of dimension-lowering techniques, such as world models Ha and Schmidhuber (2018); Hafner et al. (2020) and autoencoders Hinton and Salakhutdinov (2006), also opens up new possibilities for ES to effectively solve more complex problems by simplifying them into more manageable forms.
3 Methods
We implement three ES methods and benchmark them against three popular gradient-based DRL methods.
3.1 Gradient-Based Algorithms
We use three popular gradient-based DRL algorithms: Deep Q-learning Mnih et al. (2015), Proximal Policy Optimization Schulman et al. (2017), and Soft Actor-Critic Haarnoja et al. (2018). We summarize the main gradient-update ideas below.
3.1.1 Deep Q-Learning
Deep Q-learning (DQN) combines a deep neural network with Q-learning to learn the value function in a high-dimensional environment Mnih et al. (2015). Each experience tuple is stored in a replay buffer. The agent randomly selects a batch of experiences to update the value function. The replay buffer breaks the correlation between consecutive experiences, leading to lower variance. The primary Q-network weights are updated every training step by minimizing the expectation of the squared difference between the predicted Q-value of the current state-action pair and the target Q-value :
The weights from the primary Q-network are copied every timesteps to a separate target network to prevent large oscillations in the loss function’s target values.
3.1.2 Proximal Policy Optimization
Proximal Policy Optimization (PPO) was introduced to improve the complexity of earlier policy gradient methods Schulman et al. (2017). PPO introduces a simpler, clipped objective function:
where denotes the empirical expectation over a finite batch of samples, the probability ratio reflects the probability of an action under the current policy compared to the previous policy, is the advantage estimate at timestep , and is a hyperparameter defining the clipping range. The clipping mechanism clips the ratio within the range .
3.1.3 Soft Actor-Critic
SAC objective’s function maximizes the expected return and entropy simultaneously to ensure a balanced trade-off between exploitation and exploration:
where is the temperature parameter that scales the importance of the entropy of the policy given the state . SAC updates its Q-value estimates using a soft Bellman backup operation that includes an entropy term:
SAC employs twin Q-networks to mitigate overestimation bias and stabilize policy updates by using the minimum of their Q-value estimates.
3.2 Evolution Strategies
ES are designed for solving continuous optimization problems , where . The ES methods are used here to optimize the neural network parameters for the policy function, i.e., the ES is used for neuroevolution of the weights of the neural network that represents the policy. The methods are variants of derandomized ES and use a parameterized multivariate normal distribution to control the direction of the search. is the mean vector of the search distribution at generation in the ES, denotes the scale and the shape of the mutation distribution. The algorithm adapts the parameters of the search distribution to achieve fast convergence (Algorithm 1).
The ES samples offspring from its mutation distribution at each iteration. By selecting the most promising offspring to update its parameters, it moves to regions of higher optimality. After sorting the offspring by fitness ranking, the mean of the search distribution is updated via weighted recombination:
The ES variants adapt, with increasing complexity, the scale and shape of the mutation distribution. The Cumulative Step-size Adaptation Evolution Strategy (CSA-ES) only adapts , producing exclusively isotropic (i.e. ) mutations during optimization. The separable Covariance Matrix Adaptation Evolution Strategy (sep-CMA-ES) additionally adapts the diagonal entries of the covariance matrix , producing mutation steps with arbitrary scaling parallel to each coordinate axis. Finally, the CMA-ES adapts the full covariance matrix, which allows the mutation distribution to scale to arbitrary rotations. Figure 2 illustrates the evolution of the mutation distribution for each of these three methods when optimizing a two-dimensional quadratic function. The figure shows that the mutation distribution guides the search, favoring selected mutation steps with high probability Hansen and Ostermeier (2001). The CSA-ES uses a process called cumulation of historically selected mutation steps in order to update the value of the global step size parameter . We implemented the algorithm following Chotard et al. (2012), using recommended hyperparameter settings. While several modifications of the CMA-ES have been developed over the years, we implemented a canonical version of the algorithm, as first introduced in Hansen and Ostermeier (2001). The update of the full covariance matrix becomes computationally impractical for , but the sep-CMA-ES, which we implemented according to Ros and Hansen (2008), does not suffer from this restriction. As shown in Figure 2, this algorithm only computes variances for each coordinate axis, which makes it applicable to much higher dimensions, as the computational complexity for the update of the mutation distribution scales only linearly with .


3.3 Network Architecture
We compare the performance of linear policies trained through neuroevolution by ES with gradient-based methods inspired by earlier studies demonstrating this approach’s feasibility Mania et al. (2018); Rajeswaran et al. (2017). For the ES, only linear policies are trained, defined as a linear mapping from states to actions, activated by either an or function for discrete and continuous action spaces, respectively (no hidden layer: a fully connected shallow network). We use the gradient-based methods to train the same linear policies for each control task. Table LABEL:tab:weights (Supplementary material) shows the number of trainable weights for each environment for a linear policy. Additionally, a network architecture based on the original studies for each of the gradient-based methods is trained for comparison. We employ the architecture from the original studies for PPO Schulman et al. (2017) and SAC Haarnoja et al. (2018). For DQN, we use the default architecture from CleanRL’s library, which has been tested across multiple control environments and showed good results Huang et al. (2022). Specifics for these architectures and other hyperparameters can be found in the supplementary material. We do not train these deep architectures using ES, as they only serve as a benchmark to demonstrate the intended usage of the gradient-based algorithms, and self-adaptation mechanisms are increasingly less useful for such high dimensions Chrabąszcz et al. (2018).
| Algorithm | CSA-ES | CMA-ES | sep-CMA | Random | Human | DQN | ES* |
| Atlantis | 84690 | 87100 | 88580 | 12850 | 29028 | 85641 | 103500 |
| B. Rider | 2215 | 1967 | 2222 | 363.9 | 5775 | 6846 | 5072 |
| Boxing | 96.0 | 96.8 | 95.1 | 0.1 | 4.3 | 71.8 | 100 |
| C. Climber | 36170 | 29290 | 32940 | 10781 | 35411 | 114103 | 57600 |
| Enduro | 65.1 | 58.9 | 69.0 | 0 | 309.6 | 301.8 | 102 |
| Pong | 5.7 | 7.4 | 7.1 | -20.7 | 9.3 | 18.9 | 21 |
| Q*Bert | 7355 | 5732 | 7385 | 163.9 | 13455 | 10596 | 14700 |
| Seaquest | 959 | 948 | 954 | 68.4 | 20182 | 5286 | 1470 |
| S. Invaders | 1640 | 1972 | 1488 | 148 | 1652 | 1976 | 2635 |
3.4 Experimental Setup
We conduct experiments on common control tasks of varying complexity levels from the Gymnasium API Towers et al. (2023). For each of the considered environments, five runs using different random seeds are conducted for each algorithm/control task combination to test the stability of each approach. Value-based DQN is only used for environments with discrete action spaces, SAC for continuous action spaces, and PPO and ES are used for both action spaces. The RL algorithms are implemented using the cleanRL library111https://github.com/vwxyzjn/cleanrl/tree/master that has been benchmarked across several environments; we removed the hidden layers for the linear network. The specifics of the Evolution Strategies (ES) implementations are detailed in the repository, the link to which is provided in the footnote222anonymized for reviewing. Since the environments are stochastic, we report the median episodic return, calculated over five test episodes. As was discussed in Salimans et al. (2017), for ES, the wall-clock time required to solve a given control task decreases linearly with the number of parallel workers available. This allows us to do many more evaluations of the environment than is feasible with gradient-based RL. For fairness of comparison, we limit the difference in the number of training time steps allowed by a single order of magnitude. Specific hyper-parameters used for each environment can be found in the supplementary material, including hardware. For the ES, we initialize each experiment with . We calculate a rolling mean and variance of the observations of the environment during each run. These values are then used to normalize each state observation to standard normal entries by subtracting this rolling mean and dividing by the standard deviation.
3.4.1 Classic RL Environments
The first set of experiments includes the classic control tasks Cartpole, Acrobot, and Pendulum. We include BipedalWalker and LunarLander from the Box2D simulations for slightly more complex dynamics. Each run uses a maximum of 500 000 timesteps for each environment. The exception to this is the BipedalWalker task, for which timesteps are used.
3.4.2 MuJoCo Simulated Robotics
We evaluate the algorithms on the MuJoCo environments Todorov et al. (2012) for higher complexity levels, including Hopper, Walker2D, HalfCheetah, Ant, Swimmer, and Humanoid. Table LABEL:tab:hyper (Supplementary material) provides training details. As was noted by Mania et al. (2018), ES methods have exploration at the policy level, whereas gradient-based methods explore on the action level. In the locomotion tasks, a positive reward is provided for each time step where the agent does not fall over. This causes the ES method to stay in a local optimum when the agent stays upright but does not move forward (the gradient-based methods do not get stuck). Following Mania et al. (2018), we modified the reward function for these environments for ES, subtracting the positive stability bonus and only rewarding forward locomotion.
3.4.3 Atari Learning Environment
Finally, we benchmark DQN against the ES with linear policies on games from the Atari suite. To demonstrate the effectiveness of linear policies for these high-dimensional tasks, we take inspiration from the approach by Cuccu et al. (2018) and separate the computer vision task from the control task. We train the ES agents on the 128 bytes of the Random Access Memory (RAM) in the simulated Atari console. This drastically reduces the input dimensionality of the controller, allowing for the training of smaller policies. This assumes that the random access memory sufficiently encodes the state of each game without having to extract the state from the raw pixel images. It should be noted that not for all games is RAM information sufficient to train a controller and that for some games, DQN is easier to train on pixel images than on RAM input Sygnowski and Michalewski (2017). Since we evaluate linear policies, we fix frame skipping to 4, with no sticky actions Machado et al. (2018), similar to the settings used in Mnih et al. (2015). For each run, the ES were trained for 20 000 episodes, where the maximum episode length was capped at 270 000 timesteps. The gradient-based methods were trained for a maximum of timesteps.
4 Results
In this section, we present the results of our experiments (more details, including training curves and tables with summary statistics, can be found in the Supplementary material). Here, we focus on a selection of environments (Figure 3).
4.1 Classics RL Environments
The first column of Figure 3 shows the training curves for the gradient-based methods and for ES on the CartPole and LunarLander environments (the Supplementary material has more). For both environments, the ES policies outperform the deep gradient-based methods with just a simple linear policy. For CartPole, the results are even more surprising, as the ES policies are able to solve the environment in the first few iterations of training through pure random sampling from a standard normal distribution. The deep gradient-based methods, on the other hand, require around timesteps in order to solve CartPole. The gradient-based methods are unable to find a good linear policy for CartPole. This pattern persists for LunarLander, where, even though the ES requires around timesteps to solve the environment, the gradient-based methods cannot find a good linear policy at all. While the deep gradient-based methods eventually seem to catch up to the ES, it still requires more than timesteps to train a stable policy for LunarLander. For the BipedalWalker task (see Supplementary material), DQN and PPO are able to find good policies, with the gradient-based methods requiring fewer timesteps. Only SAC is able to solve Pendulum within timesteps. For Acrobot, again, the ES are able to solve the environment almost instantly, while the gradient-based methods require a good number of environment interactions to do so.
4.2 MuJoCo Simulated Robotics
The center column of Figure 3 shows that the ES policies are much better at finding a policy for the Swimmer environment, while for HalfCheetah, SAC greatly outperforms all other methods. However, ES outperforms PPO. Moreover, none of the gradient-based methods are able to find a good linear policy for HalfCheetah and Swimmer. This pattern holds for almost all MuJoCo experiments; only for the Ant environment can PPO find a linear policy with decent performance. Overall, as the number of weights increases, the performance of the ES lags behind the deep gradient-based methods (see Table LABEL:tab:weights in the Supplementary material). Nevertheless, even though ES generally require more timesteps, they can still find good linear policies for most environments, which are just as effective as policies found by vastly larger networks (see Table LABEL:tab:stats in the Supplementary material). Even for the most complex of these environments, Humanoid, the ES are able, in several trials, to find a linear policy that has a higher episodic return, (averaged over 5 test episodes with different random seeds), than was found by the best deep gradient-based method, SAC. Furthermore, ES timesteps are quicker and easier to parallelize, meaning experiments are much faster to run.
4.3 Atari Learning Environment
The last column of Figure 3 shows the training curves of ES vs. DQN for the Atari games SpaceInvaders and Boxing. The figure shows that when training agents that use the controller’s RAM state as observations, ES outperform linear DQN in most cases. CrazyClimber (Supplementary material) is the only exception, for which the performance of ES and linear DQN is similar. Even comparing against deep DQN trained on RAM memory, we find that for both the games in Figure 3, the ES yield better policies and require fewer environment interactions. In addition, Table 1 shows the average highest score per trial for each of the tested games for the ES, compared against the numerical results presented in Mnih et al. (2015) for a Human, Random and a DQN player that uses pixel input. The table additionally shows the highest score attained by any ES in any trial, averaged over 5 test episodes. For both Atlantis and Boxing, an ES achieves the highest score. For all the other games tested, the DQN agent earned a higher score than all RAM-trained ES, although CMA-ES achieved a score almost identical to DQN on SpaceInvaders. This score is attained by an agent that uses a linear policy consisting of only 768 weights, while the policy trained by DQN has 1.5 (pixel-based, deep policy network). Moreover, the best-found policy by any ES is often competitive with DQN. This indicates that a linear policy, which is competitive with pixel-based DQN, does exist.
5 Discussion and Conclusion
In this study, we have studied different ways to optimize reinforcement learning policies with conventional deep learning gradient-based backpropagation methods as used in DQN, PPO, and SAC, and with three evolution strategy methods (ES). We have applied these methods to several classic reinforcement learning benchmarks. For these methods, we trained the regular deep network as conventionally used, as well as a neural network with no hidden layers, i.e., a linear mapping from states to actions, as a low-complexity controller for each environment. In many of the tested environments, the linear policies trained with the ES are on par or, in some cases, even better controllers than the deep policy networks trained with the gradient-based methods. Additionally, the gradient-based methods are often ineffective at training these simple policies, requiring much deeper networks. For our experiments on Atari, we find that by accessing the RAM memory of the Atari controller, ES methods can find a linear policy that is competitive with "superhuman" DQN Mnih et al. (2015). It should be noted that there are certain high-complexity environments where the deep gradient-based methods yield better policies, e.g. SAC for HalfCheetah. However, even for these environments, linear policies exist that are competitive and much more easily interpretable.
We conclude that conventional gradient-based methods might be overly complicated or that more complex benchmarks are required to properly evaluate algorithms. In fact, even for the most complex locomotion task included in our experiments, the Humanoid environment, the CMA-ES was able to find a linear policy that was competitive with state-of-the-art methods. As the ES are stochastic algorithms, they were not able to find these policies for every trial run, but our results show that such policies do exist. We expect the search landscapes for these environments to be deceptive and multimodal, and future work could help discover effective algorithms for more consistently training these linear policy networks, for example, using niching methods Shir and Bäck (2005). We hypothesize that gradient-based methods may struggle to find linear policies due to the multimodal nature of the search landscape, a phenomenon also seen in supervised learning Kawaguchi (2016). Counterintuitively, with gradient-based methods, it seems more straightforward to train deeper architectures than shallower ones with far fewer weights, as was also shown by Schwarzer et al. (2023). We note that gradient-based methods are essentially local search methods, requiring heuristically controlled exploration, while ES, in the early phases of optimization, are performing global search, producing more diverse solutions. This also becomes evident in the more simple environments, such as CartPole, where the ES are able to almost instantly sample the optimal policy, while the gradient-based methods have a much harder time.
Moreover, we find many counterexamples to the prevailing view that ES are less sample efficient than the gradient-based methods. For many of the low to medium-complexity environments, the ES are actually more sample efficient and require fewer environment interactions than the deep gradient-based methods. On the other hand, for the more complex environments, and with increasing dimensionality, we find that the ES can take more time steps to converge than the deep gradient-based methods. This is to be expected, as the self-adaptation mechanisms that are central to the ES become increasingly ineffective for larger dimensions Chrabąszcz et al. (2018); Müller and Glasmachers (2018). We have compared three ES, that, with increasing levels of complexity, adapt the shape of the mutation distribution in order to converge the search. Our results indicate that updates of the covariance matrix are often not required and that performing step size adaptation is sufficient. While we expect the search landscape to be multimodal, relative scaling and rotation of search coordinates seem absent, allowing isotropic mutations to be effective for these problems. This would also explain the effectiveness of the approach demonstrated in Maheswaranathan et al. (2019), which would be heavily impacted by conditioning on the search space. However, this may be explained because optimizing a single linear layer may exhibit less inherent variance and covariance than multiple layers.
Overall, we have demonstrated the potential of linear policies on popular RL benchmarks. We showed that ES are effective optimizers for these policies compared to gradient-based methods. Additionally, we note that ES are simpler in design, have fewer hyperparameters, and are trivially parallelizable. Hence, ES can perform more environment interactions within the same time frame Salimans et al. (2017). Moreover, evaluating linear policies is faster than evaluating one or sometimes several deep architectures, making the training much more expedient regarding wall-clock time. As the need for energy-efficient policy networks increases, our results warrant a closer look at ES for RL and training of simpler policies for tasks currently considered complex. For future work, we aim to extend our benchmark with more types of classical ES and strategies for multimodal optimization Preuss (2015). Additionally, it would be interesting to study the effect of the step-size adaptation methods in the presence of one or more hidden layers. Next, we will explore the potential of linear networks for other applications. Inspired by works such as Cuccu et al. (2018), we will look at more complex Atari games to see if they can also be solved by simple, energy-efficient means.
References
- Bäck et al. [1991] T Bäck, F Hoffmeister, and H-P Schwefel. A survey of evolution strategies. In Proceedings of the fourth international conference on genetic algorithms. Citeseer, 1991.
- Bäck et al. [2023] T Bäck, A V Kononova, B van Stein, H Wang, K Antonov, R Kalkreuth, J de Nobel, D Vermetten, R de Winter, and F Ye. Evolutionary algorithms for parameter optimization—thirty years later. Evolutionary Computation, 31(2):81–122, 2023.
- Bellman [1957] R Bellman. A markovian decision process. Journal of Mathematics and Mechanics, pages 679–684, 1957.
- Choromanski et al. [2019] K M Choromanski, A Pacchiano, J Parker-Holder, Y Tang, and V Sindhwani. From complexity to simplicity: Adaptive es-active subspaces for blackbox optimization. Advances in Neural Information Processing Systems, 32, 2019.
- Chotard et al. [2012] A Chotard, A Auger, and N Hansen. Cumulative step-size adaptation on linear functions. In Parallel Problem Solving from Nature-PPSN XII: 12th International Conference, Taormina, Italy, September 1-5, 2012, Proceedings, Part I 12, pages 72–81. Springer, 2012.
- Chrabąszcz et al. [2018] P Chrabąszcz, I Loshchilov, and F Hutter. Back to basics: Benchmarking canonical evolution strategies for playing atari. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI-18, pages 1419–1426. International Joint Conferences on Artificial Intelligence Organization, 2018.
- Cuccu et al. [2018] G Cuccu, J Togelius, and P Cudré-Mauroux. Playing atari with six neurons. arXiv preprint arXiv:1806.01363, 2018.
- Eimer et al. [2023] T Eimer, M Lindauer, and R Raileanu. Hyperparameters in reinforcement learning and how to tune them. In International conference on machine learning, 2023.
- Ha and Schmidhuber [2018] D Ha and J Schmidhuber. World models. arXiv preprint arXiv:1803.10122, 2018.
- Haarnoja et al. [2018] T Haarnoja, A Zhou, K Hartikainen, G Tucker, S Ha, J Tan, V Kumar, H Zhu, A Gupta, P Abbeel, et al. Soft actor-critic algorithms and applications. arXiv preprint arXiv:1812.05905, 2018.
- Hafner et al. [2020] D Hafner, T Lillicrap, J Ba, and M Norouzi. Dream to control: Learning behaviors by latent imagination. In International Conference on Learning Representations, 2020.
- Hansen and Ostermeier [2001] N Hansen and A Ostermeier. Completely derandomized self-adaptation in evolution strategies. Evolutionary computation, 9(2):159–195, 2001.
- Heidrich-Meisner and Igel [2009] V Heidrich-Meisner and C Igel. Neuroevolution strategies for episodic reinforcement learning. Journal of Algorithms, 64(4):152–168, 2009.
- Henderson et al. [2018] P Henderson, R Islam, P Bachman, J Pineau, D Precup, and D Meger. Deep reinforcement learning that matters. In Proceedings of the AAAI conference on artificial intelligence, volume 32, 2018.
- Hinton and Salakhutdinov [2006] G Hinton and R Salakhutdinov. Reducing the dimensionality of data with neural networks. science, 313(5786):504–507, 2006.
- Huang et al. [2022] S Huang, R Fernand, J Dossa, C Ye, J Braga, P Chakraborty, K Mehta, and J Araújo. Cleanrl: High-quality single-file implementations of deep reinforcement learning algorithms. Journal of Machine Learning Research, 23(274):1–18, 2022.
- Igel [2003] C Igel. Neuroevolution for reinforcement learning using evolution strategies. In The 2003 Congress on Evolutionary Computation, 2003. CEC’03., volume 4, pages 2588–2595. IEEE, 2003.
- Islam et al. [2017] R Islam, P Henderson, M Gomrokchi, and D Precup. Reproducibility of benchmarked deep reinforcement learning tasks for continuous control. In Reproducibility in Machine Learning Workshop (ICML), 2017.
- Kawaguchi [2016] K Kawaguchi. Deep learning without poor local minima. In D. Lee, M. Sugiyama, U. Luxburg, I. Guyon, and R. Garnett, editors, Advances in Neural Information Processing Systems, volume 29. Curran Associates, Inc., 2016.
- Konda and Tsitsiklis [1999] V Konda and J Tsitsiklis. Actor-critic algorithms. Advances in neural information processing systems, 12, 1999.
- Loshchilov [2014] I Loshchilov. A computationally efficient limited memory cma-es for large scale optimization. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, pages 397–404, 2014.
- Machado et al. [2018] M Machado, M Bellemare, E Talvitie, J Veness, M Hausknecht, and M Bowling. Revisiting the arcade learning environment: Evaluation protocols and open problems for general agents. Journal of Artificial Intelligence Research, 61:523–562, 2018.
- Maheswaranathan et al. [2019] N Maheswaranathan, L Metz, G Tucker, D Choi, and J Sohl-Dickstein. Guided evolutionary strategies: Augmenting random search with surrogate gradients. In International Conference on Machine Learning, pages 4264–4273. PMLR, 2019.
- Mandischer [2002] M Mandischer. A comparison of evolution strategies and backpropagation for neural network training. Neurocomputing, 42(1):87–117, 2002.
- Mania et al. [2018] H Mania, A Guy, and B Recht. Simple random search provides a competitive approach to reinforcement learning. arXiv preprint arXiv:1803.07055, 2018.
- Mnih et al. [2015] V Mnih, K Kavukcuoglu, D Silver, A A Rusu, J Veness, M G Bellemare, A Graves, M Riedmiller, A K Fidjeland, G Ostrovski, et al. Human-level control through deep reinforcement learning. Nature, 518(7540):529–533, 2015.
- Moriarty and Mikkulainen [1996] D Moriarty and R Mikkulainen. Efficient reinforcement learning through symbiotic evolution. Machine learning, 22:11–32, 1996.
- Morse and Stanley [2016] G Morse and K Stanley. Simple evolutionary optimization can rival stochastic gradient descent in neural networks. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, pages 477–484, 2016.
- Müller and Glasmachers [2018] N Müller and T Glasmachers. Challenges in high-dimensional reinforcement learning with evolution strategies. In Parallel Problem Solving from Nature–PPSN XV: 15th International Conference, Coimbra, Portugal, September 8–12, 2018, Proceedings, Part II 15, pages 411–423. Springer, 2018.
- Nomura and Ono [2022] M Nomura and I Ono. Fast moving natural evolution strategy for high-dimensional problems. In 2022 IEEE Congress on Evolutionary Computation (CEC), pages 1–8. IEEE, 2022.
- Plaat et al. [2023] A Plaat, W Kosters, and M Preuss. High-accuracy model-based reinforcement learning, a survey. Artificial Intelligence Review, pages 1–33, 2023.
- Plaat [2022] A Plaat. Deep Reinforcement Learning. Springer Verlag, Singapore, 2022.
- Preuss [2015] M Preuss. Multimodal Optimization by Means of Evolutionary Algorithms. Springer Publishing Company, Incorporated, 1st edition, 2015.
- Rajeswaran et al. [2017] A Rajeswaran, K Lowrey, E Todorov, and S Kakade. Towards generalization and simplicity in continuous control. Advances in Neural Information Processing Systems, 30, 2017.
- Rechenberg [1965] I Rechenberg. Cybernetic solution path of an experimental problem. Royal Aircraft Establishment Library Translation 1122, 1122, 1965.
- Ros and Hansen [2008] R Ros and N Hansen. A simple modification in cma-es achieving linear time and space complexity. In International conference on parallel problem solving from nature, pages 296–305. Springer, 2008.
- Salimans et al. [2017] T Salimans, J Ho, X Chen, S Sidor, and I Sutskever. Evolution strategies as a scalable alternative to reinforcement learning. arXiv preprint arXiv:1703.03864, 2017.
- Salomon [1998] R Salomon. Evolutionary algorithms and gradient search: similarities and differences. IEEE Transactions on Evolutionary Computation, 2(2):45–55, 1998.
- Schulman et al. [2017] J Schulman, F Wolski, P Dhariwal, A Radford, and O Klimov. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347, 2017.
- Schwarzer et al. [2023] M Schwarzer, J Ceron, A Courville, M Bellemare, R Agarwal, and P Castro. Bigger, better, faster: Human-level atari with human-level efficiency. In International Conference on Machine Learning, pages 30365–30380. PMLR, 2023.
- Shir and Bäck [2005] O Shir and T Bäck. Niching in evolution strategies. In Proceedings of the 7th annual conference on Genetic and evolutionary computation, pages 915–916, 2005.
- Silver et al. [2016] D Silver, A Huang, C J Maddison, A Guez, L Sifre, G Van Den Driessche, J Schrittwieser, I Antonoglou, V Panneershelvam, M Lanctot, et al. Mastering the game of go with deep neural networks and tree search. Nature, 529(7587):484–489, 2016.
- Stanley et al. [2019] K O Stanley, J Clune, J Lehman, and R Miikkulainen. Designing neural networks through neuroevolution. Nature Machine Intelligence, 1(1):24–35, 2019.
- Such et al. [2017] F P Such, V Madhavan, E Conti, J Lehman, K O Stanley, and J Clune. Deep neuroevolution: Genetic algorithms are a competitive alternative for training deep neural networks for reinforcement learning. arXiv preprint arXiv:1712.06567, 2017.
- Sutton and Barto [2018] R S Sutton and A G Barto. Reinforcement learning: An introduction. MIT press, 2018.
- Sygnowski and Michalewski [2017] J Sygnowski and H Michalewski. Learning from the memory of atari 2600. In Computer Games: 5th Workshop on Computer Games, CGW 2016, and 5th Workshop on General Intelligence in Game-Playing Agents, GIGA 2016, Held in Conjunction with the 25th International Conference on Artificial Intelligence, IJCAI 2016, New York, USA, July 9-10, 2016, Revised Selected Papers 5, pages 71–85. Springer, 2017.
- Todorov et al. [2012] E Todorov, T Erez, and Y Tassa. Mujoco: A physics engine for model-based control. In 2012 IEEE/RSJ international conference on intelligent robots and systems, pages 5026–5033. IEEE, 2012.
- Towers et al. [2023] M Towers, J Terry, A Kwiatkowski, J Balis, G de Cola, T Deleu, M Goulão, A Kallinteris, A KG, M Krimmel, R Perez-Vicente, A Pierré, S Schulhoff, J J Tai, A T J Shen, and O Younis. Gymnasium, March 2023.
- Vinyals et al. [2019] O Vinyals, I Babuschkin, W M Czarnecki, M Mathieu, A Dudzik, J Chung, D H Choi, R Powell, T Ewalds, P Georgiev, et al. Grandmaster level in starcraft ii using multi-agent reinforcement learning. Nature, 575(7782):350–354, 2019.
- Watkins and Dayan [1992] C JCH Watkins and P Dayan. Q-learning. Machine learning, 8:279–292, 1992.
- Whitley et al. [1993] D Whitley, S Dominic, R Das, and C W Anderson. Genetic reinforcement learning for neurocontrol problems. Machine Learning, 13(2–3):259–284, 1993.
- Williams [1992] R J Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8:229–256, 1992.