Some Neumann-Bessel series
and the Laplacian on polygons

Luca Guido Molinari L. G. Molinari: Physics Department Aldo Pontremoli, Università degli Studi di Milano and I.N.F.N. sez. Milano, Via Celoria 16, 20133 Milano, Italy Luca.Molinari@unimi.it

(Date: 9 nov 2020)

Abstract.

Several sums of Neumann series with Bessel and trigonometric functions are evaluated, as finite sums of trigonometric functions. They arise from a generalization of the Neumann expansion of the eigenstates of the Laplacian in regular polygons.

Key words and phrases:

Bessel function, Neumann series, Laplace equation in polygon

2010 Mathematics Subject Classification:

Primary 33C10, Secondary 35J05

Introduction

The ground state of the Laplace equation in a regular polygon with Dirichlet boundary conditions at the $n$ sides, has a natural expression as a Neumann series of Bessel and trigonometric functions,

\psi_{n}(r,\theta)=J_{0}(\lambda_{n}r)+2{\sum}_{k=1}^{\infty}h_{k,n}J_{kn}(\lambda_{n}r)\cos(kn\theta),

with coefficients $h_{k,n}$ to be found and eigenvalue $-\lambda_{n}^{2}$ that scales with the area. For the equilateral triangle and the square, the solutions are known as sums of few trigonometric functions of the coordinates $x=r\cos\theta$ and $y=r\sin\theta$ . Such solutions have a corresponding Neumann expression [7]. For the square of area $\pi$ :

(1)

\displaystyle J_{0}(\sqrt{2\pi}r)+2{\sum}_{k=1}^{\infty}J_{4k}(\sqrt{2\pi}r)\cos(4k\theta)=\tfrac{1}{2}\cos(x\sqrt{2\pi})+\tfrac{1}{2}\cos(y\sqrt{2\pi})

The triangle requires some work to establish the equivalence:

(2)		$\displaystyle J_{0}(\lambda_{3}r)+2{\sum}_{k=1}^{\infty}\frac{\cos(k\pi/2-\pi/6)}{\cos(\pi/6)}J_{3k}(\lambda_{3}r)\cos(3k\theta)=\tfrac{2}{3\sqrt{3}}\sin(\tfrac{4\pi}{3R_{3}}x+\tfrac{2\pi}{3})$
	$\displaystyle-\tfrac{2}{3\sqrt{3}}[\sin[\tfrac{2\pi}{3R_{3}}(x+y\sqrt{3})-\tfrac{2\pi}{3}]-\tfrac{2}{3\sqrt{3}}\sin[\tfrac{2\pi}{3R_{3}}(x-y\sqrt{3})-\tfrac{2\pi}{3}]$

where, for area $\pi$ , $\lambda^{2}_{3}=\frac{4\pi}{\sqrt{3}}$ and $R_{3}=\tfrac{2}{3}\sqrt{\pi\sqrt{3}}$ . In [7] I also obtained a sum that generalizes the integrable cases $n=3,4$ :

(3)		$\displaystyle f_{n}(x,y)=$	$\displaystyle J_{0}(r)+2{\sum}_{k=1}^{\infty}\frac{\cos[nk\tfrac{3\pi}{2}-\tfrac{\pi}{2n}]}{\cos(\tfrac{\pi}{2n})}J_{nk}(r)\cos(nk\theta)$
	$\displaystyle=$	$\displaystyle\frac{1}{n}{\sum}_{\ell=0}^{n-1}\frac{\cos[r\cos(\theta+\tfrac{2\pi}{n}\ell)+\tfrac{\pi}{2n}]}{\cos(\tfrac{\pi}{2n})}$
	$\displaystyle=$	$\displaystyle\frac{1}{n}{\sum}_{\ell=0}^{n-1}\frac{\cos[x\cos(\tfrac{2\pi}{n}\ell)-y\sin(\tfrac{2\pi}{n}\ell)+\tfrac{\pi}{2n}]}{\cos(\tfrac{\pi}{2n})}$

For $n\to\infty$ the Riemann sum in the second line is $\int_{0}^{2\pi}\frac{dt}{2\pi}\cos(r\cos t)=J_{0}(r)$ ; for $n=2$ it is $f_{2}(x,y)=\cos x$ . For $n=6$ :

(4)

\displaystyle f_{6}(x,y)=J_{0}(r)+2\sum_{k=1}^{\infty}(-1)^{k}J_{6k}(r)\cos(6k\theta)=\tfrac{1}{3}\cos x+\tfrac{2}{3}\cos(\tfrac{1}{2}x)\cos(\tfrac{\sqrt{3}}{2}y)

The functions $f_{n}$ are eigenfunctions of the Laplace operator with eigenvalue $-1$ but, for $n>4$ , they no longer vanish on the boundary of a $n$ -polygon.

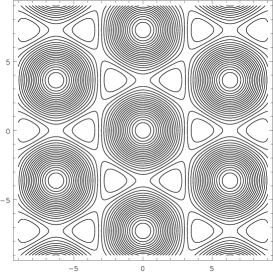
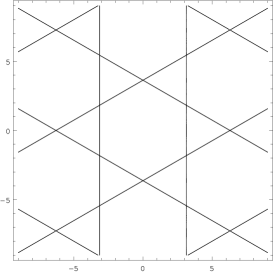
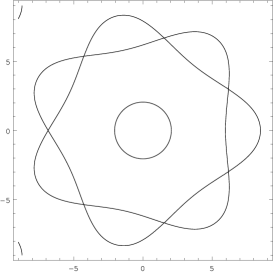
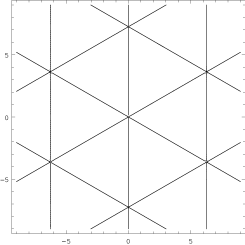
Refer to caption — Figure 1. Left: contour plots of $f_{6}$ and $f_{7}$ in eq.(3). Right: the separatrix line $f_{6}(x,y)=-1/3$ (Kagomé lattice, the eq. can be written as $0=\cos(x/2)[\cos(x/2)+\cos(\sqrt{3}y/2)]$ . Sites are the doule zeros.), and $f_{7}(x,y)=-1.9633...$ (Mathematica)

I only remark that the level curves $f_{n}(x,y)=C_{n}$ are closed around the origin (where $f_{n}=1$ ) up to a separatrix with $n$ self-intersections, with values $C_{5}=-0.334909$ , $C_{6}=-1/3$ , $C_{7}=0.19633$ , etc. The lines are shown in Fig.1.

The Laplacian in polygons has a long history. The ground state beyond the square cannot be finite sums of trigonometric functions, and has been investigated analytically and numerically in $1/n$ expansion (see for example [7, 4, 3]).

In this paper I generalize the identity (3), and obtain a number of new formulas for Neumann series whose sums contain a finite number of terms. For certain values of the parameters, they are identities that are found in the tables by Gradshteyn and Ryzhik [2], Prudnikov, Brychkov and Marichev [8], a recent paper by Al-Jarrah, Dempsey and Glasser [1], and two old papers by Takizawa and Kobayasi [9, 5]. In the last ones, the Neumann series appear as correlation functions for the heat flow in coupled harmonic oscillators.

The summation formula

The source equation of various sums in this paper is:

(5)

\displaystyle\boxed{\sum_{k=-\infty}^{+\infty}J_{kn+p}(z)e^{ikny}=\frac{1}{n}\sum_{\ell=0}^{n-1}e^{iz\sin(y+\tfrac{2\pi}{n}\ell)-ip(y+\tfrac{2\pi}{n}\ell)}}

For $y=0$ and even $n$ it is eq.1 in [9]. Sums of this sort are tabulated only for $n=1,2$ in [8].

Proof.

The result follows from the Fourier integral of a Bessel function of integer order. For fixed $z\in\mathbb{C}$ , $\sum_{k=-\infty}^{\infty}e^{ik\theta}J_{kn+p}(z)$ is uniformly convergent in $\theta$ by the bound $|J_{\pm m}(z)|\leq C|z/2|^{m}/m!$ (Nielsen, see §3.13 in [10]).

	$\displaystyle\sum_{k=-\infty}^{\infty}e^{ikny}J_{kn+p}(z)=\sum_{k=-\infty}^{\infty}e^{ikny}\int_{0}^{2\pi}\frac{d\theta}{2\pi}e^{iz\sin\theta-i(kn+p)\theta}$
	$\displaystyle=\sum_{k=-\infty}^{\infty}e^{ikny}\sum_{j=0}^{n-1}\int_{\frac{2\pi}{n}j}^{\frac{2\pi}{n}(j+1)}\frac{d\theta}{2\pi}e^{iz\sin\theta-ip\theta}e^{-ikn\theta}$

The sums are exchanged: $=\sum_{j=0}^{n-1}\sum_{k=-\infty}^{\infty}e^{ikny}\int_{0}^{\frac{2\pi}{n}}\frac{d\theta}{2\pi}e^{iz\sin(\theta+\frac{2\pi}{n}j)-ip(\theta+\frac{2\pi}{n}j)}e^{-ikn\theta}$ . The functions $\sqrt{n/2\pi}\,e^{ikny}$ are a complete orthonormal basis in L ${}^{2}(0,2\pi/n)$ . The infinite sum is the Fourier representation of $\exp[iz\sin(y+\frac{2\pi}{n}j)-ip(y+\frac{2\pi}{n}j)]$ . ∎

1

The case $p=0$ and $y=\frac{\pi}{2}+\alpha$ is an extension with angle $\alpha$ of the equations 19 and 20 in [1], where $\alpha=0$ . With $J_{-m}(z)=(-)^{m}J_{m}(z)$ :

(6)

\displaystyle J_{0}(z)+2\sum_{k=1}^{+\infty}e^{ikn\frac{\pi}{2}}J_{kn}(z)\cos(kn\alpha)=\frac{1}{n}\sum_{\ell=0}^{n-1}e^{iz\cos(\alpha+\tfrac{2\pi}{n}\ell)}

For $n=1$ , separation of even and odd parity parts in $z$ gives the Jacobi expansions (eqs. 5.7.10.4 and 5 in [8]):

(7)		$\displaystyle J_{0}(z)+2\sum_{k=1}^{\infty}(-)^{k}J_{2k}(z)\cos(2k\alpha)=\cos(z\cos\alpha)$
(8)		$\displaystyle\sum_{k=0}^{\infty}(-)^{k}J_{2k+1}(z)\cos[(2k+1)\alpha]=\tfrac{1}{2}\sin(z\cos\alpha)$

If $\alpha$ is replaced by $\alpha+\pi/2$ they are eqs. 8.514.5 and 6 in [2] and 10.4, 10.5 in [6]:

(9)		$\displaystyle J_{0}(z)+2\sum_{k=1}^{\infty}J_{2k}(z)\cos(2k\alpha)=\cos(z\sin\alpha)$
(10)		$\displaystyle\sum_{k=0}^{\infty}J_{2k+1}(z)\sin[(2k+1)\alpha]=\tfrac{1}{2}\sin(z\sin\alpha)$

1.1

For $n$ replaced by $2n$ , eq.(6) is:

(11)

\displaystyle J_{0}(z)+2\sum_{k=1}^{\infty}(-)^{kn}J_{2kn}(z)\cos(2kn\alpha)=\frac{1}{2n}\sum_{\ell=0}^{2n-1}\cos[z\cos(\alpha+\tfrac{\pi}{n}\ell)]

Since terms $\ell$ and $n+\ell$ are the same, the sum is replaced by $2\sum_{\ell=0}^{n-1}$ . The value $y=\frac{\pi}{2}$ yields eq.(23) in [1].
For $n=1$ the derivative of (11) in $\alpha=\frac{\pi}{4}$ is:

(12)

\displaystyle 2J_{2}(z)-6J_{6}(z)+10J_{10}(z)-14J_{14}(z)+...=z\tfrac{\sqrt{2}}{4}\sin(z\tfrac{\sqrt{2}}{2})

For $n=2$ eq.(11) gives

(13)

\displaystyle J_{0}(z)+2\sum_{k=1}^{\infty}J_{4k}(z)\cos(4k\alpha)=\frac{1}{2}[\cos(z\sin\alpha)+\cos(z\cos\alpha)]

The values $\alpha=0,\frac{\pi}{4}$ give eqs. 5.7.1.19. Case $n=3$ , $\alpha=0$ gives eq. 5.7.1.21 in [8].
The derivative of (13) with $n=4$ is:

(14)

\displaystyle\sum_{k=1}^{\infty}kJ_{4k}(z)\sin(4k\alpha)=\frac{z}{16}[\sin(z\sin\alpha)\cos\alpha-\sin(z\cos\alpha)\sin\alpha]

The expansion in small $\alpha$ gives:

(15)

\displaystyle\sum_{k=1}^{\infty}k^{2}J_{4k}(z)=\frac{z}{64}(z-\sin z)

1.2

For $n$ replaced by $2n+1$ , eq.(6) is:

\displaystyle J_{0}(z)+2\sum_{k=1}^{\infty}e^{i(2n+1)k\frac{\pi}{2}}J_{(2n+1)k}(z)\cos[(2n+1)k\alpha]=\frac{1}{2n+1}\sum_{\ell=0}^{2n}e^{iz\cos(\alpha+\tfrac{2\pi}{2n+1}\ell)}

The even-parity and odd-parity parts in the exchange $z\to-z$ are:

	$\displaystyle J_{0}(z)+2\sum_{k=1}^{\infty}(-)^{k}J_{(4n+2)k}(z)\cos[(4n+2)k\alpha]=\frac{1}{2n+1}\sum_{\ell=0}^{2n}\cos[z\cos(\alpha+\tfrac{2\pi}{2n+1}\ell)]$
	$\displaystyle 2\sum_{k=0}^{\infty}(-)^{n+k}J_{(2n+1)(2k+1)}(z)\cos[(2n+1)(2k+1)\alpha]=\frac{1}{2n+1}\sum_{\ell=0}^{2n}\sin[z\cos(\alpha+\tfrac{2\pi}{2n+1}\ell)]$

Examples of the second equation are

(16)		$\displaystyle\sum_{k=0}^{\infty}(-)^{k}J_{6k+3}(z)\cos[(6k+3)\alpha]=-\frac{1}{6}\sum_{\ell=0}^{2}\sin[z\cos(\alpha+\tfrac{2\pi}{3}\ell)]$
(17)		$\displaystyle\sum_{k=0}^{\infty}(-)^{k}J_{10k+5}(z)\cos[(10k+5)\alpha]=\frac{1}{10}\sum_{\ell=0}^{4}\sin[z\cos(\alpha+\tfrac{2\pi}{5}\ell)]$

The first equation with $\alpha=\pi$ is eq.22 in [1].
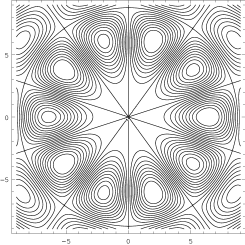
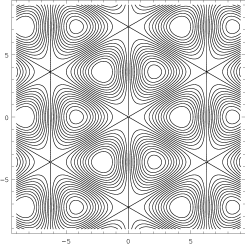
Both sums are eigenfunctions of the Laplacian with eigenvalue $\lambda=-1$ (see Fig. 2). The sum (17), with $z=r$ , $x=r\cos\alpha$ and $y=r\sin\alpha$ , is

(18)

\displaystyle f(x,y)=\sin x-2\sin(x\cos\tfrac{\pi}{5})\cos(y\sin\tfrac{\pi}{5})+2\sin(x\cos\tfrac{2\pi}{5})\cos(y\sin\tfrac{2\pi}{5})

1.3

In (5) with $p=0$ , multiply by $\exp(i\beta)$ ( $\beta$ real) and take the real part. The left hand side becomes:

	$\displaystyle J_{0}(x)\cos\beta+{\sum}_{k=1}^{\infty}J_{kn}(x)\;{\rm Re}[e^{i\beta}(e^{ikny}+e^{-ikn(y+\pi)})]$
	$\displaystyle=J_{0}(x)\cos\beta+2{\sum}_{k=1}^{\infty}\cos(\beta-kn\tfrac{\pi}{2})J_{kn}(x)\cos[kn(y+\tfrac{\pi}{2})]$

The identity (3) is obtained, when $\beta=\tfrac{\pi}{2n}$ and $y+\tfrac{\pi}{2}=\theta+\pi$ .

2

Parseval’s identity is applied to (5):

	$\displaystyle\sum_{k\in\mathbb{Z}}J^{2}_{kn+p}(x)$	$\displaystyle=\frac{1}{n^{2}}\sum_{k\ell}e^{ip\tfrac{2\pi}{n}(k-\ell)}\int_{0}^{2\pi}\frac{dy}{2\pi}e^{ix\sin(y-\tfrac{\pi}{n}(k-\ell))-ix\sin(y+\tfrac{\pi}{n}(k-\ell))}$
		$\displaystyle=\frac{1}{n^{2}}\sum_{k\ell}e^{ip\tfrac{2\pi}{n}(k-\ell)}\int_{0}^{2\pi}\frac{dy}{2\pi}e^{-i2x\cos y\sin(\tfrac{\pi}{n}(k-\ell))}$
		$\displaystyle=\frac{1}{n^{2}}\sum_{k\ell}e^{ip\tfrac{2\pi}{n}(k-\ell)}J_{0}[2x\sin(\tfrac{\pi}{n}(k-\ell))]$
		$\displaystyle=\frac{1}{n}+\frac{2}{n^{2}}\sum_{k=1}^{n-1}k\cos(\tfrac{2\pi}{n}kp)J_{0}(2x\sin\tfrac{\pi k}{n})$

The last sum is unchanged if $k$ is replaced by $n-k$ :

(19)

\displaystyle\sum_{k\in\mathbb{Z}}J^{2}_{kn+p}(x)=\frac{1}{n}+\frac{1}{n}\sum_{k=1}^{n-1}\cos(\tfrac{2\pi}{n}kp)J_{0}(2x\sin\tfrac{\pi k}{n})

The left-hand side is $J_{p}(x)^{2}+\sum_{k=1}^{\infty}J^{2}_{kn+p}(x)+J^{2}_{kn-p}(z)$ .
For the special case $p=0$ and $n\to 2n$ in (19), the sum is amenable to eq.29 in [1]:

(20)

\displaystyle J_{0}^{2}(x)+2\sum_{k=1}^{\infty}J_{2kn}^{2}(x)=\frac{1}{2n}+\frac{1}{2n}J_{0}(2x)+\frac{1}{n}\sum_{k=1}^{n-1}J_{0}(2x\cos\tfrac{\pi}{2n}k)

2.1

If $n\to 2n$ and $p=n$ in (19), with simple steps one obtains:

(21)

\displaystyle\sum_{k=0}^{\infty}J^{2}_{(2k+1)n}(x)=\frac{1}{4n}+\frac{(-)^{n}}{4n}J_{0}(2x)+\frac{1}{2n}\sum_{\ell=1}^{n-1}(-1)^{\ell}J_{0}(2x\sin\tfrac{\pi\ell}{2n})

3

In eq.(5) the variable $y$ is shifted to $y+2t$ . The equation is multiplied by $e^{iz^{\prime}\sin y-iqy}$ and integrated in $y$ :

	$\displaystyle\sum_{k=-\infty}^{+\infty}J_{p+kn}(z)$	$\displaystyle J_{q-kn}(z^{\prime})e^{i(kn+p)2t}$
(22)		$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{\ell=0}^{n-1}e^{-ip\tfrac{2\pi}{n}\ell}\int_{0}^{2\pi}\frac{dy}{2\pi}e^{iz\sin(y+2t+\tfrac{2\pi}{n}\ell)+iz^{\prime}\sin y-i(p+q)y}$

In the integral, the shift $y$ to $y-t-\frac{\pi}{n}\ell$ changes the exponent to

i(z+z^{\prime})\sin y\cos(t+\tfrac{\pi}{n}\ell)+i(z-z^{\prime})\cos y\sin(t+\tfrac{\pi}{n}\ell)-i(p+q)(y-t-\tfrac{\pi}{n}\ell)

3.1

With $z=z^{\prime}$ we obtain eq.1 in [5]:

(23)

\displaystyle\sum_{k=-\infty}^{+\infty}J_{p+kn}(z)J_{q-kn}(z)e^{2iknt}=\frac{1}{n}\sum_{\ell=0}^{n-1}e^{-i(p-q)(t+\tfrac{\pi}{n}\ell)}J_{p+q}[2z\cos(t+\tfrac{\pi}{n}\ell)]

For $n=1,2$ it is (with a shift of the index $k$ in the first identity and renaming of parameter):

(24)		$\displaystyle\sum_{k=-\infty}^{+\infty}J_{k}(z)J_{p-k}(z)e^{2ikt}=e^{ipt}J_{p}(2z\cos t)$
(25)		$\displaystyle\sum_{k=-\infty}^{+\infty}J_{p+2k}(z)J_{q-2k}(z)e^{4ikt}=\tfrac{1}{2}e^{-i(p-q)t}[J_{p+q}(2z\cos t)+i^{p-q}J_{p+q}(2z\sin t)]$

The first one is eq.8.530 [2]. The second one, for $t=\frac{\pi}{4},\frac{\pi}{2}$ , becomes:

(26)		$\displaystyle\sum_{k=-\infty}^{+\infty}(-)^{k}J_{p+2k}(z)J_{q-2k}(z)=J_{p+q}(z\sqrt{2})\cos[(p-q)\tfrac{\pi}{4}]$
(27)		$\displaystyle\sum_{k=-\infty}^{+\infty}J_{p+2k}(z)J_{q-2k}(z)=\tfrac{1}{2}J_{p+q}(2z)$

For $p=q$ the first one is eq. 5.7.11.25 [8].

3.2

Eq.(22) with $p=q=0$ and $t=0$ is:

\displaystyle J_{0}(z)J_{0}(z^{\prime})+2\sum_{k=1}^{\infty}(-)^{kn}J_{kn}(z)J_{kn}(z^{\prime})=\frac{1}{n}\sum_{\ell=0}^{n-1}\int_{0}^{2\pi}\frac{dy}{2\pi}e^{iz\sin(y+\tfrac{2\pi}{n}\ell)+iz^{\prime}\sin y}

For $n=1,2$ they are eqs. 5.7.11.1 and 5.7.11.18 in [8] and, for $z=z^{\prime}$ : eqs. 31, 32 in [1]. A new example is:

(28)

\displaystyle\sum_{k=1}^{\infty}J_{4k}(x)J_{4k}(y)=\tfrac{1}{8}[J_{0}(x+y)+J_{0}(x-y)-4J_{0}(x)J_{0}(y)+2J_{0}(\sqrt{x^{2}+y^{2}})]

4

Multiplication of (5) by $\exp(-ay)$ ( $a>0$ ) with $p=0$ and $n=1$ , and integration on $\mathbb{R}^{+}$ give:

\displaystyle\frac{1}{a}J_{0}(z)+\sum_{k=1}^{\infty}J_{2k}(z)\frac{2a}{a^{2}+4k^{2}}+\sum_{k=0}^{\infty}J_{2k+1}(z)\frac{2i(2k+1)}{a^{2}+(2k+1)^{2}}=\int_{0}^{\infty}dy\,e^{iz\sin y-ay}

The integral in the right-hand side is done by series expansion, with eqs.3.895.1 and 3.895.4 [2]. The even and odd terms are:

(29)		$\displaystyle\frac{1}{a}J_{0}(z)+\sum_{k=1}^{\infty}J_{2k}(z)\frac{2a}{a^{2}+4k^{2}}=\sum_{k=0}^{\infty}(-)^{k}\frac{z^{2k}}{a(a^{2}+4)...(a^{2}+4k^{2})}$
(30)		$\displaystyle\sum_{k=0}^{\infty}J_{2k+1}(z)\frac{2(2k+1)}{a^{2}+(2k+1)^{2}}=\sum_{k=0}^{\infty}(-)^{k}\frac{z^{2k+1}}{(a^{2}+1)(a^{2}+9)...(a^{2}+(2k+1)^{2})}$

More and more identities can be obtained by derivation, or integration with functions. Here I limited myself to simple and, hopefully, useful examples.

References

[1] A. Al-Jarrah, K. M. Dempsey, M. L. Glasser, Generalized series of Bessel functions, J. Comp. Appl. Math. 143 (2002) 1–8.
[2] I. S. Gradshteyn and I. M. Ryzhik, Table of integrals, series and products, 7th edition, Academic Press
[3] R. S. Jones, The fundamental Laplacian eigenvalue of the regular polygon with Dirichlet boundary conditions, arXiv:1712.06082 [math.NA]
Jones, R.S. Computing ultra-precise eigenvalues of the Laplacian within polygons Adv. Comput. Math. 43 1325–1354 (2017).
[4] P. Grinfeld and G. Strang, Laplace eigenvalues on regular polygons: a series in 1/N, J. Math. Anal. Appl. 385 (2012) 135–149.
[5] K. Kobayasi and Éi I. Takizawa, On an infinite sum of two Bessel functions of first kind, Chinese Journal of Physics 3 n.1 (1965) 69–71.
[6] B. G. Koronev, Bessel functions and their applications, Taylor and Francis (2002).
[7] L. Molinari, On the ground state of regular polygonal billiards, J. Phys. A: Math. Gen. 30 n.18 (1997) 6517–6424.
[8] A. P. Prudnikov, Yu. A. Brychkov. and O. I. Marichev, Integrals and Series, Vol. 2: Special functions, Gordon and Breach (1986).
[9] Éi I. Takizawa and K. Kobayasi, On an infinite series of Bessel functions, Chinese Journal of Physics 1 n.2 (1963) 83–84.
[10] G. N. Watson, A Treatise on the Theory of Bessel Functions (2nd edition), Cambridge Univ. Press, Cambridge, 1944.

Some Neumann-Bessel series and the Laplacian on polygons