Some theorems on decomposable continua
Abstract.
We prove some theorems on decomposable continua. In particular, we prove;
(i) the property of being a Wilder continuum is not a Whitney reversible property,
(ii) inverse limits of -continua with surjective monotone upper semi-continuous bonding functions are , and
(iii) there exists a -continuum which contains neither Wilder continua nor -continua.
Also, we show the existence of a Wilder continuum containing no -continua and a -continuum containing no Wilder continua.
Key words and phrases:
Whitney reversible property, Wilder continua, -continua, -continua, inverse limits2020 Mathematics Subject Classification:
Primary 54F15 ; Secondary 54F16, 54F171. Introduction
In this paper, all spaces are assumed to be metrizable. A is a continuous single-valued function. A map is said to be if for each , is connected. If is a space and is a subset of , then we denote the closure of in by . By a we mean a compact connected metric space. An is a space which is homeomorphic to the closed interval . If is an arc, then we denote the set of end points of by . A continuum is said to be if it is the union of two proper subcontinua. If a continuum is not decomposable, then is said to be .
Let be a continuum. Then, denotes the space of all closed subsets of with the topology generated by the Hausdorff metric. Also, denotes the subspace of consisting of all nonempty subcontinua of . A is a map satisfying for each , and whenever and . It is well-known that for each Whitney map and for each , is a continuum ([4, Theorem 19.9]).
A topological property is called a Whitney property if a continuum has property , so does for any Whitney map for and for any . Also, a topological property is called a Whitney reversible property provided that whenever is a continuum such that has property for each Whitney map for and for each , then has property . For information about Whitney properties and Whitney reversible properties, see [4, Chapter 8].
In this paper, we show some theorems on decomposable continua. In particular, we deal with topics on Wilder continua, -continua, -continua and -continua (definitions of these continua are given in the following section). Studies on these continua are seen in [1], [2], [10], [11], [12], [13], [14] and [18].
The paper is divided as follows:
In Section 2, we introduce some basic definitions and terminology that are used throughout this paper.
In Section 3, we show that the properties of being a Wilder continuum is not a Whitney reversible property. This result gives a partial answer to [14, Qusetion 5.2]. Note that the properties of being a Wilder continuum, being a -continuum, being a -continuum and being a -continuum are all Whitney properties (see [14]).
In Section 4, we deal with topics on inverse limits with set-valued bonding functions. The notion of inverse limits with set-valued bonding functions was introduced by Ingram and Mahavier ([5]). In Section 4, we prove that inverse limits of -continua with surjective monotone upper semi-continuous bonding functions are . This result is in contrast to [17, Examples 5.1 and 5.2], which state that there exists an inverse sequence of -continua (resp. -continua) with surjective monotone upper semi-continuous bonding functions such that is not a -continuum (resp. a -continuum).
In Section 5, we show that there exists a -continuum which contains neither Wilder continua nor -continua. Also, we show the existence of a Wilder continuum containing no -continua and a -continuum containing no Wilder continua.
2. preliminaries
In this section, we introduce some basic definitions and terminology.
Definition 2.1.
A continuum is called a Wilder continuum if for any three distinct points , there exists a subcontinuum of such that and contains exactly one of and .
Wilder introduced the notion of Wilder continua in [18].111Wilder named the continua as -continua. However, we use the term Wilder continua following the notion proposed in [8].
Let be a continuum. If is not Wilder, then there exist three distinct points such that for each subcontinuum of with and , . In this case, we say that and are - .
Definition 2.2.
Let be a continuum. Then:
-
•
The continuum is called a D-continuum if for any pairwise disjoint nondegenerate subcontinua and of , there exists a subcontinuum of such that
(i) , and
(ii) or .
-
•
The continuum is called a -continuum if for any pairwise disjoint nondegenerate subcontinua and of , there exists a subcontinuum of such that
(i) , and
(ii) .
-
•
The continuum is called a -continuum if for any pairwise disjoint nondegenerate subcontinua and of , there exists a subcontinuum of such that
(i) , and
(ii) and .
Note that a continuum is a -continuum if and only if for each and for each nondegenerate subcontinuum of with , there exists a subcontinuum of such that , and .
It is clear that every -continuum is a -continuum and every -continuum is a -continuum. Note that the -continuum is a -continuum which is not a -continuum.
In [14, Section 2], it is proven that the classes of Wilder continua and -continua are strictly contained in the class of -continua. Since every nondegenerate indecomposable continuum has uncountably many composants [16, Theorem 11.15], we can easily see that every nondegenerate -continuum is decomposable. For other relationships between the classes of the above continua and other classes of continua, see [2, Figure 6].
Let and be any compacta. Then, a set-valued function is called an - provided that for each and each open subset of containing , there exists an open subset of which contains such that if , then . The of a set-valued function is the set . We say that a set-valued function is if for each , there exists such that .
Every map induces the upper semi-continuous function defined by for each . Therefore, if necessary, we may regard a map as the upper semi-continuous function .
An is a double sequence of compacta and upper semi-continuous functions . The spaces are called the and the upper semi-continuous functions the . We denote the subspace for each of by . is also denoted by . is called the .
3. Being a Wilder continuum is not a Whitney reversible property
First, we show the following result which can yield a lot of examples of non-Wilder continua whose all positive Whitney levels are Wilder continua.
Theorem 3.1.
Let be a nondegenerate continuum and let be a Whitney map. Assume there exists a totally disconnected subset of satisfying the following property:
If and are pairwise distinct points in , then there exists a subcontinuum of such that and contains exactly one of and .
Then, is a Wilder continuum for each .
Proof.
The proof is obtained by slightly modifying the proof of [14, Theorem 4.2] as follows:
() In Case 3 of the proof of [14, Theorem 4.2], the second author and the third author chose points , and . Instead of it, choose points , and .
Then, we can prove the theorem. ∎
By the following example, we see that the property of being a Wilder continuum is not a Whitney reversible property. This result gives a partial answer to [14, Question 5.2].
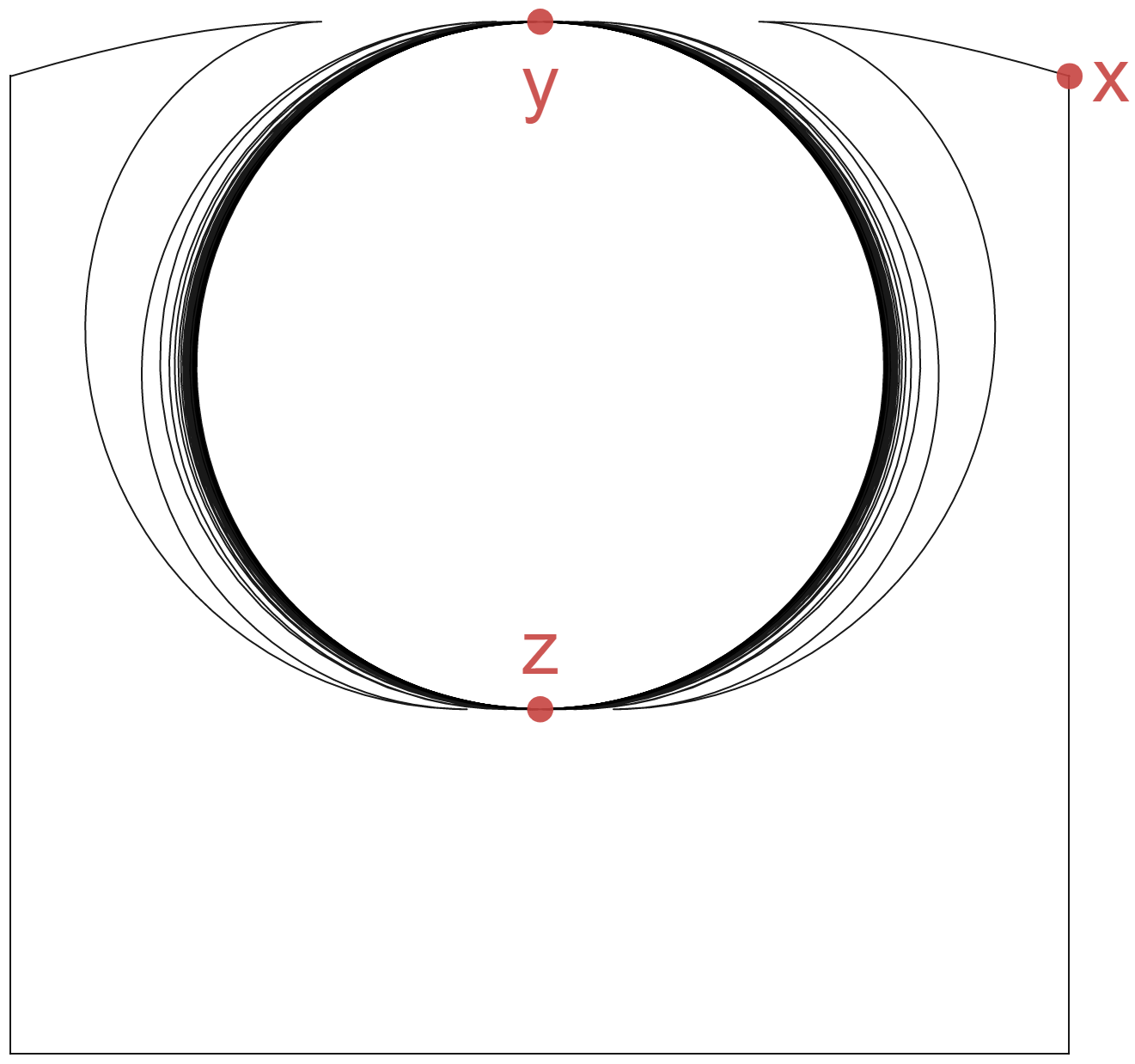
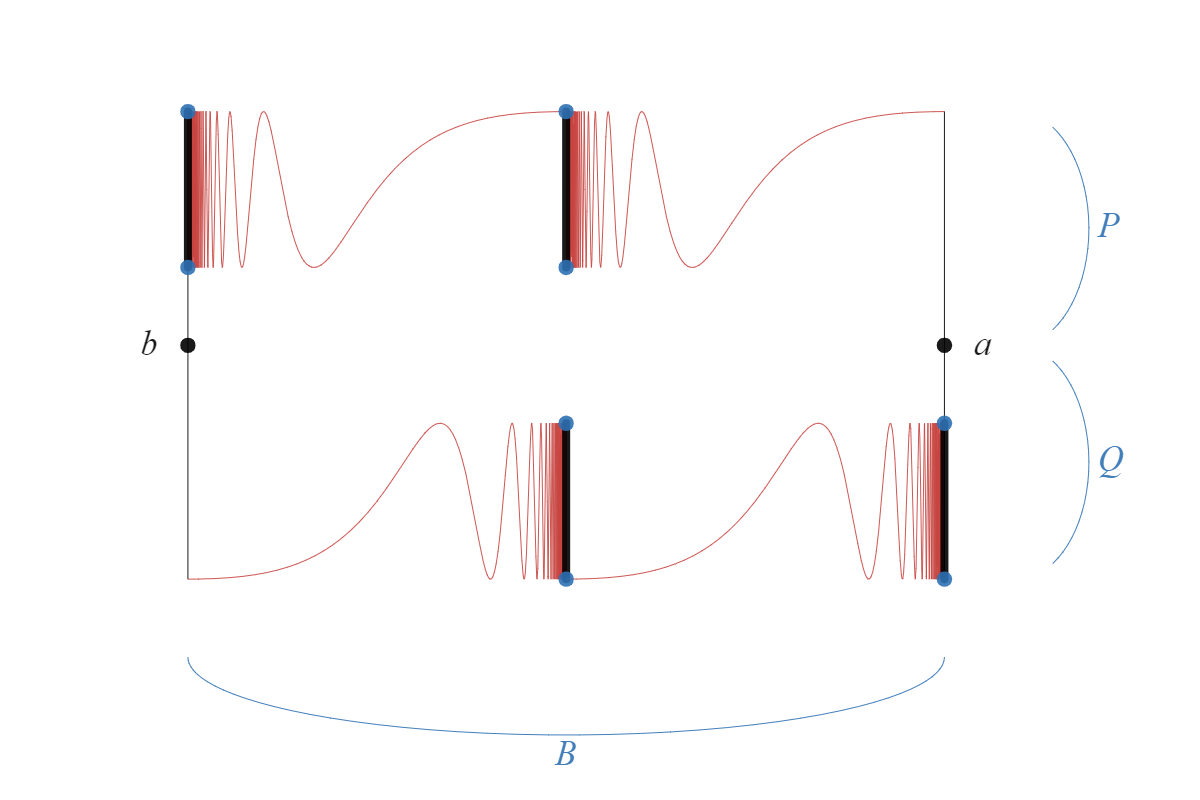
Example 3.2.
Let
(see Figure 1). has two arc components. One of them is a simple closed curve, and the other is homeomorphic to . Let , and be points in as in Figure 1. Since there does not exist a subcontinuum of which contains and exactly one of and , is not Wilder.
Let be a Whitney map. Let . Then, it is easy to see that is totally disconnected. Also, we see that if and are pairwise distinct points in , then there exists a subcontinuum of such that and contains exactly one of and . Hence, by the previous result, we see that is a Wilder continuum for each .
Remark 3.3.
In [2, Example 3.5], Espinoza and the second author constructed an example of a -continuum which is not Wilder. Compared to their example, it is easy to see that the continuum in the previous example has such properties.
Remark 3.4.
Let , , be as in Example 3.2. Let be the midpoint of the line segment . Let and let be the subcontinuum of with rotated clockwise around for each . Let and let for each . Now, let be the arc component of which is a simple closed curve, and for each , let . Let be the upper semi-continuous decomposition of defined by . Then, by similar arguments in Example 3.2, we can easily see that the quotient space is a non-Wilder continuum whose all positive Whitney levels are Wilder continua.
Question 1.
(See [14, Question 5.2].) Is the property of being a -continuum (or a -continuum, or a -continuum) a Whitney reversible property?
4. Inverse limits with monotone upper semi-continuous bonding functions
In this section, we deal with topics on inverse limits with set-valued bonding functions.
Note that if a map between compacta is monotone, then it satisfies the condition of in the following definition.
Definition 4.1 ([7, Definition 3.2]).
Let and be compacta. Then, an upper semi-continuous function is said to be monotone if each of the projection maps and is a monotone map.
The following results are proven in [17].
Theorem 4.2.
([17, Example 5.1]) There exists an inverse sequence of -continua with surjective monotone upper semi-continuous bonding functions such that is not a -continuum.
Theorem 4.3.
([17, Example 5.4]) There exists an inverse sequence of -continua with surjective monotone upper semi-continuous bonding functions such that is not a -continuum.
The main aim of this section is to prove Theorem 4.8, which is in contrast to the above results. To prove the theorem, we need Theorem 4.6 proven in [17].
Definition 4.4.
([17, Definition 3.1]) Let be a topological property of continua. Then, we say that property satisfies the monotonic condition I if for any continua and with property and for each surjective monotone upper semi-continuous function , is a continuum having property .
Definition 4.5.
([17, Definition 3.2]) Let be a topological property of continua. Then, we say that property satisfies the monotonic condition II if for any inverse sequence of continua having property with surjective monotone bonding maps, is a continuum having property .
Theorem 4.6.
([17, Theorem 3.6]) Let be a topological property of continua. Then, property satisfies the monotonic conditions I and II if and only if for each inverse sequence of continua having property with surjective monotone upper semi-continuous functions, is a continuum having property .
Furthermore, we need the following result. The proof is similar to the proof of [2, Theorem 4.3]. Hence, we omit the proof.
Lemma 4.7.
(See also [2, Theorem 4.3]) Let be an inverse sequence of -continua with surjective monotone maps. Then, is also a -continuum.
The following theorem is the main result in this section.
Theorem 4.8.
Let be an inverse sequence of compacta with surjective monotone upper semi-continuous bonding functions. If is a -continuum for each , then is also a -continuum.
Proof.
By Theorem 4.6, it is enough to show that the property of being satisfies the monotonic conditions I and II. By Lemma 4.7, it is easy to see that the property of being satisfies the monotonic condition II. Hence, we only show that the property of being satisfies the monotonic condition I.
Let and be -continua and let be a surjective monotone upper semi-continuous function. First, since is upper semi-continuous, by Theorem [5, Theorem 2.1], is compact. Also, by the monotonicity of , is connected. Hence, is a continuum.
Let and let be a nondegenerate subcontinuum of such that . Put and .
-
Case 1
and
Since is not a one point set, we may assume is not a one point set. Since is , there exists a subcontinuum such that , and . Then, is a subcontinuum of such that , and .
-
Case 2.
or .
In this case, we may assume .
-
Case 2.1.
is not a one point set.
In this case, by using the fact that is monotone, we see that is a subcontinuum of such that , and .
-
Case 2.2.
is a one point set.
In this case, note that is a nondegenerate subcontinuum of and . Since is , there exists a subcontinuum of such that , and . Then, is a subcontinuum of such that , and .
-
Case 2.1.
From the above, we see that is a -continuum. Hence, the property of being satisfies the monotonic condition I. This completes the proof. ∎
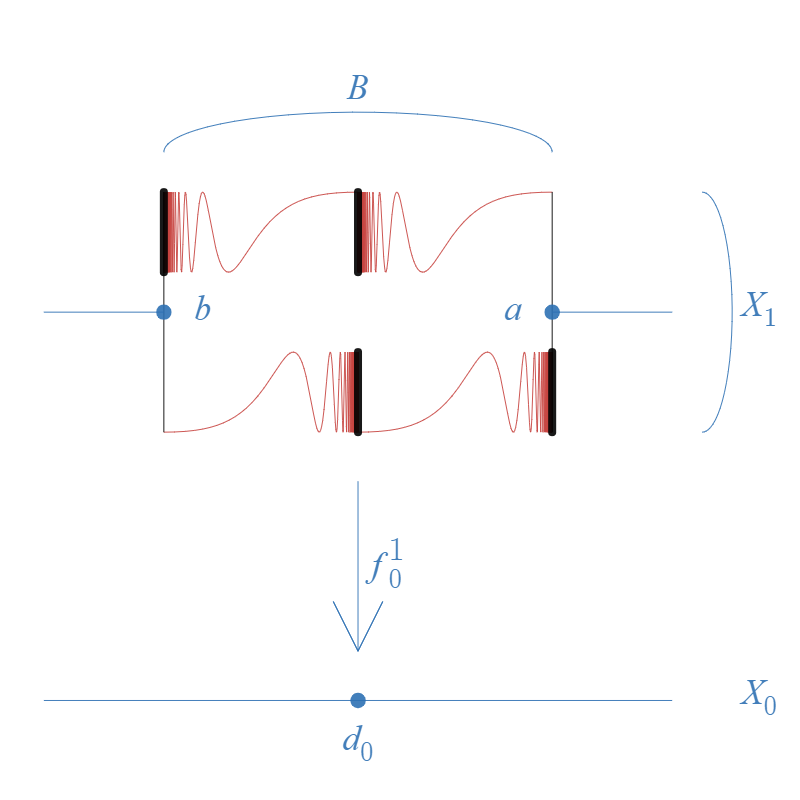
Example 4.9.
Let , , and be subspaces of defined by
Note that are pairwise disjoint. Let (see figure 2). We can see that there is a homeomorphism such that .
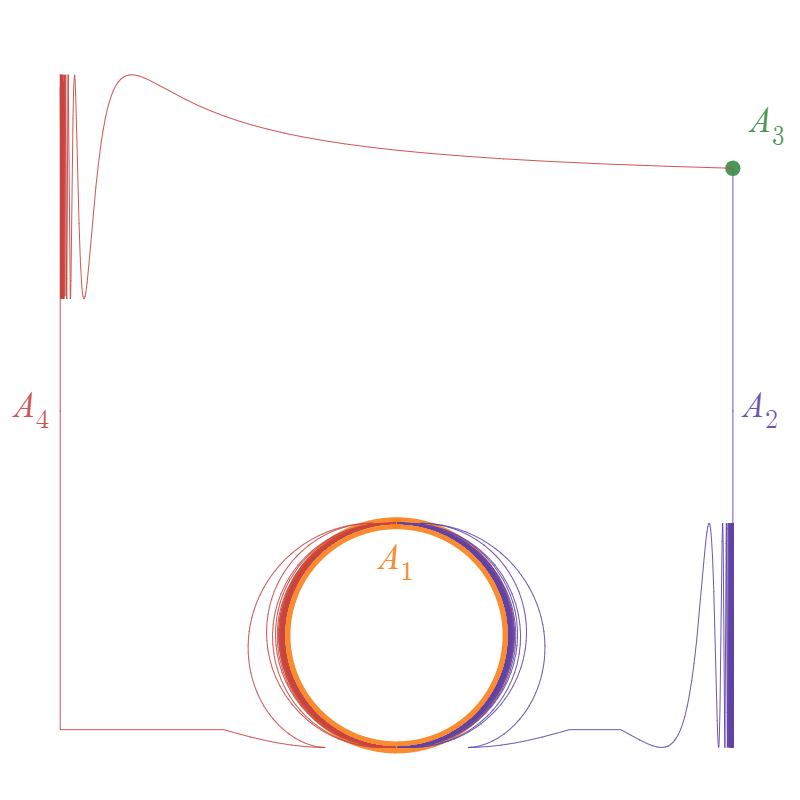
Let be the upper semi-continuous function defined by
It is easy to see that is a surjective monotone upper semi-continuous function.
For each , let and let . By Theorem 4.8, the inverse limit is a -continuum.
Remark 4.10.
The continuum in the previous example also appears in [14, Example 2.3] as an example of -continuum which is neither Wilder nor .
Remark 4.11.
In [17], the third author showed that inverse limits of Wilder continua with surjective monotone upper semi-continuous bonding functions are also Wilder continua.
5. A -continuum containing neither Wilder continua nor -continua
Let be a nondegenerate continuum. Then is said to be arc-like if for each , there exists a surjective map such that for each , . A continnuum is said to be if each of its all subcontinua is decomposable.
Theorem 5.1.
([2, Remark 5,11]) There exists an arc-like hereditarily decomosable continuum containing no -continua.
A continuum is said to be hereditarily arcwise connected if each of its subcontinuum is arcwise connected. Also, if each subcontinuum of is a Wilder continuum (resp. a -continuum, a -continuum, a -continuum), then is called a hereditarily Wilder continuum (resp. a hereditarily -continuum, a hereditarily -continuum, a hereditarily -continuum).
Theorem 5.2.
Hence, it is natural to ask whether or not there exists a hereditarily -continuum containing no -continua. The answer to this question is negative by the following result.
Corollary 5.3.
[14, Corollary 3.4]) Let be a nondegenerate continuum. Then, the following are equivalent.
-
(1)
is a hereditarily Wilder continuum;
-
(2)
is a hereditarily -continuum;
-
(3)
is a hereditarily -continuum;
-
(4)
is a hereditarily arcwise connected continuum.
However, in Theorem 5.4, we show that there exists a -continuum containing neither Wilder continua nor -continua.
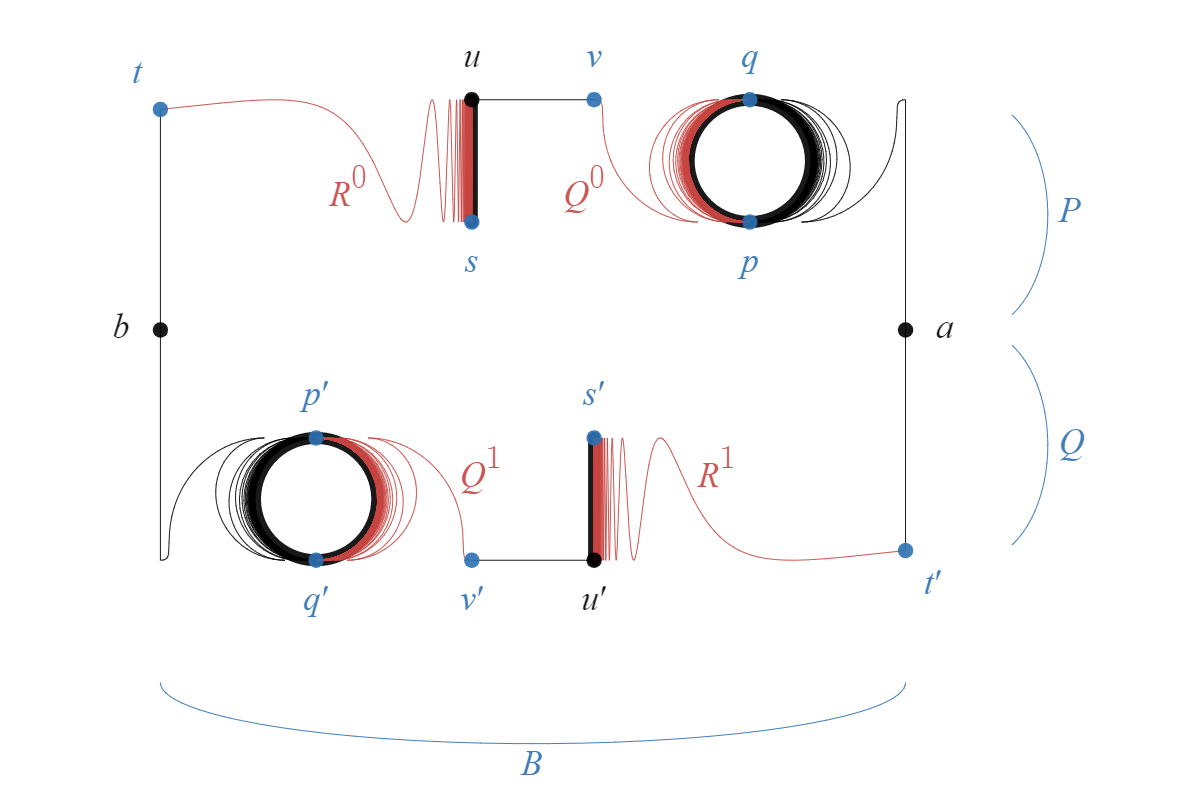
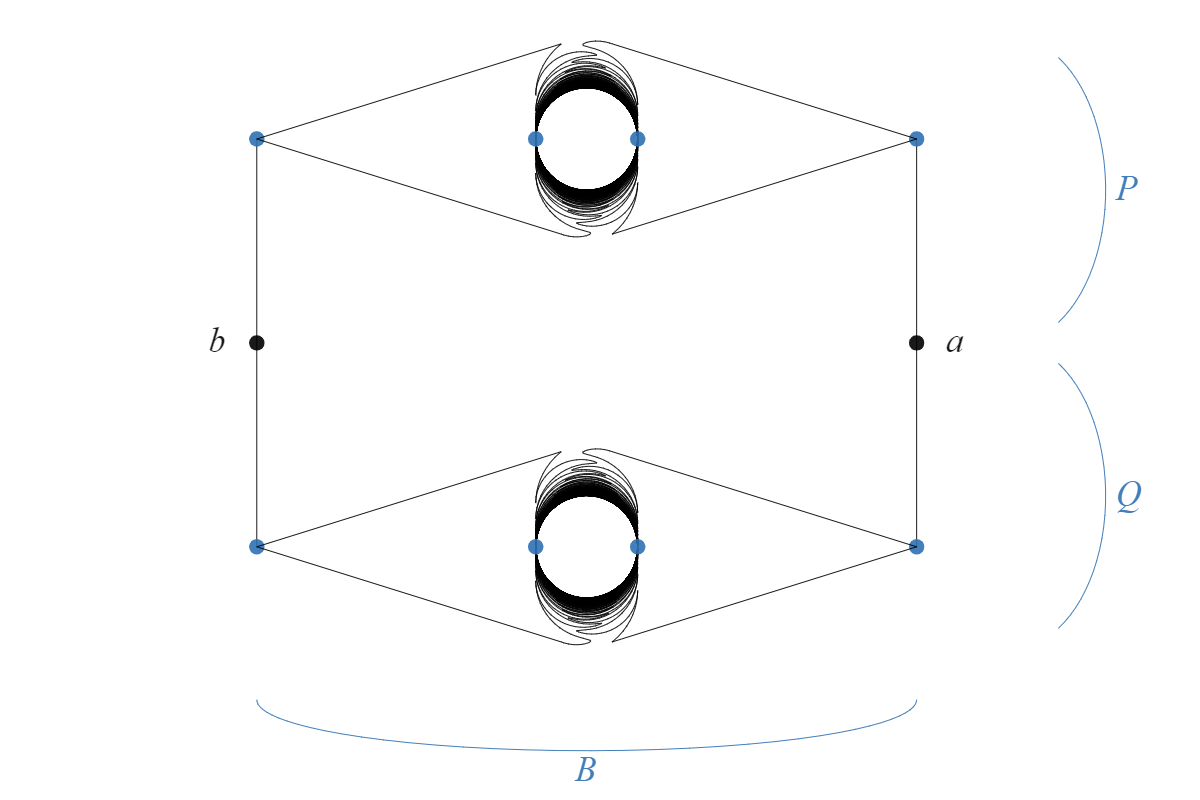
Let be the subcontinuum of defined by
(see Figure 3). Let and be the subcontinua of defined by
Also, let , , and be the subspaces of defined by
Then, , , and are homeomorphic to respectively. Also, note that , , and are homeomorphic to the -continuum. Furthermore, let , , , , , , , , , , , , , be the points as in Figure 3. Finally, let , , , , , , , , , , , , , .
In the following theorem, if is an inverse sequence with single valued bonding maps, then we denote the map by if . Also, let . Furthermore, for each , let be the projection. Finally, if is a map and is a point such that is a one point set, then we also denote the point in by .
Theorem 5.4.
There exists a -continuum containing neither Wilder continua nor -continua.
Proof.
We follow the scheme from [3, Section 3], which is originally based on the idea of the construction of Janiszewski’s hereditarily decomposable, arc-like, and arcless continuum [6]. In particular, almost all notations and terminology in the proof are taken from [3, Section 3]. In order to avoid complications, we will omit the parts of the way of construction of the required continuum that overlap with the construction of the planar arcless continuum-chainable continuum that appeared in [3]. There are three differences in construction between the continuum in [3, Section 3] and ours. Two of them are as follows:
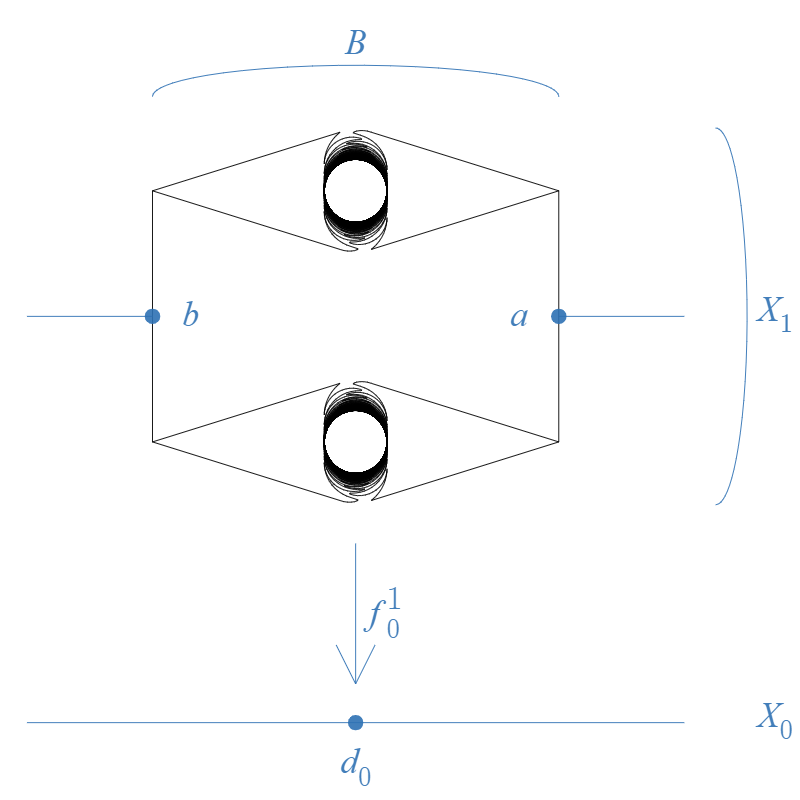
(i) Instead of in [3, Section 3], in our example, we let be the continuum defined before Theorem 5.4.
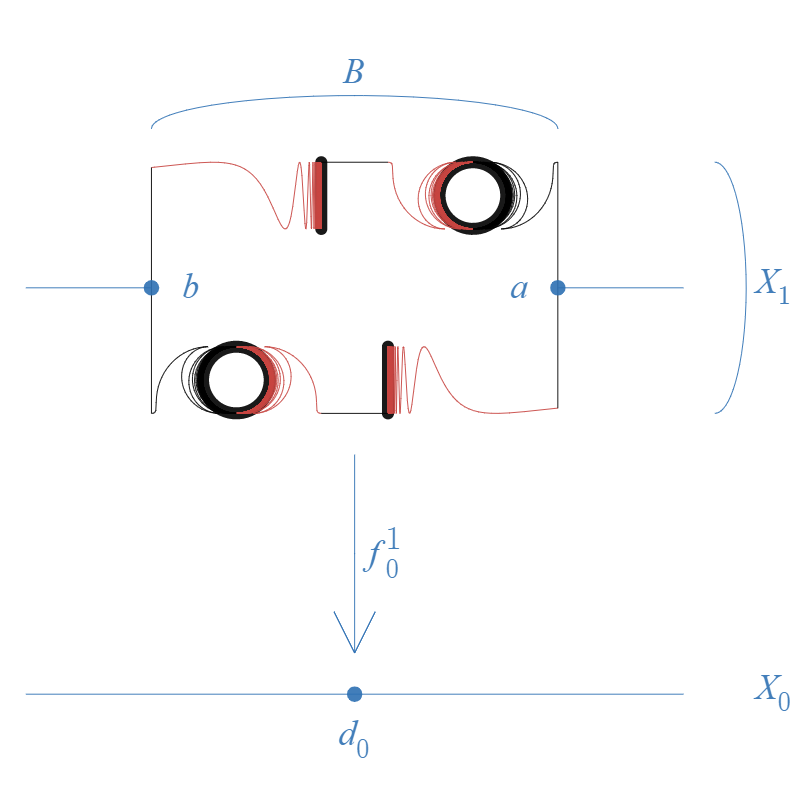
(ii) Let and . Also, let and let be the map defined by
See Figure 4. We say that is obtained from by blowing up the point to a copy of . Also, following the scheme in [3, Section 3], we continue blowing up points of an appropriately chosen sequence to copies of , and for each we can obtain from and . For each , let and let , , , , , , , , , , , , , , , , , , , be subsets and points in corresponding to , , , , , , , , , , , , , , , , , , , in respectively. Let . Also, for each , let
.
We may assume the following condition (this is the third difference in construction between the planar arcless continuum-chainable continuum that appeared in [3, Section 3]) and ours):
(iii) For each , .
Let . We show that has the required property.
Claim 1. is a -continuum.
Proof of Claim 1. To prove Claim 1, first, we prove that is a -continuum for each . To prove it , we need to prove the following subclaim.
Subclaim. Let . Let and be a subarc of such that and . Then, for each , there exists a subcontinuum of such that and .
Before the proof of Subclaim, note that the following holds:
Let and let be a subarc of such that . Then, for each , there exists a subcontinuum of such that and .
Proof of Subclaim. We prove Subclaim by induction on . If , then we can easily see the assertion holds. Let and assume that the assertion holds for . Now, we prove that the assertion holds for .
Case A. .
Case B. .
In the cases above, by using inductive assumption, we can easily find a subcontinuum of with the required properties.
Case C. .
In this case, by () it is easy to see that there is a subcontinuum of with the required properties.
Case D. , .
In this case, take a sufficiently small subarc of such that and . Then, by inductive assumption, there is a subcontinuum of such that and . Take . Then, we can take a subarc of from to the one of and , and . We may assume . Let be a subarc of such that and . Then, by , there exists a subcontinuum of such that , and . Let . Then, it is easy to see that has the required properties.
Hence, in every case we can find a subcontinuum of with the required properties. This completes the proof of Subclaim.
Now, we prove is a -continuum for each . Let be a nondegenerate subcontinuum and . Take any subarc of and any . By Subclaim, there exists a subcontinuum of such that and . Note that . Hence, we see that is a -continuum.
Therefore, is an inverse limit of -continua with surjective monotone bonding maps. Hence, by Lemma 4.7, is a -continuum. This completes the proof of Claim 1.
Claim 2. contains no Wilder continua.
Proof of Claim 2. Let be a nondegenerate subcontinuum of . Then, there exists such that is not a singleton. Take any subarc of . Let and and . Note that , , , . Since is connected, the one of the following holds:
(i) There is a subcontinuum of containing and .
(ii) There is a subcontinuum of of containing and .
Assume (i) holds. Then, it is easy to see that either or holds. Hence, we may assume . In this case, we can easily see that and are points of non-Wilderness of . Hence, if (i) holds, then is not a Wilder continuum. We also see that is not a Wilder continuum if (ii) holds. This completes the proof of Claim 2.
Claim 3. contains no -continua.
Proof of Claim 3. Let be as in the proof of Claim 2. Then, as in the proof of Claim 2, the one of the following holds:
(i) There is a subcontinuum of containing and .
(ii) There is a subcontinuum of of containing and .
Assume (i) holds. We may assume that . Let and . Then, and are pairwise disjoint subcontinua of . Also, it is not difficult to see that if is a subcontinuum of such that and , then is a subcontinuum of such that and . However, there is not such a subcontinuum in . Hence, this is a contradiction. Therefore, there is not a subcontinuum of such that and . Hence, if (i) holds, then is not a -continuum. We also see that is not a -continuum if (ii) holds. This completes the proof of Claim 3.
Thus, is a -continuum containing neither Wilder continua nor -continua. ∎
Also, we can get the following result. The proof is very similar to the proof of Theorem 5.4. The essential difference is the continuum obtained by blowing up a point of the factor space at each step. Hence, we only write about it in the proof.
Theorem 5.5.
There exists a Wilder continuum which contains no -continua.
Proof.
Furthermore, we can get the following result.
Theorem 5.6.
There exists a -continuum which contains no Wilder continua.
Proof.
As in the previous theorem, the proof of this theorem can be obtained by replacing the corresponding continua drawn in Figures 3 and 4 with the continua drawn in Figures 7 and 8 in the proof of Theorem 5.4. To be exact, let
Then, using the same idea as the proof of Theorem 5.4, we can prove this theorem. ∎
References
- [1] B. Espinoza and E. Matsuhashi, Weakly Whitney preserving maps, Topology Appl., 262 (2019), 90-108.
- [2] B. Espinoza and E. Matsuhashi, D-continua, -continua and Wilder continua, Topology Appl., 285 (2020), 25p.
- [3] C. L. Hagopian and L. G. Oversteegen, Continuum chainability without arcs, Houston J. Math., 21, No. 2 (1995), 407-411.
- [4] A. Illanes and S. B. Nadler, Jr., Hyperspaces: Fundamentals and Recent Advances, Marcel Dekker, Inc., New York, 1999.
- [5] W. T. Ingram and W. S. Mahavier, - , Houston J. Math. 32 (2006), no.1, 119-130.
- [6] J. Janiszewski, ber die Begriffe “Linie” und “Flche”, Proceedings of the Fifth International Congress of Mathematicians II, Cambridge (1912), 126-128.
- [7] J. P. Kelly. - , Topology Appl. 228, 486-500, 2017.
- [8] K. Królicki and P. Krupski, Wilder continua and their subfamilies as coanalytic absorbers, Topology Appl., 220 (2017), 146-151.
- [9] J. Krasinkiewicz and S. B. Nadler, Jr., Whitney properties, Fund. Math., 98 (1978), 165-178.
- [10] I. Lončar, Whitney map for hyperspaces of continua with the property of Kelley, JP Jour. Geometry and Topology, 4 (2004), no. 2, 147-156.
- [11] I. Lončar, -continuum admits a Whitney map for if and only if it is metrizable, Glas. Mat. Ser. III, 40(60)(2005), 333-337.
- [12] I. Lončar,Weight and metrizability of inverses under hereditarily irreducible mappings, An. \cbStiin\cbt. Univ. “Ovidius” Constan\cbta Ser. Mat. 16 (2008), no. 2, 67-82.
- [13] I. Lončar, A note on generalized Whitney maps, Mat. Vesnik, 67 (2015), no.4, 233-245.
- [14] E. Matsuhashi and Y. Oshima, Some decomposable continua and Whitney levels of their hyperspaces, Topology Appl., 326 (2023), 9p.
- [15] S. B. Nadler, Jr., Hyperspaces of sets, Marcel Dekker, Inc., New York, 1978.
- [16] S. B. Nadler, Jr., Continuum theory: an introduction, Marcel Dekker, Inc., New York, 1992.
- [17] Y. Oshima, Some Theorems on inverse limits with monotone upper semi-continuous bonding functions, Topology Proc.60 (2022), 279-294.
- [18] B. E. Wilder, Concerning point sets with a special connectedness property, Colloq. Math., 19 (1968), 221-224.