Sounds Discordant:
Classical Distance Ladder & CDM-based Determinations of the Cosmological Sound Horizon
Abstract
Type Ia Supernovae, calibrated by classical distance ladder methods, can be used, in conjunction with galaxy survey two-point correlation functions, to empirically determine the size of the sound horizon . Assumption of the CDM model, together with data to constrain its parameters, can also be used to determine the size of the sound horizon. Using a variety of cosmic microwave background (CMB) datasets to constrain CDM parameters, we find the model-based sound horizon to be larger than the empirically-determined one with a statistical significance of between 2 and 3, depending on the dataset. If reconciliation requires a change to the cosmological model, we argue that change is likely to be important in the two decades of scale factor evolution prior to recombination. Future CMB observations will therefore likely be able to test any such adjustments; e.g., a third generation CMB survey like SPT-3G can achieve a three-fold improvement in the constraints on in the CDM model extended to allow additional light degrees of freedom.
1 Introduction
Classical distance ladder (CDL) approaches using Cepheids and supernovae (Riess et al., 2018b, hereafter R18) find higher Hubble constant estimates than those derived from cosmic microwave background (CMB) data, that assume the standard cosmological model, CDM (Planck Collaboration VI, 2018). The statistical significance of this discrepancy has grown over time with fairly steady progress on the distance ladder (Riess et al., 2009, 2011, 2016) and with a sudden jump in precision of the CDM prediction with the first release of the Planck cosmology data in 2013 (Planck Collaboration XVI, 2014). Comparing the R18 value of km/s/Mpc with the value inferred from Planck CMB temperature and polarization power spectra plus CMB lensing, assuming CDM, km/s/Mpc, there is a 3.6 discrepancy (Planck Collaboration VI, 2018).
Along with the reduction of statistical errors in the Cepheids plus supernovae determination of , other supporting evidence in favor of a high value of has been growing as well. A number of independent analyses of the data have served to largely confirm the conclusions of R18 (Efstathiou et al., 2014; Cardona et al., 2017; Zhang et al., 2017; Feeney et al., 2018a; Follin & Knox, 2018). Despite claims that the CDL departs significantly from the cosmic mean due to a local void, Wu & Huterer (2017) have shown that within CDM the sample variance in the R18 measurement is only 0.3 km/sec/Mpc, or 0.2. In addition, Birrer et al. (2018) have provided the latest inference of from the H0LiCOW (Suyu et al., 2017) collaboration’s use of strong-lensing time delays: km/s/Mpc. Combining the result of this completely independent probe of the distance-redshift relation at low redshift, with that from R18, results in a 4.1 discrepancy with the Planck result quoted above. Finally, the tip of the red giant branch distance method shows consistency with Cepheid distances to a handful of supernova host galaxies (Jang & Lee, 2017; Hatt et al., 2018a, b).
Recently, Shanks et al. (2018a) claimed that corrections applied to the Gaia data (Lindegren et al., 2018) in the R18 analysis have introduced significant systematic error, a claim that has sparked a debate (Riess et al., 2018a; Shanks et al., 2018b). We simply point out here that the Riess et al. (2016) result of km/s/Mpc makes no use of Gaia data and is thus immune to this controversy, while nearly as discrepant from the CDM plus CMB-inferred values.
The case against systematic errors in CMB data as the source of this discrepancy is very strong. First of all, the result from Planck is robust to choice of frequency channels (Planck Collaboration et al., 2016), arguing against foreground modeling, or any channel-specific systematic errors as a source of bias in the inference. Further, the consistency of Planck measurements with WMAP on large angular scales (Planck Collaboration et al., 2014) and the 2500 deg2 SPT-SZ measurements on small angular scales (Hou et al., 2018; Aylor et al., 2017) also argues against any significant systematic errors on all angular scales relevant for determination of cosmological parameters from Planck data.
Additionally, the conclusion of a low from CMB data and the assumption of CDM can be reached without any use of Planck data. The inverse distance ladder results (Percival et al., 2010; Heavens et al., 2014; Aubourg et al., 2015; Cuesta et al., 2015; Bernal et al., 2016a; DES Collaboration et al., 2017; Verde et al., 2017b; Lemos et al., 2018; Joudaki et al., 2018; Feeney et al., 2018b) also show that the combination of measurement of the baryon acoustic oscillation (BAO) feature in galaxy surveys, Type Ia supernova observations, and CMB data with or without Planck (e.g., WMAP9, Bennett et al. 2013) lead to low (Planck-like) values of . Finally, Addison et al. (2018) point out that assuming the CDM model, using BAO data, and light element abundance measurements as constraints on the baryon-to-photo ratio, one infers a Planck-like value of ; i.e., without use of any CMB anisotropy data. The above results indicate that systematic errors in CMB data, and Planck CMB data in particular, are not the major driver of the discrepancies in inferences of .
Recently, some works in the literature have proposed solutions both pre- and post-recombination to address the discrepancy. For example, Karwal & Kamionkowski (2016); Evslin et al. (2018); Poulin et al. (2018) propose the existence of an early dark energy which reduces the size of the sound horizon subsequently increasing the CMB inferred value of ; Lin et al. (2018) propose a modified gravity solution at the time of recombination and Chiang & Slosar (2018) alter the duration of the recombination to reduce the tension between CMB and CDL results. On the other hand, Di Valentino et al. (2016, 2017); Joudaki et al. (2017) use an extended parameter space and point out that an interacting phantom-like dark energy with equation of state can also reduce the tension in measurements.
In this paper, to further explore what can, and what cannot, explain this discrepancy, we follow Bernal et al. (2016b) and use the sound horizon , rather than , as the point of comparison between CDL and CDM-based estimates. With this approach, the BAO data are on the CDL side: Cepheids calibrate Type Ia supernovae, which are then used to determine distances to redshifts for which BAO measurements of the angular size of the sound horizon exist, thereby revealing the size of the sound horizon. We also note that strong-lensing time delays can be used to calibrate the BAO measurements, so we convert the H0LiCOW result into a sound horizon constraint. For a more comprehensive use of data sensitive to distances and the expansion rate at low redshifs (), see Bernal & Peacock (e.g. 2018), which includes use of “cosmic clocks.”
We find use of the sound horizon as a point of comparison, to be a particularly useful way of examining the data for several reasons: first, there is added insensitivity with this method to extreme changes in the cosmology since one does not need to extrapolate to , circumventing issues with peculiar velocities brought up by Shanks et al. (2018a) ; second, the CDM predictions for the sound horizon are more robust than those for ; third, as with the inverse distance ladder, this approach clarifies that reconciliation can not be delivered by altering cosmology at . Fourth, it serves to clarify that the reconciliation of distance ladder, BAO, and CMB observations via a cosmological solution is likely to include a change to the cosmological model in the two decades of scale factor evolution prior to recombination; and finally, from CMB data, assuming CDM is four times smaller than the from the same data and assumed model.
Since Bernal et al. (2016b), we have new supernova data available (Scolnic et al., 2018), an updated supernova absolute luminosity calibration (R18), and results from the final data release from Planck (Planck Collaboration VI, 2018). We examine the tension in given these most recent data. As mentioned above, strong-lensing time delays can also be used to calibrate the distance to the BAO redshifts. So we also use the latest H0LiCOW results (Birrer et al., 2018) to produce a constraint on .
We find that the CDL-inferred sound horizons are in 2-3 tension with CDM-determined ones111The inverse distance ladder results in a more significant tension because the BAO error, in this case, gets added to the error which is fractionally smaller than the CDL error on . . While a statistical fluke could explain this discrepancy, we believe there is sufficient evidence to motivate the exploration of cosmological solutions. In Section 4, we argue that if there is to be a cosmological solution to the discrepancies in values, it is likely to be significantly different from CDM in the two decades of scale factor growth prior to recombination. Such model changes are likely to lead to predictions testable with future CMB data. We examine the predictions in the case of a two-parameter extension of the standard cosmological model, and forecasts for errors in these extended model spaces given the survey to come from SPT-3G, a third-generation camera outfitted on the South Pole Telescope (Benson et al., 2014; Bender et al., 2018).
2 Models and Data
We present here the empirical, CDL, approach to determining the sound horizon scale, , and then the more cosmological-model dependent approach. Although the former also requires modeling, we demonstrate with a parametric Spline model for the history of the expansion rate that the results are at most only mildly dependent on cosmological model assumptions. We also describe how we use the recent H0LiCOW results (Birrer et al., 2018) to determine .
2.1 using CDL
We describe the formalisms to determine empirically in this section. For this purpose, we use the BAO data from the BOSS survey (Alam et al., 2017), supernova data from the SNeIa Pantheon sample (Scolnic et al., 2018), and Cepheid data from R18.
The sound horizon leaves its imprint on the galaxy distribution as a peak in the galaxy two-point correlation function at , the comoving size of the sound horizon222More specifically, at the end of the baryon drag epoch; i.e. at as defined in Hu & Sugiyama (1996). This is often denoted , but we use to avoid confusion with the diffusion scale.. In redshift space, with galaxy positions recorded in and angular position on the sky, the sound horizon scale maps into (the difference in redshift between two galaxies with line-of-sight separation ) and (the angular separation of two galaxies separated by perpendicular to the line of sight), where is the comoving angular diameter distance. Thus BAO surveys fundamentally constrain these two quantities and analyses often summarize the constraints as constraints on and .
Type Ia Supernovae are used as “standardizable” candles, that, after suitable data-dependent corrections, can be reduced to a corrected apparent magnitude with signal modeled by
| (1) |
where runs over supernovae, the first term on the right is a global, supernova-independent, corrected absolute magnitude, and the 2nd and 3rd terms just follow from the inverse square law for fluxes and the definitions of apparent and absolute magnitudes, with the comoving luminosity distance.
Neglecting, for the moment, the BAO constraints on , the BAO and SNe constraints are very similar. Both the BAO and SNe data determine a distance-redshift relationship up to some global scaling factor. In the BAO case the scaling factor is , and in the supernova case we could take it to be Mpc333The choice of “+19” here is arbitrary; it makes Mpc for which is close to the corrected supernova absolute magnitude.. The two different distances are also very simply related, assuming conservation of photon number, via .
We can relate these observable distance ratios to , assuming negligible mean spatial curvature, via
| (2) |
with and .
Finally, there are the Cepheids. The Supernovae, H0, for the Equation of State of Dark energy (SH0eS) (Riess et al., 2018b) program has used Cepheids in 19 different host galaxies with observed SNe Ia to calibrate the mean supernova absolute magnitude. Rather than directly using that calibration, we use the value of that results from the calibration. As one can see in the equations above, the supernova data themselves are sensitive to the combination , so specifying allows one to determine ; i.e., it allows for a calibration of the supernova distance measurements.
We use BAO, SNe, and Cepheid data as just (generically) described to infer , performing our analyses with two different model spaces. One is CDM with
| (3) |
where
| (4) |
with calculated for a neutrino background with a temperature today of K , two mass eigenstates and one with mass with default value of 0.06 eV and the energy density, in units of the critical density, in a black body of photons with temperature K. The complete set of parameters of this model can be taken to be { }. Note that the sound horizon scale is a derived parameter given by .
The other model we call the Spline model. For this model, following Bernal et al. (2016b), is determined by at 5 locations in and cubic spline interpolation. The complete set of parameters for the Spline model is {} where with and , for which we assume a uniform prior over the region with . These were the redshift points used by Bernal et al. (2016b). We also consider a slightly different choice to check robustness in §3.1.2.
We note that the Spline model results are not completely free of cosmological assumptions, as the relationship between and depends on curvature. If it were not for the BAO constraints on then our Spline model-based inferences of would not have any dependence on curvature, as our parameters can just be thought of, in that case, as a means of parameterizing . The reconstructed would have curvature dependence, but the recovered would not. The inclusion of the BAO constraints on breaks that degeneracy in curvature and brings some dependence of the inferred on assumptions about curvature. We will discuss this dependence in the Results §3.
To perform joint analyses of the three datasets, we form a log likelihood (natural log of the likelihood), given by
| (5) |
We now briefly describe each of these likelihoods in turn.
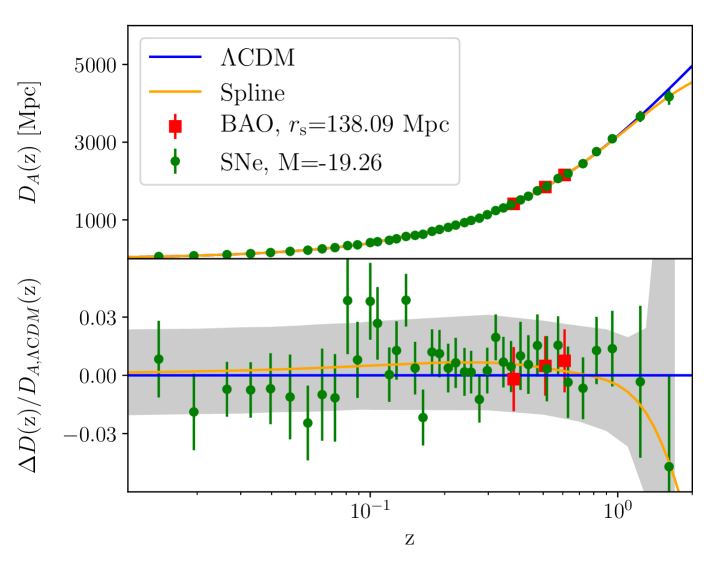
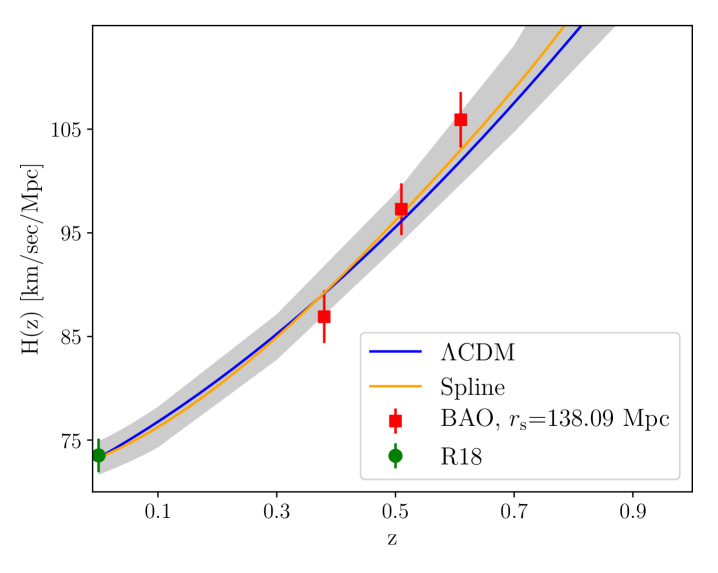
The log likelihood has the BAO means and error covariance matrix as described in the BOSS collaboration paper Alam et al. (2017), for and at the effective redshifts and 0.61. These data points are plotted as red squares in Figures 1 and 2 as constraints on and given a fiducial value of .
We do not include any other BAO data, such as from the 6df galaxy survey (Beutler et al., 2011) and from a BOSS DR12 Ly absorption cross-correlation analysis (du Mas des Bourboux et al., 2017). While they provide useful consistency tests of the standard cosmological model they are not as precise as the BOSS galaxy constraints (Alam et al., 2017) and some are also at redshifts greater than the highest redshifts for which we have supernova distance estimates, rendering them uninformative for our main purpose.
To construct the likelihood for SNe we use the Scolnic et al. (2018) dataset. They report the redshift-binned estimates of corrected band SNe apparent magnitudes, corrected to improve the approximation for some global , where is the distance modulus for redshift . We thus model the data as
| (6) |
The absolute magnitude is the more usual way of specifying the calibration of the supernovae. Taking introduced above to have the fiducial value of 1 Mpc for a fiducial value of (for specificity) then Eq. 6 can be rewritten to swap in for :
| (7) |
We form a likelihood that is Gaussian in the apparent magnitudes, with covariance matrices that include the statistical and systematic errors as reported in Scolnic et al. (2018). The data points are plotted as green circles in Fig. 1 as constraints on for a fiducial value of .
For the “Cepheids” log likelihood, we take
| (8) |
where is our model Hubble constant in km/s/Mpc and the numbers in the likelihood are from R18 measurement km/s/Mpc. Note that, just like for with the BAO data, is a derived parameter given by . The supernova absolute magnitude parameter can likewise be derived from .
2.2 and strong-lensing time delays
We also consider strong-lensing time delay (SLTD) data (Birrer et al., 2018) as a means of calibrating the BAO. A given SLTD system is sensitive to the ratio where is the distance to the lens (typically near ), the distance to a lensed quasar (typically near ), and the distance between the two. This quantity is inversely proportional to , and, in CDM, its dependence on the exact shape of (given largely by ) is weak enough to, even with very weak priors on the matter density, produce a strong constraint on . We can thus use this constraint to anchor the BAO point instead of the Cepheids without any other additional external data. In practice, we simply combine the constraint on which we get from SNe and BAO with the reported by Birrer et al. (2018), propagating Gaussian error bars in quadrature.
We note that this analysis is approximate because we have not jointly analyzed the datasets; improved constraints on the matter density from the SNe+BAO data could further tighten the H0LiCOW result. However, this effect is likely to be small given the weak dependence on the prior reported by Birrer et al. (2018). Note that this analysis does assume CDM, in particular that the shape of follows the expectation from CDM between today and the quasar redshifts of . While the SNe strongly constrain the shape at somewhat lower redshifts, there is, at least in theory, the possibility that the H0LiCOW inference of and thus our corresponding inference could be somewhat thrown off by a change to right around . We have not attempted a joint spline fit of SNe+BAO+H0LiCOW, but such a test could reveal to what extent this is a possibility (although, of course, the H0LiCOW and Cepheid determinations of are already in good agreement, arguing against this possibility).
2.3 from CDM plus CMB data
We have just reviewed how one can infer in an empirical manner using the CDL. Here we describe how one can adopt a model and directly calculate . The comoving size of the sound horizon is given by
| (9) |
where is the sound speed as a function of the scale factor and is the scale factor at the end of the baryon drag epoch. In the CDM model is completely determined by the baryon-to-photon ratio, for its influence on and , and the matter density for its influence on and . With these parameters constrained, or any other relevant parameters there might be in extended model spaces, one can then calculate a constraint on .
We use the CMB datasets from the Atacama Cosmology Telescope (ACTPol, Louis et al., 2016), Planck (Planck Collaboration VI, 2018), the South Pole Telescope: SPT-SZ (Aylor et al., 2017) and SPTpol (Henning et al., 2018), and the Wilkinson Microwave Anisotropy Probe (WMAP, Bennett et al. 2013). We look at subsets of the Planck data as well. Significant constraints on come from each of the three dominant power spectra: , and , as well as from at and at .
3 Results and Discussion
Before presenting the constraints on from different methods described in §2, in Figures 1 and 2 we display the BAO and SNe data as they constrain and . For these figures, we assume the fiducial values Mpc and , which are the best-fit values for the Spline model parameter space described in §3.1.2 given the BAO, SNe, and Cepheid data. We choose the best-fit values from the spline model, as opposed to the CDM model, primarily for specificity, and secondarily in order to have less model dependence in the resulting distance estimates.
Examining the residuals from these fits in Fig. 1 and Fig. 2 we see no obvious problems for either the CDM model or the Spline model. For the CDM model, we find for the best fit and = 3.5, summing to = 42.8 for 43 degrees of freedom (40 SNe data points, 6 BAO data points, and 3 parameters, not counting ). For the Spline model, we find the best fit and = 3.4, with = 41.4 for 40 degrees of freedom (6 parameters, once again not counting ).
Now we turn to results reporting the inferred value of using the CDL approach from the CDM and the Spline model in §3.1. This is followed by the results obtained using CMB data for the CDM model in §3.2. Next, we discuss the to tension in the value of obtained from these two methods in §3.3. In §3.4, we look at a couple model extensions and forecast the expected constraints on that can be obtained by combining Planck results with SPT-3G (Benson et al., 2014), a stage-3 CMB temperature and polarization survey. Finally, in §4,we argue that if the origin of the discrepancies is cosmological, the cosmological solution must make its important changes at times prior to recombination.
3.1 CDL based constraints
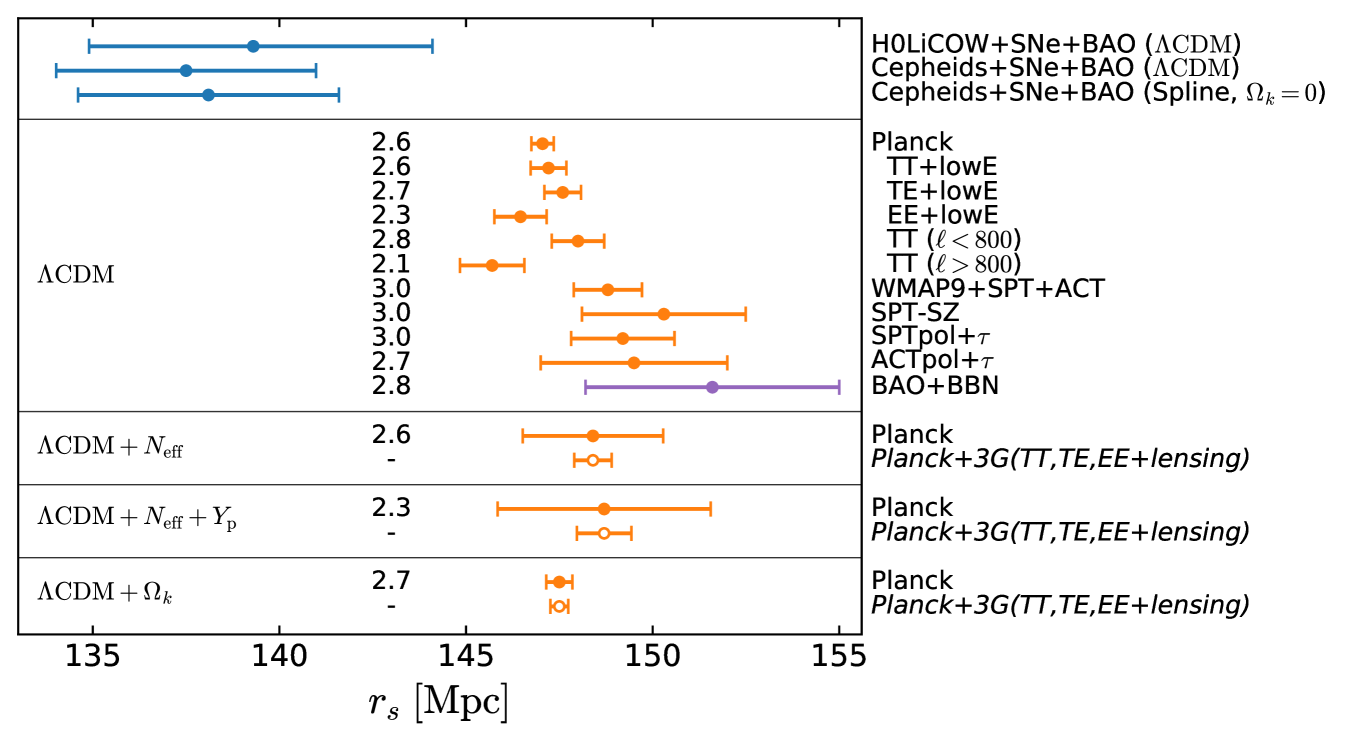
We begin our discussion with our first result from a combination of the constraint (that we refer to as “Cepheids”, R18), used for calibrating the Pantheon binned distance moduli (“SNe”, Scolnic et al. 2018), which in turn are used to calibrate the BAO distance and constraints from BOSS galaxies (“BAO”, Alam et al. 2017). The CDL based results are shown as blue circles in the top panel of Fig. 3.
3.1.1 CDL + CDM
First, we have assumed the CDM model – using it to provide the parameterized shape of . We find
| (10) |
As a point of comparison we mention a result from Addison et al. (2018). They take a more comprehensive set of BAO data, including constraints at lower redshift from galaxy surveys (Beutler et al., 2011; Ross et al., 2015), and higher redshift constraints from BOSS Lyman- (Font-Ribera et al., 2014; Delubac et al., 2015; Bautista et al., 2017) and find, from the BAO data themselves, assuming the CDM model, that km/sec. Combining this with the R18 result for it becomes
| (11) |
This result is nearly the same, in mean and standard deviation, as our own CDL + CDM result. The lack of reduction in uncertainty, despite the much greater amount of BAO data, is due in part to the lack of use of the SNeIa data, which increases uncertainty in , and therefore the shape of . The other important factor in the lack of reduction is that the BOSS galaxy data are unmatched in precision.
Our second CDL + CDM result comes from replacing Cepheids (R18) with the SLTD data from H0LiCOW (Birrer et al., 2018) like explained in §2.2. From our SNeIa + BAO data we have . Combining this with km/s/Mpc from Birrer et al. (2018) we find
| (12) |
That uncalibrated supernovae, combined with BAO data, put a strong constraint on the product was previously mentioned in Verde et al. (2017b).
3.1.2 CDL + Spline
To explore the model-dependence of the CDL method for inference, we now drop the assumption of CDM for parameterization of the shape of and replace it with our Spline model. Because our BAO results span such a small range of redshift, we can expect that there is very little sensitivity of the inferred to the choice of parameterization, as long as it is not varying rapidly on redshift intervals comparable to the redshift span of the BAO measurements. With the four-parameter model described in the previous section we indeed find a very similar result to the CDM result:
| (13) |
That this sound horizon result is a little bit larger is consistent with what we see in the residuals panel of Fig. 1. Namely, the SNe data largely sit above the CDM best-fit curve in the redshift interval with the BAO data. The increased freedom of the empirical model reduces the influence of the SNe outside of this redshift range, boosting in this interval with the result that is slightly larger. Note though that statistically, this is a very small shift of less than 0.2.
More importantly, because the CDM and Spline results for are basically the same, including in the uncertainty, we can conclude that the CDL sound-horizon determination is highly model independent. In particular, it is, at most, very weakly dependent on any assumptions about the shape of the distance-redshift relationship. As a further check, we performed an analysis with Spline points moved to {0, 0.2, 0.5, 0.8, 1.1} away from our baseline (see §2.1) and obtain Mpc indicating that our results are not highly sensitive to the choice of pivotal redshift points.
Before closing this subsection we comment on the dependence of the CDL result for on curvature. Using R16 for the constraint, Betoule et al. (2014) for the SNeIa data, and the same BOSS BAO data, Verde et al. (2017b) found, also for a phenomenological parameterization of , that Mpc assuming . This is consistent with our result to within 0.2. When they marginalize over they find Mpc. This is a shift, which indicates that were we to relax our zero curvature assumption, it might have some impact on the significance of our results. We caution against seeing this small shift as possibly leading to a resolution between the CMB and CDL data. To get the full magnitude of this shift requires the curvature to be quite far from zero. The Verde et al. (2017b) constraint on in this analysis is . Such a large value of is highly disfavored by CMB data; in the CDM+ model the Planck temperature and polarization power spectra lead to .
3.2 CDM-based constraints with and without CMB data
We now turn to the model-based determinations of the sound horizon, focusing first on the CDM model results. To examine robustness of sound-horizon determination we show results for many choices of CMB datasets (orange circles in the biggest panel of Fig. 3). We see some scatter in these inferences of , with all of them between 2 and 3 larger than the spline-based CDL result.
A curious feature of the scatter in the CDM results is that those datasets that lead to lower values of , such as using Planck temperature power spectrum (TT) data restricted to (+ lowE), which are thus more discrepant with the CDL value of , also lead to values of that are less discrepant with the CDL, and vice versa. This pattern can be understood as follows. First, recall that the comoving size of the sound horizon is given by Eq. 9, which, in the CDM model depends only on the baryon-to-photon ratio and the matter density . The fluctuations in CDM-based inferences from CMB data are almost entirely driven by fluctuations in . The short explanation for the positive correlation between and fluctuations is that upward fluctuations drive downward, and downward as well.
The positive correlation between and can be understood as follows. If the radiation density were completely negligible for the calculation of the sound horizon, then, from the Friedmann equation, so we have . The radiation softens this response to closer to (Hu et al., 2001). To keep the angular size of the sound horizon fixed (in order to stay at high CMB data likelihood), we have for the distance from here to , . For the model to achieve this softened response of the distance to the matter density (softened to a exponent as opposed to ) there has to be a fluctuation in the dark energy density that is anti-correlated with the matter density fluctuation, with the result that has the same sign from , as also explained in Hou et al. (2014). Perhaps of particular note regarding this positive correlation between and fluctuations, is that those datasets that are somewhat more consistent with the CDL for than is the case for Planck, are less consistent with the CDL for . This is the case for Planck TT (), WMAP9+SPT+ACT (Calabrese et al., 2017), SPT-SZ (Aylor et al., 2017), and SPTpol (Henning et al., 2018). These fluctuations toward higher , if they go far enough to reconcile with R18, end up being discrepant with BAO data (given the CDM model) as noted in Hou et al. (2014).
While the above results indicate robustness to the choice of the CMB data, Addison et al. (2018) have demonstrated that can be estimated, assuming CDM, without any CMB anisotropy data at all. They use a combination of BAO data and constraints on from inferences of the primordial abundance of deuterium relative to hydrogen (D/H) (Cooke et al., 2016). Within CDM is entirely determined by and via Eq. 9. Given the assumption of CDM the BAO data can be used to constrain . This constraining power arises from the degeneracy breaking power of separately parallel and perpendicular constraints at several different redshifts. The primordial D/H ratio resulting from big bang nucleosynthesis (BBN) is highly sensitive to the baryon-to-photon ratio and can therefore be used to estimate . Addison et al. (2018) combine galaxy and Lyman- forest BAO with a precise estimate of the primordial deuterium abundance (Cooke et al., 2016) to find Mpc. The BAO+BBN based is shown in Fig. 3 in purple (rather than orange like CMB) as it relies on BAO data that has also been used for the CDL determination, and whose interpretation is dependent in this case on late-time assumptions of the CDM model. This result, like the CMB-based estimates, is also discrepant with the CDL measured values of .
3.3 Tension in
The tension between these two means of inferring , the CDL measurement vs. the CDM calculation, is the main result of this paper. Cast in terms of , rather than in terms of , it is clear – as the inverse distance ladder approach also suggests – that if the solution to the discrepancies lies in cosmology, we need modifications to cosmology at early times, not late times. We need a model that, given the CMB data, produces a smaller sound horizon. We discuss this further in §4.
3.4 Extensions and Forecasts
An extension of CDM often considered for its possibility of reducing tension is to let the effective number of light and non-interacting degrees of freedom, , be a variable, freed from its CDM value of 3.046. One of the hindrances to adjustment of is that it leads to a change in the ratio of sound horizon to damping scales (Hu & White, 1996; Bashinsky & Seljak, 2004; Hou et al., 2013), a change that is not preferred by CMB data. To loosen up these damping-scale constraints, we also consider allowing the primordial fraction of baryonic mass in Helium, , to be freed from its BBN-consistent value. We see that these extensions do very little, if anything, to relieve the tension with the CDL result. They do increase the uncertainty significantly in , but the uncertainty remains sub-dominant to the CDL uncertainty, so there is not much impact on the significance of the difference.
To give an example of robustness to changes to late-time cosmology, we also show results for the extension to free mean curvature, CDM + . As expected, allowing curvature to float has very little impact, if any, on the inference of .
Next we forecast the expected constraints on to come from a combination of Planck and the final results of the SPT-3G survey that is currently underway. The constraints are presented in Fig. 3 as open circles.
In the CDM + model space the error in will reduce by a factor of 2 compared to Planck-only results. The resulting reduction in follows from this reduction plus reduction in the matter density uncertainty as well. In the CDM + model space the area of the 68% confidence region is reduced by a factor of 2.8 with the inclusion of SPT-3G compared to Planck alone. Because there is no degeneracy between and the improvement of constraint on in the CDM + model space is less dramatic.
We also see that constraints from current CMB data on do not change much with the extension from CDM to CDM+. This is expected as the inference is not sensitive to the distance to the last-scattering surface. This insensitivity to late-time physics was previously noted by Verde et al. (2017a).
4 Cosmological Solutions
The inverse distance ladder papers we cited earlier, and also Poulin et al. (2018), indicate that the combination of BAO and supernova data make a cosmological solution unlikely with changes restricted to . Here we go further and argue that any viable cosmological solution to sound horizon discrepancies is likely to differ significantly from the standard cosmological model in the two decades of scale factor expansion immediately prior to recombination. Changes that are only important earlier cannot reduce the sound horizon significantly. This is because in the standard cosmological model, near the best-fit location in parameter space given Planck data, greater than 95% of is generated in the final two decades of scale factor growth prior to recombination.
What about changes after recombination? These would have to make a fractional change in of where to bring the model values in line with the CDL values. If the changes were only important after recombination, then our calculation is unchanged so we still have so we need . To preserve (which we would need to do to stay at high likelihood given the CMB data; e.g., Pan et al. 2016) we would also need to change the angular-diameter distance to last-scattering by . However, another important length scale for interpretation of CMB data, the comoving size of the horizon at matter-radiation equality, , responds much more rapidly to changes in . We find, assuming CDM, as is appropriate here, and therefore the change in distance required to keep from changing would be 12 times greater than required to keep fixed. We can not make changes to the late-time cosmology, and therefore , that keep both of these angular scales fixed. To make this work, the changes in the post-recombination cosmology would have to introduce new anisotropies that would confuse our inference of and/or . The consistency of the CDM results for (which depend primarily on , which is inferred from ; see, e.g., Section 4 of Planck Collaboration et al. (2017) ) across angular scale argue against this possibility. We find it to be highly unlikely that whatever confuses our interpretation of the TT data (perhaps ISW effects) would also similarly confuse our interpretation of the TT data, as well as our interpretation of other data selections such as TE+lowE.
Our claim in this section, that any viable cosmological solution is likely to include significant changes from CDM in the epoch immediately prior to recombination, is an interesting one, as this is an epoch that we will probe better with improved measurements of CMB polarization (and also temperature on small angular scales). It has this exciting implication: viable cosmological solutions are likely to make predictions that are testable by so-called stage 3 CMB experiments, as well as CMB-S4.
Soon after we posted this paper on the arXiv (and prior to publication) Poulin et al. (2018) appeared on the arXiv. This paper presents a cosmological solution reconciling CMB, BAO, and Cepheid-calibrated supernova data. The solution is consistent with our analysis here: namely it has an early dark energy component contributing significantly in the scale factor window we have just described. It also leads to predictions that appear to be testable by future measurements of CMB polarization.
5 Conclusions
Following Bernal et al. (2016b) we have compared, using more recent data, empirical CDL determination of with its inference assuming the CDM model and given a variety of CMB datasets. Casting the tension between the CDL and CDM + CMB datasets in terms of , as opposed to , weakens the statistical significance, but helps to clarify the space of possible cosmologies that could reconcile these datasets. As the inverse distance ladder analyses have pointed out, modifying the shape of at can at most be a sub-dominant part of the solution.
Because SNe cover the range of redshifts of the BOSS galaxy BAO data, our CDL inferences of are highly model-independent. For the Spline model, which we prefer for this purpose over CDM due to its modest cosmological model assumptions444There is an implicit assumption of zero mean curvature. As discussed above, we expect that if we relaxed this assumption our results would only shift a small amount, as was the case for a similar analysis (Verde et al., 2017b)., from the Cepheid, SNe, and BAO datasets, we find Mpc.
This result is 2.6 lower than the result from Planck TT+TE+EE+lowE (which we have referred to simply as Planck). We calculated the statistical significance of the difference between the CDL result and the CDM + CMB data results for a variety of CMB datasets and found they ranged from 2.1 to 3.0. Perhaps of particular interest, the combination of the highest precision non-Planck data, WMAP9 + SPT-SZ + ACT, gives an that is 3.0 discrepant from the above CDL result. It is clear that the sound horizon differences cannot be explained by an unknown systematic error in the Planck data.
Expanding the model space to CDM + does not reduce the tension of the CDL with the Planck . Although the error bar for the Planck-determined increases considerably, the CDL error remains larger, and the central value for the Planck-determined shifts to a slightly higher value. Expanding further to CDM + only reduces the tension from 2.6 to 2.3. The CMB data have no significant preference for these extensions.
While the CMB data show no preference for those particular extensions, we point out here that there are hints/weak evidence of inconsistencies of the CMB data with the CDM model. Parameter constraints derived from different angular scales, such as the Planck temperature power spectra at compared to , are uncomfortably different, with a statistical significance that varies between 1.5 and 2.9 depending on details of the analysis and how the question of consistency is posed (Addison et al., 2016; Planck Collaboration et al., 2017; Kable et al., 2018). Driven by small angular scales better measured by the South Pole Telescope, there is a 2.1 tension between SPT-SZ determination of cosmological parameters and those from Planck (Aylor et al., 2017). It is possible that these are hints relevant to the sound horizon discrepancy, but current data are not yet clear on the matter, and no model has been discovered, to our knowledge, that both addresses the sound horizon discrepancy and improves CMB internal consistency.
We argued that viable cosmological model solutions are likely to include important changes from CDM in the two decades of scale factor growth prior to recombination. This statement is interesting because it has an exciting implication: significant changes in this time period are likely to lead to consequences observable with near-future precision observations of CMB polarization.
We produced forecasts for one such model adjustment: allowing for to be a free parameter, which directly alters pre-recombination dynamics. We found a three-fold improvement in the constraints on when combining Planck with the SPT-3G (Benson et al., 2014) dataset. Whether or not the solution to the discrepancy is cosmological, we can expect future observations of the CMB from SPT-3G and other future CMB surveys like AdvACT (Henderson et al., 2016); Simons Observatory (The Simons Observatory Collaboration et al., 2018), CMB-S4 (CMB-S4 Collaboration et al., 2016), and PICO (Young et al., 2018), to reveal further clues via their sensitivity to the acoustic dynamics of the plasma.
Appendix A Forecast Inputs
In §3, we presented the expected constraints on that can be achieved by SPT-3G (Benson et al., 2014) for two extensions of the CDM model: CDM+Neff and CDM+Neff+. Here, we describe the inputs for the forecast.
SPT-3G is the third generation millimeter-wave camera on the South Pole Telescope (Carlstrom et al., 2002). SPT-3G commenced operations in early 2018 and is currently observing a 1500 deg2 sky-patch in the Southern hemisphere. It is expected to achieve projected levels of noise in intensity maps of 3.0, 2.2, and 8.8 K-arcmin at 95, 150, and 220 GHz respectively at the end of five years (Bender et al., 2018). A primary goal of this SPT-3G survey is to produce a high signal-to-noise ratio CMB lensing map for delensing the BICEP Array (Hui et al., 2018) observations that overlap with the SPT-3G 1500 deg2 patch. When completed, it will be the deepest high-resolution CMB survey of any patch of this size or larger.
For the Fisher forecast, we use TT, TE, EE, and power spectra as inputs. We construct the covariance matrix assuming the T and E mode maps are fully delensed and therefore not correlated by lensing. To model the noise, we use the projected SPT-3G noise levels ( higher in polarization) to construct a foreground-reduced estimate of using the internal linear combination (ILC) method as described in Raghunathan et al. (2017). We add a knee at for the three channels in T and for channels in P to model large angular scale noise. For the lensing spectrum , we compute the noise with the minimum-variance combination of TT, TE, EE, TE, and EB quadratic estimators (Hu & Okamoto, 2002). We do not model the covariance of the common patch between Planck and SPT-3G because SPT-3G’s patch is much smaller than Planck’s and the high S/N mode coverages for each experiments overlap little.
To include Planck constraints in the forecast we “Fisher-ize” the Planck chain from the relevant parameter space: estimating the parameter covariance matrix from the chain and then inverting it to get the parameter Fisher matrix. We then add this to the SPT-3G Fisher matrix to get our final Fisher matrix. The Planck chains we use are for the data combination TT+TE+EE+lowE as explained in Planck Collaboration VI (2018).
References
- Addison et al. (2016) Addison, G. E., Huang, Y., Watts, D. J., et al. 2016, ApJ, 818, 132. doi: 10.3847/0004-637X/818/2/132. arXiv: 1511.00055
- Addison et al. (2018) Addison, G. E., Watts, D. J., Bennett, C. L., et al. 2018, ApJ, 853, 119. doi: 10.3847/1538-4357/aaa1ed. arXiv: 1707.06547
- Alam et al. (2017) Alam, S., Ata, M., Bailey, S., et al. 2017, MNRAS, 470, 2617. doi: 10.1093/mnras/stx721. arXiv: 1607.03155
- Aubourg et al. (2015) Aubourg, E., Bailey, S., Bautista, J. E., et al. 2015, Phys. Rev. D, 92, 123516. doi: 10.1103/PhysRevD.92.123516. arXiv: 1411.1074
- Aylor et al. (2017) Aylor, K., Hou, Z., Knox, L., et al. 2017, ApJ, 850, 101. doi: 10.3847/1538-4357/aa947b. arXiv: 1706.10286
- Bashinsky & Seljak (2004) Bashinsky, S., & Seljak, U. 2004, Phys. Rev. D, 69, 083002. doi: 10.1103/PhysRevD.69.083002
- Bautista et al. (2017) Bautista, J. E., Busca, N. G., Guy, J., et al. 2017, A&A, 603, A12. doi: 10.1051/0004-6361/201730533. arXiv: 1702.00176
- Bender et al. (2018) Bender, A. N., Ade, P. A. R., Ahmed, Z., et al. 2018, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 10708, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 1070803
- Bennett et al. (2013) Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20. doi: 10.1088/0067-0049/208/2/20. arXiv: 1212.5225
- Benson et al. (2014) Benson, B. A., Ade, P. A. R., Ahmed, Z., et al. 2014, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 9153, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series
- Bernal & Peacock (2018) Bernal, J. L., & Peacock, J. A. 2018, J. Cosmology Astropart. Phys, 7, 002. doi: 10.1088/1475-7516/2018/07/002. arXiv: 1803.04470
- Bernal et al. (2016a) Bernal, J. L., Verde, L., & Cuesta, A. J. 2016a, J. Cosmology Astropart. Phys, 2, 059. doi: 10.1088/1475-7516/2016/02/059. arXiv: 1511.03049
- Bernal et al. (2016b) Bernal, J. L., Verde, L., & Riess, A. G. 2016b, J. Cosmology Astropart. Phys, 10, 019. doi: 10.1088/1475-7516/2016/10/019. arXiv: 1607.05617
- Betoule et al. (2014) Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22. doi: 10.1051/0004-6361/201423413. arXiv: 1401.4064
- Beutler et al. (2011) Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017. doi: 10.1111/j.1365-2966.2011.19250.x. arXiv: 1106.3366
- Birrer et al. (2018) Birrer, S., Treu, T., Rusu, C. E., et al. 2018, ArXiv e-prints. arXiv: 1809.01274
- Calabrese et al. (2017) Calabrese, E., Hložek, R. A., Bond, J. R., et al. 2017, Phys. Rev. D, 95, 063525. doi: 10.1103/PhysRevD.95.063525. arXiv: 1702.03272
- Cardona et al. (2017) Cardona, W., Kunz, M., & Pettorino, V. 2017, J. Cosmology Astropart. Phys, 3, 056. doi: %****␣DiscordantSounds.bbl␣Line␣175␣****10.1088/1475-7516/2017/03/056. arXiv: 1611.06088
- Carlstrom et al. (2002) Carlstrom, J. E., Holder, G. P., & Reese, E. D. 2002, ARA&A, 40, 643
- Chiang & Slosar (2018) Chiang, C.-T., & Slosar, A. 2018, ArXiv e-prints, arXiv:1811.03624. arXiv: 1811.03624
- CMB-S4 Collaboration et al. (2016) CMB-S4 Collaboration, Abazajian, K. N., Adshead, P., et al. 2016, ArXiv e-prints. arXiv: 1610.02743
- Cooke et al. (2016) Cooke, R. J., Pettini, M., Nollett, K. M., & Jorgenson, R. 2016, ApJ, 830, 148. doi: 10.3847/0004-637X/830/2/148. arXiv: 1607.03900
- Cuesta et al. (2015) Cuesta, A. J., Verde, L., Riess, A., & Jimenez, R. 2015, MNRAS, 448, 3463. doi: 10.1093/mnras/stv261. arXiv: 1411.1094
- Delubac et al. (2015) Delubac, T., Bautista, J. E., Busca, N. G., et al. 2015, A&A, 574, A59. doi: 10.1051/0004-6361/201423969. arXiv: 1404.1801
- DES Collaboration et al. (2017) DES Collaboration, Abbott, T. M. C., Abdalla, F. B., et al. 2017, ArXiv e-prints. arXiv: 1708.01530
- Di Valentino et al. (2017) Di Valentino, E., Melchiorri, A., & Mena, O. 2017, Phys. Rev. D, 96, 043503, doi: 10.1103/PhysRevD.96.043503
- Di Valentino et al. (2016) Di Valentino, E., Melchiorri, A., & Silk, J. 2016, Physics Letters B, 761, 242, doi: 10.1016/j.physletb.2016.08.043
- du Mas des Bourboux et al. (2017) du Mas des Bourboux, H., Le Goff, J.-M., Blomqvist, M., et al. 2017, A&A, 608, A130. doi: 10.1051/0004-6361/201731731. arXiv: 1708.02225
- Efstathiou et al. (2014) Efstathiou, A., Pearson, C., Farrah, D., et al. 2014, MNRAS, 437, L16. doi: 10.1093/mnrasl/slt131. arXiv: 1309.7005
- Evslin et al. (2018) Evslin, J., Sen, A. A., & Ruchika. 2018, Phys. Rev. D, 97, 103511, doi: 10.1103/PhysRevD.97.103511
- Feeney et al. (2018a) Feeney, S. M., Mortlock, D. J., & Dalmasso, N. 2018a, MNRAS, 476, 3861. doi: 10.1093/mnras/sty418. arXiv: 1707.00007
- Feeney et al. (2018b) Feeney, S. M., Peiris, H. V., Williamson, A. R., et al. 2018b, ArXiv e-prints. arXiv: 1802.03404
- Follin & Knox (2018) Follin, B., & Knox, L. 2018, MNRAS, 477, 4534. doi: 10.1093/mnras/sty720. arXiv: 1707.01175
- Font-Ribera et al. (2014) Font-Ribera, A., Kirkby, D., Busca, N., et al. 2014, J. Cosmology Astropart. Phys, 5, 027. doi: 10.1088/1475-7516/2014/05/027. arXiv: 1311.1767
- Hatt et al. (2018a) Hatt, D., Freedman, W. L., Madore, B. F., et al. 2018a, ApJ, 861, 104. doi: 10.3847/1538-4357/aac9cc. arXiv: 1806.02900
- Hatt et al. (2018b) —. 2018b, ApJ, 866, 145. doi: 10.3847/1538-4357/aadfe8. arXiv: 1809.01741
- Heavens et al. (2014) Heavens, A., Jimenez, R., & Verde, L. 2014, Physical Review Letters, 113, 241302. doi: 10.1103/PhysRevLett.113.241302. arXiv: 1409.6217
- Henderson et al. (2016) Henderson, S. W., Allison, R., Austermann, J., et al. 2016, Journal of Low Temperature Physics, 184, 772. doi: 10.1007/s10909-016-1575-z. arXiv: 1510.02809
- Henning et al. (2018) Henning, J. W., Sayre, J. T., Reichardt, C. L., et al. 2018, ApJ, 852, 97. doi: 10.3847/1538-4357/aa9ff4. arXiv: 1707.09353
- Hou et al. (2013) Hou, Z., Keisler, R., Knox, L., Millea, M., & Reichardt, C. 2013, Phys. Rev. D, 87, 083008. doi: 10.1103/PhysRevD.87.083008. arXiv: 1104.2333
- Hou et al. (2014) Hou, Z., Reichardt, C. L., Story, K. T., et al. 2014, ApJ, 782, 74. doi: 10.1088/0004-637X/782/2/74. arXiv: 1212.6267
- Hou et al. (2018) Hou, Z., Aylor, K., Benson, B. A., et al. 2018, ApJ, 853, 3. doi: 10.3847/1538-4357/aaa3ef. arXiv: 1704.00884
- Hu et al. (2001) Hu, W., Fukugita, M., Zaldarriaga, M., & Tegmark, M. 2001, ApJ, 549, 669
- Hu & Okamoto (2002) Hu, W., & Okamoto, T. 2002, ApJ, 574, 566
- Hu & Sugiyama (1996) Hu, W., & Sugiyama, N. 1996, ApJ, 471, 542. doi: 10.1086/177989
- Hu & White (1996) Hu, W., & White, M. 1996, ApJ, 471, 30
- Hui et al. (2018) Hui, H., Ade, P. A. R., Ahmed, Z., et al. 2018, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 10708, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 1070807
- Jang & Lee (2017) Jang, I. S., & Lee, M. G. 2017, ApJ, 835, 28. doi: 10.3847/1538-4357/835/1/28. arXiv: 1611.05040
- Joudaki et al. (2018) Joudaki, S., Kaplinghat, M., Keeley, R., & Kirkby, D. 2018, Phys. Rev. D, 97, 123501. doi: 10.1103/PhysRevD.97.123501. arXiv: 1710.04236
- Joudaki et al. (2017) Joudaki, S., Blake, C., Heymans, C., et al. 2017, MNRAS, 465, 2033. doi: 10.1093/mnras/stw2665. arXiv: 1601.05786
- Kable et al. (2018) Kable, J. A., Addison, G. E., & Bennett, C. L. 2018, ArXiv e-prints. arXiv: 1809.03983
- Karwal & Kamionkowski (2016) Karwal, T., & Kamionkowski, M. 2016, Phys. Rev. D, 94, 103523, doi: 10.1103/PhysRevD.94.103523
- Lemos et al. (2018) Lemos, P., Lee, E., Efstathiou, G., & Gratton, S. 2018, ArXiv e-prints. arXiv: 1806.06781
- Lin et al. (2018) Lin, M.-X., Raveri, M., & Hu, W. 2018, ArXiv e-prints. arXiv: 1810.02333
- Lindegren et al. (2018) Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2. doi: 10.1051/0004-6361/201832727. arXiv: 1804.09366
- Louis et al. (2016) Louis, T., Grace, E., Hasselfield, M., et al. 2016, ArXiv e-prints. arXiv: 1610.02360
- Millea (2017) Millea, M. 2017, CosmoSlik: Cosmology sampler of likelihoods, Astrophysics Source Code Library. http://ascl.net/1701.004
- Pan et al. (2016) Pan, Z., Knox, L., Mulroe, B., & Narimani, A. 2016, MNRAS, 459, 2513. doi: 10.1093/mnras/stw833. arXiv: 1603.03091
- Percival et al. (2010) Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148. doi: 10.1111/j.1365-2966.2009.15812.x. arXiv: 0907.1660
- Planck Collaboration et al. (2014) Planck Collaboration, Ade, P. A. R., Aghanim, N., et al. 2014, A&A, 571, A1. doi: 10.1051/0004-6361/201321529. arXiv: 1303.5062
- Planck Collaboration et al. (2016) Planck Collaboration, Aghanim, N., Arnaud, M., et al. 2016, A&A, 594, A11. doi: 10.1051/0004-6361/201526926. arXiv: 1507.02704
- Planck Collaboration et al. (2017) Planck Collaboration, Aghanim, N., Akrami, Y., et al. 2017, A&A, 607, A95. doi: 10.1051/0004-6361/201629504. arXiv: 1608.02487
- Planck Collaboration VI (2018) Planck Collaboration VI. 2018, ArXiv e-prints. arXiv: 1807.06209
- Planck Collaboration XVI (2014) Planck Collaboration XVI. 2014, A&A, 571, A16. doi: %****␣DiscordantSounds.bbl␣Line␣575␣****10.1051/0004-6361/201321591. arXiv: 1303.5076
- Poulin et al. (2018) Poulin, V., Boddy, K. K., Bird, S., & Kamionkowski, M. 2018, Phys. Rev. D, 97, 123504. doi: 10.1103/PhysRevD.97.123504. arXiv: 1803.02474
- Raghunathan et al. (2017) Raghunathan, S., Patil, S., Baxter, E. J., et al. 2017, J. Cosmology Astropart. Phys, 8, 030. doi: 10.1088/1475-7516/2017/08/030. arXiv: 1705.00411
- Riess et al. (2018a) Riess, A. G., Casertano, S., Kenworthy, D., Scolnic, D., & Macri, L. 2018a, ArXiv e-prints. arXiv: 1810.03526
- Riess et al. (2009) Riess, A. G., Macri, L., Casertano, S., et al. 2009, ApJ, 699, 539. doi: 10.1088/0004-637X/699/1/539. arXiv: 0905.0695
- Riess et al. (2011) —. 2011, ApJ, 730, 119. doi: 10.1088/0004-637X/730/2/119. arXiv: 1103.2976
- Riess et al. (2016) Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56. doi: 10.3847/0004-637X/826/1/56. arXiv: 1604.01424
- Riess et al. (2018b) Riess, A. G., Casertano, S., Yuan, W., et al. 2018b, ArXiv e-prints. arXiv: 1804.10655
- Ross et al. (2015) Ross, A. J., Samushia, L., Howlett, C., et al. 2015, MNRAS, 449, 835. doi: 10.1093/mnras/stv154. arXiv: 1409.3242
- Scolnic et al. (2018) Scolnic, D. M., Jones, D. O., Rest, A., et al. 2018, ApJ, 859, 101. doi: 10.3847/1538-4357/aab9bb. arXiv: 1710.00845
- Shanks et al. (2018a) Shanks, T., Hogarth, L., & Metcalfe, N. 2018a, ArXiv e-prints. arXiv: 1810.02595
- Shanks et al. (2018b) —. 2018b, ArXiv e-prints. arXiv: 1810.07628
- Suyu et al. (2017) Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590. doi: 10.1093/mnras/stx483. arXiv: 1607.00017
- The Simons Observatory Collaboration et al. (2018) The Simons Observatory Collaboration, Ade, P., Aguirre, J., et al. 2018, ArXiv e-prints. arXiv: 1808.07445
- Verde et al. (2017a) Verde, L., Bellini, E., Pigozzo, C., Heavens, A. F., & Jimenez, R. 2017a, J. Cosmology Astropart. Phys, 4, 023. doi: 10.1088/1475-7516/2017/04/023. arXiv: 1611.00376
- Verde et al. (2017b) Verde, L., Bernal, J. L., Heavens, A. F., & Jimenez, R. 2017b, MNRAS, 467, 731. doi: 10.1093/mnras/stx116. arXiv: 1607.05297
- Wu & Huterer (2017) Wu, H.-Y., & Huterer, D. 2017, MNRAS, 471, 4946. doi: 10.1093/mnras/stx1967. arXiv: 1706.09723
- Young et al. (2018) Young, K., Alvarez, M., Battaglia, N., et al. 2018, ArXiv e-prints. arXiv: 1808.01369
- Zhang et al. (2017) Zhang, B. R., Childress, M. J., Davis, T. M., et al. 2017, MNRAS, 471, 2254. doi: 10.1093/mnras/stx1600. arXiv: 1706.07573