Source-only realizations, weakly reversible deficiency one networks and dynamical equivalence
Abstract
Reaction networks can display a wide array of dynamics. However, it is possible for different reaction networks to display the same dynamics. This phenomenon is called dynamical equivalence and makes network identification a hard problem to solve. We show that to find a strongly endotactic, endotactic, consistent, or conservative realization that is dynamically equivalent to the mass-action system generated by a given network, it suffices to consider only the source vertices of the given network. In addition, we show that weakly reversible deficiency one realizations are not unique. We also present a characterization of the dynamical relationships that exist between several types of weakly reversible deficiency one networks.
1 Introduction
It is in general difficult to analyze the dynamics exhibited by nonlinear systems. They can exhibit a wide range of behaviour ranging from periodicity, chaos, limit cycles etc. One way of analyzing dynamical systems is to represent them as reaction networks. Reaction networks are ubiquitous in biological systems. The dynamics generated by reaction networks often assume polynomial or power-law form. A key feature here is how the graphical structure of the reaction network regulates its dynamics. Such graphical properties include but are not limited to weak reversibility, complex balancing, endotacticity etc. Reaction networks possessing these properties are conjectured to to exhibit dynamical properties like persistence (which implies that no species can go extinct), permanence (which implies convergence to a compact set) and the existence of a globally attracting steady state.
It turns out that there exists networks with different graphical structures that exhibit the same dynamics. This property is called dynamical equivalence and makes the problem of network identification difficult. Dynamical equivalence has also been called “macro-equivalence” by Horn and Jackson [22] and “confoundability” by Craciun and Pantea [10]. A natural application is to infer the dynamics of networks that do not possess properties like weak reversibility or endotacticity, but are dynamically equivalent to weakly reversible or endotactic networks. A large body of literature exists on designing efficient algorithms for detecting weakly reversible or endotactic realizations, given a dynamical system and a set of source vertices. One of our contributions in this paper is to give an upper bound on the number of source vertices required for detecting certain families of reaction networks.
Another quantity that is useful in the analysis of reaction networks is the deficiency of the reaction network. Informally, deficiency is a measure of how far the reaction vectors in the network are from their general position. In particular, weakly reversible deficiency zero reaction networks exhibit robust dynamics. It is known that for weakly reversible deficiency zero reaction networks, there exists a Lyapunov function. In addition, there exists a unique steady state that is locally asymptotically stable [22]. Recently, it was shown [8] that weakly reversible deficiency zero realizations are unique, i.e., there cannot exist two different weakly reversible deficiency zero networks that generate the same dynamical system. Further, an algorithm has been proposed to check whether a weakly reversible deficiency zero realization exists given a dynamical system and a set of source vertices [6]. A natural extension is to ask whether weakly reversible deficiency one realizations are unique. We show that the answer to this question is no. Another question worth exploring is to analyze the property of dynamical equivalence between different types of weakly reversible deficiency one networks, and between weakly reversible deficiency one and weakly reversible deficiency zero networks. We attempt to answer these questions in this paper.
Our paper is organized as follows: In Section 2 we give a short primer on reaction networks. More specifically we introduce reaction networks as graphs embedded in Euclidean space. We define weakly reversible, strongly endotactic, endotactic, consistent and conservative networks. In Section 3 we introduce net vectors and ghost vertices. The idea of network corresponds to the net flux out a vertex. A ghost vertex is a source vertex whose net vector is zero. We will use both these notions later in the paper to prove results about source-only realizations and dynamical equivalence between different families of reaction networks. In Section 4 we define the notion of dynamical equivalence. We show in Lemma 4.3 that two dynamically equivalent weakly reversible or strongly endotactic realizations have the stoichiometric subspace. In Section 5 in Theorem 5.4 we show that certain families of reaction networks possess the following property: A mass-action system is dynamically equivalent to a mass-action system generated by networks from this family iff it is dynamically equivalent to a mass-action system generated by networks from this family that uses only the source vertices of . The family of such networks include weakly reversible, consistent, endotactic and strongly endotactic networks. Section 6 deals with the uniqueness and non-uniqueness of realizations. In particular, we show that weakly reversible deficiency one realizations are not unique, i.e., there exists different weakly reversible deficiency one networks that generate the same dynamics. In Theorem 6.3 we show that two weakly reversible deficiency one realizations with the property that one realization has all linkage classes of deficiency zero and the other realization has all linkage classes of deficiency zero except one which has deficiency one, cannot be dynamically equivalent.
2 Reaction Networks
Reaction networks can be characterized as directed graphs in Euclidean space called Euclidean embedded graphs [4, 5, 11, 3]. In particular, a reaction network is a tuple , where is the set of vertices (that correspond to complexes) and is the set of edges (that correspond to reactions). An edge corresponds to a reaction . Here is the source vertex and is the target vertex.
The stoichiometric subspace corresponding to a reaction network is given by the set . Given , the stoichiometric compatibility class of is the polyhedron .
A linkage class is a maximal connected component of . The deficiency of a reaction is the non-negative integer , given by the formula , where is the number of vertices, is the number of linkage classes and is the dimension of the stoichiometric subspace. Let denote the set of source vertices and let denote the convex hull of the source vertices of . Then
-
•
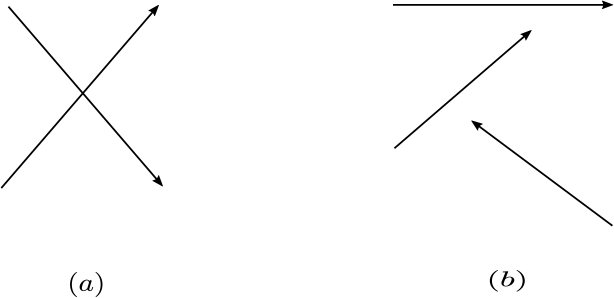
is weakly reversible if every reaction is part of a strongly connected component.
-
•
is strongly endotactic [15] if for every vector and with , there exists such that , and for all .
-
•
is endotactic [9] if for every vector and with , there exists such that , .
-
•
is consistent if there exists positive constants such that .
-
•
is conservative if there exists a vector such that .
Figure 2 shows a few examples of such networks.
The chain of inclusions among the above mentioned networks is as follows: Weakly reversible networks consisting of a single linkage class are strongly endotactic. Weakly reversible networks networks are endotactic. Strongly endotactic networks are also endotactic. Further endotactic networks are consistent. It is possible for a network to be
-
(i)
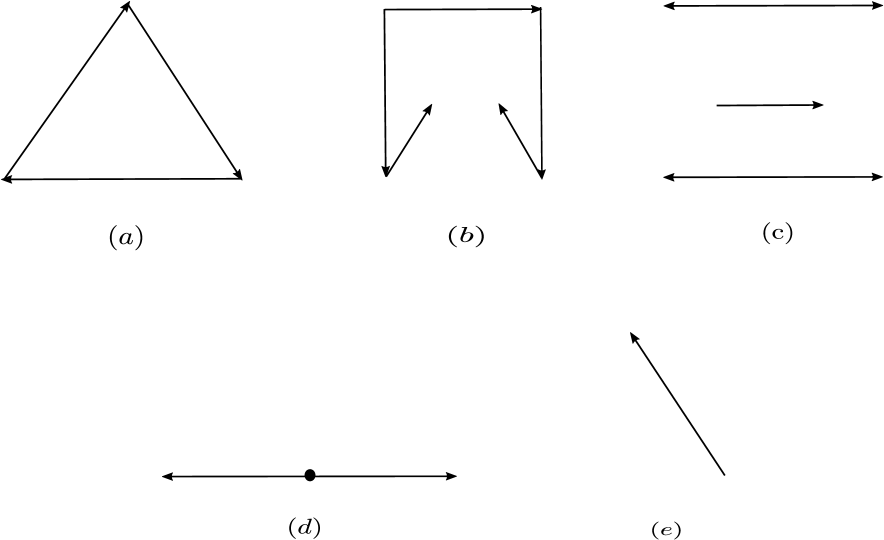
consistent, but not conservative
-
(ii)
conservative, but not consistent.
-
(iii)
consistent and conservative
-
(iv)
neither consistent nor conservative.
Figure 3 gives examples of networks that are of the four types mentioned above.
Conservative networks are also related to the notion of critical sets, which are relevant in the context of autocatalysis [12, 18, 19, 20]. It can be shown that if a network is conservative, then the set of species is not a critical set [12]. Critical sets also show up in the context of persistence; it is known that if there are no critical siphons in the network, then the dynamics exhibited by it is persistent [2].
It turns out that there is a geometrically intuitive way to deduce whether the network is endotactic or strongly endotactic. This is given by the parallel sweep test [9, 15]. The parallel sweep test for strongly endotactic networks can be summarized as follows [15]
Proposition 2.1.
Let be a reaction network. For every , we sweep with a hyperplane perpendicular to in the direction of until it hits the boundary of . Let denote this supporting hyperplane. On , if all reactions with source vertex satisfy and there exists a reaction such that , then the network passes the parallel sweep test, i.e., the network is strongly endotactic. If the network fails to satisfy the parallel sweep test, it is not strongly endotactic.
The parallel sweep test for endotactic networks can be summarized as follows [9]
Proposition 2.2.
Let be a reaction network. For every , we sweep with a hyperplane perpendicular to in the direction of until it hits the boundary of . On , check if all reactions with source vertex satisfy . If yes, and there exists a reaction such that , then the network passes the parallel sweep test, i.e., the network is endotactic. If there exists a reaction with such that , then the network fails to satisfy the parallel sweep test, i.e., it is not strongly endotactic. If we have for all reactions with source vertex , then continue sweeping with the hyperplane until you hit another source vertex and repeat the same steps as above. If you continue sweeping with the hyperplane and have covered all source vertices, then the network passes the parallel sweep test and the network is strongly endotactic.
A reaction network can generate a wide array of dynamical systems. If we assume mass-action kinetics [13, 31, 16, 32, 17, 1], the dynamical system generated by is given by
| (1) |
Let us denote vector of rate constants in this dynamical system by . Then the associated mass-action system will be represented as . A mass-action system is complex balanced if there exists a point such that for any vertex , we have
| (2) |
As remarked before, graphical properties like weak reversbility, endotacticity and complex balancing are closely related to dynamical properties like persistence, permanence and global stability. Anderson has proved the Global Attractor Conjecture, which says that complex balanced systems have a globally attracting steady state within every stoichiometric compatibility class when the associated reaction graph consists of a single linkage class. It is know from the work of Craciun, Nazarov and Pantea [9] that two-dimensional endotactic networks are permanent. This has been extended by Pantea [24] to endotactic networks with two-dimensional subspace. Gopalkrishnan, Miller and Shiu [15] have shown that strongly endotactic networks are permament. Recently, Craciun [4] has proposed a proof of the Global Attractor Conjecture.
3 Net vectors and Ghost vertices
The idea of this section is to introduce the notions of net vectors and ghost vertices, which will be used later in the paper to analyze the dynamics of several families of networks. The dynamical system generated by (given by Equation 1) can be rewritten as
| (3) |
Then will denote the net vector corresponding to the source vertex .
Remark 3.1.
Note that the net vector corresponding to the source vertex may consist of terms like where . In such cases, we set .
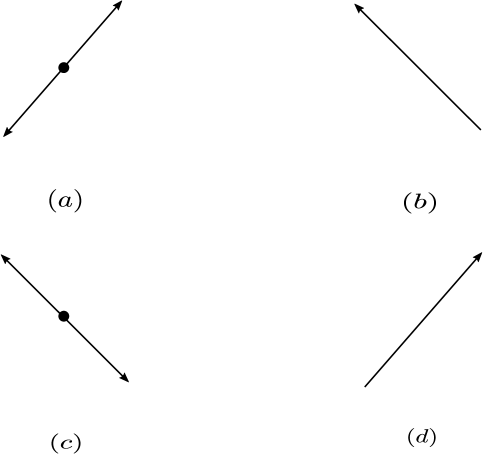
If the net reaction vector corresponding to a source vertex is zero, then will be called a ghost vertex. Previous works [7] have referred to such vertices as virtual sources. Figure 4 shows an example of a ghost vertex.
Theorem 3.2.
Consider a reaction network with deficiency . Then can have at most ghost vertices.
Proof.
For contradiction, assume that has ghost vertices where . By Remark 5.3, applying the procedure in [8][Theorems 4.8 and 4.12] times gives a reaction network of deficiency and ghost vertices, which is not possible.
∎
Corollary 3.3.
Consider a reaction network with deficiency . Then cannot have any ghost vertices.
Proof.
Follows from Theorem 3.2. ∎
Lemma 3.4.
Consider a strongly endotactic mass-action system . Let denote the net reaction vectors of . Define a matrix with as its columns. Then,
-
(i)
.
-
(ii)
If is deficiency zero, then any reaction vectors from the set are linearly independent.
Proof.
-
(i)
Note that . For contradiction, suppose that . Then there exists a vector that is orthogonal to . Now project all the source vertices on , i.e. consider the set . Let denote the set of source vertices that maximizes the dot product in . Since the network is strongly endotactic, there exists a reaction with source vertex from to a target vertex not in . Let be this reaction. This implies that .
Note that for . This gives us , contradicting that is orthogonal to .
-
(ii)
Since is a strongly endotactic mass-action system, it has a steady state say [15][Corollary 8.12]. This gives us the following equation
(4) Since , from Lemma 3.4.(i) we have . This gives . Note that the vector has positive coefficients. This implies that any reaction vectors of are linearly independent.
∎
4 Dynamical Equivalence
Associated with every reaction network is a dynamical system. However, it is possible for two different reaction networks to generate the same dynamical system. This phenomenon is called dynamical equivalence. It is also referred to as macro-equivalence [22] or confoundability [10]. We formally define the notion of dynamical equivalence below.
Definition 4.1.
Consider two mass-action systems and . Then and are said to be dynamically equivalent if the following holds true for all :
| (5) |
Remark 4.2.
It is clear from Definition 4.1 that two mass-action systems are dynamically equivalent iff they have the same set of net reaction vectors.
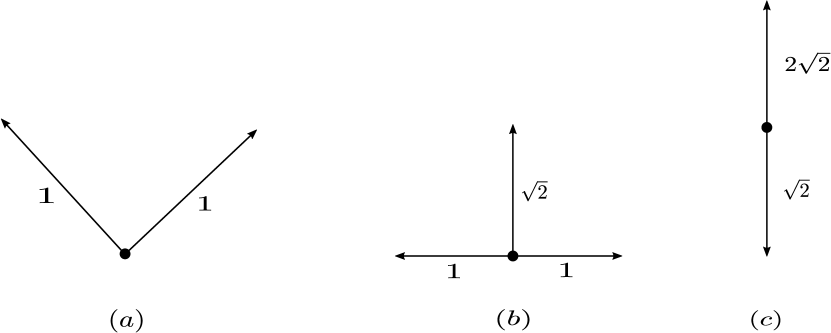
Figure 5 shows a a few examples of dynamically equivalent networks.
Dynamical systems generated by reaction networks are also sometimes referred to as realizations. The next lemma collects a useful observation about the stoichiometric subspaces of dynamically equivalent weakly reversible reaction networks.
Lemma 4.3.
Let and be two dynamically equivalent weakly reversible (strongly endotactic) realizations. Then .
Proof.
Since and are two dynamically equivalent weakly reversible (strongly endotactic) realizations, they have the same set of net reaction vectors (neglecting the ghost vertices). Since both these realizations are weakly reversible (strongly endotactic), by Lemma 3.4 or Remark 3.5, we get that and the result follows. ∎
Remark 4.4.
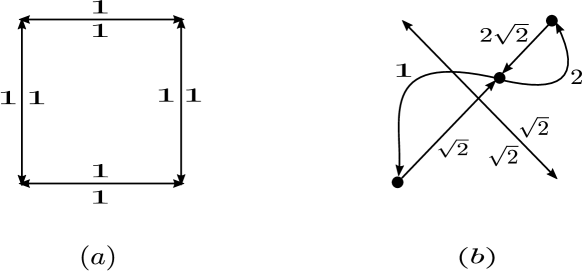
Note that two dynamically equivalent weakly reaction networks with the same deficiency may not have the same number of vertices or linkage classes. Figure 6 illustrates this point.
5 Source-only realizations
Network identification is a challenging problem in general due to the phenomenon of dynamical equivalence. However, certain properties of the network like complex balancing, weak reversibility are often required to design efficient systems [23, 30]. There exists a large body of work that design algorithms for detecting properties like weak reversibility, complex balancing or for finding dense realization, i.e., realizations that have the maximum number of reactions. Many of these approaches use techniques like linear and mixed linear integer programming to perform a constrained optimization [30, 26, 27, 25]. In such approaches, the set of source vertices is part of the input search space over which the optimization is performed. Previous works [28, 29, 7] have shown that to deduce whether a detailed balanced, complex balanced or weakly reversible realizations exists, it suffices to check over the space of input source vertices. In our paper, we show that this property extends to endotactic, strongly endotactic, consistent and conservative networks. Theorem 5.4 illustrates this point.
Before we move to Theorem 5.4, we recall the following lemma from linear algebra which will be used in the context of consistent networks.
Lemma 5.1.
(Steimke’s theorem) Let . Then exactly one the following is true
-
(i)
There exists constants such that .
-
(ii)
There exists a vector such that for all and for some .
Theorem 5.2.
Let be a reaction network such that . Then is consistent.
Proof.
For contradiction, assume that is not consistent. By Lemma 5.1, there exists a vector such that for all and for some . Note that for any . Since , we have or equivalently , a contradiction.
∎
Remark 5.3.
Using [8] 4.8 and 4.12], we get the following: Consider a dynamical system generated by a weakly reversible deficiency zero network. Then the exponents of the monomials in are the same as the vertices of the network. In particular, [8][Theorems 4.8 and 4.12] gives a procedure to decrease both deficiency and number of vertices of the reaction network by one, whilst maintaining dynamical equivalence.
Theorem 5.4.
Choose a property from among the following:
-
(i)
Strongly endotactic.
-
(ii)
Endotactic.
-
(iii)
Consistent.
-
(iv)
Conservative.
Consider a mass-action system . Then, is dynamically equivalent to a mass-action system having property if and only if it is dynamically equivalent to a mass-action system having property that uses only the source vertices of .
Proof.
-
(i)
We will first prove when the property is strongly endotactic. We will prove the contrapositive, i.e., if we have a mass-action system that is not strongly endotactic, then adding a ghost source vertex to this network still implies that the resultant network is not strongly endotactic. If lies inside the convex hull of the source vertices of , then the resultant network is not strongly endotactic since the network was not strongly endotactic to begin with. Note that if lies outside the convex hull of the source vertices of , then lies on the boundary of the convex hull of the source vertices of the resultant network. Since is a ghost vertex, the resultant network is not strongly endotactic.
-
(ii)
The proof when property is endotactic is exactly same as the proof when property is strongly endotactic.
-
(iii)
We will prove when the property is consistent. Keep on adding reaction vectors (oppositely oriented two at a time) to so that . By Theorem 5.2, we get that is consistent.
-
(iv)
We will prove when the property is conservative. Since is conservative, there exists a positive vector that is orthogonal to the stoichiometric subspace . Removing the ghost vertex generates a network with stoichiometric subspace . Therefore, we still have the positive vector that is orthogonal to , implying that it is conservative.
∎
6 Uniqueness/Non-uniqueness of realizations
As remarked before, realizations of reaction networks may not be unique due to the property of dynamical equivalence. However, under certain restrictions on the reaction network structure, one can show that the realization is unique. For example in [8], Craciun et. al. showed that weakly reversible deficiency one realizations are unique. Weakly reversible deficiency zero networks form an important class of reaction networks given the rich dynamics that they exhibit. Weakly reversible deficiency zero reaction networks are known to be complex balanced for all values of the rate constants [21]. The property of being complex balanced implies that there exists a Lyapunov function that decreases along trajectories; further there exists a unique equilibria in each stoichiometric compatibility class which is locally asymptotically stable [22]. In the language of Feinberg [14], the dynamical system is quasi-thermodynamic.
Theorem 6.1 (Deficiency zero theorem).
[21] A mass-action system is complex balanced for all values of iff it is weakly reversible and has a deficiency of zero.
Note that it follows from the deficiency zero theorem that for a deficiency zero network that is not weakly reversible, there exists no positive equilibrium for all choices of . In other words, a consistent deficiency zero reaction network is weakly reversible. Since weakly reversible deficiency zero realizations are unique [8], this implies that consistent deficiency zero realizations are unique.
A natural extension is to ask the following question: “Are weakly reversible deficiency one realizations unique?” We show that the answer to this question is no in general, i.e., weakly reversible deficiency one realizations are not unique.
A network with deficiency one can be classified into the following three types:
-
(i)
All linkages classes of deficiency zero.
-
(ii)
One linkage of deficiency one.
-
(iii)
One linkage of deficiency one and the remaining linkage classes of deficiency zero.
It is interesting to see the interplay of dynamical equivalence between the above mentioned cases in the context of weakly reversible deficiency one networks; and also the relationship between the dynamics of weakly reversible deficiency zero and deficiency one networks.
Figure 7 shows an example of two dynamically equivalent weakly reversible networks that have deficiency one and each of them consists of two linkage classes of deficiency zero.
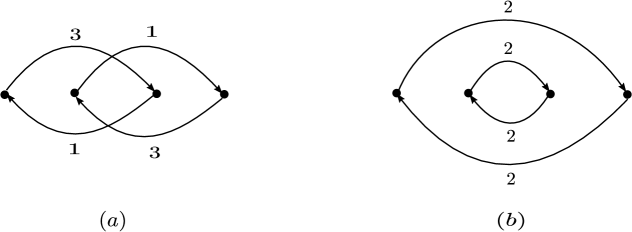
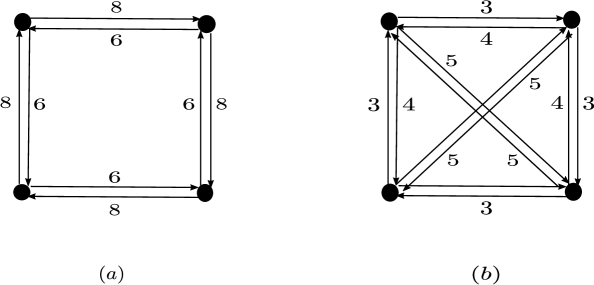
Figure 8 shows an example of two dynamically equivalent weakly reversible networks that have deficiency one and each of them consists of a single linkage class.
One can also generate examples of reaction networks consisting of different number of linkage classes. Figure 9.(a) shows a weakly reversible network of deficiency zero having two linkage classes. This is dynamically equivalent to the network in Figure 9.(b) which is a weakly reversible network of deficiency one having one linkage class.
In Theorem 6.3, we show that two reaction networks having a deficiency of one (one reaction network whose linkage classes have deficiency zero and another reaction network whose linkage classes all of deficiency zero except one which has deficiency one) and same number of linkages cannot be dynamically equivalent. Towards this, we need a result from [8] as the next remark states.
Remark 6.2.
The following is known from Lemma 3.10 in [8]: If the vertices of a weakly reversible deficiency zero reaction network consisting of a single linkage class are split between multiple linkage classes of another reaction network , then the stoichiometric subspaces of the linkage classes of are not linearly independent.
Theorem 6.3.
Consider two weakly reversible mass-action systems and having a deficiency of one and the same number of linkage classes. Let the linkage classes of be all of deficiency zero. Let the linkage classes of be all of deficiency zero except one which has deficiency one. Then and cannot be dynamically equivalent.
Proof.
For contradiction, assume that and are dynamically equivalent. Note that by Lemma 4.3, and have the same stoichiometric subspace. Since they have the same deficiency and the same number of linkage classes, they have the same number of vertices. We now claim that they have the same set of vertices. Note that each linkage class has deficiency zero. By Corollary 3.3, has no ghost vertex. Since the monomials in a dynamical system are linearly independent, and have the same set of vertices.
Note that the stoichiometric subspaces of the linkage classes of are linearly independent. Further, since the number of linkage classes in and are the same, there exists a deficiency zero linkage class in that has vertices split between multiple linkage classes of . By Remark 6.2, this implies that the stoichiometric subspaces of the linkage classes of cannot be linearly independent, a contradiction. ∎
7 Discussion
Network identification is an important problem in the analysis of biological systems. The property of dynamical equivalence makes the problem of network identification quite difficult. Identifying a particular type of realization like weakly reversible or endotactic given a dynamical system and a set of source vertices places no premature bound on the number of vertices in the network. In this paper, we show that to identify a strongly endotactic, endotactic, consistent or conservative realizations, it suffices to consider only the given source vertices. This builds upon earlier work by Craciun, Jin and Yu [7], who showed that this property is true for detailed balanced, complex balanced and weakly reversible realizations.
In addition, we have studied the uniqueness/non-uniqueness of realizations for weakly reversible networks having low deficiency. In particular, we show that weakly reversible deficiency one realizations are not unique. This builds upon earlier work by Craciun, Jin and Yu [8] who showed that weakly reversible deficiency zero realizations are unique. Further, we have tried to characterize the dynamical relationships between several types of weakly reversible deficiency one networks. In particular, Theorem 6.3 says that two weakly reversible deficiency one realizations such that one realization has all linkage classes of deficiency zero and the other realization has all linkage classes of deficiency zero except one which has deficiency one, cannot be dynamically equivalent.
A future line of research is to extend the set of inclusions obtained among several types of deficiency one networks in the context of dynamical equivalence to networks of higher deficiency. Another direction worthy of exploration is to design efficient algorithms to detect weakly reversible networks of high deficiency.
8 Acknowledgements
I thank Gheorghe Craciun for useful discussions and suggestions for improving the presentation of the paper.
References
- [1] L. Adleman, M. Gopalkrishnan, M. Huang, P. Moisset, and D. Reishus, On the mathematics of the law of mass action, A Systems Theoretic Approach to Systems and Synthetic Biology I: Models and System Characterizations, Springer, 2014, pp. 3–46.
- [2] D. Angeli, P. Leenheer, and E. Sontag, A petri net approach to persistence analysis in chemical reaction networks, Biology and Control Theory: Current Challenges, Springer, 2007, pp. 181–216.
- [3] C. Craciun, A. Deshpande, and J. Yeon, Quasi-toric differential inclusions, Discrete and Continuous Dynamical Systems - B 26 (2021), no. 5, 2343–2359.
- [4] G. Craciun, Toric differential inclusions and a proof of the global attractor conjecture, arXiv preprint arXiv:1501.02860 (2015).
- [5] , Polynomial dynamical systems, reaction networks, and toric differential inclusions, SIAM J. Appl. Algebra Geom. 3 (2019), no. 1, 87–106.
- [6] G. Craciun, J. Jin, and P. Yu, An algorithm for weakly reversible deficiency zero realizations of polynomial dynamical systems, In preparation.
- [7] , An efficient characterization of complex-balanced, detailed-balanced, and weakly reversible systems, SIAM J. Appl. Math. 80 (2020), no. 1, 183–205.
- [8] , Uniqueness of weakly reversible and deficiency zero realizations of dynamical systems, Math. Biosci. 342 (2021), 108720.
- [9] G. Craciun, F. Nazarov, and C. Pantea, Persistence and permanence of mass-action and power-law dynamical systems, SIAM J. Appl. Math. 73 (2013), no. 1, 305–329.
- [10] G. Craciun and C. Pantea, Identifiability of chemical reaction networks, J. Math. Chem. 44 (2008), no. 1, 244–259.
- [11] Gheorghe Craciun and Abhishek Deshpande, Endotactic networks and toric differential inclusions, SIAM Journal on Applied Dynamical Systems 19 (2020), no. 3, 1798–1822.
- [12] A. Deshpande and M. Gopalkrishnan, Autocatalysis in reaction networks, Bull. Math. Biol. 76 (2014), no. 10, 2570–2595.
- [13] M. Feinberg, Lectures on chemical reaction networks, Notes of lectures given at the Mathematics Research Center, University of Wisconsin (1979), 49.
- [14] , Foundations of chemical reaction network theory, (2019).
- [15] M. Gopalkrishnan, E. Miller, and A. Shiu, A geometric approach to the global attractor conjecture, SIAM J. Appl. Dyn. Syst. 13 (2014), no. 2, 758–797.
- [16] C. Guldberg and P. Waage, Studies Concerning Affinity, CM Forhandlinger: Videnskabs-Selskabet I Christiana 35 (1864), no. 1864, 1864.
- [17] J. Gunawardena, Chemical reaction network theory for in-silico biologists, Notes available for download at http://vcp. med. harvard. edu/papers/crnt. pdf (2003).
- [18] W. Hordijk, J. Hein, and M. Steel, Autocatalytic sets and the origin of life, Entropy 12 (2010), no. 7, 1733–1742.
- [19] W. Hordijk and M. Steel, Detecting autocatalytic, self-sustaining sets in chemical reaction systems, J. Theor. Biol. 227 (2004), no. 4, 451–461.
- [20] W. Hordijk, M. Steel, and S. Kauffman, The structure of autocatalytic sets: Evolvability, enablement, and emergence, Acta biotheoretica 60 (2012), no. 4, 379–392.
- [21] F. Horn, Necessary and sufficient conditions for complex balancing in chemical kinetics, Arch. Ration. Mech. Anal. 49 (1972), no. 3, 172–186.
- [22] F. Horn and R. Jackson, General mass action kinetics, Arch. Ration. Mech. Anal. 47 (1972), no. 2, 81–116.
- [23] G. Lipták, G. Szederkényi, and K. Hangos, Kinetic feedback design for polynomial systems, J. Process Control 41 (2016), 56–66.
- [24] C. Pantea, On the persistence and global stability of mass-action systems, SIAM J. Math. Anal. 44 (2012), no. 3, 1636–1673.
- [25] J. Rudan, G. Szederkényi, and K. Hangos, Computing dynamically equivalent realizations of biochemical reaction networks with mass conservation, AIP Conference Proceedings, vol. 1558, American Institute of Physics, 2013, pp. 2356–2359.
- [26] , Efficiently computing alternative structures of large biochemical reaction networks using linear programming, MATCH Commun. Math. Comput. Chem 71 (2014), 71–92.
- [27] J. Rudan, G. Szederkényi, K. Hangos, and T. Péni, Polynomial time algorithms to determine weakly reversible realizations of chemical reaction networks, J. Math. Chem. 52 (2014), no. 5, 1386–1404.
- [28] G. Szederkényi and K. Hangos, Finding complex balanced and detailed balanced realizations of chemical reaction networks, J. Math. Chem. 49 (2011), no. 6, 1163–1179.
- [29] G. Szederkényi, K. Hangos, and Z. Tuza, Finding weakly reversible realizations of chemical reaction networks using optimization, arXiv preprint arXiv:1103.4741 (2011).
- [30] G. Szederkényi, G. Lipták, J. Rudan, and K. Hangos, Optimization-based design of kinetic feedbacks for nonnegative polynomial systems, 2013 IEEE 9th International Conference on Computational Cybernetics (ICCC), IEEE, 2013, pp. 67–72.
- [31] E. Voit, H. Martens, and S. Omholt, 150 years of the mass action law, PLOS Comput. Biol. 11 (2015), no. 1, e1004012.
- [32] P. Yu and G. Craciun, Mathematical Analysis of Chemical Reaction Systems, Isr. J. Chem. 58 (2018), no. 6-7, 733–741.