Sparse M-estimators in semi-parametric copula models
Abstract
We study the large sample properties of sparse M-estimators in the presence of pseudo-observations. Our framework covers a broad class of semi-parametric copula models, for which the marginal distributions are unknown and replaced by their empirical counterparts. It is well known that the latter modification significantly alters the limiting laws compared to usual M-estimation. We establish the consistency and the asymptotic normality of our sparse penalized M-estimator and we prove the asymptotic oracle property with pseudo-observations, possibly in the case when the number of parameters is diverging. Our framework allows to manage copula-based loss functions that are potentially unbounded. Additionally, we state the weak limit of multivariate rank statistics for an arbitrary dimension and the weak convergence of empirical copula processes indexed by maps. We apply our inference method to Canonical Maximum Likelihood losses with Gaussian copulas, mixtures of copulas or conditional copulas. The theoretical results are illustrated by two numerical experiments.
Key words: Copulas; M-estimation; Pseudo-observations; Sparsity.
1 Introduction
In this paper, we consider the parsimonious estimation of copula models within the semi-parametric framework: margins are left unspecified and a parametric copula model is assumed. The sparse assumption is motivated by the model complexity that occurs in copula modelling, where the parameterization may require the estimation of a large number of parameters. For instance, the variance-covariance matrix of a -dimensional Gaussian copula involves the estimation of parameters, the components of an unknown correlation matrix; in single-index copula, the underlying conditional copula is parameterized through a link function that depends on a potentially large number of covariates and thus parameters, which may not be all relevant for describing these conditional distributions. Since the seminal work of [12], a significant amount of literature dedicated to sparsity-based M-estimators has been flourishing in a broad range of settings. In contrast, the sparse estimation of copula based M-estimators has benefited from a very limited attention so far. In [7], the authors considered a mixture of copulas with a joint estimation of the weight parameters and the copula parameters, while penalizing the former ones only. However, a strong limitation of their approach is the parametric assumption formulated for the marginals, which greatly simplifies the large sample inference. [37] specified a penalized estimating equation-based estimator for single-index copula models and derived the corresponding large sample properties but assuming known margins. A theory covering the sparse estimation for semi-parametric copulas is an important missing stone in the literature. One of the key difficulties is the treatment of the values close to the boundaries of , where some loss functions potentially “explode”. The latter situation is not pathological. It often occurs for the standard Canonical Maximum Likelihood method or CML (see, e.g., [19, 33, 34]) and many usual copula log-densities, as pointed out in [32] in particular. Since the seminal works of [31, 30], the large sample properties of the empirical copula process were established by, e.g., [16], and such properties were applied to the asymptotic analysis of copula-based maximum likelihood estimators with pseudo-observations. In that case, the empirical copula process is indexed by the likelihood function: see [34, 8], who considered some regularity conditions on the likelihood function to manage the values close to the boundaries of . Similar conditions were stated likewise in [8, 39, 22], among others, where some bracketing number conditions on a suitable class of functions are assumed. These works share a similar spirit with [36, 11], who considered a general framework of empirical processes indexed by classes of functions under entropy conditions. Thanks to a general integration by parts formula, [28] established the conditions for the weak convergence of the empirical copula process indexed by a class of functions of bounded variation, the so-called Hardy–Krause variation. Their results do not require explicit entropy conditions on the class of functions. In the same vein, [6] assumed similar regularity conditions on the indexing functions but restricted their analysis to the two-dimensional copula case. It is worth mentioning that the techniques for stating the large sample analysis of semi-parametric copulas amply differ from the fully parametric viewpoint, for which the classical M-estimation theory obviously applies.
The present paper is then motivated by the lack of links between sparsity and semi-parametric copulas. Our asymptotic analysis for sparse M-estimators in the context of semi-parametric copulas builds upon the theoretical frameworks of [6] and [28]. The contribution of our paper is fourfold: first, we provide the asymptotic theory (consistency, oracle property for variable selection and asymptotic normality in the same spirit as [12]) for general penalized semi-parametric copula models, where the margins are estimated by their empirical counterparts. In particular, our setting includes the Canonical Maximum Likelihood method. Second, these asymptotic results are extended for (a sequence of) copula models in large dimensions, a framework that corresponds to the diverging dimension case, as in, e.g., [13]. Third, we prove the asymptotic normality of multivariate-rank statistics for any arbitrary dimension , extending Theorem 3.3 of [6]. Fourth and finally, we prove the weak convergence of the empirical copula process indexed by functions of bounded variation, extending Theorem 5 of [28] to cover the prevailing situation of unbounded copula densities. We emphasize that our theory is not restricted to i.i.d. data and potentially covers the case of dependent observations, as in [28].
The rest of the paper is organized as follows. Section 2 details the framework and fix our notations. The large sample properties of our penalized estimator are provided in Section 3. The situation of conditional copulas is managed in Section 4. Section 5 discusses some examples and two simulated experiments to illustrate the relevance of our method. The theoretical results about multivariate rank statistics and empirical copula processes are stated in Appendix A. All the proofs, the theoretical results in the case of a diverging number of parameters and additional simulated experiments are provided in the Appendix.
2 The framework
This section details the sparse estimation framework for copula models when the marginal distributions are non-parametrically managed. We consider a sample of realizations of a random vector , . This sample is denoted as . The observations may be dependent or not. As usual in the copula world, we are more interested in the “reduced” random variables , , where denotes the cumulative distribution function (c.d.f.) of . Throughout this paper, we make the blanket assumption that all have continuous marginals. Then, the variables are uniformly distributed on and the joint law of is the uniquely defined copula of denoted by . To study the latter copula, it would be tempting to work with the sample instead of . Unfortunately, since the marginal c.d.f.s’ are unknown in general, this is still the case of , and the marginal c.d.f.s’ have to be replaced by consistent estimates. Therefore, it is common to build a sample of pseudo-observations , , obtained from the initial sample . Here and as usual, set for every and every , using the -th re-scaled empirical c.d.f. We will denote by , , the empirical c.d.f. of the (unobservable) random variable , i.e. The empirical c.d.f. of is , i.e. for any . We denote by the usual empirical process associated with the sample , i.e.
The natural estimator of the true underlying copula , i.e. the c.d.f. of , is the empirical copula map
| (2.1) |
and the associated empirical copula process is .
Hereafter, we select a parametric family of copulas , , and we assume it contains the true copula : there exists (the “true value” of the parameter) s.t. . We want to cover the usual case of semi-parametric dependence models, for which there is an orthogonality condition of the type for some family of loss functions . The dimension of the copula parameter will be fixed hereafter. In the Appendix, it will be allowed to tend to the infinity with the sample size . The function is usually defined as a quadratic loss or minus a log-likelihood function. Note that has not to be defined on the boundaries of at this stage because the law of was assumed to be continuous. Moreover, an important contribution of the paper will be to deal with some maps that cannot be continuously extended on .
For the sake of the estimation of , let us specify a statistical criterion. Consider a global loss function from to . The value evaluates the quality of the “fit” given for every and under . Hereafter, we assume there exists a continuous function such that
| (2.2) |
for every and every in . As usual for the inference of semiparametric copula models, the empirical loss cannot be calculated since we do not observe the realizations of in practice. Therefore, invoking the “pseudo-sample” , the empirical loss will be approximated by , a quantity called “pseudo-empirical” loss function.
Example 1.
A key example is the Canonical Maximum Likelihood method: the law of (i.e. the copula of ) belongs to a parametric family and . There, for i.i.d. data, , minus the log-copula density of w.r.t. the Lebesgue measure on .
Now, we assume that the unknown parameter is sparse and we introduce a penalization term. Our criterion becomes
| (2.3) |
when such a minimizer exists. Here, , for , is a penalty function, where is a tuning parameter which depends on the sample size and enforces a particular type of sparse structure. Throughout the paper, we will implicitly work under the following assumption.
Assumption 0.
The parameter space is a borelian subset of . The function is uniquely minimized on at , and an open neighborhood of is contained in .
Note that only the uniqueness of is required but not that of . In [12, 13], is assumed to be an open subset. Nonetheless, it may happen that belongs to the frontier of . This may be the case for the estimation of weights in mixture models (see Example 3 below), e.g. Actually, our results will apply even if does not contain an open neighborhood of . Indeed, it is sufficient that there exists a convex open neighborhood of in : for some open ball centered at and with a radius and for every parameter , every element of the segment , belongs to and is the limit of a sequence of elements in , where is the interior of . Therefore, we will define the partial derivatives of any map at some point on the frontier of (in particular ) by continuity. For example, when the derivative of exists in the interior of , for some , it will be defined at by , assuming the latter limit exists. To lighten the presentation, we will keep Assumption ‣ 2 as above. By slightly strengthening some regularity assumptions, the case of on the boundary of will be straightforwardly obtained (essentially by imposing the continuity of some derivatives around ).
Some well-known penalty functions are the LASSO, where for every , and the non-convex SCAD and MCP. The SCAD penalty of [12] is defined as: for every ,
where . The MCP due to [38] is defined for as follows: for every ,
Note that when (resp. ), the SCAD (resp. MCP) penalty behaves as the LASSO penalty since all coefficients of are equally penalized. The idea of sparsity for copulas naturally applies to a broad range of situations. In such cases, the parameter value zero usually plays a particular role, possibly after reparameterisation. This is in line with the usual previously cited penalties.
Example 2.
Consider a Gaussian copula model in dimension , whose parameter is a correlation matrix . The description of all the underlying dependencies between the components of is a rather painful task. Then, the sparsity of becomes a nice property. Indeed, the independence between two components of is equivalent to the nullity of their corresponding coefficients in .
Example 3.
The inference of mixtures of copulas may justify the application of a penalty function. Indeed, consider a set of known -dimensional copulas , . In practice, we could try to approximate the true underlying copula by a mixture , for every . Here, the underlying parameter is the vector of weights and is defined as . If a weight is estimated as zero, its corresponding copula does not matter to approximate . The latter model is generally misspecified, but our theory will apply even in this case, interpreting in (2.3) as an estimator of a “pseudo-true” value . If we apply the CML method, is the log-copula density of . When some or all copulas depend on unknown parameters that need to be estimated in addition to the weights, the penalty function could also be applied to these copula parameters.
Dealing with conditional copulas ([17], e.g.), our framework will be slightly modified. Now, the law of a random vector knowing the vector of covariates is given by a parametric conditional copula whose parameter depends on a known map of and is denoted , . Beside, the law of the margins , , given are unknown and we assume they do not depend on . In other words, the conditional law of given is assumed to be
Therefore, as for the CML method and in the i.i.d. case, an estimator of would be
Surprisingly and to the best of our knowledge, the asymptotic theory of such estimators has apparently not been explicitly stated in the literature until now. This will be the topic of Section 4.
Example 4.
Sparsity naturally applies to single-index copulas (see, e.g., [18]). The function is now specified with respect to the underlying parameter. In other words, sparsity refers to the situation where only a (small) subset of the components is relevant to describe the dependencies between the components given . Consider the conditional Gaussian copulas, as Example 4 of [18]. Here, the correlation matrix would be a function of . It may be rewritten , where denotes the conditional Kendall’s tau of given .
3 Asymptotic properties
To prove the asymptotic results, we consider two sets of assumptions: one is related to the loss function; the other one concerns the penalty function. First, define the support of the true parameter as . We will implicitly assume a sparsity assumption, i.e. the cardinal of is ”significantly” smaller than .
Assumption 1.
The map is thrice differentiable on , for every . The parameter satisfies the first order condition . Moreover, and exist and are positive definite. Finally, for every , there exists a constant such that
Assumption 2.
For any , the copula partial derivative exists and is continuous on . For every couple , the second-order partial derivative exists and is continuous on . Moreover, there exists a positive constant such that
| (3.1) |
When does not belong to (i.e. when one of its components is zero or one), we have defined . It has been pointed out in [32] that Condition 2 is satisfied for bivariate Gaussian and bivariate extreme-value copulas in particular. We formally state this property for -dimensional Gaussian copulas in Section E of the Appendix.
Assumption 3.
We will denote by (resp. ) the first order (resp. second order) derivative of , for any .
Assumption 4.
Defining
assume that and when . Moreover, there exist constants and such that
for any real numbers such that .
Assumption 1 is a standard regularity condition for asymptotically normal M-estimators. Assumptions 2 is a smoothness condition on the copula and is similar to Condition 4.1 of [32] and Condition 2.1 of [6]. It ensures that the second-order derivatives with respect to do not explode “too rapidly” when approaches the boundaries of . Assumption 3 is related to the indexing function of the copula process, here by the first, second and third order derivatives of the loss function . The -regularity of these functions ensures that they are of bounded Hardy-Krause variation - similar to assumption F of [28] - together with some integrability conditions. Here, is some fixed number in entering in the definition of a weight function , as specified in Definition A, point (ii). Such a weight function is related to the theory of weighted empirical processes applied in [6]. Assumption 4 is dedicated to the regularity of the penalty function, and includes conditions in the same vein as [13], Assumption 3.1.1. Note that the LASSO, the SCAD and the MCP penalties fulfill Assumption 4. Our first result establishes the existence of a consistent penalized M-estimator.
Theorem 3.1.
The proof is postponed in Section D of the Appendix. The factor could be replaced by any sequence that tends to the infinity with , as in Corollary A.2. It has been arbitrarily chosen for convenience. We will apply this rule throughout the article.
We now show that the penalized estimator satisfies the oracle property in the sense of [12]: the true support can be recovered asymptotically and the non-zero estimated coefficients are asymptotically normal. Denote by the (random) support of our estimator. The following theorem states the main results of this section. It uses some standard notations for concatenation of sub-vectors, as recalled in Appendix A.
Theorem 3.2.
The proof is relegated to Section D of the Appendix. The existence and the meaning of the integrals defining comes from Assumption 13. The proofs of the two latter theorems rely on a third-order limited expansion of our empirical loss w.r.t. its arguments. The negligible terms are managed thanks to a ULLN (Corollary A.2). An integration by parts formula (Theorem A.1) allows to write the main terms as sums of integrals of the empirical copula process w.r.t. some “sufficiently regular” functions. The latter ones are deduced from the derivatives of the loss, justifying the concept of regularity and Assumption 3. A weak convergence result of the weighted empirical copula process concludes the asymptotic normality proof.
Note that the previous results apply with dependent observations . Indeed, in Theorem 3.2 (ii), we only require the weak convergence of the process to . In the i.i.d. case, is a Brownian Bridge and is a Gaussian random vector. The latter assertion is still true when is a strongly stationary and geometrically alpha-mixing sequence, due to Proposition 4.4 in [6]. The existence and the meaning of the random variable come from Assumption 13. Our conditions on allow to use the SCAD or the MCP penalty, but not the LASSO because in the latter case. In other words, Theorem 3.1 may apply with LASSO but not Theorem 3.2. The fact that LASSO does not yield the oracle property has already been noted in the literature: see [40] and the references therein. Actually, consider any penalty such that does not depend on , when is sufficiently small, as for the SCAD and MCP cases. Then,
when is sufficiently large because , implying . Thus, Assumption 4 is satisfied and , for large enough. Therefore, for such penalty functions, the asymptotic law of becomes a lot simpler.
Corollary 3.3.
Theorem 3.2 establishes that the non-convex penalization procedure for semi-parametric copula models is an “oracle”: for a consistent estimator , the true sparse support is correctly identified in probability, and the non-zero estimated parameters have the same limiting law as if the support of were known. The limit is in the same vein as the one in Theorem 5 of [28]. However, in contrast to the latter result which assumes bounded indexing functions on , our framework covers the case of unbounded ones. In particular, our indexing functions are not constrained to be bounded on .
In the particular case of CML, the asymptotic law of our estimator has been stated under a set of regularity assumptions (particularly Assumption 3) that significantly differs from those that have been proposed in the literature: see the seminal papers [34] (Assumption (A.1)) and [8] (Assumptions (A.2)-(A.4)). These competing sets of assumption are apparently not nested, due to two very different techniques of proofs: a general integration by parts formula in our case, and some old results from [31, 30] in the latter cases. Our set of assumptions should most often be weaker. Indeed, we typically do not require that some expectations as are finite for some (Assumption (A.3) in [8]). Moreover and importantly, our results may directly be applied to time series, contrary to the cited papers that are strongly restricted to i.i.d. observations.
Our proofs rely on the weak convergence of multivariate rank-order statistics: see Theorem A.1 in the Appendix, that is an extension of Theorem 3.3 of [6] in an arbitrary dimension. Note that some papers have already stated similar results, but under restrictive conditions: Theorem 6 in [15] assumed the existence of continuous partial derivatives of the true copula on the whole hypercube (contrary to our Assumption 2). Theorem 2.4 in [20] relies on numerous very technical assumptions and it is unclear whether the latter result is weaker/stronger than ours. Nonetheless, it “only” states weak convergence in the space of cadlag functions equipped with the Skorohod topology.
Applying Theorem 3.2 (ii) or its corollary, it is possible to approximate by plug-in the limiting law of , for every fixed subset and assuming (an event whose probability tends to one): just replace the unknown quantities with their empirical counterparts. This is obvious concerning the matrices , and . Concerning the Gaussian random vector , an estimator of its variance is proposed in Section B of the Appendix.
4 Conditional copula models
In several situations of interest, multivariate models are defined through some conditioning laws. In other words, there exist a random vector of covariates , for some borelian subset in , and we focus on the laws of given any value of . The natural framework is given by conditional copulas and the associated Sklar’s theorem ([17], e.g.). Generally speaking, conditional copula models have to manage conditional marginal distributions on one side, and conditional copulas on the other side. In our semiparametric approach, we do not specify the former ones. Indeed, this would be a source of complexities due to the need of kernel smoothing or other non parametric techniques ([17, 2], among others). Here, we make the following simplifying assumption.
Assumption 5.
For every , the law of given does not depend on .
In other words, the conditional margins and the unconditional ones are identical. Even if the latter assumption may be considered as relatively strong, it is not implausible. For instance, in typical copula-GARCH models ([9]), the marginal dynamics are filtered in a first stage, and a parametric copula is then postulated between the residuals. It is well-known that systemic risk measures strongly depend on the economic cycle. Thus, some macroeconomic explanatory variables may have a significant impact on the latter copula. But, concerning the marginal conditional distributions, this effect could be hidden due to the first-order phenomenon of “volatility clustering”.
Under Assumption 5, our dependence model of interest will be related to the laws of given , , by keeping the same definition of as previously. Sparsity would then be related to the number of components of that are relevant to specify any copula of (or , equivalently) given . Typically, the latter copulas belong to a given parametric -dimensional family and the parameter depends on the underlying covariate: given , the law of is , for some known map , . The problem is now to evaluate the true “new parameter” , based on a sample . Compared to the previous sections, the focus has switched from to . In particular, we will assume that the new parameter set satisfies Assumption ‣ 2 instead of .
Under Assumption 5, we define the same pseudo-observations as before, and keep the notation . In addition, set . For example, the parameter may naturally be estimated without any penalty by CML as
| (4.1) |
Under sparsity and with penalties, the results of Sections 2 and 3 can be adapted to tackle this new problem and even more general ones. First of all, we need to distinguish the cases of known and/or unknown covariate distributions.
4.1 The marginal laws of the covariates are known.
Let us assume the law of is known, continuous, and denoted as , . To simplify and w.l.o.g., we can additionally impose that the joint law of is a copula.
Assumption 6.
The law of is uniform between and , for every .
If this is not the case, just replace any with . In the case of conditional copula models, the map would be replaced by . To ease the notations, we will not distinguish between and . Extending (2.3), we now consider the penalized estimator
| (4.2) |
where is a penalty. Assume the new empirical loss is associated with a continuous function so that we can write
| (4.3) |
Since the margins of are uniform by assumption, the joint law of is a -dimensional copula denoted . Instead of the empirical copula related to the , we now focus on an empirical counterpart of the copula, i.e.
| (4.4) |
for every and . The associated “empirical copula” process becomes . Obviously, the weak behavior of is the same as the one of , where
See Appendix C in [28], for instance.
We would like to state some versions of Theorems 3.1 and 3.2 for an estimator given by (4.2). Obviously,
and the limiting law of will be deduced from the asymptotic behavior of . Broadly speaking, the two main components to state such results are an integration by parts formula and a weak convergence result for (or , equivalently). The former tool will be guaranteed by applying our Theorem A.1 in the appendix. And the latter weak convergence result, will be a consequence of the weak convergence of , now the empirical process associated with the sample :
| (4.5) |
Obviously, when our observations are i.i.d., the process weakly tends to a -Brownian bridge in . Instead of (see Theorem A.1 in the appendix), the approximated empirical copula process is here
using the notations detailed in our appendix. Note that the partial derivatives of the copula have to be considered w.r.t. the first components only, i.e. the components that correspond to pseudo-observations (and not -type components).
Now, let us state the new theoretical results related to semi-parametric inference in the presence of pseudo-observations and possible complete observations. Since they can be deduced from the previous sections and proofs, we omit the details.
Assumption 7.
The map is thrice differentiable on , for every . Moreover, and exist and are positive definite. Finally, for every , there exists a constant such that
Assumption 8.
For any and , the copula partial derivative exists and is continuous on uniformly w.r.t. . For every couple and , the second-order partial derivative exists and is continuous on . Moreover, there exists a positive constant such that
| (4.6) |
Assumption 9.
Theorem 4.1.
Theorem 4.2.
In addition to the assumptions of Theorem 4.1, assume that the penalty function satisfies . Moreover, assume , and . Then, the consistent estimator of Theorem 4.1 satisfies the following properties.
-
(i)
Support recovery: , where and are related to the support of .
-
(ii)
Asymptotic normality: assume the empirical process converges weakly in to a limit process which has continuous sample paths, almost surely. If, in addition, the Assumption 13 in Appendix A (applied to instead of ) is fulfilled and , then
where , , and is a -dimensional centered random vector defined as
for , with , .
Remark 1.
In Theorems 4.1 and 4.2, it has been assumed that some -maps are regular w.r.t. (Assumption 9). Checking the latter property with may sometimes be painful, or even impossible. Beside, this task may have been done for the same parametric copula family in the (usual) unconditional case, using the weights . Unfortunately, there is no order between and and the randomness of the covariates matters in the more general situation (4.2). Hopefully, when some regularity properties are available uniformly w.r.t. , we can rely on instead of and checking regularity properties becomes simpler: see Section 4.3 below.
By a careful inspection of the proof of Proposition 3.1 in [32], the weak convergence of can be easily stated under “minimal assumptions” in the i.i.d. case. Since this result is new and of interest per se, it is now precisely stated.
Theorem 4.3.
Assume the margins are continuous. If, for any , any and any , the partial derivative exists and is continuous on uniformly w.r.t. , then
when . Moreover, weakly tends to in .
4.2 The marginal laws of the covariates are unknown.
In this case, the laws are still continuous but unknown, and the covariates belong to some arbitrary subset . Introduce the random variables , , that are uniformly distributed between zero and one. Set . We can manage this situation when the loss function is a map of , instead of as previously: define pseudo-observations related to the covariates , where for every and every , using the -th re-scaled empirical c.d.f. The penalized estimator of interest is here defined as
Thus, we recover the standard situation that has been studied in Section 3. All the results of Section 3 directly apply, replacing the -dimensional copula by the -dimensional copula , replacing by , etc. The limiting law of will not be the same as in Theorem 4.2 (ii). Indeed, the process has now to be replaced by , due to the additional amount of randomness induced by the “pseudo-covariates” .
4.3 Practical considerations
Now, let us come back to the estimator given by (4.1). The regularity assumptions of Theorems 4.1 and 4.2 have to be checked on a case-by-case basis. Nonetheless, there are some situations where things become simpler. Indeed, assume
-
(i)
the map and all its partial derivatives (up to order and w.r.t. the components of and respectively) are bounded in , denoting by a neighborhood of the true parameter in the space ;
- (ii)
-
(iii)
the latter conditions may be verified replacing the weight function by .
Note that, under (i) and (ii), the conditions of Theorems 3.1 and 3.2 are satisfied with the derivatives of the loss functions , for any fixed . Then, it can be easily checked that Theorems 4.1 and 4.2 apply. In particular, the influence of the covariates is “neutralized” through (i); moreover, noting that , (iii) is sufficient to manage the weight functions.
To illustrate, consider the case of Gumbel and Clayton copulas, for which is and respectively (under the usual parameterization of [26]). Assume that, given , the latter parameters can be rewritten for some in that satisfies Assumption ‣ 2. Moreover, assume the ranges of the maps from to are included into a compact subset of . Then, Theorems 4.1 and 4.2 apply: the associated parameters defined in 4.1 are consistent and weakly convergent. See Sections F and G of the Appendix for the technical details and for the proof that (i), (ii) and (iii) are indeed satisfied. This justifies the application of our results in the case of single-index models with Clayton/Gumbel copulas (Section 5.2 below).
5 Applications
5.1 Examples
5.1.1 M-criterion for Gaussian copulas
An important application of the latter results is Maximum Likelihood Estimation with pseudo-observations, where we observe a sample from a -dimensional distribution whose parametric copula depends on some parameter . Equipped with pseudo-observations and using the same notations as above, our penalized estimator is defined as
denoting by the copula density. In the case of Gaussian copula model, the parameter of interest is , where is the correlation matrix of such a copula. This yields
| (5.1) |
with , . Note that the are approximated realizations of the Gaussian random vector . The Gaussian copula exhibits discontinuous partial derivatives at the boundary of : see [32], Example 5.1. We have seen in Section 3 that is asymptotically normally distributed under suitable regularity conditions. In Section E of the Appendix, we check that all the conditions are satisfied so that Theorems 3.1 and 3.2 can be applied to Gaussian copula models and given by (5.1). Interestingly, the associated limiting law in Theorem 3.2 is simply .
The estimation of can be carried out using the least squares loss . In Section E of the Appendix, we verify that the latter loss satisfies the regularity conditions of Theorems 3.1 and 3.2. Our simulation experiments on sparse Gaussian copula will be based on both the Gaussian loss and the least squares loss. Set , that approximates . Interestingly, our empirical loss is equal to and for the Gaussian CML and least squares cases respectively, apart from some constant terms that do not depend on . Indeed, for the least squares loss, we have
which is equal to plus some constant terms that do not depend on . In our simulation experiment for sparse Gaussian copulas, the implemented code relies on and/or intensively, some quantities that can be quickly calculated through some matrix manipulations, even when .
5.1.2 M-criterion for mixtures of copulas
Mixing parametric copulas is a flexible way to build richly parameterized copulas. More precisely, a mixture based copula is usually specified by its density , built from the family of copula densities . Each of the copula density depends on a vector of parameters , and are some unknown weights satisfying , , and . The parameter of interest is , with , with the notations of Example 3. Let be the dimension of any parameter . Then, with our CML criterion with pseudo-observations, an estimator of the true is defined as
Such a procedure fosters sparsity among and among : when , then the corresponding copula parameter can potentially be sparse. The latter criterion is similar to Criterion (3) in [7]; however, these authors treat the marginals as known quantities, which significantly simplifies their large sample analysis.
Assume that all parametric copula families , , satisfy the regularity conditions to apply our Theorems 3.1 and 3.2. Unfortunately, in general, this does not imply their mixture model will satisfy all these properties, in particular the -regularity. Therefore, it will be necessary to do this task on a case-by-case basis. Nonetheless, in the particular case of mixtures of Gaussian copulas, our regularity conditions are satisfied by considering the least squares loss function, as in Section 5.1.1. Indeed, for this model, the variance-covariance matrix of is , denoting by the correlation matrix of parameters that is associated with , . Thus, the same arguments as for the Gaussian copula with the loss can easily be invoked. Alternatively, choosing the log-likelihood (CML) loss induces more difficulties. Nonetheless, it can be proved that our regularity conditions apply, at least when all the (true) weights are strictly positive. See Section E of the Appendix for details.
5.2 Simulated experiments
In this section, we assess the finite sample performances of our penalization procedure in the presence of pseudo-observations. To do so, we carry out simulated experiments for the sparse Gaussian copula model and some sparse conditional copulas. These experiments are meant to illustrate the ability of the penalization procedure to correctly identify the zero entries of the copula parameter with non-parametric marginals. First, let us briefly discuss the implementation procedure and the choice of .
5.2.1 Implementation and selection of
All the experiments are implemented in Matlab code and run on a Mac-OS Apple M1 Ultra with 20 cores and 128 GB Memory. A gradient descent type algorithm is implemented to solve the penalized Gaussian copula problem, a situation where closed-form gradient formulas can directly be applied. We employed the numerical optimization routine fmincon of Matlab to find the estimated parameter for sparse conditional copulas 333The code for replication is available at https://github.com/Benjamin-Poignard/sparse-copula. The tuning parameter controls the model complexity and must be calibrated for each penalty function. To do so, we employ a -fold cross-validation procedure, in the same spirit as in Section 7.10 of [23]. To be specific, we divide the data into disjoint subgroups of roughly the same size, the so-called folds. Denote the indices of that observations that belong to the -th fold by , and the size of the -th fold by . The -fold cross-validation score is defined as
| (5.2) |
where is the non-penalized loss associated to the copula model and evaluated over the -th fold of size , which serves as the test set, and is our penalized estimator of the latter copula parameter based on the sample - the training set - using as the tuning parameter. The optimal tuning parameter is then selected according to . Then, is used to obtain the final estimate of over the whole sample. Here, the minimization of the cross-validation score is performed over , where is a grid (its size is user-specified) of values set as and dim the number of parameters to estimate. The choice of the rate is standard in the sparse literature for M-estimators: see, e.g., Chapter 6 of [5] for the LASSO and [25] for non-convex penalization methods.
5.2.2 Sparse Gaussian copula models
Our first application concerns the Gaussian copula. Here, sparsity is specified with respect to the variance-covariance matrix . Its diagonal elements are equal to one and its off-diagonal elements are , so that the number of distinct free parameters is . The parameter is defined as the column vector of the components located strictly below the main diagonal. Thus, can be considered as a function of : . We still denote by the true sparse support, where is sparse when some components of are independent. Our simulated experiment can be summarized as follows: we simulate a sparse true , generate the from the corresponding Gaussian copula with parameter for a given sample size , and calculate by minimizing our penalized procedure based on the pseudo-sample; this procedure is repeated for two hundred independent batches.
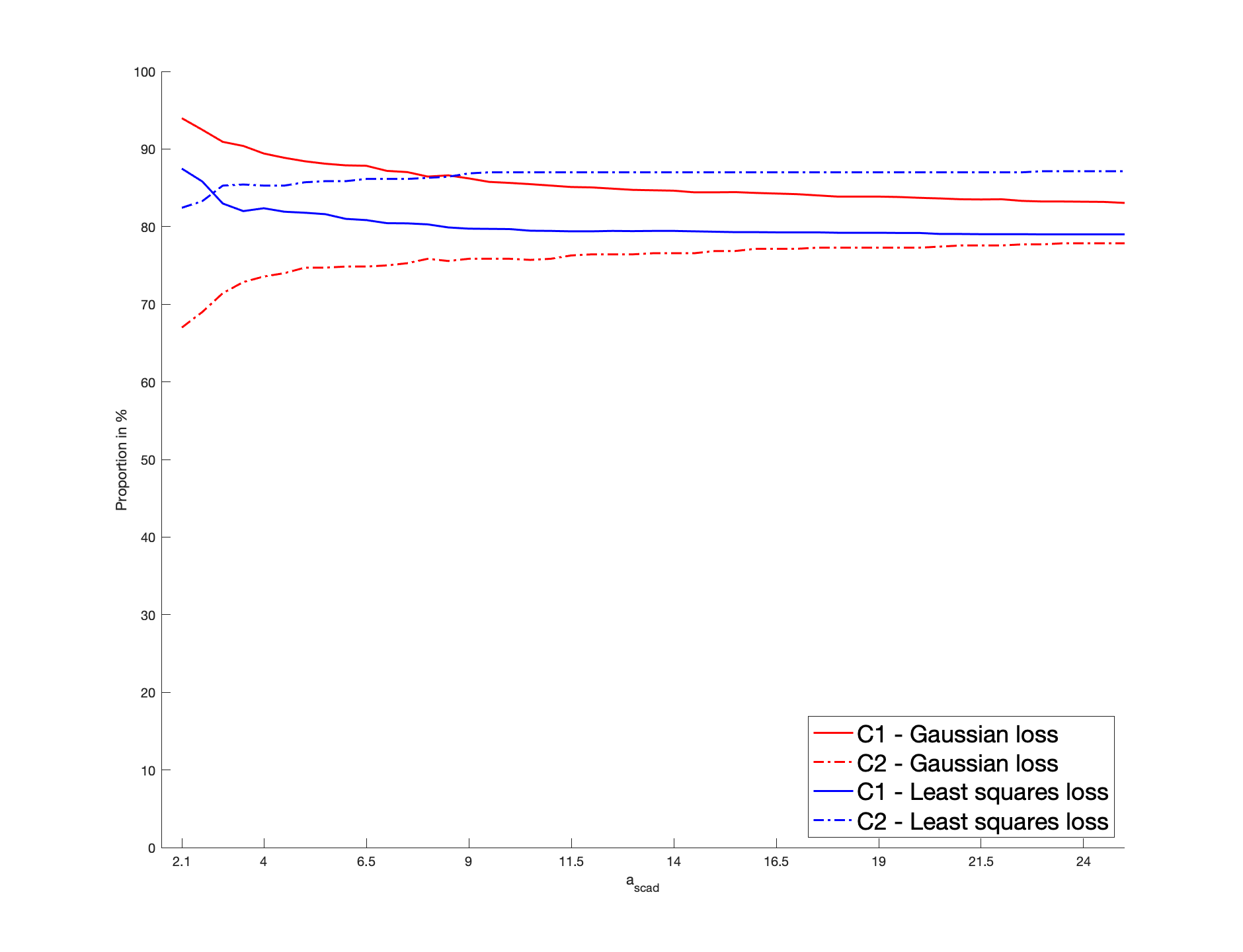
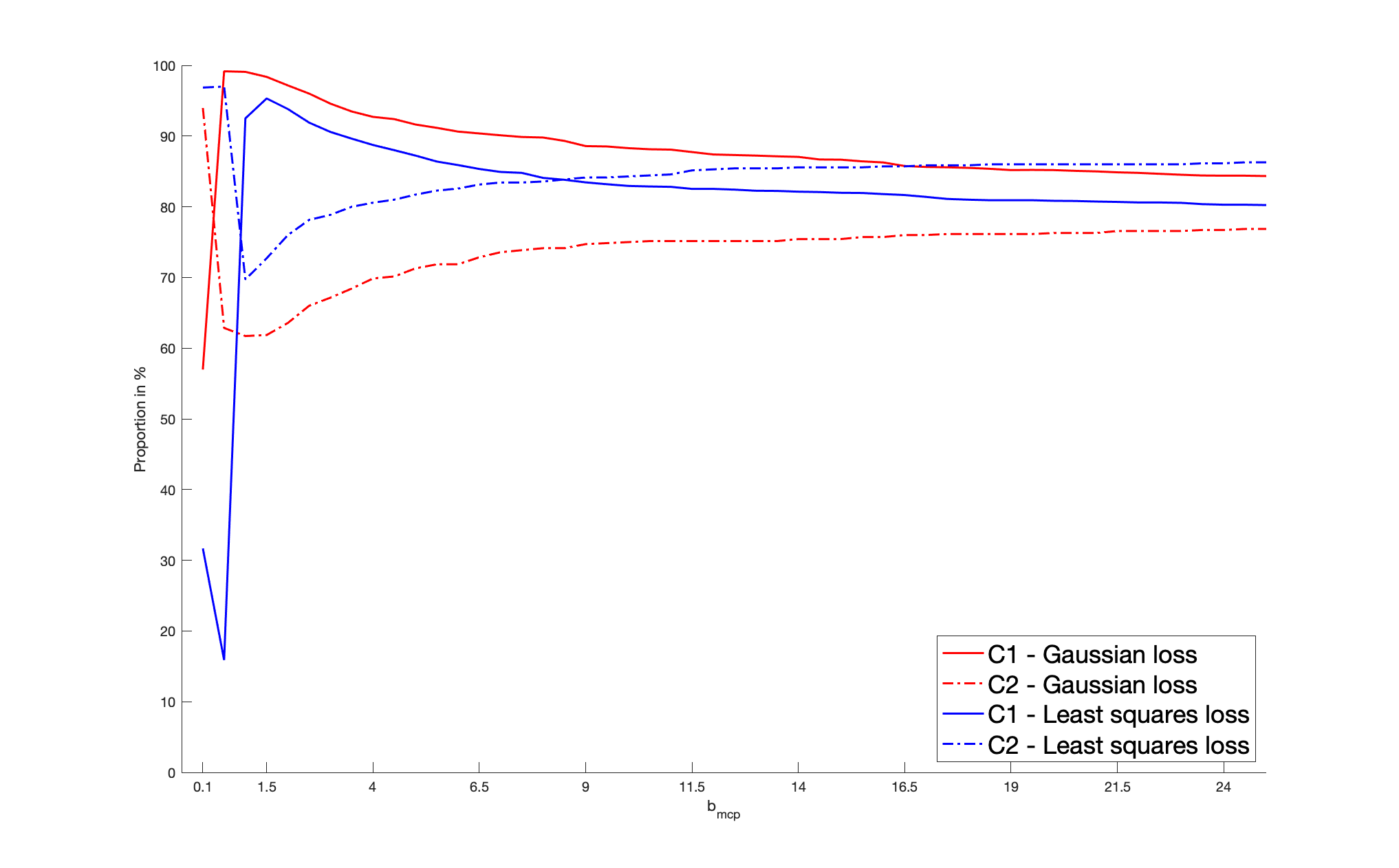
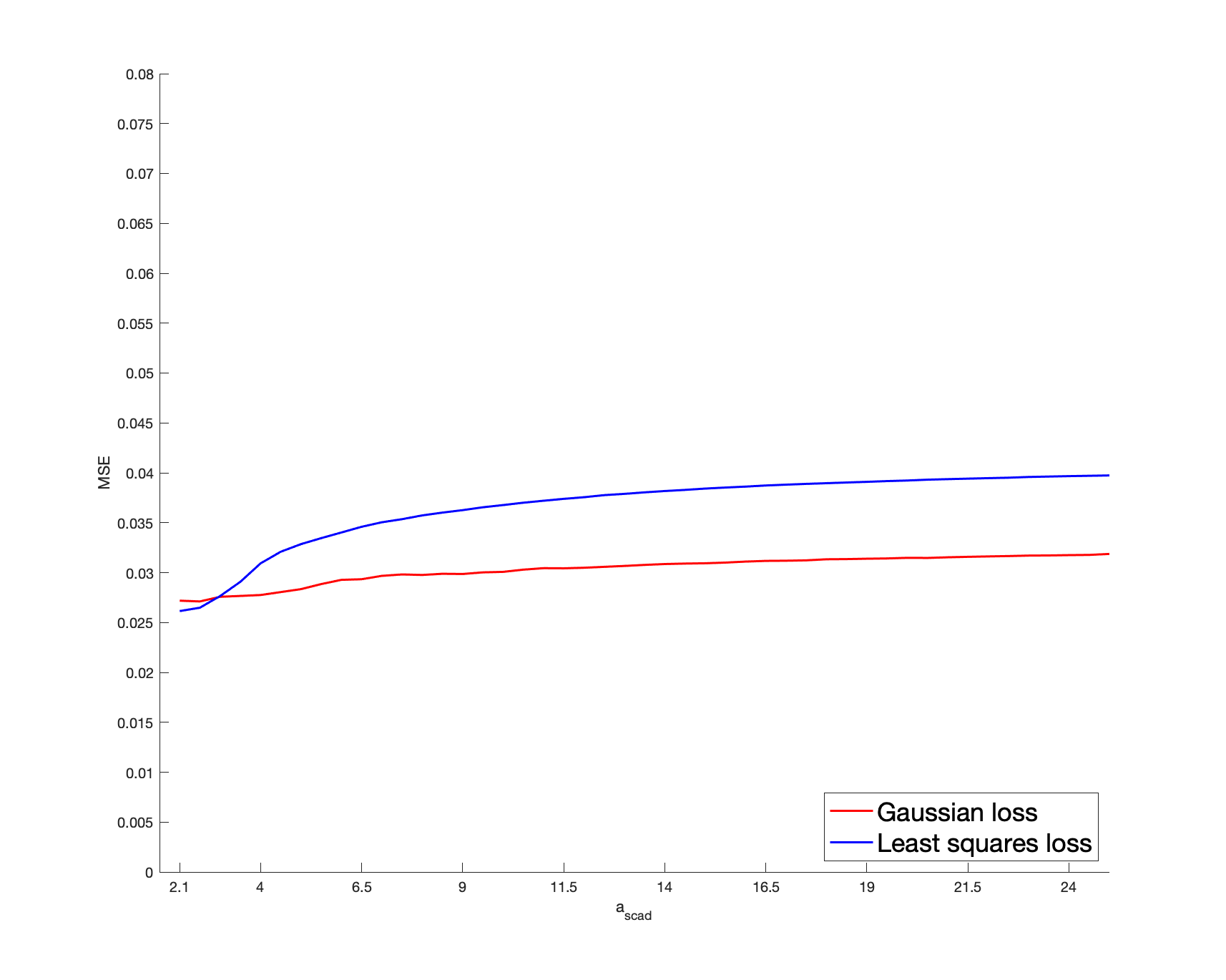
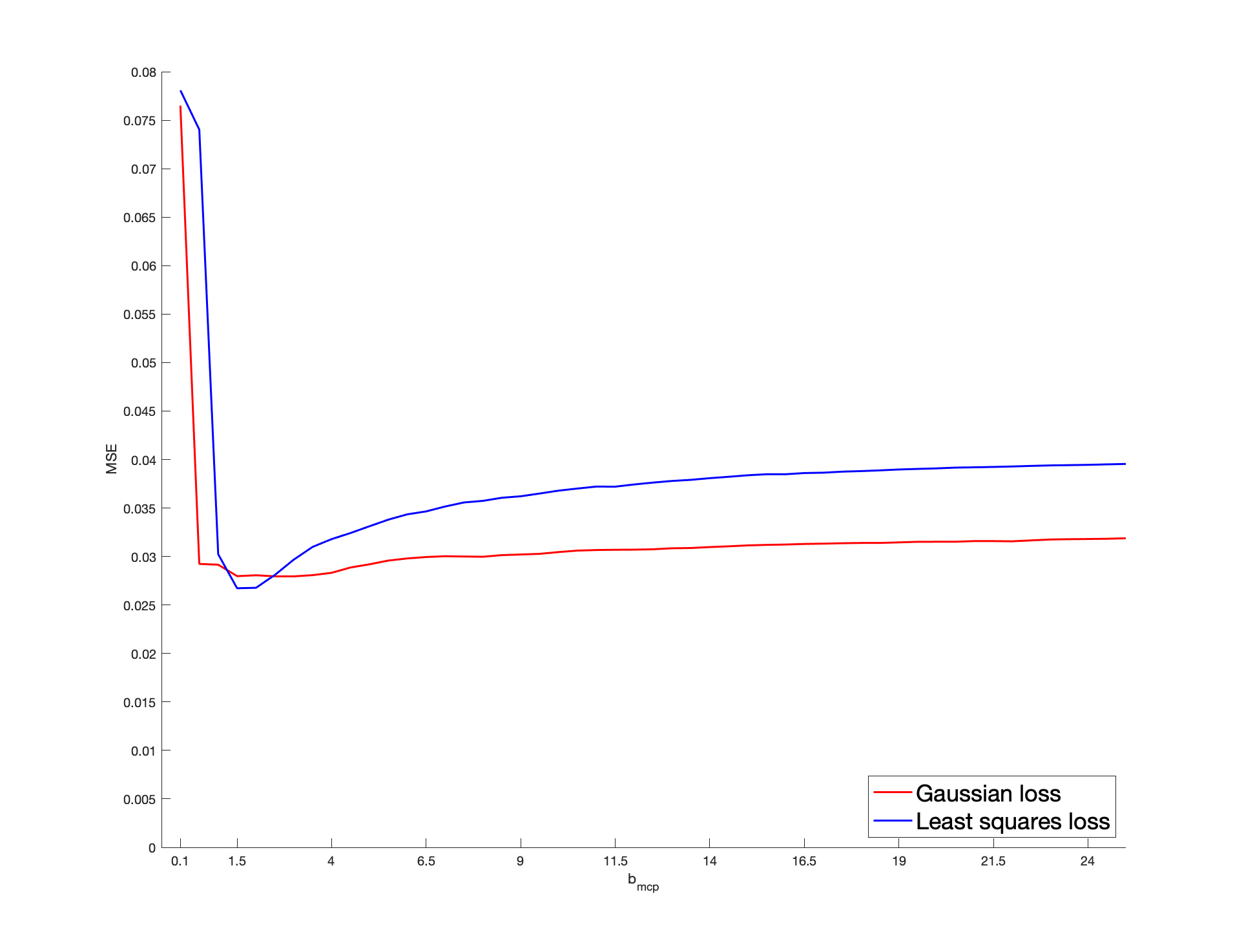
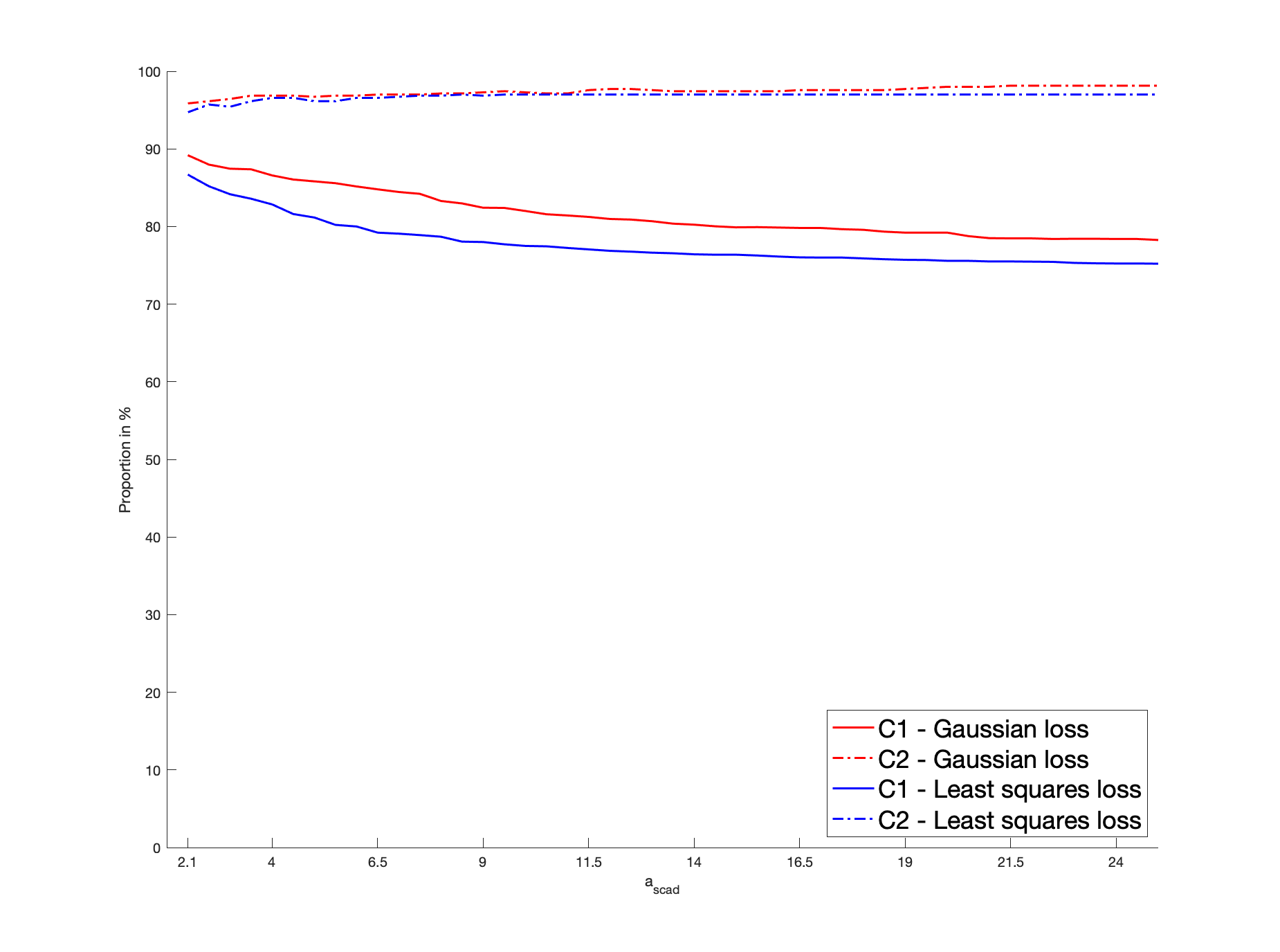
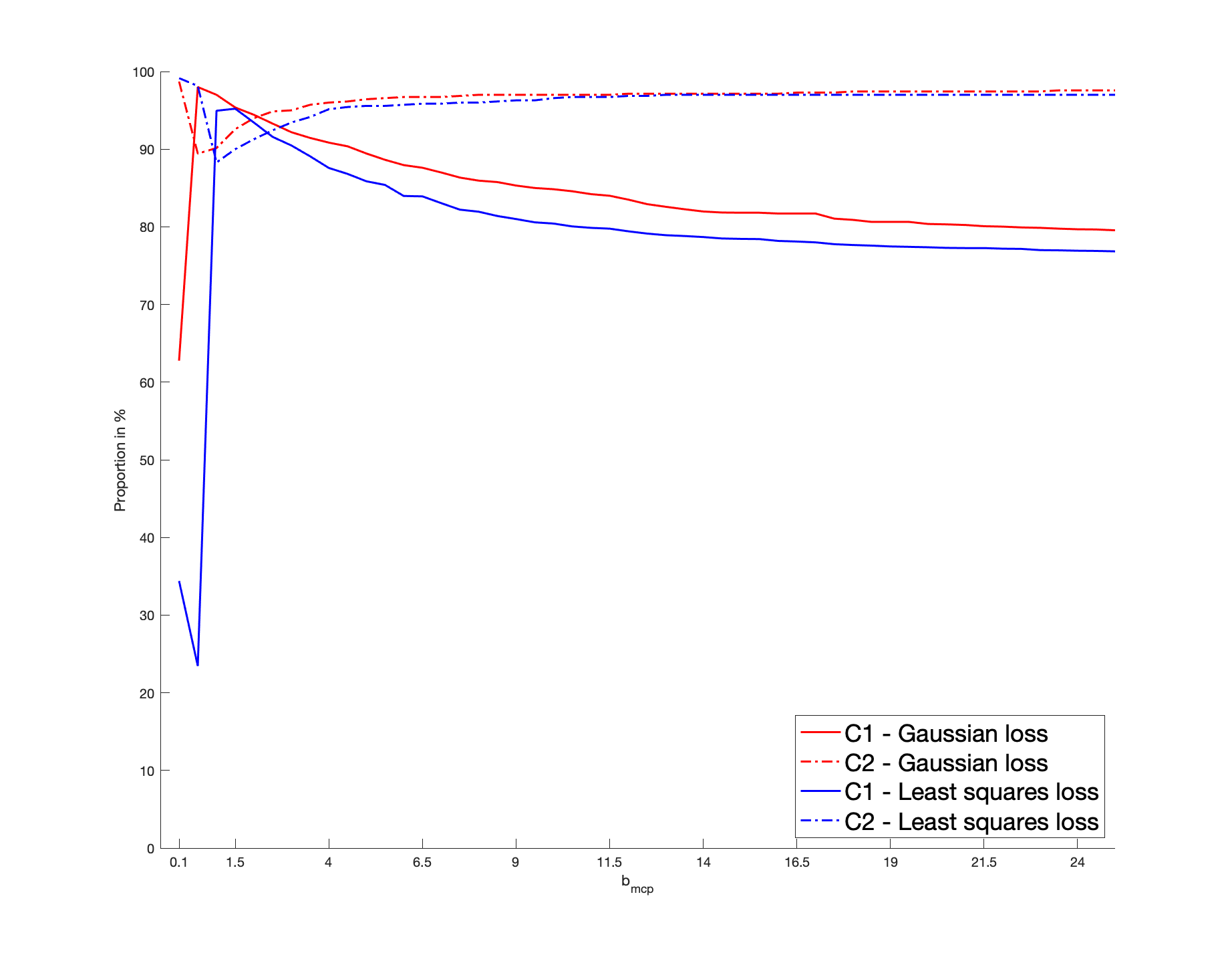
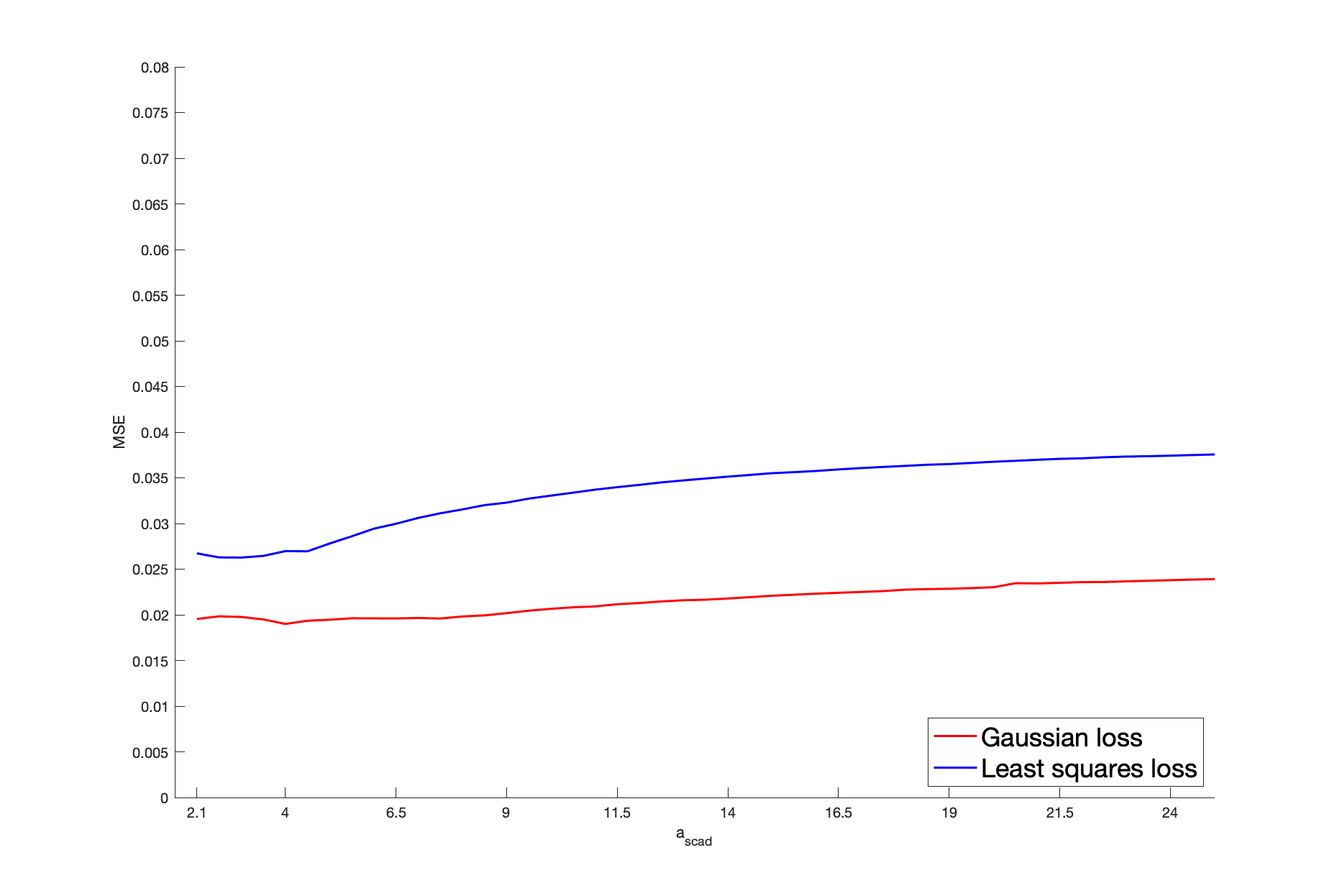
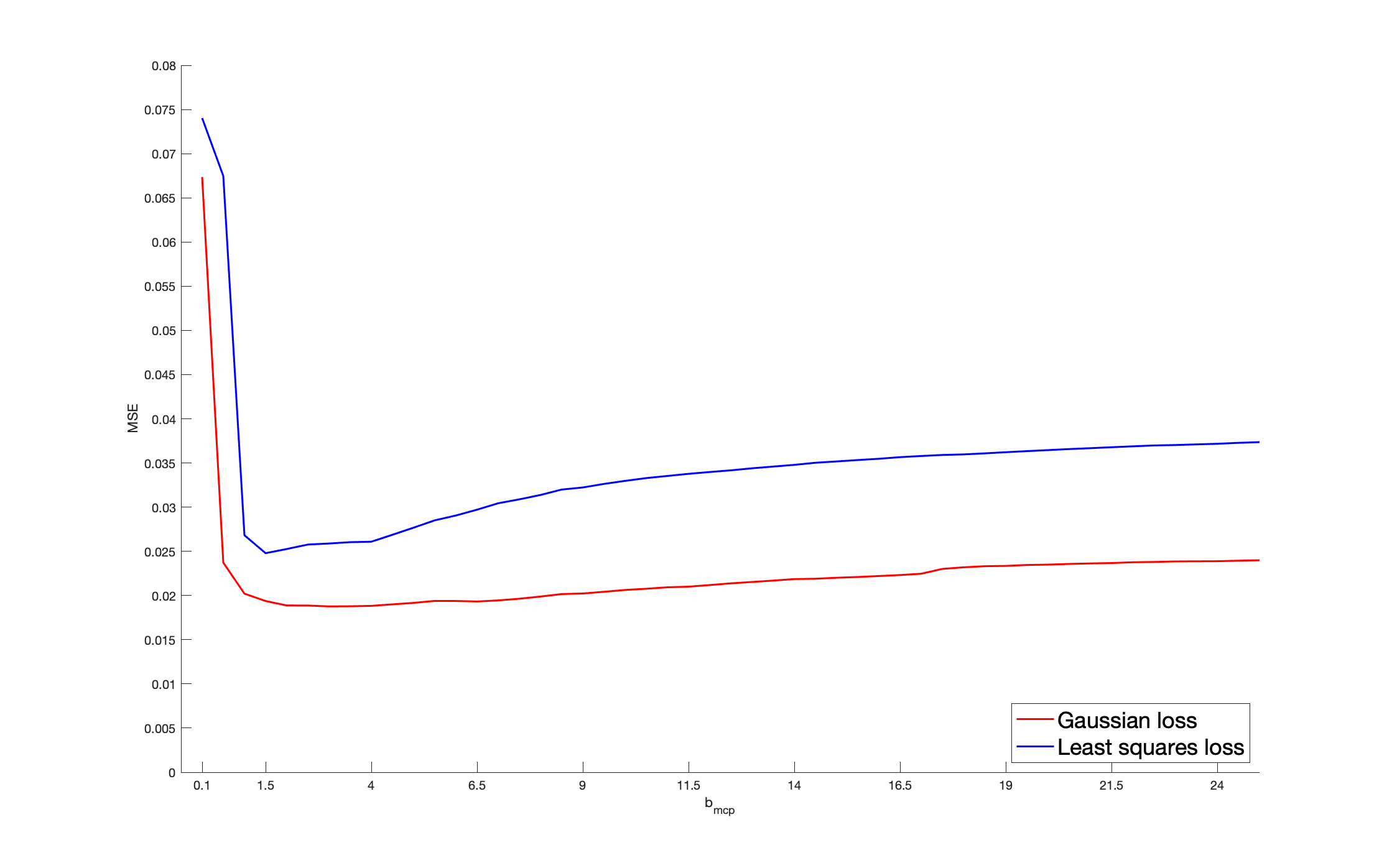
To be more specific, a sparse is randomly drawn for each batch as detailed below. Then, we generate a sample of vectors as follows: we draw , , from a Gaussian copula with parameter ; then we consider their rank-based transformation to obtain a non-parametric estimator of their marginal distribution, providing the pseudo-observations that enter the loss function. Then, we solve (2.3). The non-penalized loss is the Gaussian log-likelihood, as defined in (5.1). Alternatively, in (2.3), we consider the least squares criterion for which , where . In both cases, the penalized problem is solved by a gradient descent algorithm based on the updating formulas of Section 4.2 in [24], where the initial value is set as . The score for cross-validation purpose is defined in (5.2) with the Gaussian loss or the least squares loss. Concerning , we apply the SCAD, MCP and LASSO penalties. The non-convex SCAD and MCP ones require the calibration of and , respectively. We select , a “reference” value identified as optimal in [12] by cross-validated experiments. In the MCP case, the “reference” parameter is set as , following [24]. We investigate the sensitivity of these non-convex procedures with respect to their parameters . In particular, our results are also detailed with the values and . This case corresponds to “large” and , for which the corresponding penalty functions tend to the LASSO penalty.
We consider the dimensions , so that the dimension of is and , respectively. The cardinality of the true support is set arbitrarily as (resp. ) when (resp. ), so that the percentage of zero coefficients of is approximately (resp. ). As for the non-zero coefficients of , for each batch, they are generated from the uniform distribution , thus ensuring the minimum signal strength . As for the sample size, we consider . Note that, for each batch, the number of zero coefficients of remains unchanged but their locations may be different.
We report the variable selection performance through the percentage of zero coefficients in that are correctly estimated, denoted by C1, and the percentage of non-zero coefficients in correctly identified as such, denoted by C2. The mean squared error (MSE), defined as , is reported as an estimation accuracy measure. These metrics are averaged over the two hundred batches and reported in Table 1. For clarifying the reading of the figures, the first entry in the column “Gaussian” represents the percentage of the true zero coefficients correctly identified by the estimator deduced from the Gaussian loss function, with SCAD penalization when , for a sample size , a dimension , and averaged over two hundred batches; in the last MSE line, the value in the column “Least Squares” represents the MSE of the estimator deduced from the least squares loss function with MCP penalization when , for a sample size and , and averaged over two hundred batches. Our results highlight that, for a given loss, the SCAD/MCP-based penalization procedures provide better results in terms of support recovery compared to the LASSO for our reference values of . Furthermore, the SCAD and even more the MCP-based estimators with the Gaussian loss provide better recovery performances compared to the least squares loss. This is particularly true with the indicator C1, i.e., for the sake of identifying the zero coefficients. Interestingly, large values worsen the recovery ability. Indeed, such large values result in a LASSO-type behavior, which is biased so that small will tend to be selected. Moreover, for any given penalty function, the Gaussian loss-based MSE’s are always lower than the least squares loss-based MSE’s, which suggest that the estimator deduced from the former loss is more efficient than the estimator obtained from the latter loss. Furthermore, larger values worsen the MSE performances: when , for a given loss function, the MSE’s of SCAD/MCP are close to the LASSO. In Section I of the Appendix, we investigate further the sensitivity of the performances of the SCAD and MCP-based estimators with respect to and .
| Truth | Gaussian | Least Squares | ||
|---|---|---|---|---|
| C1 | ||||
| C2 | ||||
| MSE | ||||
| C1 | ||||
| C2 | ||||
| MSE | ||||
| C1 | ||||
| C2 | ||||
| MSE | ||||
| C1 | ||||
| C2 | ||||
| MSE | ||||
| C1 | ||||
| C2 | ||||
| MSE | ||||
| C1 | ||||
| C2 | ||||
| MSE | ||||
| C1 | ||||
| C2 | ||||
| MSE | ||||
| C1 | ||||
| C2 | ||||
| MSE |
5.2.3 Conditional copulas
Our next application is dedicated to the sparse estimation of conditional copula models with known link functions and known marginal laws of the covariates: the experiment is an application of the penalized problem detailed in Subsection 4.1. We specify the law of , given some covariates , as a parametric copula with parameter , where and ( and , with our notations of Section 4). We assume the marginal distribution of , , is unknown and does not depend on . We focus on the Clayton and Gumbel copulas, and restrict ourselves to .
In the same vein as in the previous application to sparse Gaussian copulas, for each sample size , we draw two hundred independent batches of vectors as follows: in each batch, we simulate a sparse true ; then for every , we draw the covariates , , from a uniform distribution , independently of each other; then, for a given , we sample from the Clayton/Gumbel copula with parameter ; we consider their rank-based transformation to obtain the pseudo-observations , which are plugged in the penalized criterion. Here, the copula parameters are specified in terms of Kendall’s tau: for each , define the Kendall’s tau . Using the mappings of, e.g., [26], set for the Clayton copula and for the Gumbel copula. We consider the dimension , and set the cardinality of the true support as , so that approximately of the entries of are zero coefficients. For each batch, the non-zero entries are simulated from the uniform distribution , which ensures that the following copula parameter constraints are satisfied: (resp. ) for the Clayton (resp. Gumbel) copula. For each batch, the locations of the zero/non-zero entries in are arbitrary, but the size of remains fixed. Finally, we consider the sample size . For a given batch, our criterion becomes:
where is the log-density of the Clayton/Gumbel copula with parameter . As for the penalty function, we consider the SCAD, MCP and LASSO penalty functions to estimate and . Moreover, we choose and . To assess the finite sample performance of the penalization methods and as in Section 5.2.2, we report in Table 2 the percentage of zero coefficients correctly estimated (C1), the percentage of non-zero coefficients correctly identified (C2) and the mean squared error (MSE), averaged over the two hundred batches. For both models and low/large sample sizes, our results emphasize the poor performances of the LASSO penalization in terms of support recovery (correct identification of the zero coefficients). As for non-convex penalization, the trade-off between C1 and C2 is more indicative than in the application to the Gaussian copula: small provide better C1 to the detriment of C2, which results in larger MSE since C2 worsens in that case. The MSE results are significantly improved for large. Mid-range values provide an optimal trade-off in terms of the combined C1, C2 and MSE metrics.
| Gumbel | Gumbel | Clayton | Clayton | |
| Penalty | C1 C2 MSE | C1 C2 MSE | C1 C2 MSE | C1 C2 MSE |
| SCAD, | ||||
| MCP, | ||||
| LASSO |
6 Conclusion
We studied the asymptotic properties of sparse M-estimator based on pseudo-observations, where we treat the marginal distributions entering the loss function as unknown, which is a common situation in copula inference. Our framework includes, among others, semi-parametric copula models and the CML inference method. We assume sparsity among the coefficients of the true copula parameter and apply a penalty function to recover the sparse underlying support. Our method is based on penalized M-estimation and accommodates data-dependent penalties, such as the LASSO, SCAD and MCP. We establish the consistency of the sparse M-estimator together with the oracle property for the SCAD and MCP cases for both fixed and diverging dimensions of the vector of parameters. Because of the presence of non-parametric estimators of marginal cdfs’ and potentially unbounded loss functions, it is difficult to exhibit simple regularity conditions and to derive the oracle property. This would make the large sample analysis intricate when and simultaneously diverge. We shall leave it as a future research direction. Among potential applications of our methodology, the (brute force) estimation of vine models ([10]) under sparsity seems to be particularly relevant. Nonetheless, checking our regularity assumptions for such highly nonlinear models would surely be challenging. In addition, it would be interesting to prove similar theoretical results in the case of conditional copulas for which their conditional margins would depend on covariates.
Acknowledgements
J.D. Fermanian was supported by the labex Ecodec (reference project ANR-11-LABEX-0047) and B. Poignard by the Japanese Society for the Promotion of Science (Grant 22K13377).
References
- [1] Abadir, K.M. and J.R. Magnus (2005). Matrix algebra. Cambridge University Press.
- [2] Abegaz, F., Gijbels, I. and N. Veraverbeke (2012). Semiparametric estimation of conditional copulas. Journal of Multivariate Analysis, 110: 43–73.
- [3] Abramowitz, Milton and I.A. Stegun (1972). Handbook of mathematical functions with formulas, graphs, and mathematical tables, Vol. 55, Reprint of the 1972 ed. A Wiley-Interscience Publication. Selected Government Publications, John Wiley & Sons, New York.
- [4] Aistleitner, C. and J. Dick (2015). Functions of bounded variation, signed measures, and a general Koksma-Hlawka inequality. Acta Arithmetica, 167:143–171.
- [5] Bühlmann, P. and S. van de Geer (2011). Statistics for high-dimensional data: Methods, theory and applications. 1st ed. Springer Series in Statistics. Springer, Berlin.
- [6] Berghaus, B. and Bücher, A. and S. Volgushev (2017). Weak convergence of the empirical copula process with respect to weighted metrics. Bernoulli, 23(1):743–772.
- [7] Cai, Z. and X. Wang (2014). Selection of mixed copula model via penalized likelihood. Journal of the American statistical Association, 109(506):788–801.
- [8] Chen, X. and Y. Fan (2005). Pseudo-likelihood ratio tests for semiparametric multivariate copula model selection. Canadian Journal of Statistics, 33(3):389–414.
- [9] Chen, X. and Y. Fan (2006). Estimation and model selection of semiparametric copula-based multivariate dynamic models under copula misspecification. Journal of econometrics, 135(1-2): 125–154.
- [10] Czado, C (2019). Analyzing dependent data with vine copulas. 1st ed. Lecture Notes in Statistics. Springer, Cham.
- [11] Dehling, H., Durieu, O. and M. Tusche (2014). Approximating class approach for empirical processes of dependent sequences indexed by functions. Bernoulli, 20(3):1372–1403.
- [12] Fan, J. and R. Li (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American statistical Association, 96(456):1348–1360.
- [13] Fan, J. and H. Peng (2004). Nonconcave penalized likelihood with a diverging number of parameters. The Annals of Statistics, 32(3):928–961.
- [14] Fermanian, J.-D. (1998). Contributions à l’analyse nonparamétrique des fonctions de hasard sur données multivariées et censurées. PhD thesis, Paris 6.
- [15] Fermanian, J.-D., Radulović, D. and M. Wegkamp (2002). Weak convergence of empirical copula processes, Center for Research in Economics and Statistics, Working Paper, No. 2002-06.
- [16] Fermanian, J.-D. and D. Radulović and M. Wegkamp (2004). Weak convergence of empirical copula processes. Bernoulli, 10(5):847–860.
- [17] Fermanian, J.-D. and M. Wegkamp (2012). Time-dependent copulas. Journal of Multivariate Analysis, 110:19–29.
- [18] Fermanian, J.D. and O. Lopez (2018). Single-index copulas. Journal of Multivariate Analysis, 165:27–55.
- [19] Genest, C. and Ghoudi, K. and L.-P. Rivest (1995). A semi-parametric estimation procedure of dependence parameters in multivariate families of distributions. Biometrika, 82(3):543–552.
- [20] Ghoudi, K. and B. Rémillard (2004). Empirical processes based on pseudo-observations II: the multivariate case. Fields Institute Communications, 44:381–406.
- [21] Gijbels, I., Veraverbeke, N. and O. Marel (2011). Conditional copulas, association measures and their applications. Computational Statistics & Data Analysis, 55(5), 1919–1932.
- [22] Hamori, S., Motegi, K. and Z. Zhang (2019). Calibration estimation of semiparametric copula models with data missing at random. Journal of Multivariate Analysis, 173:85–109.
- [23] Hastie, T., Tibshirani, R. and J. Friedman (2009). The elements of statistical learning: Data mining, inference, and prediction. 2nd ed.Springer Series in Statistics. Springer, New York.
- [24] Loh, P.L and M.J. Wainwright (2015). Regularized M-estimators with non-convexity: statistical and algorithmic theory for local optima. Journal of Machine Learning Research, 16:559-616.
- [25] Loh, P.L and M.J. Wainwright (2017). Support recovery without incoherence: A case for nonconvex regularization. The Annals of Statistics, 45(6):2455–2482.
- [26] Nelsen, R.B. (2006). An introduction to copulas. 2nd ed. Springer Series in Statistics. Springer, New York.
- [27] Portnoy, S. (1985). Asymptotic behavior of M-estimators of regression parameters when is large; II. Normal approximation. The Annals of Statistics, 13(4):1403–1417.
- [28] Radulović, D. and Wegkamp, M. and Y. Zhao (2017). Weak convergence of empirical copula processes indexed by functions. Bernoulli, 23(4B):3346–3384.
- [29] Rémillard, B. and O. Scaillet (2009). Testing for equality between two copulas. Journal of Multivariate Analysis, 100(3):377–386.
- [30] Ruymgaart, F.H. (1974). Asymptotic normality of nonparametric tests for independence. The Annals of Statistics, 2(5):892–910.
- [31] Ruymgaart, F.H. and Shorack, G.R. and W.R. Van Zwet (1972). Asymptotic normality of nonparametric tests for independence. The Annals of Mathematical Statistics, 43(4):1122–1135.
- [32] Segers, J. (2012). Asymptotics of empirical copula processes under non-restrictive smoothness assumptions. Bernoulli, 18(3):764–782.
- [33] Shi, J. H. and T. Louis (1995). Inferences on the association parameter in copula models for bivariate survival data. Biometrics, 51(4):1384–1399.
- [34] Tsukahara, H. (2005). Semi-parametric estimation in copula models. The Canadian Journal of Statistics, 33(3):357–375.
- [35] van der Vaart, A.W. and J. Wellner (1996). Weak convergence and empirical processes: with applications to statistics. 1st ed. Springer Series in Statistics. Springer, New York.
- [36] van der Vaart, A.W. and J.A. Wellner (2007). Empirical processes indexed by estimated functions. Asymptotics: Particles, Processes and Inverse Problems, 234–252, IMS Lecture Notes Monograph Series, 55.
- [37] Yang, B. and Hafner, C.M. and Liu, G. and W. Long (2021). Semi-parametric estimation and variable selection for single-index copula models. Journal of Applied Econometrics, 36(7):962–988.
- [38] Zhang, C.-H. (2010). Nearly unbiased variable selection under minimax concave penalty. The Annals of Statistics, 38(2):894-942.
- [39] Zhang, S. and O. Okhrin and Q.M. Zhou and P.X.-K. Song (2016). Goodness-of-fit test for specification of semiparametric copula dependence models. Journal of Econometrics, 193(1):215–233.
- [40] Zou, H. (2006). The adaptive lasso and its oracle properties. Journal of the American statistical association, 101(476):1418–1429.
Appendix A Multivariate rank statistics and empirical copula processes indexed by functions
In this section, we prove some theoretical results about the asymptotic behavior of multivariate rank statistics
for a class of maps that will be of “locally” bounded variation and sufficiently regular. Such maps will be allowed to diverge when some of their arguments tend to zero or one, i.e. when their arguments are close to the boundaries of . We will prove the asymptotic normality of , extending Theorem 3.3 of [6] to any dimension . Moreover, we will state the weak convergence seen as an empirical process indexed by , for a convenient family of maps .
To be specific, consider a family of measurable maps . As in [6] and for any , define the weight function
When , check that . Moreover, if , then . To lighten notations and when there will be no ambiguity, the map will simply denoted as hereafter. For technical reasons, we will need the map for every .
Recall the process and for any . Therefore, may be considered as a process defined on . The maps may potentially be unbounded, particularly when their arguments tend to the boundaries of the hypercube . This is a common situation when is chosen as the log-density of many copula families. Moreover, we will need to apply an integration by parts trick that has proved its usefulness in several copula-related papers, particularly [28] and [6]. To this end, we introduce the following class of maps.
-
Definition.
A map is of locally bounded Hardy Krause variation, a property denoted by , if, for any sequence and , , , , the restriction of to is of bounded Hardy-Krause variation.
The concept of Hardy-Krause variation has become a standard extension of the usual concept of bounded variation for multivariate maps: see the Supplementary Material in [6] or Section 2 and Appendix A in [28], and the references therein.
Denote the box and its complementary in , . Moreover, any sub-vector whose components are all equal to (resp. ) will be denoted as (resp. ). For any and a measurable map , the integral can be conveniently defined: see [6], Section 3.1 and its Supplementary Material.
In terms of notations, we use the same rules as [28], Section 1.1, to manage sub-vectors and the way of concatenating them. More precisely, for , denotes the cardinality of , and the unary minus refers to the complement with respect to so that . For , denotes a -tuple of real numbers whose elements are ; the vector typically belongs to . Now let , and two vectors in . The concatenation symbol “” is defined as follows: the vector denotes the point such that for and for . The vector is well defined for and when even if and remains unspecified. We use this concatenation symbol to glue together more than two sets of components: let with mutually disjoint sets such that . Then is a well defined vector in . Finally, for a function and a constant vector , the function denotes a lower-dimensional projection of onto . The integral of a function w.r.t. the measure induced by the latter map will be denoted as .
-
Definition.
A family of maps is said to be regular with respect to the weight function for some (or -regular, to be short) if
-
(i)
every is and right-continuous;
-
(ii)
the map is bounded on ,
(A.1) and, for any partition of the set of indices with ,
(A.2) Moreover, the latter sequence tends to zero when .
-
(i)
When is a singleton, one simply says that the map is -regular. Note that, if , then except when and simultaneously. In the latter case, .
Remark 2.
Consider a family of maps from to . Assume there exist subsets , s.t. every member can be written
for some maps , . Define for every . If every , is regular w.r.t. the weight function , then it is easy to see that is regular w.r.t. the weight function . This property may be invoked to prove the regularity of the Gaussian copula family, for instance (see Section E in the Appendix).
Remark 3.
Any family of maps defined on may formally be seen as a family of maps defined on a larger dimension, say , : every defines a map on by setting , , . It can be easily checked that, if is regular then this is still the case for .
Beside the regularity conditions on the family of maps , we will need that the (standard) empirical process is well-behaved. To this aim, we recall the so-called conditions 4.1, 4.2 and 4.3 in [6].
Assumption 10.
There exists such that, for all and all sequences , we have
Assumption 11.
There exists and such that, for any , any and any , we have
Assumption 12.
The empirical process converges weakly in to some limit process which has continuous sample paths, almost surely.
As pointed out in [6], such conditions 10-12 are satisfied for i.i.d. data with , and . In the latter case, the limiting process is a -Brownian bridge, such that for any and in , with the usual notation . More generally, if the process is strongly stationary and geometrically -mixing, then the assumptions 10-12 are still satisfied, with the same choice , and (Proposition 4.4 in [6]). In the latter case, the covariance of the limiting process is more complex: .
Assumption 13.
For any , , any that belongs to a regular family and for any continuous map , the sequence is convergent when . Its limit is denoted as , i.e. it is given by an integral w.r.t. a borelian measure on denoted as .
The latter regularity condition is required to get the weak convergence of our main statistic in Theorem A.1. Note that the map is not defined when one component of is one. Therefore, the way we write the limits in Assumption 13 is a slight abuse of notation. Typically, will be defined as the limit when tends to when such a limit exists. In other standard situations, there exists a measurable map such that . If it is possible to extend by continuity the map when tends to , simply set . But other more complex situations.
To get the weak convergence of the process indexed by the maps in , we will need to strengthen the latter assumption 13, so that it becomes true uniformly over .
Assumption 14.
For any and any continuous map ,
when .
Theorem A.1.
(i) Assume the assumptions 2,10 and 11 are satisfied and consider a family of maps that is -regular, for some . Then, for any , we have
| (A.3) | |||||
where , and .
(ii) In addition, assume the conditions 12 and 13 apply. Then, for any function , the sequence of random variables tends in law to the centered Gaussian r.v.
| (A.4) |
where for any .
(iii) Under the latter assumptions of (i) and (ii), in addition to Assumption 14, weakly tends in to a Gaussian process.
Points (i) and (ii) of the latter theorem yield a generalization of Theorem 3.3 in [6] for any arbitrarily chosen dimension , and uniformly over a class of functions. Note that it is always possible to set and we have proved the weak convergence of a single multivariate rank statistic. The proof is based on the integration by part formula in [28]. Note that, in dimension , for any . Thus, in the bivariate case, the limiting law of is simply the law of , as stated in Theorem 3.3 in [6]. Nonetheless, this is no longer true in dimension , explaining the more complex limiting laws in our Theorem A.1. Finally, the sum in (A.4) can be restricted to the subsets such that . Indeed, when is a singleton, then is zero a.s.
The point (iii) of Theorem A.1 extends Theorem 5 in [28]. The latter one was restricted to right-continuous maps of bounded Hardy-Krause variation and defined on the whole hypercube . For any of these maps , there exists a finite signed Borel measure bounded on such that for every (Theorem 3 in [4]). In particular, they are bounded on , an excessively demanding assumption in many cases. Indeed, for the inference of copulas, many families of relevant maps contain elements that are not of bounded variation or cannot be defined on as a whole, as pointed out by several authors, following [32]; see Section 3.4 in [28] too. This is in particular the case with the Canonical Maximum Likelihood method and Gaussian copulas. In such a case, and is the density of a Gaussian copula with correlation parameter . Therefore, we have preferred the less restrictive approach of [6], that can tackle unbounded maps (in particular copula log-densities), through the concept of locally bounded Hardy Krause variation.
We deduce from Theorem A.1 an uniform law of large numbers too.
Corollary A.2.
Remark 4.
In the literature, some ULLN for copula models have already been applied, but without specifying the corresponding rates of convergence to zero. In semi-parametric models, some authors invoked some properties of bracketing numbers (Lemma 1 in [8]; Th. 17 in the working paper version of [15]): if, for every , the bracketing number of (denoted in the literature) is finite, then tends to zero a.s.
Appendix B Asymptotic variance of
Here, we provide a plug-in estimator of the variance-covariance matrix of the vector that appeared in Theorem 3.2. The latter vector is centered Gaussian and, for every ,
In the latter formula, we will replace with . Denote the covariance function of the process as , i.e. , for every and in . Then, the covariance function of the process is
In the latter formula, every partial derivative of the copula could be empirically approximated, as in [29] for instance. Moreover, assume we have found an estimator of the map , denoted . With i.i.d data, is obviously approximated by . This would yield and estimator of , for every , that can be plugged in (B). Taking all pieces together yields an estimator of .
Appendix C Proofs of Theorem A.1 and Corollary A.2
C.1 Proof of Theorem A.1
To state (i), we follow the same paths as in the proof of Theorem 3.3 in [6]. For any , define . Note that, when , , but this property does not extend to larger dimensions. Any remainder term that tends to zero in probability uniformly w.r.t. will be denoted as . Note that, for any ,
Let us prove that . Indeed, a vector belongs to iff one of its components is smaller than or is strictly larger than . Thus, let us decompose as the disjoint union of “boxes” on such as
where and is a partition of . Note that, for any , we have
Since there exists a constant such that for every by -regularity, we have for any
that tends to zero with uniformly wrt . Therefore, we have proven that .
Moreover, invoking the integration by parts formula (40) in [28], we get
In , the ‘+’ symbol within denotes the disjoint union. In other words, the summation is taken over all partitions of into three disjoint subsets. Moreover, we have used the usual notation that is the sum of component-wise differentials of over all the vertices of the hypercube . For instance, in dimension two,
By assumptions 2, 10 and 11, Theorem 4.5 in [6] holds. Then, the term can be rewritten as
| (C.1) |
Moreover, due to Lemma 4.10 in [6] and their theorem 4.5 again, this yields
The term is a finite sum of integrals as
where is not empty and is not equal to the whole set . By the first part of Theorem 4.5 and Lemma 4.10 in [6], we obtain
If , any argument of belongs to the subset . In such a case, for any , we have
The two latter terms tend to zero with , for any sufficiently small . Indeed, the first probability tends to zero with by Lemma 4.9 in [6], and the second one may be arbitrarily small by -regularity, choosing a sufficiently small . Therefore, all the terms of for which are negligible. Moreover, if , then . By the stochastic equicontinuity of the process (Lemma 4.10 in [6]), we have
invoking again (A.2), when . Re-indexing the subsets , check that yields the sum in (A.3) plus a negligible term.
The remaining term is a sum of terms. By -regularity, all these terms are smaller than a constant times , evaluated at a -vector whose components are or . This implies these terms are equal to with the same arguments (Th. 4.5 in [6]), plus a negligible term. Due to Lemma 4.9 in [6], all of the latter terms tend to zero in probability, and then . Therefore, we have proven (A.3) and point (i).
(ii) If, in addition, the process is weakly convergent, then is weakly convergent to in , by Theorem 2.2 in [6]. For a given , define the sequence of maps as
If a sequence of maps tends to in and is continuous on , let us prove that , where
The difference is a sum of differences between integrals that come from (C.1). The first one is managed as
that tends to zero by (A.1) and Assumption 13. The other terms of are indexed by a subset , and can be bounded similarly:
Therefore, apply the extended continuous mapping (Theorem 1.11.1 in [35]) to obtain the weak convergence of (that is equal to in our case) towards in . Note that almost every trajectory of on is continuous. Since , this proves the announced weak convergence result (ii).
(iii) Our arguments are close to those invoked to prove Theorem 1 in [28]. Our point (ii) above yields the finite-dimensional convergence of in . For any (possibly random) map and any , set
Moreover, define
We have proved above (recall Equation (A.3) and (C.1)) that, for any ,
Therefore, we expect that the weak limit of in will be . It is sufficient to prove that weakly tends to the latter process.
To this end, we slightly adapt our notations to deal with functionals defined on . The weak limit of on is the Gaussian process , that is tight (Ex. 1.5.10 in [35]). Moreover, define the map as , where denotes the set on continuous maps on , endowed with the sup-norm. Similarly, define as . We now have to prove that weakly tends to on .
First, we prove that is continuous. Let be a sequence of maps in that tends to is the latter space. We want to prove that tends to in . The first term of that comes from the definition of is easily managed:
that tends to zero because of (A.1). The other terms are tackled similarly:
that tends to zero. We have used the fact that, due to (A.2) and Assumption 14, we have
As a consequence, tends to in . Therefore, by continuity, the expected weak limit of is tight on .
Then, the weak convergence of towards in is obtained if we prove that the bounded Lipschitz distance between the two processes tends to zero with (Th. 1.12.4 in [35]), i.e. if
with the supremum taken over all the uniformly bounded and Lipschitz maps , and for all . By the triangle inequality, we have
To deal with , note that
for some positive constant , due to (A.2). This proves that is Lipschitz, with a Lipschitz constant that does not depend on nor . Therefore, we get
that tends to zero because of the weak convergence of to in (Th. 4.5 in [6]).
To show that tends to zero, note that, for every , we have
Clearly, tends to zero, invoking (A.2) and the continuity of on . By Assumption 14, tends to zero a.s. Thus, we have proved that
tends to zero for almost every trajectory and when , Considering the bounded Lipschitz maps as in the definition of , deduce
Since for every , the sequence is bounded by two. And we have proved above that tends to zero a.s. Thus, the dominated convergence theorem implies that when , i.e. when .
To conclude, we have proved that and . Since the limit is tight, we get the weak convergence of to in , i.e. the weak convergence of indexed by , i.e. in , as announced.
C.2 Proof of Corollary A.2
By inspecting the proof of Theorem A.1 (i), it appears that it is sufficient to prove
for any , . For any constant , we have
| (C.4) | |||||
Check that , for any sequence of positive numbers , and with . This yields
Note that when , and set . Thus, for sufficiently large, and we get
Since , then too because all partial derivatives , , belong to (Th. 2.2.7 in [26]). Therefore, the first term on the r.h.s. of (C.4) tends to zero. Finally, the second term on the r.h.s. of (C.4) may be arbitrarily small with a large , due to (A.2), proving the result.
Appendix D Additional proofs
D.1 Proof of Theorem 3.1
We denote and we would like to prove that, for any , there exists such that, for any , we have
| (D.1) |
Now, following the reasoning of Fan and Li (2001), Theorem 1, and denoting the penalized loss , we have
| (D.2) |
and we can always impose , our choice hereafter. If the r.h.s. of (D.2) is smaller than , there is a local minimum in the ball with a probability larger than . In other words, (D.1) is satisfied and . Now, by a Taylor expansion of the penalized loss function around the true parameter, we get
for some parameter such that . Note that we have used and the positiveness of the penalty. Thus, it is sufficient to prove there exists such that
| (D.3) |
Let us deal with the non-penalized quantities. First, for any , we have
due to the first-order conditions. For any , we have assumed that the family of maps is -regular. Moreover, Assumption 10 and the compacity of implies . Then, we can apply Corollary A.2, that yields
By Cauchy-Schwarz, we deduce
The empirical Hessian matrix can be expanded as
We have assumed that the maps , , belong the a -regular family. Therefore, applying Corollary A.2, we get
As a consequence, since , this yields
that is positive by assumption, when is sufficiently large and for a probability arbitrarily close to one. By similar arguments with the family of maps , we get
Let us now treat the penalty part as in [13] (proof of Theorem 1, equations (5.5) and (5.6)). By using exactly the same method, we obtain
and the latter term is dominated by , allowing to be large enough. Thus, for such , we have
Since the latter dominant term is larger than for large enough, where denotes the smallest eigenvalue of , we deduce (D.3) and finally .
D.2 Proof of Theorem 3.2
Point (i): The proof is performed in the same spirit as in Fan and Li (2001). Consider an estimator of such that , as in Theorem 3.1, with . Using our notations for vector concatenation, as detailed in Appendix A, the support recovery property holds asymptotically if
| (D.4) |
for any constant with a probability that tends to one with . Set . To prove (D.4), it is sufficient to show that, for any such that , we have with a probability that tends to one
| (D.5) |
for any . By a Taylor expansion of the partial derivative of the penalized loss around , we obtain
for some that satisfies . The family of maps is -regular and . As a consequence, by Corollary A.2,
As for the second order term, the maps are -regular by assumption, for any . Then, by Corollary A.2, we deduce
Finally, for the remaining third order term, since the family of maps is -regular by assumption, Corollary A.2 yields
that is bounded in probability by Assumption 1. Hence putting the pieces together and using the Cauchy-Schwarz inequality, we get
Under the assumptions , and tends to the infinity, the sign of the derivative is determined by the sign of . As a consequence, (D.5) is satisfied, implying our assertion (i). Indeed, all zero components of will be estimated as zero with a high probability. And its non-zero components will be consistently estimated. Then, the probability that all the latter estimates will not be zero tends to one, when .
Point (ii): We have proved that . Therefore, for any , the event in occurs with a probability larger than for large enough. Since we want to state a convergence in law result, we can consider that the latter event is always satisfied. By a Taylor expansion around the true parameter, the orthogonality conditions yield
where and , which simplifies into a diagonal matrix since the penalty function is coordinate-separable. Obviously, is a random parameter such that . Rearranging the terms and multiplying by , we deduce
where . First, under the -regularity conditions and by Corollary A.2, we have . Second, the third order term can be managed as follows:
is a vector as size whose -th component is
for any . Invoking Corollary A.2 and Assumption 1, for any . Then, since , we obtain
Regarding the gradient in , since belongs to our -regular family for any , apply Theorem A.1 (ii): for any , we have
We then conclude by Slutsky’s Theorem to deduce the asymptotic distribution
where the -dimensional random vector defined in (D.2).
Remark 5.
It would be possible to state Theorem 3.2-(ii) under other sets of regularity conditions. Indeed, the latter result mainly requires a CLT (given by our Theorem A.1 (ii)) and a ULLN (given by our Corollary A.2). The latter one may be obtained with a condition on the bracketing numbers associated with the family of maps for some (small) : see Remark 4 at the end of the main text. This would provide an alternative way of managing the term . To deal with , a CLT for can be obtained under some regularity conditions on and its derivative w.r.t. , as introduced in [30] and [31]. See [34], Prop. 3 and Assumption (A.1), to be more specific. At the opposite, the proof of Theorem 3.2-(i) (support recovery) requires Corollary A.2 and not only a usual ULLN. Indeed, an upper bound for the rate of convergence to zero of is here required to manage the penalty functions and sparsity.
Appendix E Regularity conditions for Gaussian copulas
Let us verify that the Gaussian copula family fulfills all regularity conditions that are required to apply Theorems 3.1 and 3.2. Here, the loss function is where . Since the true underlying copula is Gaussian, the random vector in is Gaussian . The vector of parameters is , whose “true value” will be . Note that , as a function of , is a quadratic form w.r.t. , and that
| (E.1) |
Assumption 1: when is invertible, and are positive definite. This is exactly the same situation as the Hessian matrix associated with the (usual) MLE for the centered Gaussian random vector . When belongs to a small neighborhood of , the associated correlation is still invertible by continuity. Then, the third order partial derivatives of the loss are uniformly bounded in expectation in such a neighborhood, due to (E.1).
The first part of Assumption 2 is satisfied for Gaussian copulas, as noticed in [32], Example 5.1. Checking (3.1) is more complex. This is the topic of Lemma E.1 below.
Let us verify Assumption 3 for the Gaussian loss defined as , with : every member of the family has continuous and integrable partial derivatives on and then is . Moreover, any can be written as a quadratic form w.r.t. :
Note that, for every , for any and . Thus, for every , we clearly have
for every , proving the first condition for the regularity of . To check (A.1), note that is zero when . Otherwise, when , . Thus, to apply our theoretical results, it is sufficient to check Assumption 3 by replacing by , as if the loss and its derivatives were some functions of only, instead of . See the remark after the definition of the regularity too. Since (c.f. (E.2) in the proof of Lemma E.1), we obtain
for some constant , yielding (A.1). Note that we have used the inequality .
Now consider (A.2). We restrict ourselves to the case , because we are interested in the situation for which . Again, when the cardinality of is larger than two, the latter condition is satisfied because . When is a singleton, say , the absolute value of
is smaller than a constant times
We have used the identity . Note that when . Using , this yields
for some constant . The latter r.h.s. tends to zero, because ([3], 26.2.23). This reasoning can be led for every map . This proves (A.2). Importantly, we have proved that all integrals as tend to zero with . As a consequence, the limiting law in Theorem 3.2 is simply .
Assumption 13 is a direct consequence of the dominated convergence theorem and the upper bounds that have been exhibited just before.
Remark 6.
Alternatively to the Gaussian loss function, consider the least squares loss
Then, it is easy to check our regularity assumptions as above. In particular, every member of can be written as a quadratic form w.r.t. , as for the previous log-likelihood loss. Then the same techniques apply.
Remark 7.
For completeness, let us provide the gradient of the Gaussian and least squares losses w.r.t. the parameter . By the identification of the gradient following [1], the derivatives of the Gaussian and least squares functions are, respectively, given by
The Gaussian and least squares based Hessian matrices respectively follow as
and .
Lemma E.1.
Let be a -dimensional Gaussian copula. Then, there exists a constant s.t., for every in and every ,
Obviously, the constant depends on the dimension and on the correlation matrix . We prove the latter property below. In dimension two, it had been announced in [32] and [6], but without providing the corresponding (non trivial) technical details.
Proof.
First assume that and . Note that the random vector is Gaussian . The extra diagonal coefficient of is . Moreover, , where is the bivariate cdf of , and . With obvious notations, simple calculations provide
Since , we deduce
But there exists a constant such that
| (E.2) |
Indeed, when tends to zero, ([3], 26.2.23). Then, the map is bounded. As a consequence, . Similarly, by symmetry, , proving the announced inequality for crossed partial derivatives in the bivariate case.
Second, assume that and . We the same notations as above, simple calculations provide
Note that
implying
| (E.3) |
Indeed, it is easy to check that the map is bounded, because (resp. ) when (resp. ). Moreover,
Then, after an integration w.r.t. , we get
for some constant . This yields
| (E.4) |
Globally, (E.3) and (E.4) imply the announced result in this case.
Third, assume and choose the indices , w.l.o.g. By the definition of partial derivatives, we have
applying the previously proved result in dimension . Thus, the latter inequality is extended for any dimension , at least concerning crossed partial derivatives.
Concerning the second-order derivative of w.r.t. (to fix the ideas) and when , we can mimic the bivariate case. For any , set with , . We obtain
Note that, with for every , we have
| (E.5) | |||||
The latter upper bound does not depend on . Therefore, we get
| (E.6) |
for some constant . Moreover, for some constants and that depend on only, we have
| (E.7) |
It can be proved that there exist some constants and s.t.
| (E.8) |
where appears on the r.h.s. of (E.8). Indeed, the multiplicative factors , , inside the integral sum in (E.7) do not prevent the use of the same change of variable trick that had been used in the bivariate case for the treatment of above. Therefore, after integrations, the -function that would remain is the same as for , apart from a multiplicative factor. Since the latter quantity is due to Equation (E.5), this yields
| (E.9) |
Thus, (E.6) and (E.9) provide the result when , for the second-order derivatives of w.r.t. . ∎
Now, consider the case of a mixture of Gaussian copulas, i.e. the true underlying copula density is
where , and is a Gaussian copula density with a correlation matrix , . Here, is the concatenation of the first weights and the unknown parameters of every Gaussian copula. The latter ones are given by the lower triangular parts of the correlations matrices . Assume the true weights are strictly positive. The -order partial derivatives of the loss function w.r.t. and/or w.r.t. its arguments are linear combinations of maps as
| (E.10) |
where for every , and . Here, the derivatives of order have to be understood w.r.t. the corresponding parameters and/or the arguments of the copula , possibly multiple times. The latter derivatives may be written as
for some polynomials of the variables . When all the weights are positive, every map given by (E.10) with be (in absolute value) smaller than times a constant, that is itself a polynomial in terms of ’s components. Checking our Assumption 3, the single problematic one, is then reduced to checking this assumption for polynomials of . This task is easy and details are left to the reader. To conclude, the penalized CML method can be used with mixtures of Gaussian copulas, at least when the underlying true weights are strictly positive. In practice, penalization should then be restricted to the copulas parameters.
Appendix F Regularity conditions for Gumbel copulas
We now verify that the Gumbel copula family fulfills all regularity conditions that are required to apply Theorems 3.1 and 3.2 when the loss is chosen as the opposite of the log-copula density. A -dimensional Gumbel copula is defined by where , , for some parameter . Note that , . The associated density is
and the considered loss will be . Simple calculations show that for every , where
for some coefficients that depend on . Since , deduce
Assumption 1 is satisfied because all the derivatives of are nonzero and given by some polynomial maps of , of the quantities and , , or by the logarithm of such maps. The latter maps are clearly integrable, even uniformly w.r.t. in a small neighborhood of . This may be seen by doing the changes of variables , in the corresponding integrals.
To state Assumption 2 and w.l.o.g., let us focus on the cross-derivatives of the true copula w.r.t. its first two components. Note that
setting , denoted also by when there is no ambiguity. Since for every and , we have Then, we deduce
Since , this easily yields
To check Assumption 3 (the regularity of the partial derivatives of the loss function), it is sufficient to verify this assumption for every term , .
Study of and Assumption 3: by simple calculations, we get
Let us prove that is -regular for any . For convenience, will simply be denoted as hereafter.
Since is bounded on , for any triplet of positive numbers, the map is bounded on for any positive .
To verify (A.1), it is necessary to calculate
By tedious calculations, it can be shown that
for some map that is a power function of the quantities , , , and . Therefore, by symmetry, we have
For any s.t. , for some map that is a power function of the quantities and . Therefore, after integrations w.r.t. successively, we get
for some constant . Note that . After another integration w.r.t. , there exists another constant s.t.
This means (A.1) is satisfied for .
The same technique can be applied to check (A.2), assuming . Set , . For every , , we have
in every case, except when and simultaneously. W.l.o.g., let us assume that the components indexed by are the first ones, i.e. are . Note that
| (F.1) | |||||
for some map defined on that is a power function of the quantities , , , , and .
Let us first deal with the case and . Here,
when . The reasoning is then exactly the same as for checking (A.1), starting from (F.1), noting that and by doing integrations on instead of . In the calculation of the latter integrals, the single difference w.r.t. (A.1) comes from the terms instead of . This will not change the conclusion and we have stated (A.2).
Incidentally, Assumption 13 is easily checked by applying the dominated convergence theorem. This statement is general and will not be repeated hereafter for the other terms.
When or , note that
Thus, after integration on , we obtain
for some constants and . The latter term on the r.h.s. is , proving (A.2) when or when .
With exactly the same techniques, it can be proved that and (the family given by the second and third order derivatives of ) are -regular for any , even when the parameter is free to belong to a neighborhood of .
Study of and Assumption 3: Since is the Laplace transform of a stable distribution, it is completely monotone and for every . Thus, , . By definition, By recursion, it can be proved that , that is not zero because . Moreover, . Therefore, there exists a positive constant s.t.
| (F.2) |
for any . Note that we can write , for some constants and . As above and to lighten notations, denote , also denoted simply. Simple calculations yield
Moreover, successive derivatives yield
and, by iteration, we get
Note that, for every positive integer , there exists some constants and s.t.
| (F.3) |
As before, we have by symmetry
Deduce from (F.2) and (F.3) that the first latter term is smaller than a linear combination of integrals as
| (F.4) |
for some , , and But, for any , there exist some positive constants and s.t.
| (F.5) |
Moreover, there exist some positive constants and s.t.
for any . In the “worst case”, the latter integral (F.4) is smaller than a constant times
| (F.6) | |||||
after integrations w.r.t. successively. The r.h.s. of (F.6) is smaller than
By choosing , the latter integral is finite because
This proves that is finite.
Similarly, is smaller than a linear combination of integrals as
| (F.7) |
for some , , and Reminding (F.5), note that
Therefore, the “worst situation” to manage is to evaluate
| (F.8) |
When , integrate the latter integral w.r.t. successively, and we obtain a scalar times the integral
that is finite because
for some sufficiently small constant .
When , first integrate (F.8) w.r.t. , but on instead of . This will yield an upper bound of the -type term (F.8). In such a case, note that
with obvious notations. Thus, the term in (F.7) can be replaced by that does not depend on . The new integral w.r.t. is then
and we will choose . To bound (F.8), we are restricted to the evaluation of
Now, integrate w.r.t. successively. We obtain a scalar times the integral
that is finite for any , because
for some sufficiently small constant . This means (A.1) is satisfied for .
The same technique can be applied to check (A.2) for , mimicking the reasonings we led for .
With exactly the same techniques, it can be proved that and (here defined through ) are -regular for any . Actually, this is still the case for any higher-order -derivatives of the loss function. Indeed, the effect of such derivatives will be to add some multiplicative factors , , and such factors do not play any role to check -regularity.
Since Assumption 3 is trivially satisfied with , we have proven the validity of this assumption for the Gumbel family.
Remark 8.
Note that we have proved the regularity assumptions as if the weight function were replaced by , implying a stronger requirement.
Appendix G Regularity conditions for Clayton copulas
We now verify that the Clayton copula family fulfills all regularity conditions that are required to apply Theorems 3.1 and 3.2 when the loss is chosen as the opposite of the log-copula density. A -dimensional Clayton copula is defined by where , , for some parameter . Note that , and
The associated density on is
and the considered loss will be the . Note that
where is a positive map of only.
Assumption 1 is satisfied because is nonzero and integrable for any , even uniformly w.r.t. in a small neighborhood of . This can be easily seen by noting that
for every because , , and is finite for every .
To state Assumption 2 and w.l.o.g., let us focus on the cross-derivative w.r.t. the first two components of the true copula. By simple calculations, we get
setting . Since , deduce
Let us check Assumption 3, i.e. the regularity of the partial derivatives of the loss function. We will do the task for only. The task for and , or even for every higher-order derivatives of the loss w.r.t. , is obtained by exactly similar reasonings. Simple calculations yield
First, let us show that the map is bounded on for any positive . We will replace by hereafter, to weaken our notations. W.l.o.g., assume that . Then, . We deduce
that is a bounded function of .
Second, by simple calculations, it can be easily seen that , for some map that is a linear combination of the maps
for every .
Let us check (A.1) for all the latter maps. Concerning , this means we have to show
| (G.1) |
Indeed, by symmetry, we have
By an integration w.r.t. , the latter integral is smaller than a constant times
By integrating w.r.t. successively, we obtain a constant times
proving (G.1). To manage for any , note that, for any , there exist some positive constants and s.t.
Then, apply the same technique as for . The upper bound is here reduced to a constant times , that is finite by choosing . The same ideas apply to deal with : for some constant , and we recover the case. We have then proved (A.1) for .
The same technique can be applied to check (A.2), assuming . Denote , . W.l.o.g., let us assume that the components indexed by are the first ones, i.e. are . By simple calculations, it can be easily seen that , for some map whose absolute value is smaller than a linear combination of the maps
for every , by setting
We will check Assumption (A.2) for all latter maps.
For every , , note that
when or . For the moment, let us assume this is the case.
To deal with , we have by symmetry
First integrate w.r.t. between and . The absolute value of the latter integral w.r.t. can be bounded by a constant times
Then, successively integrate w.r.t. using the same type of upper bounds for every integral. We finally obtain an -integral of order
that is and then tends to zero with for any . Thus, (A.2) is proven in the case of the integrand . The terms are managed similarly by noting that when .
The task is similar with : after integrations w.r.t. , , etc, , we get
for any . The terms are managed similarly by noting that when .
Thus, it remains to consider the case and to check (A.2). Apply the same technique as above, invoking for every . Moreover, after every integration stage, it is possible to replace by in the denominators. For instance, in the case of , the integration w.r.t. yields
because in our case. After integration stages, we obtain
that is finite, as required. This is still the case for term , obviously, when because . The terms are managed similarly because for every and The same ideas apply with the terms , because To conclude, we have checked (A.2) in every situation.
Since Assumption 3 is now satisfied with , we have proven the validity of our assumptions in the case of the Clayton family.
Remark 9.
As for the Gumbel copula family, we have proved the regularity assumptions for the Clayton family as if the weight function were replaced by , a stronger property.
Appendix H Asymptotic properties for parameters of varying dimensions
In this section, we deal with the case of copula parameters whose dimensions are functions of the sample size. More formally, we consider a sequence of parametric copula models , for some subsets , . Therefore, the number of unknown parameters may vary with the sample size . In particular, the sequence could tend to the infinity with , i.e. when , but it is not mandatory.
As a consequence, in this section only, we introduce a sequence of loss functions , which hereafter enters in an associated map (whose notation remains unchanged, to simplify): for every , the map defines the “global loss” map
| (H.1) |
for every and every in .
Assumption 15.
For every , the parameter space is a borelian subset of . The function is uniquely minimized on at , and an open neighborhood of is contained in .
Exactly as detailed in the core of the main text (see the discussion after Assumption ‣ 2), our theory applies when belongs to the frontier of . Technical details are left to the reader. Let us illustrate the relevance of the diverging dimension case for copula selection.
Example 5 (Example 3 cont’d).
Consider an infinite sequence of given copulas in dimension . The true underlying copula will be estimated by a sequence of finite mixtures, given by the weighted sum of the first copulas , . If we choose the CML method, the loss function is the log-copula density associated with . In theory, we could extend the latter framework by assuming that every depends on an unknown parameter that has to be estimated in addition to the weights, but the numerical estimation of the enlarged unknown vector of parameters will surely become numerically challenging.
Example 6.
A probably more relevant application is related to single-index copulas with a diverging number of underlying factors and a known link function : in the same spirit as Example 4, the conditional copula of given would be the -dimension copula for some parameter to be estimated and a given parametric copula family .
We have now to consider a sequence of estimators defined as
| (H.2) |
We will focus on the distance between and .
Remark 10.
Note that we do not evaluate the distance between (or ) and an hypothetical “true parameter” , because they generally do not live in the same spaces. In some cases, it is possible to “dive” into and/or into a (correctly specified) parametric family of copulas. To illustrate, in Example 5, assume the true copula is an infinite sum of known copulas, i.e. . Setting , some identification constraints have to be found and they depend on the selected copulas . Therefore, it would be possible to compare the two infinite sequences and . Nonetheless, in such cases, the distance between and is strongly model-dependent. Since this is no longer an inference problem but rather a problem of model specification, we will not go further in this direction.
In terms of notations, for every , the sparse subset of parameters is , and will denote the cardinality of . Let us rewrite some of our latter assumptions that have to be adapted to the new framework.
Assumption 16.
The map is thrice differentiable on , for every . Any pseudo-true value satisfies the first-order condition, i.e. . Moreover, and exist, are positive definite and . Denoting by the smallest eigenvalue of , there exists a positive constant such that for every . Finally, for every , there exists a positive constant such that
Assumption 17.
For some , the family of maps , , from to is -regular, with
for some constant .
Assumption 18.
Define
We assume that and when . Moreover, there exist some constants and such that for any real numbers such that .
This set of assumptions extends the regularity conditions of Section 3 to the diverging dimension case. In particular, our assumptions 16 and 18 are in the same vein as in [13], assumption (F) and condition 3.1.1. respectively. Note that our Assumption 2 in the main text does not need to be altered as remains fixed.
Theorem H.1.
Note that is allowed to diverge to the infinity, but not too fast, since by assumption.
Proof.
The arguments are exactly the same as those given for the proof of Theorem 3.1. With the same notations, the dominant term in the expansion comes from and is larger than , for some vector , . By a careful inspection of the previous proof, the result follows if we satisfy
The latter conditions will be satisfied under our assumptions, choosing some vectors whose norm is sufficiently large and setting . ∎
As in the fixed dimension case, we establish the asymptotic oracle property, i.e. the conditions for which the true support is recovered and the non-zero coefficients are asymptotically normal. We denote by the estimated support of our estimator for the -th model, i.e. . For convenience and w.l.o.g., we assume that the supports are related to the first components of the true parameters, i.e. and . Therefore, every (true or estimated) parameter will be split as , where (resp. ) is related to the (resp. ). components. The statement of the asymptotic distribution with a diverging dimension requires the introduction of a sequence of deterministic real matrices , being of size , for some fixed . Denote . Define the sequences of maps , , from to by
In addition to Condition 17, the next assumption allows to obtain the -regularity of the latter maps.
Assumption 19.
Moreover, we need to introduce a limit for the sequences of maps .
Assumption 20.
There exist maps that are -regular and such that
Denote . The use of the sequence of matrices is classical and inspired here by Theorem 2 of [13]. This technicality allows to obtain convergence towards a finite -dimensional distribution. A similar technique was employed in Theorem 3.2 of [27], which established the normal distribution of the least squares based M-estimator when the dimension diverges. Our regularity assumptions differ from the latter ones, due to different techniques of proofs. For instance, Theorem 2 of [13] assume and imposes the convergence of . In our case, we need and the boundedness of the sequence of row-sum norms (Assumption 19). In light of our criterion, since Theorem A.1 will be applied to , , contrary to our Theorem 3.2 that applied the same corollary to , , this motivates Assumptions 19 and 20.
Theorem H.2.
Note that the property (i) is related to the zero coefficients of the true parameters , as in [13]. There is a subtle difference with the oracle property established for a fixed dimension, where both true zero and non-zero coefficients are correctly identified, a property termed “support recovery”. Herer, the so-called “sparsity property” actually does not preclude the possibility that, for every , some components of ’s support may be estimated as zero.
Remark 11.
Assume the minimum signal condition (H) of [13], i.e., as - a condition standard for sparse estimation with diverging dimensions - is satisfied. Such a property is closely related to the unbiasedness property for non-convex penalization: see, e.g., condition 2.2.-(vii) of [25]. Then, if the penalty is SCAD or MCP, the quantities are zero when is sufficiently large. Therefore, the conclusion of Theorem H.2 (ii) becomes
Remark 12.
It can be checked that our assumptions in Theorem H.2 can be satisfied by some sequences . Restricting ourselves to some powers of , set , and , for some positive constants , and . The subset
yields an acceptable choice for .
Proof.
Point (i): The proof of (i) follows exactly the same lines as the proof of the first point in Theorem 3.2. Due to the diverging number of parameters and Theorem H.1, we now consider . By the same reasoning as above, particularly Equation (D.2), the result is proved if we satisfy
| (H.3) |
keeping in mind that the estimated parameters we consider satisfies . Note that we have invoked an uniform upper bound for the second and third order partial derivatives of the loss (Assumption 16). It can be easily checked that (H.3) is satisfied under our assumptions on the sequence . Indeed, (H.3) if satisfied if
Since and , then . Is is then sufficient to check that
that is a direct consequence of our assumptions.
Point (ii): We proved the sparsity property . Therefore, for any , the event occurs with a probability larger than for large enough. Since we want to state a convergence in law result, we can consider that the latter event is satisfied everywhere. By a Taylor expansion around the true parameter, as in the proof of Theorem 3.2, and after multiplying by the matrix , we get
where . Obviously, is a random parameter such that . Due to Assumptions 17 and 19, the family of maps from to defined as
is -regular, with the same as in Assumption 17. Invoking Corollary A.2, we obtain
Second, the third order term is a vector as size whose -th component, , is
Conditions 17 and 19 imply that the maps
are -regular. Then, apply Corollary A.2 to the latter family. This yields , by setting
for every . By Assumption 16, we get
With our assumptions about , we obtain .
It remains to show that is asymptotically normal. To this end, note that
for any . Setting this implies that , due the first order conditions.
Now, denote . Remind that is -regular (Assumption 20). Thus, the family of maps is -regular, due to the -regularity of (Assumption 17) and Assumption 19. Moreover, satisfies Assumption 14 (replacing with ). Therefore, all the conditions of application of Theorem A.1 (iii) are fullfilled and is weakly convergent in . By the stochastic equicontinuity of the process defined on , the random vector weakly tends to , with obvious notations.
We then conclude with an application of Slutsky’s Theorem to deduce the following asymptotic distribution:
where is the -dimensional random vector defined in the statement of the theorem. ∎
Appendix I Additional simulated experiment
In this subsection, we investigate how the calibration of and alters the performances of the SCAD and MCP penalty functions, respectively. Following the experiment on sparse Gaussian copula performed in the main text, we set and specify two true sparse correlation matrices . The true parameters , which stack the lower triangular part of , respectively, excluding the diagonal terms, belong to with . The number of zero coefficients in is , i.e., approximately of their total number of entries are zero coefficients. The non-zero entries are generated from the uniform distribution . For them, we have , ; , . Moreover, the true vector contains three non-zero entries smaller (in absolute value) than . The latter parameters and will be left fixed hereafter.
Then, for the sample size , we draw , , from the sparse Gaussian copula with parameter and apply the rank-based transformation to obtain the . Equipped with the pseudo-sample , , we solve the same penalized criteria as in the main text for the Gaussian copula (Gaussian loss and least squares loss) with SCAD and MCP penalty functions. We will use a grid of different and values: and . We repeat this procedure for independent batches. The same experiment is performed with the true Gaussian copula parameter .
Figure 1 and Figure 2 display the metrics C1/C2 and MSE, respectively, averaged over these batches, when the true parameter is . Figure 3 and Figure 4 display the same metrics when the true parameter is . For instance, on Figure LABEL:scad_c1_c2_case1, the red solid line represents the percentage of the true zero coefficients in that are correctly recovered by when deduced from the Gaussian loss penalized by the SCAD penalty for different values of and averaged over the batches. Similarly, on Figure LABEL:mcp_c1_c2_case1, the blue dash-dotted line represents the percentage of the true non-zero coefficients in correctly recovered by when deduced from the least squares loss penalized by the MCP penalty for some values of and averaged over the batches.
Figures LABEL:scad_c1_c2_case1 and LABEL:mcp_c1_c2_case1 highlight the existence of a trade-off between the recovery of the zero and non-zero coefficients, particularly for the Gaussian loss: smaller and provide better C1 but to the detriment of C2, whereas larger values imply worse C1, but better C2. Interestingly, a different recovery pattern of the true non-zero coefficients is displayed in Figure LABEL:scad_c1_c2_case2 and Figure LABEL:mcp_c1_c2_case2: the metric C2 is close to for all (excluding the values in the MCP case). Since contains a true minimum signal sufficiently large, the penalization procedure can correctly recover all its non-zero entries. On the other hand, includes three values smaller than . In that case, the penalization tends to estimate the true small non-zero entries as zero entries, thus worsening the C2 metric. The pattern of C1 for both penalty functions and loss functions is not much affected by . For both cases, and for both SCAD and MCP, the Gaussian loss-based criterion tends to generate more zero coefficients than the least squares-based criterion. Furthermore, the performances in terms of estimation accuracy (MSE) are in favor of the Gaussian loss-based criterion. Larger and values result in larger MSE, which is in line with the findings in the main text: large and values result in a LASSO penalization, a situation where the penalty increases linearly with respect to the absolute value of the coefficient, thus generating more bias. Moreover, the MSE metric is smaller when the true parameter is : compare Figure 2 and Figure 4. This is in line with the fact that the support recovery is better for than for .
A point worth mentioning are the poor performances of the MCP method for too small values of . In the latter case, the set is likely to be active, and the penalty becomes , so that the penalization is almost vanishing, which results in lower C1 and larger C2, as depicted in Figure LABEL:mcp_c1_c2_case1 when . But a low C1 implies that the penalization misses a large number of true zero entries, which prompts large MSE patterns.
This simulated experiment on sparse Gaussian copula suggests the existence of an interval of “optimal” values of and , where optimality refers to the ideal situation of perfect recovery of the zero and non-zero coefficients with a low MSE. Such coeffficients should not be too small and too large: for the SCAD, provides an optimal compromise between C1 and C2 with low MSE; this is the case for the MCP when .