Sparse Quadratic Optimisation over the
Stiefel Manifold with Application to
Permutation Synchronisation

We start by ensuring that, under the assumption that $Z_{t}(U_{t})$ is full rank, the sequence $\{U_{t}\}$ generated by Algorithm 1 converges to the dominant subspace of $W$. This can straightforwardly be shown by using the following result.

Thus, if $Z_{t}(U_{t})$ is full rank for each $t$, we can identify our Algorithm 1 with Algorithm A in Lemma 3, and conclude that the sequence $\{U_{t}\}$ converges to the dominant subspace of $W$ as $t\rightarrow\infty$. This is because Algorithm B in Lemma 3 corresponds to the Orthogonal Iteration algorithm, which is known to converge to the dominant subspace of $W$ [21].

We continue by investigating the behaviour at the limit where the columns of $U_{t}$ are in the dominant subspace of $W$. Let us consider the update $U_{t+1}R_{t+1}\leftarrow WU_{t}Z(U_{t})$ of Algorithm 1, and further assume that the $d$ largest eigenvalues of $W$ are equal, which is for example the case for synchronisation problems assuming cycle consistency (cf. Sec. 4).

Hence, under the assumptions in Lemma 4, the columns of $U_{t^{\prime}}$ span the dominant subspace of $W$ for any $t^{\prime}\geq t$. The update in Algorithm 1 reduces to the form

i.e. updating $U_{t}$ to obtain $U_{t+1}$ simplifies to multiplication of $U_{t}$ with the $Q$-matrix from the QR-factorisation of $Z(U_{t})$.

We now turn our attention to the choice of $Z(U_{t})$ in Algorithm 1. We know that, as long as $Z(U_{t})$ is full rank in each iteration $t$, the columns of $U_{t}$ converge to the dominant subspace of $W$. In addition to our objective function $f$ in Problem (1), we now introduce the secondary objective

where for $p$ being a positive integer the notation $U.^{\wedge p}$ means to raise each element in $U$ to the power $p$. For $U\in\operatorname{St}(m,d)$ and $p$ larger than $2$, the maximisation of $g$ promotes sparsity in a relaxed sense. To be specific, if $p$ is odd, a few larger elements (with value close to 1) lead to a larger value of $g$ compared to many smaller elements (with value close to 0), so that sparsity and non-negativity are simultaneously promoted. Analogously, if $p$ is even, a few elements with value closer to $\pm 1$ lead to a larger value of $g$ compared to many smaller elements close to $0$.

Let us consider the maximisation of

with respect to $Q$, where $h(U,Q)=(UQ)^{T}((UQ).^{\wedge(p-1)}),$ $Q\in\mathbb{O}^{d}$, and $U\in\operatorname{St}(m,d)$. This means that we want to rotate $U$ by $Q$ in such a way that the secondary objective $g$ is maximised after the rotation. By applying the rotation from the right, we ensure that the columns $U$ span the same space after the rotation, but a higher objective value is achieved for the secondary objective $g$ in (4).

The extrinsic gradient with respect to $Q$ (for $Q$ relaxed to be in $\mathbb{R}^{d\times d}$) of $g(UQ)$ at $Q=\mathbf{I}$ is $p{\cdot}h(U,\mathbf{I})$. Thus the (manifold) gradient of $g(UQ)$ at $Q=\mathbf{I}$ is given by the projection of the extrinsic gradient at $Q=\mathbf{I}$ onto the tangent space, which reads

For a small step size $\alpha$, we can perform a first-order approximation of gradient ascent if we choose $Z=\mathbf{I}+\alpha p(h(U,\mathbf{I})-h^{T}(U,\mathbf{I}))$, and then update $U$ in terms of the Q-matrix of the QR-factorisation of $Z$. Now, let us assume that we investigate the behaviour at the limit under the assumptions in Lemma 4, i.e. that the $d$ largest eigenvalues of $W$ are equal. In this context the Q-matrix of the QR-factorisation is a retraction [3] and serves as a first-order approximation of the exponential map. With that, the updates become

This choice of the matrix $Z(U_{t})$ ensures that it is full rank, since adding the identity matrix and a skew-symmetric matrix results in a full rank matrix. Hence, for sufficiently small step size $\alpha$, we iteratively move in an ascent direction on $\mathbb{O}^{d}$ by utilising the QR-retraction.

Permutation synchronisation is a procedure to improve matchings between multiple objects [23, 34], and related concepts have been utilised to address diverse tasks, such as multi-alignment [7, 5, 25], multi-shape matching [22, 24, 20], multi-image matching [51, 42, 9, 13, 12], or multi-graph matching [48, 6, 41], among many others. Permutation synchronisation refers to the process of establishing cycle consistency in the set of pairwise permutation matrices that encode correspondences between points in multiple objects. In computer vision there is a typical application where the points are feature descriptors or key-points, and the objects are images, as shown in Fig. 2.

Let $k$ denote the number of objects, where each object $i$ contains $m_{i}$ points. For $\mathbf{1}_{p}$ being a $p$-dimensional vector of all ones, and vector inequalities being understood in an element-wise sense, let $P_{ij}\in\mathbb{P}_{m_{i}m_{j}}:=\{X\in\{0,1\}^{m_{i}\times m_{j}}:X\mathbf{1}_{m_{j}}\leq\mathbf{1}_{m_{i}},\mathbf{1}_{m_{i}}^{T}X\leq\mathbf{1}_{m_{j}}^{T}\}$ be the partial permutation matrix that represents the correspondence between the $m_{i}$ points in object $i$ and the $m_{j}$ points in object $j$. In the case of bijective permutations, the set of pairwise permutations $\mathcal{P}:=\{P_{ij}\}_{i,j=1}^{k}$ is said to be cycle-consistent if for all $i,j,\ell$ it holds that $P_{i\ell}P_{\ell j}=P_{ij}$.

We define the set of partial permutation matrices with full row-rank as $\overline{\mathbb{P}}_{m_{i}d}:=\{X\in\mathbb{P}_{m_{i}d}:X\mathbf{1}_{d}=\mathbf{1}_{m_{i}}\}$, where $d$ denotes the total number of distinct points across all objects. Cycle consistency is known to be equivalent to the existence of so-called object-to-universe matchings $\mathcal{U}:=\{P_{i}\in\overline{\mathbb{P}}_{m_{i}d}\}_{i=1}^{k}$ such that for all $i,j$ we can write $P_{ij}=P_{i}P_{j}^{T}$ (see [23, 34] for details). The object-to-universe characterisation of cycle consistency is also valid for the case of non-bijective (i.e. partial) permutations (see [42, 8] for details).

Given the noisy (i.e. not cycle-consistent) set of pairwise permutations $\mathcal{P}=\{P_{ij}\}_{i,j=1}^{k}$, permutation synchronisation can be phrased as the optimisation problem

where for $m:=\sum_{i}m_{i}$ we define the set $\mathbb{U}:=\overline{\mathbb{P}}_{m_{1}d}\times\ldots\times\overline{\mathbb{P}}_{m_{k}d}\subset\mathbb{R}^{m\times d}$, the $(m{\times}d)$-dimensional block matrix $P=[P_{1}^{T},\ldots,P_{k}^{T}]^{T}$, and the block matrix $W:=[P_{ij}]_{ij}\in\mathbb{R}^{m\times m}$ in order to allow for a compact matrix representation of the objective.

The core idea of existing spectral permutation synchronisation approaches [34, 39, 31] is to replace the feasible set $\mathbb{U}$ in Problem (9) with the Stiefel manifold $\operatorname{St}(m,d)$, so that we obtain an instance of Problem (1). We utilise Algorithm 1 to obtain a (globally optimal) solution $U^{*}\in\operatorname{St}(m,d)$ of this spectral formulation. In our algorithm we choose $p=3$ to promote sparsity and non-negativity in the resulting $U^{*}$ via the function $g(U)=\operatorname{tr}(U^{T}(U.^{\wedge 2}))=\sum_{i=1}^{m}\sum_{j=1}^{d}U_{ij}^{3}$. With that, in addition to $U^{*}$ being an orthogonal matrix, it contains few large elements that are close to 1 and many smaller elements that are close to 0. As such, we can readily project the matrix $U^{*}$ onto the set $\mathbb{U}$ in terms of a Euclidean projection. The Euclidean projection is given by projecting each of the $k$ blocks of $U^{*}=[U_{1}^{*T},\ldots,U_{k}^{*T}]^{T}$ individually onto the set of partial permutations, i.e. $P_{i}=\operatorname{proj}_{\overline{\mathbb{P}}_{m_{i}d}}(U_{i}^{*})=\operatorname*{arg\,max}_{X\in\overline{\mathbb{P}}_{m_{i}d}}\operatorname{tr}(X^{T}U_{i}^{*})$, see e.g. [8], which amounts to a (partial) linear assignment problem [32, 11] that we solve based on the efficient implementation in [10].

We experimentally compare our proposed approach with various methods for permutation synchronisation and perform an evaluation on both real and synthetic datasets. In particular, our comparison includes two existing spectral approaches, namely MatchEig [31] and Spectral [34], where for the latter we use the efficient implementation from the authors of [51]. In addition, we also compare against the alternating minimisation method MatchALS [51], and against the non-negative matrix factorisation approach NmfSync [8]. To emphasise that the methods MatchEig and MatchALS do not guarantee cycle consistency (but instead aim to improve the initial matchings), in all plots we show results of respective methods as dashed lines. We use the fscore to measure the quality of obtained multi-matchings, which is defined as the fraction $f=\frac{2\cdot p\cdot r}{p+r}$, where $p$ and $r$ denote the precision and recall, respectively. All experiments are run on a Macbook Pro (2.8 GHz quad core i7, 16 GB RAM), where for $\epsilon=10^{-5}$ we use $f(U_{t})/f(U_{t+1})\geq 1-\epsilon$ as convergence criterion in Algorithm 1, and a step size of $\alpha_{t}=\|h(U_{t},\mathbf{I})-h^{T}(U_{t},\mathbf{I})\|_{\infty}^{-1}$ in (7).

Real data. In this experiment we use the CMU house image sequence [1] comprising $111$ frames within the experimental protocol of [34]. We generate a sequence of permutation synchronisation problem instances with a gradually increasing number of objects $k$ by extracting respective pairwise matchings for $k$ objects. To this end, we vary $k$ from $20$ to $111$ and sample the pairwise matchings evenly-spaced from the $111\times 111$ pairwise matchings. Quantitative results in terms of the fscore, the objective value of Problem (9), and the runtimes are shown in Fig. 1, in which the individual problem instances vary along the horizontal axis. We can see that our proposed method dominates other approaches in terms of the fscore and the objective value (the reported objective values are divided by $k^{2}$ to normalise the scale in problems of different sizes), while being among the fastest. Note that we do not report the objective value for MatchEig and MatchALS, since they do not lead to cycle-consistent matchings so that the obtained solution does not lie in the feasible set of Problem (9). Qualitative results of the matching between one pair of images for $k=111$ are shown in Fig. 2. As expected, our proposed approach clearly outperforms the Spectral baseline, since our method is guaranteed to converge to the same same subspace that is spanned by the spectral solution, while at the same time providing a sparser and less negative solution that is thereby closer to the feasible set $\mathbb{U}$.

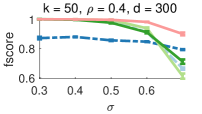
Synthetic data. We reproduce the procedure described in [8] for generating synthetic instances for the synchronisation of partial permutations. Four different parameters are considered for generating a problem instance: the universe size $d$, the number of objects $k$ that are to be matched, the observation rate $\rho$, and the error rate $\sigma$ (see [8] for details). One of these parameters varies in each experimental setting, while the others are kept fixed. Each individual experiment is repeated $5$ times with different random seeds. In Fig. 3 we compare the performance of MatchEig [31], MatchALS [51], Spectral [34], NmfSync [8] and Ours. The first row shows the fscore, and the second row the respective runtimes. Note that we did not run MatchALS on the larger instances since the runtime is prohibitively long. The methods MatchEig and MatchALS do not guarantee cycle consistency, and are thus shown as dashed lines. It can be seen that in most settings our method obtains superior performance in terms of the fscore, while being almost as fast as the most efficient methods that are also based on a spectral relaxation (MatchEig and Spectral).

The key contribution of this paper is an effective and efficient optimisation algorithm for addressing sparse optimisation problems over the Stiefel manifold. Given the fundamental nature of our contribution, we do not see any direct ethical concerns or negative societal impacts related to our work.

Overall, there are numerous opportunities to use the proposed method for various types of multi-matching problems over networks and graphs. The problem addressed is highly relevant within the fields of machine learning (e.g. for data canonicalisation to faciliate efficient learning with non-Euclidean data), computer vision (e.g. for 3D reconstruction in structure from motion, or image alignment), computer graphics (e.g. for bringing 3D shapes into correspondence) and other related areas.

The true power of permutation synchronisation methods appears when the number of objects to synchronise is large. With large quantities of data becoming increasingly available, the introduction of our scalable optimisation procedure that can account for orthogonality – while promoting sparsity and non-negativity – is an important contribution to the synchronisation community on the one hand. Moreover, on the other hand, it has the potential to have an impact on more general non-convex optimisation problems, particularly in the context of spectral relaxations of difficult and large combinatorial problems.

JT was supported by the Swedish Research Council (2019-04769).