Sparse random graphs: Eigenvalues and Eigenvectors

In this paper, we consider two models of random graphs, the Erdős-Rényi random graph $G(n,p)$ and the random regular graph $G_{n,d}$. Given a real number $p=p(n)$,$0\leq p\leq 1$, the Erdős-Rényi graph on a vertex set of size $n$ is obtained by drawing an edge between each pair of vertices, randomly and independently, with probability $p$. On the other hand, $G_{n,d}$, where $d=d(n)$ denotes the degree, is a random graph chosen uniformly from the set of all simple $d$-regular graphs on $n$ vertices. These are basic models in the theory of random graphs. For further information, we refer the readers to the excellent monographs $\cite[cite]{[\@@bibref{}{bollobas}{}{}]},\cite[cite]{[\@@bibref{}{janson}{}{}]}$ and survey [33].

Given a graph $G$ on $n$ vertices, the adjacency matrix $A$ of $G$ is an $n\times n$ matrix whose entry $a_{ij}$ equals one if there is an edge between the vertices $i$ and $j$ and zero otherwise. All diagonal entries $a_{ii}$ are defined to be zero. The eigenvalues and eigenvectors of $A$ carry valuable information about the structure of the graph and have been studied by many researchers for quite some time, with both theoretical and practical motivations (see, for example, $\cite[cite]{[\@@bibref{}{bauer}{}{}]},\cite[cite]{[\@@bibref{}{bhamidi}{}{}]},\cite[cite]{[\@@bibref{}{feige}{}{}]},\cite[cite]{[\@@bibref{}{semerjian}{}{}]}$ $\cite[cite]{[\@@bibref{}{FK1981}{}{}]},\cite[cite]{[\@@bibref{}{fried1991}{}{}]},\cite[cite]{[\@@bibref{}{fried2003}{}{}]}$, $\cite[cite]{[\@@bibref{}{fried1993}{}{}]},\cite[cite]{[\@@bibref{}{tvrandom}{}{}]},\cite[cite]{[\@@bibref{}{erdos2009semi}{}{}]}$, $\cite[cite]{[\@@bibref{}{shi2000}{}{}]},\cite[cite]{[\@@bibref{}{pothen1990}{}{}]}$).

The goal of this paper is to study the eigenvalues and eigenvectors of $G(n,p)$ and $G_{n,d}$. We are going to consider:

• •

  The global law for the limit of the empirical spectral distribution (ESD) of adjacency matrices of $G(n,p)$ and $G_{n,d}$. For $p=\omega(1/n)$, it is well-known that eigenvalues of $G(n,p)$ (after a proper scaling) follows Wigner’s semicircle law (we include a short proof in the Appendix A for completeness). Our main new result shows that the same law holds for random regular graph with $d\rightarrow\infty$ with $n$. This complements the well known result of McKay for the case when $d$ is an absolute constant (McKay’s law) and extends recent results of Dumitriu and Pal [9] (see Section 1.2 for more discussion).

• •

  Bound on the infinity norm of the eigenvectors. We first prove that the infinity norm of any (unit) eigenvector $v$ of $G(n,p)$ is almost surely $o(1)$ for $p=\omega(\log n/n)$. This gives a positive answer to a question raised by Dekel, Lee and Linial [7]. Furthermore, we can show that $v$ satisfies the bound $\|v\|_{\infty}=O\left(\sqrt{\log^{2.2}g(n){\log n}/{np}}\right)$ for $p=\omega(\log n/n)=g(n)\log n/n$, as long as the corresponding eigenvalue is bounded away from the (normalized) extremal values $-2$ and $2$.

We finish this section with some notation and conventions.

Given an $n\times n$ symmetric matrix $M$, we denote its $n$ eigenvalues as

$${\lambda}_{1}{(M)}\leq{\lambda}_{2}{(M)}\leq\ldots\leq{\lambda}_{n}{(M)},$$

and let $u_{1}(M),\ldots,u_{n}(M)\in\mathbb{R}^{n}$ be an orthonormal basis of eigenvectors of $M$ with

$$Mu_{i}(M)={\lambda}_{i}u_{i}(M).$$

The empirical spectral distribution (ESD) of the matrix $M$ is a one-dimensional function

$$F^{\bf M}_{n}(x)=\frac{1}{n}|\{1\leq j\leq n:\lambda_{j}(M)\leq x\}|,$$

where we use $|\mathbf{I}|$ to denote the cardinality of a set $\mathbf{I}$.

Let $A_{n}$ be the adjacency matrix of $G(n,p)$. Thus $A_{n}$ is a random symmetric $n\times n$ matrix whose upper triangular entries are iid copies of a real random variable $\xi$ and diagonal entries are $0$. $\xi$ is a Bernoulli random variable that takes values $1$ with probability $p$ and $0$ with probability $1-p$.

$$\mathbb{E}\xi=p,\mathbb{V}ar{\xi}=p(1-p)={\sigma}^{2}.$$

Usually it is more convenient to study the normalized matrix

$$M_{n}=\frac{1}{\sigma}(A_{n}-pJ_{n})$$

where $J_{n}$ is the $n\times n$ matrix all of whose entries are 1. $M_{n}$ has entries with mean zero and variance one. The global properties of the eigenvalues of $A_{n}$ and $M_{n}$ are essentially the same (after proper scaling), thanks to the following lemma

The main advantage of this definition is that if we have a polynomial number of events, each of which holds with overwhelming probability, then their intersection also holds with overwhelming probability.

Asymptotic notation is used under the assumption that $n\rightarrow\infty$. For functions $f$ and $g$ of parameter $n$, we use the following notation as $n\rightarrow\infty$: $f=O(g)$ if $|f|/|g|$ is bounded from above; $f=o(g)$ if $f/g\rightarrow 0$; $f=\omega(g)$ if $|f|/|g|\rightarrow\infty$, or equivalently, $g=o(f)$; $f=\Omega(g)$ if $g=O(f)$; $f=\Theta(g)$ if $f=O(g)$ and $g=O(f)$.

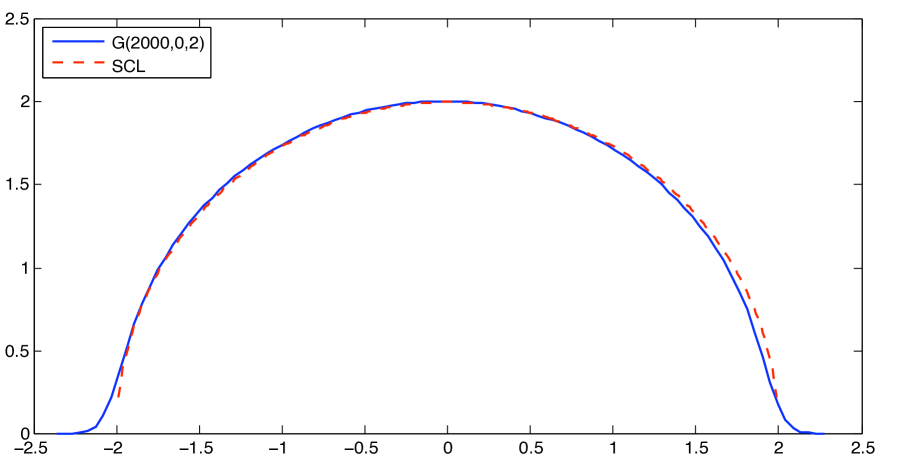
In 1950s, Wigner [32] discovered the famous semi-circle for the limiting distribution of the eigenvalues of random matrices. His proof extends, without difficulty, to the adjacency matrix of $G(n,p)$, given that $np\rightarrow\infty$ with $n$. (See Figure 1 for a numerical simulation)

If $np=O(1)$, the semicircle law no longer holds. In this case, the graph almost surely has $\Theta(n)$ isolated vertices, so in the limiting distribution, the point $0$ will have positive constant mass.

The case of random regular graph, $G_{n,d}$, was considered by McKay [21] about 30 years ago. He proved that if $d$ is fixed, and $n\rightarrow\infty$, then the limiting density function is

$$\displaystyle f_{d}(x)=\left\{\begin{array}[]{ll}\frac{d\sqrt{4(d-1)-x^{2}}}{2\pi(d^{2}-x^{2})},&\mbox{if $|x|\leq 2\sqrt{d-1}$};\\ \\ 0&\mbox{otherwise}.\end{array}\right.$$

This is usually referred to as McKay or Kesten-McKay law.

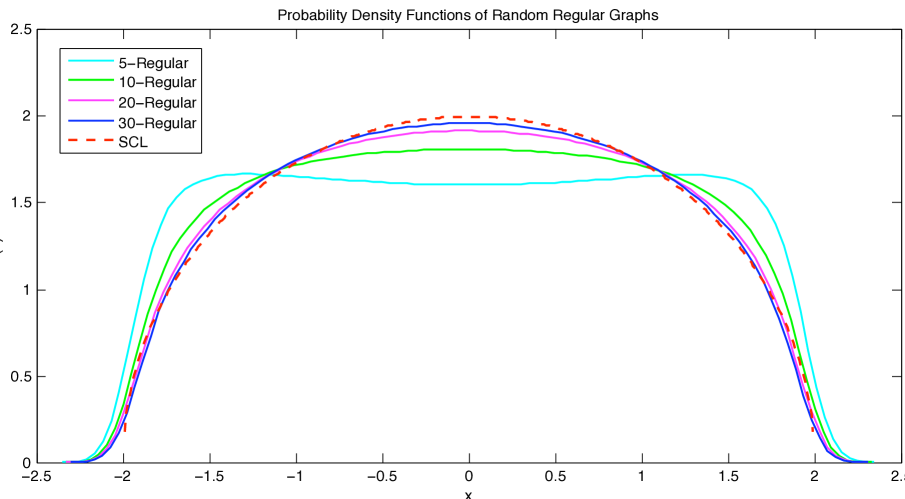
It is easy to verify that as $d\rightarrow\infty$, if we normalize the variable $x$ by $\sqrt{d-1}$, then the above density converges to the semicircle distribution on $[-2,2]$. In fact, a numerical simulation shows the convergence is quite fast(see Figure 2).

It is thus natural to conjecture that Theorem 1.3 holds for $G_{n,d}$ with $d\rightarrow\infty$. Let $A^{\prime}_{n}$ be the adjacency matrix of $G_{n,d}$, and set

$$M^{\prime}_{n}=\frac{1}{\sqrt{\frac{d}{n}(1-\frac{d}{n})}}(A^{\prime}_{n}-\frac{d}{n}J).$$

Nothing has been proved about this conjecture, until recently. In [9], Dimitriu and Pal showed that the conjecture holds for $d$ tending to infinity slowly, $d=n^{o(1)}$. Their method does not extend to larger $d$.

We are going to establish Conjecture 1.4 in full generality. Our method is very different from that of [9].

Without loss of generality we may assume $d\leq n/2$, since the adjacency matrix of the complement graph of $G_{n,d}$ may be written as $J_{n}-A^{\prime}_{n}$, thus by Lemma 1.1 will have the spectrum interlacing between the set $\{-\lambda_{n}(A^{\prime}_{n}),\dots,-\lambda_{1}(A^{\prime}_{n})\}$. Since the semi-circular distribution is symmetric, the ESD of $G_{n,d}$ will converges to semi-circular law if and only if the ESD of its complement does.

Theorem 1.5 is a direct consequence of the following stronger result, which shows convergence at small scales. For an interval $I$ let $N^{\prime}_{I}$ be the number of eigenvalues of $M^{\prime}_{n}$ in $I$.

Relatively little is known for eigenvectors in both random graph models under study. In [7], Dekel, Lee and Linial, motivated by the study of nodal domains, raised the following question.

Later, in their journal paper [8], the authors added one sharper question.

The bound $n^{-1/2+o(1)}$ was also conjectured by the second author of this paper in an NSF proposal (submitted Oct 2008). He and Tao [30] proved this bound for eigenvectors corresponding to the eigenvalues in the bulk of the spectrum for the case $p=1/2$. If one defines the adjacency matrix by writting $-1$ for non-edges, then this bound holds for all eigenvectors [30, 29].

The above two questions were raised under the assumption that $p$ is a constant in the interval $(0,1)$. For $p$ depending on $n$, the statements may fail. If $p\leq\frac{(1-\epsilon)\log n}{n}$, then the graph has (with high probability) isolated vertices and so one cannot expect that $\|u\|_{\infty}=o(1)$ for every eigenvector $u$. We raise the following questions:

Similarly, we can ask the above questions for $G_{n,d}$:

As far as random regular graphs is concerned, Dumitriu and Pal [9] and Brook and Lindenstrauss [5] showed that for any normalized eigenvector of a sparse random regular graph is delocalized in the sense that one can not have too much mass on a small set of coordinates. The readers may want to consult their papers for explicit statements.

We generalize our questions by the following conjectures:

In this paper, we focus on $G(n,p)$. Our main result settles (positively) Question 1.8 and almost Question 1.10 . This result follows from Corollary 2.3 obtained in Section 2.

For Questions 1.9 and 1.11, we obtain a good quantitative bound for those eigenvectors which correspond to eigenvalues bounded away from the edge of the spectrum.

For convenience, in the case when $p=\omega(\log n/n)\in(0,1)$, we write

$$p=\frac{g(n)\log n}{n},$$

where $g(n)$ is a positive function such that $g(n)\rightarrow\infty$ as $n\rightarrow\infty$ ($g(n)$ can tend to $\infty$ arbitrarily slowly).

The proofs are adaptations of a recent approach developed in random matrix theory (as in [30],[29],[10], [11]). The main technical lemma is a concentration theorem about the number of eigenvalues on a finer scale for $p=\omega(\log n/n)$.

We use the method of comparison. An important lemma is the following

For the range $p\geq\log^{2}n/n$, Lemma 2.1 is a consequence of a result of Shamir and Upfal [26] (see also [20]). For smaller values of $np$, McKay and Wormald [23] calculated precisely the probability that $G(n,p)$ is $np$-regular, using the fact that the joint distribution of the degree sequence of $G(n,p)$ can be approximated by a simple model derived from independent random variables with binomial distribution. Alternatively, one may calculate the same probability directly using the asymptotic formula for the number of $d$-regular graphs on $n$ vertices (again by McKay and Wormald [22]). Either way, for $p=o(1/\sqrt{n})$, we know that

$${\hbox{\bf P}}(G(n,p)\text{ is }np\text{-regular})\geq\Theta(\exp(-n\log(\sqrt{np})).$$

which is better than claimed in Lemma 2.1.

Another key ingredient is the following concentration lemma, which may be of independent interest.

Apply Lemma 2.2 for the normalized adjacency matrix $M_{n}$ of $G(n,p)$ with $K=1/\sqrt{p}$ we obtain

By Corollary 2.3 and Lemma 2.1, the probability that $N_{I}$ fails to be close to the expected value in the model $G(n,p)$ is much smaller than the probability that $G(n,p)$ is $np$-regular. Thus the probability that $N_{I}$ fails to be close to the expected value in the model $G_{n,d}$ where $d=np$ is the ratio of the two former probabilities, which is $O(\exp(-cn\sqrt{np}\log np))$ for some small positive constant $c$. Thus, Theorem 1.6 is proved, depending on Lemma 2.2 which we turn to next.

Assume $I=[a,b]$ and $a-(-2)<2-b$.

We will use the approach of Guionnet and Zeitouni in [18]. Consider a random Hermitian matrix $W_{n}$ with independent entries $w_{ij}$ with support in a compact region $S$. Let $f$ be a real convex $L$-Lipschitz function and define

$$Z:=\sum_{i=1}^{n}f(\lambda_{i})$$

where $\lambda_{i}$’s are the eigenvalues of $\frac{1}{\sqrt{n}}W_{n}$. We are going to view $Z$ as the function of the atom variables $w_{ij}$. For our application we need $w_{ij}$ to be random variables with mean zero and variance 1, whose absolute values are bounded by a common constant $K$.

The following concentration inequality is from [18]

In order to apply Lemma 2.5 for $N_{I}$ and $M$, it is natural to consider

$$Z:=N_{I}=\sum_{i=1}^{n}\chi_{I}(\lambda_{i})$$

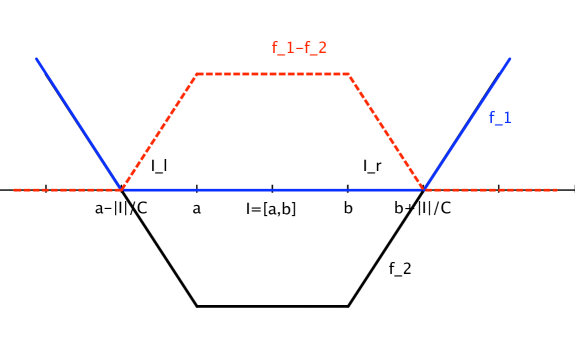
where $\chi_{I}$ is the indicator function of $I$ and $\lambda_{i}$ are the eigenvalues of $\frac{1}{\sqrt{n}}M_{n}$. However, this function is neither convex nor Lipschitz. As suggested in [18], one can overcome this problem by a proper approximation. Define $I_{l}=[a-\frac{|I|}{C},a]$, $I_{r}=[b,b+\frac{|I|}{C}]$ and construct two real functions $f_{1},f_{2}$ as follows(see Figure 3):

$$f_{1}(x)=\Bigg{\{}\begin{array}[]{ll}-\frac{C}{|I|}(x-a)-1&\text{if }x\in(-\infty,a-\frac{|I|}{C})\\ 0&\text{if }x\in I\cup I_{l}\cup I_{r}\\ \frac{C}{|I|}(x-b)-1&\text{if }x\in(b+\frac{|I|}{C},\infty)\end{array}$$

$$f_{2}(x)=\Bigg{\{}\begin{array}[]{ll}-\frac{C}{|I|}(x-a)-1&\text{if }x\in(-\infty,a)\\ -1&\text{if }x\in I\\ \frac{C}{|I|}(x-b)-1&\text{if }x\in(b,\infty)\end{array}$$

where $C$ is a constant to be chosen later. Note that $f_{j}$’s are convex and $\frac{C}{|I|}$-Lipschitz. Define

$$X_{1}=\sum_{i=1}^{n}f_{1}(\lambda_{i}),\ X_{2}=\sum_{i=1}^{n}f_{2}(\lambda_{i})$$

and apply Lemma 2.5 with $T=\frac{\delta}{8}n\int_{I}\rho_{sc}(t)dt$ for $X_{1}$ and $X_{2}$. Thus, we have

$\displaystyle{\hbox{\bf P}}(|X_{j}-{\hbox{\bf E}}(X_{j})|\geq\frac{\delta}{8}n\int_{I}\rho_{sc}(t)dt)$

$\displaystyle\leq 4\exp(-c\frac{\delta^{2}n^{2}|I|^{2}(\int_{I}\rho_{sc}(t)dt)^{2}}{K^{2}C^{2}}).$

At this point we need to estimate the value of $\int_{I}\rho_{sc}(t)dt$. There are two cases: if $I$ is in the “bulk” i.e. $I\subset[-2+\epsilon,2-\epsilon]$ for some positive absolute constant $\epsilon$, then $\int_{I}\rho_{sc}(t)dt=\alpha|I|$ where $\alpha$ is a constant depending on $\epsilon$. But if $I$ is very near the edge of $[-2,2]$ i.e. $a-(-2)<|I|=o(1)$, then $\int_{I}\rho_{sc}(t)dt=\alpha^{\prime}|I|^{3/2}$ for some absolute constant $\alpha^{\prime}$. Thus in both case we have

$${\hbox{\bf P}}(|X_{j}-{\hbox{\bf E}}(X_{j})|\geq\frac{\delta}{8}n\int_{I}\rho_{sc}(t)dt)\leq 4\exp(-c_{1}\frac{\delta^{2}n^{2}|I|^{5}}{K^{2}C^{2}})$$

Let $X=X_{1}-X_{2}$, then

$${\hbox{\bf P}}(|X-{\hbox{\bf E}}(X)|\geq\frac{\delta}{4}n\int_{I}\rho_{sc}(t)dt)\leq O(\exp(-c_{1}\frac{\delta^{2}n^{2}|I|^{5}}{K^{2}C^{2}})).$$

Now we compare $X$ to $Z$, making use of a result of Götze and Tikhomirov [17]. We have ${\hbox{\bf E}}(X-Z)\leq{\hbox{\bf E}}(N_{I_{l}}+N_{I_{r}})$. In [17], Götze and Tikhomirov obtained a convergence rate for ESD of Hermitian random matrices whose entries have mean zero and variance one, which implies that for any $I\subset[-2,2]$

$$|{\hbox{\bf E}}(N_{I})-n\int_{I}\rho_{sc}(t)dt|<\beta n\sqrt{\frac{M_{4}}{n}},$$

where $\beta$ is an absolute constant, $M_{4}=\sup_{i,j}{\hbox{\bf E}}(|\omega_{ij}|^{4})$. Thus

$${\hbox{\bf E}}(X)\leq{\hbox{\bf E}}(Z)+n\int_{I_{l}\cup I_{r}}\rho_{sc}(t)dt+\beta n\sqrt{\frac{M_{4}}{n}}.$$

In the “edge” case we can choose $C=(4/\delta)^{2/3}$, then because $|I|\geq\Omega(\delta^{-2/3}(M_{4}/n)^{1/3})$, we have

$$n\int_{I_{l}\cup I_{r}}\rho_{sc}(t)dt=\Theta(n(\frac{|I|}{C})^{3/2})>\Omega(n\sqrt{\frac{M_{4}}{n}})$$

and

$$n\int_{I_{l}\cup I_{r}}\rho_{sc}(t)dt+\beta n\sqrt{\frac{M_{4}}{n}}=\Theta(n(\frac{|I|}{C})^{3/2})=\Theta(\frac{\delta}{4}n\int_{I}\rho_{sc}(t)dt).$$

In the “bulk” case we choose $C=4/\delta$, then

$$n\int_{I_{l}\cup I_{r}}\rho_{sc}(t)dt+\beta n\sqrt{\frac{M_{4}}{n}}=\Theta(n\frac{|I|}{C})=\Theta(\frac{\delta}{4}n\int_{I}\rho_{sc}(t)dt).$$

Therefore in both cases, with probability at least $1-O(\exp(-c_{1}\frac{\delta^{4}n^{2}|I|^{5}}{K^{2}}))$, we have

$$Z\leq X\leq{\hbox{\bf E}}(X)+\frac{\delta}{4}n\int_{I}\rho_{sc}(t)dt<{\hbox{\bf E}}(Z)+\frac{\delta}{2}n\int_{I}\rho_{sc}(t)dt.$$

The convergence rate result of Götze and Tikhomirov again gives

$${\hbox{\bf E}}(N_{I})<n\int_{I}\rho_{sc}(t)dt+\beta n\sqrt{\frac{M_{4}}{n}}<(1+\frac{\delta}{2})n\int_{I}\rho_{sc}(t)dt,$$

hence with probability at least $1-O(\exp(-c_{1}\frac{\delta^{4}n^{2}|I|^{5}}{K^{2}}))$

$$Z<(1+\delta)n\int_{I}\rho_{sc}(t)dt,$$

which is the desires upper bound.

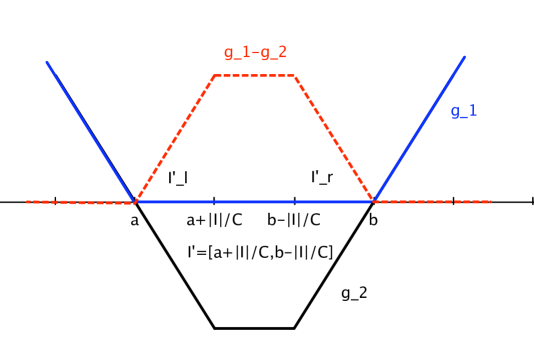
The lower bound is proved using a similar argument. Let $I^{\prime}=[a+\frac{|I|}{C},b-\frac{|I|}{C}]$, $I^{\prime}_{l}=[a,a+\frac{|I|}{C}]$, $I^{\prime}_{r}=[b-\frac{|I|}{C},b]$ where $C$ is to be chosen later and define two functions $g_{1}$, $g_{2}$ as follows (see Figure 3):

$$g_{1}(x)=\Bigg{\{}\begin{array}[]{ll}-\frac{C}{|I|}(x-a)&\text{if }x\in(-\infty,a)\\ 0&\text{if }x\in I^{\prime}\cup I^{\prime}_{l}\cup I^{\prime}_{r}\\ \frac{C}{|I|}(x-b)&\text{if }x\in(b,\infty)\end{array}$$

$$g_{2}(x)=\Bigg{\{}\begin{array}[]{ll}-\frac{C}{|I|}(x-a)&\text{if }x\in(-\infty,a+\frac{|I|}{C})\\ -1&\text{if }x\in I^{\prime}\\ \frac{C}{|I|}(x-b)&\text{if }x\in(b-\frac{|I|}{C},\infty)\end{array}$$

Define

$$Y_{1}=\sum_{i=1}g_{1}(\lambda_{i}),\ Y_{2}=\sum_{i=1}g_{2}(\lambda_{i}).$$

Applying Lemma 2.5 with $T=\frac{\delta}{8}n\int_{I}\rho_{sc}(t)dt$ for $Y_{j}$ and using the estimation for $\int_{I}\rho(t)dt$ as above, we have

$${\hbox{\bf P}}(|Y_{j}-{\hbox{\bf E}}(Y_{j})|\geq\frac{\delta}{8}n\int_{I}\rho_{sc}(t)dt)\leq 4\exp(-c_{2}\frac{\delta^{2}n^{2}|I|^{5}}{K^{2}C^{2}}).$$

Let $Y=Y_{1}-Y_{2}$, then

$${\hbox{\bf P}}(|Y-{\hbox{\bf E}}(Y)|\geq\frac{\delta}{4}n\int_{I}\rho_{sc}(t)dt)\leq O(\exp(-c_{2}\frac{\delta^{2}n^{2}|I|^{5}}{K^{2}C^{2}})).$$

We have ${\hbox{\bf E}}(Z-Y)\leq{\hbox{\bf E}}(N_{I^{\prime}_{l}}+N_{I^{\prime}_{r}})$. A similar argument as in the proof of the upper bound (using the convergence rate of Götze and Tikhomirov) shows

$${\hbox{\bf E}}(Y)\geq{\hbox{\bf E}}(Z)-n\int_{I^{\prime}_{l}\cup I^{\prime}_{r}}\rho_{sc}(t)dt-\beta n\sqrt{\frac{M_{4}}{n}}>E(Z)-\frac{\delta}{4}n\int_{I}\rho_{sc}(t)dt.$$

Therefore with probability at least $1-O(\exp(-c_{2}\frac{\delta^{2}n^{2}|I|^{5}}{K^{2}C^{2}}))$, we have

$$Z\geq Y\geq{\hbox{\bf E}}(Y)-\frac{\delta}{4}n\int_{I}\rho_{sc}(t)dt>{\hbox{\bf E}}(Z)-\frac{\delta}{2}n\int_{I}\rho_{sc}(t)dt,$$

and by the convergence rate, with probability at least $1-O(\exp(-c2\frac{\delta^{2}n^{2}|I|^{5}}{K^{2}C^{2}}))$

$$Z>(1-\delta)n\int_{I}\rho_{sc}(t)dt.$$

Thus, Theorem 2.2 is proved.

$A_{n}$ is the adjacency matrix of $G(n,p)$. In the proofs of Theorem 1.16 and Theorem 1.17, we actually work with the eigenvectors of a perturbed matrix

$$A_{n}+\epsilon N_{n},$$

where $\epsilon=\epsilon(n)>0$ can be arbitrarily small and $N_{n}$ is a symmetric random matrix whose upper triangular elements are independent with a standard Gaussian distribution.

The entries of $A_{n}+\epsilon N_{n}$ are continuous and thus with probability 1, the eigenvalues of $A_{n}+\epsilon N_{n}$ are simple. Let

$$\mu_{1}<\ldots<\mu_{n}$$

be the ordered eigenvalues of $A_{n}+\epsilon N_{n}$, which have a unique orthonormal system of eigenvectors $\{w_{1},\ldots,w_{n}\}$. By the Cauchy interlacing principle, the eigenvalues of $A_{n}+\epsilon N_{n}$ are different from those of its principle minors, which satisfies a condition of Lemma 3.2.

Let $\lambda_{i}$’s be the eigenvalue of $A_{n}$ with multiplicity $k_{i}$ defined as follows:

$$\ldots\lambda_{i-1}<\lambda_{i}=\lambda_{i+1}=\ldots=\lambda_{i+k_{i}}<\lambda_{i+k_{i}+1}\ldots$$

By Weyl’s theorem, one has for every $1\leq j\leq n$,

$$|\lambda_{j}-\mu_{j}|\leq\epsilon||N_{n}||_{\text{op}}=O(\epsilon\sqrt{n})$$

(3.1)

Thus the behaviors of eigenvalues of $A_{n}$ and $A_{n}+\epsilon N_{n}$ are essentially the same by choosing $\epsilon$ sufficiently small. And everything (except Lemma 3.2) we used in the proofs of Theorem 1.16 and Theorem 1.17 for $A_{n}$ also applies for $A_{n}+\epsilon N_{n}$ by a continuity argument. We will not distinguish $A_{n}$ from $A_{n}+\epsilon N_{n}$ in the proofs.

The following lemma will allow us to transfer the eigenvector delocaliztion results of $A_{n}+\epsilon N_{n}$ to those of $A_{n}$ at some expense.