The Daya Bay Collaboration

Spectral measurement of electron antineutrino oscillation amplitude and frequency at Daya Bay

F.P. An Institute of High Energy Physics, Beijing East China University of Science and Technology, Shanghai A.B. Balantekin University of Wisconsin, Madison, Wisconsin, USA H.R. Band University of Wisconsin, Madison, Wisconsin, USA W. Beriguete Brookhaven National Laboratory, Upton, New York, USA M. Bishai Brookhaven National Laboratory, Upton, New York, USA S. Blyth Department of Physics, National Taiwan University, Taipei R.L. Brown Brookhaven National Laboratory, Upton, New York, USA I. Butorov Joint Institute for Nuclear Research, Dubna, Moscow Region G.F. Cao Institute of High Energy Physics, Beijing J. Cao Institute of High Energy Physics, Beijing R. Carr California Institute of Technology, Pasadena, California, USA Y.L. Chan Chinese University of Hong Kong, Hong Kong J.F. Chang Institute of High Energy Physics, Beijing Y. Chang National United University, Miao-Li C. Chasman Brookhaven National Laboratory, Upton, New York, USA H.S. Chen Institute of High Energy Physics, Beijing H.Y. Chen Institute of Physics, National Chiao-Tung University, Hsinchu S.J. Chen Nanjing University, Nanjing S.M. Chen Department of Engineering Physics, Tsinghua University, Beijing X.C. Chen Chinese University of Hong Kong, Hong Kong X.H. Chen Institute of High Energy Physics, Beijing Y. Chen Shenzhen Univeristy, Shenzhen Y.X. Chen North China Electric Power University, Beijing Y.P. Cheng Institute of High Energy Physics, Beijing J.J. Cherwinka University of Wisconsin, Madison, Wisconsin, USA M.C. Chu Chinese University of Hong Kong, Hong Kong J.P. Cummings Siena College, Loudonville, New York, USA J. de Arcos Department of Physics, Illinois Institute of Technology, Chicago, Illinois, USA Z.Y. Deng Institute of High Energy Physics, Beijing Y.Y. Ding Institute of High Energy Physics, Beijing M.V. Diwan Brookhaven National Laboratory, Upton, New York, USA E. Draeger Department of Physics, Illinois Institute of Technology, Chicago, Illinois, USA X.F. Du Institute of High Energy Physics, Beijing D.A. Dwyer Lawrence Berkeley National Laboratory, Berkeley, California, USA W.R. Edwards Lawrence Berkeley National Laboratory, Berkeley, California, USA Department of Physics, University of California, Berkeley, California, USA S.R. Ely Department of Physics, University of Illinois at Urbana-Champaign, Urbana, Illinois, USA J.Y. Fu Institute of High Energy Physics, Beijing L.Q. Ge Chengdu University of Technology, Chengdu R. Gill Brookhaven National Laboratory, Upton, New York, USA M. Gonchar Joint Institute for Nuclear Research, Dubna, Moscow Region G.H. Gong Department of Engineering Physics, Tsinghua University, Beijing H. Gong Department of Engineering Physics, Tsinghua University, Beijing Y.A. Gornushkin Joint Institute for Nuclear Research, Dubna, Moscow Region W.Q. Gu Shanghai Jiao Tong University, Shanghai M.Y. Guan Institute of High Energy Physics, Beijing X.H. Guo Beijing Normal University, Beijing R.W. Hackenburg Brookhaven National Laboratory, Upton, New York, USA R.L. Hahn Brookhaven National Laboratory, Upton, New York, USA G.H. Han College of William and Mary, Williamsburg, Virginia, USA S. Hans Brookhaven National Laboratory, Upton, New York, USA M. He Institute of High Energy Physics, Beijing K.M. Heeger Department of Physics, Yale University, New Haven, Connecticut, USA Y.K. Heng Institute of High Energy Physics, Beijing P. Hinrichs University of Wisconsin, Madison, Wisconsin, USA yk. Hor Center for Neutrino Physics, Virginia Tech, Blacksburg, Virginia, USA Y.B. Hsiung Department of Physics, National Taiwan University, Taipei B.Z. Hu Institute of Physics, National Chiao-Tung University, Hsinchu L.J. Hu Beijing Normal University, Beijing L.M. Hu Brookhaven National Laboratory, Upton, New York, USA T. Hu Institute of High Energy Physics, Beijing W. Hu Institute of High Energy Physics, Beijing E.C. Huang Department of Physics, University of Illinois at Urbana-Champaign, Urbana, Illinois, USA H.X. Huang China Institute of Atomic Energy, Beijing H.Z. Huang University of California, Los Angeles, California, USA X.T. Huang Shandong University, Jinan P. Huber Center for Neutrino Physics, Virginia Tech, Blacksburg, Virginia, USA G. Hussain Department of Engineering Physics, Tsinghua University, Beijing Z. Isvan Brookhaven National Laboratory, Upton, New York, USA D.E. Jaffe Brookhaven National Laboratory, Upton, New York, USA P. Jaffke Center for Neutrino Physics, Virginia Tech, Blacksburg, Virginia, USA S. Jetter Institute of High Energy Physics, Beijing X.L. Ji Institute of High Energy Physics, Beijing X.P. Ji School of Physics, Nankai University, Tianjin H.J. Jiang Chengdu University of Technology, Chengdu J.B. Jiao Shandong University, Jinan R.A. Johnson Department of Physics, University of Cincinnati, Cincinnati, Ohio, USA L. Kang Dongguan University of Technology, Dongguan S.H. Kettell Brookhaven National Laboratory, Upton, New York, USA M. Kramer Lawrence Berkeley National Laboratory, Berkeley, California, USA Department of Physics, University of California, Berkeley, California, USA K.K. Kwan Chinese University of Hong Kong, Hong Kong M.W. Kwok Chinese University of Hong Kong, Hong Kong T. Kwok Department of Physics, The University of Hong Kong, Pokfulam, Hong Kong W.C. Lai Chengdu University of Technology, Chengdu W.H. Lai Institute of Physics, National Chiao-Tung University, Hsinchu K. Lau Department of Physics, University of Houston, Houston, Texas, USA L. Lebanowski Department of Engineering Physics, Tsinghua University, Beijing J. Lee Lawrence Berkeley National Laboratory, Berkeley, California, USA R.T. Lei Dongguan University of Technology, Dongguan R. Leitner Charles University, Faculty of Mathematics and Physics, Prague A. Leung Department of Physics, The University of Hong Kong, Pokfulam, Hong Kong J.K.C. Leung Department of Physics, The University of Hong Kong, Pokfulam, Hong Kong C.A. Lewis University of Wisconsin, Madison, Wisconsin, USA D.J. Li University of Science and Technology of China, Hefei F. Li Institute of High Energy Physics, Beijing G.S. Li Shanghai Jiao Tong University, Shanghai Q.J. Li Institute of High Energy Physics, Beijing W.D. Li Institute of High Energy Physics, Beijing X.N. Li Institute of High Energy Physics, Beijing X.Q. Li School of Physics, Nankai University, Tianjin Y.F. Li Institute of High Energy Physics, Beijing Z.B. Li Sun Yat-Sen (Zhongshan) University, Guangzhou H. Liang University of Science and Technology of China, Hefei C.J. Lin Lawrence Berkeley National Laboratory, Berkeley, California, USA G.L. Lin Institute of Physics, National Chiao-Tung University, Hsinchu S.K. Lin Department of Physics, University of Houston, Houston, Texas, USA Y.C. Lin Chengdu University of Technology, Chengdu J.J. Ling Brookhaven National Laboratory, Upton, New York, USA J.M. Link Center for Neutrino Physics, Virginia Tech, Blacksburg, Virginia, USA L. Littenberg Brookhaven National Laboratory, Upton, New York, USA B.R. Littlejohn Department of Physics, University of Cincinnati, Cincinnati, Ohio, USA D.W. Liu Department of Physics, University of Illinois at Urbana-Champaign, Urbana, Illinois, USA Department of Physics, University of Houston, Houston, Texas, USA H. Liu Department of Physics, University of Houston, Houston, Texas, USA J.C. Liu Institute of High Energy Physics, Beijing J.L. Liu Shanghai Jiao Tong University, Shanghai S.S. Liu Department of Physics, The University of Hong Kong, Pokfulam, Hong Kong Y.B. Liu Institute of High Energy Physics, Beijing C. Lu Joseph Henry Laboratories, Princeton University, Princeton, New Jersey, USA H.Q. Lu Institute of High Energy Physics, Beijing K.B. Luk Lawrence Berkeley National Laboratory, Berkeley, California, USA Department of Physics, University of California, Berkeley, California, USA Q.M. Ma Institute of High Energy Physics, Beijing X.B. Ma North China Electric Power University, Beijing X.Y. Ma Institute of High Energy Physics, Beijing Y.Q. Ma Institute of High Energy Physics, Beijing K.T. McDonald Joseph Henry Laboratories, Princeton University, Princeton, New Jersey, USA M.C. McFarlane University of Wisconsin, Madison, Wisconsin, USA R.D. McKeown College of William and Mary, Williamsburg, Virginia, USA Y. Meng Center for Neutrino Physics, Virginia Tech, Blacksburg, Virginia, USA I. Mitchell Department of Physics, University of Houston, Houston, Texas, USA Y. Nakajima Lawrence Berkeley National Laboratory, Berkeley, California, USA J. Napolitano Department of Physics, Applied Physics, and Astronomy, Rensselaer Polytechnic Institute, Troy, New York, USA D. Naumov Joint Institute for Nuclear Research, Dubna, Moscow Region E. Naumova Joint Institute for Nuclear Research, Dubna, Moscow Region I. Nemchenok Joint Institute for Nuclear Research, Dubna, Moscow Region H.Y. Ngai Department of Physics, The University of Hong Kong, Pokfulam, Hong Kong W.K. Ngai Department of Physics, University of Illinois at Urbana-Champaign, Urbana, Illinois, USA Z. Ning Institute of High Energy Physics, Beijing J.P. Ochoa-Ricoux Lawrence Berkeley National Laboratory, Berkeley, California, USA A. Olshevski Joint Institute for Nuclear Research, Dubna, Moscow Region S. Patton Lawrence Berkeley National Laboratory, Berkeley, California, USA V. Pec Charles University, Faculty of Mathematics and Physics, Prague J.C. Peng Department of Physics, University of Illinois at Urbana-Champaign, Urbana, Illinois, USA L.E. Piilonen Center for Neutrino Physics, Virginia Tech, Blacksburg, Virginia, USA L. Pinsky Department of Physics, University of Houston, Houston, Texas, USA C.S.J. Pun Department of Physics, The University of Hong Kong, Pokfulam, Hong Kong F.Z. Qi Institute of High Energy Physics, Beijing M. Qi Nanjing University, Nanjing X. Qian Brookhaven National Laboratory, Upton, New York, USA California Institute of Technology, Pasadena, California, USA N. Raper Department of Physics, Applied Physics, and Astronomy, Rensselaer Polytechnic Institute, Troy, New York, USA B. Ren Dongguan University of Technology, Dongguan J. Ren China Institute of Atomic Energy, Beijing R. Rosero Brookhaven National Laboratory, Upton, New York, USA B. Roskovec Charles University, Faculty of Mathematics and Physics, Prague X.C. Ruan China Institute of Atomic Energy, Beijing B.B. Shao Department of Engineering Physics, Tsinghua University, Beijing H. Steiner Lawrence Berkeley National Laboratory, Berkeley, California, USA Department of Physics, University of California, Berkeley, California, USA G.X. Sun Institute of High Energy Physics, Beijing J.L. Sun China Guangdong Nuclear Power Group, Shenzhen Y.H. Tam Chinese University of Hong Kong, Hong Kong H.K. Tanaka Brookhaven National Laboratory, Upton, New York, USA X. Tang Institute of High Energy Physics, Beijing H. Themann Brookhaven National Laboratory, Upton, New York, USA S. Trentalange University of California, Los Angeles, California, USA O. Tsai University of California, Los Angeles, California, USA K.V. Tsang Lawrence Berkeley National Laboratory, Berkeley, California, USA R.H.M. Tsang California Institute of Technology, Pasadena, California, USA C.E. Tull Lawrence Berkeley National Laboratory, Berkeley, California, USA Y.C. Tung Department of Physics, National Taiwan University, Taipei B. Viren Brookhaven National Laboratory, Upton, New York, USA V. Vorobel Charles University, Faculty of Mathematics and Physics, Prague C.H. Wang National United University, Miao-Li L.S. Wang Institute of High Energy Physics, Beijing L.Y. Wang Institute of High Energy Physics, Beijing L.Z. Wang North China Electric Power University, Beijing M. Wang Shandong University, Jinan N.Y. Wang Beijing Normal University, Beijing R.G. Wang Institute of High Energy Physics, Beijing W. Wang College of William and Mary, Williamsburg, Virginia, USA W.W. Wang Nanjing University, Nanjing X. Wang College of Electronic Science and Engineering, National University of Defense Technology, Changsha Y.F. Wang Institute of High Energy Physics, Beijing Z. Wang Department of Engineering Physics, Tsinghua University, Beijing Z. Wang Institute of High Energy Physics, Beijing Z.M. Wang Institute of High Energy Physics, Beijing D.M. Webber University of Wisconsin, Madison, Wisconsin, USA H. Wei Department of Engineering Physics, Tsinghua University, Beijing Y.D. Wei Dongguan University of Technology, Dongguan L.J. Wen Institute of High Energy Physics, Beijing K. Whisnant Iowa State University, Ames, Iowa, USA C.G. White Department of Physics, Illinois Institute of Technology, Chicago, Illinois, USA L. Whitehead Department of Physics, University of Houston, Houston, Texas, USA T. Wise University of Wisconsin, Madison, Wisconsin, USA H.L.H. Wong Lawrence Berkeley National Laboratory, Berkeley, California, USA Department of Physics, University of California, Berkeley, California, USA S.C.F. Wong Chinese University of Hong Kong, Hong Kong E. Worcester Brookhaven National Laboratory, Upton, New York, USA Q. Wu Shandong University, Jinan D.M. Xia Institute of High Energy Physics, Beijing J.K. Xia Institute of High Energy Physics, Beijing X. Xia Shandong University, Jinan Z.Z. Xing Institute of High Energy Physics, Beijing J. Xu Beijing Normal University, Beijing J.L. Xu Institute of High Energy Physics, Beijing J.Y. Xu Chinese University of Hong Kong, Hong Kong Y. Xu School of Physics, Nankai University, Tianjin T. Xue Department of Engineering Physics, Tsinghua University, Beijing J. Yan Xi’an Jiaotong University, Xi’an C.G. Yang Institute of High Energy Physics, Beijing L. Yang Dongguan University of Technology, Dongguan M.S. Yang Institute of High Energy Physics, Beijing M. Ye Institute of High Energy Physics, Beijing M. Yeh Brookhaven National Laboratory, Upton, New York, USA Y.S. Yeh Institute of Physics, National Chiao-Tung University, Hsinchu B.L. Young Iowa State University, Ames, Iowa, USA G.Y. Yu Nanjing University, Nanjing J.Y. Yu Department of Engineering Physics, Tsinghua University, Beijing Z.Y. Yu Institute of High Energy Physics, Beijing S.L. Zang Nanjing University, Nanjing L. Zhan Institute of High Energy Physics, Beijing C. Zhang Brookhaven National Laboratory, Upton, New York, USA F.H. Zhang Institute of High Energy Physics, Beijing J.W. Zhang Institute of High Energy Physics, Beijing Q.M. Zhang Xi’an Jiaotong University, Xi’an S.H. Zhang Institute of High Energy Physics, Beijing Y.C. Zhang University of Science and Technology of China, Hefei Y.H. Zhang Institute of High Energy Physics, Beijing Y.M. Zhang Department of Engineering Physics, Tsinghua University, Beijing Y.X. Zhang China Guangdong Nuclear Power Group, Shenzhen Z.J. Zhang Dongguan University of Technology, Dongguan Z.P. Zhang University of Science and Technology of China, Hefei Z.Y. Zhang Institute of High Energy Physics, Beijing J. Zhao Institute of High Energy Physics, Beijing Q.W. Zhao Institute of High Energy Physics, Beijing Y.B. Zhao Institute of High Energy Physics, Beijing L. Zheng University of Science and Technology of China, Hefei W.L. Zhong Institute of High Energy Physics, Beijing L. Zhou Institute of High Energy Physics, Beijing Z.Y. Zhou China Institute of Atomic Energy, Beijing H.L. Zhuang Institute of High Energy Physics, Beijing J.H. Zou Institute of High Energy Physics, Beijing

(July 28, 2025)

Abstract

A measurement of the energy dependence of antineutrino disappearance at the Daya Bay Reactor Neutrino Experiment is reported. Electron antineutrinos ( $\overline{\nu}_{e}$ ) from six $2.9$ GW_th reactors were detected with six detectors deployed in two near (effective baselines 512 m and 561 m) and one far (1579 m) underground experimental halls. Using 217 days of data, 41589 (203809 and 92912) antineutrino candidates were detected in the far hall (near halls). An improved measurement of the oscillation amplitude $\sin^{2}2\theta_{13}=0.090^{+0.008}_{-0.009}$ and the first direct measurement of the $\overline{\nu}_{e}$ mass-squared difference $|\Delta m^{2}_{ee}|=(2.59_{-0.20}^{+0.19})\times 10^{-3}\ {\rm eV}^{2}$ is obtained using the observed $\overline{\nu}_{e}$ rates and energy spectra in a three-neutrino framework. This value of $|\Delta m^{2}_{ee}|$ is consistent with $|\Delta m^{2}_{\mu\mu}|$ measured by muon neutrino disappearance, supporting the three-flavor oscillation model.

neutrino oscillation, neutrino mixing, reactor, Daya Bay

pacs:

14.60.Pq, 29.40.Mc, 28.50.Hw, 13.15.+g

Experimental measurements of neutrino oscillations have clearly established that neutrinos have mass and that the mass eigenstates mix Beringer et al. (2012). The Daya Bay experiment recently reported the discovery of the disappearance of reactor antineutrinos over kilometer-long baselines, providing the most precise measurement of the mixing angle $\theta_{13}$ An et al. (2012a, 2013). Other experiments have made consistent $\theta_{13}$ measurements Ahn et al. (2012); Abe (2012); Adamson et al. (2013a); Abe et al. (2013). Precise knowledge of neutrino mixing and mass differences enables experimental searches for CP violation, tests of the neutrino mass hierarchy and precision tests of oscillation theory. In particular, the relatively large value of $\theta_{13}$ facilitates a rich program of future neutrino oscillation research Bishai et al. ; Y. F. Li, J. Cao, Y. F. Wang, and L. Zhan (2013); Balantekin et al. . It also allows the Daya Bay experiment to report in this Letter an independent measurement of the neutrino mass-splitting via the distortion of the reactor antineutrino energy spectrum.

In the framework of three-flavor neutrino mixing in vacuum, the probability that an $\overline{\nu}_{e}$ produced with energy $E$ is detected as an $\overline{\nu}_{e}$ at a distance $L$ is given by

	$\displaystyle P_{\overline{\nu}_{e}\rightarrow\overline{\nu}_{e}}$	$\displaystyle=$	$\displaystyle 1-\cos^{4}\theta_{13}\sin^{2}2\theta_{12}\sin^{2}\Delta_{21}\hfill$
		$\displaystyle-$	$\displaystyle\sin^{2}2\theta_{13}(\cos^{2}\theta_{12}\sin^{2}\Delta_{31}+\sin^{2}\theta_{12}\sin^{2}{\Delta_{32}}),$

where $\Delta_{ji}\equiv 1.267{\Delta}m^{2}_{ji}({\rm eV}^{2})\frac{L({\rm m})}{E({\rm MeV})}$ , and ${\Delta}m^{2}_{ji}$ is the difference between the mass-squares of the mass eigenstates $\nu_{j}$ and $\nu_{i}$ . Since $\Delta m_{21}^{2}\!\!\!\!\ll\!\!\!\left|\Delta m_{31}^{2}\right|\!\!\!\approx\!\!\!\left|\Delta m_{32}^{2}\right|$ Beringer et al. (2012), the short-distance ( $\sim$ km) reactor $\overline{\nu}_{e}$ oscillation is due primarily to the $\Delta_{3i}$ terms and naturally leads to the definition of the effective mass-squared difference $\sin^{2}\Delta_{ee}\equiv\cos^{2}\theta_{12}\sin^{2}\Delta_{31}+\sin^{2}\theta_{12}\sin^{2}{\Delta_{32}}\,$ ¹¹1Our $\Delta m_{ee}^{2}$ definition is consistent with H. Minakata, H. Nunokawa, S. J. Parke and R. Zukanovich Funchal, Phys. Rev. D 74, 053008 (2006). .

The Daya Bay experiment previously determined $\sin^{2}2\theta_{13}$ using only the relative rates of $\overline{\nu}_{e}$ detected in three antineutrino detectors (ADs) located near to and three ADs located far from six nuclear reactor cores An et al. (2012a, 2013). The effective mass splitting $|\Delta m^{2}_{\mu\mu}|$ measured in $\nu_{\mu}$ disappearance Adamson et al. (2011) provided a good approximation of $|{\Delta}m^{2}_{ee}|$ in the rate-only measurement. This Letter presents a combined analysis of the $\overline{\nu}_{e}$ rates and energy spectra measured for the six detector data-taking period from 24 December 2011 to 28 July 2012. This represents a 48% increase in statistics over the most recent result An et al. (2013). The $\sin^{2}2\theta_{13}$ uncertainty is reduced by inclusion of the spectral information and the statistics of the complete six-AD data period. The spectral distortion due to the $\sin^{2}\Delta_{ee}$ term provides a strong confirmation that the observed $\overline{\nu}_{e}$ deficit is consistent with neutrino oscillations and allows the first direct measurement of $|{\Delta}m^{2}_{ee}|$ .

A detailed description of the Daya Bay experiment can be found in An et al. (2012b, ). Each of the three experimental halls (EHs) contains functionally identical, three-zone ADs surrounded by a pool of ultra-pure water segmented into two regions, the inner water shield (IWS) and outer water shield (OWS), which are instrumented with photomultiplier tubes (PMTs). In each AD, light created as a result of particle interactions in the innermost zone, defined by an inner acrylic vessel (IAV) containing gadolinium-doped liquid scintillator (LS), and the surrounding undoped LS zone, is collected by 192 radially-positioned 20-cm PMTs in the outermost mineral-oil region. The AD trigger threshold of 45 hit PMTs or a summed charge of $\sim\!65$ photoelectrons in all PMTs corresponds to about 0.4 MeV in the Gd-doped volume. The trigger inefficiency for events above 0.7 MeV is negligible. Charge and timing information for each PMT are available for energy calibration and reconstruction, as described in Ref. An et al. (2012b). The detectors have a light yield of $\sim\!165$ photoelectrons/MeV and a reconstructed energy resolution of $\sigma_{E}/E\approx 8\%$ at 1 MeV.

Reactor antineutrinos are detected via the inverse $\beta$ -decay (IBD) reaction, $\overline{\nu}_{e}+p\to e^{+}+n$ . The delayed gamma rays (totalling $\sim\!8$ MeV) generated from the neutron capture on Gd with a mean capture time of $\sim\!30~\mu{\rm s}$ enable powerful background suppression. The prompt light from the $e^{+}$ gives an estimate of the incident $\overline{\nu}_{e}$ energy, $E_{\overline{\nu}_{e}}=E_{\rm prompt}+{}\mkern 3.0mu\overline{\mkern-3.0muE}_{n}+0.78$ MeV, where $E_{\rm prompt}$ is the prompt event energy including the positron kinetic energy and the annihilation energy, and ${}\mkern 3.0mu\overline{\mkern-3.0muE}_{n}$ is the average neutron recoil energy ( $\sim\!10$ keV).

Interpretation of the observed prompt energy spectra requires characterization of the detector response to $e^{+}$ , $e^{-}$ and $\gamma$ , which maps the true energy ( $E_{\rm true}$ ) to the reconstructed energy ( $E_{\rm rec}$ ). $E_{\rm rec}$ is determined by scaling the measured total charge with a position-dependent correction An et al. (2012b, 2013). For a $\gamma$ or $e^{-}$ , $E_{\rm true}$ is the kinetic energy; for a positron $E_{\rm true}$ is the sum of the kinetic energy and the energy from annihilation. The energy response is not linear due to scintillator and electronics effects and is taken into account by two functions, $f_{\rm scint}$ and $f_{\rm elec}$ , respectively. The scintillator nonlinearity is particle- and energy-dependent, and is related to intrinsic scintillator quenching and Cherenkov light emission. The quenching effects are constrained by standalone measurements with a fast neutron beam as well as by neutron source data and radioactive $\alpha$ -decays in the AD. The Cherenkov contribution is also affected by absorption and reemission in the liquid scintillator. The scintillator nonlinearity for electrons is described by an empirical model $f_{\rm scint}(E_{\rm true})=E_{\rm vis}/E_{\rm true}=(p_{0}+p_{3}\cdot E_{\rm true})/(1+p_{1}\cdot e^{-p_{2}\cdot E_{\rm true}})$ , where $E_{\rm vis}$ is the total visible light generated by the particle and $p_{i}$ are the model parameters. A GEANT4-based Agostinelli et al. (2003); Allison et al. (2006) Monte-Carlo simulation (MC) is used to relate the $e^{-}$ scintillator nonlinearity to the response for $\gamma$ and $e^{+}$ . The electronics nonlinearity, $f_{\rm elec}(E_{\rm vis})$ , is introduced due to the interaction of the scintillation light time profile and the charge collection of the front-end electronics. Given the similar timing profiles for $e^{\pm}$ and $\gamma$ s, it is modeled as an exponential function of $E_{\rm vis}$ as determined by studying the time profile of charge in the data and MC.

The energy model, $f=f_{\rm scint}\times f_{\rm elec}$ , is determined by a fit to monoenergetic $\gamma$ lines from radioactive sources and the continuous $\beta+\gamma$ spectrum extracted from ¹²B data. Sources were deployed at the center of all ADs regularly (⁶⁸Ge, ⁶⁰Co, ²⁴¹Am-¹³C) An et al. (2012b) and during a special calibration period in summer 2012 (¹³⁷Cs, ⁵⁴Mn, ⁴⁰K, ²⁴¹Am-⁹Be, Pu-¹³C) with AD1 and AD2 in near-hall EH1. In addition, gamma peaks in all ADs which could be identified with singles and correlated spectra in data (⁴⁰K, ²⁰⁸Tl, $n$ capture on H, C, and Fe) were included. For source data with multiple gamma-line emissions, $f_{\rm scint}$ is computed for each gamma then summed up, whereas $f_{\rm elec}$ is computed based on the total $E_{\rm vis}$ . The ¹²B isotopes are produced cosmogenically at the rate of about 900 (60) events/day/AD at the near (far) site. The measured relative nonlinearity of $<\!0.3\%$ among 6 ADs An et al. (2013) is negligible in the context of the energy model.

Figure 1 compares the best-fit energy model with the single-gamma, multi-gamma and continuous ¹²B data used to determine the model parameters. As additional validation, the energy model prediction for the continuous $\beta+\gamma$ spectra from ²¹²Bi, ²¹⁴Bi and ²⁰⁸Tl decays was compared with the data and found to be consistent.

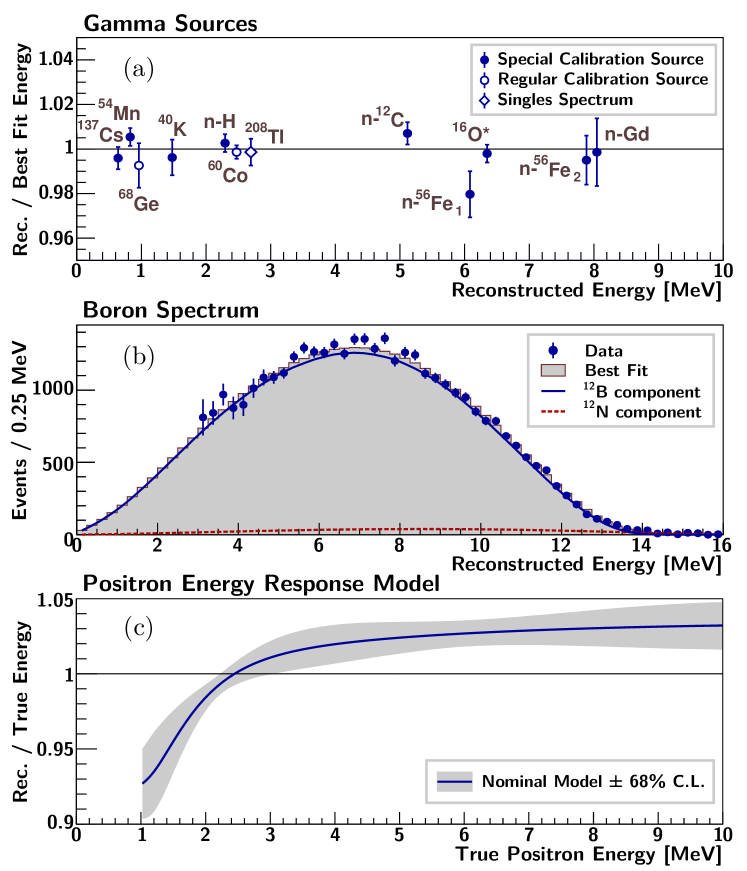
Refer to caption — Figure 1: (a) Ratio of the reconstructed to best-fit energies of $\gamma$ lines from calibration sources and singles spectra as described in the text. The error bars represent the total uncertainty on each ratio. The $\gamma$ from the second-excited state of ¹⁶O in the Pu-¹³C source is denoted ${}^{16}{\rm O}^{*}$ . The n- ${}^{56}{\rm Fe}_{1}$ and n- ${}^{56}{\rm Fe}_{2}$ labels denote the $\sim\!\!6$ MeV and $\sim\!\!7.6$ MeV $\gamma$ s, respectively, resulting from the capture of neutrons from the AmC sources parked on top of the AD. (b) Reconstructed energy spectrum (points) compared to the sum (shaded area) of the ¹²B (solid line) and ¹²N (dashed line) components of the best-fit energy response model. The error bars represent the statistical uncertainties. (c) AD energy response model for positrons.

Alternative energy response models, based on different methodologies, were constructed. The second method builds the scintillator nonlinearity based on Birks’ formula Birks (1951) and Cherenkov radiation theory. The model is characterized by Birks’ constant $k_{B}$ and the Cherenkov light contribution $k_{c}$ . $f_{\rm elec}$ is determined from the residual nonlinearity of the same $\gamma$ and $\beta$ -decay calibration data set. The third method does not use $\gamma$ data but only uses $\beta$ -decay from ¹²B, as well as the internal radioactive $\beta$ -decays of ²¹²Bi, ²¹⁴Bi and ²⁰⁸Tl, to construct the energy model.

All positron energy response models were consistent with each other to $\sim\!1.5\%$ . The uncertainty in the $e^{+}$ energy response, shown in Fig. 1, is conservatively estimated by combining the calibration and model uncertainties. The energy response has a marginal effect on the measured oscillation parameters because it is essentially identical for all ADs.

The observed prompt energy spectrum is modified because positrons from IBD interactions near the IAV can deposit energy in the acrylic without generating scintillation light. This significantly affects $\sim\!1\%$ of all IBD positrons causing an enhancement near $E_{\rm rec}\approx 1$ MeV that is taken into account using MC.

The analysis used for previous Daya Bay results An et al. (2012a, 2013) has been repeated with the full six-AD data sample. The rate uncertainty of the background is slightly reduced compared to the previous analysis due to the increased statistics. The rate-only analysis yields $\sin^{2}2\theta_{13}=0.090\pm 0.010$ with $\chi^{2}/{\rm NDF}=0.6/4$ . The analysis has also been updated to include spectral information by applying the energy nonlinearity correction to the positron spectrum and measuring the spectral distribution of the five background sources. The spectral uncertainties of the five backgrounds are included as uncorrelated among energy bins in the $\chi^{2}$ fit of the oscillation parameters, to allow all possible spectral models consistent with the data. The combined rate and spectral analysis yields $\sin^{2}2\theta_{13}=0.092\pm 0.008$ and $|\Delta m^{2}_{ee}|=(2.57^{+0.20}_{-0.22})\times 10^{-3}{\rm eV}^{2}$ with $\chi^{2}/{\rm NDF}=166/171$ which are consistent with the results to be described in this Letter.

This Letter presents the results of an analysis that is largely independent of the analysis described in An et al. (2012a, 2013). The two analyses differ in terms of event reconstruction, energy calibration, IBD selection, background estimation and construction of the $\chi^{2}$ used for determination of the oscillation parameters. The selected IBD candidates differ by 3.7% (11%) at the far (near) sites. A “blind analysis” strategy was implemented by concealing the reactor history and thermal power information for all cores for the new data period.

IBD candidates are selected with the criteria that follows. First, events caused by PMT light emission are efficiently removed using the techniques of An et al. (2013). Candidates are then selected by requiring a prompt-like signal ( $0.7-12$ MeV) in coincidence with a delayed-like signal ( $6-12$ MeV) separated by $1-200~\mu{\rm s}$ . Candidate pairs are vetoed if their delayed-like events occur (i) within a ( $-2~\mu{\rm s}$ , $600~\mu{\rm s}$ ) time-window with respect to an IWS or OWS trigger with a PMT multiplicity $>$ 12, (ii) within a ( $-2~\mu{\rm s}$ , $1400~\mu{\rm s}$ ) time-window with respect to triggers in the same AD with a total light yield larger than $3000$ photoelectrons, or (iii) within a ( $-2~\mu{\rm s}$ , $0.4~{\rm s}$ ) time-window with respect to triggers in the same AD with a total light yield higher than $3\times 10^{5}$ photoelectrons. This targeted muon veto allows for efficient removal of spurious triggers that follow a muon as well as most muon-induced spallation products. Finally, a multiplicity cut is applied to remove any ambiguities in the IBD pair selection. This cut requires no additional prompt-like signals $400~\mu{\rm s}$ before the delayed event, and no delayed-like signals $200~\mu{\rm s}$ after the delayed event. The muon veto efficiency ( $\epsilon_{\mu}$ ) and multiplicity cut efficiency ( $\epsilon_{m}$ ) are calculated directly from data with negligible uncertainties for each AD. The average values of $\epsilon_{\mu}\cdot\epsilon_{m}$ are summarized in Tab. 1.

A detailed treatment of the absolute and relative efficiencies, as well as their corresponding uncertainties, has been reported in An et al. (2012b, 2013). The uncertainties of the absolute efficiencies are correlated among ADs and thus play a negligible role in the extraction of the oscillation parameters. All differences among ADs are treated as uncorrelated uncertainties. In the rate-only analysis, the uncorrelated uncertainties are dominated by the delayed-energy cut (0.12%) and Gd capture fraction ( $<$ 0.1%). In the spectral analysis, additional uncorrelated uncertainty comes from the relative energy scale difference between ADs. Based upon the relative response in all ADs to identified gamma and alpha peaks from numerous sources that span the IBD positron energy range, a 0.35% uncertainty is assigned.

Five sources of background are identified. The accidental background, defined as any pair of otherwise uncorrelated signals that happen to satisfy the IBD selection criteria, is the largest background in the antineutrino sample. The rate and energy spectra of this background can be accurately determined by measuring the singles rates of prompt- and delayed-like signals and then calculating the probability that the two randomly satisfy the selection criteria. Alternative estimation methods yield consistent results. The relative uncertainty of this background is 0.3% and is dominated by the statistics in the rate of delayed-like signals.

The correlated $\beta-n$ decays from cosmogenic ⁹Li and ⁸He can mimic IBD interactions. The rate of correlated background from this source is estimated by fitting the distribution of the time elapsed since the last muon with the known ⁹Li and ⁸He decay lifetimes L. J. Wen, J. Cao, K. B. Luk, Y. Q. Ma, Y. F. Wang, and C. G. Yang (2006). The 20% systematic uncertainty takes into account the uncertainty in ⁹Li and ⁸He production by muons with energy below the showering muon threshold. The rate is assumed to be the same for ADs at the same site. The fraction of ⁹Li events in this background is estimated to be $95\%\pm 5\%$ based on data and MC. The spectra are calculated with a model that simulates the decay chain of each isotope into their daughters based on external data Nyman et al. (1990); Bjornstad et al. (1981). The spectral uncertainty of this background is estimated by assigning large variations to the energy response model, particularly for the neutron and alpha daughter particles.

Neutrons from the $\sim\!\!0.7$ Hz Am-C calibration sources inside the automated calibration units on top of the ADs can occasionally mimic IBD events by inelastically scattering with nuclei in the shielding material and then capturing on Fe/Cr/Mn/Ni. This produces two $\gamma$ rays that both enter the scintillating region. The MC is used to estimate the rate of this background. The normalization is constrained by the measured rate of single delayed-like candidates from this source. A special Am-C source, approximately 80 times more potent than the calibration sources, was temporarily deployed during summer 2012. Results from this source are used to benchmark the MC and provide the estimate of the 45% uncertainty in the rate normalization. The energy spectrum of this background is modeled as an exponential, the parameters of which are constrained by these data.

Through elastic scattering with protons and the subsequent thermalization and capture on gadolinium, energetic neutrons produced by cosmic rays can mimic IBD interactions. The energy of the proton-recoil signal ranges from sub-MeV up to several hundred MeV. If the prompt energy criterion is loosened to (0.7 - 50) MeV, a flat spectrum is observed up to $50$ MeV, which is extrapolated into the IBD energy region. The flat spectrum assumption is corroborated through the study of fast neutrons associated with muons identified by the muon veto system and by MC. A $50\%$ systematic uncertainty in the rate is assigned. The rate is assumed to be the same for ADs in the same experimental hall.

The ¹³C( $\alpha$ ,n)¹⁶O background is determined from a simulation adjusted with the measured alpha-decay rates from ${}^{238}{\rm U}$ , ${}^{232}{\rm Th}$ , ${}^{227}{\rm Ac}$ and ${}^{210}{\rm Po}$ decay chains. This background represents only about $0.01\%$ and $0.05\%$ of the total IBD sample in the near and far sites, respectively.

The estimated IBD and background rates are summarized in Tab. 1 and displayed in Fig. 2. Backgrounds amount to about $5\%$ (2%) of the IBD candidate sample in the far (near) sites.

	EH1		EH2	EH3
	AD1	AD2	AD3	AD4	AD5	AD6
IBD candidates	101290	102519	92912	13964	13894	13731
DAQ live time (days)	191.001		189.645	189.779
$\epsilon_{\mu}\cdot\epsilon_{m}$	0.7957	0.7927	0.8282	0.9577	0.9568	0.9566
Accidentals (per day)	9.54 $\pm$ 0.03	9.36 $\pm$ 0.03	7.44 $\pm$ 0.02	2.96 $\pm$ 0.01	2.92 $\pm$ 0.01	2.87 $\pm$ 0.01
Fast-neutron (per AD per day)	0.92 $\pm$ 0.46		0.62 $\pm$ 0.31	0.04 $\pm$ 0.02
⁹Li/⁸He (per AD per day)	2.40 $\pm$ 0.86		1.20 $\pm$ 0.63	0.22 $\pm$ 0.06
Am-C correlated (per AD per day)	0.26 $\pm$ 0.12
¹³C( $\alpha$ , n)¹⁶O background (per day)	0.08 $\pm$ 0.04	0.07 $\pm$ 0.04	0.05 $\pm$ 0.03	0.04 $\pm$ 0.02	0.04 $\pm$ 0.02	0.04 $\pm$ 0.02
IBD rate (per day)	653.30 $\pm$ 2.31	664.15 $\pm$ 2.33	581.97 $\pm$ 2.07	73.31 $\pm$ 0.66	73.03 $\pm$ 0.66	72.20 $\pm$ 0.66

Table 1: Summary of signal and backgrounds. The background and IBD rates are corrected for the product of the muon veto and multiplicity cut efficiencies

\epsilon_{\mu}\cdot\epsilon_{m}

The $\overline{\nu}_{e}$ spectrum from a reactor with thermal power $W_{\rm th}(t)$ at energy $E$ and on a given day $t$ is

	$\displaystyle\frac{d^{2}\!N(E,t)}{dEdt}=$	$\displaystyle\sum_{i}\left(\frac{W_{\rm th}(t)}{\sum_{j}f_{j}(t)e_{j}}\,f_{i}(t)\,S_{i}(E)\,c^{\rm ne}_{i}(E,t)\right)$
		$\displaystyle+S_{\rm SNF}(E,t),$

with the fission fractions from each isotope $f_{i}(t)$ , the thermal energy released per fission for each isotope $e_{i}$ , the $\overline{\nu}_{e}$ yield per fission for each isotope $S_{i}(E)$ , the correction to the $\overline{\nu}_{e}$ yield due to reactor non-equilibrium effects $c^{\rm ne}_{i}(E,t)$ and the spent nuclear fuel $S_{\rm SNF}(E,t)$ . The nuclear reactor operators provide daily effective livetime-corrected thermal power as well as periodic burn-up and simulation-based fission fraction data that are used to calculate daily fission fractions. The $\overline{\nu}_{e}$ flux at each detector is calculated by summing the contributions of all reactors. The treatment of $W_{\rm th}$ , $f_{i}$ , $e_{i}$ , $c^{\rm ne}_{i}$ and $S_{\rm SNF}$ terms are described in An et al. (2012a, 2013). The integrated, livetime-corrected, exposure for the EH3 ADs is $168.8\ {\rm kton}\!\cdot\!{\rm GW}_{\rm th}\!\cdot\!{\rm day}$ with mean fission fractions ${}^{235}{\rm U}\!:\!{}^{238}{\rm U}\!:\!{}^{239}{\rm Pu}\!:\!{}^{241}{\rm Pu}=0.573\!:\!0.076\!:\!0.301\!:\!0.050$ . Due to the relative measurement of near and far detectors, the measurement of oscillation parameters is insensitive to the choice of $S_{i}(E)$ K. Schreckenbach, G. Colvin, W. Gelletly, and F. von Feilitzsch (1985); Hahn et al. (1989); von Feilitzsch et al. (1982); Vogel et al. (1981); Huber (2011); Mueller et al. (2011).

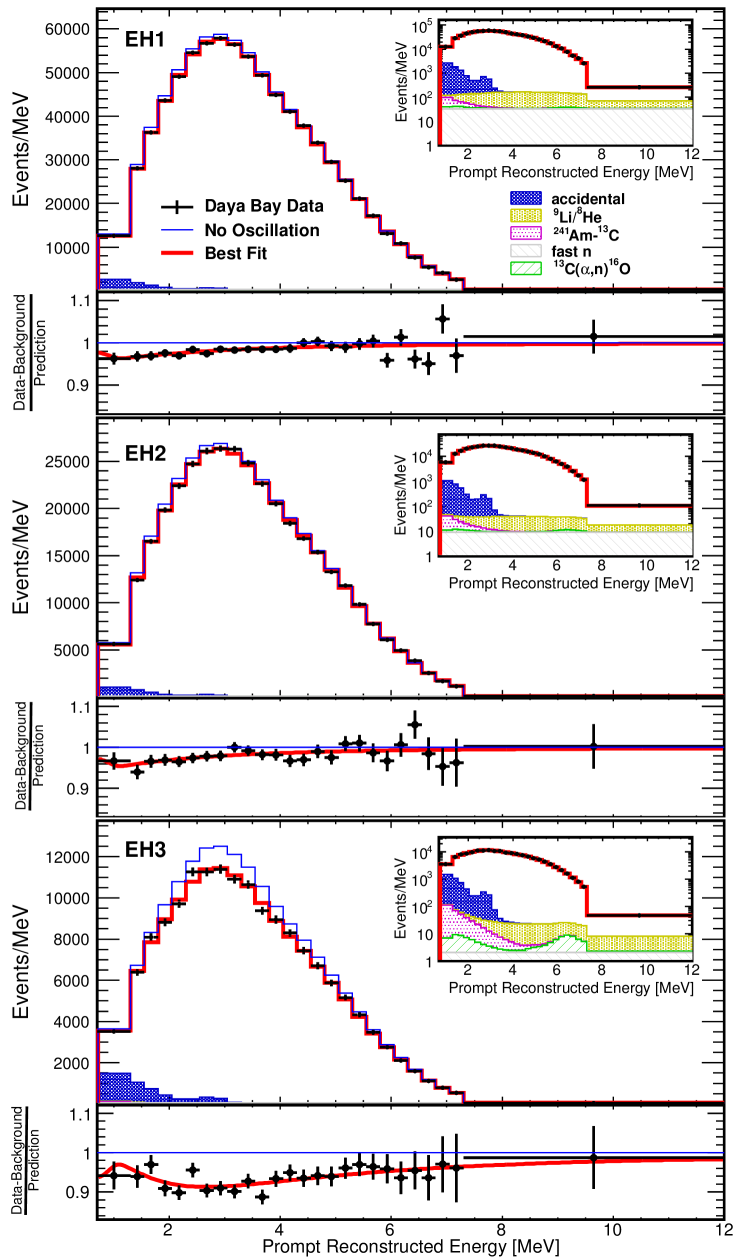
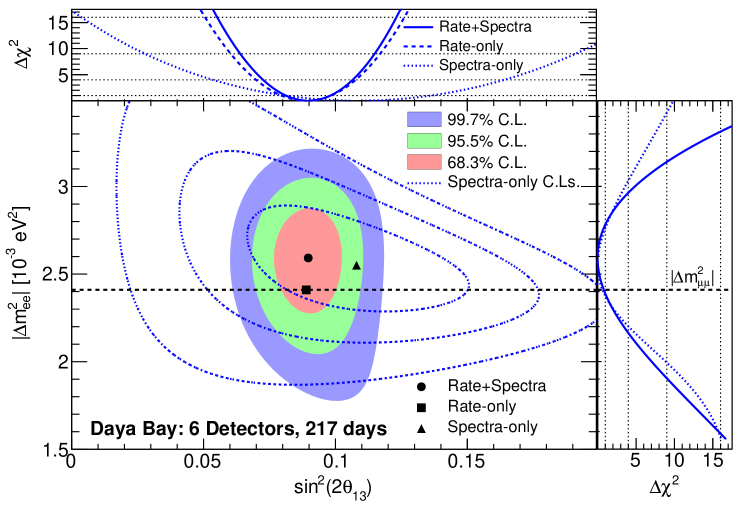
The oscillation parameters are extracted from a fit that takes into account the antineutrino rate, spectral information and the $\overline{\nu}_{e}$ survival probability (Eqn. Spectral measurement of electron antineutrino oscillation amplitude and frequency at Daya Bay). In order to properly account for the systematic effects and correlations among energy bins, a $\chi^{2}$ is constructed using nuisance parameters for detector response and background and a covariance matrix for reactor-related uncertainties. The absolute normalization of the $\overline{\nu}_{e}$ flux is a free parameter in the fit. The fit uses $\sin^{2}2\theta_{12}=0.857\pm 0.024$ and $\Delta m^{2}_{21}=(7.50\pm 0.20)\times 10^{-5}{\rm eV}^{2}$ Beringer et al. (2012). The best-fit values are $\sin^{2}2\theta_{13}=0.090^{+0.008}_{-0.009}$ and $|\Delta m^{2}_{ee}|=(2.59_{-0.20}^{+0.19})\times 10^{-3}\ {\rm eV}^{2}$ with $\chi^{2}/{\rm NDF}=163/153$ (68.3% confidence level (C.L.) intervals) ²²2See Supplemental Material at [URL will be inserted by publisher] for a table of $\chi^{2}-\chi^{2}_{\rm min}$ as a function of $(\sin^{2}2\theta_{13}$ , $|\Delta m_{ee}^{2}|)$ .. The prompt energy spectra observed in each of the experimental halls are compared to the spectra expected for no oscillation and with the best-fit oscillation parameters in Fig. 2. The $68.3\%$ , $95.5\%$ , and $99.7\%$ C.L. allowed regions in the $|{\Delta}m^{2}_{ee}|$ vs. sin ${}^{2}2\theta_{13}$ plane are shown in Fig. 3. Under the assumption of the normal (inverted) neutrino mass hierarchy Beringer et al. (2012), this result is equivalent to $|\Delta m^{2}_{32}|=(2.54_{-0.20}^{+0.19})\times 10^{-3}\ {\rm eV}^{2}$ ( $|\Delta m^{2}_{32}|=(2.64_{-0.20}^{+0.19})\times 10^{-3}\ {\rm eV}^{2}$ ). The result is consistent with $|{\Delta}m^{2}_{\mu\mu}|=({2.41}^{+0.09}_{-0.10})\times 10^{-3}\ {\rm eV}^{2}$ as measured via $\nu_{\mu}$ and $\overline{\nu}_{\mu}$ disappearance Adamson et al. (2013b) noting the small ${\cal O}(0.04\times 10^{-3}\ {\rm eV}^{2})$ effects due to other neutrino oscillation parameters. Figure 4 compares the IBD data from all experimental halls with the $\overline{\nu}_{e}$ survival probability (Eqn. Spectral measurement of electron antineutrino oscillation amplitude and frequency at Daya Bay) using the best-fit values. Almost one full oscillation cycle is visible, demonstrating both the amplitude and frequency of short-baseline reactor $\overline{\nu}_{e}$ oscillation.

The total uncertainty on both oscillation parameters is dominated by statistics. The most significant contributions to the $\sin^{2}2\theta_{13}$ systematic uncertainty are the reactor, relative-detector-efficiency and energy-scale components ³³3Define the contribution of the $i^{\rm th}$ component to the total uncertainty ( $\sigma_{\rm tot}$ ) as $\sigma_{i}^{2}/\sigma_{\rm tot}^{2}$ . The contributions to the $\sin^{2}2\theta_{13}$ ( $|\Delta m_{ee}^{2}|$ ) uncertainty are then 0.73 (0.65), 0.18 (0.02), 0.13 (0.21), 0.11 (0.01), and 0.04 (0.06) for the statistical, reactor, relative-energy and efficiency, absolute-energy, and background components, respectively. Note that $\sum_{i}\sigma_{i}^{2}/\sigma_{\rm tot}^{2}\neq 1$ due to correlations.. The $|\Delta m^{2}_{ee}|$ systematic uncertainty is dominated by the relative energy scale and efficiency. Consistent results are obtained with an independent approach that uses minimal reactor model assumptions and directly predicts the far spectra from the near spectra. Similarly, analysis with a purely nuisance-parameter-based $\chi^{2}$ or purely covariance-matrix-based $\chi^{2}$ yields consistent results. The rate-only result is $\sin^{2}2\theta_{13}=0.089\pm 0.009$ with $\chi^{2}/{\rm NDF}=0.5/4$ with $|\Delta m^{2}_{ee}|$ constrained by the measurement of $|\Delta m^{2}_{\mu\mu}|$ Adamson et al. (2013b). The spectra-only result, obtained by fixing the predicted event rate in each AD to the measured rate, is $\sin^{2}2\theta_{13}=0.108\pm 0.028$ and $|\Delta m^{2}_{ee}|=(2.55^{+0.21}_{-0.18})\times 10^{-3}\ {\rm eV}^{2}$ with $\chi^{2}/{\rm NDF}=161/148$ , and rules out $\sin^{2}2\theta_{13}=0$ at $>\!\!3$ standard deviations.

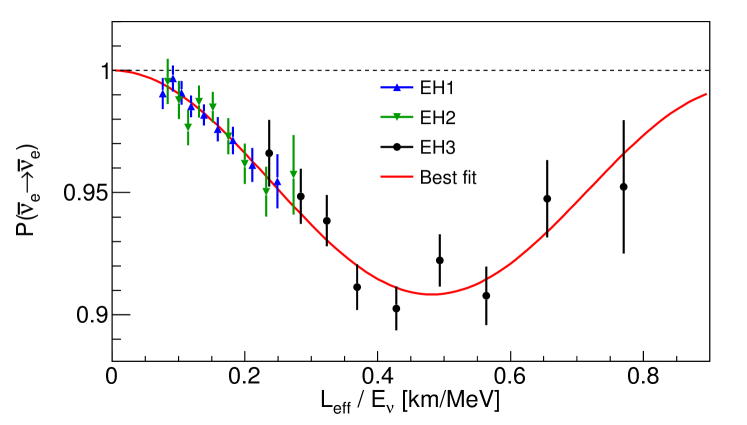
In summary, the relative deficit and spectral distortion observed between three far and three near antineutrino detectors at Daya Bay provides the first independent measurement of $|\Delta m^{2}_{ee}|=(2.59_{-0.20}^{+0.19})\times 10^{-3}\ {\rm eV}^{2}$ and the most precise estimate of $\sin^{2}2\theta_{13}=0.090^{+0.008}_{-0.009}$ to date. Following a special calibration campaign in summer 2012, data collection using all eight antineutrino detectors began in October 2012, and an eventual reduction to a few percent uncertainty in both oscillation parameters is anticipated. On-going analysis of the special calibration data is expected to yield improvements in the energy response model and the knowledge of the absolute $\overline{\nu}_{e}$ detection efficiency. These improvements will enable a future high-statistics measurement of the absolute reactor $\overline{\nu}_{e}$ flux and energy spectra that will provide a valuable reference for studies of reactor neutrinos.

The Daya Bay Experiment is supported in part by the Ministry of Science and Technology of China, the United States Department of Energy, the Chinese Academy of Sciences, the National Natural Science Foundation of China, the Guangdong provincial government, the Shenzhen municipal government, the China Guangdong Nuclear Power Group, Shanghai Laboratory for Particle Physics and Cosmology, the Research Grants Council of the Hong Kong Special Administrative Region of China, University Development Fund of The University of Hong Kong, the MOE program for Research of Excellence at National Taiwan University, National Chiao-Tung University, and NSC fund support from Taiwan, the U.S. National Science Foundation, the Alfred P. Sloan Foundation, the Ministry of Education, Youth and Sports of the Czech Republic, Charles University in Prague, Yale University, the Joint Institute of Nuclear Research in Dubna, Russia, and the NSFC-RFBR joint research program. We acknowledge Yellow River Engineering Consulting Co., Ltd. and China Railway 15th Bureau Group Co., Ltd. for building the underground laboratory. We are grateful for the ongoing cooperation from the China Guangdong Nuclear Power Group and China Light & Power Company.

References

Beringer et al. (2012) J. Beringer et al. (Particle Data Group), Phys. Rev. D 86, 010001 (2012), Section 13.
An et al. (2012a) F. P. An et al. (Daya Bay Collaboration), Phys. Rev. Lett. 108, 171803 (2012a).
An et al. (2013) F. P. An et al. (Daya Bay Collaboration), Chin. Phys. C 37, 011001 (2013).
Ahn et al. (2012) J. Ahn et al. (RENO Collaboration), Phys. Rev. Lett. 108, 191802 (2012).
Abe (2012) Y. Abe (Double Chooz Collaboration), Phys. Rev. Lett. 108, 131801 (2012).
Adamson et al. (2013a) P. Adamson et al. (MINOS Collaboration), Phys. Rev. Lett. 110, 171801 (2013a).
Abe et al. (2013) K. Abe et al. (T2K Collaboration), Phys. Rev. D 88, 032002 (2013).
(8) M. Bishai et al., arXiv:1203.4090 (2012) .
Y. F. Li, J. Cao, Y. F. Wang, and L. Zhan (2013) Y. F. Li, J. Cao, Y. F. Wang, and L. Zhan, Phys. Rev. D 88, 013008 (2013).
(10) A. Balantekin et al., arXiv:1307.7419 (2013) .
Note (1) Our $\Delta m_{ee}^{2}$ definition is consistent with H. Minakata, H. Nunokawa, S. J. Parke and R. Zukanovich Funchal, Phys. Rev. D 74, 053008 (2006).
Adamson et al. (2011) P. Adamson et al. (MINOS Collaboration), Phys. Rev. Lett. 106, 181801 (2011).
An et al. (2012b) F. P. An et al. (Daya Bay Collaboration), Nucl. Inst. Meth. A 685, 78 (2012b).
(14) F. P. An et al. (Daya Bay Collaboration), arXiv:hep-ex/0701029 (2007) .
Agostinelli et al. (2003) S. Agostinelli et al., Nucl. Inst. Meth. A 506, 250 (2003).
Allison et al. (2006) J. Allison et al., IEEE Trans. Nucl. Sci. 53, 270 (2006).
Birks (1951) J. B. Birks, Phys. Rev. 84, 364 (1951).
L. J. Wen, J. Cao, K. B. Luk, Y. Q. Ma, Y. F. Wang, and C. G. Yang (2006) L. J. Wen, J. Cao, K. B. Luk, Y. Q. Ma, Y. F. Wang, and C. G. Yang, Nucl. Inst. Meth. A 564, 471 (2006).
Nyman et al. (1990) G. Nyman et al., Nucl. Phys. A 510, 189 (1990).
Bjornstad et al. (1981) T. Bjornstad et al. (ISOLDE Collaboration), Nucl.Phys. A366, 461 (1981).
K. Schreckenbach, G. Colvin, W. Gelletly, and F. von Feilitzsch (1985) K. Schreckenbach, G. Colvin, W. Gelletly, and F. von Feilitzsch, Phys. Lett. B 160, 325 (1985).
Hahn et al. (1989) A. Hahn et al., Phys. Lett. B 218, 365 (1989).
von Feilitzsch et al. (1982) F. von Feilitzsch, A. Hahn, and K. Schreckenbach, Phys. Lett. B 118, 162 (1982).
Vogel et al. (1981) P. Vogel, G. K. Schenter, F. M. Mann, and R. E. Schenter, Phys. Rev. C 24, 1543 (1981).
Huber (2011) P. Huber, Phys. Rev. C 84, 024617 (2011).
Mueller et al. (2011) T. Mueller et al., Phys. Rev. C 83, 054615 (2011).
Note (2) See Supplemental Material at [URL will be inserted by publisher] for a table of $\chi^{2}-\chi^{2}_{\rm min}$ as a function of $(\mathop{sin}\nolimits^{2}2\theta_{13}$ , $|\Delta m_{ee}^{2}|)$ .
Adamson et al. (2013b) P. Adamson et al. (MINOS Collaboration), Phys. Rev. Lett. 110, 251801 (2013b).
Note (3) Define the contribution of the $i^{\rm th}$ component to the total uncertainty ( $\sigma_{\rm tot}$ ) as $\sigma_{i}^{2}/\sigma_{\rm tot}^{2}$ . The contributions to the $\mathop{sin}\nolimits^{2}2\theta_{13}$ ( $|\Delta m_{ee}^{2}|$ ) uncertainty are then 0.73 (0.65), 0.18 (0.02), 0.13 (0.21), 0.11 (0.01), and 0.04 (0.06) for the statistical, reactor, relative-energy and efficiency, absolute-energy, and background components, respectively. Note that $\sum@\slimits@_{i}\sigma_{i}^{2}/\sigma_{\rm tot}^{2}\not=1$ due to correlations.