Spectrally Sparse Signal Recovery via Hankel Matrix Completion with Prior Information
Abstract
This paper studies the problem of reconstructing spectrally sparse signals from a small random subset of time domain samples via low-rank Hankel matrix completion with the aid of prior information. By leveraging the low-rank structure of spectrally sparse signals in the lifting domain and the similarity between the signals and their prior information, we propose a convex method to recover the undersampled spectrally sparse signals. The proposed approach integrates the inner product of the desired signal and its prior information in the lift domain into vanilla Hankel matrix completion, which maximizes the correlation between the signals and their prior information. Theoretical analysis indicates that when the prior information is reliable, the proposed method has a better performance than vanilla Hankel matrix completion, which reduces the number of measurements by a logarithmic factor. We also develop an ADMM algorithm to solve the corresponding optimization problem. Numerical results are provided to verify the performance of proposed method and corresponding algorithm.
Index Terms:
Maximizing correlation, Hankel matrix completion, spectrally sparse signals, prior information.I Introduction
Spectrally sparse signal recovery refers to recovering a spectrally sparse signal from a small number of time domain samples, which is fundamental in various applications, such as medical imaging[1], radar imaging[2], analog-to-digital conversion[3] and channel estimation[4]. Let denote the one-dimensional spectrally sparse signal to be estimated. Each entry of the desired signal is a weighted superposition of complex sinusoids
where , and denote the normalized frequencies and amplitudes for the sinusoids, respectively, and for .
In many practical applications, we only have access to a small subset of signal samples. For example, in the field of computed tomography (CT), only part of the desired signals can be observed to protect the patients from high-dose radiation[5]; in wideband signal sampling, it’s challenging to build analog-to-digital converter according to Shannon sampling theorem, and hence only a small number of samples of the wideband signals can be acquired for reconstruction[3]. Therefore, we have to figure out a way to recover the original signal from its random undersampled observations
where denote the index set of the entries we observe, denotes the -th canonical basis of , and denotes the projection operator on the sampling index set , i.e., for .
In order to reconstruct , structured low-rank completion methods have been proposed by using the low-rank Hankel structure of the spectrally sparse signals in the lifting domain
| (1) | ||||
where returns the rank of matrix, and is a linear lifting operator to generate the Hankel low-rank structure. In particular, for a vector , the Hankel matrix is defined as
where denotes the matrix pencil parameter, and .
By using Vandermonde decomposition, the Hankel matrix can be decomposed as
where and , . When the frequencies are all distinct and , is a low-rank matrix with .
Since Eq. (1) is a non-convex problem and solving it is NP-hard, an alternative approach based on convex relaxation is proposed to complete the low rank matrix, that is, Hankel matrix completion program [6, 7]
| (2) | ||||
where denotes the nuclear norm. Theoretical analysis was given to show that samples are enough to recover the desired signal with high probability [6].
Apart from the sparsity constraint in the spectral domain, a reference signal that is similar to the original signal sometimes is available to us. There are two main sources of this kind of prior information. The first source comes from natural (non-self-constructed) signals. In high resolution MRI [8, 9, 10], adjacent slices show good similarity with each other; in multiple-contrast MRI [11, 12, 13], different contrasts in the same scan are similar in structure; in dynamic CT [14], the scans for the same slice in different time have similar characteristics. The second source comes from self-constructed signals. One way is to use classical method to construct a similar signal. For example, filtered backprojection reconstruction algorithm from the dynamic scans was used to construct the prior information in dynamic CT [15]; smooth method was used to generate prior information in sparse-view CT [16]; the standard spectrum of dot object was used as the prior information in radar imaging [17]. The other way is to use machine learning to generate a similar signal. In [18], the authors generated the reference image by using a CNN network; similarly, other algorithms from deep learning can be used to create reference signals, see e.g. in [19, 20].
In this paper, we propose a convex approach to integrate prior information into the reconstruction of spectrally sparse signals by maximizing the correlation between signal and prior information in the lifting domain
| (3) | ||||
where is a tradeoff parameter, is a composition operator, is the inner product and returns the real part of a complex number. Here, is a suitable operator to be designed in the sequel. Theoretical guarantees are provided to show that our method has better performance than vanilla Hankel matrix completion when the prior information is reliable. In addition, we propose an Alternating Direction Method of Multipliers (ADMM)-based optimization algorithm for efficient reconstruction of the desired signals.
I-A Related Literature
Recovery of spectrally sparse signals has attracted great attentions in the past years. Conventional compressed sensing [21, 22] was used to estimate the spectrally sparse signals when the frequencies are located on a grid. In many practical applications, however, the frequencies lie off the grid, leading to the mismatch for conventional compressed sensing.
To recover the signals with off-the-grid frequencies, two kinds of methods are proposed: atomic norm minimization and low-rank structured matrix completion. By promoting the sparsity in a continuous frequency domain, atomic norm minimization [23, 24] demonstrated that random samples are sufficient to recover the desired signals exactly with high probability when the frequencies are well separated. Due to the fact that the sparsity in frequency domain leads to the low-rankness in the lifting time domain, low rank structured matrix completion [6, 7] was proposed to promote the low-rank structure in the lifting time domain. Their results showed that random samples are enough to correctly estimate the original signals with high probability when some incoherence conditions are satisfied.
Besides the sparse prior knowledge, other kinds of prior information are used to further improve the recovery performance. By using the similarity between original signal and reference signal, an adaptive weighted compressed sensing approach was considered in [25], which presented a better performance than conventional approach. Assuming that some frequency intervals or likelihood of each frequency of the desired signal is known a priori, a weighted atomic norm method was studied in [26, 27], which outperforms standard atomic norm approach.
While the above work considered spectrally sparse signal recovery with prior information based on conventional compressed sensing or atomic norm minimization, little work incorporates the prior information into low-rank structured matrix completion.
Recently, we proposed a novel method to recover structured signals by using the prior information via maximizing correlation [28, 29]. By introducing a negative inner product of the prior information and the desired signal into the objective function, theoretical guarantees and numerical results illustrated that the matrix completion approach proposed in [29] outperforms standard matrix completion procedure in [30, 31, 32, 33] when the prior information is reliable.
Inspired by [29], this paper leverages the transform low-rank information in the lifting domain to recover the undersampled spectrally sparse signals with the help of the prior information. Different from [29], this paper studies the low-rank property in the lifting domain while the previous approach studies the low-rank property in original domain, leading to the change of the desired matrix from random matrix to Hankel random matrix. Accordingly, the sampling operator changes from sampling random entries to sampling random skew-diagonal. Therefore, different theoretical guarantees should be given to analyze the proposed approach. The analysis also should be extended from real number domain to complex number domain since the spectrally sparse signals are complex.
I-B Paper Organization
The structures of this paper are arranged as follows. Preliminaries are provided in Section II. Performance guarantees are given in Section III. An extension to multi-dimensional models is provided in Section IV. The ADMM optimization algorithm is presented in Section V. Simulations are included in Section VI, and the conclusion is drawn in Section VII.
II Preliminaries
In this section, we introduce some important notation and definitions, which will be used in the sequel.
Let be an orthonormal basis of Hankel matrices [7, 34], which is defined as
where
and returns the cardinality of the set . Then can be expressed as
| (4) |
where for .
Let denote the compact singular value decomposition (SVD) of with , and . Let the subspace denote the support of and be its orthogonal complement. Let denote the sign matrix of , where denotes the compact SVD of .
III Theoretical Guarantees
In this section, we start by giving the theoretical guarantees for the proposed method. Then we extend the analysis to noisy circumstance. Our main result shows that when the prior information is reliable, the proposed approach (3) can outperform previous approach (2) by a logarithmic factor.
Theorem 1.
Let be a rank- matrix and satisfy the standard incoherence condition in Eq. (5) with parameter . Consider a multi-set whose indicies are i.i.d. and follow the uniform distribution on . If the sample size satisfies
and the prior information satisfies
where is an absolute constant,
and
then is the unique minimizer for the approach (3) with high probability.
Remark 1 (Comparison with [7, Theorem 1]).
Remark 2 (The choice of operator ).
It should be noted that the choice of operator will influence the performance of the proposed program. According to the definition of , it’s not hard to see that is a suitable choice to improve the sampling bound. In this case, the value of will be very small when the subspace information of is very similar to that of and . Accordingly, the program becomes
Remark 3 (The choice of weight ).
Note that the sampling lower bound is determined by the value of and the best choice of is the one that minimizes . The expression of can be rewritten as
So the optimal weight is
Let as Remark 2. When the prior information is close to the desired signal, should be around . On the contrary, when the prior information is extremely different from the desired signal, should be around .
Remark 4 (The wrap-around operator).
When is replaced with the following operator with the wrap-around property
where , it is straightforward to obtain the lower bound for sample size by following the proof in [7]
In this case, samples are enough to exactly reconstruct the original signals when the prior information is reliable, which outperforms the atomic norm minimization in [23, 24].
| (12) |
By straightly following [35, Theorem 7], an extension to the noisy version with bounded noise can be shown as follows.
Corollary 1.
Let be a rank- matrix and satisfy the standard incoherence condition in Eq. (5) with parameter . Consider a multi-set whose indicies are i.i.d. and follow the uniform distribution on . Suppose the noisy observation , where denotes bounded noise. Let be the solution of the noisy version program
If the sample size satisfies
and the prior information satisfies
then the solution satisfies that
with high probability.
IV Extensions to multi-dimensional models
In this section, we extend the analysis from one-dimensional signal to multi-dimensional signal. Consider a -way tensor , each of whose entries can be denoted as
for . Denote as the frequency vector for .
Similar to the one-dimensional case, we use multi-level Hankel operator to lift to a low-rank matrix. See Eq. (12), where . When , the above operator degrades to normal Hankel operator. According to [6], the rank of the lifted matrix satisfies by using high-dimensional Vandermonde decomposition. Let denote the prior information of . We can complete the -way tensor by using the following nuclear norm minimization
| (13) | ||||
where denotes the index set of known entries of and denotes the inner product of the -way tensors.
Let be the canonical basis in the domain , and define the following orthonormal basis,
where
and
So each -way tensor can be rewritten as
It’s straightforward to extend the theoretical guarantee from one-dimensional case to multi-dimensional case.
Theorem 2.
Let be a multi-set consisting of random indices where are i.i.d. and follow the uniform distribution on . Suppose, furthermore, that is of rank- and satisfies the standard incoherence condition in (5) with parameter . Then there exists an absolute constant such that is the unique minimizer to (3) with high probability, provided that
and
where
and
Here, if the lifting operator has the wrap-around property; if the lifting operator doesn’t have the wrap-around property.
V Optimization Algorithm
Due to the high computational complexity of low rank methods, we decide to use the non-convex method to solve the problem. First we use matrix factorization to decompose to two low complexity matrices, i.e. with and . Then we use Alternating Direction Method of Multipliers (ADMM) [36] to solve the problem.
First of all, we denote the nuclear norm as follows [37, Lemma 8]
| (14) |
Then, we start ADMM by the following argumented Lagrange function
| (15) |
where is an absolute constant, and is an indicator function
By simple calculations, we can obtain
where denotes the projection operator on and denotes the Penrose-Moore pseudo-inverse mapping corresponding to .
Then, by taking the derivative of the other two problems and setting them to zero, we can otain
and
The last question is how to initialize and . In order to converge quickly, the authors in [38] uses an algorithm named LMaFit [39], which is
| (16) |
However, LMaFit only uses the undersampled measurements and cannot guarantee that has the lifting matrix structure. Instead, we can take advantage of the reference image to initialize and by using truncated SVD when the reference image is reliable. Here, we use the value of as a criterion to choose the suitable initialization strategy.
Then we can give the corresponding algorithm in Algorithm 1. Here, returns the results of truncated SVD. And denotes the algorithm in (16).
VI Simulations
In this section, we carry on numerical simulations to show the improvement of the proposed method (3) compared to standard Hankel matrix completion (2). Besides, we compare the performance under two different solvers: CVX solver and ADMM-solver. Here, we use CVX package[40, 41] to get the convex results and use Algorithm 1 to get the ADMM results.
VI-A Simulations for 1-D signals
We begin by giving the numerical results for one-dimensional signals.
Consider a one-dimensional spectrally sparse signal and the signal is a weighted superposition of complex sinusoids with unit amplitudes. The reference signal is created by , where the entries of the real and imaginary part of follow i.i.d. standard Gaussian distribution, i.e., for .
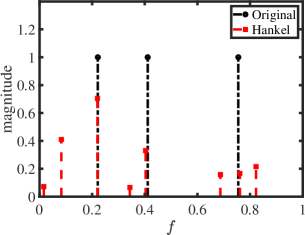
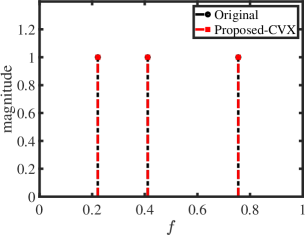
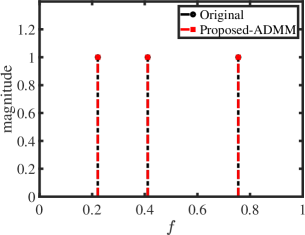
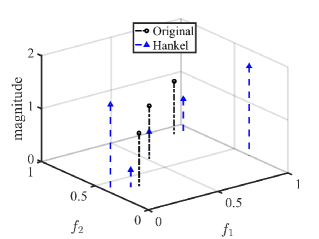
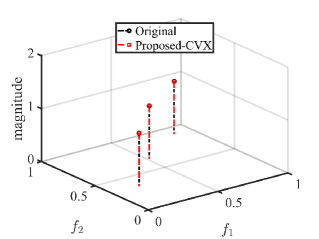
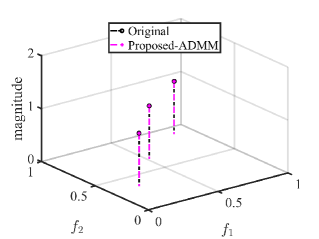
We first show the reconstruction results for standard Hankel matrix completion, the proposed method with CVX solver and the proposed method with ADMM solver. We set , , and . The matrix pencil method is used to estimate the location and amplitude of frequencies [42]. The frequency estimation results are shown in Fig. 1. As expected, with the reliable reference signal, the proposed scheme with different solvers exactly reconstructs the original signal,which has a better performance than standard Hankel matrix completion.
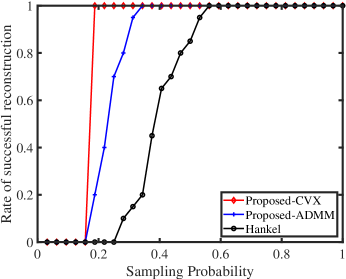
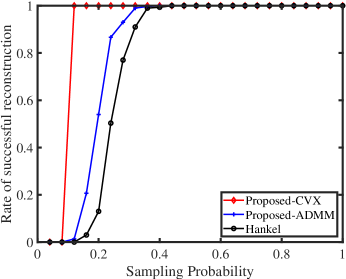
We next provide the successful reconstruction rate as a function of sampling probability standard Hankel matrix completion, the proposed method with CVX solver and the proposed method with ADMM solver. We set , , . We set for CVX solver and for ADMM solver since CVX solver gets the exact solution while ADMM solver has performance degradation due to finite iteration. For each sampling probability, we sample the desired signals in time domain randomly and the results are averaged over 300 independent trials. Then we count the number of successful trials, and calculate the related probability. Here, we claim a trial as a successful trial if the solution satisfies
The results are presented in Fig. 2. The results indicate that the proposed approach (3) outperforms the standard Hankel matrix completion with reliable reference.
| Methods | |||
|---|---|---|---|
| Proposed-CVX | 0.483s | 3.185s | 21.456s |
| Proposed-ADMM | 0.003s | 0.017s | 0.028s |
We then compare the running time for the proposed method with different solvers when the dimension of signals is 16,64 and 96. The numerical simulations are carried on an Intel desktop with 2.5 GHz CPU and 8 GB RAM. The results in Table I show that ADMM solver can dramatically improve the running time. Besides, the proposed scheme with ADMM solver has a much better performance compared with the standard Hankel matrix completion.
VI-B Simulations for 2-D signals
We proceed by giving the numerical results for two-dimensional signals.
Consider a two-dimensional spectrally sparse signal and the signal is a weighted superposition of complex sinusoids with unit amplitudes. The reference signal is created by , where the entries of the real and imaginary part of follow i.i.d. standard Gaussian distribution, i.e., for .
We first show the recovery results for the proposed method and standard Hankel matrix completion. We set and . 2D-MUSIC is applied to obtain the location and amplitude of frequencies[43]. The results are presented in Fig. 3. The results show that the proposed method with different solvers can exactly recover the desired signals while Hankel matrix cannot.
We next present the successful reconstruction rate as a function of sampling probability standard Hankel matrix completion, the proposed method with CVX solver and the proposed method with ADMM solver. We set and . We increase the number of samples from 1 to 100. We Fig. 4 gives the simulation results. As expected, the proposed scheme with the CVX solver performs the best, followed by the proposed scheme with ADMM solver and standard Hankel matrix completion.
| Methods | |||
|---|---|---|---|
| Proposed-CVX | 1.420s | 3.449s | 12.847s |
| Proposed-ADMM | 0.399s | 0.529s | 0.786s |
Finally, Table II compares the running time for the proposed method with different solvers when , and . The results present that the proposed scheme with ADMM solver has smaller running time than that with CVX solver, especially when the dimension of signals is large.
VII Conclusion
In this paper, we have integrated prior information to improve the performance of spectrally sparse signal recovery via structured matrix completion problem and have provided the related performance guarantees. Furthermore, we have designed corresponding ADMM algorithm to reduce the computational complexity. Both the theoretical and experimental results show that the proposed scheme outperforms standard Hankel matrix completion.
Appendix A Proof of Theorem 1
Dual certification is used to deviate the theoretical results. In particular, we use the golfing method from [33] to proceed the process. And we adjust the methods from [6, 7] to suit our model.
Recall the definition of the operator by
Then each is an orthogonal projection onto the one-dimensional subspace spanned by . The orthogonal projection onto the subspace spanned by is given as . Let denote the orthogonal complement of . The summation of the rank-1 projection operators in is denoted by , i.e., . Since is a multi-set and there may exist repetitions in , may be not a projection operator. The summation of distinct elements in is denoted by , which is a valid orthogonal projection.
Before proving the theorem, let’s review the proposed program
We begin by presenting two lemmas, which are necessary for the proof.
Lemma 1 ([7, Lemma 19] & [6, Lemma 3]).
Suppose that
So we have
| (17) | ||||
Then for any small constant , one has
| (18) |
with probability exceeding , provided that for some universal constant and .
Lemma 2.
Consider a multi-set that contains random indices. Suppose that the sampling operator obeys
| (19) |
If there exists a matrix satisfying
| (20) |
| (21) |
and
| (22) |
then the program (3) can achieve exact recovery, i.e., is the unique minimizer.
Proof:
See Appendix B. ∎
As shown in [6], we generate independent random multi-sets and each set contains entries. Note that the distribution of and is the same. Then we construct of a dual certificate via the golfing scheme:
-
1.
Define ;
-
2.
For every (), set
-
3.
Define .
By the construction, it’s easy to see that is in the range space of , then
| (23) |
Let
| (26) |
then we have
| (27) |
except with a probability at most , as long as
For the last condition, using triangle’s inequality yields
According to the result of [6, VI. E], we have
as long as
where from [7, Appendix E]. Set
If , we have
Therefore, we conclude, if
then with high probability, we can achieve the unique minimum.
Remark 5.
Form the operator with wrap-around property, according to [7, Appendix E]. Therefore, we can get the following bound of sample size
Appendix B Proof of Lemma 2
Let be the minimizer to (3). We will show that . Then by the injectivity of the operator , we achieve , so we have .
According to case 2 in the proof of [7, Lemma 20], leads to . So we only need to prove that when
| (28) |
we also have . In the subsequent analysis, we assume that the condition (28) is correct.
According to the definition of nuclear norm, there exists such that and . Then is a sub-gradient of the nuclear norm at . Then it follows that
| (29) | ||||
We can get as shown in [7, A.33-A.34]. In addition, we have
Then the inequality (29) becomes
| (30) |
Next, we are going to derive
Noting that for , it’s enough to prove
By using the triangle inequality, we have
| (31) |
Using Holder’s inequality and the properties of (Eqs. (21) and (22)) yields
| (32) |
By using Eq. (28), we obtain
| (33) |
Therefore, we get
| (34) |
Since be the minimizer to (3), we also have
| (35) |
References
- [1] M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1182–1195, 2007.
- [2] L. C. Potter, E. Ertin, J. T. Parker, and M. Cetin, “Sparsity and compressed sensing in radar imaging,” Proc. IEEE, vol. 98, no. 6, pp. 1006–1020, 2010.
- [3] J. A. Tropp, J. N. Laska, M. F. Duarte, J. K. Romberg, and R. G. Baraniuk, “Beyond nyquist: Efficient sampling of sparse bandlimited signals,” arXiv preprint arXiv:0902.0026, 2009.
- [4] J. L. Paredes, G. R. Arce, and Z. Wang, “Ultra-wideband compressed sensing: Channel estimation,” IEEE J. Sel. Topics Signal Process., vol. 1, no. 3, pp. 383–395, 2007.
- [5] D. J. Brenner and E. J. Hall, “Computed tomography—an increasing source of radiation exposure,” N. Engl. J. Med., vol. 357, no. 22, pp. 2277–2284, 2007.
- [6] Y. Chen and Y. Chi, “Robust spectral compressed sensing via structured matrix completion,” IEEE Trans. Inf. Theory, vol. 60, no. 10, pp. 6576–6601, Oct 2014.
- [7] J. C. Ye, J. M. Kim, K. H. Jin, and K. Lee, “Compressive sampling using annihilating filter-based low-rank interpolation,” IEEE Trans. Inf. Theory, vol. 63, no. 2, pp. 777–801, 2017.
- [8] J. P. Haldar, D. Hernando, S.-K. Song, and Z.-P. Liang, “Anatomically constrained reconstruction from noisy data,” Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, vol. 59, no. 4, pp. 810–818, 2008.
- [9] X. Peng, H.-Q. Du, F. Lam, S. D. Babacan, and Z.-P. Liang, “Reference-driven MR image reconstruction with sparsity and support constraints,” in Biomedical Imaging: From Nano to Macro, 2011 IEEE International Symposium on. IEEE, 2011, pp. 89–92.
- [10] B. Wu, R. P. Millane, R. Watts, and P. J. Bones, “Prior estimate-based compressed sensing in parallel MRI,” Magn. Reson. Med., vol. 65, no. 1, pp. 83–95, 2011.
- [11] B. Bilgic, V. K. Goyal, and E. Adalsteinsson, “Multi-contrast reconstruction with bayesian compressed sensing,” Magn. Reson. Med., vol. 66, no. 6, pp. 1601–1615, 2011.
- [12] X. Qu, Y. Hou, F. Lam, D. Guo, J. Zhong, and Z. Chen, “Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator,” Med. Image Anal., vol. 18, no. 6, pp. 843–856, 2014.
- [13] J. Huang, C. Chen, and L. Axel, “Fast multi-contrast MRI reconstruction,” Magn. Reson. Imaging, vol. 32, no. 10, pp. 1344–1352, 2014.
- [14] M. Selim, E. A. Rashed, and H. Kudo, “Low-dose multiphase abdominal ct reconstruction with phase-induced swap prior,” in Developments in X-Ray Tomography X, vol. 9967. International Society for Optics and Photonics, 2016, p. 99671P.
- [15] G.-H. Chen, J. Tang, and S. Leng, “Prior image constrained compressed sensing (piccs): a method to accurately reconstruct dynamic ct images from highly undersampled projection data sets,” Med. Phys., vol. 35, no. 2, pp. 660–663, 2008.
- [16] M. Selim, E. A. Rashed, M. A. Atiea, and H. Kudo, “Image reconstruction using self-prior information for sparse-view computed tomography,” in 2018 9th Cairo International Biomedical Engineering Conference (CIBEC). IEEE, 2018, pp. 146–149.
- [17] Y. Li, X. Wang, Z. Ding, X. Zhang, Y. Xiang, and X. Yang, “Spectrum recovery for clutter removal in penetrating radar imaging,” IEEE Trans. Geosci. Remote Sens., 2019.
- [18] M. Vella and J. F. Mota, “Single Image Super-Resolution via CNN Architectures and TV-TV Minimization,” arXiv preprint arXiv:1907.05380, 2019.
- [19] C. Dong, C. C. Loy, K. He, and X. Tang, “Image super-resolution using deep convolutional networks,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 38, no. 2, pp. 295–307, 2015.
- [20] J. Kim, J. Kwon Lee, and K. Mu Lee, “Accurate image super-resolution using very deep convolutional networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 1646–1654.
- [21] E. J. Candès, J. Romberg, and T. Tao, “Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,” IEEE Trans. Inf. Theory, vol. 52, no. 2, pp. 489–509, 2006.
- [22] D. L. Donoho, “Compressed sensing,” IEEE Trans. Inf. Theory, vol. 52, no. 4, pp. 1289–1306, 2006.
- [23] G. Tang, B. N. Bhaskar, P. Shah, and B. Recht, “Compressed sensing off the grid,” IEEE Trans. Inf. Theory, vol. 59, no. 11, pp. 7465–7490, 2013.
- [24] G. Tang, B. N. Bhaskar, and B. Recht, “Near minimax line spectral estimation,” IEEE Trans. Inf. Theory, vol. 61, no. 1, pp. 499–512, 2014.
- [25] L. Weizman, Y. C. Eldar, and D. Ben Bashat, “Reference-based MRI,” Med. Phys., vol. 43, no. 10, pp. 5357–5369, 2016.
- [26] K. V. Mishra, M. Cho, A. Kruger, and W. Xu, “Spectral super-resolution with prior knowledge,” IEEE Trans. Signal Process., vol. 63, no. 20, pp. 5342–5357, 2015.
- [27] Y. Li, X. Zhang, Z. Ding, and X. Wang, “Compressive multidimensional harmonic retrieval with prior knowledge,” arXiv preprint arXiv:1904.11404, 2019.
- [28] X. Zhang, W. Cui, and Y. Liu, “Recovery of structured signals with prior information via maximizing correlation,” IEEE Trans. Signal Process., vol. 66, no. 12, pp. 3296–3310, June 2018.
- [29] ——, “Matrix completion with prior subspace information via maximizing correlation,” arXiv preprint arXiv:2001.01152, 2020.
- [30] M. Fazel, “Matrix rank minimization with applications,” Ph.D. dissertation, PhD thesis, Stanford University, 2002.
- [31] B. Recht, M. Fazel, and P. A. Parrilo, “Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization,” SIAM Rev., vol. 52, no. 3, pp. 471–501, 2010.
- [32] E. J. Candès and B. Recht, “Exact matrix completion via convex optimization,” Found. Comput. Math., vol. 9, no. 6, p. 717, 2009.
- [33] D. Gross, “Recovering low-rank matrices from few coefficients in any basis,” IEEE Trans. Inf. Theory, vol. 57, no. 3, pp. 1548–1566, 2011.
- [34] J.-F. Cai, T. Wang, and K. Wei, “Fast and provable algorithms for spectrally sparse signal reconstruction via low-rank hankel matrix completion,” Appl. Comput. Harmon. Anal., vol. 46, no. 1, pp. 94–121, 2019.
- [35] E. J. Candes and Y. Plan, “Matrix completion with noise,” Proc. IEEE, vol. 98, no. 6, pp. 925–936, 2010.
- [36] S. Boyd, N. Parikh, E. Chu, B. Peleato, J. Eckstein et al., “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Foundations and Trends® in Machine learning, vol. 3, no. 1, pp. 1–122, 2011.
- [37] N. Srebro, “Learning with matrix factorizations,” Ph.D. dissertation, Massachusetts Institute of Technology, 2004.
- [38] K. H. Jin, D. Lee, and J. C. Ye, “A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank hankel matrix,” IEEE Trans. Comput. Imaging, vol. 2, no. 4, pp. 480–495, Dec 2016.
- [39] Z. Wen, W. Yin, and Y. Zhang, “Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm,” Mathematical Programming Computation, vol. 4, no. 4, pp. 333–361, 2012.
- [40] M. Grant and S. Boyd, “CVX: Matlab software for disciplined convex programming, version 2.1,” http://cvxr.com/cvx, Mar. 2014.
- [41] ——, “Graph implementations for nonsmooth convex programs,” in Recent Advances in Learning and Control, ser. Lecture Notes in Control and Information Sciences, V. Blondel, S. Boyd, and H. Kimura, Eds. Springer-Verlag Limited, 2008, pp. 95–110.
- [42] Y. Hua and T. K. Sarkar, “Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise,” IEEE Trans. Acoust., Speech, Signal Process., vol. 38, no. 5, pp. 814–824, 1990.
- [43] C. R. Berger, B. Demissie, J. Heckenbach, P. Willett, and S. Zhou, “Signal processing for passive radar using ofdm waveforms,” IEEE J. Sel. Topics Signal Process., vol. 4, no. 1, pp. 226–238, 2010.