Spectroscopy of high-energy states of lanthanide ions
Abstract
We discuss recent progress and future prospects for the analysis of the 4fN-15d excited states of lanthanide ions in host materials. We demonstrate how ab-initio calculations for Ce3+ in LiYF4 may be used to estimate crystal-field and spin-orbit parameters for the 4f1 and 5d1 configurations. We show how excited-state absorption may be used to probe the electronic and geometric structure of the 4fN-15d excited states in more detail and we illustrate the possibilities with calculations for Yb2+ ions in SrCl2.
Michael F. Reida, Liusen Hub,a, Sebastian Franka,c,
Chang-Kui Duand, Shangda Xiab, and Min Yinb
aDepartment of Physics and Astronomy and
MacDiarmid Institute for Advanced Materials and Nanotechnology,
University of Canterbury, Christchurch, New Zealand
Email: mike.reid@canterbury.ac.nz
bDepartment of Physics, University of Science and
Technology of China, Hefei 230026, China
cPresent Address: Department of Theoretical Physics,
University of Bayreuth, 95440 Bayreuth, Germany
dInstitute of Modern Physics, Chongqing University of
Post and Telecommunications, Chongqing 400065, China
Keywords: lanthanide, rare earth, crystal field, ab initio calculations, UV/vis spectroscopy, laser spectroscopy
1 Introduction
The electronic structure of the 4fN configuration of lanthanide ions in condensed matter environments has been a field of intense study since the 1960s. The parametric models that were developed in the 1960s [1, 2, 3] gained further sophistication through the 1970s and 1980s (see, for example, Ref [4]). For a recent review see Ref. [5].
Many applications of lanthanide materials, such as scintillators, lasers, and phosphors, involve the 4fN-15d excited configuration. An understanding of these states, and other high-energy states, such as charge-transfer, conduction-band, and exciton states [6, 7, 8, 9], is crucial to the development of better materials for such applications.
Transitions to the 4fN-15d excited states of lanthanide ions have been studied for a long time, particularly for divalent ions [10, 11] and for Ce3+ [12], which have transitions in the UV region. The availability of VUV synchrotron radiation from the 1970s allowed systematic experimental studies and some limited calculations to be carried out for the trivalent ions [13, 14]. Good availability of VUV beamlines during the past two decades has led to renewed interest in these energy levels, and detailed analyses have been made over the past ten years [15, 16, 17, 18]. These analyses have been reviewed in Ref. [19].
Though the extension of the parametrized model is straightforward, its application to the 4fN-15d configuration is different from application to the 4fN configuration. The 4fN spectra consist of sharp lines, allowing detailed identification of energy levels and accurate fitting of parameters. In contrast, transitions between 4fN and 4fN-15d configurations consist mainly of broad vibronic lines, so interpretation of the spectra is not so straightforward, and accurate determination of the parameters is difficult. The crystal-field splittings of the 4fN-15d configuration are large compared to the splittings caused by the Coulomb interaction. Whereas for the 4fN configuration the crystal field can be considered as a minor perturbation to the free ion, this is not the case for the 4fN-15d configuration, where the crystal field dominates the structure of the spectra.
It is now possible to make reasonably accurate ab-initio calculations for the 4fN and 4fN-15d configurations of lanthanide ions in crystals [20, 21, 22, 23, 24, 25]. This raises the possibility of determining crystal-field and other parameters from such calculations. A method for doing this was developed in Ref. [26], and here is demonstrated for Ce3+ ions in LiYF4.
Ab-initio calculations can also give information about excited-state bonding and geometry [21, 22, 23, 25]. Some excited states have shorter bond lengths than the ground state, and some longer, consistent with various experiments.
More information about the stucture and dynamics of the 4fN-15d states may be obtained by using excited-state absorption (ESA). We discuss how ESA might be used to reveal detailed electronic structure of the 4fN-15d configuration. Transitions where the 5d electron does not change orbitals should give sharp-line spectra because there is no change in bond length. On the other hand, transitions between states where the 5d electron changes to a different orbital will again give broad bands, with the width of the band a measure of the change in excited-state bond length.
2 Analysis of the 4fN and 4fN-15d
configurations of
lanthanide ions in crystals
Modelling of the 4fN and 4fN-15d configurations by parametrized calculations has been reviewed in Ref. [19]. Such “crystal field” calculations make use of an “effective Hamiltonian” [27, 28, 29] that acts solely within the 4fN and 4fN-15d configurations. Rather than solving for the eigenvalues and eigenstates of the full Hamiltonian, the effective Hamiltonian is diagonalized within the model space (4fN and 4fN-15d configurations), and the expectation values of the effective operators are evaluated between the model-space eigenvectors.
The effective Hamiltonian for the 4fN configuration may be written as [4, 5]:
| (1) | |||||
is the energy difference between the ground-state energy and the configuration center of gravity and is included to allow the ground-state energy to be set to zero. The Coulomb interaction between the 4f electrons is parametrized by the radial electronic integrals and the spin-orbit interaction by . These parameters are multiplied by appropriate tensor operators. The , , , , , and parameters represent higher-order Coulomb and magnetic interactions. The major features of the spectra are determined by the and parameters, with the other parameters giving small, but crucial, adjustments.
The are “crystal-field” parameters, which represent the interaction of the 4f electrons with the surrounding ions. For 4f electrons the non-zero parameters have , 4, 6, and values determined by symmetry [1, 2, 5].
For lanthanide 4fN configurations the Coulomb interaction gives splittings of tens of thousands of cm-1, the spin-orbit interaction splittings of a few thousand cm-1, and the crystal-field interaction splittings of a few hundred cm-1. Thus, the positions of the electronic multiplets are quite similar in different crystals, leading to the useful concept of a “Dieke diagram”, which summarises the energy levels of the entire lanthanide series [2, 4, 5]
Transitions between states are parity forbidden, so the transitions are rather weak, consisting of magnetic-dipole and “forced” electric-dipole transitions. The latter are parametrized according to the “Judd-Ofelt” approach [30, 31, 32].
To extend the model to the 4fN-15d configuration we must add more terms to our Hamiltonian. The extra terms are:
| (2) | |||||
In this equation represents the energy difference between the 4fN and 4fN-15d configurations, the and direct and exchange Coulomb interactions between the 4f and 5d electrons, and the crystal-field interaction of the 5d electron with the surrounding ions. This interaction is generally about twenty times larger than the interaction for the 4f electrons, so the splittings due to this interaction are tens of thousands of cm-1, the same magnitude as the Coulomb interaction.
This difference in interaction strength of the 4f and 5d electrons with the ligands results in a shift in the excited-state geometry, and hence the broad bands seen in transitions between the 4fN and 4fN-15d configurations. Since transitions between the 4fN and 4fN-15d configurations generally consist of broad bands, rather than sharp lines, analyses have made use of a variety of ways to reducing the number of parameters, such as by using atomic calculation for the “free ion” parameters. Examination of spectra for ions across the series is also helpful, since certain features may be used to calibrate the model. For example, the splitting between spin-allowed and spin-forbidden transitions in the second half of the series may be used to estimate the parameters for the Coulomb interaction between the 4f and 5d electrons [18].
Calculations based on the above Hamiltonians give a 4f 4fN-15d spectrum with hundreds or thousands of transitions. But since many of the details are obscured by the vibronic bands comparison with experiment is not straightforward. Therefore, it is helpful to have some simple ways to catalog some of the experimental results. Dorenbos [33, 34, 6] has given simple formulae to relate the lowest-energy 4fN to 4fN-15d transition energies, and also charge transfer transition energies, across the lanthanide series. In another approach, Duan and co-workers [35, 36] have used a “simplified model”, where the Coulomb interaction is approximated by a simple exchange potential. Such models are helpful to rationalizing the important features of the spectra.
There have been some attempts to treat the excited state vibrations in more detail. Perturbations of the energies of the excited states by electron-phonon coupling, which has been discussed in detail by Malkin and co-workers [37]. In some cases the individual vibrations can be resolved, in which case the spectra may be analysed to obtain excited state coordinate shifts. See, for example, [38, 39].
3 Extracting parameters from ab-initio calculations
First-principles (ab-initio) calculations of the electronic structure of the 4fN and 4fN-15d configurations of lanthanide ions in solids are now becoming common [21, 24, 20, 25]. Ishii, Ogasawara and co-workers [40, 41, 42, 20, 43] have applied the DV-X method for ions across the entire lanthanide series. Similar calculations have been performed by other workers [24, 44]. Seijo and co-workers [21, 22, 23] have concentrated on a smaller number of systems and have used a sophisticated quantum-mechanical embedding scheme to calculate realistic excited-state geometries and potential-energy surfaces.
Though quite good agreement can now be obtained between ab-initio calculations and experimental energies, it is desirable to compare the ab-initio calculations with the parametric models. As discussed in the previous section, parametric calculations are useful in part because they give a way to compare spectra across the lanthanide series. Parameters obtained in one ion may be extrapolated to others. This may be helpful in applying ab-initio calculations. For example, crystal-field parameters may be calculated for Ce3+, where there is only one valence electron, and the parameters extrapolated to ions with more complex electronic structure for which ab-inito calculations are much more time consuming.
Comparisons at the level of parameters could also provide more detailed tests of the ab-initio calculations. For example, it may be easier to deduce which effects are being poorly represented in the ab-initio calculations by extrating parameters from the calcuations. For example, if correlation is poorly represented then the correlation parameters in Eq. (1) will be calculated to be too small.
In some cases, particularly in high symmetries, such as Oh, the parameters may be determined from ab-initio calculations by fitting them to the calculated energy levels [45]. However, this is not always possible in low symmetry, where, for Ce3+ there are often more free parameters than energy levels. However, it is possible to determine the 4fN or 4fN-15d “effective Hamiltonian” [27], and therefore the parameters, directly, if one has the eigenvectors, as well as the energies, for the relevant states. A straight-forward way of doing this has been discussed recently [26].
We illustrate this method for the crystal-field and spin-orbit parameters for the 4f1 and 5d1 configurations of Ce3+ in LiYF4. Further details and calculations for other hosts will be presented elsewhere. For these calculations we use the rather unsophisticated DV-Xα method with a simple Madelung embedding. This has many shortcomings, as discussed in Refs. [21, 22, 23]. However, our purpose here is to illustrate the method, and this code is quite suitable for that. In particular, it is easy to extract the eigenvectors from the calculation.
The DV-Xα technique was originally developed by Ellis and co-workers for quantum chemical calculations of electronic and structural properties of molecular systems [46]. It was further developed by Adachi and co-workers [47] and it has been used for various calculations on lanthanide systems [40, 41, 42, 43, 24, 44]. These calculations are fully relativistic and so automatically include the spin-orbit interaction.
The coordinates for LiYF4 were taken from Ref. [48]. For the calculations reported here we used a small (CeF8)5- cluster, as used in Refs. [41, 42, 43].
The calculated energy levels are presented in Table 1. Also shown are the experimental 5d1 energies and the results of similar calculations by Ogasawara and co-workers [42, 43]. Since the main focus of this work is the crystal-field splitting of the 4f1 and 5d1 configurations the average energy of the 5d1 configuration in our calculation has been shifted to match the experimental average. The average before this adjustment is given in the last line of the Table.
For Ce3+ there is only one valence electron so the Hamiltonian only includes the crystal-field and spin-orbit interactions. In LiYF4 the energy levels consist of seven and five Kramer’s doublets for 4f1 and 5d1 respectively. Taking into account the S4 site symmetry, the Hamiltonian may be written as:
| (3) |
In S4 symmetry the parameters are complex. However, we may rotate about the axis to make one of our calculated parameters real (e.g. see [1, 49]). If we perform the rotation to make (f) real we find that in practise the imaginary parts of the other parameters are small. Since the experimental parameters are derived assuming a higher D2d symmetry, where all parameters are real, we report real parameters by calculating the magnitude and using the sign of the real part.
To use the approach of Ref. [26] we must identify 4f1 and 5d1 energy levels and eigenvectors. This is straightforward for the small cluster used here. In Table 2 we list the crystal-field parameters for 4f1 and 5d1. We list experimental parameters for Pr3+ and Nd3+, as well as Ce3+, since the crystal-field parameters for Ce3+ are difficult to determine because there are the same number of parameters as energy levels.
The calculated crystal-field parameters and spin-orbit parameters agree quite well with experiment. However, as mentioned above, the DV-Xα method has many shortcomings and more sophisticated calculations would be required to obtain accurate results. We note that we could not have determined crystal-field parameters from only the calculated energies since there are as many parameters as energies. Thus, knowledge of the wave-functions are crucial to such a calculation.
For the small cluster the 4f and 5d orbitals can only mix with F- orbitals. When we attempted calculations with a larger cluster the shortcomings of the method became apparent and there was considerable mixing of 5d orbitals with Y3+ orbitals. This has been previously noted in Ref. [40]. While interactions with the conduction band has an important effect on the high-energy states, as is well-known from the lack of structure observed in the spectra and from direct measurements of photoconductivity [7], the mixing we obtained was too large to be physical.
4 Probing electronic and geometrical structure with
excited-state absorption
The ab-initio calculations by Seijo and co-workers [21, 22, 23] have challenged some common assumptions. It is often assumed that the bond lengths always increase when a lanthanide ion is excited from 4fN to 4fN-15d. However, the recent first-principles calculations cited above suggest that for the lowest-energy 4fN-15d states the bond lengths are shorter than for the 4fN configuration. Only the magnitude, not the sign, of this change in bond length may be easily estimated from ground-state aborption (GSA) spectra. Various evidence, such as pressure measurements [50] and EXAFS experiments in the excited state [51], may be used to confirm these calculations
These calculations also suggest that useful information may be obtained by performing excited-state absorption (ESA) measurements between the 4fN-15d states. We now give a sketch of how such measurements might be carried out.
For ions with the lowest 4fN-15d states have a higher spin than the ground 4fN states and the lowest states with the same spin as the ground state lie a few thousand cm-1 higher. Luminescence is observed in many cases from both the “High Spin” (HS) and the higher-energy “Low Spin” (LS) states of trivalent ions has been observed [18]. Observation of Emission from more than one excited state is particularly common for divalent ions (e.g. [52, 53].
In these cases it is possible to perform a very sensitive ESA experiment by first populating the lower 4fN-15d states. ESA may then be obeserved by using a second excitation source by monitoring the higher-energy emission. Such “upconversion” has already been observed in Tm2+ systems [53]. However, those experiments only demonstrated the effect by exciting at a single frequency. An ESA spectrum was not reported.
The ab-initio calculations by Seijo and co-workers, such as [23], suggest that for some excited-state transtions the bond-length will not change because the 5d electron stays in the same orbital. These transitions should be sharp, whereas those for which the 5d electron changes to a different orbital will be broad. If the bond lengths when the 5d electron is in the lowest 5d orbitals are more contracted than when it is in a 4f orbital and the bond lengths when the electron is in a higher 5d orbital are more expanded, as indicated by the calculations of Seijo and co-workers [21, 22, 23], then some of the transitions within the 4fN-15d configuration will have even broader vibronic bands than the 4fN to 4fN-15d transitions.
These observations suggest that signficantly more information may be obtained from ESA experiments than from conventional one-photon experiments. The observation of sharp transitions within the 4fN-15d configuration (rather than the broad bands observed with ground-state absopption) will allow a much more detailed analysis of the elctronic structure of the excited states. Detailed analyis of the vibrational spectrum for transitions that do change bond length, such as in Refs.[38, 39] will give information about changes in excited state geometry.
We illustrate the information that might be obtained from ESA measurements by considering the case of Yb2+ in SrCl2. This system has been analysed in detail by Piper et al. [11], and more recently by Pan et al. [52]. These calculations make use of our simple crystal-field model. Much more accurate simulations based on ab-initio calculations such as Ref. [23] should be possible, but our point here is to illustrate the issues.
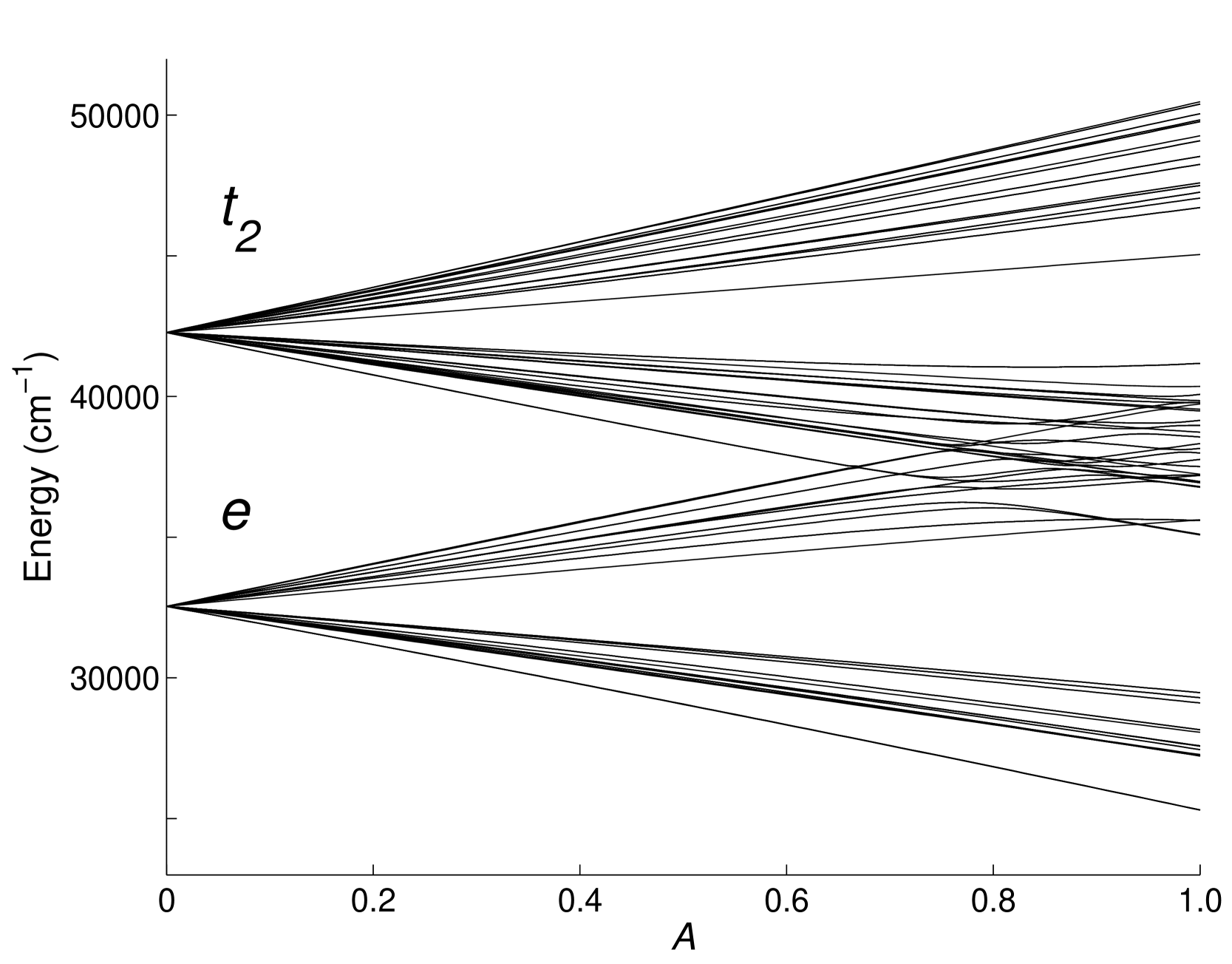
In Figure 1 we show the effect of “switching on” the Hamiltonian, apart from the 5d crystal field. In Oh symmetry there is only one independent 5d crystal-field parameter, , and the Hamiltonian may be written as:
| (4) |
where contains all other interactions apart from the 5d crystal field (and thus is not truly “atomic”, since it contains the 4f crystal field). In Figure 1 the parameter is varied from 0 to 1. When we have only the 5d crystal-field splitting, with the lowest states having the 5d electron in an orbital and the higher states having the 5d electron in a orbital. When we reproduce the calculation of Ref. [52].
Though the lowest 4f135d state has the 5d electron in an orbital, it is clear that some states for which the d electron is in an or a orbital overlap and mix when . We may calculate this mixing by expressing the eigenvectors for as linear combinations of the eigenvectors for . This allows us to simulate the ESA spectrum by assigning appropriate line-widths for the various transitions.
In Figure 2 we show calculated GSA and ESA spectra. The GSA transitions are assigned a vibronic linewidth of 650 cm-1. We assume, for simplicity, that the 5d: states are contracted and the 5d: states expanded by the same amount relative to the 4f14 ground state. Therefore, we assign a small linewidth (50 cm-1) to ESA transitions to pure 5d: states and a linewidth twice the GSA linewidth to ESA transitions to pure 5d: states. Mixed states have intermediate linewidths according to there proportion of 5d:. In the Oh site symmetry of Yb2+ in SrCl2 the ESA transitions within the 4f135d configuration are only magnetic-dipole allowed, and so their dipole strengths are about 1000 times smaller than the electric-dipole allowed GSA transitions. However, they are still strong compared to typical 4fN transitions, and we note that ESA experiments similar to those discussed here have been carried out for transitions within the 4f7 configuration of Gd3+ [54].
The transition to the HS state is forbidden, so does not appear in the simulated GSA spectrum at about 25,000 cm-1. It is clear from Figure 2 that an ESA spectrum could give much more information than the GSA spectrum.
Yb2+ in SrCl2 has drawbacks for this sort of experiment. It is difficult to populate the lowest excited state due to the transition from the ground state to the lowest excited state being electric-dipole and magnetic-dipole forbidden due to point-group selection rules and the non-radiative relaxation from higher states being very slow [52]. More promising candidates are Tm2+ systems, for which up-conversion has already been observed [53] and experiments on these systems are currently underway.
5 Conclusions
It is clear that there are many interesting aspects of excited states of lanthanide ions remaining to be explored. We have demonstrated that it is possible to calculate crystal-field parameters from ab-initio calculations and have suggested excited-state absorption experiments that should allow the exploration of excited states involving 5d electrons in much more detail than in the past.
Acknowledgements
M.F.R. acknowledges travel support from the MacDiarmid Institute and
support from the International Conference on f-Elements.
L.H. acknowledges support from a Chinese Government
Scholarship for his visit to New Zealand.
C.-K.D acknowledges National Science Foundation of China Grant No. 10874173 for financial support.
References
- [1] Wybourne BG. Spectroscopic properties of rare earths. Wiley-Interscience, New York, 1965.
- [2] Dieke GH. Spectra and energy levels of rare earth ions in crystals. Interscience, 1968.
- [3] Carnall WT, Fields PR, Rajnak K. J. Chem. Phys. 1968; 49:4424–4442.
- [4] Carnall W, Goodman G, Rajnak K, Rana R. J. Chem. Phys. 1989; 90:3443–3457.
- [5] Liu GK, Jacquier B ( eds.). Properties of Rare Earths in Optical Materials. Springer, 2005.
- [6] Dorenbos P. J. Less Common Metals 2009; 488:568.
- [7] Pedrini C, Joubert MF, McClure DS. J. Luminescence 2007; 125:230.
- [8] Grinbeg M, Mahlik S. J. Non-Cryst. Sol. 2008; 354:4163.
- [9] Dorenbos P. J. Phys. Condensed Matter 2003; 15(2645).
- [10] McClure DS, Kiss Z. J. Chem. Phys. 1963; 39:3251.
- [11] Piper TS, Brown JP, McClure DS. J. Chem. Phys. 1967; 46:1353.
- [12] Schesinger M, Whippey PW. Phys. Rev. 1968; 171:361.
- [13] Elias LR, Heaps WS, Yen WM. Phys. Reve. B 1973; 8:4989.
- [14] Heaps WS, Elias LR, Yen WM. Phys. Rev. B 1975; 13:94.
- [15] Reid MF, van Pieterson L, Wegh RT, Meijerink A. Phys. Rev. B 2000; 62:14 744–14 749.
- [16] Laroche M, Doualan JL, Girard S, Margerie J, Moncorgé R. J. Opt. Soc. Am. B 2000; 17:1291.
- [17] van Pieterson L, Reid MF, Wegh RT, Soverna S, Meijerink A. Phys. Rev. B 2002; 65:045 113–1–16.
- [18] van Pieterson L, Reid MF, Burdick GW, Meijerink A. Phys. Rev. B 2002; 65:045 114–1–13.
- [19] Burdick GW, Reid MF. Handbook on the Physics and Chemistry of the Rare Earths, vol. 37, Gschneidner Jr KA, Bunzli JC, Percharsky VK eds.. chap. 232, North Holland, 2007; 61–91.
- [20] Ogasawara K, Watanabe S, Toyoshima H, Brik MG. Handbook on the Physics and Chemistry of Rare Earths, vol. 37. chap. 231, Elsevier, 2007.
- [21] Ruiperez F, Barandiaran A, Seijo L. J. Chem. Phys. 2005; 123:244 703.
- [22] Pascual JL, Schamps J, Barandiarán Z, Seijo L. Phys. Rev. B 2006; 74:104 105.
- [23] Sánchez-Sanz G, Seijo L, Barndarán Z. J. Chem. Phys. 2009; 131:024 505.
- [24] Ying J, Zhi Z, Xia S, Yin M. Journal of Rare Earths 2005; 23:148–152.
- [25] Andriesson J, van der Kolk E, Dorenbos P. Phys. Rev. B 2007; 76:075 124.
- [26] Reid MF, Duan CK, Zhou H. J. Alloys Comp. 2009; 488:591 – 594.
- [27] Hurtubise V, Freed KF. Adv. Chem. Phys. 1993; 83:465.
- [28] Bryson AR, Reid MF. J. Alloys Comp. 1998; 275-277:284–287.
- [29] Lee MJ, Reid MF, Faucher MD, Burdick GW. J. Alloys Comp. 2001; 323-324:636–639.
- [30] Judd BR. Phys. Rev. 1962; 127:750–761.
- [31] Ofelt GS. J. Chem. Phys. 1962; 37:511–520.
- [32] Reid MF. Spectroscopic Properties of Rare Earths in Optical Materials, Liu G, Jacquier B eds.. chap. 2, Springer, 2005; 95–127.
- [33] Dorenbos P. J. Luminescence 2000; 91:155–176.
- [34] Dorenbos P. J. Phys. Condensed Matter 2003; 15(575).
- [35] Duan C, Xia S, Reid M, Ruan G. Phys. Stat. Sol. B 2005; 242:2503–2508.
- [36] Xia SD, Duan CK, Deng Q, Ruan G. J. Solid State Chem. 2005; 178:2643.
- [37] Malkin BZ, Solovyev OV, Malishev AY, Saikin SK. J. Luminescence 2007; 125:175.
- [38] Liu GK, Chen XY, Edelstein NM, Reid MF, Huang J. J. Alloys Comp. 2004; 366:240–244.
- [39] Karbowiak M, Urbaniowicz A, Reid MF. Phys. Rev. B 2007; 76:115 125.
- [40] Ishii T, Tohei T, Fujimura T, Ogasawara K, Adachi E. The 4th Pacific Rim Conference on Lasers and Electro-Optics, vol. 2. 2001; 80.
- [41] Ogasawara K, Watanabe S, Toyoshima H, Ishii T, Brik MG, Ikeno H, Tanaka I. J. Solid State Chem. 2005; 178:412.
- [42] Watanabe S, Ishii T, Fujimura K, Ogasawara K. First-principles calculations of spectral properties of reare earth and transition metal ions in crystals, ad K Ogasawara MGB (ed.). Transworld Research Network, 2006; 81.
- [43] Watanabe S, Ogasawra K. J. Phys. Soc. Jap. 2008; 77(084702).
- [44] Wang DJ, Xia SD, Yin M. J. Rare Earths 2008; 26:439.
- [45] Duan CK, Reid MF, Xia S. J. Luminescence 2007; 122:939–941.
- [46] Rosen A, Ellis DE. J. Chem. Phys. 1975; 62:3039.
- [47] Adachi H, Tsukada M, Satoko C. J. Phys. Soc. Jap. 1978; 45:875.
- [48] Garcia E, Ryan RR. Acta Cryst. 1993; C49:2053.
- [49] Burdick GW, Reid MF. Mol. Phys. 2004; 102:1141–1147.
- [50] Valiente R, Rodriguez F, Gonzalez J, Güdel HU, Martin-Rodriguez R, Nataf L, Sanz-Ortiz MN, Kramer K. Chem. Phys. Lett. 2009; 481:149.
- [51] Barandiaran A, Edelstein NM, Ruiperez F, Seijo L. J. Solid State Chem. 2005; 178:464–469.
- [52] Pan Z, Duan CK, Tanner PA. Phys. Rev. B 2008; 77:085 114.
- [53] Beurer E, Grimm J, Gerner P, Güdel HU. Inorg. Chem. 2006; 45:9901.
- [54] Peijzel PS, Vermeulen P, Schrama WJM, Meijerink A, Reid MF, Burdick GW. Phys. Rev. B 2005; 71:125 126.
- [55] van Pieterson L, Wegh RT, Meijerink A, Reid MF. J. Chem. Phys. 2001; 115:9382–9392.
- [56] Görller-Walrand C, Binnemans K. Handbook on the Physics and Chemistry of Rare Earths, vol. 23, K A Gschneidner J, Eyring L eds.. North-Holland: Amsterdam, 1996; 121–283.
| Experiment [55] | Calculation (this work) | Calculation(Ref. [42]) | |
|---|---|---|---|
| 4f1 | 0 | 0 | 0 |
| 616 | 129 | ||
| 672 | 492 | ||
| 2604 | 2807 | ||
| 2971 | 2896 | ||
| 3316 | 3041 | ||
| 3461 | 3646 | ||
| 5d1 | 33400 | 33764 | 40086 |
| 41200 | 43078 | 45974 | |
| 48600 | 48145 | 51781 | |
| 50500 | 48739 | 52829 | |
| 53000 | 52662 | 56781 | |
| 5d average | 45277 | 30864 | 49490 |
| Parameter | Calculation | Experiment | ||
|---|---|---|---|---|
| Ce3+a | Pr3+ b | Nd3+c | ||
| B(f) | 1228 | 481 | 489 | 409 |
| B(f) | 538 | 1150 | 1043 | 1135 |
| B(f) | 1001 | 1228 | 1242 | 1216 |
| B(f) | 12 | 89 | 42 | 27 |
| B(f) | 723 | 1213 | 1213 | 1083 |
| (f) | 748 | 615 | 731 | 871 |
| B(d) | 5338 | 4673 | 7290 | |
| B(d) | 12155 | 18649 | 14900 | |
| B(d) | 23448 | 23871 | 17743 | |
| (d) | 894 | 1082 | 906 | |