Spin dependence in the -wave resonance of
Abstract
We measured the spin dependence in a neutron-induced -wave resonance by using a polarized epithermal neutron beam and a polarized nuclear target. Our study focuses on the 0.75 eV -wave resonance state of 139La+, where largely enhanced parity violation has been observed. We determined the partial neutron width of the -wave resonance by measuring the spin dependence of the neutron absorption cross section between polarized and polarized neutrons. Our findings serve as a foundation for the quantitative study of the enhancement effect of the discrete symmetry violations caused by mixing between partial amplitudes in the compound nuclei.
I Introduction
The spin dependence of the strong interaction between a neutron and a nucleus can lead to a spin-dependent cross section proportional to , where and are unit vectors parallel to the spins of the neutron and the nucleus, respectively. This spin-dependent cross section can be observed through a spin-dependent transmission through a polarized nuclear target. At a neutron-nucleus resonance, this observable can directly determine the spin of compound resonance states. Consequently, it has been employed in measuring -wave resonances for a select few nuclides, utilizing both a polarized neutron beam and a polarized target Keyworth et al. (1973a, b); Alfimenkov et al. (1994). In the case of -wave resonances, the spin-dependent cross section imparts valuable information not only regarding the spin of the resonance but also the partial neutron widths.
These widths enable the exploration of symmetry violation enhancement effects in the compound nucleus. Enhancements in parity violation, exceeding magnitudes of nucleon-nucleon interactions by a factor of 106, have been observed in -wave resonances of nuclei with a mass number of medium-heavy or heavy nuclei Mitchell et al. (2001). These enhancements can be understood as a result of parity mixing between - and - compound nuclear resonances. This is referred to as the - mixing model Mitchell et al. (2001); Sushkov and Flambaum (1982); Bunakov and Gudkov (1983). Theory suggests that this mechanism can lead to an enhancement of fundamental time reversal violation, which could be utilized to search for beyond the Standard Model physics by measuring a T-odd cross section at the -wave resonance using a polarized target and a polarized neutron beam Gudkov (1991). We can quantify the enhancement factors associated with both P- and T-violations by determining the partial neutron width Gudkov (1992); Gudkov and Shimizu (2018); Okudaira et al. (2018, 2021); Yamamoto et al. (2020); Koga et al. (2022); Endo et al. (2022); Okudaira et al. (2023).
This paper presents the first measurement of the spin-dependent cross section at the -wave compound resonance, employing a polarized epithermal neutron beam and a polarized nuclear target. As our target nucleus, we selected 139La, which displays an exceedingly large enhanced parity violation at the 0.75 eV -wave resonance Yuan et al. (1991).
II Experiment
II.1 Experimental setup
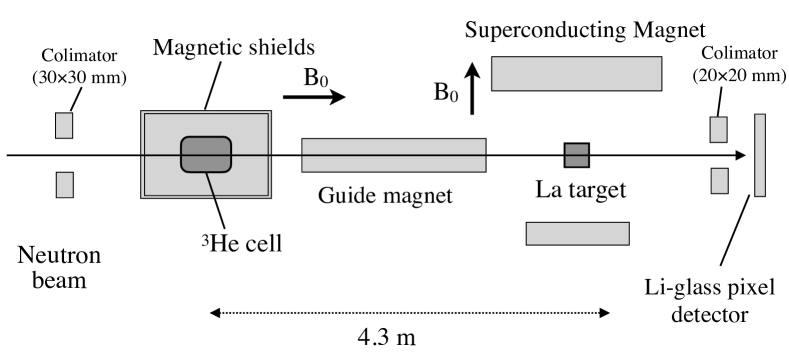
The experiment was performed with a pulsed epi-thermal neutron beam at the RADEN beamline of the Material and Life Science Experimental Facility (MLF) at the Japan Proton Accelerator Research Complex (J-PARC) Shinohara et al. (2020). The experimental setup is depicted in Fig. 1. The La target is placed 23.0 m from the moderator surface. A 2.0 cm cubic lanthanum metal cooled with a dilution refrigerator was used as the target. A 6.8 Tesla transverse magnetic field was applied using a superconducting magnet to polarize the target nuclei. The neutron beam, collimated to a 3 cm by 3 cm size, was stripped of thermal neutrons using a cadmium filter upstream of the beamline to reduce the heat load on the La target induced by the neutron beam. The beam was polarized with a neutron polarizer using polarized 3He gas (3He spin filter), located 4.3 m upstream of the polarized target. The 3He spin filter was polarized using the spin exchange optical pumping method (SEOP) with a 110 W laser system constructed outside of the beamline and then installed on the beamline with a coil and a double magnetic shield to maintain the 3He polarization Okudaira et al. (2020). The 3He cell was 45 mm in diameter by 70 mm in length and the pressure was 0.31 MPa. The neutron beam, longitudinally polarized by the 3He spin filter, was guided using a guide magnet. The spin direction was adiabatically rotated to the transverse direction utilizing the stray magnetic field of the superconducting magnet. The neutron spin was flipped every 30 minutes by flipping the spin of 3He gas using adiabatic fast passage (AFP) NMR. The loss of the 3He polarization was per flip, which was negligibly small. Transmitted neutrons were recorded in list mode using a 256-pixel lithium glass scintillator detector located at 24.71 m from the moderator surface Satoh (2015). Downstream of the La target, another collimator was installed to reduce the beam divergence. The neutron energy was determined using the neutron time-of-flight (TOF) and the flight path length. The proton beam power was 750 kW during the experiment.
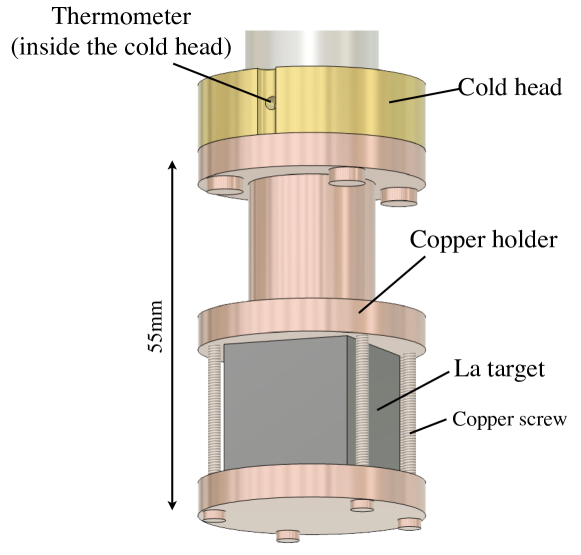
Figure 2 illustrates the configuration around the La target. The La target was held in place between upper and lower copper holders, fastened using copper screws. The upper holder was connected to the cold head of the dilution refrigerator, enabling cooling of the La target through thermal conduction. The temperature was monitored with a ruthenium oxide thermometer installed in the cold head. We performed the experiment in two conditions: (a) low temperature condition ( ) and (b) high temperature condition (). The measurement times were 22 hours and 6 hours, respectively. In the condition (a), the temperature increase by the beam irradiation to the La target was approximately 1 mK, indicating that the temperature difference between the cold head and the La target can be considered negligible. The temperature fluctuation was also around 1 mK, which was caused by beam interruptions in the accelerator due to malfunctions.
II.2 Measurement of the asymmetry
The cross sections for parallel and antiparallel polarized neutron and nucleus can be written with the spin-independent cross section and spin-dependent cross section as
| (1) |
where and denote the parallel and antiparallel spins, respectively. The asymmetry of neutron counts for parallel and anti-parallel spins transmitted through the polarized lanthanum target, defined as
| (2) |
where and are the neutron counts for parallel and anti-parallel spins, was measured. The neutron counts are expressed using the neutron polarization and nuclear vector polarization as
| (3) |
where , , , and are number of incident neutrons, detection efficiency of a neutron detector, number density of the nuclear target, and the thickness of the nuclear target, respectively. The spin-dependent asymmetry can be described using Eq.3 as
| (4) |
In this paper, the measurement and analysis were performed using resonance parameters of La+n reactions listed in Table 1, which were recently measured by Endo et al. Endo et al. (2023) using both neutron transmission and (, ) reaction with an intense pulsed neutron beam at J-PARC.
| Isotope | |||||
|---|---|---|---|---|---|
| 34610 | |||||
| 4 | |||||
| 11/2 | |||||
| 3 |
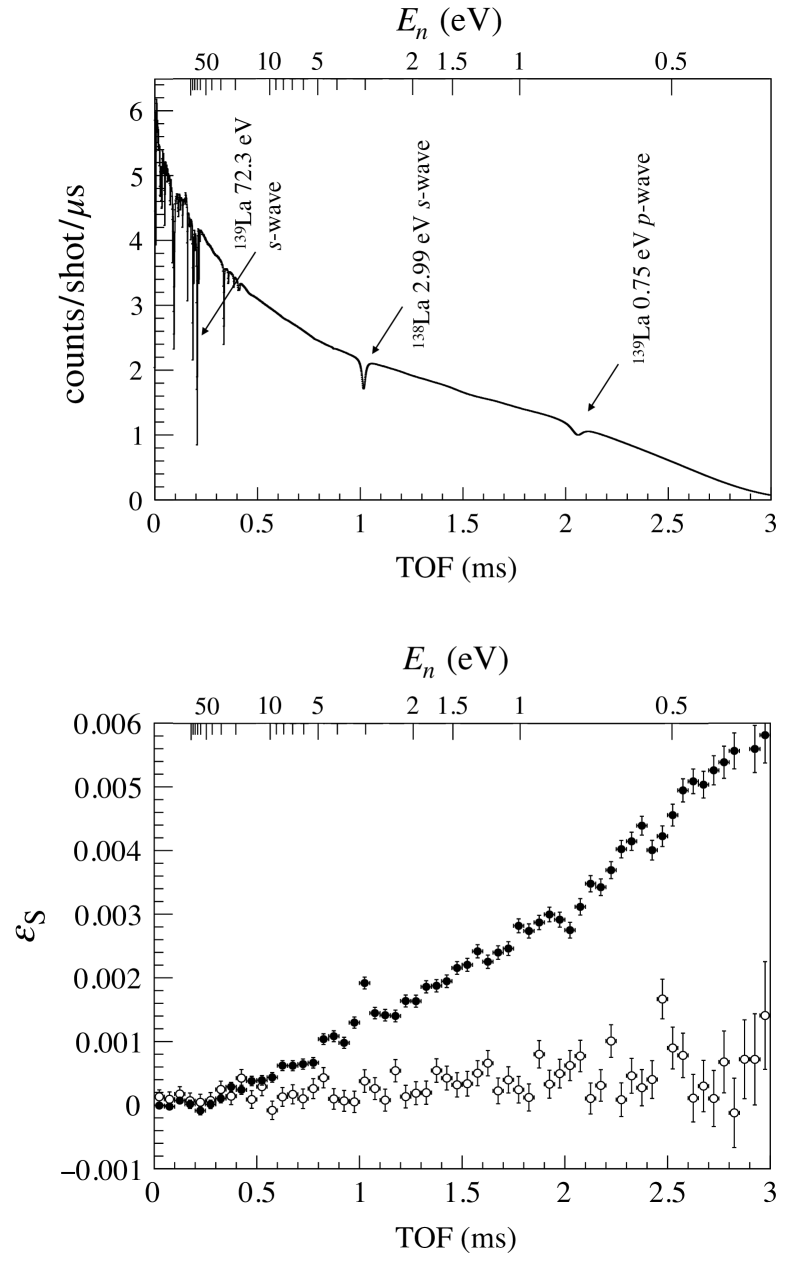
Figure 3 shows the TOF spectra of the transmitted neutrons and asymmetry in conditions (a) and (b). We observed a significant asymmetry in condition (a), corresponding to a high nuclear polarization, while the asymmetry disappeared in condition (b) due to the lower nuclear polarization. The peak and dip structures were observed at the 2.99 eV and 0.75 eV resonances. The global structure observed less than 0.3 ms is attributed to the spin-dependent cross section of the negative -wave resonance.
II.3 Neutron polarization
The neutron polarization was obtained using the 3He polarization of the 3He spin filter. The 3He polarization was determined with the ratio of the transmitted neutrons for polarized and unpolarized 3He spin filter. The ratio of the transmitted neutrons is described as
| (5) |
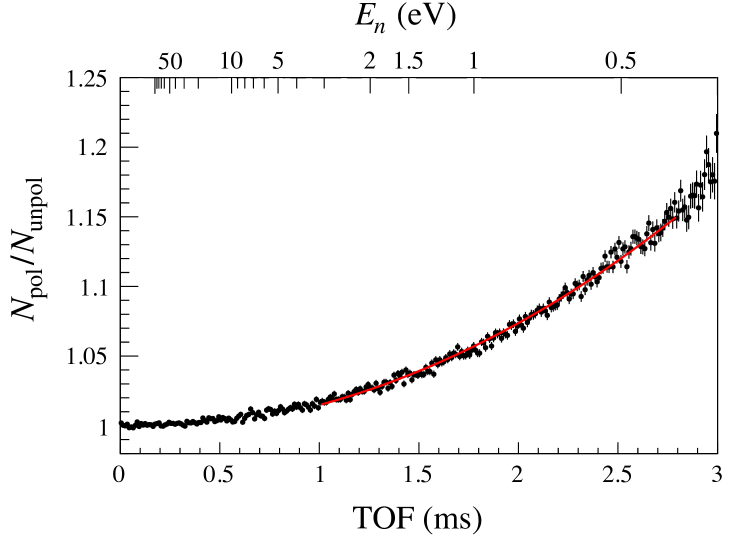
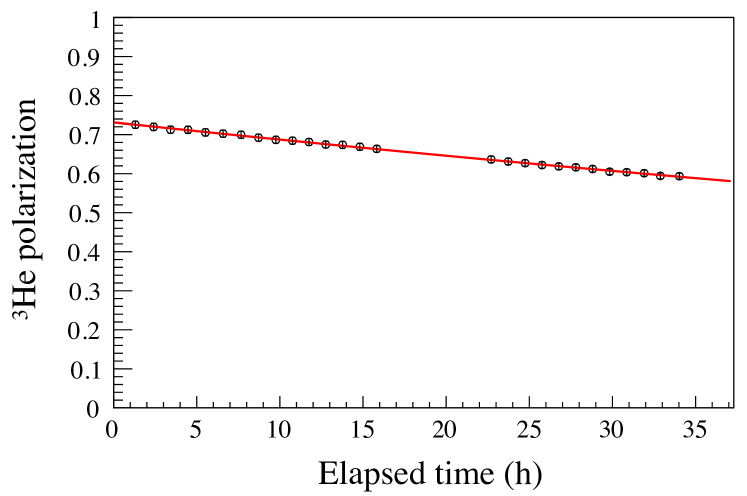
where, , , and are the 3He polarization, neutron absorption cross section of 3He, and areal density of 3He gas, respectively. Here, is defined as for cancelling the spin-dependent asymmetry derived from the polarization of the La target. The areal density was obtained from the measurement of the ratio of transmitted neutrons for unpolarized 3He spin filter and empty glass cell as 21.4 atmcm. The 3He polarization was obtained for each flip by fitting the TOF dependence of using Eq. 5 with a fit parameter of as shown in Fig 4. Figure 5 shows the time dependence of the 3He polarization. The relaxation time of the 3He polarization , which was obtained by fitting with , was 161 h. The averaged 3He polarization during the measurement was %.
The neutron polarization transmitted through the 3He spin filter is determined as
| (6) |
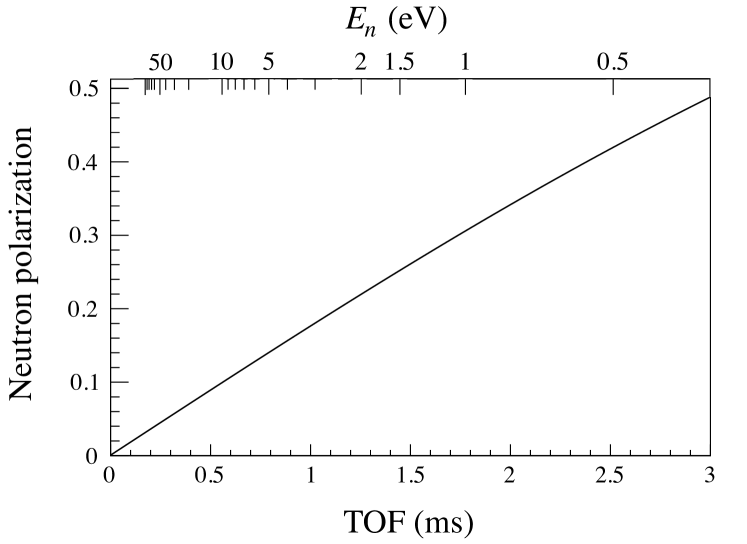
Figure 6 shows an averaged neutron polarization as a function of the neutron energy calculated from the averaged 3He polarization. The averaged neutron polarization at 0.75 eV was %.
II.4 Nuclear polarization determined by spin-dependent asymmetry
The 139La nuclear polarization was determined utilizing the spin-dependent asymmetry at the 2.99 eV -wave resonance of 138La. The spin-dependent asymmetry at the 2.99 eV resonance, after subtracting of the negative -wave component, was obtained as
| (7) |
The spin-dependent cross section of the 2.99 eV resonance can be theoretically described using the resonance parameters listed in Table 1 as
| (8) |
where , , and are the resonance energy, neutron width, and total width of the 2.99 eV s-wave resonance, respectively. The nuclear polarization of 138La can be determined using Eqs. 4, 7 and 8, taking into account its natural abundance and the neutron polarization at 2.99 eV, yielding a value of 4.90.7%. The target temperature was calculated based on a Boltzmann distribution and using the magnetic moment and nuclear spin listed in Table 2, resulting in , which is consistent with the temperature measured at the cold head of 67 mK. Under the assumption that the spin temperature of 139La is the same as that of 138La, the corresponding 139La nuclear polarization was determined to be .
| Isotope | Abundance | ||
|---|---|---|---|
| 0.09% |
II.5 Spin-dependent cross sections at the resonances
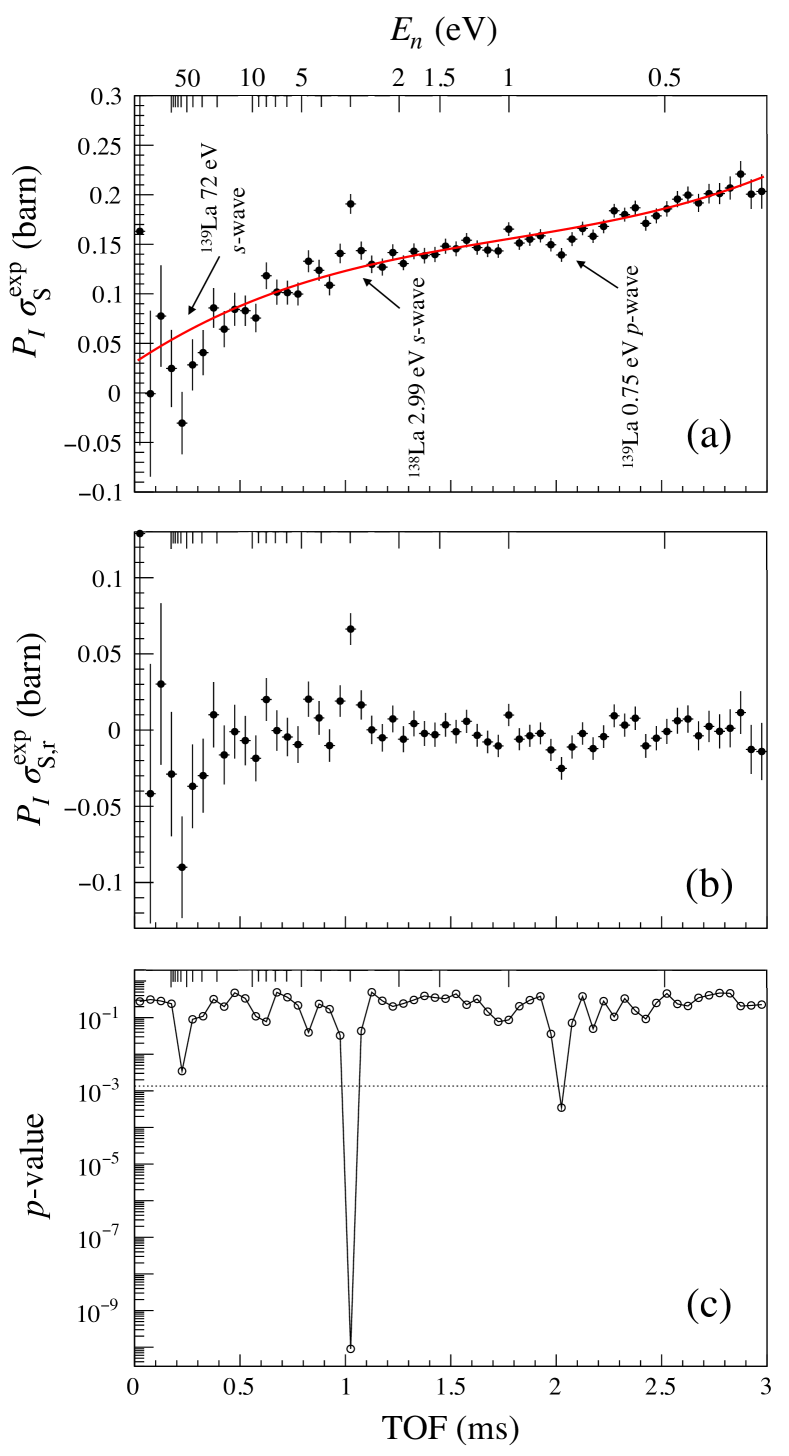
The experimental value of the spin-dependent cross section was obtained from the asymmetry using Eq. 4. The resonance component was isolated by fitting the global structure attributed to the negative -wave component with a third order polynomial function. The resonance regions listed in the Table 1 are excluded from the fitting. Figure 7 shows the TOF dependence of and . Note that Fig. 7 was calculated using the areal density of 139La. A -value, defined as , where C.L. is the confidence level of the non-zero asymmetry, is also depicted to show the significance of in Fig. 7. The p-value indicates the probability to observe a non-zero value of in the hypothesis of no asymmetry. A confidence level of over 99.7% corresponds to a p-value less than . The spin-dependence cross section was first observed at the -wave resonance with over 99.7% C.L. as shown in Fig 7.
The spin-dependent cross section in the -wave resonance region of after the subtraction of the negative -wave component, defined as , is obtained using the nuclear polarization in Section II.4 as
| (9) |
where and are the resonance energy and total width of the -wave resonance, shown in Table 1. Here, the total width is defined as . The asymmetry of the spin-dependent cross section relative to the spin-independent cross section of the -wave component was also obtained as
| (10) | |||||
The spin-independent cross section was theoretically calculated with a Breit-Wigner formula, defined as,
| (11) |
When using the nuclear polarization calculated from the temperature measured at the cold head, the differences of and from the values in Eq. 9 and Eq. 10 were and , respectively. These differences were smaller than the statistical error.
III Analysis
Under the experimental conditions, the spin-dependent assymetry can be approximated as
| (12) |
as described in the Appendix A, where is the coefficient in Eq.(10) in Ref. Gudkov and Shimizu (2020) representing the spin-spin interaction in the forward angle scattering amplitude. The following subsections will discuss the implications of the experimental results to the partial neutron width of the -wave resonance and the spins of the -wave resonances.
III.1 Determination of partial neutron width using spin-dependent cross section
The partial neutron width can also be extracted from the angular correlations of -rays emitted from -wave resonances, which arise from interference between - and -wave amplitudes Okudaira et al. (2018, 2021); Yamamoto et al. (2020); Koga et al. (2022); Endo et al. (2022). The advantage of using the spin-dependent cross section is that the neutron partial width can be directly determined without assuming the interference between partial amplitudes and the final state spin after the decay.
The spin-dependent cross section at the -wave resonance can be calculated using the explicit theoretical expression of as Gudkov and Shimizu (2020)
| (13) | |||||
where and are ratios of the neutron partial width of the channel spin, defined as
| (14) | |||||
| (15) |
The neutron partial widths of the neutron total angular momentum and components, denoted as and , are expressed by and defined as
| (16) |
where and satisfy . The corresponding mixing angle can be defined as
| (17) |
as discussed in Ref Gudkov and Shimizu (2020). The broadening effect by the pulse shape of the neutron beam at 0.75 eV was negligibly small compared with the total width of the -wave resonance and the statistical error, and therefore, the spin-dependent cross section obtained in Eq. 9 can be directly compared with the theoretical calculation. By calculating the Breit-Wigner function over the region in Eq. 13, we obtained the following equation.
| (18) |
| (19) | |||||
The corresponding and values are also obtained as
| (20) | |||||
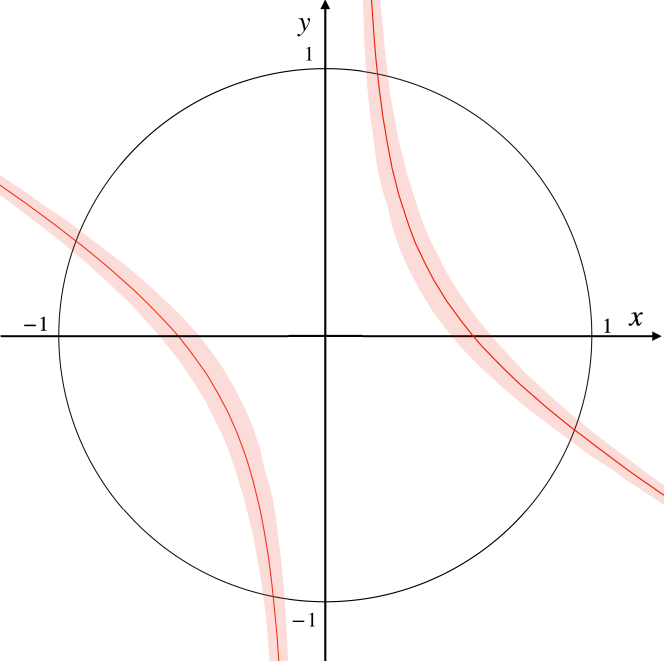
The visualization of is shown in Fig. 8. Equation 18 is described as the curved line in the plane. The intersections of the curved lines and unit circle show the solutions of .
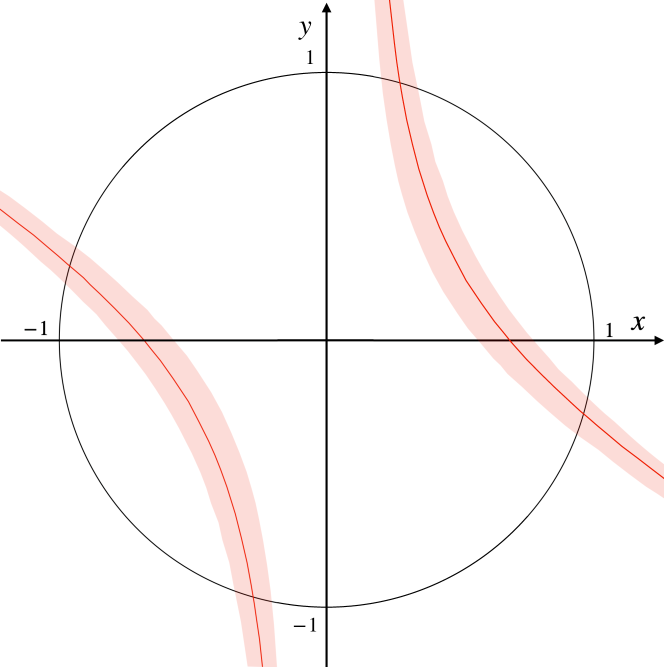
The above analysis was also performed using the resonance parameters reported by other groups in Appendix B. The differences in the analysis results that arose from differences in the resonance parameters were within the statistical error. We confirmed that these differences stemming from the resonance parameters do not affect the conclusions of this paper.
III.2 Spin of -wave resonances
For the -wave resonances, the spin can be directly determined from the asymmetry. The positive (negative) sign of the asymmetry indicates that neutrons with parallel (anti-parallel) spin are likely to be absorbed by nuclei. The sign of the asymmetry in Fig. 7 (a) and (b) implies: for the negative -wave resonance of 139La, whose spin is ; for the 2.99 eV -wave resonance of 138La, whose spin is 5; and for the 72.3 eV -wave resonance of 139La. The spins of the -wave resonances determined in this experiment are consistent with the reference values in Table 1.
IV Conclusion
We observed the spin-dependent cross section at the 0.75 eV -wave of 139La+ using a polarized lanthanum target and a polarized pulsed neutron beam. The partial neutron width of the -wave resonance was determined. In a separate paper, these results will be compared with other experimental results of (,) reactions Okudaira et al. (2018, 2021); Yamamoto et al. (2020); Koga et al. (2022); Endo et al. (2022); Okudaira et al. (2023) in terms of the - mixing model and will be used for improving a quantitative understanding the symmetry violation enhancement mechanism.
Acknowledgements.
The authors would like to thank the staff of beamline 22 for the maintenance, the low temperature sample environment team for the operation of the superconducting magnet and the dilution refrigerator, and MLF and J-PARC for operating the accelerators and the neutron production target. T. Okudaira would like to especially thank S. Ohira-Kawamura and M. Matsuura for their assistance designing the La holder. The neutron scattering experiment was approved by the Neutron Scattering Program Advisory Committee of IMSS and KEK (Proposals Nos. 2018S12). The neutron experiment at the Materials and Life Science Experimental Facility of the J-PARC was performed under a user program (Proposal No. 2022A0101). This work was supported by JSPS KAKENHI Grant Nos. 20K14495, 23K13122, JST SPRING Grant No. JPMJSP2125, and the US National Science Foundation PHY-1913789 and PHY-2209481. R. Nakabe acknowledges support from the Interdisciplinary Frontier Next-Generation Researcher Program of the Tokai Higher Education and Research System. W. M. Snow acknowledges support from the Indiana University Center for Spacetime Symmetries. J. G. Otero Munoz acknowledges support from the National GEM consortium. V. Gudkov acknowledges support from the U.S. Department of Energy Office of Science, Office of Nuclear Physics program under Award No. DE-SC0020687.Appendix A Neutron spin behavior in the polarized target and its approximation
We employ the optical description of the neutron spin behavior in polarized target material as described in Ref. Kabir (1988); Stodolsky (1986) to describe the measured asymmetry as
| (21) |
The coefficients , , , and are related to the forward angle scattering amplitude given in Ref. Gudkov and Shimizu (2020) as
| (22) |
where
| (23) |
Here, , , and denote the external magnetic field, neutron magnetic moment, and mass, respectively. and are unit vectors parallel to the neutron momentum and the nuclear spin. The , and represent the target nuclear polarization of 1st-rank (vector), 2nd-rank, and 3rd-rank spherical tensors, respectively, and amounts , , in the present experimental conditions.
Non-zero values of the originate from the beam divergence up to the maximum value of .
The valuables - are the coefficients of correlation terms in the forward scattering amplitude for polarized 139La nuclei and polarized neutrons defined as Gudkov and Shimizu (2020):
| (24) |
The magnitude of coefficients , , , , and are of the same order or less than and on the basis of the explicit expressions in Eq. (28)-(37) of Ref. Gudkov and Shimizu (2020). The magnitudes of P-odd, T-even term and P-odd, T-odd term are smaller than and by more than two orders of magnitudes. Consequently, the value of can be approximated as and we obtain
| (25) |
The numerical value of is about , which leads to
| (26) |
Appendix B Analysis using resonance parameters reported in other references
For the 0.75 eV -wave resonance, the measurements using neutron transmission or (, ) reaction have been reported by several groups listed in Table 3 Terlizzi et al. (2007); Alfimenkov et al. (1983); Shwe et al. (1967); J.A.Harvey et al. (1959). The details of each measurement of the resonance parameters are summarized in Ref. Endo et al. (2023).
| Reference | [eV] | [meV] | [meV] | |
|---|---|---|---|---|
| Endo et al. (2023) Endo et al. (2023) | ||||
| Terlizzi et al. (2007) Terlizzi et al. (2007) | ||||
| Alfimenkov et al. (1983) Alfimenkov et al. (1983) | ||||
| Shwe et al. (1967) Shwe et al. (1967) | ||||
| Harvey et al. (1959) J.A.Harvey et al. (1959) |
|
[barn] | ||||
|---|---|---|---|---|---|
| Endo et al. | |||||
| Terlizzi et al. | |||||
| Alfimenkov et al. | |||||
| Shwe et al. | |||||
| Harvey et al. |
Tables 4 shows , , and values obtained using resonance parameters reported by each group. The central values for show agreement within an accuracy of 10% or less with the exception of that based on resonance parameters reported by Terilzzi et al.. The central value of using this resonance parameters exhibit a difference of around 30%, which is attributed to Terilzzi et al.’s being reported as approximately 30% larger than in other references. Consequently, the values obtained using resonance parameters reported by Terilzzi et al. show difference compared to the analysis using other resonance parameters, as illustrated in Fig. 9. However, these differences remain consistent within the statistical errors obtained in the present experiment.
References
- Keyworth et al. (1973a) G. A. Keyworth, C. E. Olsen, F. T. Seibel, J. W. T. Dabbs, and N. W. Hill, Phys. Rev. Lett. 31, 1077 (1973a).
- Keyworth et al. (1973b) G. A. Keyworth, J. R. Lemley, C. E. Olsen, F. T. Seibel, J. W. T. Dabbs, and N. W. Hill, Phys. Rev. C 8, 2352 (1973b).
- Alfimenkov et al. (1994) V. P. Alfimenkov, Y. D. Mareev, V. V. Novitskii, L. B. Pikel‘ner, and V. R. Skoi, Physics of Atomic Nuclei 57 (1994).
- Mitchell et al. (2001) G. Mitchell, J. Bowman, S. Penttila, and E. Sharapov, Physics Reports 354, 157 (2001).
- Sushkov and Flambaum (1982) O. P. Sushkov and V. V. Flambaum, Sov. Phys. Uspekhi 25, 1 (1982).
- Bunakov and Gudkov (1983) V. E. Bunakov and V. P. Gudkov, Nuclear Physics A 401, 93 (1983).
- Gudkov (1991) V. Gudkov, Nuclear Physics A 524, 668 (1991).
- Gudkov (1992) V. P. Gudkov, Phys. Rep. 212, 77 (1992).
- Gudkov and Shimizu (2018) V. Gudkov and H. M. Shimizu, Phys. Rev. C 97, 065502 (2018).
- Okudaira et al. (2018) T. Okudaira, S. Takada, K. Hirota, A. Kimura, M. Kitaguchi, J. Koga, K. Nagamoto, T. Nakao, A. Okada, K. Sakai, H. M. Shimizu, T. Yamamoto, and T. Yoshioka, Phys. Rev. C 97, 034622 (2018).
- Okudaira et al. (2021) T. Okudaira, S. Endo, H. Fujioka, K. Hirota, K. Ishizaki, A. Kimura, M. Kitaguchi, J. Koga, Y. Niinomi, K. Sakai, T. Shima, H. M. Shimizu, S. Takada, Y. Tani, T. Yamamoto, H. Yoshikawa, and T. Yoshioka, Phys. Rev. C 104, 014601 (2021).
- Yamamoto et al. (2020) T. Yamamoto, T. Okudaira, S. Endo, H. Fujioka, K. Hirota, T. Ino, K. Ishizaki, A. Kimura, M. Kitaguchi, J. Koga, S. Makise, Y. Niinomi, T. Oku, K. Sakai, T. Shima, H. M. Shimizu, S. Takada, Y. Tani, H. Yoshikawa, and T. Yoshioka, Phys. Rev. C 101, 064624 (2020).
- Koga et al. (2022) J. Koga, S. Takada, S. Endo, H. Fujioka, K. Hirota, K. Ishizaki, A. Kimura, M. Kitaguchi, Y. Niinomi, T. Okudaira, K. Sakai, T. Shima, H. M. Shimizu, Y. Tani, T. Yamamoto, H. Yoshikawa, and T. Yoshioka, Phys. Rev. C 105, 054615 (2022).
- Endo et al. (2022) S. Endo, T. Okudaira, R. Abe, H. Fujioka, K. Hirota, A. Kimura, M. Kitaguchi, T. Oku, K. Sakai, T. Shima, H. M. Shimizu, S. Takada, S. Takahashi, T. Yamamoto, H. Yoshikawa, and T. Yoshioka, Phys. Rev. C 106, 064601 (2022).
- Okudaira et al. (2023) T. Okudaira, Y. Tani, S. Endo, J. Doskow, H. Fujioka, K. Hirota, K. Kameda, A. Kimura, M. Kitaguchi, M. Luxnat, K. Sakai, D. C. Schaper, T. Shima, H. M. Shimizu, W. M. Snow, S. Takada, T. Yamamoto, H. Yoshikawa, and T. Yoshioka, Phys. Rev. C 107, 054602 (2023).
- Yuan et al. (1991) V. W. Yuan, C. D. Bowman, J. D. Bowman, J. E. Bush, P. P. J. Delheij, C. M. Frankle, C. R. Gould, D. G. Haase, J. N. Knudson, G. E. Mitchell, S. Penttilä, H. Postma, N. R. Roberson, S. J. Seestrom, J. J. Szymanski, and X. Zhu, Phys. Rev. C 44, 2187 (1991).
- Shinohara et al. (2020) T. Shinohara, T. Kai, K. Oikawa, T. Nakatani, M. Segawa, K. Hiroi, Y. Su, M. Ooi, M. Harada, H. Iikura, H. Hayashida, J. D. Parker, Y. Matsumoto, T. Kamiyama, H. Sato, and Y. Kiyanagi, Review of Scientific Instruments 91, 043302 (2020).
- Okudaira et al. (2020) T. Okudaira, T. Oku, T. Ino, H. Hayashida, H. Kira, K. Sakai, K. Hiroi, S. Takahashi, K. Aizawa, H. Endo, S. Endo, M. Hino, K. Hirota, T. Honda, K. Ikeda, K. Kakurai, W. Kambara, M. Kitaguchi, T. Oda, H. Ohshita, T. Otomo, H. Shimizu, T. Shinohara, J. Suzuki, and T. Yamamoto, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 977, 164301 (2020).
- Satoh (2015) S. Satoh, JPS Conf. Proc. 8, 051001 (2015).
- Endo et al. (2023) S. Endo, S. Kawamura, T. Okudaira, H. Yoshikawa, G. Rovira, A. Kimura, S. Nakamura, O. Iwamoto, and N. Iwamoto, (2023), arXiv:2308.08802 [nucl-ex] .
- Mughabghab (2006) S. F. Mughabghab, Atlas of Neutron Resonances 5th ed. (Elsevier, Amsterdam, 2006).
- Gudkov and Shimizu (2020) V. Gudkov and H. M. Shimizu, Phys. Rev. C 102, 015503 (2020).
- Kabir (1988) P. K. Kabir, Phys. Rev. D 37, 1856 (1988).
- Stodolsky (1986) L. Stodolsky, Physics Letters B 172, 5 (1986).
- Terlizzi et al. (2007) R. Terlizzi et al., Phys. Rev. C 75, 035807 (2007).
- Alfimenkov et al. (1983) V. P. Alfimenkov, S. B. Borzakov, V. V. Thuan, Y. D. Mareev, L. B. Pickelner, A. S. Khrykin, and E. I. Sharapov, Nucl. Phys. A 398, 93 (1983).
- Shwe et al. (1967) H. Shwe, R. E. Coté, and W. V. Prestwich, Phys. Rev. 159, 1050 (1967).
- J.A.Harvey et al. (1959) J.A.Harvey, R.C.Block, and G.G.Slaughter, Bull. Am. Phys. Soc. 4, 385 (1959).