Spin-Valley Polarized Quantum Anomalous Hall Effect and a Valley-Controlled Half Metal in Bilayer Graphene
Abstract
We investigate topological phases of bilayer graphene subject to antiferromagnetic exchange field, interlayer bias, and irradiated by light. We discover that at finite bias and light intensity the system transitions into a previously unknown spin-valley polarized quantum anomalous Hall (SVP-QAH) insulator state, for which the subsystem of one spin is a valley Hall topological insulator (TI) and that of the other spin is a QAH insulator. We assess the TI phases occurring in the system by analytically calculating the spin-valley dependent Chern number, and characterize them by considering edge states in a nanoribbon. We demonstrate that the SVP-QAH edge states lead to a unique spin rectification effect in a domain wall. Along the phase boundary, we observe a bulk half-metal state with Berry’s phase of .
pacs:
72.80.Vp, 73.43.Nq, 03.65.Vf, 75.70.TjI I. Introduction
Bernal-stacked bilayer graphene (BLG) consists of two honeycomb lattices coupled by van der Waals interaction Ohta . Due to its novel electronic properties, such as low-energy states with Berry’s phase of NovMc and an electrically-tunable band gap McCann ; ZhaTan , BLG has recently attracted much attention both theoretically and experimentally, see e.g. Refs. MarBlan, ; WeAll, ; JrJing, ; McKosh, ; RenQiao, ; JuWang, . In particular, BLG became popular for studies of phenomena related to the valley degree of freedom RenQiao ; ZhangJung ; ZhangMac ; LiZhang ; JaskPelc , resulting in discovery of non-trivial topological states of matter. Recently, a striking finding was the discovery of the quantum valley Hall (QVH) effect in BLG, for which the edge states in the gap driven by an interlayer bias are valley-polarized and provide the conductance quantization with the step of JuShi ; LiWang ; YinJiang ; JiangShi . Theoretical studies have predicted that the usual QVH insulator in BLG undergoes a transition to a valley-polarized quantum spin Hall insulator under effect of Rashba spin-orbit interaction QiaoTse ; ZhaiJ .
Another attractive topological state of matter is the quantum anomalous Hall (QAH) state, generally characterized by chiral edge states in the gap and nonzero charge Chern numbers ChangZh ; Ezawa1 ; ZhaiJin . The QAH state in BLG has been suggested to be induced by Rashba interaction and internal magnetization TseQiao or by strong circularly polarized light MohanRao ; QuZhang ; LagoMo , differently from the mechanism of Landau-level quantization in quantum Hall effect. Most recently, the valley-polarized QAH state possessing the properties of both the QVH and QAH states has been proposed in other 2D systems PanLi ; ZhSun similar to BLG. Interestingly, this QAH state can possess edge states which are not complectly chiral PanLi .
In this work, we present the light and voltage controlled phase diagram of BLG in contact with layered antiferromagnetic (LAF) exchange field and discover a variety of topological insulator (TI) states in this system. We argue that this AFM BLG itself is a quantum anomalous valley Hall (QAVH) insulator CarSor , that it undergoes a transition to a usual QVH insulator as interlayer bias increases, and that it is switched to a normal QAH (N-QAH) insulator, a system with chiral edge states, as light intensity increases. Remarkably, we discover that if both voltage and light are applied, the system can be in a spin-valley polarized QAH (SVP-QAH) insulator state, for which the subsystem of one spin is in a QVH state and that of the other spin is in a QAH state. To our knowledge, this state has not been previously described in the literature and it is distinct from the single-valley spin-polarized QAH states QuZhang ; ZhSun and the QAH states with no spin or valley polarizations PanLi ; ZhangJung ; LiZhang ; ChangZh ; Ezawa1 ; ZhaiJin ; JuShi ; LiWang ; YinJiang .
The TI states in the system are discriminated by the spin-valley dependent Chern number RenQiao , which we calculate analytically. We further characterize these TIs by edge states in a zigzag ribbon and show transport differences in domain walls (DWs). In the phase boundary, we discover that the 2D bulk system can host a half-metal state with Berry’s phase of , and the number of gap-closing valleys is tunable.
Our paper is organized as follows. In Sec. II, we introduce the system Hamiltonian and topological theory. In Sec. III, we show the phase diagram and give the low-energy formulism. In Sec. IV, we analytically derive the Chern numbers and show the domain-wall (DW) transport. In the final section, we present the discussion and conclusions.
II II. System Hamiltonian and Topological Theory
The BLG system we consider is described by the eight-band tight-binding model
| (1) |
where creates an electron with spin polarization at site , and / run over all the nearest and next nearest neighbor hopping sites. The subscript denotes “in plane” (“out of plane”), indicates that site lies in the bottom (top) layer, is the -component of Pauli matrix in the spin subspace, and holds if the next nearest hopping is anticlockwise (clockwise). In Eq. (1), the first and second terms are the intralayer and interlayer nearest neighbor hoppings with McKosh eV and eV. The third term, , is the LAF exchange field, which can be applied by depositing BLG between 2D magnetic insulators CrI3 CarSor (7 meV can be achieved). The fourth term, , is the interlayer bias with being up to 125 meV in experiment ZhaTan ; JrJing . The fifth term, , is the Haldane mass term Haldane , which can be applied QuZhang by irradiating BLG with circularly polarized light [see Supplemental Material (SM) SupMater and Refs. KitaBra ; Ezawa2 ]. Estimated from the band width in BLG, the light frequency would typically lie in the range QuZhang ; SupMater – Hz, leading to the estimate of 10 meV.
The QAH effect is characterized by the charge Chern number PanLi ; TseQiao ; ChangZh ; Ezawa1 ; ZhaiJin
| (2) |
where is the momentum-space Berry curvature RenQiao in the out-of-plane direction for the -th subband
| (3) |
The summation is over all occupied valence bands in the first Brilloin zone below the bulk band gap, is the Bloch state, and is the velocity operator along the direction.
One can label a state a TI if it has at least one nonzero topological invariant TseQiao ; QuZhang ; ZhSun ; CarSor ; Haldane ; KitaBra ; Ezawa2 ; MohanRao ; LagoMo . Because electrons in BLG here have a mixture of charge, spin and valley degrees of freedom, the index can not identify the spin or valley polarized TI phases. To solve this problem, we employ a decomposed, spin and valley dependent Chern number RenQiao ; Ezawa2 , which is well defined in half of the first Brilloin zone around () or () points for spin-up () or spin-down () electrons. On basis of , the spin and valley Chern numbers RenQiao can be defined as and , respectively. The charge Chern number satisfies .
III III. Phase diagram and Low-energy Formulism
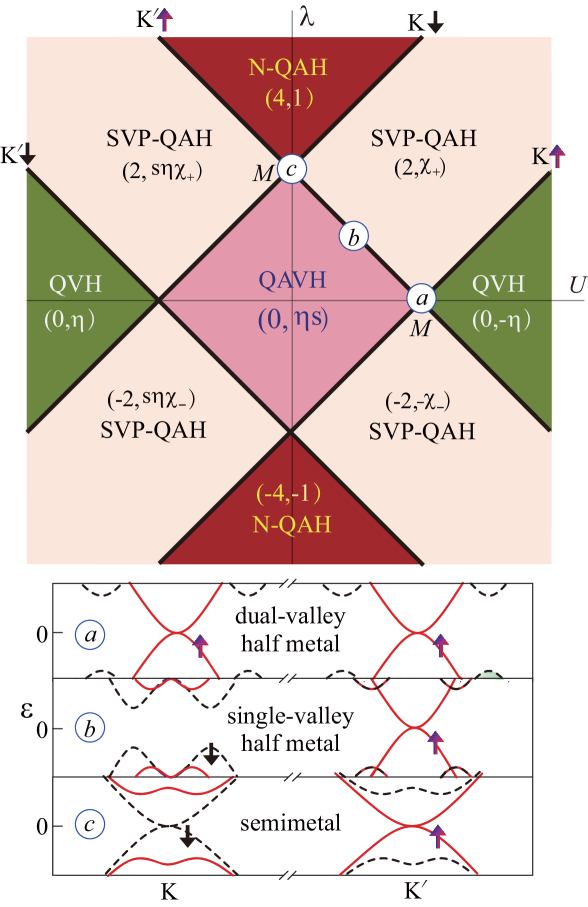
We present our result as the phase diagram in Fig. 1 by tuning and . The topological numbers are used to index the TI phases, including QAVH, QVH, N-QAH and SVP-QAH. We show how to derive the analytical expressions for the phase boundary and the Chern numbers from low-energy theory later. Because the sign changes of and only influence the signs of Chern numbers (no novel phases appear), one only needs to characterize the phases for (, ). To describe the edge states, some typical cases are chosen to calculate the bands in a zigzag ribbon (SM SupMater ). The edge states in real space for each TI are illustrated in Figs. 2(a)-2(d), where the moving directions (hollow arrows) for electrons agree with Eqs. (9-12). At the phase boundary, the bulk gap closes [Eq. (6)].
We first discuss the QAVH state, for which CarSor . The nonzero value of in this phase arises from the inversion symmetry breaking dominated by . Although the QAVH phase has metallic in-gap edge states near and , the index is zero. The anomalous property of the state is that the subsystem of each spin is a QVH insulator [ in Fig. 2(a)], while the whole system is not valley polarized (). The result indicates the edge states in each valley behaves as a quantum spin Hall state QiaoTse ; Ezawa1 in spite of . If we include non-zero voltage , the system eventually undergoes a transition to a normal QVH insulator [ in Fig. 2(b)] due to the competition of and . The QAVH insulator transitions to an N-QAH insulator [ in Fig. 2(c)] as increases due to the time-reversal symmetry breaking. Each transition is associated with with a process of the closing and reopening of the gap.
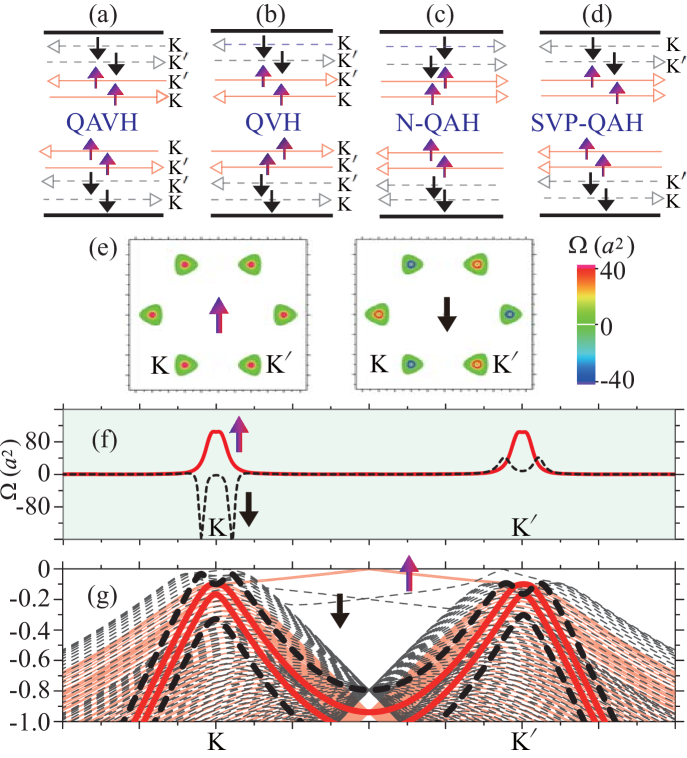
Our most significant result is the SVP-QAH phase, which appears in regions where and occupies a major part of the phase diagram. For a SVP-QAH state , four spin-down edge states in the gap appear near and , but four spin-up edge states appear away from and [Figs. 2(d) and 2(g)]. Correspondingly, the Berry curvature in the plane [Fig. 2(e)] and specifically along - direction [Fig. 2(f)] is shown. We find that the spin-down subsystem is a QVH insulator [, , ], whereas the spin-up subsystem is a normal QAH insulator [, , ], and then is achieved. To our knowledge, this SVP-QAH insulator is a new type of a QAH state, which differs obviously from the single-valley spin-polarized QAH QuZhang ; ZhSun , spin-unpolarized QAH PanLi ; RenQiao ; ZhangJung ; ZhangMac ; LiZhang , and valley-unpolarized QAH Ezawa1 ; Ezawa2 ; RenQiao states discovered previously.
At the phase boundaries, see bold lines in Fig. 1, there exists a 2D bulk state that is half-metallic SonCohen (gap closing at or ), as shown by the completely spin-polarized band structures (bottom) near the Fermi level for the marked points and . In contrast, point corresponds to a dual-valley half-metal (valley degeneracy), while point refers to a single-valley half-metal (the other valley is insulating). For the marked point , spin-down (spin-up) subbands near the Fermi level are locked to the valley, resulting in a spin-valley locked semimetal. Thus gap closing of the valleys in which one or two is tunable. Notably, the bulk half-metal state here has the Berry’s phase of [Eq. (8)].
To further explore the physics underlying the phase diagram, we analyze the low-energy effective Hamiltonian derived from the lattice model (1) after Fourier transformation, and reveal the physics of electrons near and . For simplicity, we set and below. Because two opposite spins are decoupled in Eq. (1), the effective Hamiltonian can be written as a matrix
| (4) |
where . Note that and only occur as a product , and thus the reversal of the sign of is equivalent to the reversal of spin orientation. We will assume . By matrix diagonalization, we derive the band structure as
| (5) |
Note that the electron-hole symmetry is present in Eq. (5), from which one can prove that the gap is closed only under , which requires [at ()] and simultaneously
| (6) |
According to the topological theory RenQiao , this gap-closing condition in Eq. (6) precisely describes the phase boundary as given in Fig. 1. Specifically at , the energy gap reads
| (7) |
Judging from Eq. (6), the system is a dual-valley half-metal for and a spin-valley locked semimetal for . Except for these points, the system is a single-valley half-metal in the phase boundary. The effective Hamiltonian used in Ref. NovMc, can be derived to describe the low-energy half-metal subbands with parabolic dispersion. The half-metal Bloch state ( being the azimuthal angle of the momentum) here has the Berry phase ZJ2014
| (8) |
which can induce a spin-polarized integer quantum Hall effect with a missing zero-level plateau NovMc .
IV IV. Chern numbers and domain-wall (DW) transport
We see from Eq. (6), Fig. 1 and our band calculations SupMater that the QAVH, QVH, N-QAH and SVP-QAH insulator states hold under , , , , respectively. Usually, the topological invariants are associated with the signs of the parameters for a TI state RenQiao ; Ezawa2 . For the QAVH, QVH, and N-QAH insulators here, the index is respectively determined by
| (9) |
and correspondingly , , are expressed as
| (10) |
where is the sign function. For the SVP-QAH insulator, we calculate to be
| (11) |
and the other Chern numbers satisfy
| (12) |
Here, is the Kronecker delta function. We see from Eqs. (9) and (11), always holds for each TI case.
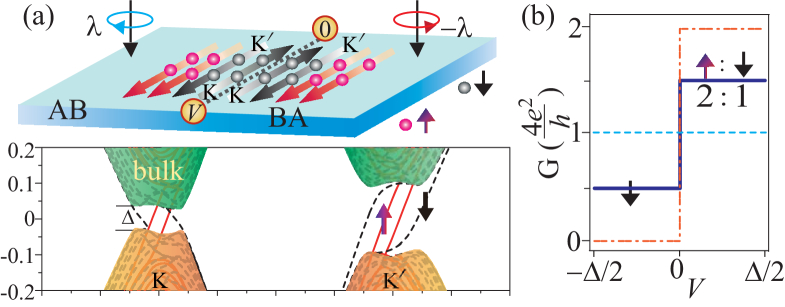
To distinguish and detect the SVP-QAH state, we consider a DW between AB- and BA-stacked GBL JuShi in Fig. 3(a), where the conducting channels and band structure are shown when has the opposite values in AB and BA regions. By using Green’s function method Datta , we show the DW conductance [, where is the current (bias)] in Fig. 3(b) and predict a unique spin rectification effect (solid line) for the SVP-QAH edge states. We assume here that the DW is much shorter than the electron mean free path, and thus scattering is ignored. The ratio of channel numbers for and is for , while only channels contribute to transport for . In contrast, no charge or spin rectifications occur for the QAVH or QVH states. The N-QAH state acts as a charge diode, however, still no spin rectification occurs.
The spin/valley filter or diode can be further realized by tuning the types of DW and fields (SM SupMater ). Specifically, a unipolar spin diode ZhaiWen (only spin-up electrons are unidirectionally conducting) works if the DW in Fig. 3(a) is of the armchair type due to the absence of the QVH edge states RenQiao ; JuWang ; JaskPelc ; ZhangMac .
V V. Discussion and conclusions
Realization of the SVP-QAH state in BLG depends strongly on the LAF field, , which is not induced by the electron-electron interaction QuZhang but by proximity, such as a van der Waals system consisting of BLG and magnetic insulator CrI3 CarSor ( meV can be achieved). Possibilities of proximity induced by other 2D magnets, such as CrBr3 or Cr2Ge2Te6 GongZhang , requires more research. Magnetic insulator EuS is an alternative candidate to induce on basis of the relevant experimental evidence WeiLee . Beyond model (1), the Coulomb interaction might induce a gap about meV JrJing ; QuZhang , which is usually disregarded when other interactions are stronger ZhaTan ; JuShi ; LiWang ; YinJiang as we assume. Notably, the LAF order can not be easily broken by light in spite of magneto-optical Kerr or spin-phonon coupled effects SunZ ; HuangCenker . If the LAF system becomes ferromagnetic, e.g. by applying magnetic field CarSor , the SVP-QAH phase disappears.
In particular, the time-periodic optical field can be safely reduced to the time-averaged static term under high-frequency (3J) condition Ezawa2 ; LagoMo ; MohanRao ; QuZhang , when the Chern number is well defined to characterize the quantized current DehghOka ; Kundu ; Manghi of edge states near . This is further carefully checked (SM SupMater ) by using the full-time Floquet theory. Because the light absorbance per graphene layer is only about 2.3% MakSfe , the band population is presumably intact. For the SVP-QAH DW transport in Fig. 3(a), the electron mean free path nm was found by experiment JuShi ; YinJiang ; LiWang ; JiangShi . Ignoring the contact resistance, the dependence of ballistic conductance on DW length reads Datta ; JuShi , where is the integer for quantized plateau in Fig. 3(b). For the lower-frequency light, other complex effects such as FoaPerez ; SenCla ; WangStein time-averaged densities of states in addition to edge states can break the conductance quantization SupMater .
The exchange proximity effect in Graphene/2D-magnet may be rather small that pressure is usually needed to induce a measurable QAH effect ZhangZhao . Certainly, small details related to the physics close to the Fermi level such as bands hybridization, charge transfer, exchange proximity or bias effects may change the phase diagram at the level of ab-initio calculations CarSor , reduce the conductivity and even hamper the observation of the SVP-QAH phase. Therefore, more efforts both in theory and experiment are still needed to explore and confirm the SVP-QAH phase in GBL/2D-magnet systems.
Another striking result revealed by Eq. (11) is that, without optical fields, the SVP-QAH phase holds in the systems with intrinsic spin-orbit coupling (by replacing with ). A promising alternative system to obverse the SVP-QAH phase is the experimentally-available LAF Eu/bilayer silicene/Eu structure TokAver . Our further calculations SupMater indicate the SVP-QAH is robust against weak Rashba interactions.
In summary, the concept of van der Waals LAF order applied to 2D valleytronics, rarely noticed before, opens a novel avenue for engineering small devices with ultra-low dissipation. The explored topological transitions modulated by photon and electric voltage will motivate the experimental exploration of novel 2D QAH insulators with rich spin or valley physics in the integrated systems between layered 2D materials, van der Waals magnets and correlated valley materials, for which the combination of spintronics, valleytronics and topology promises discoveries of novel condensed matter phases.
VI Acknowledgments
This work was supported by the NSFC with Grant No. 61874057, QingLan Project of Jiangsu Province (2019), 1311 Talent Program “DingXin Scholar” of NJUPT (2018), and Jiangsu Government Scholarship for Overseas Studies.
References
- (1) T. Ohta, A. Bostwick, T. Seyller, K. Horn, and E. Rotenberg, Science 313, 951 (2006).
- (2) K. S. Novoselov, E. McCann, S. V. Morozov, V. I. Fal’ko, M. I. Katnelson, U. Zeitler, D. Jiang, F. Schedin, and A. K. Geim, Nat. Phys. 2, 177 (2006).
- (3) E. McCann, Phys. Rev. B 74, 161403(R) (2006).
- (4) Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, C. C. Martin, A. Zettl, M. F. Crommie, Y. R. Shen, and F. Wang, Nature 459, 820 (2009).
- (5) I. Martin, Y. M. Blanter, and A. F. Morpurgo, Phys. Rev. Lett. 100, 036804 (2008).
- (6) R. T. Weitz, M. T. Allen, B. E. Feldman, J. Martin, and A. Yacoby, Science 330, 812 (2010).
- (7) J. Velasco Jr, L. Jing, W. Bao, Y. Lee, P. Kratz, V. Aji, M. Bockrath, C. N. Lau, C. Varma, R. Stillwell, D. Smirnov, F. Zhang, J. Jung, and A. H. MacDonald, Nat. Nanotechnol. 7, 156 (2012).
- (8) E. McCann and M. Koshino, Rep. Prog. Phys. 76, 056503 (2013).
- (9) Y. Ren, Z. Qiao, and Q. Niu, Rep. Prog. Phys. 79, 066501 (2016).
- (10) L. Ju, and L. Wang, T. Cao, T. Taniguchi, K. Watanabe, S. G. Louie, F. Rana, J. Park, J. Hone, F. Wang, and P. L. McEuen, Science 358, 907 (2017).
- (11) W. Jaskólski, M. Pelc, G. W. Bryant, L. Chico, and A. Ayuela, 2D Mater. 5, 025006 (2018).
- (12) F. Zhang, A. H. MacDonald, and E. J. Mele, Proc. Natl. Acad. Sci. 110, 10551 (2013).
- (13) F. Zhang, J. Jung, G. A. Fiete, Q. Niu, and A. H. MacDonald, Phys. Rev. Lett. 106, 156801 (2011).
- (14) X. Li, F. Zhang, Q. Niu, and A. H. MacDonald, Phys. Rev. Lett. 113, 116803 (2014).
- (15) L. Ju, Z. Shi, N. Nair, Y. Lv, C. Jin, J. Velasco Jr, C. Ojeda-Aristizabal, H. A. Bechtel, M. C. Martin, A. Zettl, J. Analytis, and F. Wang, Nature 520, 650 (2015).
- (16) J. Li, K. Wang, K. J. McFaul, Z. Zern, Y. Ren, K. Watanabe, T. Taniguchi, Z. Qiao, and J. Zhu, Nat. Nanotechnol. 11, 1060 (2016).
- (17) L.-J. Yin, H. Jiang, J.-B. Qiao, and L. He, Nat. Commun. 7, 11760 (2016).
- (18) L. Jiang, Z. Shi, B. Zeng, S. Wang, J.-H. Kang, T. Joshi, C. Jin, L. Ju, J. Kim, T. Lyu, Y.-R. Shen, M. Crommie, H.-J. Gao, and F. Wang, Nat. Mater. 15, 840 (2016).
- (19) Z. Qiao, W.-K. Tse, H. Jiang, Y. Yao, and Q. Niu, Phys. Rev. Lett. 107, 256801 (2011).
- (20) X. Zhai and G. Jin, Phys. Rev. B 93, 205427 (2016).
- (21) C.-Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei, L.-L. Wang, Z.-Q. Ji, Y. Feng, S. Ji, X. Chen, J. Jia, X. Dai, Z. Fang, S.-C. Zhang, K. He, Y. Wang, L. Lu, X.-C. Ma, and Q.-K. XUe, Science 340, 167 (2013).
- (22) M. Ezawa, Phys. Rev. Lett. 109, 055502 (2012).
- (23) X. Zhai and G. Jin, Phys. Rev. B 89, 235416 (2014).
- (24) W.-K. Tse, Z. Qiao, Y. Yao, A. H. MacDonald, and Q. Niu, Phys. Rev. B 83, 155447 (2011).
- (25) P. Mohan and S. Rao, Phys. Rev. B 98, 165406 (2018).
- (26) C. Qu, C. Zhang, and F. Zhang, 2D Mater. 5, 011005 (2018).
- (27) V. Dal Lago, E. Suarez Morell, and L. E. F. Foa Torres, Phys. Rev. B 96, 235409 (2017).
- (28) H. Pan, Z. Li, C.-C. Liu, G. Zhu, Z. Qiao, and Y. Yao, Phys. Rev. Lett. 112, 106802 (2014).
- (29) J. Zhou, Q. Sun, and P. Jena, Phys. Rev. Lett. 119, 046403 (2017).
- (30) C. Cardoso, D. Soriano, N. A. García-Martínez, and J. Fernández-Rossier, Phys. Rev. Lett. 121, 067701 (2018).
- (31) F. D. M. Haldane, Phys. Rev. Lett. 61, 2015 (1988).
- (32) See Supplemental Material for details on the item , the bands in a zigzag ribbon, the realization of spin/valley filter or diode, the transport in full-time Floquet theory, and an alternative system to realize the SVP-QAH effect.
- (33) T. Kitagawa, T. Oka, A. Brataas, L. Fu, and E. Demler, Phys. Rev. B 84, 235108 (2011).
- (34) M. Ezawa, Phys. Rev. Lett. 110, 026603 (2013).
- (35) Y.-W. Son, M. L. Cohen, and S. G. Louie, Nature 444, 347 (2006).
- (36) X. Zhai and G. Jin, Phys. Rev. B 89, 085430 (2014).
- (37) S. Datta, Electronic Transport in Mesoscopic Systems (Cambridge University Press, Cambridge, England, 1995).
- (38) X. Zhai, R. Wen, X. Zhou, W. Chen, W. Yan, L.-Y. Gong, Y. Pu, and X. Li, Phys. Rev. Appl. 11, 064047 (2019).
- (39) C. Gong and X. Zhang, Science 363, 706 (2019).
- (40) P. Wei, S. Lee, F. Lemaitre, L. Pinel, D. Cutaia, W. Cha, F. Katmis, Y. Zhu, D. Heiman, J. Hone, J. S. Moodera, and C.-T. Chen, Nat. Mater. 15, 711 (2016).
- (41) A. Kundu, H. A. Fertig, and B. Seradjeh, Phy. Rev. Lett. 113, 236803 (2014).
- (42) H. Dehghani, T. Oka, and A. Mitra, Phys. Rev. B 91, 155422 (2015).
- (43) F. Manghi, M. Puviani, and F. Lenzini, Adv. Condens. Matter Phys. 2018, 5703197 (2018).
- (44) L. E. F. Foa Torres, P. M. Perez-Piskunow, C. A. Balseiro, and G. Usaj, Phys. Rev. Lett. 113, 266801 (2014).
- (45) M. A. Sentef, M. Claassen, A. F. Kemper, B. Moritz, T. Oka, J. K. Freericks, and T. P. Devereaux, Nat. Commun. 6, 7047 (2015).
- (46) Y. H. Wang, H. Steinberg, P. Jarillo-Herrero, and N. Gedik, Science 342, 453 (2013).
- (47) K. F. Mak, M. Y. Sfeir, Y. Wu, C. H. Lui, J. A. Misewich, and T. F. Heinz, Phys. Rev. Lett. 101, 196405 (2008).
- (48) Z. Sun, Y. Yi, T. Song, G. Clark, B. Huang, Y. Shan, S. Wu, D. Huang, C. Gao, Z. Chen, M. McGuire, T. Cao, D. Xiao, W.-T. Liu, W. Yao, X. Xu, and S. Wu, Nature 572, 497 (2019).
- (49) B. Huang, J. Cenker, X. Zhang, E. L. Lay, T. Song, T. Taniguchi, K. Watanabe, M. A. McGuire, D. Xiao, X. Xu, Nat. Nanotechnol. 15, 212 (2020).
- (50) J. Zhang, B. Zhao, T. Zhou, Y. Xue, C. Ma, and Z. Yang, Phys. Rev. B 97, 085401 (2018).
- (51) A. M. Tokmachev, D. V. Averyanov, O. E. Parfenov, A. N. Taldenkov, I. A. Karateev, I. S. Sokolov, O. A. Kondratev, and V. G. Storchak, Nat. Commun. 9, 1672 (2018).