Spin-wave dynamics controlled by tunable ac magnonic crystal

Spin waves are the collective wave excitations in the magnetically ordered system, which have the frequencies typically ranged from GHz up to even THz. The utilization of spin waves for the purposes of quantum-information exchange was proposed long ago [7]. The later studies [8, 9] showed that the spin waves excited in yttrium iron garnet (YIG) can have both lifetime and coherence time longer than $100$ ns. In addition, the ability of exciting exchange spin waves with wavelengths down to the nanometer range [10, 11] allows one to build compact spin-wave-based devices at the submicron scale. All these properties make the low-damping coherent spin waves a suitable candidate for performing rapid data processing and wave computing [12, 13, 14, 15, 16, 17].

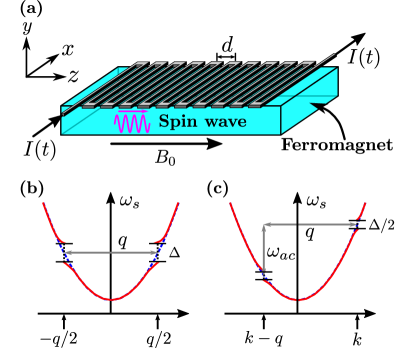
As an efficient way to control spin waves, magnonic crystals have been studied both experimentally and theoretically [20, 18, 19, 21, 22]. A prototypical current-induced magnonic crystal for ferromagnet is schematically depicted in Fig. 1(a) (cf. Refs. [18, 19]). If a dc current, $I(t)=I_{0}$, is supplied through a metallic meander structure with a period $d$, a spatially modulated static magnetic field generates a magnonic crystal for the spin waves propagating along the direction of the modulation. For the spin waves with a symmetric spectrum, the dc magnonic crystal resonantly couples the spin waves with wave vectors around $\pm q/2$, where $q=2\pi/d$ is determined by the period of the spatial modulation. As shown in Fig. 1(b), the coupling of the two degenerate waves opens a band gap $\Delta$, which is $\propto I_{0}$ [18, 19]. In practice, for an incident spin-wave packet, after switching on the dc magnonic crystal, the spin-wave components that are under the resonant scattering conditions start to alternate between the forward- and backward-propagating states; while the out-of-resonance spectral components are unaffected by the perturbation and propagate unidirectionally.

In this paper, we consider the same experimental setup as was exploited in Refs. [18, 19], but extend the discussion to an ac modulated magnonic crystal, i.e., when the current $I(t)=I_{0}\cos(\omega_{ac}t+\varphi_{ac})$. We show that under the limit $\omega_{ac}\gg\Delta$ a spin-wave pair with wave vectors $k$ and $k-q$ can be controlled by a tunable ac magnonic crystal that satisfies the shifted resonance condition $|\omega_{s}(k)-\omega_{s}(k-q)|=\omega_{ac}$ [cf. Fig. 1(c)].

Next, at $t=0$, one switches on the ac modulated magnonic crystal, which for $t>0$ is described by $\Delta B_{0}\cos(\omega_{ac}t+\varphi_{ac})\cos(qz)\bm{e}_{z}$. Here, $\Delta B_{0}$ is the intensity of the magnonic crystal controlled by $I_{0}$, the frequency of the ac modulation is given by $\omega_{ac}$, while $\varphi_{ac}$ is the initial phase determined at the moment $t=0$. In the discussed geometry, the spin-wave propagation is effectively one-dimensional. To find what will be the dynamics of the spin wave after $t=0$, one needs to solve $S^{+}(z,t)$ from the equation [23]

by matching the solution for $t>0$ with the free spin-wave solution for $t<0$.

The magnonic crystal term in Eq. (Spin-wave dynamics controlled by tunable ac magnonic crystal) couples the spin-wave state $k$ to the state $k-q$ as long as $|\omega_{s}(k)-\omega_{s}(k-q)|\approx\omega_{ac}$. To better understand the spin-wave dynamics under the ac magnonic crystal, we look for the solution of Eq. (Spin-wave dynamics controlled by tunable ac magnonic crystal) in the form

Here, we introduced four complex time-dependent coefficients $\mathcal{S}_{p/m}(t)$ and $\mathcal{C}_{p/m}(t)$ in front of the basis functions $\sin(k_{\pm}z)$ and $\cos(k_{\pm}z)$, respectively. Solution (Spin-wave dynamics controlled by tunable ac magnonic crystal) describes the mutual scatterings between a pair of the spin waves with the wave vectors $k=k_{+}=q/2+\delta k$ and $k-q=-k_{-}=-q/2+\delta k$. Although the scattering occurs between the spin waves with the oppositely directed wave vectors, the wave vectors $k_{\pm}$ are defined here as their absolute values and, therefore, are positive (we assume that $-q/2<\delta k<q/2$). Note that, in Eq. (Spin-wave dynamics controlled by tunable ac magnonic crystal), the contributions from the spin waves with wave vectors $\pm 3q/2+\delta k$ and higher are neglected.

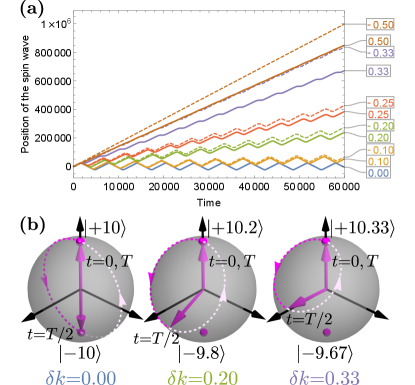
In Fig. 2(a) we plot a momentary “position” of the spin wave with wave vector $q/2+\delta k$ as a function of time for different $\delta k$ after the dc magnonic crystal is switched on at $t=0$. [The “position” was determined by tracking numerically the most left zero-crossing point of the imaginary part of the spin-wave solution (Spin-wave dynamics controlled by tunable ac magnonic crystal) within a sufficiently large spatial interval.] As one can see from Fig. 2(a), at $\delta k=0$, the dependence of spin-wave position on time is a zigzag curve around the horizontal axis which indicates the resulting to-and-fro propagation of the spin wave. The period of this zigzag curve is extracted to be $T_{\downarrow\uparrow}\approx 6283\approx 2\pi/\gamma\Delta B_{0}$, which indicates that the gap $\Delta$ induced by the dc magnonic crystal is equal to $\gamma\Delta B_{0}$. Moreover, from Fig. 2(a), one may conclude that the to-and-fro motion exists only for a limited interval of $\delta k$ when $|\delta k|<\delta k_{c}\approx 0.33$ in units of $(2\pi/1000)$. The critical value $\delta k_{c}$ is roughly determined by the criterion $\Delta\omega_{s}(\delta k_{c})=\gamma\Delta B_{0}$. For the chosen parameters, we get $\Delta\omega_{s}(0.33)\approx 0.00104$ while $\gamma\Delta B_{0}=0.001$.

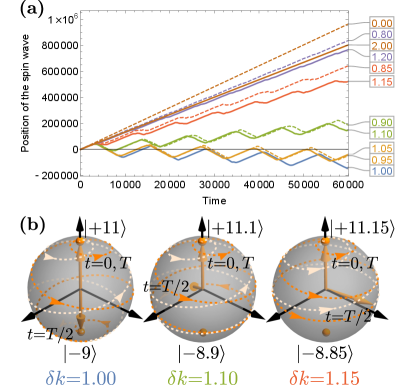
By properly tuning $\omega_{ac}$, the resonant spin-wave wave vector can be noticeably shifted from $q/2$. As one may observe from Fig. 3(a), if $\omega_{ac}$ is set to be $0.00316$, only the spin waves around $k=11$ perform the to-and-fro motion accurately enough. For the chosen parameters, namely, $A=2$ and $q=20$, one has $\Delta\omega_{s}(\delta k=1)\approx 0.00316$ and, therefore, the shifted resonance indeed happens at $\tilde{\xi}\approx 0$.

Furthermore, in Fig. 3(a), the period of the zigzag curves around the horizontal axis is doubled as compared with the one in Fig. 2(a). In addition, the width of the $\delta k$ intervals at which the to-and-fro motion develops becomes approximately half of the one in the dc case. For example, in Fig. 3(a), the to-and-fro motion can be observed within the interval $10.85\lesssim k\lesssim 11.15$, while for the dc magnonic crystal presented in Fig. 2(a) it develops when the spin-wave wave vectors are within $9.67\lesssim k\lesssim 10.33$. All these observations are consistent with our understanding based on the solutions presented by Eqs. (Spin-wave dynamics controlled by tunable ac magnonic crystal) and (Spin-wave dynamics controlled by tunable ac magnonic crystal).

The state $\ket{\text{SW}}$ described by Eq. (Spin-wave dynamics controlled by tunable ac magnonic crystal) can be represented by a vector, whose ending point is moving on the surface of a Bloch sphere with $\ket{k}$ and $\ket{k-q}$ to be its north and south poles. The motion of the states with different initial wave vectors $k$ on the Bloch spheres, after turning on the dc and ac magnonic crystal, are shown in Figs. 2(b) and 3(b), respectively. As demonstrated by Fig. 2(b), at the resonance (i.e., when $\delta k=0$), during the first period of the to-and-fro motion, the spin-wave state, which is initially located at the north pole, starts to move to the south pole, and then, after passing the south pole, returns to the north pole. Note that, the spin wave is propagating forward when the state is on the north hemisphere, and vice versa. However, at $\delta k=0.2$, the trajectory does not pass through the south pole, and its portion below the equator becomes less than the one above the equator. Finally, when $\delta k=\delta k_{c}\approx 0.33$, the full trajectory is on the north hemisphere only, which indicates the disappearance of the to-and-fro motion.

Figure 3(b), plotted for an ac magnonic crystal with $\omega_{ac}=0.00316$, shows a more complicated behavior, which includes a non-trivial precession of the states on the Bloch spheres. In the presented case, the resonant spin-wave wave vector is shifted to $k\approx 11$ (and $9$).

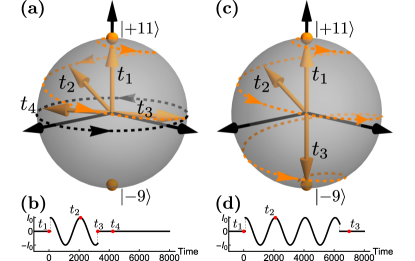
(ii) When the spin wave is at the exact shifted resonance (i.e., $\tilde{\xi}=0$), Eq. (Spin-wave dynamics controlled by tunable ac magnonic crystal) is reduced to $\ket{\text{SW}}=e^{-i\varphi_{g}(t)}\allowbreak\left\{\cos\left[\theta(t)/2\right]\ket{k}+\sin\left[\theta(t)/2\right]e^{i\phi(t)}\ket{k-q}\right\}$. Here, $\theta(t)\equiv\omega_{R}t$ and $\phi(t)\equiv\omega_{ac}t+\varphi_{ac}-\pi/2$. This state can be considered as a spin-wave “qubit”, which is characterized by the polar angle $\theta(t)$ and azimuthal angle $\phi(t)$. Recall that $\omega_{R}(\tilde{\xi}=0)=\gamma\Delta B_{0}/2\propto I_{0}$; therefore, the time evolution of this “qubit” [i.e., $\theta(t)$ and $\phi(t)$] is fully controlled by the intensity and the ac modulation of the magnonic crystal. Consequently, one can manipulate this spin-wave based macroscopical “qubit” using a properly designed ac pulse. For example, Fig. 4(a) demonstrates that one can bring the state from the north pole to the equator on the Bloch sphere utilizing a $\pi/2$ pulse shown in Fig. 4(b). It is also possible to flip the spin-wave “qubit” by the $\pi$ pulse, see, e.g., Figs. 4(c) and 4(d), and more discussions in SM. Note that the spin-wave “qubit” controlled by the ac magnonic crystal has a nonzero energy mismatch $\Delta\omega_{s}=\omega_{ac}$. This leads to a time-dependent $\phi(t)$ and, thereby, opens a way to manipulate the azimuthal angle of this “qubit” and makes all single-qubit operations possible [32].

(iii) Finally, we discuss the feasibility of the proposed scheme. To make the RWA valid, $\omega_{ac}$ has to be much greater than $\gamma\Delta B_{0}$. In addition, to minimize the higher-order effects from the spin-wave states with wave vectors $k+q$, $k\pm 2q$, $\cdots$, the inequalities of the kind $||\omega_{s}\left(k+q\right)-\omega_{s}\left(k\right)|-\omega_{ac}|\gg\gamma\Delta B_{0}/2$ need to be fulfilled. In particular, one may require $|\omega_{s}(q)-\omega_{s}(0)|-\omega_{ac}\gg\gamma\Delta B_{0}/2$. Let us take the experimental parameters in Ref. [19] as an example. In this measurement, the value of $\gamma\Delta B_{0}$ was $2\pi\times 11$ MHz, while $|\omega_{s}(q)-\omega_{s}(0)|$ was roughly $2\pi\times 100$ MHz. In this case, an ac modulation with $\omega_{ac}$ around $2\pi\times 50$ MHz would be suitable for the experimental studies of the shifted resonance. Spin-wave attenuation and decoherence are the two other factors that need to be considered. Let us estimate the operation time required to bring the spin-wave state from the north to the south pole. Using the same value of $\gamma\Delta B_{0}$, we find this time to be $2\pi/\gamma\Delta B_{0}\approx 91$ ns, which is shorter than both lifetime and coherence time of spin waves in YIG (cf. Refs. [8, 9, 14]). In the end, we estimate the length of the device. In practice, the slopes of the curves plotted in Figs. 2(a) and 3(a) are determined by the group velocities of the incident and reflected spin-wave packets, which may vary dramatically for different magnetic material and geometries. In the case of the magnetostatic spin waves studied in Ref. [19], the spin-wave group velocity $|v_{g}|$ was found to be about $27404$ m/s. Such a spin-wave packet would perform to-and-fro motion with maximum displacement $|v_{g}|\times 2\pi/\gamma\Delta B_{0}\approx 2.5$ mm, and therefore, the meander structure must have a size of at least $2.5$ mm in order to confine this bouncing packet. In principle, the operating range of $\omega_{ac}$ can be enlarged to a GHz range by fabricating a meander structure with a shorter period $d$, and the operation time can be further reduced by applying a bigger $I_{0}$.

With the use of the techniques accessible nowadays, the tunable ac magnonic crystal can be exploited for controlling spin waves with different wave vectors. One can excite and detect many spin waves with different frequencies in a magnetic sample at the same time through one antenna setup [33]. The tunability of the ac magnonic crystal allows one to use a single hardware (the meander pattern) to simultaneously manipulate multiple spin-wave pairs in one waveguide. Each pair formed by waves with different frequencies is independently operated by a suitable ac pulse that satisfies the shifted resonance. As a result, the tunable ac magnonic crystal can serve as a new building block of the computing device studied in Ref. [6] and improve its spatial scalability with no compromise on computational time.