∎
2Department of Mathematics and Computer Science, Islamic Azad University, Bardaskan Branch, Bardaskan, Iran. 11email: mehdidelkhosh@yahoo.com.
SPSMAT: GNU Octave software package for spectral and pseudospectral methods
Abstract
SPSMAT (Spectral/Pseudospectral matrix method) is an add-on for Octave, that helps you solve nonfractional-/fractional ordinary/partial differential/integral equations. In this version, as the first version, the well-defined spectral or pseudospectral algorithms are considered to solve differential and integral equations. The motivation is that there are few software packages available that make such methods easy to use for practitioners in the field of scientific computing. Additionally, one of the most practical platforms in computation, MATLAB, is currently not supporting beneficial and free numerical method for the solution of differential equations–to the best author’s knowledge. To remedy this situation, this paper provides the description of its relevant uploaded open source software package and is a broad guidance to describe how to work with this toolbox.
Keywords: Spectral methods, PseudoSpectral methods, Matrix computation, Octave software package
1 Introduction
During the recent years getting our hands dirty of working with spectral and pseudospectral methods, when it comes to solving differential/integral equations, we feel like there is a huge lack amongst a myriad of papers published in the field of solving differential/integral equations. The instant problem to detect is that all the scientists and researchers solve problems without using others’ codes and packages. Undoubtedly, having a fixed platform and inviting the scientist to develop their work can reduce the time and effort in solving these similar-based problems.
Over these years, we have known that the works of these scientists are of giant works and worth admiring, but we always ask ourself ”what if we gather the works of all current scientific computer scientist in order to design a package to use easier and grownup methods for the solutions of ODEs and PDEs?”.
To do so, it has been attempted to provide consistent and user-friendly high-level functions that allow experimental scientists to work properly and beneficially on their equations.
Furthermore, users and developers can easily extend the functionality and implement new
algorithms due to the modular design functionalities and facilities, and in higher expectation, harness them in other software packages.
This package and its documentation are freely available from This address.
The SPSMAT toolbox consists of approximately 80
high-level and other low-level functions.
We are to say that the high-level functions give a consistent
and easy-to-use interface of the functionality and reusability to the users and developers, allowing them to do the analysis in such well-defined manners. The
low-level functions implement the core functionality and are not needed to be shown to the end-users, these functions are set and called inside other functions. In addition to handy functions, some constructive examples are given in terms of guidance and showing the handling of the functions.
SPSMAT has been believed to be portable and open source. At this
aim, SPSMAT has been developed using Octave, which is a kind of free MATLAB clone and runs on the
commonest operating systems, such as Unix, Linux, Windows, and Mac OS X.
To the best of our knowledge, SPSMAT is also the first free scientific computing package which runs on GNU/Octave platform.
2 Features of SPSMAT
The SPSMAT package is
self-contained; it only needs an Octave environment
with
standard toolboxes [See
Octave ].
SPSMAT is released under the free and open source GNU GENERAL PUBLIC LICENSE (GPL)
(Version 3, 29 June 2007). The accompanying source code and the documentation of the toolbox have been enriched with numerous comments, examples, and detailed instructions for extensions.
This is the first in a series of papers on implementing different numerical techniques in term of an open source
GNU Octave toolbox. The intention of this ongoing project is
to provide a rapid prototyping package
for using spectral and pseudospectral methods in solving integral and differential equations.
Here, we highlighted some of the outstanding features of SPSMAT:
-
•
highly modular; the reasons beyond highly modular design are:
-
–
* The combinations of the approximation techniques.
-
–
* The easy construction and embedding of other novel techniques; the library aims to utilize the well-known spectral and pesudospectral methods as transparent as possible to the user. A small alternation and enhancing the code to fit one’s assumption is easy to handle.
-
–
* Having a well-defined structure for the modules also simplifies the maintenance of the code.
-
–
* Their immediate application in other packages. The modular design facilitates reuse of source code in other software. It ignites the collaboration with current developers and with developers of other software packages to broaden their work and understandings.
-
–
-
•
Free and open source; explained in next sections.
-
•
Multi-platform toolbox; SPSMAT is multi-platform: it has been extensively tested on Windows and Linux; since it is made of standard Octave files, it is expected to work on alternative platforms as well.
-
•
Following ”all-in-one” philosophy. By this, we tried to represent one particular function with different inputs to encompass all possible outputs and purposes. For instance, in order to have functions for Jacobi polynomials and their derivatives, we defined a function with input 0 to show the Jacobi polynomials and with input 1 to give the first order derivative of this polynomials.
2.1 Why numerical methods?
After delving through different books, we know that they concentrated on ODEs based on linear problems. The trouble is most ODE problems including almost all nonlinear ones can’t be solved analytically. A numerical one, however, can be obtained by computer. The very important advantage of numerical approximations is that they can be obtained for almost any ODE. In addition to the speed of these methods, the nature of numbers helps scrutinize results obtained numerically even apply different analysis method to a problem and compare them with one another. On another hand, it is not easy to compare two exact formulas, but it is beneficial to compare two numbers, even as numbers or visually in plots therifeten . That simply can be detected as a reason for designing a numerical package rather than the analytical one.
2.2 Why No User Interface (UI)?
We never assume that we are familiar with everything that a user might want to do. A great feature of the SPSMAT toolbox is that it does not have a Graphical User Interface (GUI). Instead, the user is interacting directly with the functions on the command line or in scripts and is able to mix and build his new insight in order to solve a problem. Providing a GUI prevent the user to mix, match, and test the SPSMAT high-level functions experimentally. Data and code, in fact, are in the hands of the end users to reshape them suitable to their need.
2.3 Why Open source and Octave?
MATLAB is widely known and used in the science communities including scientific computing. Although MATLAB has a rich feature set and flexibility, it is relatively and ridiculously expensive. MATLAB environment is a commercial and ”closed” product, thus MATLAB kernel and libraries cannot be modified nor freely distributed. To allow exchanging insights and contributing scientific research, both the toolbox and the platform on which a toolbox runs must be completely free.
Mathworks like other proprietary firms has its own policies that may not help you freely use and develop some packages.
That was maybe the ultimate motive to use an open source platform. In addition to it, as what an Iranian proverb saying one clap is not audible, we
required
the users extend the analyses with their own code and be exchanged between users, and between students and
their supervisors, facilitating collaboration and knowledge over Github where they can even transfer their proper contribution with us.
Nonetheless, these are not such limitation for MATLAB users at all. They can even download the package and use it.
2.4 Why Fractional?
Due to the accuracy of fractional differential and integral equations in modeling various natural phenomena, fractional calculus has become the focus of many researchers. Fractional differential equations provide an outstanding instrument to describe the complex phenomena in fields of viscoelasticity, electromagnetic waves, diffusion equations, and so on. Moreover, the fractional order models of real systems are more sufficient in comparison with the integer order cases. Therefore, the field of fractional calculus has motivated the interest of researchers in various fields like physics, chemistry, engineering and even finance where all of their scientists and students need to work with numerical methods of solving these fractional equations. We broadly aim at this spectrum and wanted to produce a package for all of these practitioners.
2.5 Why Jacobi?
The classical Jacobi polynomials, have been used extensively in mathematical
analysis and practical applications, and play a pivotal role in the analysis and implementation of spectral and pseudospectral methods bhrawy2 .
It is easily proven that the Jacobi polynomials are the polynomials arising as eigenfunctions of a singular
Sturm–Liouville problem bhrawy2 .
The usual spectral method by Legendre or Chebyshev approximation, and available only for non-singular problems on rectangular bounded domains. However, the general Jacobi method can be used in a wide array of
problems bhrawy3 .
In addition to this, in this version, also for the simplicity’s sake, we cover Jacobi polynomials which are wide-ranging polynomials encompassing Gegenbauer (ultraspherical), Chebyshev, and Legendre polynomials. But, for those who are not into these polynomials, we also offered the derived subcategories including Gegenbauer, Chebyshev (all four kinds), and Legendre polynomials.
2.6 Why Now?
Over the recent years, many researchers have been interested in studying the properties of various equations and providing robust and accurate analytical and numerical methods for solving these equations and recorded their work in their published papers: what we have seen at this moment is to see and gather their works in one single work. Moreover, some of the high-qualified state-of-the-art methods and landmark works are done and analyzed perfectly that let us code them in the best shape that is readable and understandable, and specifically, beneficial. In addition to this, other works done on spectral methods are out-dated; like the work of Funaro/Matlab that is done in 1993 via Fortran (See Funaro package). What these packages lack are that at that time fractional calculus, operational matrices and Lagrangian bases had not been developed like today. The other FORTRAN package, PseudoPack 2000 is implemented by Don and Costas and is available in [PseudoPack package]. In this work parallel computers capability involved to solve problems and suffer the same misfortunes we issued here. In the newest work by Trefethen in Chebfun package, a huge and broad work done to refer a tool for researchers. But the light version, and more importantly, the specification for solving differential and integral equation in terms of spectral and pseudospectral was not its first goal.
SPSMAT, lo and behold, was created to address some of these issues.
2.7 Why Matrix method?
As the operations in MATLAB and Octave are based on the concept of matrix, and in some extends their performance is optimal for matrices, we have given a matirx-based method in order to reach the best action of MATLAB or Octave. Another reason is the parallel computation that is said to be feasible and meaningful when it comes to matrix operations like multiplications and so forth. In this version, we have not considered matrix parallel computation methods, but in due course, we will work on it and report its relevant results.
2.8 Why Spectral?
The well-defined Spectral methods, by using computer power, have been developed rapidly through the recent years for the numerical solutions of ordinary/partial differential/integral equations. They have been providing a satisfying accuracy compared with other numerical methods and have wide applications in many mathematical problems. As we have realized, the spectral methods have been developed in different ways to provide accurate solutions for linear and nonlinear ordinary/partial differential/integral equations. Additionally, spectral methods have received considerable attention in dealing with various problems. As their most significant characteristics, they reduce problems to those of solving a system of algebraic equations; this makes them easier for solving. Also, they have excellent error properties and they offer exponential rates of convergence for smooth problems. Such methods have matured over the last 50 years and, in many cases, meet the robustness and computational efficiency standards required in practice.
2.9 Why Pseudospectral?
In general, there are two ways to construct a polynomial approximation to the solution : One is to use an interpolating polynomial between the values at some points . The other is to use a series expansion in terms of Lagrange or orthogonal polynomials like Jacobi polynomials. Here, the latter idea is pursued, and both the Jacobi and Lagrange Jacobi polynomials are constructed and the difference between employing them are also represented. In fact, the pseudospectral methods (here using Lagrange polynomials) are based on the spectral techniques. In pseudospectral methods, there are particularly two steps to achieve a numerical approximation for a differential equation. Firstly, a proper finite or discrete representation of the solution should be selected– this can be done by polynomial interpolation of the solution based on some appropriate nodes. On another hand, it is known that the Lagrange interpolation polynomial based on equidistant points does not yield a satisfactory approximation to general smooth functions. As a matter of fact, when the number of collocation points increases, interpolant polynomials notably diverge. However, satisfying results are obtained by relating the collocation points to the structure of classical orthogonal polynomials, such as the well-established Jacobi-Gauss-Lobatto points. That can be figured as a cogent reason for choosing these points in defining Lagrange polynomials. The use of global polynomials together with Gaussian quadrature collocation points (here Jacobi-Gauss-Lobatto points) is known to provide accurate approximations that converge exponentially for problems whose solutions are smooth kidderlatifi ; fokkerlatifi ; delkhosh ; delkhosh2 ; div .
2.10 What is the prerequisite and who is this package for?
This software package is intended for those who have a taste for solving ODEs, PDEs, integral equations and Optimal Controls. Practitioners with a not-so-deep understanding of Matlab or Octave can use this package without any difficulty. But basically this package is meant to be useful to solve different differential and integral equations; so it stipulates that the users have a grasp of Numerical analysis beforehand.
Undergraduate students taking a course in scientific computing and any relevant course can find this package as a test machine to check different things with orthogonal polynomials and develop their work with this package: this is your lightweight companion. In nutshell, whoever you are, we aim to increase your appreciation of this fundamental subject.
3 Solving a nonlinear PDE with SPSMAT
In this section, firstly we discuss the orthogonal Gegenbauer polynomials. The orthogonal Gegenbauer polynomial of order is defined over bahram :
As said, this package helps solve partial and ordinary differential equations. To show its capability, we have considered nonlinear Fokker-Plank equation:
where and with the initial and boundary conditions , and . The exact solution is and .
For solving this problem, with help of Crank-Nicolson method fokkerlatifi , we discretized the variable and solved the equation in different iterations fokkerlatifi .
Notice that and .
Using where and applying Crank-Nicolson method we have got
| (3) |
in which is unknown and is supposed to be determined. Simplifying the last equation we have
| (4) |
Now by defining
then Eq. (3) will be
Now for solving this equation, we use an approximation expansion with Generalized Lagrange polynomials: , where , are the unknown coefficients, and are the Generalized Lagrange polynomials defined in kidderlatifi ; fokkerlatifi . Then
| (5) |
and with Gegenbauer Gauss Lobatto points , and roots of which are calculated with:

Setting
and considering Eq. (3), by using Gegenbauer Gauss Lobatto points, we will get a matrix form as
| (6) |
in which is the coefficient matrix and is the unknown vector.
By implementing boundary condition, is rewritten as:
by which
where and are the Generalized Lagrange first and second order derivative matrices that are calculated in kidderlatifi ; fokkerlatifi .


Also applying initial condition leads to .

The completed code file contains more of these functions which are mostly discussed here.
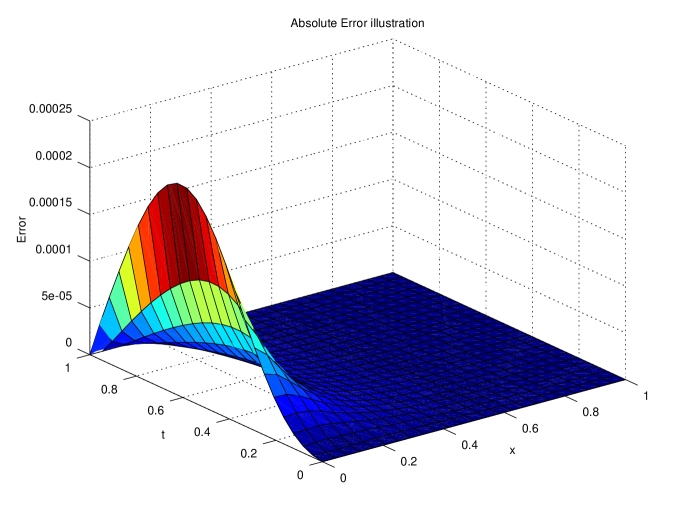
Acknowledgements.
In the end, we owe some researchers a thank who were at our disposal when we were in dire need. We thank profusely Mohammad Hemami and Dr. Saeed Kazem.References
- (1) Trefethen L.N., Á Birkisson, and TA Driscoll. Exploring ODEs. SIAM. (2017): 157
- (2) Doha, E. H., A. H. Bhrawy, and S. S. Ezz-Eldien. ”A new Jacobi operational matrix: an application for solving fractional differential equations.” Applied Mathematical Modelling 36.10 (2012): 4931-4943.
- (3) Doha, E. H., and A. H. Bhrawy. ”Efficient spectral-Galerkin algorithms for direct solution of fourth-order differential equations using Jacobi polynomials.” Applied Numerical Mathematics 58.8 (2008): 1224-1244.
- (4) Parand, K., Latifi, S., Delkhosh, M., and Moayeri, M. M. ”Generalized Lagrangian Jacobi Gauss collocation method for solving unsteady isothermal gas through a micro-nano porous medium.” The European Physical Journal Plus 133.1 (2018): 28.
- (5) Parand, K., Latifi, S., Moayeri, M. M., and Delkhosh, M. ”Generalized Lagrange Jacobi Gauss-Lobatto (GLJGL) Collocation Method for Solving Linear and Nonlinear Fokker-Planck Equations.” Communications in Theoretical Physics 69.5 (2018): 519.
- (6) Delkhosh, M., and Parand, K. ”Generalized Pseudospectral Method: Theory and Application”, Journal of Computational Science 34 (2019): 11-32.
- (7) Delkhosh, M., Parand, K., and Hadian-Rasanan A.H., ”A development of Lagrange interpolation, Part I: Theory”, arXiv:1904.12145 (2019): 1-12.
- (8) Garg, D., Patterson, M., Hager, W. W., Rao, A. V., Benson, D. A., and Huntington, G. T. ”A unified framework for the numerical solution of optimal control problems using pseudospectral methods.” Automatica 46.11 (2010): 1843-1851.
- (9) Parand K, Bahramnezhad A, Farahani H. ”A numerical method based on rational Gegenbauer functions for solving boundary layer flow of a Powell–Eyring non-Newtonian fluid”. Computational and Applied Mathematics. 37(5) (2018):6053-6075.