Stability frontiers in the AM₆X₆ kagome metals: The LnNb₆Sn₆ (Ln:Ce–Lu,Y) family and density-wave transition in LuNb₆Sn₆

Single crystal growth of LnNb₆Sn₆ (Ln:Ce–Tm,Y) single crystals was performed using the self-flux technique. Elemental reagents were combined in a ratio of 8:2:90 Ln:Nb:Sn. The exact ratio of Ln:Nb:Sn is flexible and growths have succeeded with compositions as rich as 12% rare-earth and as as poor as 4%. We utilized Ames Lab rare-earth metals (Ce-Lu, Y), Nb powder (Alfa, 99.9%), and Sn shot (Alfa, 99.9%). Reagents were placed into 5 mL Al₂O₃ (Canfield) crucibles fitted with a catch crucible/porous frit and sealed within fused quartz ampoules with approximately 0.6–0.7 atm of argon cover gas.[41] Samples were heated to 1150°C and thermalized for 18 h. For growths utilizing Ce–Tm (and Y), samples are cooled to 780°C at a rate of 2°C/hr before centrifugation at 780°C. Growths targeting LuNb₆Sn₆ are cooled to 900°C at a rate of 0.5-1°C/hr and subsequently centrifuged at 900°C.

Single crystals are small, well-faceted, gray-metallic, hexagonal plates and blocks. The samples are stable in air, water, and common solvents. Crystals resist attack by concentrated HCl and dilute HNO₃, with the exception of LuNb₆Sn₆.

Single crystals were mounted on kapton loops with Paratone oil for single crystal x-ray diffraction (SCXRD). Diffraction data at 100 K was collected on a Bruker D8 Advance Quest diffractometer with a graphite monochromator. Supplementary diffraction data at 45 K for LuNb₆Sn₆ were collected with a Rigaku XtaLab PRO equipped with a Rigaku HyPix6000HE detector and an Oxford N-HeliX cryocooler. Both instruments used Mo K$\alpha$ radiation ($\lambda$ = 0.71073 Å). Data integration, reduction, and structure solution was performed using the Bruker APEX4 software package, Rigaku Oxford Diffraction CrysAlisPro[42], JANA,[43] or Shelx.[44] Diffuse X-ray scattering measurements were performed at the Cornell High Energy X-ray Synchrotron Source (CHESS), beamline IDB4-QM2 ($\lambda$ = 0.27021Å). The experiment was conducted in transmission geometry using a 6-megapixel photon-counting pixel-array detector with a silicon sensor layer and a flowing He cryostream for temperature control. Temperature-dependent powder diffraction was performed on a PANalytical Xpert Pro diffactometer ($\lambda$ = 1.5406 Å) equipped with a Oxford PheniX closed-cycle helium cryostat. Diffuse data was analyzed and visualized using the NeXpy/NXRefine software package.[45, 46] The Topas V6 software package[47] was used to analyze the polycrystalline data.

The ARPES experiments were performed at beamline 21-ID-1 of NSLS-II at BNL. The LuNb₆Sn₆ samples were cleaved in-situ under vacuum ($<$3$\times$10^-11 Torr). Measurements were taken using an incident energy of 79 eV and a energy resolution of 15 meV.

Magnetization measurements (300–1.8 K) on crystals of LnNb₆Sn₆ (Ln:Ce–Lu,Y) were performed in a 7 T Quantum Design Magnetic Property Measurement System (MPMS3) SQUID magnetometer in vibrating-sample magnetometry (VSM) mode. Additional measurements below 1.8 K utilized the Quantum Design iHe-3 insert for the MPMS3 (1.8–0.4 K). For consistency, the same sample was utilized for both measurements wherever possible. The data sets were matched at 1.8 K, with deference given to the MPMS3 (lower background) dataset. Small errors (5–10% of the absolute magnetization) can often be observed when transitioning to the ³He regime, predominately attributed to the difficulty of aligning the small crystals in the ³He setup. Both field-cooled (FC) and zero-field-cooled (ZFC) measurements were performed, though ZFC curves are only shown where hysteresis is noted. Measurements were made for both H $\parallel$ c and H $\perp$ c. When possible, orientations with H $\perp$ c are also oriented such that H $\parallel$ a. Temperature-dependent measurements are typically performed at an applied field of 500 Oe, except for the non-magnetic YNb₆Sn₆ and LuNb₆Sn₆ ($H=$ 10 kOe).

Heat capacity measurements (300–1.8 K) on crystals of LnNb₆Sn₆ (Ln:Gd–Lu,Y) were performed in a Quantum Design 9 T Dynacool Physical Property Measurement System (PPMS), and a Quantum Design 14 T PPMS equipped with a ³He (9–0.4 K) insert. Additional measurements were performed for LnNb₆Sn₆ (Ln:Ho–Lu,Y) utilizing a Quantum Design dilution refrigerator insert (4–0.1 K) for the 9 T Dynacool PPMS. The same samples were used for both measurements wherever possible. Similar to magnetization measurements, curves were matched in the crossover regime around 2 K. A systematic thermometry offset of approximately 0.2 K is observed in the ³He data.

Resistivity measurements (300–1.8 K) were performed using a Quantum Design 9 T Dynacool Physical Property Measurement System (PPMS). Resistivity bars were constructed from single crystals of LnNb₆Sn₆ (Ln:Gd–Lu,Y) via polishing. Naturally faceted crystals were mounted on a Struers AccuStop sample holder using Crystalbond 509 and polished into rectangular prisms with approximate dimensions of $1\times 0.3\times 0.1$ mm. Crystalbond was subsequently removed using acetone. Where possible, samples were polished such that $I\,\parallel$ a. Electrical contact was achieved using silver paint (DuPont cp4929N-100) and platinum wire (Alfa, 0.05 mm Premion 99.995%) in a four-wire configuration.

First-principles calculations were performed within the density functional theory[48] approximation using the linearized augmented plane-wave (LAPW) method [49, 50, 51] as implemented in the WIEN2K code.[52] The LAPW “muffin-tin” spheres of radii 2.5 Bohr for all three components, with $RK_{\text{max}}$ = 9.0 were used. The experimental lattice parameters were used for all calculations, and atomic positions were relaxed until atomic forces fell below 1 mRy/Bohr. The exchange-correlation energy was calculated within generalized gradient approximation [53] with the parametrization by Perdew, Burke, and Ernzerhof (PBE).[54] Spin-orbit coupling was included using the second-variation approach.[55] Brillouin zone (BZ) summation in electronic system self-consistency procedure was carried out over 13$\times$13$\times$6 $k$-points mesh, while Fermi surface was built using 22$\times$22$\times$11 mesh. To build the Fermi surface the FermiSurfer [56] and XCrySDen [57] graphical packages were used.

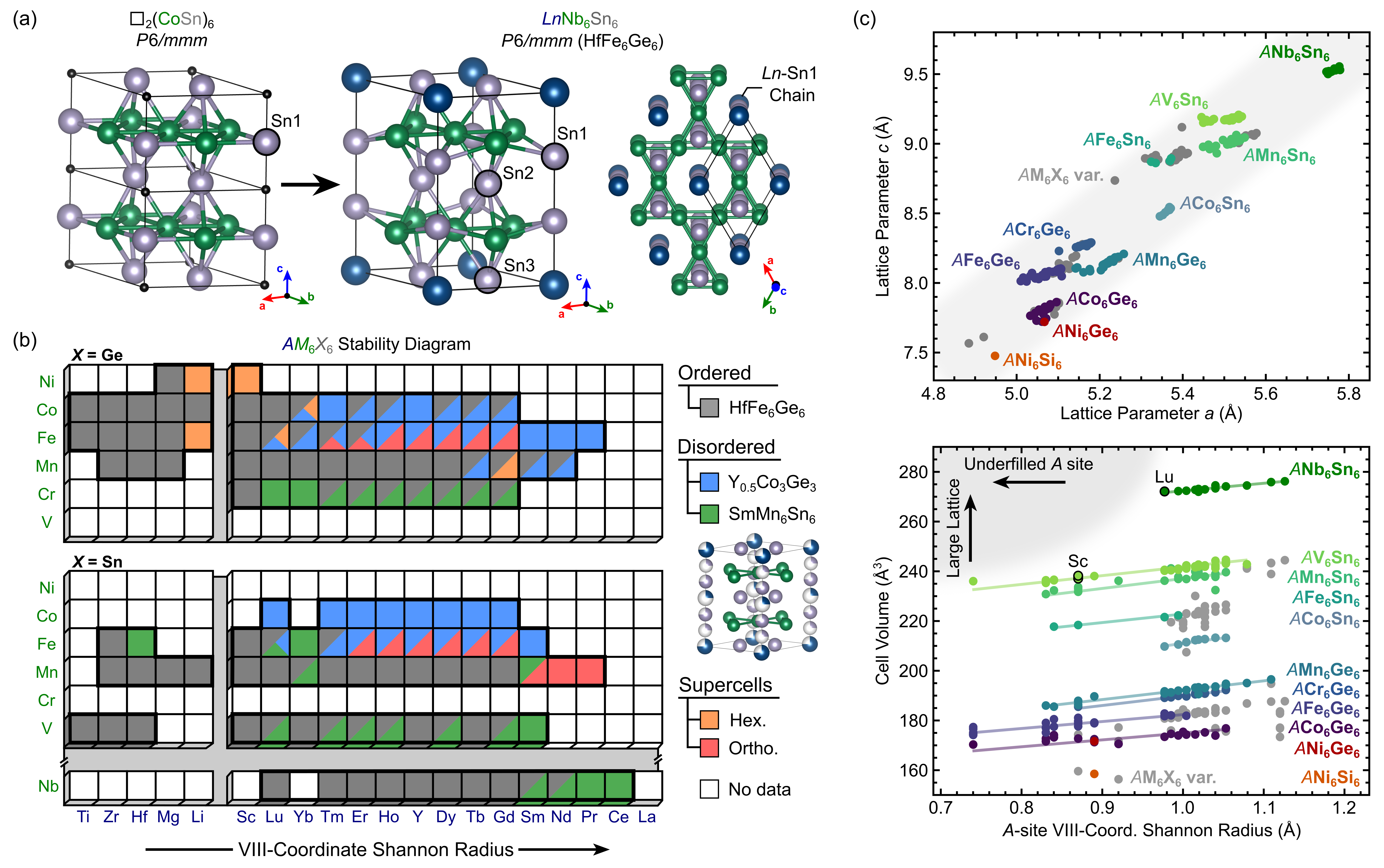
Of the binary kagome compounds, the CoSn prototype is one of the most fundamental families. The simple unit cell and isolated kagome planes leads to an electronic structure that clearly exhibits the hallmark flat-bands, Dirac points, and saddle points predicted by theory.[124] Unfortunately, the family is limited in scope, and only CoSn, FeGe, NiIn, FeSn, PtTl, and RhPb are known.[125] It has been proposed that the limited stability of the CoSn structure may relate to the low density structure, which is filled with large interstitial voids.[126, 127] Figure 1(a) shows two stacked CoSn unit cells, highlighting the interstitial voids with small black spheres. This unusual feature of CoSn allows integration of “filler” atoms, producing AM₆X₆-type structures. The most frequently encountered AM₆X₆ structure is the HfFe₆Ge₆ prototype, formed when the (0,0,0) position in the $1\times 1\times 2$ CoSn supercell is filled with electropositive cations. As one may expect, the connection between the filler size and host lattice sterics is complex, producing vast structural and stacking diversity in the AM₆X₆ family. Over 100 unique compounds are known.[58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 67, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 72, 85, 86, 87, 88, 89, 90, 91, 28, 92, 93, 30, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 128, 104, 105, 106, 107, 108, 109, 79, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122] with a plethora of stacking variations, intergrowths, and incommensurate structures.[126, 129]

The most recognizable AM₆X₆ prototype is the HfFe₆Ge₆ structure. Fig. 1(a) shows the relationship between the filled CoSn supercell and the HfFe₆Ge₆ prototype, represented here by our LnNb₆Sn₆ family. Note that the volumetric expansion from the filler atoms pushes the in-plane (Sn1) atoms out of the (0,0,1/4) and (0,0,3/4) kagome plane. Where the original Sn1–Sn1 distance in CoSn was nearly 4.3 Å, the new Sn1–Sn1 bond is $\approx$3.2 Å. This is comparable with other bonding distances in the AM₆X₆ cell ($d_{\text{Nb-Nb}}\approx$2.9 Å, $d_{\text{Nb-Sn}}\approx$3.0 Å).

Furthermore, the length of the Sn1–Sn1 bond is highly sensitive to the choice of the filler atom. Between the largest (e.g. NdNb₆Sn₆) and smallest (e.g. LuNb₆Sn₆) members of the family, the Sn1–Sn1 bond length compresses nearly 4% from 3.29 Å  (Lu) to less than 3.16 Å with large atoms (Nd). Compression of the Sn1–Sn1 bond appears to be the structure’s preferred means to relieve strain from the incorporation of large atoms. For comparison, from NdNb₆Sn₆ to LuNb₆Sn₆, the $c$-axis lattice parameter only expands 0.6%, the volume expands $<$2%, and the $z$-position of the kagome lattice shifts only 0.4%. Thus, it appears that the Nb-(Sn2,3) sublattices act as a largely rigid scaffolding interlaced with flexible Ln1–Sn1–Sn1–Ln1 chains.

These flexible, less constrained $Ln$1–Sn1–Sn1–$Ln1$ chains are key to our prior work detailing a “rattling” bond modulation in ScV₆Sn₆,[30] previously identified as a potential CDW instability.[28] The “rattling” is more constrained than the analogous terminology applied in the Skutterudites and filled clathrates, but draws from similar steric principles.[130, 131, 132, 133] Thus, we have an interesting confluence of chemical pressures inside the AM₆X₆ compounds. The filler atom stabilizes compositions by filling anomalously large interstitial voids, but it clearly affects the bond distances and crystal structure in a highly non-isotropic manner. It naturally follows that some filler atoms will be too large, while others will be too small. The boundaries between the structural stability and internal strain is the impetus for our discussion – a AM₆X₆ stability field.

Figure 1(b) presents a stability diagram of all known AM₆X₆ phases where X is Ge or Sn. Given the limited number of silicon-based compounds (MgNi₆Si₆, ScNi₆Si₆, LiNi₆Si₆)[63, 134], we have omitted the corresponding silicide diagram. The M-site has been organized according to atomic number, and the A-site has been organized based on the VIII-coordinate Shannon radius. This diagram is an agglomeration of all publicly available structural data on the AM₆X₆ compounds.[58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 67, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 72, 85, 86, 87, 88, 89, 90, 91, 28, 92, 93, 30, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 102, 104, 105, 106, 107, 108, 109, 79, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123] In our diagram, there are five major categories of structures: 1) HfFe₆Ge₆ (gray), 2) disordered SmMn₆Sn₆ (green), 3) disordered Y_0.5Co₃Ge₃ (blue), 4) “other” hexagonal cells (orange), and 5) “other” orthorhombic cells (red). We have preserved the classification given by the author of each work.

The HfFe₆Ge₆ cell is what is typically regarded as the “pristine,” ordered, AM₆X₆-type compound. However, we can clearly see that many compounds exhibit varying degrees of disorder. Both disordered SmMn₆Sn₆ and Y_0.5Co₃Ge₃ are characterized by partial suboccupancy of the A-site and partial occupancy on the (normally vacant) (0,0,0.5) site. In the case of Y_0.5Co₃Ge₃, the (0,0,0.5) and (0,0,0) site are both nearly half occupied, causing the unit cell to reduce to a smaller, single kagome-layer compound. We suspect a similar phenomenon occurs in our PrNb₆Sn₆ and CeNb₆Sn₆, which exhibit clear signatures of disorder in diffraction and subtle changes in crystal habit. For the purposes of this work we classify them as non-HfFe₆Ge₆ structures, though we hope the ordered structure can be stabilized with more refined synthesis methods.

We note that the Y_0.5Co₃Ge₃ and SmMn₆Sn₆-type structures seem to appear on opposite sides of the diagram. Empirically, Y_0.5Co₃Ge₃ seems to favor the smaller Co- and Fe- host lattices, whereas SmMn₆Sn₆-type occurs more frequently in larger V- and Cr-based lattices. The other observation of note is the striking and complex variations in stacking seen in the iron-containing compounds, with HfFe₆Ge₆, ErFe₆Sn₆, HoFe₆Sn₆, YFe₆Sn₆, DyFe₆Sn₆, and TbFe₆Sn₆ all representing unique commensurate superstructures arising from variations in the stacking/filling of the host lattice.[79, 129] We have only examined those compounds with AM₆X₆-type stoichiometry, though many other structures and stackings (e.g. AM₃X₄ kagome metals)[135, 136, 137, 138, 139, 140, 141, 142] can be derived from the CoSn and HfFe₆Ge₆ prototypes.

On our diagram, the LnNb₆Sn₆ family stands apart as the only 4$d$-element series of AM₆X₆ compounds. Hints of the family’s existence were noted with both YNb₆Sn₆ and TbNb₆Sn₆ reported as side products in exploratory reactions, and served as a launching point for our synthetic endeavors.[121, 120] The LnNb₆Sn₆ system appears to tolerate larger (e.g. Sm, Nd) and reject smaller (e.g. Sc) A-site filler atoms, with the notable absence of YbNb₆Sn₆. The inclusion of Nb will produce the largest M₆X₆ scaffolding and the largest interstitial voids. To assist in visualiation, Figure 1(c,top) presents a plot of the a and c lattice parameters for all AM₆X₆ compounds. Notable series of HfFe₆Ge₆-type AM₆X₆ have been colored to highlight chemical families, with the various structural distortions and disordered compounds left gray. The exception is ACo₆Sn₆, which is highlighted even though no HfFe₆Ge₆ representatives exist for the stannides. The general trends are visually striking, with the LnNb₆Sn₆ family sitting isolated from the rest of the data.

Meier et al.[30] previously proposed that the structural instability in ScV₆Sn₆ arises from underfilling of the interstitial voids.[30] Figure 1(c,bottom) provides a graphical interpretation of this hypothesis by plotting the A-site Shannon radius (filler size) and the unit cell volume (proxy for host lattice voids). Based on the model, we expect the “rattling” DW instability to be favored for the combination of a small A-atom and a large host lattice (shaded gray region in upper left). We have marked the two known DW compounds, ScV₆Sn₆ and the our newly discovered LuNb₆Sn₆, with black-bordered points. Coincidentally, while writing this manuscript, Feng. et al. computationally cataloged the instabilities in the broader AM₆X₆ compounds, suggesting that the “hypothetical” Nb-based [143] compounds would be unstable to Sn1-Sn1 bond modulation mode.

Both LuNb₆Sn₆ and ScV₆Sn₆ are among the smallest A-site end members of the V- and Nb-based AM₆X₆ series, respectively, which agrees with expectations. One point of curiosity on Figure 1(c, bottom), however, would be the three V-based compounds with even smaller Shannon radii than ScV₆Sn₆. These compounds correspond to the recently reported TiV₆Sn₆, ZrV₆Sn₆ and HfV₆Sn₆.[91] TiV₆Sn₆ likely exhibits some Ti${}_{\text{V}}$ disorder, but the absence of a structural (DW-like) instability in the Hf- and Zr-based compounds is curious. However, unlike the rare-earth compounds, it is unlikely that Hf and Zr can be treated within the ionic (Zr⁴⁺, Hf⁴⁺, 8-coordinate) limit. Further, recent computational assessments have indicated that Ti, Zr, and Hf-based compounds are not expected to show bond modulations, suggesting the importance of appropriate band-filling and $d$-orbital states.[143] Fermi level alignment with the prototypical kagome bands is persistent theme in kagome metal research – and thus we turn to examine the characteristic electronic structure of the LnNb₆Sn₆ family.

The tight-binding model of the kagome motif provides an underlying motivation for research into kagome metals,[8, 9, 10, 11] though the actual manifestation of “kagome” bands in real materials is often substantially more complex. Figure 2 presents the electronic structure of non-magnetic LuNb₆Sn₆, which serves as a convenient proxy for the electronic structure of the wider LnNb₆Sn₆ family. Here we are intentionally neglecting the influence of magnetism for the other rare-earth compounds in an effort to simplify the discussion and provide a general perspective on the electronic structure in the Nb-Sn compounds. We anticipate that more in-depth computational works will follow, particularly with regards to some of the more complex magnetic members.

Figure 2 demonstrates the density functional theory (DFT) calculation for LuNb₆Sn₆ within $\sim$2 eV of the Fermi level. We have shown data with (blue) and without (gray) spin-orbit coupling. Figure 2(b) provides a magnified view of the electronic structure within 1 eV of the Fermi level for the $\Gamma$-$K$-$M$-$\Gamma$ path. From both figures, there are several key features that are easily identified. There is a flat-band (red arrow) that extends throughout much of the Brilluoin zone at approximately +0.6 eV. While the distant flat band is unlikely to have an appreciable effect on the physical properties, both a Van Hove singularity (VHS) at $M$ and a Dirac-like feature at $K$ are within 0.1 eV of the calculated Fermi level. Several other VHS’s (green arrows) and Dirac-like features (black arrows) have been highlighted on Figure 2(a,b). We note that spin-orbit coupling (relevant with heavier Nb) gaps many of the Dirac cones, including the one near the Fermi level at $K$.

To verify the electronic structure near the Fermi level, and to check the alignment of the computationally derived Fermi level, we performed a series of ARPES measurements ($T=30$ K) on cleaved single crystals of LuNb₆Sn₆. Figure 2(c) is a reconstructed image of the ARPES intensity along the $\Gamma$-$K$-$M$-$\Gamma$ high symmetry path. While the ARPES measurements were performed at $k_{z}=\pi$, we observe minimal changes in $k_{z}$-dependent scans and are comfortable utilizing the data for a qualitative comparison with DFT. A overlay of the DFT band structure has been provided as a faint white trace. We see generally good agreement between the DFT and theory, particularly with regards to the high DOS near the Van Hove singularity at $K$, and the faint signal from the Dirac-like feature at $M$. Figure 2(d) highlights a series of Fermi surface contours at different isoenergy cuts from which the band structure in Fig. 2(c) is derived.

Prior knowledge from ScV₆Sn₆ helps to identify substantial signal from surface-states in both the reconstructed band dispersions and the Fermi surface maps. The potential for topologically non-trivial surface states is an intriguing prospect. Within ScV₆Sn₆, there have been many recent ARPES, STM, and computational efforts directed at investigating surface states.[144, 29] Given their chemical similarity, we suspect LuNb₆Sn₆ to exhibit equally complex features. Though our ARPES results are below the DW transition temperature (68 K), we did not observe strong changes in the ARPES intensities above and below the transition. The ScV₆Sn₆ system also shows relatively subtle changes through the DW transition. However, more detailed studies have shown a rich landscape of subtle changes,[35, 145, 146, 147, 148] and while the evolution of the surface states and DW in ARPES is intriguing, these efforts are beyond the scope of this manuscript. A more in-depth investigation into the ARPES and scattering results are anticipated in our follow-up work.

The DW instability in the structurally analogous ScV₆Sn₆[28] manifests with thermodynamic signatures remarkably similar to those observed in the CDW AV₃Sb₅ systems.[22, 21, 23, 24] This led to initial claims of an analogous CDW state in ScV₆Sn₆. Combined with the similarities in their electronic structures and the near alignment with the VHS ($M$-point) and Dirac point ($K$-point), this was a reasonable hypothesis. However, we now understand the transition in ScV₆Sn₆ as more analogous to a bond-modulated DW, and can use this knowledge to help interpret the transition in LuNb₆Sn₆.

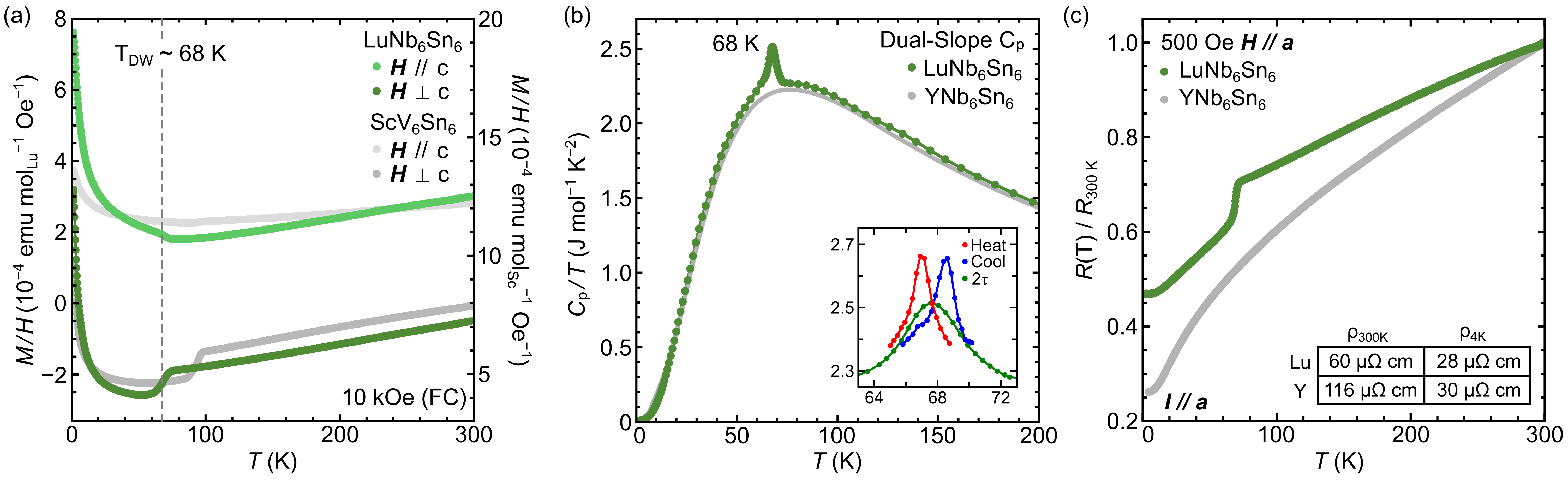
Figure 3(a) shows the magnetic susceptibility for single crystals of LuNb₆Sn₆ (green) measured using a 10 kOe magnetic field. A sample of ScV₆Sn₆ was measured as well (gray) and is included as a reference. A sharp decrease in the susceptibility occurs around 68 K, coinciding with the onset of the DW transition. There is a relatively strong shift in the magnetization between the H $\parallel$ c and H $\perp$ c orientations, which is likely tied to anisotropy of Landau diamagnetism. A similar, albeit weaker effect can be seen in ScV₆Sn₆.

The step in magnetic susceptibility directly corresponds an anomaly in the specific heat (Fig. 3(b)). We have identified that the transition is first-order, with strong differences between data analyzed using the standard $2\tau$ (dual-slope, 2% rise) and data analyzed with the large pulse (single-slope, 20–30% rise) methodology. The inset shows the clear splitting between heating and cooling curves. The 2$\tau$ heat capacity for YNb₆Sn₆, corrected for a small difference in the molar mass of YNb₆Sn₆ and LuNb₆Sn₆ is shown for comparison.

Figure 3(c) shows the electrical resistivity of single crystal LuNb₆Sn₆ polished into a rectangular bar with approximate dimensions of $1\times 0.3\times 0.1$ mm. A precipitous drop in the resistivity is observed at 68 K, corresponding to the susceptibility drop and the heat capacity anomaly. Current was applied along the [100] direction. A weak 500 Oe field was applied along the [001] direction to quench trace superconductivity arising from elemental Sn. The field has no other appreciable effects on the transport. As before, an analogous result on YNb₆Sn₆ is shown for comparison. The data has been scaled according to $R/R_{\text{300~K}}$, but quantitative resistivity values have been provided in the figure as well. Both samples exhibit similar resistivity values at 4 K ($\sim$30 µ$\Omega$ cm), but with different RRR values.

We’ve established the presence of a suspected DW-like, first-order phase transition near 68 K. We now turn to examine the temperature-dependent scattering data for evidence of an emergent superlattice and diffuse scattering. Figure 4 presents a suite of X-ray scattering results for both polycrystalline and single crystal samples of LuNb₆Sn₆. All results are indexed in the standard $1\times 1\times 1$ hexagonal unit cell. Beginning with Fig. 4(a), we examine the temperature dependence of the lattice parameters for both LuNb₆Sn₆ and YNb₆Sn₆. The transition is clear, predominately observed in the abrupt change of the $c$-axis lattice parameter. Remarkably, the $a$-axis is nearly unperturbed, contracting at a rate consistent with the featureless YNb₆Sn₆ reference.

While cooling the sample, yet well above the transition temperature (e.g. 220–100 K), we observed clear evidence of diffuse X-ray scattering by LuNb₆Sn₆. Figure 4(b) presents a slice of the diffuse scattering on the $HK$($L$=9.5) plane (CHESS-QM2 data). A remarkable tiling of hollow triangles appear across the entire dynamic range. The inset shows a higher resolution scan (BNL 21-ID-1) over a smaller range, clearly showing the hollow triangles and highlighting some finer features like the increased scattering intensity on triangle corners. The temperature dependence of the diffuse scattering (Fig. 4(c)) increases in intensity immediately above the phase transition before coalescing into superlattice peaks below 68 K. Intriguingly, we observed that the diffuse pattern arises most strongly on planes where $L=3n+0.5$ (e.g. 6.5, 9.5), nearly vanishes on $L=3n+1.5$ (e.g. 7.5, 10.5), and is only weakly visible on $L=3n+2.5$ (e.g. 8.5, 11.5).

Though the hollow triangles are a feature seemingly unique to LuNb₆Sn₆, to first-order, the diffuse scattering at half integer $L$ is reminiscent of our prior results in ScV₆Sn₆ [34, 31, 149]. We previously revealed that the diffuse scattering in ScV₆Sn₆ could be reproduced using a minimal model of two-dimensional Ising-like displacements of Sn atoms that are frustrated via repulsive strain fields across the kagome network.[149] A rough application of our previous methods with a similar number of interchain interactions did not readily reproduce the hollow triangles, suggesting that a more complex analysis may be needed. However, an in-depth analysis of the diffuse data is beyond the scope of this foundational work.

Figure 4(d,e) show three different slices through reciprocal space to visualize the emergent superlattice that forms at low temperatures. All graphics show the same sample at high temperature (280 K) and deep within the DW phase (50 K) to help omit artifacts from the diffraction experiment (e.g. background, $\lambda$/3 monochromator contamination). Figure 4(d) is a reconstructed slice of the $HHL$ plane,[46] clearly indicating superlattice peaks with a wavevector of (1/3,1/3,1/3). The bright streaks extending from the zone center are artifacts from the $HHL$ reconstruction, and are to be ignored. Figure 4(e) shows two slices through the raw data $HK(L=6.66)$ and $(H=0.66)KL$ to highlight the (1/3,1/3,1/3) wavevector. The superlattice peaks are relatively weak, nearly three orders of magnitude weaker than typical integer Bragg reflections. Note that the streaking in Fig. 4(e) arises from the bleed-over of the much stronger integer $HKL$ reflections into the $H$=0.66 cut.

The refined structural modulation in LuNb₆Sn₆  is essentially identical to that observed in ScV₆Sn₆.[28] We refined the data both using a supercell and a supersymmetry approach. The supercell method indexes the sample using the rotated $\sqrt{3}\times\sqrt{3}\times 3$ supercell, which produces the structural solution in Figure 4(f). For graphical clarity, the displacement of individual atoms has been exaggerated by a factor of 3, and shaded arrows have been added to help indicate the atomic shifts. Owing to the large unit cell, only a slice through the (110) plane has been shown. Similar to ScV₆Sn₆, the primary distortion arises along the Lu1–Sn1–Sn1–Lu1 chains with very little distortion occurring within the kagome network. The superspace approach results in a qualitatively similar result, utilizing the superspace group $P\bar{3}$1$m$(1/3 1/3 $g$)000 and a large crenel-type occupation and sinusoidal displacement modulation for the Lu1 atom and the neighboring Sn1 atom along the $c$-axis.

The bottom of Fig. 4(f) is provided to help visualize the displacements. $\Delta z_{\text{DW}}$ represents the shift in the $z$-coordinate of the atomic position relative to the parent (high-temperature) phase. Positive shifts indicate atoms moving “up” on Fig. 4(f), and negative values indicate atoms moving “down.” The displacements for three different chains are shown (0,0,$z$), (2/3,1/3,$z$), and (1/3,2/3,$z$). As one chain shifts up, the other chains shift down (or remain neutral) to compensate for the shifting strain fields within the material.

Besides the recent search for DW-like distortions in the nonmagnetic kagome metals, one of the hallmark strengths of the AM₆X₆ family is the extraordinary chemical flexibility and choice of magnetic $A$ and $M$ sublattices. Like the LnV₆Sn₆ series, the Nb-based kagome sublattice in the LnNb₆Sn₆  is nonmagnetic, leaving the rare-earth $A$ sublattice to dictate the magnetism. Here we aim to provide a broad, high-level overview of the magnetic properties of the LnNb₆Sn₆ system to help the community identify potentially interesting materials for subsequent studies. As alluded to before, we have observed some deleterious disorder for large rare-earth elements, particularly in the cases of PrNb₆Sn₆ and CeNb₆Sn₆. As a conservative approach, we will only investigate the magnetic properties of the LnNb₆Sn₆ (Ln:Gd–Tm), which are well-described by the HfFe₆Ge₆ structure.

Figure 5 shows a grid of the primary physical property measurements (magnetization, heat capacity, electronic transport) for single crystals of the LnNb₆Sn₆ where (Ln:Gd–Tm). For rapid comparison across the series, we have chosen to normalize several of the units ($M/gJ$, $M/M_{\text{max}}$, and $R/R_{\text{300\,K}}$), where $gJ$ is the expected free-ion saturation magnetization, $M_{\text{max}}$ is the maximum magnetization (peak), and $R_{\text{300\,K}}$ is the resistivity at 300 K. The top row presents the isothermal magnetization at the ³He base temperature ($T=0.4$ K). All compounds effectively saturate to $\pm$5-10% of the expected $gJ$ by a 4-6 T applied field. For each composition we have shown measurements with both H $\parallel$ c and H $\perp$ c, and have further indicated the increasing and decreasing field directions for samples what exhibit field hysteresis.

The second row presents field-cooled cooling (FC-C) temperature-dependent magnetization measurements for the series, and additionally highlights zero-field-cooled cooling (ZFC-C) measurements where a difference betweem FC-C and ZFC-C was noted. Between the step-like metamagnetic isothermal magnetization curves and the temperature-dependent magnetization, it is clear that the majority of the series are low-temperature antiferromagnets with strong anisotropy. Most compounds clearly order by 0.4 K in the exception of ErNb₆Sn₆ and TmNb₆Sn₆. TbNb₆Sn₆ stands apart as a particularly complicated system, even in the context of other Tb-containing AM₆X₆ compounds.[95, 101, 99, 98, 150, 151, 67]

To help visualize the magnetization data, faint gray bars have been drawn through the main features in the temperature-dependent magnetization. Immediately below we have displayed the zero-field heat capacity on the same $\log(T)$ scale to provide rapid comparison of the magnetization data and any corresponding heat capacity anomalies. Each heat capacity plot includes a trace of the nonmagnetic, featureless YNb₆Sn₆ as a lattice comparison. Any relevant phase transitions are included as a linearly scaled inset. To augment the magnetic measurements (which end at 0.4 K) the heat capacity of HoNb₆Sn₆, ErNb₆Sn₆, and TmNb₆Sn₆ were performed using a dilution refrigerator down to approximately 0.1 K to search for any lower temperature transitions. We suspect that ErNb₆Sn₆ may order near 0.15 K, though the convolution with a rare-earth nuclear Schottky peak (which occurs in several of the compounds) impedes a clear determination.

Due to the strong magnetic signatures of the rare-earth compounds, any signatures of potential DW-like behavior in the Gd–Tm compounds would be completely obscured in the magnetization data. Heat capacity measurements should capture any higher temperature transitions, though we can also use the electrical resistivity as a good screening tool given the strong electrical response of LuNb₆Sn₆ at the DW transition. The lowest row of Fig. 5 shows the electrical resistivity normalized to the resistivity at 300 K. Quantitative data for 4 K and 300 K is written in each plot for completeness, though geometrical factors will play a large role in samples of this size (ca. 1$\times$0.3$\times$0.1 mm).

We do not observe any clear signature of DW-like instabilities in the electronic resistivity of the magnetic compounds down to 4 K. Note that the resistivity measurements do not go sufficiently low in temperature to probe the magnetic transition, though we note a curious trend in $R/R_{\text{300K}}$ where large rare-earth compounds exhibit stronger temperature-dependence and higher RRR. The effect reverses as we integrate progressively smaller filler atoms, which may be indicative of a tendency towards the “rattling” instability that ultimately yields the superlattice in LuNb₆Sn₆. Sub-linear resistivity vs temperature in proximity to structural modulations also appears in ScV₆Sn₆ and $A$V₃Sb₅.[152]

Until now, ScV₆Sn₆ was the only member of the HfFe₆Ge₆ family to exhibit a density wave-like transition. Prior work highlighted that Sc was substantially smaller than all other LnV₆Sn₆ compounds, leaving extra room along the chains for the Sn1-Sc-Sn1 trimers[31] to rattle and driving the Sn1-Sn1 bond modulation.[28, 36, 35, 33] The sharp contrast in size between Sc and the next smallest compound (LuV₆Sn₆) made it difficult to compare the effect of a slightly larger atom without alloying. With the introduction of LuNb₆Sn₆ we have a more gradual series of rare-earth sizes, as the size of the next smallest ion (Tm) is only slightly larger than Lu. Yet we are left with the same question; why is LuNb₆Sn₆ the only member of this series to display a structural transition?

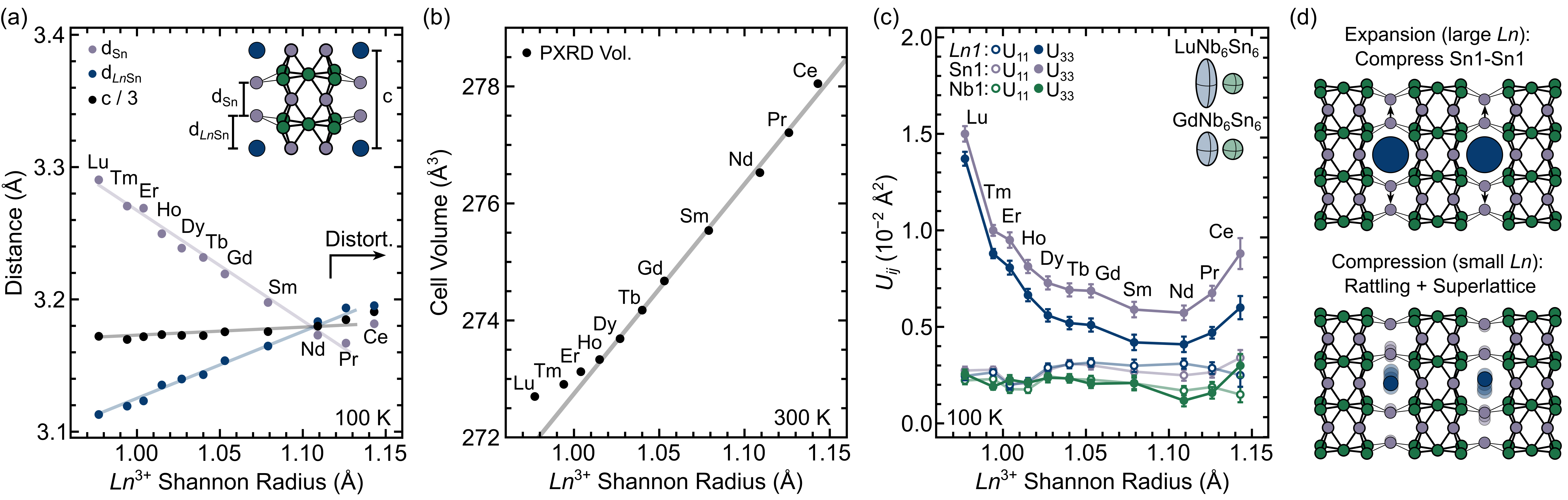
Recall that the AM₆X₆ family of compounds can be thought of as a long-range, ordered, filled variant of CoSn. Large filler atoms intuitively place an expansive pressure on the surrounding lattice, which drives the motion of the Sn1 atoms and the ultimate evolution of the HfFe₆Ge₆ structure (see Fig. 1(a)). Figure 6(a) helps provide a graphical representation of this effect in the LnNb₆Sn₆ series extracted from single crystal diffraction results. Here we show three sets of data: 1) the Sn1-Sn1 bond distance (gray), 2) the $Ln$1-Sn1 bond distance (blue), and 3) 1/3 of the $c$-axis lattice parameter (black). The $c$ lattice parameter is divided by 3 in order to provide a convenient, scaled proxy for the expansion along $c$. Since PrNb₆Sn₆ and CeNb₆Sn₆ still index into the hexagonal $1\times 1\times 1$ unit cell we have opted to include the results, though we caution that their details are unknown and should be viewed cautiously.

The first anomalous observation is the slow expansion of $c$, expanding by only 0.02 Å across the series even though the Shannon radius is 0.13 Å larger.[153] If we considered the atomic positions largely static, this would be an irreconcilable difference, even for a toy model. However, despite the feeble trend in ($c/3$), both the Sn1-Sn1 bond distance ($d_{\text{Sn}}$) and the $Ln$1-Sn1 bond distance ($d_{Ln\text{Sn}}$) show dramatic changes. Notably, the Sn1-Sn1 bond is compressed by 0.12 Å across the series, indicating that the structure accommodates large atoms by preferentially compressing the Sn1-Sn1 bond, which is observed in the $A$V₆Sn₆ series as well.[30]

Clearly the expansive effect of large rare-earth atoms on the $c$ axis is mitigated by the flexible Sn1–Sn1 bonds, but we should still expect a general expansion of the overall lattice. In many rare-earth containing series the cell volume still trends nearly linearly with the Shannon radius of the rare-earth element.[154] However, in contrast to the usual lanthanide trend, Fig. 6(b) reveals a markedly nonlinear plot of cell volume vs Shannon radius. Pawley fits to powder X-ray diffraction data have been used for more accurate lattice parameters. As we integrate smaller rare-earth elements, the volumetric contraction of the lattice progressively slows, which originates from the stunted contraction of the $c$-axis. We suspect that upon switching to small rare-earth species, the structure switches into a different regime, where the rigid Nb–Sn scaffolding (Fig. 1(a)) accommodates the size mismatch, supporting the structure and preventing further collapse.

Panels (a) and (b) of Fig. 6 paint a picture of the rigid Nb-Sn network that supports the lattice and the steric compression of the Sn1–Sn1 bonds through the incorporation of larger filler atoms. Both of these effects should have a strong impact on the thermal motion of the atoms and be strongly reflected in the anisotropic displacement parameters (ADPs). Figure 6(c) presents the single crystal ADPs as a function of the Shannon radius at 100 K. Two of the curves immediately stand apart – $U_{33}$ for both Ln1 and Sn1. These values show a dramatic enhancement for the smallest rare earths, representing increasingly large displacements along the c direction. These large displacements are not seen in the $ab$-plane ($U_{11}$) for Ln1 or Sn1. The Nb1, Sn2, and Sn3 (Sn2, Sn3 not shown) show largely isotropic and small ADPs, supporting our interpretation of the Nb–Sn rigid scaffolding. The inset in Fig. 6(c) depicts the size of the thermal ellipsoids for the rare-earth Lu1 site (light blue) and Nb1 (light green) to scale. The large dynamic displacements of Lu1 and Sn1 in LuNb₆Sn₆ are certainly the origin of the diffuse scattering presented in Fig. 4. Note that the increased ADPs for PrNb₆Sn₆ and CeNb₆Sn₆ are likely a consequence of static site disorder, and not true anisotropic motion.

Figure 6(d) summarizes the how rare earth atoms impact filling of the LnNb₆Sn₆ structure using a schematic of the Nb–Sn scaffolding and exaggerated filler atoms. Yet, a lingering question remains – what is the filling threshold for that leads to the structural modulations observed in the LnNb₆Sn₆ and $A$V₆Sn₆ families? This question was difficult to approach in the ScV₆Sn₆ system, as the difference in size between Sc and the next smallest element (Lu) is quite dramatic. In the LuNb₆Sn₆ system, however, TmNb₆Sn₆ does not exhibit a DW despite the similar size of the Lu and Tm ions. Frustratingly, YbNb₆Sn₆ has not been realized at this time. Thus, we now have the converse problem observed in ScV₆Sn₆ – there are no rare-earth (or rare-earth-like) atoms incrementally smaller than Lu.

Based on the similarities with the ScV₆Sn₆ series,[28, 30] we expect pressure and doping to have profound effects on the DW stability. We predict that the structural transition temperature in LuNb₆Sn₆ will be suppressed by applied pressure due to the compression of the Nb-Sn scaffolding.[155] In addition, doping with different sized rare earths should modify the room available in the $Ln$-Sn1 columns. Therefore, we anticipate scandium doping for Lu should enhance the transition temperature in LuNb₆Sn₆ and Tm should reduce it. Pursuing these avenues forward will direct our research towards our ultimate goal – realizing a DW-like structural modulation in the HfFe₆Ge₆ compounds with a magnetic rare-earth sublattice, allowing us to explore how the atomic shifts modify the exchange coupling between rare earth sites how it potentially impacts the magnetic order.