Stabilizing Linear Systems under Partial Observability:
Sample Complexity and Fundamental Limits
Abstract
We study the problem of stabilizing an unknown partially observable linear time-invariant (LTI) system. For fully observable systems, leveraging an unstable/stable subspace decomposition approach, state-of-art sample complexity is independent from system dimension and only scales with respect to the dimension of the unstable subspace. However, it remains open whether such sample complexity can be achieved for partially observable systems because such systems do not admit a uniquely identifiable unstable subspace. In this paper, we propose LTS-P, a novel technique that leverages compressed singular value decomposition (SVD) on the “lifted” Hankel matrix to estimate the unstable subsystem up to an unknown transformation. Then, we design a stabilizing controller that integrates a robust stabilizing controller for the unstable mode and a small-gain-type assumption on the stable subspace. We show that LTS-P stabilizes unknown partially observable LTI systems with state-of-the-art sample complexity that is dimension-free and only scales with the number of unstable modes, which significantly reduces data requirements for high-dimensional systems with many stable modes.
1 Introduction
Learning-based control of unknown dynamical systems is of critical importance for many autonomous control systems [Beard et al., 1997; Li et al., 2022; Bradtke et al., 1994; Krauth et al., 2019; Dean S. Mania, 2020]. However, existing methods make strong assumptions such as open-loop stability, availability of initial stabilizing controller, and fully observable systems [Fattahi, 2021; Sarkar et al., 2019]. However, such assumptions may not hold in many autonomous control systems. Motivated by this gap, this paper focuses on the problem of stabilizing an unknown, partially-observable, unstable system without an initial stabilizing controller. Specifically, we consider the following linear-time-invariant (LTI) system:
| (1) |
where and are the state, control input, and observed output at time step , respectively. The system also has additive observation noise .
While there are works studying system identification for partially observable LTI systems [Fattahi, 2021; Sun et al., 2020; Sarkar et al., 2019; Oymak and Ozay, 2018b; Zheng and Li, 2020], none of these works address the subsequent stabilization problem; in fact, many assume open-loop stability [Fattahi, 2021; Sarkar et al., 2019; Oymak and Ozay, 2018b]. Other adaptive control approaches can solve the learn-to-stabilize problem in (1) and achieve asymptotic stability guarantees [Pasik-Duncan, 1996; Petros A. Ioannou, 2001], but the results therein are asymptotic in nature and do not study the transient performance.
Recently, in the special case when , i.e. fully-ovservable LTI system, Chen and Hazan [2020] reveals that the transient performance during the learn-to-stabilize process suffers from exponential blow-up, i.e. the system state can blow up exponentially in the state dimension. This is mainly due to that in order to stabilize the system, system identification for the full system is needed, which takes at least samples on a single trajectory, during which the system could blow up exponentially for steps.
To relieve this problem, Hu et al. [2022] proposed a framework of separating the unstable component of the system and stabilizing the entire system by stabilizing the unstable subsystem. This reduces the sample complexity to only grow with the number of the unstable eigenvalues (as opposed to the full state dimension ). This result was later extended to noisy setting in Zhang et al. [2024], and such a dependence on the number of unstable eigenvalues is the best sample complexity so far for the learn-to-stabilize problem in the fully observable case. Compared with this line of work, our work focuses on partially observable systems, which is fundamentally more difficult than the fully observable case. First, partially observable systems typically need a dynamic controller, which renders stable feedback controllers in the existing approach not applicable [Hu et al., 2022]. Second, the construction in “unstable subspace” in Hu et al. [2022] is not uniquely defined in the partially observable case. This is because the state and the matrices are not uniquely identifiable from the learner’s perspective, as any similarity transformation of the matrices can yield the same input-output behavior. Given the above discussions, we ask the following question:
Is it possible to stabilize a partially observable LTI system by only identifying an unstable component (to be properly defined) with a sample complexity independent of the overall state dimension?
Contribution. In this paper, we answer the above question in the affirmative. Firstly, we propose a novel definition of “unstable component” to be a low-rank version of the transfer function of the original system that only retains the unstable eigenvalues. Based on this unstable component, we propose LTS-P, which leverages compressed singular value decomposition (SVD) on a “lifted” Hankel matrix to estimate the unstable component. Then, we design a robust stabilizing controller for the unstable component, and show that it stabilizes the full system under a small-gain-type assumption on the norm of the stable component. Importantly, our theoretical analysis shows that the sample complexity of the proposed approach only scales with the dimension of unstable component, i.e. the number of unstable eigenvalues, as opposed to the dimension of the full state space. We also conduct simulations to validate the effectiveness of LTS-P, showcasing its ability to efficiently stabilize partially observable LTI systems.
Moreover, the novel technical ideas behind our approach are also of independent interest. We show that by using compressed singular value decomposition (SVD) on a properly defined lifted Hankel matrix, we can estimate the unstable component of the system. This is related to the classical model reduction [Dullerud and Paganini, 2000, Chapter 4.6], but our dynamics contain unstable modes with a blowing up Hankel matrix as opposed to the stable Hankel matrix in Dullerud and Paganini [2000] and the system identification results in Fattahi [2021]; Sarkar et al. [2019]; Oymak and Ozay [2018b]. Interestingly, the norm condition on the stable component, derived from the small gain theorem, is a necessary and sufficient condition for stabilization, revealing the required subspace to be estimated in order to stabilize the unknown systems. Such a result not only suggests the optimality of LTS-P but also informs the fundamental limit on stabilizability.
Related Work. Our work is mostly related to adaptive control, learn-to-control with known stabilizing controllers, learn-to-stabilize on multiple trajectories, and learn-to-stabilize on a single trajectory. In addition, we will also briefly cover system identification.
Adaptive control. Adaptive control enjoys a long history of study [Pasik-Duncan, 1996; Petros A. Ioannou, 2001; Chen and Astolfi, 2021]. Most classical adaptive control methods focus on asymptotic stability and do not provide finite sample analysis. The more recent work has started to study non-asymptotic sample complexity of adaptive control when a stabilizing controller is unknown [Chen and Hazan, 2020; Faradonbeh, 2017; Lee et al., 2023; Tsiamis and Pappas, 2021; Tu and Recht, 2018]. Specifically, the most typical strategy to stabilize an unknown dynamic system is to use past trajectory to estimate the system dynamics and then design the controller [Berberich et al., 2020; De Persis and Tesi, 2020; Liu et al., 2023]. Compared with those works, we can stabilize the system with fewer samples by identifying and stabilizing only the unstable component.
Learn to control with known stabilizing controller. Extensive research has been conducted on stabilizing LTI under stochastic noise [Bouazza et al., 2021; Jiang and Wang, 2002; Kusii, 2018; Li et al., 2022]. One branch of research uses the model-free approach to learn the optimal controller [Fazel et al., 2019; Jansch-Porto et al., 2020; Li et al., 2022; Wang et al., 2022; Zhang et al., 2020]. Those algorithms typically require a known stabilization controller as an initialization policy for the learning process. Another line of research utilizes the model-based approach, which requires an initial stabilizing controller to learn the system dynamics for controller design [Cohen et al., 2019; Mania et al., 2019; Plevrakis and Hazan, 2020; Zheng et al., 2020]. On the other hand, we focus on learn-to-stabilize. Our method can be used as the initial policy in these methods to remove their requirement on initial stabilizing controllers.
Learn-to-stabilize on multiple trajectories. There are also works that do not assume open-loop stability and learn the full system dynamics before designing a stabilizing controller while requiring complexity [Dean S. Mania, 2020; Tu and Recht, 2018; Zheng and Li, 2020]. Recently, a model-free approach via the policy gradient method offers a novel perspective with the same complexity [Perdomo et al., 2021]. Compared with those works, the proposed algorithm requires fewer samples to design a stabilizing controller.
Learn-to-stabilize on a single trajectory. Learning to stabilize a linear system in an infinite time horizon is a classic problem in control [Lai, 1986; Chen and Zhang, 1989; Lai and Ying, 1991]. There have been algorithms incurring regret of which relies on assumptions of observability and strictly stable transition matrices [Abbasi-Yadkori and Szepesvári, 2011; Ibrahimi et al., 2012]. Some studies have improved the regret to [Chen and Hazan, 2020; Lale et al., 2020]. Recently, Hu et al. [2022] proposed an algorithm that requires samples. While these techniques are developed for fully observable systems, LTS-P works for partially observable unstable systems, which requires significantly greater technical challenges as detailed above.
System identification. Our work is also related to works in system identification, which focuses on determining the parameters of the system [Oymak and Ozay, 2018a; Sarkar and Rakhlin, 2018; Simchowitz et al., 2018; Xing et al., 2022]. Our work utilizes a similar approach to partially determine the system parameters before constructing the stabilizing controller. While these works focus on identifying the system dynamics, we close the loop and provide state-of-the-art sample complexity for stabilization.
2 Problem Statement
Notations. We use to denote the -norm for vectors and the spectral norm for matrices. We use to represent the conjugate transpose of . We use and to denote the smallest and largest singular value of a matrix, and to denote the condition number of a matrix. We use the standard big , , notation to highlight dependence on a certain parameter, hiding all other parameters. We use , , to mean respectively while only hiding numeric constants.
For simplicity, we primarily deal with the system where . For the case where , we can easily estimate in the process and subtract to obtain a new observation measure not involving control input. We briefly introduce the method for estimating and how to apply the proposed algorithm in the case when in Appendix D.
Learn-to-stabilize. As the unknown system as defined in (1) can be unstable, the goal of the learn-to-stabilize problem is to return a controller that stabilizes the system using data collected from interacting with the system on rollouts. More specifically, in each rollout, the learner can determine and observe for a rollout of length starting from , which we assume for simplicity of proof.
Goal. The sample complexity of stabilization is the number of samples, , needed for the learner to return a stabilizing controller. Standard system identification and certainty equivalence controller design need at least samples for stabilization, as is the number of samples needed to learn the full dynamical system. In this paper, our goal is to study whether it is possible to stabilize the system with sample complexity independent from .
2.1 Background on control
In this section, we briefly introduce the background of -infinity control. First, we define the open loop transfer function of system (1) from to to be
| (2) |
which reflects the cumulative output of the system in the infinite time horizon. Next, we introduce the space on transfer functions in the -domain.
Definition 2.1 (-space).
Let denote the Banach space of matrix-valued functions that are analytic and bounded outside of the unit sphere. Let denote the real and rational subspace of . The -norm is defined as
where the second equality is a simple application of the Maximum modulus principle. We also denote be the complement of the unit disk in the complex domain. For any transfer function , we say it is internally stable if .
The norm of a transfer function is crucial in robust control, as it represents the amount of modeling error the system can tolerate without losing stability, due to the small gain theorem [Zhou and Doyle, 1998]. Abundant research has been done in control design to minimize the norm of transfer functions [Zhou and Doyle, 1998]. In this work, control play an important role as we treat the stable component (to be defined later) of the system as a modeling error and show that the control we design can stabilize despite the modeling error.
3 Algorithm Idea
In this paper, we assume the matrix does not have marginally stable eigenvalues, and the eigenvalues are ordered as follows:
The high-level idea of the paper is to first decompose the system dynamics into the unstable and stable components (Section 3.1), estimate the unstable component via a low-rank approximation of the lifted Hankel matrix (Section 3.2), and design a robust stabilizing for the unstable component that stabilizes the whole system (Section 3.3).
3.1 Decomposition of Dynamics
Given the eigenvalues, we have the following decomposition for the system dynamics matrix:
| (3) |
where , and the columns of are an orthonormal basis for the invariant subspace of the unstable eigenvalues , with inheriting eigenvalues from . Similarly, columns of form an orthonormal basis for the invariant subspace of the unstable eigenvalues and inherit all the stable eigenvalues .
Given the decomposition of the matrix , our key idea is to only estimate the unstable component of the dynamics, which we define below. Consider the transfer function of the original system:
| (8) | ||||
| (13) | ||||
| (18) | ||||
| (19) |
Therefore, the original systrem is an additive decomposition into the unstable transfer function , which we refer to as the unstable component, and the stable transfer function , which we refer to as the stable component.
3.2 Approximate low-rank factorization of the lifted Hankel matrix
In this section, we define a “lifted” Hankel matrix, show it admits a rank approximation, based on which the unstable component can be estimated.
If each rollout has length , we can decompose and estimate the folloing “lifted” Hankel matrix where the -th block is where , . In other words,
| (20) |
for some that we will select later. We call this Hankel matrix “lifted” as it starts with . This “lifting” is essential to our approach, as raising to the power of can separate the stable and unstable components and facilitate better estimation of the unstable component, which will become clear later on.
Define
| (21) | ||||
| (22) |
Then we have the factorization , indicating that is of rank at most .
Rank approximation. We now show that has a rank approximation corresponding to the unstable component. Given the decomposition of in (3), we can write each block of the lifted Hankel matrix as
If is resonably large, using the fact that , we can have . Therefore, we know that when is reasonably large, we have can be approximately factorized as where:
| (23) |
| (24) |
As has columns, has (at most) rank-. We also use the notation
| (25) |
to denote this rank- approximation of Hankel. As from to , the only thing that are omitted are of order , it is reasonable to expect that , i.e. this rank approximation has exponentially decaying error in , as shown in Lemma A.3.
Estimating unstable component of dyamics. In the actual algorithm (to be introduced in Section 4), is to be estimated and therefore not known perfectly.However, to illustrate the methodology of the proposed method, for this subsection, we consider to be known perfectly and show that the unstable component can be recovered perfectly.
Suppose we have the following factorization of for some , (which has infinite possible solutions), We show in Lemma B.1 there exists an invertible , such that:
Therefore, from the construction of in (23) and in (24), we see that , where represent the first block submatrix of .444For row block or column block matrics , we use to denote its ’th block, and to denote the submatrix formed by the ’th block. Solving for for the equation , we can get . After which we can get , and . In summary, we get the following realization of the system:
| (26a) | ||||
| (26b) | ||||
whose transfer function is exactly , the unstable component of the original system.
3.3 Robust stabilizing controller design
After the unstable component is estimated, we can treat the unobserved part of the system as a disturbance and then synthesize a robust stabilizing controller. Suppose we design a controller for , and denote its sensitiviy function as:
Now let’s look at what if we applied the same to the full system in (19). In this case, the closed loop system is stable if and only if the transfer function is analytic for all , see e.g. Chapter 5 of Zhou and Doyle [1998]. Note that,
| (27) |
The Small Gain Theorem shows a necessary and sufficient condition for the system to have a stabilizing controller:
Lemma 3.1 (Theorem 8.1 of Zhou and Doyle [1998]).
Given , the closed loop transfer function defined in (27) is internally stable for any if and only if
We already know is stable and therefore has bounded norm, so it suffices to find a controller such that
| (28) |
in order to stabilize the original full system.
4 Algorithm
Based on the ideas developed in Section 3, we now design an algorithm that learns to stabilize from data. The pseudocode is provided in Algorithm 1.
Step 1: Approximate Low-Rank Lifted Hankel Estimation. Section 3 shows that if defined in (25) is known, then we can design a controller satisfying (28) to stabilize the system. In this section, we discuss a method to estimate with singular value decomposition (SVD) of the lifted Hankel metrix.
Data collection and notation. Consider we sample trajectories, each with length . To simplify notation, for each trajectory , we organize input and output data as
| (29) | ||||
| (30) |
where each are independently selected. We also define the a new matrix for the observation noise as
| (31) |
respectively. To substitute the above into (1), we obtain
| (32) |
We further define an upper-triangular Toeplitz matrix
| (33) |
and we define the following notations:
| (34) |
Note that the lifted Hankel matrix in (20) can be recovered from (34) as they contain the same block submatrices.
Estimation low rank lifted Hankel from measurement. The measurement data (32) in each rollout can be written as
| (35) |
Therefore, we can estimate by the following ordinary least square problem:
| (36) |
We then estimate the lifted Hankel matrix as follows:
| (37) |
Let denote the singular value decomposition of , and we define the -th order estimation of :
| (38) |
where () is the matrix of the top left (right) singular vector in (), and is the matrix of the top singular values in .
Step 2: Esitmating unstable transfer function F. With the SVD , we further do the following factorization:
| (39) |
With the above, we can estimate similar to the procedure introduced in Section 3.2:
| (40) |
To reduce the error of estimating and and avoid compounding error caused by raising to the ’th power, we also directly estimate from both and .
| (41) |
| (42) |
In practice, the estimation obtained from (41) and (42) are very similar, and we can use either one to estimate . Lastly, we estimate and as follows:
| (43) |
where for simplicity, we use to denote the invserse of . We will provide accuracy bounds for those estimations in Section 6. With the above estimations, we are ready to design a controller with the following transfer function.
| (44) |
Step 3: Designing robust controller. After estimating the system dynamics and obtain the estimated transfer function in (44) as discussed in Section 3.3, we can design a stabilizing controller by existing control methods to minimize . The details on how to design the robust controller can be found in robust control documentations, e.g. Chapter 7 of Dullerud and Paganini [2000].
What if is not known a priori? The proposed method requires knowledge of , the number of unstable eigenvalues. If is not known, we show in Lemma 6.1 and Lemma A.3 that the first singular values of and increase exponentially with , and the remaining singular values decrease exponentially with . Therefore, with a reasonably sized and if are chosen to be larger than , there will be a large spectral gap among the singular values of . The learner can use the location of the spectral gap to determine the value of .
5 Main Results
In this section, we provide the sample complexity needed for the proposed algorithm to return a stabilizing controller. We first introduce a standard assumption on controllabilty and observability.
Assumption 5.1.
The LTI system is controllable, and is observable.
We also need an assumption on the existence of a controller that meets the small gain theorem’s criterion (28).
Assumption 5.2.
There exists a controller that stabilizes plant . Further, for some fixed ,
To state our main result, we introduce some system theoretic quantity.
Controllability/observability Gramian for unstable subsystem. For the unstable subsystem , its -observability Gramian is
and its -controllability Gramian is . Per Lemma F.1 and 5.1, we know the subsystem is both controllable and observable, and hence we can select to be the smallest integer such that both are rank-. Note that we always have . Our main theorem will use the following system-theoretic parameters: , (the condition numbers of respectively), and (the smallest singular values of respectively).
Umbrella upper bound . We use a constant to upper bound the norms . We will use the Jordan form decomposition for , and let upper bound . We also use in . Lastly, we use to upper bound the constant in Gelfand’s formula (Lemma F.2) for and . Specifically we will use , , .
With the above preparations, we are ready to state the main theorem.
Theorem 5.3.
Suppose 5.1, 5.2 holds and is diagonalizable. In the regime where , , are small,555This regime is the most interesting and challenging regime. For more general values of , , , see the bound in (125) which takes a more complicated form. we set (recall throughout the paper only hides numerical constants)
and we set (hence each trajectory’s length is and the number of trajectories
for some . Then, with probability at least , obtained by Algorithm 1 stabilizes the original dynamical system (2).
The total number of samples needed for the algorithm is . In the bound in Theorem 5.3, the only constant that explicitly grows with is the controllability/observability index which appears in the bound for . Therefore, the sample complexity grows quadratically with and independent from system state dimension .In the regime , this significantly reduces the sample complexity of stabilization compared to methods that estimate the full system dynamics. To the best of our knowledge, this is the first result that achieves stabilization of unknown partially observable LTI system with sample complexity independent from the system state dimension .
Dependence on system theoretic parameters. As the system becomes less observable and controllable, , increases and decreases, increasing and the sample complexity grows in the order of . Moreover, when are closer to , the sample complexity also increases in the order of . This makes sense as the unstable and stable components of the system would become closer to marginal stability and harder to distinguish apart. Lastly, if the in 5.2 becomes smaller, we have a smaller margin for stabilization, which also increases the sample complexity in the order of .
Non-diagonalization case. Theorem 5.3 assumes is diagonalizable, which is only used in a single place in the proof in Lemma B.1. More specifically, we need to upper bound for some Jordan block and integer , and in the diagonalizable case an upper bound is as the Jordan block is size . In the case that is not diagonalizable, a similar bound can still be proven with dependence on the size of the largest Jordan block of , denoted as . Eventually, this will lead to an additional multiplicative factor in the sample complexity on (cf. (141)), whereas the requirements for is the same. The derivations can be found in Appendix E. In the worst case that ( consists of a single Jordan block), the sample complexity will be worsend to but still independent from .
Necessity of Assumption 5.2. 5.2 is needed if one only estimates the unstable component of the system, treating the stable component as unknown. This is because the small gain theorem is an if-and-only-if condition. If 5.2 is not true, then no matter what controller one designs, there must exist an adversarially chosen stable component (not known to the learner) causing the system to be unstable, even if is perfectly learned. For a specific construction of such a stability-breaking , see the proof of the small gain theorem, e.g. Theorem 8.1 of Zhou and Doyle [1998]. Although Hu et al. [2022]; Zhang et al. [2024] do not explictly impose this assumption, they impose similar assumptions on the eigenvalues, e.g. the in Theorem 4.2 of Zhang et al. [2024], and we believe the small gain theorem and 5.2 is the intrinsic reason underlying those eigenvalue assumptions in Zhang et al. [2024]. We believe this requirement of 5.2 is the fundamental limit of the unstable + stable decomposition approach. One way to break this fundamental limit is that instead of doing unstable + stable decomposition, we learn a larger component corresponding to eigenvalues for some , which effectively means we learn the unstable component and part of the stable component of the system. Doing so, 5.2 will be easier to satisfy as when approaches , will approach . We leave this as a future direction.
Relation to hardness of control results. Recently there has been related work on the hardness of the learn-to-stabilize problem [Chen and Hazan, 2020; Zeng et al., 2023]. Our setting does not conflict these hardness results for the following reasons. Firstly, our result focuses on the regime. In the regime , our result does not improve over other approaches. Secondly, our 5.2 is related to the co-stabilizability concept in Zeng et al. [2023], as 5.2 effectively means the existence of a controller that stabilizes the system for all possible . In some sense, our results complements these results showing when is learn-to-stabilize easy under certain assumptions.
6 Proof Outline
In this section, we will give a high-level overview of the key proof ideas for the main theorem. The full proof details can be found in Appendix A (for Step 1), Appendix B (for Step 2), and Appendix C (for Step 3).
Proof Structure. The proof is largely divided into three steps following the idea developed in Section 3. In the first step, we examine how accurately the learner can estimate the low-rank lifted Hankel matrix . In the second step, we examine how accurately the learner estimates the transfer function of the unstable component from . In the last step, we provide a stability guarantee.
Step 1. We show that obtained in (38) is an accurate estimate of .
Lemma 6.1.
With probability at least , the estimation obtained in (38) satisfies
where is the estimation error for that decays in the order of ; is the error that decays in the order of . See Theorem A.2 and Lemma A.3 for the exact constants.
We later (in Step 2, 3) will show that for a sufficiently small , the robust controller produced by the algorithm will stabilize the system in (1). We will invoke Lemma 6.1 at the end of the proof in Step 3 to pick values that achieve the required (in Appendix C).
Step 2. In this step, we will show that can be estimated up to an error of and up to a similarity transformation, given that .
Lemma 6.2.
The estimated system dynamics satisfies the following bound for some invertible matrix :
where are constants depending on system theoretic parameters, and is a quantity that grows with . See Lemma B.1 for the definition of these quantities.
Lemma 6.3.
Lemma 6.4.
Up to transformation ( is the same as the one in Lemma 6.2), we can bound the difference between and the unstable component of the system as follows:
Step 3. We show that, under sufficiently accurate estimation, the controller returned by the algorithm stabilizes plant and hence is well defined. This is done via the following helper proposition.
Proposition 6.5.
Recall the definition of the estimated transfer function in (44). Suppose the estimation errors are small enough such that . Then, the following two statements hold: (a) If stabilizes and , then stabilizes plant as well; (b) similarly, if stabilizes with , then stabilizes plant as well.
Then, we upper bound and use small gain theorem (Lemma 3.1) to show that the stable mode does not affect stability either, and therefore, the controller stabilizes the full system, in (19). Leveraging the error bounds in Step 2 and Step 1, we will also provide the final sample complexity bound. The detailed proof can be found in Appendix C.
7 Simulations
In this section, we compare our algorithm to the two existing benchmarks: nuclear norm regularization in Sun et al. [2020] and the Ho-Kalman algorithm in Zheng and Li [2020]. We use a more complicated system than (1):
| (45) |
where there are both process noise and observation noise . we fix the unstable part of the LTI system to dimension , i.e. , and observe the effect of increasing dimension on the system. For each dimension , we randomly generate a matrix with unstable eigenvalues and stable eigenvalues . The basis for these eigenvalues is also initialized randomly. In both parts of the simulations, we fix and for the proposed algorithm, LTS-P.
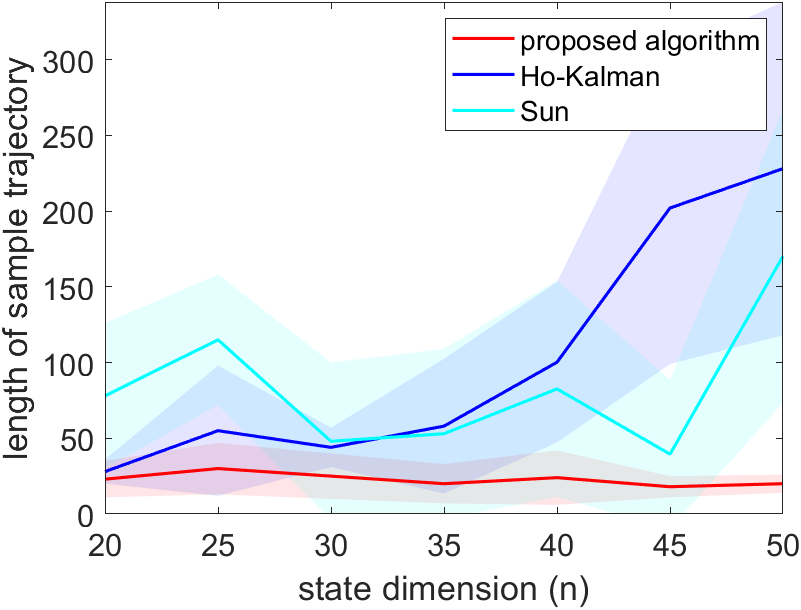
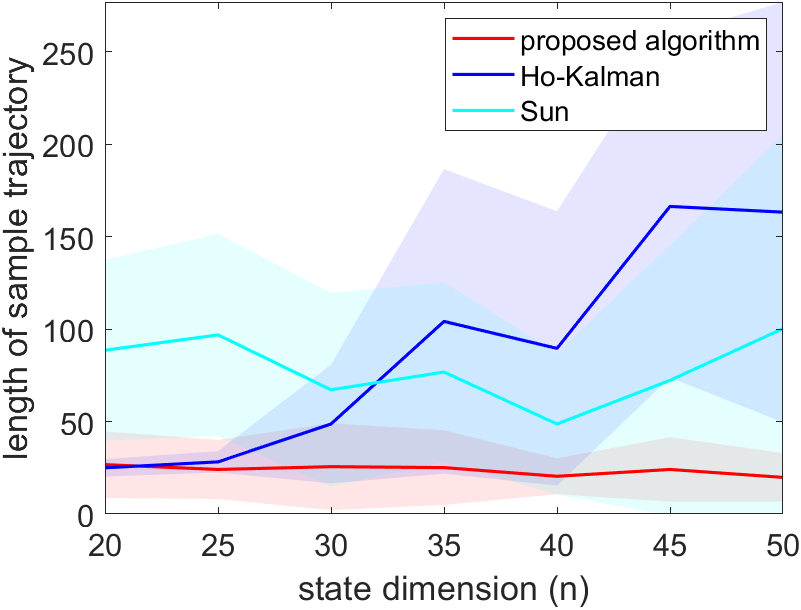
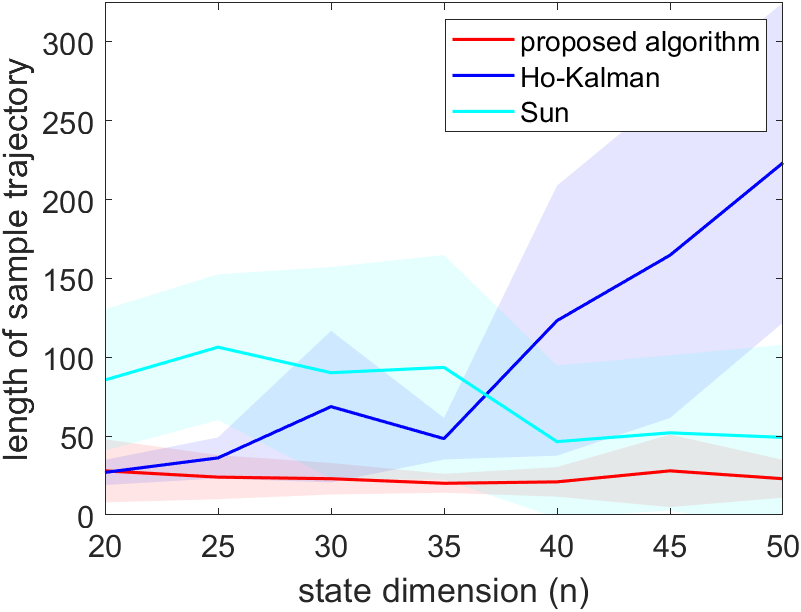
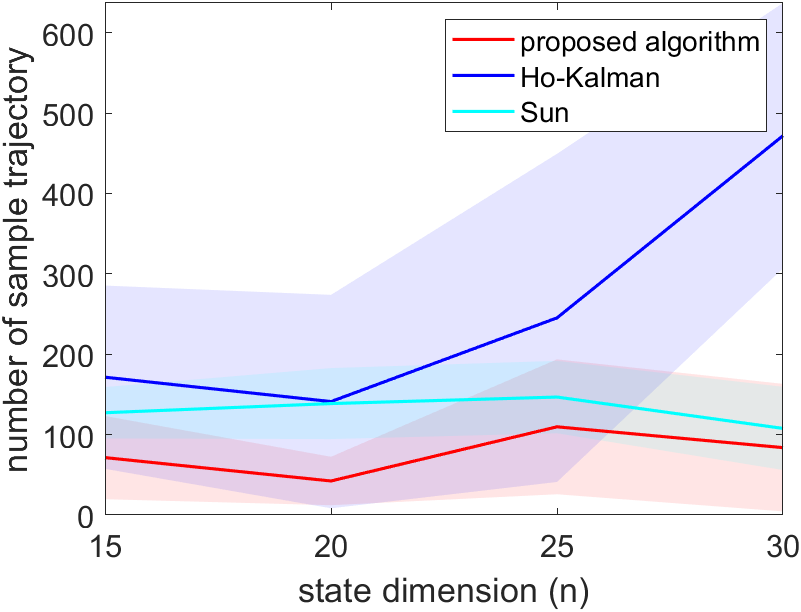
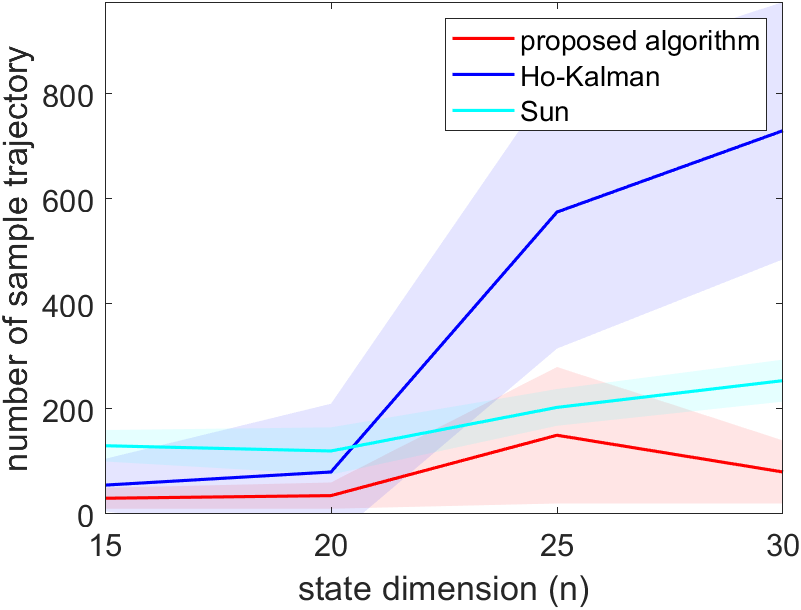
In the first part of the simulations, we fix the number of rollouts to be times the dimension of the system and let the system run with an increasing length of rollouts until a stabilizing controller is generated. The system is simulated in three different settings, each with noise , with . For each of the three algorithms, the simulation is repeated for 30 trails, and the result is shown in Figure 1. The proposed method requires the shortest rollouts. The algorithm in Sun et al. [2020] roughly have the same length of rollouts across different dimensions. This is to be expected, as Sun et al. [2020] only uses the last data point of each rollout, so a longer trajectory does not generate more data. However, unlike the proposed algorithm, Sun et al. [2020] still needs to estimate the entire system, which is why it still needs a longer rollout. The length of the rollouts of Zheng and Li [2020] grows linearly with the dimension of the system. We also see fluctuations of the length of rollouts required for stabilization in Figure 1 because the matrix generated for each has a randomly generated eigenbasis, which influences the amount of data needed for stabilization, as shown in Theorem 5.3. Overall, this simulation shows that the length of rollouts of the proposed algorithm remains regardless of the dimension of the system .
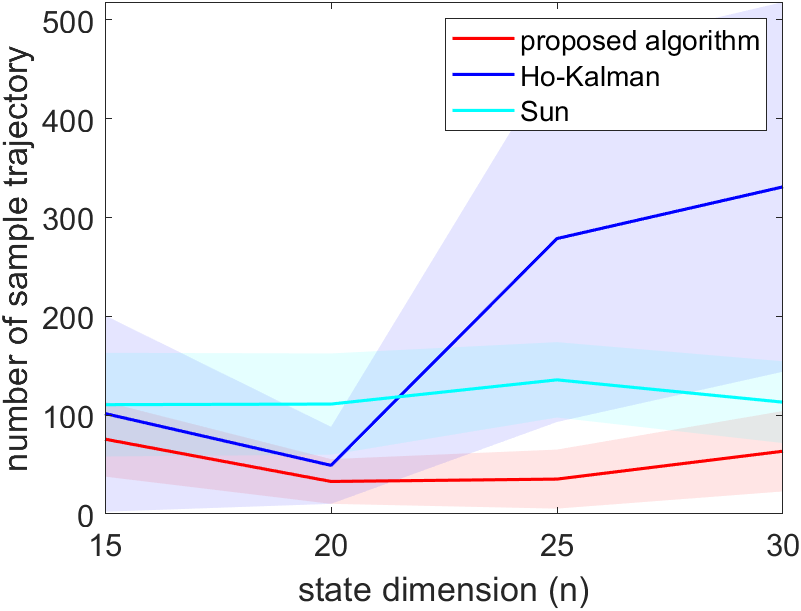
In the second part of the simulation, we fix the length of each trajectory to and examine the number of trajectories needed before the system stabilizes. We do not increase the length of trajectory in this part of the simulation with increasing , since Sun et al. [2020] only uses the last data point, and does not show significant performance improvement with longer trajectories, as shown in the first part of the simulation, so it would be an unfair comparison if the trajectory is overly long. Similar to the first part, the system is simulated in three different settings and the result is shown in Figure 2. Overall, the proposed method requires the least number of trajectories. When the , the proposed algorithm requires a similar number of data with Zheng and Li [2020], as the proposed algorithm is the same to that in Zheng and Li [2020] when . When , the proposed algorithm out-performs both benchmarks.
References
- Abbasi-Yadkori and Szepesvári [2011] Y. Abbasi-Yadkori and C. Szepesvári. Regret bounds for the adaptive control of linear quadratic systems. In S. M. Kakade and U. von Luxburg, editors, Proceedings of the 24th Annual Conference on Learning Theory, volume 19 of Proceedings of Machine Learning Research, pages 1–26, Budapest, Hungary, 09–11 Jun 2011. PMLR.
- Ahlfors [1966] L. V. Ahlfors. Complex Analysis. McGraw-Hill Book Company, 2 edition, 1966.
- Beard et al. [1997] R. W. Beard, G. N. Saridis, and J. T. Wen. Galerkin approximations of the generalized hamilton-jacobi-bellman equation. Automatica, 33(12):2159–2177, 1997. ISSN 0005-1098. doi: https://doi.org/10.1016/S0005-1098(97)00128-3.
- Berberich et al. [2020] J. Berberich, J. Köhler, M. Muller, and F. Allgöwer. Data-driven model predictive control with stability and robustness guarantees. IEEE Transactions on Automatic Control, PP:1–1, 06 2020. doi: 10.1109/TAC.2020.3000182.
- Bouazza et al. [2021] L. Bouazza, B. Mourllion, A. Makhlouf, and A. Birouche. Controllability and observability of formal perturbed linear time invariant systems. International Journal of Dynamics and Control, 9, 12 2021. doi: 10.1007/s40435-021-00786-4.
- Bradtke et al. [1994] S. Bradtke, B. Ydstie, and A. Barto. Adaptive linear quadratic control using policy iteration. Proceedings of the American Control Conference, 3, 09 1994. doi: 10.1109/ACC.1994.735224.
- Chen and Zhang [1989] H.-F. Chen and J.-F. Zhang. Convergence rates in stochastic adaptive tracking. International Journal of Control, 49(6):1915–1935, 1989. doi: 10.1080/00207178908559752.
- Chen and Astolfi [2021] K. Chen and A. Astolfi. Adaptive control for systems with time-varying parameters. IEEE Transactions on Automatic Control, 66(5):1986–2001, 2021. doi: 10.1109/TAC.2020.3046141.
- Chen and Hazan [2020] X. Chen and E. Hazan. Black-box control for linear dynamical systems. CoRR, abs/2007.06650, 2020.
- Cohen et al. [2019] A. Cohen, T. Koren, and Y. Mansour. Learning linear-quadratic regulators efficiently with only regret. In K. Chaudhuri and R. Salakhutdinov, editors, Proceedings of the 36th International Conference on Machine Learning, volume 97 of Proceedings of Machine Learning Research, pages 1300–1309. PMLR, 09–15 Jun 2019.
- De Persis and Tesi [2020] C. De Persis and P. Tesi. Formulas for data-driven control: Stabilization, optimality, and robustness. IEEE Transactions on Automatic Control, 65(3):909–924, 2020. doi: 10.1109/TAC.2019.2959924.
- Dean S. Mania [2020] N. e. a. Dean S. Mania, H. Matni. On the sample complexity of the linear quadratic regulator. Foundations of Computational Mathematics, 20:633–679, 2020. doi: https://doi.org/10.1007/s10208-019-09426-y.
- Dullerud and Paganini [2000] G. E. Dullerud and F. Paganini. A Course in Robust Control Theory. Springer, New York, NY, 2000.
- Faradonbeh [2017] M. K. S. Faradonbeh. Non-Asymptotic Adaptive Control of Linear-Quadratic Systems. PhD thesis, University of Michigan, 2017.
- Fattahi [2021] S. Fattahi. Learning partially observed linear dynamical systems from logarithmic number of samples. In A. Jadbabaie, J. Lygeros, G. J. Pappas, P. A. Parrilo, B. Recht, C. J. Tomlin, and M. N. Zeilinger, editors, Proceedings of the 3rd Conference on Learning for Dynamics and Control, volume 144 of Proceedings of Machine Learning Research, pages 60–72. PMLR, 07 – 08 June 2021.
- Fazel et al. [2019] M. Fazel, R. Ge, S. M. Kakade, and M. Mesbahi. Global convergence of policy gradient methods for the linear quadratic regulator, 2019.
- Horn and Johnson [1985] R. A. Horn and C. R. Johnson. Matrix Analysis. Cambridge University Press, 1985.
- Horn and Johnson [2012] R. A. Horn and C. R. Johnson. Matrix Analysis. Cambridge University Press, USA, 2nd edition, 2012. ISBN 0521548233.
- Hu et al. [2022] Y. Hu, A. Wierman, and G. Qu. On the sample complexity of stabilizing lti systems on a single trajectory. In Neurips, pages 1–2, 2022. doi: 10.1109/Allerton49937.2022.9929403.
- Ibrahimi et al. [2012] M. Ibrahimi, A. Javanmard, and B. V. Roy. Efficient reinforcement learning for high dimensional linear quadratic systems. In Neural Information Processing Systems, 2012.
- Jansch-Porto et al. [2020] J. P. Jansch-Porto, B. Hu, and G. E. Dullerud. Policy learning of mdps with mixed continuous/discrete variables: A case study on model-free control of markovian jump systems. CoRR, abs/2006.03116, 2020. URL https://arxiv.org/abs/2006.03116.
- Jiang and Wang [2002] Z.-P. Jiang and Y. Wang. A converse lyapunov theorem for discrete-time systems with disturbances. Systems & Control Letters, 45(1):49–58, 2002. ISSN 0167-6911. doi: https://doi.org/10.1016/S0167-6911(01)00164-5.
- Krauth et al. [2019] K. Krauth, S. Tu, and B. Recht. Finite-time analysis of approximate policy iteration for the linear quadratic regulator. Advances in Neural Information Processing Systems, 32, 2019.
- Kusii [2018] S. Kusii. Stabilization and attenuation of bounded perturbations in discrete control systems. Journal of Mathematical Sciences, 2018. doi: https://doi.org/10.1007/s10958-018-3848-3.
- Lai [1986] T. Lai. Asymptotically efficient adaptive control in stochastic regression models. Advances in Applied Mathematics, 7(1):23–45, 1986. ISSN 0196-8858. doi: https://doi.org/10.1016/0196-8858(86)90004-7.
- Lai and Ying [1991] T. L. Lai and Z. Ying. Parallel recursive algorithms in asymptotically efficient 496 adaptive control of linear stochastic systems. SIAM Journal on Control and Optimization, 29(5):1091–1127, 1991.
- Lale et al. [2020] S. Lale, K. Azizzadenesheli, B. Hassibi, and A. Anandkumar. Explore more and improve regret in linear quadratic regulators. CoRR, abs/2007.12291, 2020. URL https://arxiv.org/abs/2007.12291.
- Lee et al. [2023] B. D. Lee, A. Rantzer, and N. Matni. Nonasymptotic regret analysis of adaptive linear quadratic control with model misspecification, 2023.
- Li et al. [2022] Y. Li, Y. Tang, R. Zhang, and N. Li. Distributed reinforcement learning for decentralized linear quadratic control: A derivative-free policy optimization approach. IEEE Transactions on Automatic Control, 67(12):6429–6444, 2022. doi: 10.1109/TAC.2021.3128592.
- Liu et al. [2023] W. Liu, Y. Li, J. Sun, G. Wang, and J. Chen. Robust control of unknown switched linear systems from noisy data. ArXiv, abs/2311.11300, 2023.
- Mania et al. [2019] H. Mania, S. Tu, and B. Recht. Certainty equivalence is efficient for linear quadratic control. Proceedings of the 33rd International Conference on Neural Information Processing Systems, 2019.
- Oymak and Ozay [2018a] S. Oymak and N. Ozay. Non-asymptotic identification of lti systems from a single trajectory. 2019 American Control Conference (ACC), pages 5655–5661, 2018a.
- Oymak and Ozay [2018b] S. Oymak and N. Ozay. Non-asymptotic identification of lti systems from a single trajectory. 2019 American Control Conference (ACC), pages 5655–5661, 2018b. URL https://api.semanticscholar.org/CorpusID:49275079.
- Pasik-Duncan [1996] B. Pasik-Duncan. Adaptive control [second edition, by karl j. astrom and bjorn wittenmark, addison wesley (1995)]. IEEE Control Systems Magazine, 16(2):87–, 1996.
- Perdomo et al. [2021] J. C. Perdomo, J. Umenberger, and M. Simchowitz. Stabilizing dynamical systems via policy gradient methods. ArXiv, abs/2110.06418, 2021.
- Petros A. Ioannou [2001] J. S. Petros A. Ioannou. Robust adaptive control. Autom., 37(5):793–795, 2001.
- Plevrakis and Hazan [2020] O. Plevrakis and E. Hazan. Geometric exploration for online control. In Proceedings of the 34th International Conference on Neural Information Processing Systems, NIPS’20, Red Hook, NY, USA, 2020. Curran Associates Inc. ISBN 9781713829546.
- Sarkar and Rakhlin [2018] T. Sarkar and A. Rakhlin. Near optimal finite time identification of arbitrary linear dynamical systems. In International Conference on Machine Learning, 2018.
- Sarkar et al. [2019] T. Sarkar, A. Rakhlin, and M. A. Dahleh. Finite-time system identification for partially observed lti systems of unknown order. ArXiv, abs/1902.01848, 2019.
- Simchowitz et al. [2018] M. Simchowitz, H. Mania, S. Tu, M. I. Jordan, and B. Recht. Learning without mixing: Towards a sharp analysis of linear system identification. Annual Conference Computational Learning Theory, 2018.
- Sun et al. [2020] Y. Sun, S. Oymak, and M. Fazel. Finite sample system identification: Optimal rates and the role of regularization. In A. M. Bayen, A. Jadbabaie, G. Pappas, P. A. Parrilo, B. Recht, C. Tomlin, and M. Zeilinger, editors, Proceedings of the 2nd Conference on Learning for Dynamics and Control, volume 120 of Proceedings of Machine Learning Research, pages 16–25. PMLR, 10–11 Jun 2020.
- Tsiamis and Pappas [2021] A. Tsiamis and G. J. Pappas. Linear systems can be hard to learn. In 2021 60th IEEE Conference on Decision and Control (CDC), pages 2903–2910, 2021. doi: 10.1109/CDC45484.2021.9682778.
- Tu and Recht [2018] S. Tu and B. Recht. The gap between model-based and model-free methods on the linear quadratic regulator: An asymptotic viewpoint. In Annual Conference Computational Learning Theory, 2018.
- Wang et al. [2022] W. Wang, X. Xie, and C. Feng. Model-free finite-horizon optimal tracking control of discrete-time linear systems. Appl. Math. Comput., 433(C), nov 2022. ISSN 0096-3003. doi: 10.1016/j.amc.2022.127400.
- Xing et al. [2022] Y. Xing, B. Gravell, X. He, K. H. Johansson, and T. H. Summers. Identification of linear systems with multiplicative noise from multiple trajectory data. Automatica, 144:110486, 2022. ISSN 0005-1098. doi: https://doi.org/10.1016/j.automatica.2022.110486.
- Zeng et al. [2023] X. Zeng, Z. Liu, Z. Du, N. Ozay, and M. Sznaier. On the hardness of learning to stabilize linear systems. 2023 62nd IEEE Conference on Decision and Control (CDC), pages 6622–6628, 2023.
- Zhang et al. [2020] K. Zhang, B. Hu, and T. Basar. Policy optimization for linear control with robustness guarantee: Implicit regularization and global convergence. In A. M. Bayen, A. Jadbabaie, G. Pappas, P. A. Parrilo, B. Recht, C. Tomlin, and M. Zeilinger, editors, Proceedings of the 2nd Conference on Learning for Dynamics and Control, volume 120 of Proceedings of Machine Learning Research, pages 179–190. PMLR, 10–11 Jun 2020.
- Zhang et al. [2024] Z. Zhang, Y. Nakahira, and G. Qu. Learning to stabilize unknown lti systems on a single trajectory under stochastic noise, 2024.
- Zheng and Li [2020] Y. Zheng and N. Li. Non-asymptotic identification of linear dynamical systems using multiple trajectories. IEEE Control Systems Letters, PP:1–1, 12 2020. doi: 10.1109/LCSYS.2020.3042924.
- Zheng et al. [2020] Y. Zheng, L. Furieri, M. Kamgarpour, and N. Li. Sample complexity of linear quadratic gaussian (lqg) control for output feedback systems. Conference on Learning for Dynamics & Control, 2020.
- Zhou and Doyle [1998] K. Zhou and J. C. Doyle. Essentials of Robust Control. Prentice-Hall, 1998.
Appendix A Proof of Step 1: Bounding Hankel Matrix Error
To further simplify notation, define
| (46) | ||||
| (47) | ||||
| (48) |
so (36) can be simplified to
| (49) |
respectively. An analytic solution to (49) is , where is the right psuedo-inverse of . In this paper, we will use to recover , and we want to bound the error between and .
| (50) |
where the third equality used (35). We can bound the estimation error (50) by
| (51) |
We then prove a lemma that links the difference between and Hankel matrix .
Lemma A.1.
Given two Hankel matrices constructed from with (37), respectively, then
Proof.
We then bound the gap between and by adapting Theorem 3.1 of Zheng and Li [2020]. For completeness, we put the theorem and proof below:
Theorem A.2.
For any , the following inequality holds when with probability at least :
Proof.
By Lemma A.1, we have
Bounding and with Proposition 3.1 and Proposition 3.2 of Zheng and Li [2020] gives the result in the theorem statement. ∎
Lemma A.3.
Proof.
We are now ready to prove Lemma 6.1.
Proof of Lemma 6.1.
We first provide a bound on . As is the rank- approximation of , we have , then
| (56) |
where we use Theorem A.2 and Lemma A.3. Therefore, we obtain the following bound
| (57) |
∎
Appendix B Proof of Step 2: Bounding Dynamics Error
In the previous section, we proved Lemma 6.1 and provided a bound for . In this section, we use this bound to derive the error bound for our system estimation. We start with the following lemma that bounds the difference between and and the difference between and up to a transformation.
Lemma B.1.
Given is diagnalizable, and recall denotes the eigenvalue decomposition of , where is the diagonal matrix of eigenvalues. Consider and , where we recall are obtained by doing SVD and setting (cf. (39)). Suppose , then there exists an invertible -by- matrix such that
-
(a)
and ,
-
(b)
there exists such that , where given in (68),
-
(c)
we can bound and as follows:
Proof.
Proof of part(a). Recall the definition of
We can represent and as follows:
| (58) |
| (59) |
Next, note that
| (60) |
Therefore, we have
| (61) |
where we have defined the matrix above. We can also expand as follows:
| (62) |
Further, the last term in the last equation in (61) can be written as,
| (63) |
Putting (61), (63) together, we have
| (64) |
which proves one side of part (a). To finish part(a), we are left to bound . With the expression of in (62), we obtain
Let so . By (61) and (63), we obtain
| (65) |
and
Therefore, we can obtain the following inequalities:
Substituting (64), we get
where the last inequality requires
| (66) |
which we will verify at the end of the proof of Theorem 5.3 that our selection of algorithm parameters guarantees is true.
Proof of part(b). We first examine the relationship between and . Recall is the maximum of the controllability and observability index. Therefore, the matrix
which is exactly , is full column rank. For any full column rank matrix , let’s denote its Moore-Penrose inverse that satisfies . With this, for nonnegative integer we define the following matrix, which is essentially “divided by” in the Moore-Penrose sense:
| (67) |
As in the main Theorem 5.3 we assumed the is diagonalizable, is a diagonal matrix with possibly complex entries. As such, is a diagonal matrix with all entries having modulus .666This is the only place where the diagonalizability of is used in the proof of Theorem 5.3. If is not diagonalizable, will be block diagonal consisting of Jordan blocks, and we can still bound with dependence on the size of the Jordan block. See Appendix E for more details. Therefore, we have
| (68) |
for all . Recall the condition in the main theorem 5.3 requires . Without loss of generality, we can assume divides and ,777If does not divide or , then the last block in (69) will take a slightly different form but can still be bounded similarly. then and can be related in the following way:
| (69) |
With the above relation, we are now ready to bound the norm of . We calculate
| (70) |
If we examine the middle term , we can expand it as
| (71) |
Using Lemma F.3 on (71), we obtain
Therefore, we can bound :
| (72) |
where we used and , as is the block-diagonal matrix of (cf. (68), (69)). Therefore, plugging (72) into (70), we are ready to bound has follows:
| (73) |
Similarly,
| (74) |
If we further pick such that
| (75) |
(73) and (74) can be simplified as
| (76) |
Proof of part (c). Observe that . Therefore,
Similarly, we have
∎
We are now ready to prove Lemma 6.2
Proof of Lemma 6.2.
Let , by Lemma B.1, . Moreover, and . Given that , we have , where we have used by the condition in the main theorem,
| (77) |
so that is full column rank. Recall is estimated by
| (78) |
Given that , we have
| (79) | ||||
| (80) | ||||
| (81) |
where . Substituting (81) into (78), we obtain
Therefore,
where the last inequality requires (66). ∎
Following similar arguments from the above proof for the estimation of in (41), we have the following collarary.
Corollary B.2.
We have
Proof.
Let , then . Moreover, and . Given that , we have , where we have used by the condition in the main theorem,
| (82) |
so that is full column rank. Recall in (41), we estimate by
| (83) |
Given that , we have
| (84) | ||||
| (85) | ||||
| (86) |
where . Substituting (86) into (83), we obtain
| (87) | ||||
| (88) |
Therefore,
| (89) | ||||
| (90) |
where (89) requires
| (91) |
which we will verify at the end of the proof of Theorem 5.3, and (90) requires (66). ∎
By using an idental argument, we can also prove a similar corollary for . The proof is omitted.
Corollary B.3.
Assuming , we have
With the above two corallaries, we are now ready to prove Lemma 6.3.
Proof of Lemma 6.3.
By the definition of in (23), we have
| (92) |
Furthermore, we recall by the way is estimated in (43), we obtain
| (93) |
Let . Substituting it in (93) leads to
Substituting in (92), we have
| (94) |
By Corollary B.2, we obtain
| (95) | ||||
| (96) | ||||
| (97) |
where (95) is by Lemma B.1 and requires (91), and (97) requires
| (98) |
∎
The proof of Lemma 6.4 undergoes a very similar procedure.
Appendix C Proof of Step 3
Before we analyze the analytic condition of the transfer functions, we need to analyze the values of and on the unit circle through the following lemma:
Lemma C.1.
We have
Proof.
We have that
| (106) |
Moreover,
| (107) |
Substituting (107) into (106), we obtain
| (108) | ||||
| (109) |
where (108) requires , which in turn requires, by Lemma 6.2,
| (110) |
where the last step uses . Eq. (109) uses , which requires
| (111) |
We will verify (110) and (111) at the end of the proof of Theorem 5.3 to make sure it is met by our choice of algorithm parameters. Lastly, substituting and using give the desired result. ∎
We are now ready to prove Proposition 6.5,
Proof of Proposition 6.5.
We only prove part (a). The proof of part (b) is similar and is hence omitted. Suppose is a controller that satisfies the condition in part(a). Our goal is to show this stabilizes , or in other words, is analytic on . Let , we have
Note that to show that is analytic on , we only need to show has the same number of zeros on as that of , because we know is non-singular (i.e. has no zeros) on . Given (110), we also know and has the same number of poles on . By Rouche’s Theorem (Theorem F.4), has the same number of zeros on as if
where the last condition is satisfied by the condition in part (a) of this proposition. Therefore, has no zeros on and the proof is concluded.
∎
We are now ready to prove Theorem 5.3.
Proof of Theorem 5.3.
Suppose for now the number of samples is large enough such that the condition in Proposition 6.5 holds: . At the end of the proof we will provide a sample complexity bound for which this holds.
By 5.2, there exists that stabilizes with
Therefore, by Proposition 6.5, stabilizes plant as well. Therefore, is well defined and can be evaluated by only taking sup over :
| (112) |
where we substituted in 5.2 in the last inequality. In Algorithm 1, we find a controller that stabilizes and minimizes . As stabilizes and satisfies the upper bound in (112), the returned by the algorithm must stabilize and is such that is upper bounded by the RHS of (112). By Proposition 6.5, we know stabilizes as well. Therefore, is well defined and can be evaluated on taking the sup over :
| (113) |
As is such that satisfies the upper bound by the RHS in (112), we have
| (114) |
Therefore, by small gain theorem (Lemma 3.1), we know the controller stabilizes the original full system.
For the remaining of the proof, we analyze the number of samples required to satisfy the condition in Proposition 6.5, i.e.
where the middle step is by Lemma C.1. By Lemma 6.2, Lemma 6.4 and Lemma 6.3, we obtain the following sufficient condition,
By simple computation, we obtain the following sufficient condition:
which can be simplified into the following sufficient condition:
| (115) |
Moreover, we also need to satisfy (66),(75),(98),(105),(110),(111), which requires
| (116) |
A sufficient condition that merges both (115) and (116) is:
| (117) |
Plugging in the definition of , we have , where we recall means the condition number of a matrix. Further, as , we have Therefore, the condition (117) can be replaced with the following sufficient condition
| (118) |
where the above only hides numerical constants.
To meet (77), (82), we set . We also set large enough so that the right hand side of (118) is lower bounded by . Using the simple fact that for , , and replacing with , a sufficient condition for such an is
| (119) |
Recall that . With the above condition on , it now suffices to require . Plugging in the definition of in Theorem A.2,Lemma A.3, we need
| (120) | ||||
| (121) | ||||
| (122) |
To satisfy (121), recall . Let us also require
| (123) |
so that , so we have . Therefore, it suffices to require to satisfy (121).
To satisfy (122), we need
| (124) |
To summarize, collecting the requirements on (119),(123),(124) and also (91), we have the final complexity on :
| (125) | ||||
| (126) |
The final requirement on is,
| (127) |
The final complexity on the number of trajectories is
| (128) |
Lastly, in the most interesting regime that , , is small, we have , , . In this case, (125) can be simplified:
| (129) |
∎
Appendix D System identification when
In the case when in (1), the recursive relationship of the process and measurement data will change from (32) to the following:
| (130) |
Therefore, we can estimate each block of the Hankel matrix as follows:
| (131) |
from which we can easily obtain the matrix and use to design the controller, as in the rest of the main text. Fortunately, from (130), we see that can also be estimated via (36), i.e.
| (132) |
In particular, we see that even in the case where , the estimation error of does not affect the estimation of or . Therefore, the error bound of in Lemma 6.2, Lemma 6.3,Lemma 6.4 still holds. The error of estimating can be bounded as follows:
Lemma D.1 (Corollary 3.1 of Zheng and Li [2020]).
Let denote the first block submatrix in (132), then
where is a constant depending on , the dimension constants , and the variance of control and system noise .
We leave how the estimation error of affects the error bound of stabilization to the future works.
Appendix E Bounding when is not diagonalizable
In proving Theorem 5.3, we used the diagonalizability assumption in Lemma B.1. More specifically, it was used in (67) to upper and lower bound for , which is reflected in the value of . In the diagonalizable case, is a diagonal matrix with all entries having modulus regardless of the value of . Now in the non-diagonalizable case, we bound , provide new values for , and analyze how it affect the final sample complexity.
Consider
| (133) |
where is the number of Jordan blocks, and each is a Jordan block that is either a scalar or a square matrix with eigenvalues on the diagonal, ’s on superdiagona1, and zeros everywhere else.
Without loss of generality, assume is the largest Jordan block with eigenvalue satisfying and size , then , where is the nilpotent super-diagonal matrix of ’s such that for all . Therefore, we have
and
where is the conjugate of . Because has modulus , we have
| (134) |
We can then calculate,
where the second inequality requires , and the last inequality uses . To calculate the smallest singular value, note that is an upper triangular matrix with diagonal entries being , therefore its smallest singular value is lower bounded by . Therefore, we have
| (135) | |||
| (136) |
As such, the constants in (68) need to be modified to
| (137) | |||
| (138) |
This will affect the sample complexity calculation step in (118), which will become
| (139) |
where the only difference is the additional factor in the denominator highlighted in blue. As this factor is only polynomial in , we can merge it with the exponential factor such that
Therefore, (119) will be changed into:
| (140) |
and lastly, the final simplified complexity on will be changed into
| (141) |
which only adds a multiplicative factor in and the additional in the . Given such a change in the bound for , the bound for other algorithm parameters is the same (except for the changes caused by their dependance on ).
Appendix F Additional Helper Lemmas
Lemma F.1.
Given 5.1 is satisfied, then is observable, is controllable.
Proof.
Let denote any unit eigenvector of with eigenvalue , then
Therefore, is an eigenvector of . As is observable, by PBH test, this leads to
By PBH Test, this directly leads to is observable.The controllability part is similar.
∎
Lemma F.2 (Gelfand’s formula).
For any square matrix , we have
In other words, for any , there exists a constant such that
Further, if is invertible, let denote the eigenvalue of with minimum modulus, then
The proof can be found in existing literatures (e.g. Horn and Johnson [2012].
Lemma F.3.
For two matrices , .
Proof.
For the upper bound, notice that
Therefore, we have
| (142) |
For the lower bound, we have
where in the last inequality, we used (142). Rearrange the terms, we get the lower bound.
∎
Theorem F.4 (Rouche’s theorem).
Let be a simply connected domain, and two meromorphic functions on with a finite set of zeros and poles . Let be a positively oriented simple closed curve which avoids and bounds a compact set . If along , then
where (resp. ) denotes the number of zeros (resp. poles) of within , counted with multiplicity (similarly for ).
For proof, see e.g. Ahlfors [1966].