Texas A&M University, College Station, TX 77843, USAbbinstitutetext: Department of Physics, Lehigh University, 16 Memorial Drive East, Bethlehem, PA 18018, USAccinstitutetext: Institute for Mathematics and Institute for Theoretical Physics
Ruprecht-Karls-Universität Heidelberg, 69120 Heidelberg, Germany
Stabilizing massless fields with fluxes in Landau-Ginzburg models
Abstract
Recent work on flux compactifications suggests that the tadpole constraint generically allows only a limited number of complex structure moduli to become massive, i.e., be stabilized at quadratic order in the spacetime superpotential. We study the effects of higher-order terms systematically around the Fermat point in the Landau-Ginzburg model. This model lives at strong coupling and features no Kähler moduli. We show that indeed massless fields can be stabilized in this fashion. We observe that, depending on the flux, this mechanism is more effective when the number of initially massless fields is large. These findings are compatible with both the massless Minkowski conjecture and the tadpole conjecture but are violating the refined version of the tadpole conjecture. Along the way, we complete the classification of integral flux vectors with small tadpole contribution. Thereby we are closing in on a future complete understanding of all possible flux configurations in the Landau-Ginzburg model.
1 Introduction
In the context of string model building, moduli stabilization refers to the lifting of flat directions in the deformation space of string compactifications by symmetry breaking and dynamical effects. It has been at the forefront of research in string phenomenology for more than two decades. The influential early work that proposed various promising scenarios and constructions is reviewed, for example, in Grana:2005jc ; Douglas:2006es ; Blumenhagen:2006ci . Explicit model building has however been hampered by many computational challenges as well as deep conceptual problems. In recent years, the swampland program has emerged as a hopeful guiding principle to disentangle these complications. Reversing the burden of proof, it calls into question the very existence of low-energy effective theories that would naturally be expected as part of the string landscape, but have proven difficult to realize in practice. This encompasses 4-dimensional Anti-de Sitter, Minkowski, and de Sitter vacua with specific conditions on spectrum and interactions. Given the absence of massless scalar fields in our universe, moduli stabilization remains the greatest current challenge among all of these. Continued effort as well as the development of new techniques and approaches are required to tackle this profound problem.
In this paper we continue our study Becker:2006ks ; Becker:2007ee ; Becker:2007dn ; Bardzell:2022jfh ; Becker:2022hse ; Cremonini:2023suw ; Becker:2023rqi of this problem in an orientifold of the Landau-Ginzburg model that is mirror dual to a rigid Calabi-Yau manifold. It describes the compactification on a “non-geometric” Calabi-Yau manifold with . The absence of Kähler moduli makes it an excellent test case in which to study the stabilization of complex structure moduli in type IIB flux compactifications. The seminal GKP construction Giddings:2001yu described how fluxes stabilize the complex structure moduli. Early explicit realizations Giryavets:2003vd ; Denef:2004dm ; Denef:2005mm seemed to confirm the expectation that generic fluxes will stabilize all complex structure moduli. In the last few years this expectation has been examined more closely and called into question. In the concrete example of the sextic Calabi-Yau fourfold, it was observed that there is a tension between satisfying the tadpole constraint and stabilizing all complex structure moduli Braun:2020jrx . This tension has been formalized in the tadpole conjecture in Bena:2020xrh .
The tadpole conjecture states that the fluxes used to stabilize moduli contribute to the D3-brane
tadpole by an amount that grows in an unacceptable way the more moduli one wishes to stabilize. In
quantitative terms, the conjecture says that the number of moduli that are
stabilized111We will discuss the precise definition of this notion momentarily. for a
specific choice of flux, and the contribution of this flux to the D3-brane tadpole
satisfy the constraint222The first version of this paper did not have the factor of 2 in the equation below and concluded that the Landau-Ginzburg model does not seem to violate the refined tadpole conjecture. This factor of 2 arises from us defining the flux tadpole in equation (37) in the covering space following Becker:2006ks . The original tadpole conjecture paper Bena:2020xrh has in equation (2.1) a factor of 1/2 in front of the flux contribution, effectively counting the flux contribution in the quotient space.
The tadpole conjecture was further studied in non-geometric LG models in Becker:2024ayh ; Rajaguru:2024emw , where this point is further clarified. We thank Daniel Junghans for bringing this to our attention.
| (1) |
where the refined tadpole conjecture states that . To preserve supersymmetry, all other contributions to the D3-brane tadpole are positive. They can only be cancelled by the fixed contribution from the orientifold plane. If (1) is correct, this implies that it is not possible to stabilize large numbers of moduli using fluxes.
The tadpole conjecture has been scrutinized extensively in the asymptotics of moduli space Bena:2021wyr ; Bena:2021qty ; Plauschinn:2021hkp ; Lust:2021xds ; Marchesano:2021gyv ; Grana:2022dfw ; Tsagkaris:2022apo ; Coudarchet:2023mmm ; Braun:2023pzd and at special points with discrete symmetries Lust:2022mhk . Our work contributes to a better understanding in the deep interior of moduli space. Related work on the sextic Calabi-Yau fourfold appears in Braun:2023edp .
The quantities and appearing in (1) are of paramount interest for the physics of moduli stabilization. The statement however is in principle of purely Hodge theoretic nature, as pointed out in particular in Grana:2022dfw ; Becker:2022hse . The conjecture is therefore amenable to a completely rigorous analysis. Of course, this depends on a precise definition of the problem, and in particular of the notion of “stabilization of moduli”. As pointed out in Becker:2022hse , this is more subtle than one might naively expect. On a first approach, one might be tempted to simply require that there be no massless fields left in the supersymmetric vacuum. In mathematical terms, this means that the critical point of the superpotential induced by the flux should be non-degenerate. For the purposes of the tadpole conjecture, the quantity would then be defined as the number of erstwhile moduli that have become massive after turning on the flux. Mathematically, this corresponds to the rank of the Hessian at the critical point, and leads to a stronger version of the tadpole conjecture.
| (2) |
Note that we are here (and also in (3) below) being imprecise in the distinction between AdS and Minkowski vacua. In fact, for geometric compactifications, there are the well-known GKP type Minkowski vacua with imaginary self-dual (ISD) fluxes Giddings:2001yu and related AdS vacua with ISD fluxes that appear in the KKLT construction Kachru:2003aw . For non-geometric compactifications, fluxes have to be ISD only for Minkowski vacua that we study in this paper. For AdS vacua fluxes can contribute with either sign to the tadpole cancellation condition Becker:2007dn ; Ishiguro:2021csu ; Bardzell:2022jfh . The tadpole conjecture therefore seems mute in that case.
From the physical point of view, massless scalars could be tolerated as long as all flat directions of the potential are lifted, possibly at higher order in the field expansion. Consider, for example, a massless scalar field subject to a pure potential. Such a field will still mediate long-range forces. However, cosmological solutions in which it rolls at small constant are impossible. Perturbation theory around the vacuum is in principle well-defined. In fact, one expects radiative corrections to render the field massive at very low energies. Mathematically, this means that one should merely require that the critical point of the superpotential be isolated, but allow that it is possibly degenerate. For this weaker version of the tadpole conjecture, one would define as the co-dimension of the critical locus.
| (3) |
We understand, of course, that the critical locus need not be a smooth manifold. It can also consist of several components that intersect at the origin. We will see that this might very well be true in the case at hand. If so, we define as the minimum co-dimension of all these components.
The relation between (2) and (3) follows from the inequality
| (4) |
Namely, (2) requires less for (1) to be true than (3). It is hence more difficult to disprove, and therefore physically stronger in that sense.333In the reverse (mathematical) sense, (3) is stronger since it claims more than (2). The distinction between the two versions does not appear in the original literature cited above. This appears to be due, at least in part, to the absence of any discussion of higher-order terms in the context of moduli stabilization. In our view, it is only the weaker version (3) that, if true, would really jeopardize “stabilization of complex structure moduli by fluxes in the sense of GKP etc.” Some initial considerations of higher-order terms in the model can be found in Becker:2022hse . The main aim of the present work is to analyze this more systematically, in light of the weaker version of the tadpole conjecture. We will find that indeed higher-order terms can stabilize some more massless moduli. For computational reasons, we have not been able to decide whether the critical points first found in Becker:2006ks are degenerate or not. The technique that we develop along the way however is general. It can also be applied in other contexts.
We anticipate some other features and limitations of our analysis. As in previous works, we will study the superpotential around the Fermat point in moduli space. This allows for an easy calculation of the periods as complete power series, and hence the higher-order terms in the superpotential. The analysis around other points in moduli space is possible, but more complicated. We will also restrict the axio-dilaton to . Thus, we are clearly at strong coupling. We can nevertheless perform exact calculations, if we restrict to supersymmetric Minkowski vacua. This is because string loop corrections only enter the Kähler potential Becker:2006ks , while the critical point condition remains holomorphic. The absence of Kähler moduli in the Landau-Ginzburg model entails that if we were able to stabilize all moduli, we would in fact not only disprove the weaker version of the tadpole conjecture, but we would immediately produce Minkowksi vacua of string theory without any flat directions. It is interesting to remark that by itself this would not disprove the recently proposed Massless Minkowski conjecture Andriot:2022yyj . This conjecture states that any supersymmetric vacuum will admit some massless fields. Again, these massless fields do not have to give rise to true flat directions. If the stronger form of the tadpole conjecture, based on (2) remains true, it would imply the persistence of massless fields that could nevertheless be stabilized at higher order.
We will also pursue the classification of flux configurations that can stabilize (some of) the moduli at the Fermat point in the model. This question was also first raised in Becker:2006ks . It arises naturally due to the high rank of the supersymmetric flux lattice. A systematic study was initiated in the recent paper Becker:2023rqi . Specifically, it was explained how to find many linearly independent integral vectors in the flux lattice that have a small tadpole contribution . In particular, this led to a solution of the shortest vector problem for the model. Concretely, using exhaustive computer searches, it was shown that there are no quantized flux solutions that contribute less than to the tadpole cancellation condition. Furthermore, the authors presented a large set of flux configurations that give . In this paper we now present all flux configuration with such a small contribution to the tadpole. For the orientifold the flux contribution is bounded Becker:2006ks . Given that there are probably no flux configuration with and part of the flux configurations have already been classified in Becker:2023rqi , this puts a full classification of all flux configuration for the model within reach.
The outline of the paper is as follows: In section 2 we review the Landau-Ginzburg model and the ingredients of moduli stabilization. In section 3 we describe what is known about the set of supersymmetric 3-form fluxes in the model. In particular, we show that the recent paper Becker:2023rqi covers almost all flux configurations with 8 non-zero components in the -basis (defined in section 2) and . We complete this list. In section 4 we evaluate order by order higher terms in the superpotential and identify the number of massless fields that are stabilized through higher order terms. We summarize our findings in section 5.
2 Review of the model
The mirror dual of a rigid Calabi-Yau threefold, i.e., a CY3 manifold with , would have and hence does not admit a Kähler manifold description. Instead, one can resort to the more general class of orbifoldized Landau-Ginzburg models vafaOrbifoldized , as first studied in the context of moduli stabilization in Becker:2006ks . In general, an Landau-Ginzburg model can be attached to any world-sheet superpotential that is a holomorphic and (weighted-)homogeneous function of a set of chiral fields . The worldsheet action is of the form
| (5) |
Here, is the (worldsheet) Kähler potential. It is conjectured that determines uniquely at the IR fixed point of the renormalization group flow Vafa:1988uu . is therefore not required for the specification of the model. The superpotential itself is invariant along the flow (up to wavefunction renormalization). The central charge of the IR CFT is given by . Here, the are the R-charges of the . They are normalized such that has charge . To construct a 4-dimensional string background, one requires . It is then possible to orbifold by a subgroup of phase symmetries to project the model onto integral R-charges. This ensures a spacetime supersymmetric string background. We will deal exclusively with the simplest such model in this paper. This is the so-called model. It has chiral fields , and superpotential
| (6) |
The orbifold is by a group generated by the following action on the chiral fields:
| (7) |
Here, and throughout this paper, .
In general, the rings formed by chiral and anti-chiral fields in the left- and right-moving sectors of the above superconformal field theory are analogous to cohomology rings of Calabi-Yau manifolds, of dimension equal to the central charge. They correspond to left/right Ramond ground states by spectral flow. Specifically, the ring arises from the states in the untwisted sector of the Hilbert space of the theory, and is given by the invariant part of the Jacobi ring. In the case at hand this is
| (8) |
As a complex vector space, this ring has dimension . It is spanned by monomials of the form
| (9) |
where satisfies for all and . The elements with are the monomials with . They form a basis for the allowed marginal deformations of the superpotential .
| (10) |
The deformation parameters are analogous to complex structure moduli of a geometric compactification. Together with the axio-dilaton they give rise to massless spacetime fields that we wish to stabilize. On the other hand, the Kähler moduli are contained in the ring. This ring arises from the twisted sector of the orbifold. The model orbifolded as in (7) has only two non-trivial twisted sectors. Therefore, the ring contains no marginal deformations. In particular, there is no volume modulus. This is one way to see that the model does not have an interpretation as a geometric compactification manifold.
2.1 Middle-dimensional (co-)homology
Because the model is non-geometric, it is not possible to study Ramond and Neveu-Schwarz fluxes in the usual fashion in the supergravity approximation. However, the vertex operators creating the corresponding spacetime fields still exist in the worldsheet theory. Their interactions with the moduli induce a superpotential completely analogous to the geometric formulation. The fluxes are also subject to the same quantization and tadpole cancellation conditions. We refer to Becker:2006ks for a rigorous justification of these statements. Here, we only broach some ideas, and summarize the results. Crucially, to describe the wrapped fluxes, we require an integral homology basis, and to understand the space-time superpotential and tadpole cancellation, the pairing with cohomology. Physically, one can think of integral homology in terms of supersymmetric cycles wrapped by D-branes. In type IIB, the cycles that can be threaded by fluxes are represented by A-branes. The cycles that support the orientifold planes and carry (the analogues of) the D3/D7-brane tadpole are represented by B-branes.
The undeformed model is an orbifolded tensor product of minimal models with smallest possible central charge . This has a Landau-Ginzburg representation with a single chiral field, and superpotential
| (11) |
The A-branes of this model are represented by contours in the -plane that asymptote to regions in which HoriIqbalVafa . There are three such contours, , shown in Fig. 1 below. These are not independent cycles, but satisfy the one relation,
| (12) |
Under the action (7), they transform as
| (13) |
Somewhat fancily, one can think of the charge lattice of A-branes in the minimal model as fitting into the exact sequence,
| (14) |
where the middle is generated by the , , , and represents the relation (12).
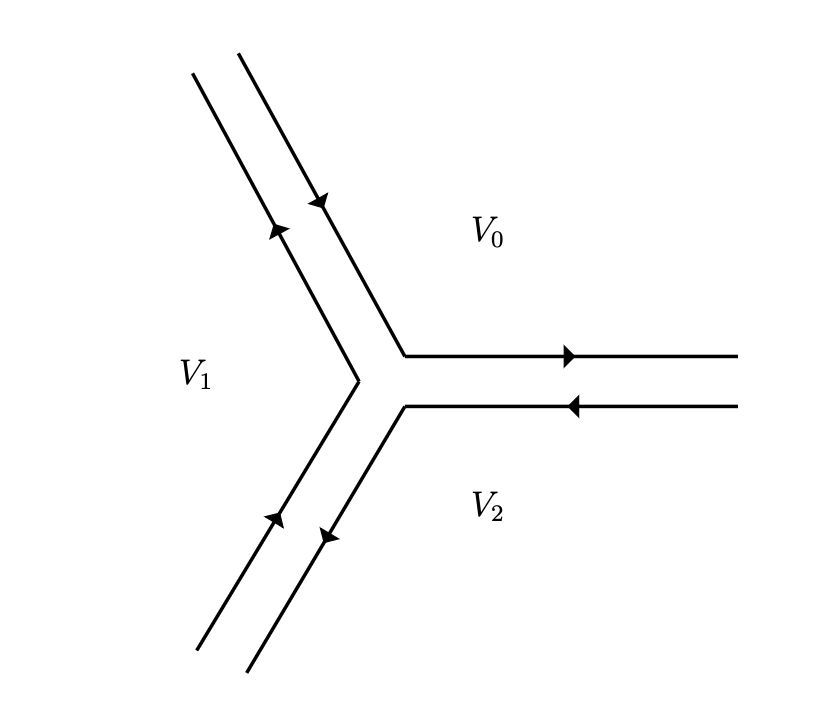
The chiral ring of the minimal model is spanned by the elements . These correspond by spectral flow to Ramond-Ramond ground states traditionally labelled as with
| (15) |
The overlap between these Ramond ground states and the boundary states represented by the (the disk one-point function) can be calculated (after supersymmetric localization) as a contour integral HoriIqbalVafa . Up to normalization, we have
| (16) |
where and . The same integral also calculates the variation of the overlaps under the deformation .
| (17) |
This vanishes when because the integrand is exact in this case. The fact that it does not vanish when (but not ), when formally is zero by the equations of motion, is physically a result of “contact terms” in the operator product expansion. Mathematically, this amounts to integration by parts. The formula (17) will be the basis for the calculation of the higher-order terms in the superpotential in section 4.
To determine the contribution of the fluxes to the D3-brane tadpole, we require the intersection form on the charge lattice. Physically, the intersection of and can be defined as the open string Witten index between the respective branes. Mathematically, it is the geometric intersection between a small counter-clockwise rotation of and HoriIqbalVafa . In matrix form Brunner:1999jq ,
| (18) |
where is the matrix representation of (13). The fact that (18) is neither symmetric nor anti-symmetric reflects that a single minimal model is not yet Calabi-Yau.
The calculations are expedited if one uses the Poincaré duals of the Ramond ground states as basis for the charge lattice. This was emphasized in Becker:2006ks ; Becker:2023rqi . Defining for
| (19) |
with inverse relation
| (20) |
we find from (18)
| (21) |
and
| (22) |
Thus, by comparison with (16),
| (23) |
All these relations are compatible with (12) and when . Eqs. (19) and the reality of the also imply that complex conjugation acts on the via
| (24) |
In combination with (21), this produces the -metric on the RR ground states Cecotti:1991me .
The full orbifoldized model can now be worked out straightforwardly. The Ramond ground states are tensor products labelled as with , , and divisible by in order to satisfy the orbifold projection. These correspond to the basis of the chiral ring (8) by spectral flow and can be classified by Hodge type as shown in table 1.
| 9 | 12 | 15 | 18 | |
|---|---|---|---|---|
An (over-complete) integral basis of cycles is obtained by taking tensor products of the to for , , and summing over images.
| (25) |
where and . On the tensor product of (14),
| (26) |
the action is free except on the very first term, where it is trivial. This shows that the rank of the lattice spanned by the is . This is equal to the dimension of the chiral ring (8). The overlap integrals (16) become
| (27) |
where , and one factor of is owed to (25). The intersection form is obtained by orbifolding the tensor product (18).
| (28) |
In the Poincaré dual basis
| (29) |
the intersection form becomes
| (30) |
We will refer to this as the “-basis”. Complex conjugation acts on it by
| (31) |
where , and . The form (30) is anti-symmetric following the orbifold projection.
2.2 Supersymmetric fluxes and tadpole cancellation
We are now in a position to describe supersymmetric 3-form fluxes in the model. There are two ways to do this. The first is to expand the standard combination of Ramond and Neveu-Schwarz fluxes in terms of the integral cohomology basis given by the . Writing
| (32) |
the should be integer. They are not uniquely determined because the are not linearly independent. The spacetime superpotential induced by this flux is given by the Landau-Ginzburg version of the standard GVW formula Gukov:1999ya
| (33) |
Here, we have used table 1 to identify the holomorphic three-form with the ground state . The overlap should be evaluated with the help of (27). The first (and higher) derivatives of the superpotential with respect to the moduli (including the axio-dilation ) can be evaluated with the help of (17), see subsection 2.3. Setting them to zero will constrain to be of a certain Hodge type as usual. This gives a set of linear equations on the , , which have to be solved over the integers. The precise formula also depends on the spacetime Kähler potential, see section 3.
The alternative approach is to expand in the -basis
| (34) |
This allows to directly constrain its Hodge type by simply setting the undesired to . Flux quantization is equivalent to the condition that in
| (35) |
which is again to be evaluated with (27), the and have to be integer. They are related to the integers in (32) by lowering indices with the help of the symplectic intersection form (28).
The two formulations (32) and (34) are of course equivalent as far as the parametrization of the supersymmetric fluxes is concerned. However, the calculation of the higher-order terms in the superpotential is considerably more efficient in the -basis. We therefore prefer it.
The final ingredients are the orientifold projection and the comparison between the O-plane charge and flux tadpole. These were determined in Becker:2006ks using the general formulas provided in Hori_2008 . We will restrict to the orientifold of the model that is generated by dressing worldsheet parity with the exchange of the first two coordinates. This has to be accompanied by a phase rotation in order to guarantee invariance of the superpotential term in (5). Namely, we are orientifolding by
| (36) |
There are invariant monomials under this orientifold. Including the axio-dilaton, this gives a total of moduli that we wish to stabilize. The above orientifold projection breaks the initial permutation group of the model to a subgroup. We will later use this group to connect different flux configurations. The O-plane associated with the orientifold projection in equation (36) is of “O3-plane type”. Its charge is equal to in natural units. This induces a RR tadpole that must be cancelled by the fluxes that we turn on, as well as possibly adding background D3-branes. The precise condition is that
| (37) |
The overlap of fluxes is to be evaluated with the help of (30) or (31), if working with the -basis.
2.3 The all-order superpotential
By combining (17) with (25), we obtain the following explicit formula for an arbitrary multi-derivative of the space-time superpotential (33) in the -basis
| (38) |
with respect to the deformation parameters in (10) labelled by , with having nine entries, six of which are and three of which are .
| (39) |
Here, as always, , and we have abbreviated with
| (40) |
The normalization in (39) is the same as in (27). Transforming to the -basis
| (41) |
with the help of (29), we find Becker:2022hse
| (42) |
Here, the Kronecker- is understood in all 9 components. Taking account of the product of ’s, we find that the derivative in equation (42) vanishes whenever or mod 3 for any . Since all and are either or , the second condition is equivalent to , where , and . Because has six entries equal to and entries equal to , we can simplify
| (43) |
Moreover, by the functional equation of the Gamma-function, the product is always a rational multiple of . The importance of the result (43) is computational. It means that before calculating the derivative explicitly, we can check whether . This substantially speeds up the calculation of higher order terms. We also note that the derivative does not depend on the individual but rather only on their sum.
We now turn to mixed multi-derivatives involving both complex structure moduli and the axio-dilaton. Since by (33), is linear in , we only need to worry about first partial derivatives with respect to . The derivative with respect to can be calculated from (32) and the reality of , as usual
| (44) |
In the -basis, this reduces a multi-derivative of the type
| (45) |
to (39) with the same ’s, but summed only against ’s. In the -basis, we can use (31) to similarly reduce to (42). However, we have to be careful to take into account that in general the coefficients will be complex numbers and also have to be complex conjugated along the way. For a single complex with we have
| (46) |
Using the result (43), this becomes
| (47) |
where we defined to be the vacuum expectation value of the axio-dilaton. Again, this can be evaluated quite speedily on a computer using only modular arithmetic. Note however that the contributions from are proportional to and are not rationally related to those from .
By combining all of the above, the exact superpotential for a generic flux with complex prefactors becomes
| (48) | ||||
| (49) |
For the purposes of moduli stabilization, this function has to be restricted to the orientifold fixed locus . Following Becker:2023rqi , we do this in practice by ordering the ’s alphabetically and dropping orientifold repetitions. We identify
| (50) |
with and include the axio-dilaton via
| (51) |
This gives us finally a flux-dependent and highly transcendental function of variables whose critical behaviour at the origin is the subject of the following sections.
3 The supersymmetric flux lattice
In most studies of moduli stabilization, one begins with a fixed choice of -form flux within the tadpole bound. The moduli that give rise to vacua preserving spacetime supersymmetry are then solutions of the F-term equations . Here, the index runs over all moduli including the axio-dilaton, . The covariant derivative of the Gukov-Vafa-Witten superpotential (33) depends on the Kähler potential . In geometric compactifications, with the standard dependence of , the moduli have to be adjusted such that is imaginary self-dual (ISD) Giddings:2001yu . This defines a subset in the product of the complex structure moduli space with the upper half-plane that has been called “the supersymmetric locus”. The tadpole conjecture Bena:2020xrh is concerned with the co-dimension of this locus, as explained in the introduction. This is a stringent constraint because, as emphasized in Denef_2004 the tadpole is positive definite for ISD fluxes.
In the setting of the non-geometric Landau-Ginzburg model Becker:2006ks ; Bardzell:2022jfh ; Becker:2022hse , we describe fluxes that are supersymmetric at the Fermat point in moduli space. We also fix the axio-dilaton to a particular value. We call the set of such fluxes the “supersymmetric flux lattice”.444The condition that the flux be invariant under the orientifold will usually be left implicit. For any point on this lattice, the superpotential is critical by definition. We are then interested in the behaviour of the superpotential around that point, in dependence on the contribution to the D3-brane tadpole. An important distinction to the geometric situation, emphasized in Becker:2007dn , is that the Kähler potential needs to be determined by mirror symmetry. Type IIA string theory compactified on a rigid () leads to the Kähler potential for the Kähler moduli and axio-dilaton Grimm:2004ua
| (52) |
Mirror symmetry exchanges the Kähler moduli with complex structure moduli. The Kähler potential is given by
| (53) |
or rather its Landau-Ginzburg analogue, see section 2. Crucially, this differs by a factor of from geometric type IIB compactifications to 4d Grimm:2004uq . As a consequence, the equations do not restrict to be ISD. This was exploited in Becker:2007dn ; Becker:2007ee ; Ishiguro:2021csu ; Becker:2022hse . In this work, we will restrict to supersymmetric Minkowski vacua. This imposes the additional constraint . Then the equations become independent of the Kähler potential. They are not affected by string loop corrections. The candidate instantons that could correct the superpotential are absent Becker:2006ks ; Becker:2007dn ; Kim:2022jvv . The solutions are identical to geometric type IIB compactifications to Minkowski space, , except that in non-geometric settings there are no Kähler moduli and it is in principle possible to stabilize all moduli with fluxes.
3.1 An integral basis of the flux lattice
We will now write out these conditions in terms of the cohomology basis reviewed in section 2. In order to satisfy flux quantization, the coefficients with respect to the integral basis must be integral periods of the torus with complex structure . In order to be supersymmetric, should be purely of Hodge type . In the dual expansions
| (54) |
the , are integer, and the are zero except when . The and are related by (29), (25). If this relation (the “period matrix” of the Landau-Ginzburg model) were completely generic, these conditions would have no non-trivial solution at all. In the situation at hand, in which all period coefficients are integral linear combinations of and , there are very many. More precisely, as observed in Becker:2006ks , there are still no solutions unless the axio-dilaton is of the form
| (55) |
with integer , , , . This is easiest to see by writing the second condition in (54) as unless . For simplicity, we will restrict to . For this choice, it follows from (27) that one may set all but one in (54) to zero. Namely, for any with ,
| (56) |
(but no smaller multiple of ) is an integral flux of type . Here, and from now on, we will replace the subscript ‘3’ on with labels for various explicit solutions. We will indicate their physical characteristics by a superscript as they become available. We observe that and are linearly independent over the integers (in fact, the reals). When or , the flux is invariant under the orientifold (36). Its contribution to the D3-brane tadpole is given by (37) in terms of its length (30),
| (57) |
When , we need to add the respective orientifold image. The tadpole contribution doubles. In total, we obtain linearly independent primitive integral flux vectors
| (58) |
The first entry in the superscript square brackets gives the number of non-zero components in the -basis, and the second, the tadpole contribution. We also use an additional subscript to label different flux choices with the same square bracket superscripts. As a result, the supersymmetric flux lattice in fact has full maximal rank.
All the fluxes in (58) have a tadpole in excess of the orientifold charge (equal to , see (37)). Fluxes with smaller tadpole can be constructed by taking suitable linear (but non-integral!) combinations of (58). For example, one may verify that the flux
| (59) |
where and , is integral for and has tadpole as indicated. The flux
| (60) |
has tadpole , and
| (61) |
which was first found in Becker:2006ks , has tadpole . The latter two fluxes can hence be used to construct supersymmetric Minkowski vacua.
To describe the full set of physical flux configurations (in particular, to enumerate integral flux vectors of tadpole ), it is important to first find an integral basis of the supersymmetric flux lattice consisting of vectors of smallest length possible.555An integral basis of a lattice is a basis of the vector space with respect to which any lattice vector has integral coefficients. Eq. (58) are not an integral basis, because (for example) it does not contain (59) in its -span. Finding lattice vectors of small(est) length in high-dimensional lattices is famously a very hard computational problem. This problem was tackled in Becker:2023rqi , and solved in a two-step process. First, a lucky coincidence that we describe momentarily yields an integral basis containing individual vectors of possibly rather large length. Second, by some judicious computational efforts, one transforms this into another integral basis with smaller lengths. We do not know whether the result is optimal.
The number of ’s of Hodge-type is , and the corresponding complex coefficients in equation (54) parameterize the flux. This amounts to real parameters, which we assemble in a vector of . The flux quantization conditions (35), explicitly
| (62) |
are linear, complex constraints between the and the integers , . (Actually, only of these are independent because of the orientifold.) Separating real and imaginary parts, and viewing the set as coordinatizing integral points , we can recast (62) in terms of a real linear map666It is to be noted that equation (63) are not (real and imaginary parts of) equation (35) on the nose, but a linear transform of it by an invertible matrix. from to as
| (63) |
According to (58), this map hits a lattice of rank inside . In particular, the matrix has full rank . (This is true on general grounds.) We can pick -linearly independent rows from this system. We term the ’s in the corresponding rows independent flux quantum numbers, and denote them . One can then solve the system
| (64) |
to obtain the as linear functions of : . Having done this, it is still a non-trivial demand that the remaining flux numbers are integral. Luckily, this in fact is true, as the linearly dependent equations in (63) are -linear combinations of the independent ones. This means that the columns of are an integral basis of the supersymmetric flux lattice Becker:2023rqi . Many of the elements in this basis have large tadpole values. One would like to swap them for fluxes of smaller length, such as (60), (61) and those presented below. In Becker:2023rqi , it was shown that this can be done via a convenient transformation. This guarantees that the result is still an integral basis. See appendix B of Becker:2023rqi for the explicit list.
Having described the rank and an integral basis, we now turn to the problem of finding the finite set of vectors satisfying the tadpole cancellation condition within the infinite lattice. For a generic flux , the contribution made by each summand to the flux-tadpole is determined completely by its coefficient because of equations (30), (31). Doing this in practice, one finds Becker:2022hse ; Becker:2023rqi that the contribution to the flux tadpole from each turned-on is a homogeneous quadratic in the with positive integer coefficients and hence positive integer-valued. Therefore, to catalogue all physical solutions with , we only need to turn on at most of the ’s. This process has been initiated in Becker:2023rqi where the search for physical solutions was organized by the number of ’s turned on. In the remainder of this section, we summarize some of these results of Becker:2023rqi to get a sense of the flux vectors satisfying the tadpole constraint, and their simplest physical characteristics. We also provide some additional details on the classification of solutions in this model.
3.2 Taxonomy of massive moduli
By construction, the superpotential (48) computed in subsection 2.3
| (65) |
as a function of the moduli remaining after the orientifold and its first derivatives vanish at the origin , for any in the supersymmetric flux lattice described in the previous subsection. The simplest non-trivial physical invariant is the Hessian,
| (66) |
We think of it as the “holomorphic mass matrix”. As shown in Bardzell:2022jfh ; Becker:2022hse , its rank gives the number of moduli that are rendered massive by turning on the flux. This is appearing in the stronger version (2) of the tadpole conjecture. The result is interesting already for the simplest fluxes listed in (58) (which mind you are non-physical because their tadpole is too large). For the “-” fluxes with tadpole , it turns out that when has , the rank of is . When , it is . For the “-” fluxes, i.e., (tadpole ), it is also . For the record, under the symmetry group, the - solutions , organize into distinct orbits, and the - solutions, in three.
We then proceed by increasing the number of non-zero coefficients in . It was found in Becker:2023rqi not to be possible to satisfy the tadpole constraint (37) with - or - fluxes, so we skip the details such as minimum- solutions of these types and the ranks of the corresponding mass matrices. The interested reader may consult Becker:2023rqi . With four ’s one can produce physical fluxes satisfying (37). The smallest value of in this class is , and is attained by precisely distinct orbits of solutions. Representatives from these orbits are given in equations (67), (68), (69).
| (67a) | ||||
| (67f) | ||||
all of which have massive moduli. The solution given in equations (90) and (106) in the next section belongs to the orbit of the first of these with .
| (68a) | ||||
| (68g) | ||||
all of which have massive moduli. The solution given in (104) belongs to the orbit of the first of these with .
| (69a) | ||||
| (69k) | ||||
all of which have massive moduli. The solution given in (105) belongs to the orbit of the first of these with .
Continuing in this way, it is possible to classify all physical solutions in this model given sufficient CPU-hours. We leave this tedious but straightforward task for future work. In anticipation, we have generated a large set of fluxes that are small linear combination of the integral basis vectors, and evaluated their tadpole and mass matrix rank, by the following process: we generated all linear combinations of up to 4 basis vectors with magnitude one coefficients and for these we computed the tadpole and the mass matrix rank. This is shown in Fig. 2, where we plot only results with . By construction this gives small tadpole fluxes but the set of generated fluxes is, of course, only a subset of all possible fluxes for the displayed range of parameters.
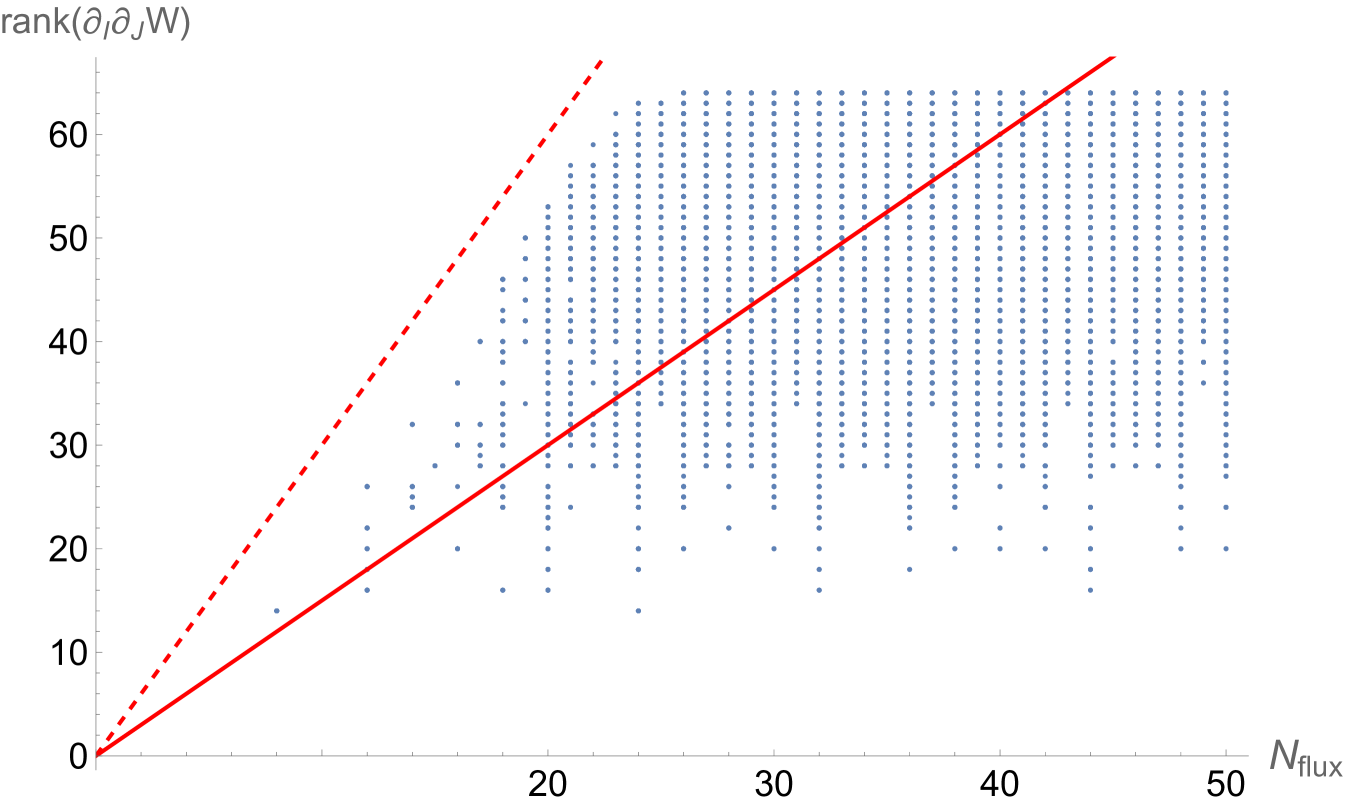
In our data set, the largest mass matrix rank to ratio is . The corresponding flux is
| (70) |
The above flux and many other data points violate the refined tadpole conjecture in equation (1), which required a value smaller than 3/2. However, our data points show a linear relationship as proposed by the tadpole conjecture, albeit with a factor that is closer to 3, see the red dotted line in figure 2.
We find the smallest tadpole contribution of a flux that makes all moduli massive is . (We do however not know whether this is absolutely the smallest possible.) One such solution is given explicitly as
| (71) |
3.3 Complete classification of the shortest vector solutions
In the recent paper Becker:2023rqi , two of the present authors solved the shortest vector problem for the model. This result was derived using the observation that having exactly of the coefficients non-zero in results in a crude lower bound for the flux tadpole: Becker:2022hse . Already in Becker:2006ks the solution , given below in equation (100), was found to have tadpole 8. By turning on up to 7 ’s, an exhaustive search was launched for solutions with tadpole smaller or equal to 7. None was found, proving that 8 is the smallest value of for Minkowski solutions in this model.
To find more solutions that saturate this bound, an Ansatz was made:
| (72) |
where the vectors are indexed in a certain way (see Becker:2023rqi for more details). The space of 8- combinations being too large for an exhaustive search, this simplifying Ansatz was made inspired by the case of 4- solutions where the solutions generating the lowest value belong to families of the form
| (73) |
The flux quantization condition, combined with the Ansatz above, implies that
| (74) |
significantly reducing the number of 8- combinations allowed. An exhaustive search then yielded 14 different 8- solutions with tadpole 8, each having 14 massive moduli. Despite the success in finding solutions, one finds the lack of proper justification of the Ansatz somewhat unsatisfactory. Furthermore, this Ansatz was restricted to only non-orientifold fluxes, meaning vectors of the kind and .
Prompted by this, we have now relaxed this Ansatz and made an exhaustive search through all possible 8- combinations, including cases where one, two, three, or four orientifold fluxes are turned on. We find that the only choices of distinct ’s that can yield tadpole 8 are the ones presented in Becker:2023rqi . Moreover, all solutions arising from one of these 8- choices can be mapped to those from the remaining ones via transformations, which explains why all of the solutions in Becker:2023rqi have the same number of massive moduli. Therefore, it suffices to look for solutions of the form
| (76) | |||||
with , which belong to the first family presented in section 3.2.3 of Becker:2023rqi , such that the flux is properly quantized and has tadpole 8. One finds a set of 162 solutions, which can be further modded by the action of the subgroup of that keeps the choice of the above eight vectors invariant. There are exactly 21 distinct solutions (all of them have massive moduli) up to the action of this stability subgroup. These correspond to:
| (84) |
This leads to the conclusion that, up to the symmetries of the model, there are 21 shortest vectors in this lattice. The solution , found originally in Becker:2006ks and given above in equation (61), is in the orbit of the first solution in (84) with .
4 Moduli stabilization at higher order
In this section, we study the stabilization of massless fields via the higher-order terms in the superpotential that we discussed in subsection 2.3. We will use previously studied flux choices and calculate explicitly the higher-order terms and how they stabilize massless fields.
4.1 The algorithm and its limitations
The main idea, sketched in Becker:2022hse and discussed in detail in the introduction, is to address the tadpole conjecture in its weaker form, in which is defined not as the number of massive moduli, but as the number of fields whose vacuum expectations values are not free parameters, but determined by the field equations, possibly in terms of other fields that themselves remain massless to all orders in the expansion. Mathematically, this is the difference between the Zariski and Krull co-dimension of the critical locus of the superpotential at the origin. To explain this concretely, consider a superpotential
| (85) |
that is known as a (formal or convergent) power series in the erstwhile moduli , including the axio-dilaton as , and assume that corresponds to a supersymmetric Minkowksi vacuum. This just means that the first non-vanishing term in the expansion of is the holomorphic mass matrix from (66), i.e., we have
| (86) |
where is completely symmetric and denotes higher order terms. In the following, we will use the shorthand notation for the terms in that are of order in the . Thus by definition . There are then two key ideas to study the effect of the for on the vacuum structure for arbitrary numbers of fields.
The first point is to shift the focus from the critical point equations as a geometric locus to the Jacobi ring of the space-time superpotential,
| (87) |
Mathematically, is known as the Milnor ring of the function germ defined by . This ring is finite-dimensional as a complex vector space precisely if and only if the origin is an isolated singularity. Physically, (87) contains those physical operators that remain non-trivial and independent after imposing the (static) field equations. This is of course just the space-time analogue of (8). Intuitively, flat directions in , say one parameterized (possibly non-linearly) by a field , will be detected by the infinite number of independent operators , , , …. In principle, the nature of the critical locus, its decomposition into branches, their singularities, etc. is all contained in the algebraic properties of the ring and can be analyzed with standard computer algebra packages. In practice however, this is computationally very expensive when the number of moduli becomes large, and one wishes to obtain exact statements that depend on terms for arbitrary large .
The second idea, then, is to return to a more geometric picture, but proceed order by order in the field expansion. For example, including terms up to gives us equations of the form
| (88) |
where are elements of generated by cubic operators. If has full rank, these equations have a unique solution in the neighborhood of the origin, which is the origin itself. Namely, all moduli have become massive. When is less than maximal, eqs. (88) only allow us to eliminate that many linear combinations of operators, in terms of the remaining ones. This means that the Zariski dimension, intuitively defined as
| (89) |
where and are the elements of generated by linear and quadratic operators, respectively, remains non-zero. Eliminating these linear operators corresponds to “solving” of the equations (88). Doing this, and neglecting any cubic terms as indicated, the remaining equations reduce to a set of quadratic equations in the same number of independent variables. Some of these equations might vanish identically (this happens quite regularly in our examples). Moreover, the number of linearly independent quadratic equations might be larger than the co-dimension of the subspace they cut out.777A most famous example for this phenomenon is the so-called twisted cubic space curve, image of , which is cut out by the three quadrics , , , but no subset of two of these. Alternatively, this can be thought of as eliminating this many quadratic operators in favor of the independent ones. These statements will be modified by the cubic terms in (88) originating from . The linear operators that we eliminated in the first step will acquire cubic terms. The intersection of the non-trivial quadrics will also be deformed. It might go down in dimension in the process. Finally, some of the equations that vanished identically before, might become non-trivial. And so on it goes to higher order.
In practice, we begin by picking a subset of fields , that we eliminate by solving the respective linear equations originating from . These fields could appear either quadratically, like in , in which case we solve by setting or they only appear linearly like in which case we can solve for and for . If say appears in another such term, like , then really is not on the list of ’s and we solve , while remains unstabilized at this order. It is appealing to think of the variables as “massive fields”. Strictly speaking, we can not decide which combination actually acquires a physical mass without knowledge of the Kähler potential. It was shown in Bardzell:2022jfh that the rank of the physical mass matrix is equal to . At the level of counting degrees of freedom, the procedure is completely correct. Although, there is some arbitrariness in the selection of the .
Solving linear equations for the massive fields does not only work at this order but actually extends to all orders. Once we have the linear order solutions , where are linear polynomials in independent, so-far unstabilized fields found by solving all the , we can make the Ansatz and plug this into to get linear equations for the . We can solve these linear equations and find quadratic polynomials in unstabilized fields as solutions for the . We can proceed like this to higher order and solve only linear equations to get , where each of the is a polynomial of -th power in the ’s that are unstabilized at this order. The upshot is that the can easily be solved for and thereby we satisfy all the equations to arbitrary order in for all the massive fields in any given example.
We now focus on the fields that are not massive and their corresponding derivatives of the superpotential. Concretely, by solving for the massive fields above we have ensured that for all when plugging in . However, at cubic order we have to solve . Plugging in solves a subset of these equations, however, generically there remain additional non-trivial quadratic equations that we need to solve. Here things get a bit more complicated. Generically, solving quadratic and higher order equations is a non-algebraic operation. It typically involves taking square roots of other combinations of fields. Luckily, in our examples this never happens. For reasons that can be traced back to the selection rules in (43) and (47), the relevant polynomials always involve a sufficient number of fields that appear only linearly. We can solve for them by merely inverting some of the remaining, independent variables. Similar statements hold at higher order in the expansion, at least as far as we have explored. The only remaining complication is that these solutions might involve different “branches” that need to be studied independently. For example, equations give rise to two components with different numbers of stabilized fields: or .
For the purposes of notation, we append the variables that we thereby eliminate to the list of ’s, but include an additional index that indicates at which order we have done so. Thus, for , corresponding to the massive fields, for those that we eliminate by solving the independent quadratic equations, etc. Note again that the number of ’s with given cannot be deduced from the number of independent non-trivial equations that appear at that order alone, and moreover will depend on the branch on which we are working. We will not introduce explicit notation to distinguish these branches, although this is of course essential in practice. The number of fields that are stabilized up to order will be denoted . Thus, , , etc.
An important observation is that we cannot trivially solve the next higher order by adding quadratic terms to the with . For example, we usually find linear solutions for the quadratic equations: . We can and have to extend those as but when we plug these back into then not all will actually appear. We can only solve a subset of these equations using the because some quadratic equations have terms like , where both . If both then the corresponding , do not appear at all. While this statement seems contrived, this actually does happen in some examples. So, at this stage, things become more complicated but we can generically solve some of the higher-order equations by fixing higher-order terms in already stabilized fields. If there are then still unsolved equations that involve the so far not stabilized fields only, then we stabilize some more fields at this order and proceed to the next higher order.
Given that we start with a finite number of moduli, , initially, the procedure must eventually stabilize, in the sense that there exists an such that for all . This can happen at different times on different branches, but again there is a maximum order after which the only effect can be a change of the explicit shape of the branches, but not their dimension. If on all branches, this means that all fields have been stabilized. Otherwise, the minimum over all branches is what we take as in the weak form (3) of the tadpole conjecture. Mathematically, this corresponds to the Krull co-dimension of the critical locus at the origin.
The algorithm that we just described in principle allows to decide how many moduli are stabilized by any given flux. It can also be applied in other background models. Some of the phenomena that we alluded to however are not easily captured by toy models. So to make the generic discussion more concrete and accessible, we work through the details of a particular example up to cubic order in the model in the next subsection. Then we summarize the results of some further calculations up to order . There are two important challenges.
-
1.
While the formulas of subsection 2.3 allow us to in principle calculate all higher order terms, their number grows quickly. At cubic order, we have just from the 63 complex structure moduli terms, which is easy to calculate. At septic order, there are 1,078,897,248 terms and it becomes problematic to calculate and store them when using a normal laptop.
-
2.
When analysing the stabilization of higher order terms we have to solve . When including cubic terms in we have to solve generically a large number of coupled quadratic equations, which is difficult. At higher order, this would then very quickly become an impossible task. However, we surprisingly find that the higher order polynomials remain usually relatively simple and we can normally solve them without getting square or higher roots. This might be due to the large number of symmetries in this model but it would be important to understand this better.
4.2 A fully worked example
In this subsection we discuss a non-trivial example with massless stabilized fields to cubic order in the superpotential. The flux, which was first presented in Becker:2023rqi is given by
| (90) |
It has and it was shown in Becker:2022hse that it has 16 massive complex scalars and that its cubic terms lead to 10 linearly independent quadratic constraints. Indeed, the quadratic terms in the superpotential (48) being
| (91) |
where
| (92) |
We can easily solve in terms of the sixteen “massive” fields
| (93) |
This fixes for example and . The latter equation shows that there is an ambiguity in which fields we identify as “massive”. However, as mentioned above, without knowledge of the Kähler potential this cannot be resolved. Note that we have already been careful in allowing for higher order terms in the massive fields that will become important once we go to higher order. Concretely for this example the cubic terms in the super potential are
| (94) |
where .
Solving the 16 equations for the 16 massive fields in equation (93), we find up to this order
| (95) |
However when looking at all 64 equations we find the additional ten linearly independent quadratic relations
| (96) |
One can calculate the Groebner basis for the above set of polynomial equations and finds the Krull co-dimension of the ideal to be 6. This means that 6 additional massive fields get stabilized. However, at higher order or in more complicated examples below, it becomes computationally too expensive to do such an analysis and therefore we quickly review how the above equations can be solved explicitly. This leads to different branches or components as briefly mentioned above. Concretely, there are components along which 6 fields are stabilized and others along which seven fields are fixed: Let us look at the fifth equation, solve it, plug the solution in the other equations and keep solving. For ease of presentation we present only two of the different branches that arise:
| (97) | |||
| (98) |
The branch 1) fixes only six fields and the branch 2) fixes seven fields. Given that all branches fix either six or seven fields, one might then be tempted to conclude that there are six stabilized fields and one could discard the other branches with 7 fixed fields. However, there are two reasons to keep track of all different components of solutions: Firstly, it is possible that at higher order the branch with less stabilized fields suddenly stabilizes more fields than another branch. We do not find an explicit example of this below. Secondly, it is possible that we cannot pursue the branch with the lowest number of stabilized fields to higher order because it is too complicated. If one is able to pursue another branch to higher order, then this other branch provides an upper bound on the number of fields that can get stabilized to higher order. We do find an instance of that were we cannot pursue the branch with the smallest number of stabilized fields beyond cubic order but we can pursue another branch up to , thereby providing a useful upper bound on the maximal number of stabilized fields.
4.3 More examples and results
Here we will carry out the above-described procedure for many more explicit examples to higher order and summarize the results. The first example was called in Becker:2022hse and appeared already above in equation (61) but we repeat it here for convenience
| (100) | |||||
The above solution has massive fields and as was observed in Becker:2022hse , there are no further quadratic constraints. So, even when including there are no further stabilized fields at this order, although at this order all 63 complex structure moduli and the axio-dilaton do appear in the superpotential. Surprisingly, we find that the same holds true when including . So, even when including sextic terms in the superpotential we can solve the 64 equations purely in terms of the 14 massive fields of . Given this one might wonder whether one can prove that no further stabilization is possible at all. Clearly, this cannot result from the unstabilized moduli not being present in since they already do all appear in as remarked above. In general, one can prove that all moduli always appear the latest in (see appendix A). Thus, one would have to find a more elaborate proof that shows that (some) flat directions remain because (some) unstabilized fields appear only in a very particular way combined with the massive fields so that to all orders. We did not succeed with this and it is possible that some higher orders are non-zero. We thus leave this as a challenge for the future to study this flux choice to higher order.
Before discussing flux choices that lead to the stabilization of massless fields via higher order terms in , we list more examples (see Becker:2022hse ; Becker:2023rqi ) that exhibit the same behavior as above. The flux choice
| (101) |
leads to and massive fields. The flux choices
| (102) |
| (103) |
have both and 26 massive fields Becker:2022hse .
Two new solutions were presented in Becker:2023rqi that are given by
| (104) | |||||
| (105) |
These solutions and have both and 22 or 26 massive fields, respectively.
For all the solutions , , , , , above we find that no massless fields are being stabilized even when including up to sextic terms in the superpotential .
Now let us look at the more interesting and complicated example
| (106) |
This example was discussed in detail in the previous subsection 4.2 up to cubic order in . As we have seen there, we have to solve 10 linearly independent quadratic equations and can do so without generating square roots since none of the variables appear quadratically. There are different components and they fix either six or seven massless fields. We can now pursue the different components to higher order, keeping in mind that the total number of stabilized fields is the smallest number of fixed fields, which is six in this case up to this order. Since we do not know how many more fields will get stabilized at higher it is worthwhile to keep track of all components.
Concretely, there is one component where we have 16 massive fields plus six stabilized massless fields that allow us to solve the higher order constraints up to . So, for this component, we find no further stabilized fields and have a total of 22 stabilized fields, 16 of which are massive and 6 of which are massless. There are other components where in addition to the 16 massive fields there are , and fixed massless fields. The smallest number of fixed fields is the number of stabilized fields which turns out to be 22 up to order in . We have summarized this in table 2, where a question mark means that we have not been able to solve the corresponding polynomial equations. Note that the model with was not violating the refined tadpole conjecture because it had only 16 massive fields, which is smaller than . However, upon including higher order stabilization all models in table 2 violate the refined version of the tadpole conjecture.
| Model | massive | 3rd power | 4th power | 5th power | 6th power |
| 14 | 0 | 0 | 0 | 0 | |
| 22 | 0 | 0 | 0 | 0 | |
| 26 | 0 | 0 | 0 | 0 | |
| 26 | 0 | 0 | 0 | 0 | |
| 22 | 0 | 0 | 0 | 0 | |
| 26 | 0 | 0 | 0 | 0 | |
| 16 | 6 | 0 | 0 | 0 | |
| 16 | 6 | 0 | 0 | ? | |
| 16 | 6 | 4 | 0 | 0 | |
| 16 | 7 | 1 | 0 | 0 | |
| 16 | 7 | 4 | 0 | 0 | |
| 20 | 2 | 0 | 4 | 1 | |
| 20 | 2 | 0 | 0 | 0 | |
| 18 | 2 | ? | ? | ? | |
| 18 | 4 | 0 | 0 | 0 |
There are two previously discussed solutions Becker:2022hse for which we calculated the higher order terms and for which we also find that there are stabilized but massless fields. For
| (107) |
which has 20 massive fields, we encounter an interesting feature that has not appeared before. While usually, whenever we found no further fixed massless fields at a particular order, then this persisted up until sextic terms in . However, for this solution , we encounter 2 stabilized fields at cubic order and then for a particular component 0 stabilized fields at quartic order, followed again by 4 fixed fields at quintic order and 1 fixed field at sextic order in . It shows explicitly that even if we encounter at a certain low order no further stabilization this could change again at higher order.
The solution below has 18 massive fields
| (108) |
We find that the quadratic equations resulting from cubic terms in give rise to two components. For one component we have four fixed fields and all higher order equations up to sextic terms in are then automatically solved in terms of the higher order terms in the 18 massive and 4 fixed fields. Another component has only 2 stabilized fields but this component is so complicated that we have not been able to solve higher order constraints, leading to the question marks in the table. This example exemplifies an interesting point. We would say that we have 18 massive and 2 stabilized massive fields at cubic order in . It is in principle possible that more fields get stabilized if we were able to pursue the first component to quartic or quintic order. However, from the last row in the table we know that even when going to sextic power in the superpotential we cannot stabilized more than 4 massless fields in this model.
We have also calculated cubic, quartic and quintic terms for the solution above that has the largest mass matrix rank to tadpole contribution and that is given above in (70). Note this is not a physical solution since . We find that there are no further stabilized fields up to quintic order in the superpotential. This is in line with the empirical observation from table 2 that models with the largest mass matrix rank do not have fields that get stabilized at higher order in this model.
5 Conclusion
In this paper we have continued the study of an orientifold of the Landau-Ginzburg model. The shortest vector problem in this model was solved in Becker:2023rqi . Specifically, it was shown that any (non-zero) quantized -flux in contributes at least to the tadpole cancellation condition: . In a convenient basis one can write the flux as and each non-zero flux component will contribute at least 1 to . Thus, any quantized flux configuration in this model can have at most 12 non-zero flux components Becker:2022hse . An exhaustive search in Becker:2023rqi proved that quantized flux solutions only exist for 4, 8 or more non-zero flux components. Furthermore, all solutions with 4 components were classified and a large class of 8 flux component solutions was presented. In this paper we have proven that this large class actually contains all 8 flux component solutions. These solutions are all related by an symmetry that is preserved after the orientifold projection so that there is essentially only one such solution with 8 flux components. There are no known solutions with 9, 10 and 11 flux components but several different ones with 12 flux components. It remains an important challenge for the future to fully classify the flux configurations with 12 flux components and to prove the absence of solutions with 9, 10 or 11 components or to find such solutions. However, the full classification of all possible flux configurations in this model seems now to be within reach.
Given the importance of moduli stabilization in trying to connect string theory to the real world, 4d Minkowski vacua in this model were studied in Becker:2022hse . It was found that all known solutions and some newly constructed ones have a large number of massless moduli. Out of the 64 complex scalar fields only between 14 and 26 were massive due to the presence of the fluxes Becker:2022hse . In this paper we have generated a large number of flux configuration with relatively small tadpole and calculated the number of massive fields. The scatter plot above in figure 2 shows the tadpole contribution vs the the number of massive fields. We find a linear behavior as predicted by the tadpole conjecture but some of our solutions violate the refined version of the tadpole conjecture. For solutions within the tadpole bound we find and more generically we find a solution with that violates the refined tadpole conjecture by almost a factor of 2.
Lastly, we developed a procedure for systematically calculating higher order terms in the superpotential and checking whether there are massless fields that are stabilized in these Minkowski vacua. In addition to the eight different solutions discussed in Becker:2022hse , we performed such a study of higher order stabilization for two more solutions from Becker:2023rqi . In the latter paper it was found that the flux configuration with only four flux components come in three families with either 16, 22 or 26 massive fields. We have included one representative from all three of those, a representative from the single family with eight flux components discussed above and several solutions with twelve flux components. Thereby making this a relatively complete set of examples.
Our findings are summarized in table 2 above and are interesting in many aspects. First, we actually find that some flux configurations do not stabilize massless fields via higher terms in the superpotential, even when including cubic, quartic, quintic and sextic terms. This might be due to the large symmetry group of this model and it would be interesting to understand better Grimm:2024fip . For setups where higher order constraints appear, we are faced with solving polynomial equations in many variables and one might have expected that this is an insurmountable task. However, we actually found that these constraint equations are often solvable and they lead to the stabilization of several massless fields. We have found three example where massless fields get stabilized when including up to sextic terms in the superpotential. The total number of stabilized fields is then in all examples larger than the maximum number allowed by the refined version of the tadpole conjecture. Given that there is an infinite number of higher order terms in the superpotential it is not clear whether and how many more moduli will be stabilized at even higher order. We are currently at the limit of what can be calculated with a normal computer and it would be interesting to use more powerful computers or to develop more sophisticated techniques to extend our result to higher order. We leave this as an exciting challenge for the future.
Acknowledgments
We would like to thank James Gray and Daniel Junghans for useful discussions, and Mariana Graña for valuable feedback on an initial draft. The work of KB and AS is supported in part by the NSF grant PHY-2112859. MR acknowledges the support of the Dr. Hyo Sang Lee Graduate Fellowship from the College of Arts and Sciences at Lehigh University. The work of MR and TW is supported in part by the NSF grant PHY-2210271. This research was supported in part by grant NSF PHY-2309135 to the Kavli Institute for Theoretical Physics (KITP). JW thanks the International Centre for Mathematical Sciences, Edinburgh, for support and hospitality during the ICMS Visiting Fellows programme where this work was completed. This work was supported by EPSRC grant EP/V521905/1. This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2181/1 — 390900948 (the Heidelberg STRUCTURES Excellence Cluster).
Appendix A Proof that all appear in
Given that it is difficult to stabilize all fields, one might ask whether one can show that flat directions arise due to the simple fact that some fields do not appear in the superpotential at all. This is however not the case and in this appendix, we prove that the dilaton and all 63 complex structure moduli do appear (at higher order) in for any non-zero flux choice.
Let us assume that we turn on some flux and generate thereby a mass term for some fields, i.e., we assume that for some . This is true for any non-zero flux choice and implies from equation (40) above that
| (109) |
Now we ask whether a exists that does not appear in . The answer is no as can be seen as follows: Since contains only 0’s and 1’s we have that . So at quintic order in the superpotential, there is a term proportional to since we have
| (110) |
Thus at quintic order, every will appear for sure. However, it will do so in a rather simple way multiplied by terms that already appeared at quadratic order and thus these terms cannot really stabilize . In concrete examples, we usually find that all fields already appear when including quartic terms in .
References
- (1) M. Grana, Flux compactifications in string theory: A Comprehensive review, Phys. Rept. 423 (2006) 91 [hep-th/0509003].
- (2) M.R. Douglas and S. Kachru, Flux compactification, Rev. Mod. Phys. 79 (2007) 733 [hep-th/0610102].
- (3) R. Blumenhagen, B. Kors, D. Lust and S. Stieberger, Four-dimensional String Compactifications with D-Branes, Orientifolds and Fluxes, Phys. Rept. 445 (2007) 1 [hep-th/0610327].
- (4) K. Becker, M. Becker, C. Vafa and J. Walcher, Moduli Stabilization in Non-Geometric Backgrounds, Nucl. Phys. B 770 (2007) 1 [hep-th/0611001].
- (5) K. Becker, Y.-C. Chung and G.-Y. Guo, Metastable Flux Configurations and de Sitter Spaces, Nucl. Phys. B 790 (2008) 240 [0706.2502].
- (6) K. Becker, M. Becker and J. Walcher, Runaway in the Landscape, Phys. Rev. D 76 (2007) 106002 [0706.0514].
- (7) J. Bardzell, E. Gonzalo, M. Rajaguru, D. Smith and T. Wrase, Type IIB flux compactifications with h1,1 = 0, JHEP 06 (2022) 166 [2203.15818].
- (8) K. Becker, E. Gonzalo, J. Walcher and T. Wrase, Fluxes, vacua, and tadpoles meet Landau-Ginzburg and Fermat, JHEP 12 (2022) 083 [2210.03706].
- (9) S. Cremonini, E. Gonzalo, M. Rajaguru, Y. Tang and T. Wrase, On asymptotic dark energy in string theory, JHEP 09 (2023) 075 [2306.15714].
- (10) K. Becker, N. Brady and A. Sengupta, On fluxes in the 19 Landau-Ginzburg model, JHEP 11 (2023) 152 [2310.00770].
- (11) S.B. Giddings, S. Kachru and J. Polchinski, Hierarchies from fluxes in string compactifications, Phys. Rev. D 66 (2002) 106006 [hep-th/0105097].
- (12) A. Giryavets, S. Kachru, P.K. Tripathy and S.P. Trivedi, Flux compactifications on Calabi-Yau threefolds, JHEP 04 (2004) 003 [hep-th/0312104].
- (13) F. Denef, M.R. Douglas and B. Florea, Building a better racetrack, JHEP 06 (2004) 034 [hep-th/0404257].
- (14) F. Denef, M.R. Douglas, B. Florea, A. Grassi and S. Kachru, Fixing all moduli in a simple f-theory compactification, Adv. Theor. Math. Phys. 9 (2005) 861 [hep-th/0503124].
- (15) A.P. Braun and R. Valandro, flux, algebraic cycles and complex structure moduli stabilization, JHEP 01 (2021) 207 [2009.11873].
- (16) I. Bena, J. Blåbäck, M. Graña and S. Lüst, The tadpole problem, JHEP 11 (2021) 223 [2010.10519].
- (17) K. Becker, N. Brady, M. Graña, M. Morros, A. Sengupta and Q. You, Tadpole conjecture in non-geometric backgrounds, JHEP 10 (2024) 021 [2407.16758].
- (18) M. Rajaguru, A. Sengupta and T. Wrase, Fully stabilized Minkowski vacua in the 26 Landau-Ginzburg model, JHEP 10 (2024) 095 [2407.16756].
- (19) I. Bena, J. Blåbäck, M. Graña and S. Lüst, Algorithmically Solving the Tadpole Problem, Adv. Appl. Clifford Algebras 32 (2022) 7 [2103.03250].
- (20) I. Bena, C. Brodie and M. Graña, D7 moduli stabilization: the tadpole menace, JHEP 01 (2022) 138 [2112.00013].
- (21) E. Plauschinn, The tadpole conjecture at large complex-structure, JHEP 02 (2022) 206 [2109.00029].
- (22) S. Lüst, Large complex structure flux vacua of IIB and the Tadpole Conjecture, 2109.05033.
- (23) F. Marchesano, D. Prieto and M. Wiesner, F-theory flux vacua at large complex structure, JHEP 08 (2021) 077 [2105.09326].
- (24) M. Graña, T.W. Grimm, D. van de Heisteeg, A. Herraez and E. Plauschinn, The tadpole conjecture in asymptotic limits, JHEP 08 (2022) 237 [2204.05331].
- (25) K. Tsagkaris and E. Plauschinn, Moduli stabilization in type IIB orientifolds at h2,1 = 50, JHEP 03 (2023) 049 [2207.13721].
- (26) T. Coudarchet, F. Marchesano, D. Prieto and M.A. Urkiola, Symmetric fluxes and small tadpoles, JHEP 08 (2023) 016 [2304.04789].
- (27) A.P. Braun, B. Fraiman, M. Graña, S. Lüst and H. Parra de Freitas, Tadpoles and gauge symmetries, JHEP 08 (2023) 134 [2304.06751].
- (28) S. Lüst and M. Wiesner, The tadpole conjecture in the interior of moduli space, JHEP 12 (2023) 029 [2211.05128].
- (29) A.P. Braun, H. Fortin, D.L. Garcia and R.V. Loyola, More on -flux and General Hodge Cycles on the Fermat Sextic, 2401.00470.
- (30) S. Kachru, R. Kallosh, A.D. Linde and S.P. Trivedi, De Sitter vacua in string theory, Phys. Rev. D 68 (2003) 046005 [hep-th/0301240].
- (31) K. Ishiguro and H. Otsuka, Sharpening the boundaries between flux landscape and swampland by tadpole charge, JHEP 12 (2021) 017 [2104.15030].
- (32) D. Andriot, L. Horer and P. Marconnet, Exploring the landscape of (anti-) de Sitter and Minkowski solutions: group manifolds, stability and scale separation, JHEP 08 (2022) 109 [2204.05327].
- (33) C. Vafa, String Vacua and Orbifoldized L-G Models, Mod. Phys. Lett. A 4 (1989) 1169.
- (34) C. Vafa and N.P. Warner, Catastrophes and the Classification of Conformal Theories, Phys. Lett. B 218 (1989) 51.
- (35) K. Hori, A. Iqbal and C. Vafa, D-branes and mirror symmetry, hep-th/0005247.
- (36) I. Brunner, M.R. Douglas, A.E. Lawrence and C. Romelsberger, D-branes on the quintic, JHEP 08 (2000) 015 [hep-th/9906200].
- (37) S. Cecotti and C. Vafa, Topological antitopological fusion, Nucl. Phys. B 367 (1991) 359.
- (38) S. Gukov, C. Vafa and E. Witten, CFT’s from Calabi-Yau four folds, Nucl. Phys. B 584 (2000) 69 [hep-th/9906070].
- (39) K. Hori and J. Walcher, D-brane categories for orientifolds—the Landau-Ginzburg case, Journal of High Energy Physics 2008 (2008) 030.
- (40) F. Denef and M.R. Douglas, Distributions of flux vacua, Journal of High Energy Physics 2004 (2004) 072.
- (41) T.W. Grimm and J. Louis, The Effective action of type IIA Calabi-Yau orientifolds, Nucl. Phys. B 718 (2005) 153 [hep-th/0412277].
- (42) T.W. Grimm and J. Louis, The Effective action of N = 1 Calabi-Yau orientifolds, Nucl. Phys. B 699 (2004) 387 [hep-th/0403067].
- (43) M. Kim, D-instanton superpotential in string theory, JHEP 03 (2022) 054 [2201.04634].
- (44) T.W. Grimm and D. van de Heisteeg, Exact Flux Vacua, Symmetries, and the Structure of the Landscape, 2404.12422.