STaCK: Sentence Ordering with Temporal Commonsense Knowledge
Abstract
Sentence order prediction is the task of finding the correct order of sentences in a randomly ordered document. Correctly ordering the sentences requires an understanding of coherence with respect to the chronological sequence of events described in the text. Document-level contextual understanding and commonsense knowledge centered around these events are often essential in uncovering this coherence and predicting the exact chronological order. In this paper, we introduce STaCK—a framework based on graph neural networks and temporal commonsense knowledge to model global information and predict the relative order of sentences. Our graph network accumulates temporal evidence using knowledge of `past' and `future' and formulates sentence ordering as a constrained edge classification problem. We report results on five different datasets, and empirically show that the proposed method is naturally suitable for order prediction. The implementation of this work is publicly available at: https://github.com/declare-lab/sentence-ordering.
1 Introduction
Coherence is an essential quality for any natural language text Halliday and Hasan (1976). Correct ordering of sentences is a necessary attribute of coherence. As such, there has been much research in correct sentence order detection due to its application in various down-stream tasks, such as, retrieval QA Yu et al. (2018), multi-document summarization Barzilay et al. (2002), automated content addition to text Mostafazadeh et al. (2016), text generation Mostafazadeh et al. (2016), and others. It also has potential applications in the evaluation of the quality of machine-generated documents. Existing approaches to sentence order prediction can be broadly classified into two categories: (1) sequence generation methods, and (2) pair-wise methods Zhu et al. (2021); Prabhumoye et al. (2020). While the former consider tagging the entire sequence, the latter takes one sentence pair at a time and predicts their relative order. Pair-wise methods ignore the importance of document level global information, i.e., while predicting the relative order of two sentences , other sentences from the same document do not play any role.

Global document information is especially important while predicting the relative order of sentences that are further apart, as it can provide essential contextual cues. As an example, consider the two highlighted sentences in the two sample documents shown in Figure 1. Although the sentences describe seemingly identical events, they have a different relative order in the two documents because of their different contexts. We recognize this fundamental limitation in existing methods, and we hypothesize that global information is essential for predicting the relative order of a sentence pair. It encompasses not only the semantic information of the discourse, but also commonsense knowledge centered around all the sentences of the document.
In this paper, we propose a graph-based framework to represent sentences in a document and their relations. Using a a two-layer relational graph convolutional network (RGCN) applied on this graph, we build a classifier that is able to learn the relative order of sentences in a document by accounting for the global document information encoded in the graph. We further infuse commonsense knowledge (CSK) information into this graph to improve the model performance. The key motivation is that temporal commonsense knowledge can bring important information about events that may occur before or after an event described in a sentence.
Our paper makes two important contributions. Firstly, we show how we can construct a document graph that captures global context information about the document. We employ a RGCN to encode the information in this graph and build an edge classifier that predicts the relative order of sentence pairs. Unlike previous work attempting to predict the relative order of sentence pairs, our approach explicitly accounts for global document-level information. Secondly, we infuse temporal commonsense knowledge into our graph convolutional neural network to further improve its performance. To the best of our knowledge, there is no prior work that attempted the use of CSK for sentence order prediction. Our results suggest that the graph representation encoding global document information and the temporal CSK are both effective to determine the order of sentences.
Sequence generation vs pair-wise methods for sentence ordering: In the literature, the sentence ordering task is also addressed using generative modeling Chowdhury et al. (2021) where the goal is to generate the correct positions of the sentences of a shuffled document as an integer sequence. In contrast, our method first classifies the sentence pairs followed by topological ordering. Despite achieving impressive performance, there exist some key differences that make the generative approaches fundamentally different and incomparable from the family of sentence pair classification-based or pair-wise approaches:
-
1.
The generative models for sentence ordering take sequences as input that contains temporal information in the form of learned positional embeddings. One could argue that this temporal information is noisy and thus would not provide any useful information to the model. However, this does not remove all the temporal information from the input that could assist the model, e.g., a shuffled order still contains valid temporal sequence or information i.e., sentence precedes sentence , and , sentence precedes sentence . Hence, a sequence generation model that accepts positional encoding of the sentences can still get confounding temporal signal despite the shuffling.
-
2.
The generative models for sentence ordering tend not to work when the sentence count during inference exceeds the highest sentence count observed in training. For instance, we found in our experiments that generative models trained on samples with five sentences would only generate tokens during inference, even if the test document has more sentences. This raises serious questions about such models' reasoning ability in zero-shot situations. One future direction to tackle such issues would be passing the input sequence length as a prompt or input to the generative model. The use of sequence length embedding could also be a possible solution. Contrary to this, pair-wise methods are robust at handling any number of sentences.
2 Background
Coherence and the problem of sentence order prediction have been extensively studied in literature due to their applicability in various downstream problems. Early work in this direction mainly used domain knowledge and handcrafted linguistic features to model the relation between sentences in a document Lapata (2003); Barzilay and Lee (2004); Barzilay and Lapata (2008). Sentence ordering methods in recent literature are primarily based on neural network architectures, and can be broadly categorized into two main families - i) Sequence generation methods and ii) Pair-wise methods.
Sequence generation methods use the entire sequence of the randomly ordered document to model local and global information. This information is then used to predict the correct order. The sentences and documents are typically encoded using a recurrent or transformer-based network Gong et al. (2016); Yin et al. (2020); Kumar et al. (2020). Hierarchical encoding schemes are also common Wang and Wan (2019). Prediction is then generally performed with a pointer network decoder Vinyals et al. (2015) based on beam search. Alternatively, ranking losses Xia et al. (2008) have also been explored to circumvent the expensive beam search algorithm Kumar et al. (2020). Such models predict a score for each sentence, which are then sorted to obtain the final order. The Pair-wise methods are motivated by a different principle of sentence ordering. These models aim to predict the relative order of each pair of sentences in the document. The final order is then constrained on all of the predicted relative orders. The constraint solving problem is generally tackled with topological sorting Prabhumoye et al. (2020), or more sophisticated neural network models Zhu et al. (2021).
Our proposed STaCK framework falls under this family of Pair-wise models. In STaCK, temporal commonsense is modelled using the Commonsense Transformers (COMET) model Hwang et al. (2020). The COMET model uses a BART Lewis et al. (2020) sequence-to-sequence encoder decoder framework and is pretrained on the commonsense knowledge graph Hwang et al. (2020). The pretraining objective is to take a triplet from the knowledge graph, and generate the object phrase from concatenated subject and relation phrase and . The set of relations include temporal relations `is before' and `is after'. COMET is pretrained on approximately 50,000 of such temporal triplets along with other commonsense relations from . The pretraining on commonsense knowledge ensures that COMET is capable of distinguishing cause-effects (causality), past-future (temporality), and other event-centered commonsense knowledge.
3 Methodology
An overall illustration of the proposed STaCK framework is shown in Fig. 2. We represent document consisting of sentences as a directed graph , with nodes and directed labeled edges , where is the relation type of the edge between and . Initial node embeddings are denoted as .
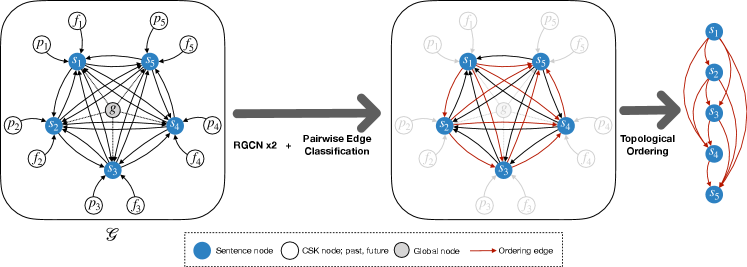
3.1 Graph Construction
The graph is constructed from the given document as follows:
Nodes and Node Embeddings:
We consider three different types of nodes in :
Sentence nodes. Each sentence in is a sentence node in the graph. We pass the sentence through a DeBERTa He et al. (2020) model and use the final layer vector corresponding to starting token <s> as the node embedding.
CSK nodes. For each sentence , we have a past and future node and , respectively. The CSK node embeddings are initialized from the BART encoder of the COMET model. Following COMET, we append temporal relation specific tokens isAfter [GEN] and isBefore [GEN] with the sentence . The concatenated text sequence is passed through the BART encoder and final layer vector corresponding to <s> is used as the node embedding for and .
Global node. The entire document is considered as an additional global node in . We pass the document through a non-positional (position embeddings removed) RoBERTa model Liu et al. (2019), and use the final layer vector corresponding to starting token <s> as the global node embedding. This non-positional model is insensitive to the sequence of tokens passed into it. The usage of a non-positional model is essential, as the model must not have any information about the relative order of the sentences. For a document consisting sentences, we have total nodes in .
Edges and Relations:
We construct edges with different relations based on the constituent nodes: Sentence edges. Each sentence node in is connected to all other sentence nodes (where ) in with relation . The directed edge is denoted as . Our formulation leads to bidirectional edges between each sentence pair, i.e. both and .
CSK edges. Each CSK node and , has an edge with the corresponding sentence node: , and . The relation is set different for past and future CSK nodes. The direction of the edge is from the CSK node to the sentence node.
Global edges. The global node has an edge with every sentence node: , for . As indicated, the direction of the edge is taken from the global node to the sentence node.
3.2 Graph Encoder: RGCN
We use a two-layer Relational Graph Convolutional Network (RGCN) Schlichtkrull et al. (2018) as our graph encoding model. The RGCN model is able to accumulate relational evidence in multiple inference steps from the neighborhood around a given node. The RGCN model is a natural choice of encoding algorithm as it enables the modelling of different relations across our graph. In RGCN, the transformation of node embeddings are performed as follows: .
where indicates the neighbouring nodes of under relation ; is a normalization constant which either can be learned in a gradient-based learning setup, or can be set in advance, such that, and , are learnable parameters of the transformation. The self-dependent connection with weight is added to ensure direct information among same nodes in consecutive layers in the graph framework.
For node , we start with initial node embeddings (Section 3.1), and transform it to , following the two layer RGCN transformation process.
3.3 Graph Decoder: Pairwise Edge Classifier
The final module in our graph network is built upon the principle of pairwise edge classification. This module predicts the relative order between any two sentences in by using the initial input embeddings and output activations from the RGCN encoder. For example, let us take two sentences and , where , i.e. appears earlier in , and appears later. In this formulation, we will first consider the bidirectional edges between and in — and . The classification objective is then to classify the first edge as 1 and second edge as 0. In other words, if the originating sentence of the directed edge appears earlier than the destination sentence in the original document, then we predict the class of the edge as 1, otherwise 0.
To achieve this, we use a function , which takes the concatenated feature vectors and and outputs a single scalar value as a score. We compute , and and normalize them with softmax activation to output two probabilities for the two edges and . The softmax operation ensures that, . During training, the probabilities are pushed towards 1 and 0 for the paired edges. During inference, for sentences and , if > then we predict appears earlier than (), or vice versa ().
Naturally the function has to be sensitive to the order of its inputs in this formulation. The more different the outputs scores are, the more the normalized probabilities are pushed towards 0 and 1. From our experiments, we find that functions that have an anti-symmetric component are most suitable for . In particular we use, , where and the sine operation is performed element-wise. is the learnable parameter of the function. The sine operation is the anti-symmetric component in our function, as, . Other functions such as outer product performed worse than the sine function in our experiments.
3.4 Topological Sorting
The topological sorting method Prabhumoye et al. (2020) is used to obtain the final ordered sequence of sentences from the all the pairwise classifications. If the pairwise classifier predicts that > i.e. , then the sorting method ensures comes before in the final ordering .
| Dataset | Min | Max | Avg | Train | Val | Test |
|---|---|---|---|---|---|---|
| NeurIPS | 1 | 15 | 6 | 2448 | 409 | 402 |
| AAN | 1 | 20 | 5 | 8569 | 962 | 2626 |
| NSF | 2 | 40 | 8.9 | 96017 | 10185 | 21573 |
| SIND | 5 | 5 | 5 | 40155 | 4990 | 5055 |
| ROCStory | 5 | 5 | 5 | 78529 | 9816 | 9816 |
4 Experimental Setup
| Method | NeurIPS | AAN | NSF | SIND | ROCStory | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| PMR | PMR | PMR | PMR | PMR | ||||||
| LSTM Pointer Net | 0.7373 | 20.95 | 0.7394 | 38.30 | 0.5460 | 10.68 | 0.4833 | 12.96 | 0.6787 | 28.24 |
| Hierarchical Attention Net | 0.7008 | 19.63 | 0.6956 | 30.29 | 0.5073 | 8.12 | 0.4814 | 11.01 | 0.6873 | 31.73 |
| Sentence Entity Graph | 0.7370 | 24.63 | 0.7616 | 41.63 | 0.5602 | 10.94 | 0.4804 | 12.58 | 0.6852 | 31.36 |
| ATTOrderNet TwoLoss | 0.7357 | 23.63 | 0.7531 | 41.59 | 0.4918 | 9.39 | 0.4952 | 14.09 | 0.7302 | 40.24 |
| RankTxNet ListMLE | 0.7462 | 24.13 | 0.7748 | 39.18 | 0.5798 | 9.78 | 0.5652 | 15.48 | 0.7602 | 38.02 |
| B-TSort | 0.7824 | 30.59 | 0.8064 | 48.08 | 0.4813 | 7.88 | 0.5632 | 17.35 | 0.7941 | 48.06 |
| Constraint Graphs | 0.8029 | 32.84 | 0.8236 | 49.81 | 0.6082 | 13.67 | 0.5856 | 19.07 | 0.8122 | 49.52 |
| STaCK w/o CSK Nodes, Edges | 0.8035 | 33.67 | 0.8365 | 51.10 | 0.6567 | 11.79 | 0.6154 | 19.84 | 0.8391 | 53.04 |
| STaCK | 0.8166 | 37.31 | 0.8556 | 54.01 | 0.6582 | 12.26 | 0.6194 | 20.79 | 0.8534 | 55.96 |
| same CSK Edges: | 0.8146 | 37.06 | 0.8472 | 52.25 | 0.6642 | 12.41 | 0.6172 | 20.03 | 0.8470 | 54.32 |
4.1 Datasets
We benchmark the proposed STaCK framework on five different datasets. NeurIPS, AAN, NSF Abstracts. These three datasets contain abstracts from NeurIPS papers, AAN papers, and the NSF Research Award abstracts respectively Logeswaran et al. (2018) . The number of sentences in each abstract varies significantly, ranging from two to forty. SIND. This is a sequential vision to language dataset Huang et al. (2016) used for the task of visual storytelling. Each story contains five images and their descriptions in natural language. ROCStory. Mostafazadeh et al. (2016) introduce a dataset of short stories capturing a rich set of causal and temporal commonsense relations between daily events. The dataset has been used for evaluating story understanding, generation, and script learning. All stories have five sentences. For ROCStory, we use the train, val, test split as used in Zhu et al. (2021). For the other datasets, we use the splits following the original papers. Some statistics about the datasets is shown in Table 1.
4.2 Evaluation Metrics
Kendall's is an automatic metric widely used for evaluating text coherence. It measures the distance between the predicted order and the correct order of sentences in terms of number of inversions. It is calculated as, , where I is the number of pairs predicted with incorrect relative order and n is the number of sentences in the paragraph. The score ranges from -1 to 1, with 1 indicating perfect prediction order. PMR (Perfect Match Ratio) measures the percentage of instances for which the entire order of the sequence is correctly predicted. It is a more strict metric, as it only gives credit to sequences that are fully correct, and does not give credit to partially correct sequences.
4.3 Training Setup
Training is performed by optimizing the binary cross-entropy loss function for pairwise edge classification. We use the AdamW optimizer with a learning rate of 1e-6 for the parameters of the transformer models used in extracting node embeddings. For the parameters of the RGCN encoder and edge classifier, we use the Adam optimizer with a learning rate of 1e-4. We train our models for 10 epochs with a batch size of 8 documents. Test results are reported corresponding to the best validation .
5 Results and Analysis
| Method | STaCK | STaCK w/o CSK | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| First | Last | Abs | LCS | D-Win=1 | First | Last | Abs | LCS | D-Win=1 | |
| NeuRIPS | 93.3 | 78.8 | 63.6 | 83.1 | 87.5 | 92.2 | 76.1 | 59.9 | 81.1 | 86.3 |
| AAN | 93.2 | 82.6 | 71.6 | 86.6 | 92.0 | 91.9 | 79.9 | 68.0 | 85.1 | 90.5 |
| NSF | 86.2 | 56.9 | 33.9 | 65.6 | 58.7 | 85.4 | 58.0 | 33.6 | 65.4 | 58.3 |
| SIND | 83.2 | 66.3 | 54.2 | 77.4 | 84.1 | 82.7 | 65.6 | 53.1 | 76.9 | 83.5 |
| ROCStory | 96.1 | 82.1 | 76.7 | 89.2 | 95.2 | 95.6 | 81.7 | 76.1 | 88.9 | 94.8 |
5.1 Baselines and State-of-the-art Methods
We compare STaCK against the following methods: LSTM Pointer Net Gong et al. (2016): A word2vec embedding based LSTM model with pointer network decoder. Hierarchical Attention Net Wang and Wan (2019): A word and sentence based hierarchical network with LSTMs and multihead attention encoder coupled with a multihead attention decoder. Sentence Entity Graph Yin et al. (2019): A model based on sentence entity graph with graph recurrent network encoder and pointer network decoder. ATTOrderNet TwoLoss Yin et al. (2020): An improved version of Attention Order Net with a pointer network decoder enhanced by two pairwise ordering prediction modules RankTxNet ListMLE Kumar et al. (2020) uses a BERT sentence encoder and predicts a score for each sentence which are sorted to obtain to sentence order. The ListMLE function Xia et al. (2008) is used as the objective function. BERT Topological Sort (BT-Sort) Prabhumoye et al. (2020): A pairwise model which applies the BERT-base encoder on concatenated sentence pairs to predict the relative order. For sentence pair (s1, s2), the input to the BERT encoder is <CLS> s1 <SEP> s2 <SEP>, and the classification is performed from the <CLS> token vector. Topological sort is then used to obtain the final prediction order from all relative orders. Constraint Graphs Zhu et al. (2021): Another pairwise model which also applies the BERT-base encoder on concatenated sentence pairs to predict the relative order of the sentences. Constraints from the relative orders are then represented as a constraint graphs and integrated into the sentence representation by using Graph Isomorphism Networks (GINs). All sentence representations from the GINs are fused together to predict the final score of sentences. The ListMLE objective function Xia et al. (2008) is then used on these scores to predict the final order.
Among the above methods, BT-Sort and Constraint Graphs are of our main interest for comparative study. Constraint Graphs model is the current state-of-the-art for sentence order prediction.
5.2 Main Results
Table 2 shows the results across all the datasets for the baseline methods and our proposed model. STaCK achieves improved scores over the previous state-of-the-art across almost all the datasets on both evaluation metrics. Interestingly, we observe that the improvement in the metric is more significant in NSF and SIND. However, for NeuRIPS, AAN, and ROCStory the improvement in more prominent in the PMR metric. A modification of model which don't use any commonsense knowledge (STaCK: w/o CSK Nodes, Edges) also surpass previous state-of-the-art results in most cases. We expand upon the obtained results and report a number of analysis studies next.
5.3 Novelty of the Proposed Graph-based Model with CSK Nodes and Edges
State-of-the-art models BT-Sort and Constraint Graphs use sentence pair concatenation method to perform the relative order prediction between a pair of sentences. This method is widely used in GLUE style classification tasks. As illustrated before, this method doesn't consider any document level information for the relative order prediction. We also compare our proposed graph model without any CSK nodes and edges to the state-of-the-art methods. We report the results for this model in Table 2 in row STaCK: w/o CSK Nodes, Edges. It can be observed that even after removing the CSK components, our graph model achieves improved scores in all datasets except the PMR metric in NSF. BT-Sort and our proposed model uses the same topological sort method to infer the final order of sentences. The significant improvement of STaCK: w/o CSK Nodes, Edges over BT-Sort can thus be directly attributed to the integration of document level information in our graph. Furthermore, even though Constraint Graphs uses a parametric neural network model to infer the final order of the sentences (compared to non-parametric topological sort of ours), it records an overall poorer performance across most metrics. From the empirical results, we conclude that document level information is indeed crucial for the task of sentence order prediction. In the future, the topological sorting employed in our work can be replaced with a more complex neural network-based sorting approach as used in the Constraint Graphs by Zhu et al. (2021). A natural question might arise — what if we use a different transformer encoder for the state-of-the-art models? We find that this change doesn't improve the results of the state-of-the-art models due to a mismatch in pretraining objective functions and the GLUE style classification setting. Other choices of encoders such as RoBERTa, ALBERT, or DeBERTa perform poorly compared to BERT for both BT-Sort and Constraint Graphs Zhu et al. (2021). These encoders are not pretrained with the next sentence prediction (NSP) objective used in BERT. The NSP objective is similar to the concatenated sentence pair classification strategy used in BT-Sort and Constraint Graphs, enabling BERT to obtain the best possible performance.
| Method | BT-Sort | CG | Ours | |||
|---|---|---|---|---|---|---|
| F | L | F | L | F | L | |
| AAN | 89.5 | 79.8 | 91.5 | 80.4 | 93.2 | 82.6 |
| SIND | 78.1 | 58.4 | 79.8 | 60.4 | 83.2 | 66.3 |
| NeuRIPS | 89.8 | 75.1 | - | - | 93.3 | 78.8 |
| NSF | - | - | - | - | 86.2 | 56.9 |
| ROCStory | - | - | - | - | 96.1 | 82.1 |
5.4 Effect of Commonsense Knowledge
To compare the effect of commonsense knowledge, we propose another model without the CSK components. The CSK nodes and edges are discarded, and the resulting model contains only sentence nodes, global node, sentence edges, and global edges. We call this model STACK w/o CSK Nodes, Edges. Note that this model surpasses previously reported state-of-the-art results in most datasets. To have a better understanding of how CSK helps, we compare this model with STaCK across several metrics in Table 3. We use the following metrics for this evaluation:
First, Last, Absolute Accuracy: The accuracy of correctly predicting the first sentence, the last sentence, and the absolute position of any sentence in the document. Longest Common Subsequence (LCS) is the ratio of longest common subsequence between the predicted order and the actual order Gong et al. (2016). Consecutiveness is not considered necessary. The ratio is measured in percentage, and higher ratios are considered better. Displacement is measured by calculating the % of sentences for which the predicted location is within distance 1 of the original location. The displacement can occur in either direction (left or right). A higher % of this metric indicates less displacement. We denote this metric as Displacement-Window=1 or D-Win=1. We compare the models with and without CSK in Table 3 and conclude the following: i) For both CSK and w/o CSK models, predicting the correct first sentence is relatively straightforward. This is followed by correctly predicting the last sentence, and then the sentences in between. ii) Incorporation of CSK always helps, except for one particular case in NSF. iii) CSK is most helpful in NeuRIPS, followed by AAN. CSK is the least helpful in NSF. iv) Improvement brought by CSK varies in different degrees across the evaluation metrics. In NeuRIPS and AAN, the last sentence prediction accuracy and the absolute accuracy are improved the most after integrating CSK.
5.5 Ablation Study
Extending the commonsense specific analysis above (Section 5.4), we further perform some ablation study on the CSK specific components of our proposed model. The results are reported in Table 2. For the first ablation setting, we consider the edges with past () and future () nodes to have the same relation i.e. . The resultant performance is slightly worse in most cases apart from the NSF dataset. The most significant drop is observed in the PMR metric of AAN, where the result is almost 2% poorer. For NSF, this ablation setting results in improved performance, suggesting that the distinction of temporal directionality (past and future) is not essential for this dataset.
The other ablation setting corresponds to the model without the CSK components, which is the same as STaCK w/o CSK Nodes, Edges in Section 5.4. For this setting, we observe a sharp drop in performance across most of the datasets. The decrease in performance is most significant in the PMR metric of NeuRIPS and AAN. Considerable reduction in performance is also observed across various metrics in SIND and ROCStory. The ablation study with respect to CSK components coupled with the more detailed analysis in Table 3 indicates that commonsense knowledge is indeed beneficial and helps in the sentence order prediction task with varying degrees across different datasets and metrics.
We experimented with different sentence encoders and found the embeddings created by DeBERTa perform the best, followed by RoBERTa and BERT. ALBERT, on the other hand, perform the worst with around 2% drop in and 4% drop in PMR. We also experimented by removing the global node from the STaCK graph, resulting performance drop around 1%-2% across the datasets.
5.6 Prediction of First and Last Sentence
The correct prediction of the first sentence and the last sentence is often paid more importance due to their crucial positions in a paragraph Kumar et al. (2020); Zhu et al. (2021). We compare STaCK against BT-Sort and Constraint Graphs in Table 4 for the task of predicting the first and last sentence correctly. Results are reported for BT-Sort and Constraint Graphs wherever available. First of all, we observe a common trend present in all the three methods — the accuracy of correctly predicting the first sentence is significantly better compared to correctly predicting the last sentence. This is an interesting aspect which has been observed by other previous works as well Kumar et al. (2020); Yin et al. (2019, 2020). Next, we compare the results across the three methods and find that our proposed model is significantly better than BT-Sort in predicting both the first and last sentences accurately. The difference in performance ranges from 2.8% - 7.9% across different datasets. We also obtain improved results over Constraint Graphs in AAN and SIND, with margins between 1.7% - 5.9%.
5.7 Visualization of Learned Representations
5.7.1 Manifold of sentence embeddings
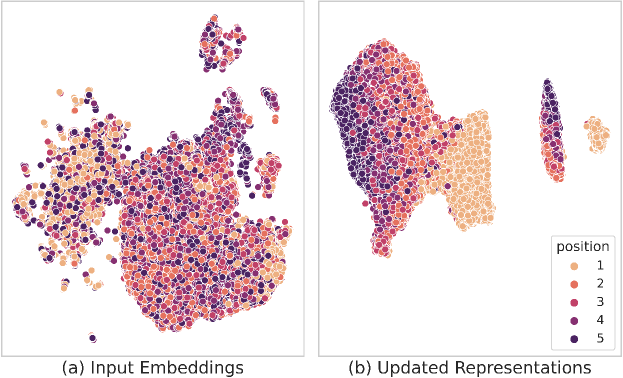
We illustrate the manifold of learned embeddings using the UMAP McInnes et al. (2018) algorithm in Fig. 3. The visualization shows the test document sentences in ROCStory dataset. Sentences are colour-coded by their position (1-5) in the story. The plot on the left shows the initial sentence embeddings () for a non-finetuned DeBERTa model. The plot on the right shows the final node embeddings () in the trained graph model. Visually it is evident that the initial input embeddings do not carry much order information. However, the updated representations are much more significantly grouped together by their position. Interestingly, sentences corresponding to positions 1 (first) and 5 (last) are the most separable after the UMAP transformation. However, sentences at positions (2-4) did not separate quite so cleanly. The results indicate that sentences appearing at the beginning and the end of a document are much easier to identify than the ones in the middle. Same conclusion can be drawn from the reported results in Table 3.
| Model | PMR | Abs | LCS | |
|---|---|---|---|---|
| NeuRIPS | ||||
| B-TSort | 0.0 | 39.43 | 0.74 | 71.68 |
| STaCK | 7.69 | 44.02 | 0.74 | 74.84 |
| AAN | ||||
| B-TSort | 0.0 | 36.86 | 0.69 | 72.01 |
| STaCK | 15.38 | 44.02 | 0.73 | 71.69 |
| NSF | ||||
| B-TSort | 0.67 | 28.57 | 0.64 | 64.86 |
| STaCK | 0.12 | 24.42 | 0.59 | 59.67 |
5.7.2 Manifold of temporal knowledge
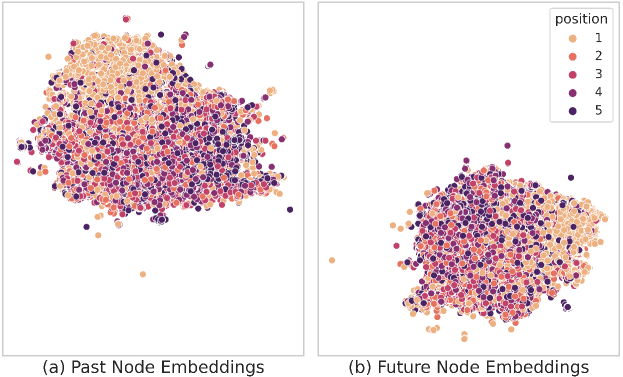
We visualize the manifold of temporal commonsense embeddings in Fig. 4. It shows the UMAP transformation of `past' and `future' node embeddings for the test sentences in ROCStory. Interestingly, embeddings corresponding to commonsense knowledge of the first sentences are grouped together more cleanly as compared to the other sentences. This pattern further substantiates the hypothesis, drawn from Table 3, that the first sentences are the easiest to identify. In contrast, the embeddings corresponding to the other sentences are noisier and cannot be distinguished clearly.
| Gold | STaCK |
|
CG | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
5.8 Order Prediction in Longer Documents
We report order prediction results for documents having more than ten sentences in Table 5. The Constraint Graphs paper does not report this result, and thus we compare STaCK with the BT-Sort method. We report results only in NeuRIPS, AAN, and NSF, as SIND and ROCStory have exactly five sentences in all documents. From the results, we conclude that STaCK is significantly better than BT-Sort for long documents in NeuRIPS and AAN. The perfect match ratio, and absolute accuracy are several percentage point higher for STaCK compared to BT-Sort. For NSF, both the models perform very poorly in the PMR metric, with scores lesser than 1%. However, BT-Sort has superior performance compared to STaCK across the other metrics. Note that the overall result of BT-Sort was worse compared to STaCK (Table 2). Results from Table 5 and Table 2 suggest that, BT-Sort is better for longer documents and STaCK is better for shorter documents in NSF.
5.9 Case Studies
We report a few case studies in Table 6. Gold order of three documents from ROCStory and SIND dataset are shown on the left. The columns on the right depicts the order predicted by our framework with and without CSK, and the Constraint Graphs (CG) model. STaCK predicts the sentence order most accurately, whereas STaCK w/o CSK often swaps absolute positions or shifts consecutive sentences. CG predicts the first sentence correctly in all cases, but suffers from predicting contextual discrepancies. For instance, He couldn't wait to cook in it! is predicted after The first time, he turned it on and smoke billowed out. In the third example, temporal commonsense around the event I called 911 to report the accident is aligned to the event The police soon arrived through the relation isBefore in COMET. Such commonsense knowledge helps in predicting the entire order correctly. We note that CG predictions for this example are displaced within window 1, with I called 911 to report the accident and The police soon arrived having wrong relative order. Such instances of the importance of document information and CSK are prevalent throughout the dataset.
5.10 Effect of COMET
We experimented by adding other temporal and causal commonsense relations in COMET such as causes, as-a-result, desires, requires as nodes to the proposed graph in STaCK. However, they did not result in any significant performance improvements. We posit this could be due to the fact that there exists a large overlap between the generated output of isBefore, isAfter and the four relations as mentioned above. Nonetheless, we think all types of CSK relations available in COMET can be used in the task. The graph structure to accommodate those additional CSK is left as future work.
5.11 Choice of Transformer Encoder
The choice of the transformer encoder plays a crucial role in the sentence order prediction task. Several choices of transformer-based models are available, such as BERT Devlin et al. (2019), RoBERTa Liu et al. (2019), ALBERT Lan et al. (2019), DeBERTa He et al. (2020), etc. Different objective functions are used to pre-train these models, which directly affects how these models perform on the downstream sentence ordering task. In particular, BERT is pre-trained with the masked language modelling (MLM) and the next sentence prediction (NSP) objective. RoBERTa and DeBERTa models are pre-trained only with the MLM objective. ALBERT model is pre-trained with the masked language modelling (MLM) and a sentence order prediction (SOP) objective.
BT-Sort and Constraint Graphs are the current state-of-the-art models which use a BERT encoder. Both models are of pair-wise nature (Section 2), that first predict the relative order between each pair of sentences in the document. The final order is then inferred from all the relative orders. The relative order prediction is performed by concatenating the sentence pairs with a <SEP> token and then passing through BERT encoder. This setting directly aligns with the NSP objective of BERT, and is capable of achieving state-of-the-art results. However, as reported in Zhu et al. (2021), replacing the BERT encoder with a RoBERTa encoder results in poorer performance because of the absence of the NSP objective. Interestingly, using ALBERT encoder also results in a performance drop, even though ALBERT was pre-trained with a sentence order prediction objective (albeit rather differently). Furthermore, we also experimented by replacing the the BERT encoder of BT-Sort with DeBERTa and found that the performance does not surpass the reported results of BERT. Our proposed model is also a pair-wise model. However, the graph-based encoding technique is different from the commonly used sentence pair concatenating method. We found that for our graph model, sentence embeddings created by DeBERTa perform the best, followed by RoBERTa and BERT. Sentence embeddings produced by ALBERT perform the worst.
6 Conclusion
In this work, we presented STaCK, a framework that uses Relational Graph Convolutional Network (RGCN) to model document-level contextual information and temporal commonsense knowledge for sentence order prediction. In the graph network, the edge classification objective was applied for pair-wise relative order prediction of the sentence pairs. This was followed by a topological sorting for the final order prediction of the sentences. STaCK achieves state-of-the-art results in several benchmark datasets.
Acknowledgments
This work is supported by the AcRF MoE Tier-2 grant titled: ``CSK-NLP: Leveraging Commonsense Knowledge for NLP'' and the A*STAR under its RIE 2020 Advanced Manufacturing and Engineering (AME) programmatic grant, Award No. - A19E2b0098.
References
- Barzilay et al. (2002) Regina Barzilay, Noemie Elhadad, and Kathleen R. McKeown. 2002. Inferring strategies for sentence ordering in multidocument news summarization. J. Artif. Int. Res., 17(1):35–55.
- Barzilay and Lapata (2008) Regina Barzilay and Mirella Lapata. 2008. Modeling local coherence: An entity-based approach. Computational Linguistics, 34(1):1–34.
- Barzilay and Lee (2004) Regina Barzilay and Lillian Lee. 2004. Catching the drift: Probabilistic content models, with applications to generation and summarization. In Proceedings of the Human Language Technology Conference of the North American Chapter of the Association for Computational Linguistics: HLT-NAACL 2004, pages 113–120.
- Chowdhury et al. (2021) Somnath Basu Roy Chowdhury, Faeze Brahman, and Snigdha Chaturvedi. 2021. Reformulating sentence ordering as conditional text generation. arXiv preprint arXiv:2104.07064.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 4171–4186.
- Gong et al. (2016) Jingjing Gong, Xinchi Chen, Xipeng Qiu, and Xuanjing Huang. 2016. End-to-end neural sentence ordering using pointer network. arXiv preprint arXiv:1611.04953.
- Halliday and Hasan (1976) Michael Alexander Kirkwood Halliday and Ruqaiya Hasan. 1976. Cohesion in English.
- He et al. (2020) Pengcheng He, Xiaodong Liu, Jianfeng Gao, and Weizhu Chen. 2020. Deberta: Decoding-enhanced bert with disentangled attention. arXiv preprint arXiv:2006.03654.
- Huang et al. (2016) Ting-Hao K. Huang, Francis Ferraro, Nasrin Mostafazadeh, Ishan Misra, Jacob Devlin, Aishwarya Agrawal, Ross Girshick, Xiaodong He, Pushmeet Kohli, Dhruv Batra, et al. 2016. Visual storytelling. In 15th Annual Conference of the North American Chapter of the Association for Computational Linguistics (NAACL 2016).
- Hwang et al. (2020) Jena D Hwang, Chandra Bhagavatula, Ronan Le Bras, Jeff Da, Keisuke Sakaguchi, Antoine Bosselut, and Yejin Choi. 2020. Comet-atomic 2020: On symbolic and neural commonsense knowledge graphs. arXiv preprint arXiv:2010.05953.
- Kumar et al. (2020) Pawan Kumar, Dhanajit Brahma, Harish Karnick, and Piyush Rai. 2020. Deep attentive ranking networks for learning to order sentences. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 8115–8122.
- Lan et al. (2019) Zhenzhong Lan, Mingda Chen, Sebastian Goodman, Kevin Gimpel, Piyush Sharma, and Radu Soricut. 2019. Albert: A lite bert for self-supervised learning of language representations. arXiv preprint arXiv:1909.11942.
- Lapata (2003) Mirella Lapata. 2003. Probabilistic text structuring: Experiments with sentence ordering. In Proceedings of the 41st Annual Meeting of the Association for Computational Linguistics, pages 545–552.
- Lewis et al. (2020) Mike Lewis, Yinhan Liu, Naman Goyal, Marjan Ghazvininejad, Abdelrahman Mohamed, Omer Levy, Veselin Stoyanov, and Luke Zettlemoyer. 2020. Bart: Denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 7871–7880.
- Liu et al. (2019) Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. 2019. Roberta: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692.
- Logeswaran et al. (2018) Lajanugen Logeswaran, Honglak Lee, and Dragomir Radev. 2018. Sentence ordering and coherence modeling using recurrent neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 32.
- McInnes et al. (2018) Leland McInnes, John Healy, Nathaniel Saul, and Lukas Großberger. 2018. Umap: Uniform manifold approximation and projection. Journal of Open Source Software, 3(29):861.
- Mostafazadeh et al. (2016) Nasrin Mostafazadeh, Nathanael Chambers, Xiaodong He, Devi Parikh, Dhruv Batra, Lucy Vanderwende, Pushmeet Kohli, and James Allen. 2016. A corpus and cloze evaluation for deeper understanding of commonsense stories. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pages 839–849, San Diego, California. Association for Computational Linguistics.
- Prabhumoye et al. (2020) Shrimai Prabhumoye, Ruslan Salakhutdinov, and Alan W Black. 2020. Topological sort for sentence ordering. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 2783–2792.
- Schlichtkrull et al. (2018) Michael Schlichtkrull, Thomas N Kipf, Peter Bloem, Rianne Van Den Berg, Ivan Titov, and Max Welling. 2018. Modeling relational data with graph convolutional networks. In European semantic web conference, pages 593–607. Springer.
- Vinyals et al. (2015) Oriol Vinyals, Meire Fortunato, and Navdeep Jaitly. 2015. Pointer networks. In NIPS.
- Wang and Wan (2019) Tianming Wang and Xiaojun Wan. 2019. Hierarchical attention networks for sentence ordering. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 7184–7191.
- Xia et al. (2008) Fen Xia, Tie-Yan Liu, Jue Wang, Wensheng Zhang, and Hang Li. 2008. Listwise approach to learning to rank: theory and algorithm. In Proceedings of the 25th international conference on Machine learning, pages 1192–1199.
- Yin et al. (2020) Yongjing Yin, Fandong Meng, Jinsong Su, Yubin Ge, Lingeng Song, Jie Zhou, and Jiebo Luo. 2020. Enhancing pointer network for sentence ordering with pairwise ordering predictions. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 9482–9489.
- Yin et al. (2019) Yongjing Yin, Linfeng Song, Jinsong Su, Jiali Zeng, Chulun Zhou, and Jiebo Luo. 2019. Graph-based neural sentence ordering. arXiv preprint arXiv:1912.07225.
- Yu et al. (2018) Adams Wei Yu, David Dohan, Quoc Le, Thang Luong, Rui Zhao, and Kai Chen. 2018. Fast and accurate reading comprehension by combining self-attention and convolution. In International Conference on Learning Representations.
- Zhu et al. (2021) Yutao Zhu, Kun Zhou, Jian-Yun Nie, Shengchao Liu, and Zhicheng Dou. 2021. Neural sentence ordering based on constraint graphs. arXiv preprint arXiv:2101.11178.