Star Formation Patterns and Hierarchies

Local Open Clusters in the compilation by Piskunov et al. (2006) seem at first to have a random distribution in the galactic plane, with the local spiral arms barely visible and no obvious age gradients or patterns. They have been known to be grouped into star complexes (Efremov, 1995) and moving groups (Eggen, 1989) for a long time, but there has been little other patterning recognized. Now this is beginning to change. The groupings and complexes are better mapped using new velocity and distance information. Piskunov et al. (2006) and Kharchenko et al. (2005) catalogued “Open Cluster Complexes,” in which many clusters have similar positions, velocities and ages inside each complex. For example, one is in the Hyades region and another is in Perseus-Auriga. Perseus-Auriga surrounds the Sun and lies in the galactic plane over a region 1 kpc in size with a log(age) between 8.3 and 8.6, in years. Gould’s Belt is another Open Cluster Complex. It has a log age less than 7.9 and lies in a thin plane tilted to the main galactic disk by an angle of 20^∘ surrounding the Sun.

de la Fuente Marcos & de la Fuente Marcos (2008) identified five Open Cluster Complexes from the positions and velocities of clusters within 2.5 kpc of Sun. These are: Scutum-Sagittarius at a galactic longitude of $l=12^{\circ}$ and a distance of 1300 pc, Cygnus at $l=75^{\circ}$ and 1400 pc, Cassiopeia-Perseus at $l=132^{\circ}$ and 2000 pc, Orion at $l=200^{\circ}$ and 500 pc, and Centaurus-Carina at $l=295^{\circ}$ and 2000 pc. These authors suggest that Open Cluster Complexes are fragments from common gas clouds. Within their limiting distance of 2.5 kpc, the total gas mass in the Milky Way is $\sim 5\times 10^{7}\;M_{\odot}$, considering a disk thickness of 300 pc and an average density of 1 cm^-3. This means that each of the 5 giant gas clouds that made these Open Cluster Complexes had a mass of $\sim 10^{7}\;M_{\odot}$. This is the Jeans mass in the galactic disk ($\sim\sigma^{4}/[G^{2}\Sigma_{\rm gas}]$ for dispersion $\sigma$ and mass column density $\Sigma_{\rm gas}$), as discussed in Lecture 1. Open Cluster Complexes could be the remnants of star formation in giant clouds formed by gravitational instabilities in the Milky Way gas layer.

Elias, Alfaro & Cabrera-caño (2009) studied Gould’s Belt using the Catalogue of Open Cluster Data (Kharchenko et al., 2005). They found an interesting correlation that the cluster fraction is large for the Orion OB association region and small for the Sco-Cen association. The cluster fraction is the ratio of the stellar mass that forms in bound clusters to the total stellar mass that forms at the same time. The rest of the stars form in unbound groups and associations. There is a gradient in the young cluster (age $<10$ Myr) fraction of star formation and in the cluster density over the 700 pc distance separating these two associations. This suggests that star formation prefers clusters when the pressure is high, as in Orion, which is a more active region than Sco-Cen. High pressure could be a factor in bound cluster formation if high-pressure cores are more difficult to disrupt and their star formation efficiencies end up higher when star formation stops. High pressure also corresponds to a broader density probability distribution function, and so a higher mass fraction of gas exceeding the critical efficiency for bound cluster formation (Sect. 7).

This lecture reviews interstellar and stellar hierarchical structure, which gives patterns in the positions and ages of young stars and clusters. Related to this is the formation of the bound clusters themselves, and the cluster mass function. A more complete review of this topic is in Elmegreen (2010).

The hierarchy of star formation begins on the scale of Jeans-mass cloud complexes. Giant molecular clouds (GMCs) form by molecular line shielding and condensation inside these giant clouds, and star complexes build up from the combined star formation (Elmegreen & Elmegreen, 1983). Each GMC makes a single OB association at any one time. Hierarchical structure has been known to be important in star-forming regions for a long time (e.g., Larson, 1981; Feitzinger & Galinski, 1987). Early reviews of large-scale hierarchical structure are in Scalo (1985, 1990). Interstellar hierarchies have also been thought to have a possible role in the stellar initial mass function (e.g., Larson, 1973, 1982, 1991).

The nearby galaxy M33 has a clear pattern of giant HI clouds, with masses of $10^{6}-10^{7}\;M_{\odot}$, containing most of the GMCs and CO emission (Engargiola et al., 2003). Giant star complexes occur in these regions (Ivanov, 2005), often extending beyond the HI clouds because of stellar drift. The high-definition image of M51 made by the ACS camera on the Hubble Space Telescope shows exquisite examples of stellar clustering on a wide variety of scales, with similar patterns of clustering for dust clouds, which are the GMCs (Fig. 1). Clearly present are giant clouds (1 kpc large with $M\sim 10^{7}\;M_{\odot}$) that are condensations in spiral arm dust lanes, star formation inside these clouds with no noticeable time delay after the spiral shock, and scattered star formation downstream. The downstream activity has the form of lingering star formation in cloud pieces that come from the disassembly of spiral arm clouds, in addition to triggered star formation in shells and comet-shaped clouds that are also made from the debris of spiral arm clouds (see Lectures 2 and 4).

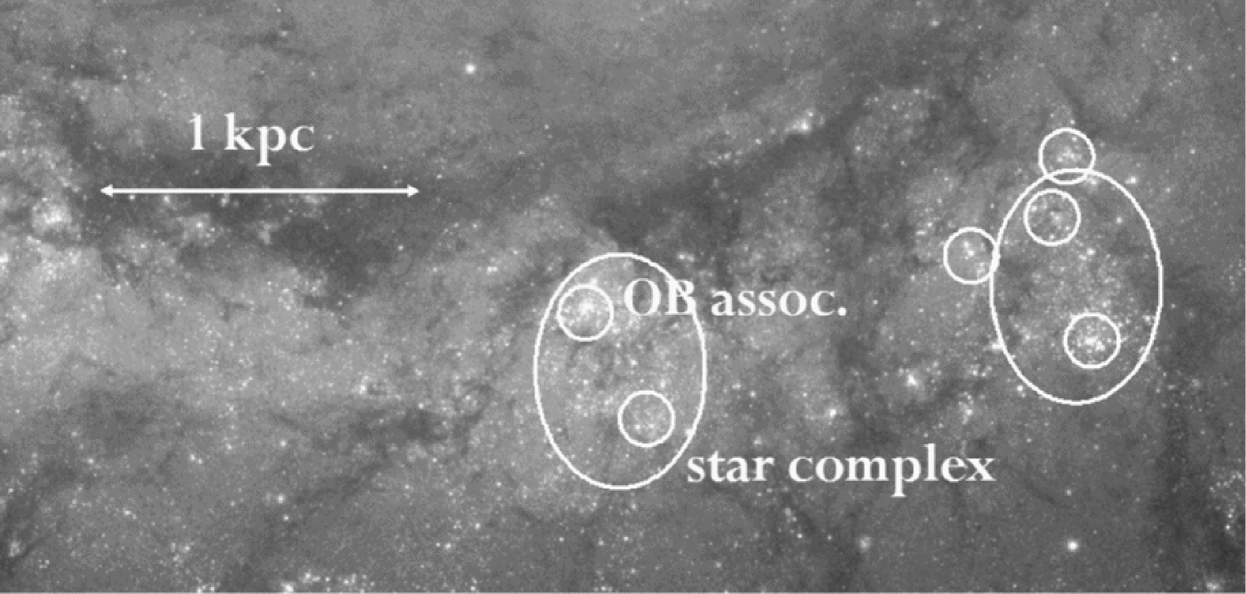
Star clusters in M51 observed with HST have been studied by Scheepmaker et al. (2009). The overall distribution of clusters in the M51 disk shows no obvious correlations or structures, aside from spiral arms. But autocorrelation functions for three separate age bins show that the youngest sample is well correlated: it is hierarchical with a fractal dimension of $\sim 1.6$. This means that there are clusters inside cluster pairs and triplets, that are inside clusters complexes and so on, up to $\sim 1$ kpc. Clusters in the Antennae galaxy are also auto-correlated out to $\sim 1$ kpc scales (Zhang, Fall, & Whitmore, 2001).

Sánchez & Alfaro (2008) surveyed the positions of HII regions in several galaxies. They found that the fractal dimension, $D_{\rm c}$, of the distribution of HII regions decreases with increasing HII region brightness. For NGC 6946, $D_{\rm c}=1.64$ for high-brightness HII regions, $D_{\rm c}=1.82$ for medium-brightness, and $D_{\rm c}=1.79$ for low-brightness. They also found that among galaxies with more than 200 HII regions, the fractal dimension decreases slightly with decreasing galaxy brightness.

The fractal dimension is the ratio of the log of the number $N$ of substructures in a region to the log of the relative size $S$ of these substructures. If we imagine a square divided into $3\times 3$ subsquares, which are each divided into $3\times 3$ more subsquares, and so on, then the size ratio is $S=3$ for each level. If 6 of these subsquares actually contain an object like an HII region (so the angular filling factor is 6/9), then $N=6$ and the fractal dimension is $\log 6/\log 3=1.63$. If all 9 regions contain substructure, then the fractal dimension would be $\log 9/\log 3=2$, which is the physical dimension of the region, viewed in a 2-dimensional projection on the sky. Thus a low fractal dimension means a small filling factor for each substructure in a hierarchy of substructures. If the brightest HII regions have the smallest fractal dimension in a galaxy, then this means that the brightest HII regions are more clustered together into a smaller fraction of the projected area. This greater clustering is also evident from maps of the HII region positions as a function of brightness (Sánchez & Alfaro, 2008). The brightest HII regions tend to be clustered tightly around the spiral arms. Similarly, fainter galaxies have more tightly clustered HII regions than brighter galaxies.

The size distributions of star-forming regions can also be found by box-counting. Elmegreen et al. (2006) blurred an HST/ACS image of the galaxy NGC 628 in successive stages and counted all of the optical sources at each stage with the software package SExtractor. The cumulative size distribution of structures, which are mostly star-forming regions, was a power law with power 2.5 for all available passbands, B, V, and I, i.e., $n(>R)dR\propto R^{-2.5}dR$ for size $R$. The H$\alpha$ band had a slightly shallower power. They compared this distribution with the distribution of structures in a projected 3D model galaxy made as a fractal Brownian motion density field. They got good agreement when the power spectrum for the model equalled the 3D power spectrum of Kolmogorov turbulence, which has a slope of 3.66. Other power spectra gave either too little clumpiness of the structures (lower $n[>R]$ slope) or too much clumpiness (higher slope).

Azimuthal intensity profiles of optical light from galaxies have power-law power spectra like turbulence too. Elmegreen et al. (2003) showed that young stars and dust clouds in NGC 5055 and M81 have the same scale-free distribution as HI gas in the LMC (Elmegreen et al., 2001), both of which have a Kolmogorov power spectrum of structure. For azimuthal scans, the power spectrum slope was $\sim-5/3$ in all of these cases. Block et al. (2009) made power spectra of Spitzer images of galaxies. They included M33, which is patchy at 8$\mu$m where PAH emission dominates, and relatively smooth at $3.6\mu$m and $4.5\mu$m where the old stellar structure dominates. The power spectra showed this difference too: the slopes were the same as those of pure noise power spectra for the stellar images, and about the same as Kolmogorov turbulence for the PAH images. The grand-design galaxy M81 had the same pattern. Block et al. also reconstructed images of the galaxies over the range of Fourier components that gave the power-law power spectrum. These images highlight the resolved hierarchical parts of the galaxies. These parts are primarily star complexes and young stellar streams.

The central regions of some galaxies show highly structured dust clouds in HST images. The central disk in the ACS image of M51 shows this, for example. In the central regions of these galaxies, there are large shear rates, strong tidal-forces, sub-threshold column densities, strong radiation fields, and lots of holes and filaments in the dust. The origin of the holes is not known, although it is probably a combination of radiation pressure, stellar winds, and turbulence. Irregular dust in the center of NGC 4736 was studied by Elmegreen et al. (2002) using two techniques. One used unsharp mask images, which are differences between two smoothed images made with different Gaussian smoothing functions. Unsharp masked images show structure within the range of scales given by the smoothing functions. They also made power spectra of azimuthal scans. The power spectra were found to be power laws with a slope of around $-5/3$, the same as the slope for HI in the LMC and optical emission in NGC 5055 and M81. A possible explanation for the power-law dust structure in galactic nuclei is that this is a network of turbulent acoustic waves that have steepened into shocks as they move toward the center (Montengero et al., 1999).

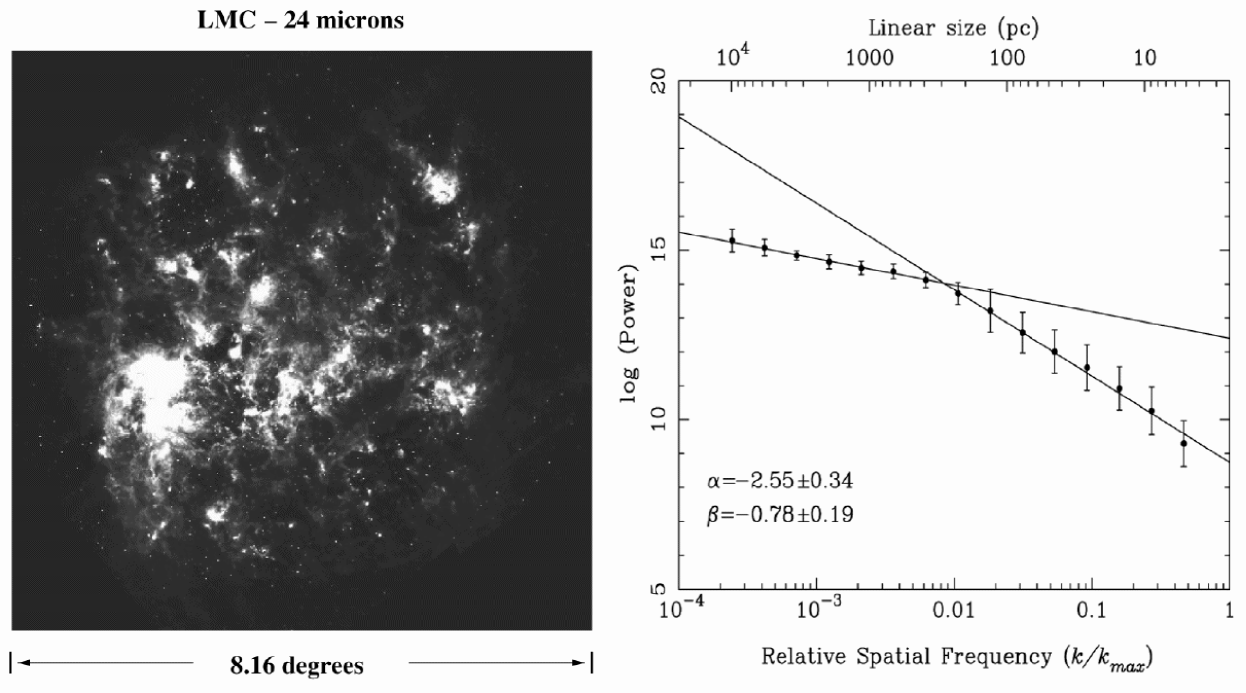
Block et al. (2010) made power spectra of the Spitzer images of the Large Magellanic Cloud at $160\mu$, $70\mu$, and $24\mu$ (see Figure 2). Again the power spectra are power laws, but now the power laws have breaks in the middle, as found previously in HI images of the LMC (Elmegreen et al., 2001). These breaks appear to occur at a wavenumber that is comparable to the inverse of the disk line-of-sight thickness. On scales smaller than the break, the turbulence is 3D and has the steep power spectrum expected for 3D, and on larger scales the turbulence is 2D and has the expected shallower spectrum. The LMC is close enough that each part of the power spectrum spans nearly two orders of magnitude in scale. The slopes get shallower as the wavelength of the observation decreases, so there is more small-scale structure in the hotter dust emission.

Power-law power spectra in HI emission from several other galaxies were studied by Dutta and collaborators. Dutta et al. (2008) obtained a power spectrum slope of $-1.7$ covering a factor of 10 in scale for NGC 628. Dutta et al. (2009a) found two slopes in NGC 1058 with a steepening from $-1$ to $-2.5$ at an extrapolated disk thickness of 490 pc (although their spatial resolution did not resolve this length). H$\alpha$ and HI power spectra of dwarf galaxies showed single power laws (Willett et al., 2005; Begum et al., 2006; Dutta et al., 2009b), as did the HI emission (Stanimirovic et al., 1999) and dust emission (Stanimirovic et al., 2000) of the Small Magellanic Cloud. The SMC has an interesting contrast to the LMC, both of which are close enough to make a power spectrum over a wide range of spatial scales. The LMC has a two component power spectrum, but the SMC has only a single power-law slope. The difference could be because the line-of-sight depth is about as long as the transverse size for the SMC, while the line-of-sight depth is much smaller than the transverse size for the LMC.

In addition to being correlated in space, clusters are also correlated in time. Efremov & Elmegreen (1998) found that the age difference between clusters in the LMC increases with the spatial separation as a power-law, age $\propto$ separation^1/2. Elmegreen & Efremov (1996) found the same age-separation correlation for Cepheid variables in the LMC. de la Fuente Marcos & de la Fuente Marcos (2009a) showed that this correlation also applies to clusters in the solar neighborhood. In both cases, the correlation is strongest for young clusters with a separation less than $\sim 1$ kpc, and it goes away for older clusters. Presumably the young clusters follow the correlated structure that the gas had when the clusters formed. Clusters form faster in regions with higher densities out to a kpc or so, which is probably the ISM Jeans length. This means that small star-forming regions (e.g., cluster cores) come and go during the life of a larger star-forming region (an OB association), and then the larger regions come and go during the life of an even larger region (a star complex). Eventually, the clusters, associations and complexes disperse when they age, taking more random positions after $\sim 100$ Myr. The correlation is about the same as the size-linewidth relation for molecular clouds (Larson, 1981), considering that the ratio of the size to the linewidth is a timescale.

Correlated star formation implies that some clusters should form in pairs. Cluster pairs were discovered in the LMC by Bhatia & Hatzidimitriou (1988) and in the SMC by Hatzidimitriou & Bhatia (1990). An example is the pair NGC 3293 and NGC 3324 near eta Carinae. de la Fuente Marcos & de la Fuente Marcos (2009b) studied these and other pairs. For NGC 3292/3324, the clusters are apparently weakly interacting and the age difference is 4.7 My. NGC 659 and NGC 663 are also weakly interacting and the age difference is 19.1 My. Dieball et al. (2002) determined the distribution function of the number of cluster members per cluster group in the LMC. They found a statistical excess of clusters in pairs compared to the expectation from random groupings.

Individual young stars are correlated in position too. Gomez et al. (1993) studied the 2-point correlation function for stars in the local star-forming region Taurus. For 121 young stars, there was a power law distribution of the number of stars as a function of their separation, which means that the stars are hierarchically correlated. (A similar correlation might arise from an isothermal distribution of stars without any hierarchical structure, as in a relaxed star cluster, but the Taurus region is not like this.) The correlation in Taurus extended from $0.15^{\prime\prime}$ of arc separation to at least $2^{\circ}$ separation – nearly 3 orders of magnitude. Larson (1995) extended this survey to smaller scales and found a break in the correlation at 0.04 pc. He suggested that smaller scales formed binary stars by fragmentation in clumps, and larger scales formed hierarchical groups by gas-related fragmentation processes, including turbulence.

Low mass x-ray stars in Gould’s Belt (i.e., T Tauri stars) show a hierarchical structure in all-sky maps (Guillout et al., 1998). This means that large groupings of T Tauri stars contain smaller sub-groupings and these contain even smaller sub-sub groupings. This is a much bigger scale than the Taurus region studied by Gomez et al. (1993). There has been no formal correlation of the large-scale structure in x-ray stars yet. The all-sky coverage suggests that the Sun is inside a hierarchically clumped complex of young stars.

To study hierarchical structure in a different way, Cartwright & Whitworth (2004) introduced a parameter, $Q$. This is the ratio of the average separation in a minimum spanning tree to the average 2-point separation. For example, suppose there are 5 stars clustered together in one region with a typical separation of 1 unit, and another 5 stars clustered together in another region with a typical separation of 1 unit, and these two regions are separated by 10 units. Then the minimum spanning tree has 4 separations of 1 unit in each region and 1 separation of 10 units (for the two closest stars among those two regions), for an average of $(8\times 1+1\times 10)/(8+1)=2$ units length. The average separation for all possible pairs is counted as follows: there are 5 stars with separation from another star equal to about 1 in each region, so that means 5 stars taken 2 at a time in each region, or 10 pairs with a separation of 1 in each region, or 20 pairs with this separation total, plus each star in one group has a separation of 10 units from each star in the other group, which is $5\times 5$ separations of 10 units. The average is $(20\times 1+25\times 10)/(20+25)=6$. The ratio of these is $Q=2/6=0.33$. Smaller $Q$ means more subclumping because for multiple subgroups, the mean 2-point separation has a lot of distances equal to the overall size of the region, so the denominator of $Q$ is large, but the minimum spanning tree has only a few distances comparable to the overall size of the system, one for each subgroup, and then the numerator in $Q$ is small.

Bastian et al. (2009) looked at the correlated properties of stars in the LMC, using a compilation from Zaritsky et al. (2004). There were about 2000 sources in each of several age ranges on the color-magnitude diagram. Bastian et al. determined the zero-points and slopes of the two point correlation function for each different age. They found that younger regions have higher correlation slopes and greater correlation amplitudes, which means more hierarchical substructure. Most of this substructure is erased by 175 Myr. They also evaluated the Cartwright & Whitworth (2004) Q parameter and found a systematic decrease in $Q$ with decreasing age, meaning more substructure for younger stars. Gieles et al. (2008) did the same kind of correlation and $Q$ analysis for stars in the Small Magellanic Cloud, and found the same general result.

In a hierarchically structured region, the average density increases as you go down the levels of the hierarchy to smaller and smaller scales. If there are dense star-forming cores at the bottom of the hierarchy, where the densities are largest and the sizes are smallest, then the fractional mass in the form of these cores increases as their level is approached. This is because more and more interclump gas is removed from the scale of interest as the densest substructures are approached. The fractional mass of cores is proportional to the instantaneous efficiency of star formation if the cores form stars. Therefore the local efficiency of star formation in a hierarchical cloud increases as the average density increases. The efficiency on the scale of a galaxy where the average density is low is $\sim 1$%; on the scale of an OB association it is $\sim 5$%, and in a cloud core where a bound cluster forms, it is $\sim 40$%. Bound cluster formation requires a high efficiency so there is a significant gravitating mass of stars remaining after the gas leaves. It follows that in hierarchical clouds, the probability of forming a bound cluster is automatically highest where the density is highest. Star clusters are the inner bound regions of a hierarchy of stellar and gaseous structures (Elmegreen 2008).

Outside the inner region, stars that form are not as likely to be bound to each other after the gas leaves. Then there are loose stellar groups, unbound OB subgroups, OB associations, and so on up to star complexes. Flocculent spiral arms and giant spiral-arm clouds are the largest scale on which gravitational instabilities drive the hierarchy of cloud and star-formation structures.

The hierarchy of young stellar structure continues inside bound clusters as well. Smith et al. (2005) found several levels of stellar subclustering inside the rho-Ophiuchus cloud, and Dahm & Simon (2005) found 4 subclusters with slightly different ages ($\pm 1$ Myr) in NGC 2264. Feigelson et al. (2009) observed X-rays from young stars in NGC 6334. The x-ray maps are nearly complete to stars more massive than $1\;M_{\odot}$ and their distribution is hierarchical, with clusters of clusters inside this region. Gutermuth et al. (2005) studied azimuthal profiles of clusters and found that they have intensity fluctuations that are much larger than what would be expected from the randomness of stellar positions; the stars are sub-clustered in a statistically significant way. Sánchez & Alfaro (2009) measured the fractal dimension and hierarchical-$Q$ parameter for 16 Milky Way clusters, using the ratio of cluster age to size as a measure of youth. They found that stars in younger and larger clusters are more clumped than stars in older and smaller clusters. Greater clumping means they have lower $Q$ and lower fractal dimension. Schmeja et al. (2008) measured $Q$ for several young clusters. For IC 348, NGC 1333, and Ophiuchus, $Q$ is lower (more clumpy) for class 0/1 objects (young) than for class 2/3 objects (old). Among four of the subclumps in Ophiuchus, $Q$ is lower and the region is more gassy where class 0/1 dominates; $Q$ is also lower for class 0/1 alone than it is for class 2/3 in Ophiuchus.

Pretellar cores are spatially correlated too. Johnstone et al. (2000) derived a power-law 2-point correlation function from $10^{3.8}$ AU to $10^{4.6}$ AU for 850$\mu$m sources in Ophiuchus, which means they are spatially correlated in a hierarchical fashion. Johnstone et al. (2001) found a similar power-law from $10^{3.6}$ AU to $10^{5.1}$ AU for 850$\mu$m sources in Orion. Enoch et al. (2006) showed that 1.1 $\mu$m pre-stellar clumps in Perseus have a power-law 2-point correlation function from $10^{4.2}$ AU to $10^{5.4}$ AU. Young et al. (2006) found similar correlated structure for pre-stellar cores from $10^{3.6}$ AU to $10^{5}$ AU in Ophiuchus. These structures could go to larger scales, but the surveys end there.

In summary, clusters form in the cores of the hierarchy of interstellar structures and they are themselves the cores of the stellar hierarchy that follows this gas. Presumably, this hierarchy comes from self-gravity and turbulence. Gas structure continues to sub-stellar scales. The densest regions, which are where individual stars form, are always clustered into the next-densest regions. Stars form in the densest regions, some independently and some with competition for gas, and then they move around, possibly interact a little, and ultimately mix together inside the next-lower density region. That mixture is the cluster. More and more sub-clusters mix over time until the cloud disrupts. Simulations of such hierarchical merging have been done by many groups, such as Bonnell & Bate (2006) and Maschberger et al. (2010). Because of hierarchical structure, the efficiency is automatically high on small scales where the gas is dense.

Barba et al. (2009) examined the giant star-forming region NGC 604 in M33 with NICMOS, finding mostly unclustered stars. Maíz-Apellániz (2001) categorized star formation regions according to three types: compact clusters with weak halos, measuring $50\times 50$ pc², compact clusters with strong halos measuring $100\times 100$ pc², and hierarchical, but no clusters, called “Scaled OB Associations” (SOBAs), measuring $100\times 100$ pc². Why do stars form in clusters some of the time but not always?

The occurrence of bound clusters in star forming regions could depend on many factors, but the pressure of the region relative to the average pressure should be important. Higher pressure regions should produce proportionally more clusters. Recall, that Elias, Alfaro & Cabrera-caño (2009) found a higher clustering fraction for the high-pressure Orion region compared to the low-pressure Sco-Cen region. One reason for a possible pressure dependence was discussed in Elmegreen (2008) and is reviewed here.

Turbulence produces a log-normal density probability distribution function (Vazquez-Semadeni, 1994; Price et al., 2010), and this corresponds to a log-normal cumulative mass fraction $f_{\rm M}(>\rho)$, which is the fraction of the gas mass with a density larger than the value $\rho$. This is a monotonically decreasing function of $\rho$. If the densest clumps have a density $\rho_{\rm c}$, and the star formation rate per unit volume is the dynamical rate for all densities with an efficiency (star-to-gas mass fraction) that depends on density, i.e., $SFR=\epsilon(\rho)\rho\left(G\rho\right)^{1/2}$, then the mass fraction of the densest clumps inside a region of average density $\rho$ is

$$\epsilon(\rho)=\epsilon_{\rm c}\left(\rho_{\rm c}/\rho\right)^{1/2}\left[f_{\rm M}(>\rho_{\rm c})/f_{\rm M}(>\rho)\right].$$

(1)

This function $\epsilon(\rho)$ increases with $\rho$ for intermediate to high density. If stars form in the densest clumps with local efficiency $\epsilon_{\rm c}$ ($\sim 0.3$), then $\epsilon(\rho)$ is the efficiency of star formation, i.e., the mass fraction going into stars for each average density. Bound clusters form where the efficiency is highest, and this is where the average density is highest. If we consider the density where $\epsilon(\rho)$ exceeds a certain minimum value for a bound cluster, then most star formation at this density or larger ends up in bound clusters.

Note that the observation of cluster boundedness appears to be independent of cluster mass and therefore independent of the presence of OB stars in the cluster. Bound clusters with highly disruptive OB stars form in dense cloud cores, just like clusters without these stars. The efficiency of star formation is therefore not related in any obvious way to the presence or lack of disruptive stars. The implication is that essentially all of the stars in a cluster form before OB-star disruption occurs. Perhaps the highly embedded nature of OB star formation, in ultracompact HII regions, for example, shields the rest of the cloud core from disruption for a long enough time to allow the lower mass cores to collapse into stars.

The pressure dependence for cluster boundedness arises in the theory of Elmegreen (2008) because at a fixed density for star formation, the slope of the $f_{\rm M}(>\rho)$ curve decreases for higher average density (the log-normal shifts to higher density), and the slope also decreases for higher Mach number because the log-normal gets broader. With a shallower slope at the density of star formation, the density where $\epsilon(\rho)$ exceeds the limit for bound cluster formation decreases, and the fraction of the mass exceeding this density increases. Thus forming a bound cluster happens at a lower density relative to the threshold for star formation when the pressure is high. A higher fraction of the gas then goes into bound clusters. The qualitative nature of this conclusion is independent of the details of the density pdf.

This discussion of cluster formation in a hierarchical medium assumes that the gas structure is already in place when star formation begins, and then the densest clumps, which are initially clustered together, form stars. The discussion can be made more dynamical if we consider that the denser regions fragment faster. This is what happens during a collapse simulation: the dense regions make more subcondensations and the low density regions collapse on to the dense regions. The result is a clustering of dense sub-condensations and a hierarchical clustering of stars.

The cluster mass function is a power law and it is natural to look for explanations of this that are related to the other power laws in star formation, including the hierarchical structure. If we imagine a cloud divided hierarchically into clumps and sub-clumps, then the mass distribution function of the nodes in this hierarchy is $dN/d\log M\sim 1/M$, or $dn/dM\sim 1/M^{2}$, because there is an equal total mass in all levels ($MN[M]d\log M=$ constant). This is the same as the mass function for star clusters. Also in such a hierarchy, the probability that a mass between $M$ and $2M$ is selected is proportional to $1/M$, as given by the number of levels and clouds at those levels having a mass in that range.

Cluster mass functions typically are a power law with a slope equal to this value, $dn/dM\sim M^{-\beta}$ for $\beta\sim 2$. This slope was found by Battinelli et al. (1994) for the solar neighborhood and Elmegreen & Efremov (1997) for the LMC, where the clusters were subdivided according to age. A second study of LMC clusters (Hunter et al., 2003) found the same slope for discrete cluster age intervals. It is important to consider clusters within a narrow age interval because older clusters are dimmer and the selection effects for clusters depend on their age. Zhang & Fall (1999) found $\beta=1.95\pm 0.03$ for young clusters in the Antenna galaxy, and $\beta=2.00\pm 0.08$ for old clusters. de Grijs & Anders (2006) looked at the LMC again and found $\beta=1.85\pm 0.05$ for various age intervals. de Grijs et al. (2003) found similar results in two other galaxies: $\beta=2.04\pm 0.23$ for NGC 3310 and $\beta=1.96\pm 0.15$ for NGC 6745.

The HII region luminosity function is about the same as the cluster mass function, having a slope of around $-2$ for linear intervals of luminosity. The first large study was by Kennicutt et al. (1989). Many other surveys have obtained about the same result (e.g., Banfi et al., 1993). Bradley et al. (2006) included 53 spiral galaxies and got a steeper slope at $\log L>38.6$ (for $L$ in erg s^-1), suggesting that larger HII regions were density bounded, and they also got a steep fall-off at $\log L>40$, suggesting an upper limit for cluster mass. The same general power law for HII regions has been obtained in detailed studies of individual galaxies (e.g., NGC 3389: Abdel-Hamid et al. (2003); M81: Lin et al. 2003; NGC 1569: Buckalew & Kobulnicky 2006; NGC 6384: Hakobyan et al. 2007; the Milky Way: Paladini et al. 2009).

There is growing evidence for an upper mass cutoff in the cluster mass function. In Gieles et al. (2006a, b), mass functions in M51 were fit to a double power law, i.e., with an increased slope at higher mass, or to a power law with $\beta=2$ throughout and an upper mass cutoff of around $10^{5}\;M_{\odot}$. A power law with an exponential cutoff is a Schechter function, $dN/dM=M^{-\beta}\exp(-M/M_{\rm c})$ for cutoff mass $M_{\rm c}$.

For several local galaxies, Larsen (2009) fit the brightest cluster and the 5th brightest cluster with a mass function having a cutoff. Larsen found that rich and poor spirals have about the same cluster mass functions, both with a cutoff, and that the cutoffs are independent of position in a galaxy. The origin of an upper mass limit for clustering is not known.

Gas is hierarchical in space and time, presumably because the gas is compressed by turbulent motions in a scale-free fashion. The self-gravitational force is scale free also at masses far above the thermal Jeans mass ($\sim 1\;M_{\odot}$). For a typical relationship between velocity dispersion and size that scales as $\sigma\propto R^{1/2}$, clouds of all masses at constant pressure have the same degree of gravitational self-binding.

Hierarchical cloud structure means that stars form in hierarchical patterns, and it follows then that the efficiency of star formation ($M_{\rm stars}/M_{\rm total}$) increases with the average density. Bound star clusters, which require a high efficiency, therefore form at high density. This explains at a very fundamental level why bound clusters form in the first place. Variations in the fraction of star formation that goes into bound clusters may be explained in the same way, with pressure playing an important role.

Hierarchical structure ensures that the clusters start with a mass function that is a power law with a slope close to $-2$. There could be an upper mass cut off.