Starbursts in Isolated Galaxies: the influence of the ISM model

Christian Theis Joachim Köppen

Abstract

We study the stability properties of isolated star forming dwarf galaxies which undergo dynamically driven star bursts induced by stellar feedback. Here we focus on the impact of the adopted ISM model, i.e. either a diffuse or a clumpy ISM. We apply a one-zone model extended for active dynamical evolution. This allows for a coupling between the dynamical state of the galaxy and its internal properties like star formation activity or the thermal state (or dynamical pressure, respectively) of the interstellar medium (ISM).

We found two major types of repetitive star bursts: one set (type A) of quasi-periodic star bursts is related to the dynamical timescale of the galaxy. In that case, the star formation follows the variations of the gas density induced by decaying virial oscillations. The second set (type B) of recurrent star bursts is characterized by a long quiescence period given by the sum of the dynamical and the dissiptional timescale: after a first burst, the inserted energy leads to a substantial expansion of the system, by this stopping any significant SF activity. A next burst might occur, when the gas reaches high densities again, i.e. after the gas recollapsed and the energy injected by stellar feedback is dissipated.

In case of a diffuse ISM model, type A bursts are the most common type due to the high efficiency of radiative cooling (no type B bursts are found). Bursts occur then mainly during an initial transitory phase. In case of a clumpy ISM model (i.e. dissipation by inelastic cloud-cloud collisions), the dissipative timescale is of the order of the dynamical time or longer. This allows for both, type A and type B bursts. Whereas initial transitory bursts are quite common, type B bursts are only found in a small mass range for given feedback and dissipation parameters.

Institute of Astronomy, University of Vienna, Türkenschanzstr. 17, 1180 Vienna, Austria

Observatoire Astronomique de Strasbourg, 11, rue de l’Université, F-67000 Strasbourg, France

1. Introduction

Starbursts are a well known phenomenon in some dIrrs (e.g. Gallagher & Hunter gallagher84 (1984); for a critical discussion of the exact definition of starbursts see Knapen & James knapen09 (2009)). They imply a mechanism to organise large-scale star formation which cannot operate all the time due to fast gas consumption. Moreover, the instability leading to an episodic SFR should work in a small parameter range only, because most of the isolated dIrrs seem to evolve in a highly self-regulated manner.

The first theoretical models dealing with the variability of the star formation rate in galaxies were based on closed-box models. For reasonable models of the interstellar medium (ISM) it turned out that stellar feedback is rather efficient in suppressing instabilities (e.g. Ikeuchi & Tomita ikeuchi83 (1983), Scalo & Struck-Marcell scalo86 (1986)). These models only allow for a burst-like behaviour when a long time-delay between star formation and stellar feedback is introduced. Köppen et al. (koeppen95 1995, hereafter KTH95) corroborated this result by investigating a simple numerical model motivated by full chemodynamical simulations. They demonstrated that the effective SFR is almost independent of the detailed recipe for the stellar birth function, provided a negative feedback due to the thermal state of the ISM is considered in the stellar birth function.

These box models, however, suffer from neglecting galactic dynamics. Several attempts have been made to study the evolution of isolated dwarf galaxies by taking full dynamics, as well as star formation and stellar feedback, into account (Kruegel et al. kruegel83 (1983), and later Hensler et al. hensler04 (2004), Pelupessy et al. pelupessy04 (2004), Struck struck05 (2005)). Though these calculations differ in many details, they agree in producing large-scale star formation variations on dynamical timescales which indicates the crucial role dynamics plays for episodic starbursts.

A major disadvantage of numerical simulations is their complexity. This often prevents a detailed investigation of the parameter space. Instead of analysing dwarf galaxies by such detailed models, we apply a set of equations that is as simple as possible, but still incorporating the generic features of the complex numerical simulations. We use an extended version of the analytical models of KTH95 that allows us to deal with the dynamical evolution of a galaxy in a simple way (for details cf. to Theis & Köppen theis09 (2009)). Here we compare the evolution of dwarf galaxies for two different ISM models: in the diffuse ISM model energy is dissipated by radiation, whereas in the clumpy ISM model energy is lost via inelastic cloud collisions.

2. Results

Diffuse ISM models. Fig. 1 shows the evolution for the diffuse ISM model. Due to strong cooling, the gas temperature drops almost immediately to values near $10^{4}{\rm K}$ bringing the system far out of virial equilibrium. In the ongoing collapse the density increases and the gas temperature drops even more. The cooling and density enhancement continue, until star formation becomes more prominent after about 100 Myr. The first stars reinject energy to the ISM leading to the quasi-equilibrium stage known from the box models of KTH95. However, different to them, the density still increases due to the ongoing collapse. Though the star formation and, by this, the stellar energy injection grows, the feedback cannot stop further collapse, because cooling is too efficient to prevent the gas from reaching virial equilibrium. The collapse proceeds until the angular momentum barrier becomes dominant and the system expands. Then the first star burst episode finishes and the gas is quickly heated to $10^{4}{\rm K}$ . However, due to the strong enhancement of the cooling rate at temperatures beyond $10^{4}{\rm K}$ , the gas never reaches the virial temperature.

The longterm evolution of this model shows that the previously discussed bursts are just transitory phenomena. The oscillations are almost completely damped after 2 Gyr. Such a behaviour, i.e. only an initial burst, was found in almost all models with radiative cooling as source of dissipation.

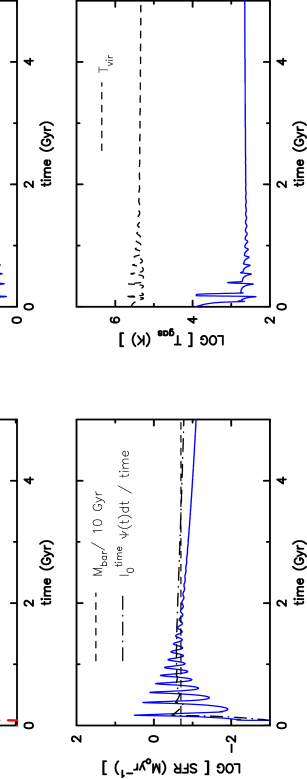
Refer to caption — Figure 1.: Evolution of a model with a baryonic mass of $2\cdot 10^{9}\,{\rm M}_{\odot}$ . Shown are the masses of the baryonic components (upper left), the mean radius of the system (upper right), the total SFR (lower left), and the gas temperatures, i.e. the actual temperature and the virial temperature (lower right).

Clumpy ISM models. The evolutionary behaviour changes when applying the clumpy ISM model. Though the structure of the equations remains identical, the dissipational timescale differs substantially from the previous case in which the cooling timescale was much shorter than other involved timescales. For cloud-cloud collisions, the timescale $\tau_{\rm coll}$ becomes of the order of Gyrs.

Driven by stellar feedback and the much longer dissipational time the ISM expands after the first burst (Fig. 2, upper right). The dark matter halo, however, prevents the gas from being blown-away. Therefore, it collapses again reaching a dynamical equilibrium after about 2 Gyrs. This can be seen from a comparison between the actual kinetic temperature (velocity dispersion of the cloud system) and the virial temperature of the system. The ongoing evolution is governed by a slow loss of energy due to dissipation. During this stage of slow shrinkage the evolution is close to virial equilibrium. After 6 Gyrs the system lost sufficient energy to start with the next run-away collapse resulting in another starburst event after a long period of quiescence. Finally, the galaxy produces stars on a mean rate of about $0.1M_{\hbox{$\odot$}}\mathrm{yr}^{-1}$ .

Discussion

The main difference between the two model scenarios is the ratio $r$ between the dissipational timescale $\tau_{\rm diss}$ and the dynamical timescale $\tau_{\rm dyn}$ . In case of the diffuse ISM model (small $r$ ) the energy input by the stars is almost instantaneously radiated away. Therefore, the radial oscillations are only decaying initial virial oscillations acting on a dynamical timescale. This behaviour turned out to be rather robust against variations of model parameters like stellar heating, gas mass, initial size or stellar birth function.

On the other hand, when $r$ becomes of the order of one or larger (i.e. for the clumpy ISM model), two timescales are important: the dynamical timescale and the dissipational timescale. After a first burst, a long period ( $\tau_{\rm dyn}+\tau_{\rm diss}$ ) of quiescence follows, before the next star formation episode starts.

During most of the quiescence phase the gas is semi-adiabatically accreted with an average infall velocity of only a few km s^-1. The related extended gas reservoirs are known around many dwarf galaxies (e.g. NGC 4449). They are very sensitive to perturbations by other galaxies. E.g. a substantial amount of the gas might be stripped off, by this reducing the strength of the second burst.

After the second burst the galaxy enters a phase with continuous star formation up to the present (here: 10 Gyr). This is in agreement with observations of several dIrrs which still show a substantial, more or less continous star formation ongoing over the last one or few Gyrs (e.g. Greggio et al. greggio93 (1993)).

Acknowledgments.

CT gratefully acknowledges support by the Univ. of Vienna and by the DFG Priority Programme 1177 ‘Galaxy Evolution’.

References

(1)
(2) Gallagher, J.S., Hunter, D. 1984, ARA&A, 22, 37
(3) Greggio, L., Marconi, G., Tosi, M., & Focardi, P. 1993, AJ, 105, 894
(4) Hensler, G., Theis, Ch., Gallagher, J. 2004, A&A, 426, 25
(5) Ikeuchi, S., Tomita, H. 1983, PASJ, 35, 77
(6) Knapen, J.H., & James, P.A. 2009, ApJ, 698, 1437
(7) Köppen, J., Theis, Ch., & Hensler, G. 1995, A&A, 296, 99
(8) Kruegel, E., Tutukov, A., & Loose, H. 1983, A&A, 124, 89
(9) Pelupessy F.I., van der Werf, P.P., Icke, V. 2004, A&A, 422q, 55
(10) Scalo, J., Struck-Marcell, C. 1986, ApJ, 301, 77
(11) Struck, C. 2005, in Proc. of Starbursts: From 30 Doradus to Lyman Break Galaxies, Cambridge, UK, R. de Grijs & R.M. Gonzalez-Delgado (eds.), Ap&SS, 329, 163
(12) Theis, Ch., & Köppen, J. 2009, A&A, 502, 45