Statistical and Analytical Approaches
to
Finite Temperature Magnetic Properties of SmFe12 compound
Abstract
To investigate the magnetic properties of SmFe12, we construct an effective spin model, where magnetic moments, crystal field (CF) parameters, and exchange fields at 0 K are determined by first principles. Finite temperature magnetic properties are investigated by using this model. We further develop an analytical method with strong mixing of states with different quantum number of angular momentum (-mixing), which is caused by strong exchange field acting on spin component of electrons. Comparing our analytical results with those calculated by Boltzmann statistics, we clarify that the previous analytical studies for Sm transition metal compounds over-estimate the -mixing effects. The present method enables us to make quantitative analysis of temperature dependence of magnetic anisotropy (MA) with high-reliability. The analytical method with model approximations reveals that the -mixing caused by exchange field increases spin angular momentum, which enhances the absolute value of orbital angular momentum and MA constants via spin-orbit interaction. It is also clarified that these -mixing effects remain even above room temperature. Magnetization of SmFe12 shows peculiar field dependence known as first-order magnetization process (FOMP), where the magnetization shows an abrupt change at certain magnetic field. The result of the analysis shows that the origin of FOMP is attributed to competitive MA constants between positive and negative . The sign of appears due to an increase in CF potential denoted by the parameter () caused by hybridization between -electrons of Fe on () site and and valence electrons on Sm site. It is verified that the requirement for the appearance of FOMP is given as .
pacs:
Valid PACS appear hereI Introduction
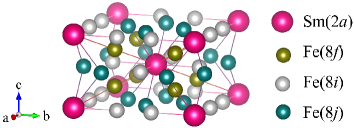
There have been intensive studies on developing new rare-earth () lean permanent magnetic materials which have strong magnetic properties comparable to those of Nd-Fe-B. Nitrogenated compounds as NdFe12N or NdFe11TiN have been considered to be candidates of such materials, and thus series of experimental and theoretical efforts have been made to figure out the magnetic properties of these materials Miyake ; Hirayama1 . SmFe12 with the ThMn12 structure (Fig. 1) is also a possible candidate and has attracted renewed interest because it exhibits excellent intrinsic magnetic properties such as uniaxial magnetocrystalline anisotropy Hadjipanayis . Although SmFe12 itself is thermodynamically unstable, it has been known that the substitution of Fe with a stabilizing element, such as Ti or V, can remove this difficulty Ohashi1 ; Ohashi2 ; Hu ; Kuno ; Schoenhoebel . In these systems, however, the saturated magnetization is reduced due to anti-parallel alignment of magnetic moments of Ti and V relative to those of Fe. Recent development of the synthesis technology made it possible to fabricate highly textured single phase samples of SmFe12 thin film Kato ; Hirayama2 ; Ogawa1 ; Ogawa2 ; Sepehri-Amin3 , and it has been shown experimentally that Co substitution for Fe enhances their magnetic properties, such as Curie temperature and magnetic anisotropy (MA) Hirayama2 . Thus, SmFe12-based systems belong to one of the most promising hard magnetic materials, and therefore to clarify the basic magnetic properties of SmFe12 is crucially important.
So far many attempts have been performed for microscopic understanding of the magnetic properties of based permanent magnets Evans ; Toga ; Nishino ; MiyakeAkai ; Yoshioka ; Tsuchiura2 . Among them a powerful method is to combine the first-principle calculations for electronic states at the ground state with a suitable model for finite temperature properties Yamada ; Sasaki ; Miura-direct ; Miura-pl ; Kuzminlinear ; Kuzmin2nd ; Kuzminlimit ; Millev ; Kuzminmix ; Magnani . As for SmFe12, Harashima et al. (2015) Harashima , Körner et al (2016) Koerner and Delonge et al (2017) Delange performed the first-principle calculations and model analysis of magnetic properties. In the theoretical study of Sm-based intermetallic compounds, however, there remains a basic issue how to deal with the formidably strong -mixing effects in Sm. This is the problem studied for a long period on the Sm-based magnets VanVleck ; Sankar ; Wijin . There are some attempts to include the -mixing in the analytical form by the first-order perturbation for the crystal fields (CFs) Kuzminmix ; Magnani . However, Kuz’min pointed out that the Sm-based magnetic materials are exceptional for application of the method Kuzminmix .
We have recently developed a similar method Yoshioka ; Tsuchiura2 , in which the model parameters are calculated by the first-principles and the finite temperature magnetic properties are calculated in a statistical way, and applied it to Fe14B systems. By taking into account CF parameters up to 6-th order, the model satisfactorily explained the experimental results for magnetization curves and the temperature dependence of MA constants Yoshioka ; Tsuchiura2 . Using the method we recently calculated the temperature dependence of the MA constants of SmFe12 and showed that and in consistence with experimental results Ogawa2 . The report of the work, however, contains only the final results and no details of computational procedure have been presented. As a results no explanations on the mechanism for the results that and have been given.
The purpose of the present study is thus to clarify the origin of the finite temperature magnetic properties of SmFe12 compound by statistical and analytical ways. To this end, we describe the details of the statistical method and develop a novel analytical method. The analytical procedure is able to derive simple relations between the temperature dependence of magnetic properties and parameters determined by first-principles electronic structure calculations. The treatment of the -mixing effects adopted previously by the other groups Kuzminmix ; Magnani will be modified, and the results will be compared with the statistical results of the temperature dependence of magnetic properties of SmFe12. Good agreement between the analytical and statistical results guarantees the applicability of the modified analytical formula to Sm compounds.
In the following, we give the model Hamiltonian, the parameters of which are determined by the first-principles, and present the calculation procedure for finite temperatures, especially the statistical method to obtain the MA constants and magnetization curves, and explain the modified analytical method. The latter method may clarify the relations among the free energy of the system, the CF, and the exchange field. Using the analytical method, we will show that the mechanism of and in SmFe12 is attributed to the characteristic lattice structure around Sm ions, that is, crystallographic 2-sites on -axis adjacent to Sm are vacant. We also present results on the magnetization process and nucleation fields by calculating Gibbs free energy. As pointed out in Ref. Tsuchiura2 , this analytical spin model can be easily extended to Sm ions around the intergranular phases, which is crucially important in the coercivity mechanism Sepehri-Amin1 ; Sepehri-Amin2 ; Sepehri-Amin3 .
This paper is organized as follows. The model Hamiltonian is explained in Section II, and the procedure of the statistical and analytical method are explained in Section III. Section IV shows the results of temperature dependence of magnetic properties calculated in the statistical and analytical methods. A summary of our work is given in Section V.
II Model Hamiltonian
We adopt a following Hamiltonian to investigate the magnetic properties of transition metal () compounds:
| (1) |
where is a Hamiltonian for ion on -th site and is the number of ion in the unit cell volume . Second and third term represent the phenomenological treatment of MA energy and Zeeman term on sublattice, where and are the temperature dependent anisotropy constant and magnetization vector of sublattice, respectively, and is the polar angle of against the -axis. is given as by using the absolute value of the sublattice magnetization and a directional vector of . is defined by a part of magnetization subtracting the electron contribution from the total magnetization. is an applied field.
II.1 Hamiltonian of Single Ion
The Hamiltonian for shell in -th ion in Eq. (1) is
| (2) |
with
| (3) |
The first and second terms in Eq. (2) represent the single electron contribution and the electron-electron repulsion in shell, respectively, where is the number of electrons, and are the vacuum permittivity and the elementary charge, respectively. in Eq. (3) is the Hamiltonian for -th electron on -th site, where the first term in Eq. (3) is the spin-orbit interaction (SOI) between spin () and orbital () angular momenta, with a coupling constant . The second term represents the exchange interaction between spin moment and temperature dependent exchange field on -th site, where is the Bohr magneton. The third and fourth terms are the CF and Zeeman terms, respectively. In the expression of CF, and are Coulomb potential and radial parts of the wave function on -th site, respectively. Note that the kinetic energy and screened central potential terms are effectively taken into account in the formation of orbital.
To obtain the electronic properties at , we apply the first-principles and determine the parameters in the Hamiltonians in Eq. (3). We use the full-potential linearized augmented plane wave plus local orbitals (APW+lo) method implemented in the WIEN2k code wien2k . The Kohn-Sham equations are solved within the generalized-gradient approximation (GGA). To simulate localized states, we treat states as atomic-like core states, which is so called opencore method Richter1 ; Novak ; Hummler0 ; Richter2 ; Divis1 ; Divis2 .
We calculate the ground state properties of SmFe12 such as Coulomb potential, charge distribution, and sublattice magnetizations. In accord with the previous theoretical studies for SmFe12 Harashima ; Koerner ; Delange , we assume that Sm ion has trivalent-like electronic structure. The exchange fields at are determined from an energy increase caused by spin flip of electrons Brooks ; Yoshioka , and CFs acting on -th electron are directly estimated from Coulomb potential acting on -th site. It is noted that the single ion Hamiltonian thus determined for -th ions includes effects of atoms surrounding the ions as a mean field.
Practically, the CF term is rewritten as the following formula Novak ; Richter2 :
| (4) | ||||
| (5) |
where is CF parameter on -th site, is a numerical factor Hutchings , is tesseral harmonic function of a solid angle , and is a cut-off radius.
Values of CF parameters in Eq. (5), exchange field in Eq. (3), -sublattice magnetization in Eq. (1) in SmFe12 are shown in TABLE 1. The lattice constants used in this calculations are the experimental values Å and Å Hirayama2 . For Wycoff positions, we apply the theoretically optimized ones given in Ref. Harashima . The crystal structure of SmFe12 is shown in Fig. 1.
| (0) | ||||||
|---|---|---|---|---|---|---|
| -71.4 | -21.3 | -49.3 | 5.9 | 3.0 | 296.1 | 51.6 |
II.2 Single Ion Hamiltonian
in Coupling Regime
We here apply the concept of coupling to the single electron Hamiltonian of Eq. (3) with Russell Saunders states , due to the strong Coulomb interaction between electrons. According to the Hund’s rule, we specify the quantum number of total orbital (spin) moment . Total angular momentum is varied from to , and is the magnetic quantum number. Thus the single ion Hamiltonian in Eq. (2) can be reduced to:
| (6) | ||||
| (7) | ||||
| (8) | ||||
| (9) | ||||
| (10) |
Hereafter, the site index is omitted for single-ion quantity. and are total orbital and spin momenta of electrons, respectively, and for , and . In the treatment of SOI, we should note that the eigenstates of coupling are specified by the quantum number of . In general, the term is dominating in Eq. (6). Thus is a good quantum number in most of the - systems. Because the coupling in Sm compounds is weak compared with other ones, it is necessary to include excited -multiplets. Hereafter, we abbreviate the states as .
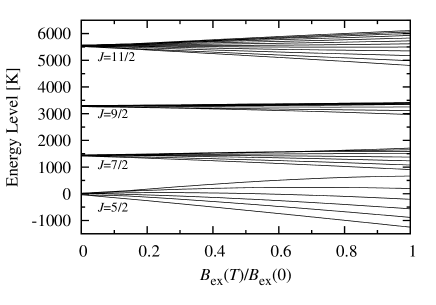
The energy levels of Sm- states in SmFe12 depend on and applied field . Fig. 2 shows the dependence of the energy levels for =, which is a unit vector parallel to -axis, and for . The data needed are given in TABLE 1. As for SOI constant, we use experimental value of K Elliott . At the is strongly coupled with to form a Kramers doublet with a total angular momentum due to the large coupling with fine CF splitting. With increasing , the exchange field breaks the time-reversal symmetry and lift the degeneracy.
II.3 Phenomenological Model for Sublattice
For finite temperature magnetic properties of TM, we apply a phenomenological formula assuming uniform and . For , we apply the Kuz’min formula Kuzminmag :
| (11) | ||||
| (12) |
where, is Curie temperature and is a fitting parameter. The temperature dependence of has been expressed by an extended power law Miura-pl :
| (13) |
where and are fitting parameters.
In present study for SmFe12 compound, we use values of and K in Eq. (12), as used by Hirayama . Hirayama2 . They showed that the magnetization agrees well with experimental measurement for SmFe12. The values of , and in Eq. (13) are determined as , and K, respectively, by fitting the expression to observed data for YFe11Ti in Ref. Nikitin .
III Method of Model Calculations
III.1 Statistical Method
To calculate the finite temperature magnetic properties, we use the model Hamiltonian and calculate MA and magnetic moment for Sm electrons using the statistical method for the partial system. Using the eigenvalues of the Hamiltonian Eq. (6), we express the free energy density as,
| (14) | ||||
| (15) | ||||
| (16) |
where is Gibbs free energy for - partial system, and are the eigenvalue and the partition function of -th Hamiltonian [Eq. (6)] for given , respectively. The direction of the magnetization is treated as an external parameter. The equilibrium condition of the system for given and is:
| (17) |
where is the direction of sublattice magnetization in the equilibrium. In practice, we determine the minimal numerically by changing .
The MA energy is given by the free energy with different directional vector . In the tetragonal symmetry, in is formally expressed as Kuzminlinear ; Miura-pl :
| (18) |
where and are polar and azimuthal angle of , respectively, indicates the greatest integer of , and and are out-of-plane and in-plane MA constant for -th ion. The is an angle independent constant. The series expansion does not guarantee the convergence Kuzmin2nd ; Kuzminlimit , however, for finite , can be obtained from the comparison between Taylor series of of Eqs. (15) and (18) with respect to for a fixed Sasaki ; Miura-direct as:
and
respectively, which are resulting in
| (19) | ||||
| (20) |
etc. Using MA energy on the single ion in Eq. (18), the total MA constants are obtained as
| (21) | |||||
| (22) |
where and are out-of-plane and in-plane MA constant in whole system.
The orbital and spin components of the magnetic moment of a single ion in the equilibrium, can be calculated by:
| (23) | ||||
| (24) |
respectively, where and is the -th eigenstate for , and the total magnetization is given as,
| (25) |
with .
Finally, to confirm the convergence of the probability weights for excited- multiplet states at , we define a following weight function:
| (26) |
In the case of SmFe12 crystal, the value of is independent of site index .
| 5/2 | 7/2 | 9/2 | 11/2 | |
|---|---|---|---|---|
| =0 | 0.93217 | 0.06548 | 0.00229 | 0.00005 |
| 0.90536 | 0.09049 | 0.00406 | 0.00009 |
The results are shown in TABLE 2, which indicates good convergence of weight for the number of the excited -multiplets even at K. Thus in the calculation using statistical method for SmFe12, we take the excited -multiplets up to . In the analytical calculation, the -mixing effects are approximately treated only for the lowest- multiplet by using unitary transformation.
III.2 Analytical Method
According to hierarchy of energy scale in intermetallic compounds: , we develop an analytical method for finite temperature magnetic properties, which enables us to connect the thermodynamic properties directly to our model parameters based on electronic states. Practically, we generalize the analytical expression of Gibbs free energy Yamada ; Kuzminlinear to include the effects of -mixing using a first-order perturbation for the CF potential and Zeeman energy. We also derive an analytical expression for the magnetization curve, which enables us to estimate the CF potential using the observed results. The procedure of the formalism consists of (i) construction of starting Hamiltonian for single ion, (ii) approximation for diagonal matrix element of an effective Hamiltonian, (iii) finite temperature perturbation for single ion, and (iv) thermodynamic analysis.
III.2.1 Effective Lowest- Multiplet Hamiltonian
for Single Ion
To restrict in low-energy subspace for , the effective lowest- multiplet Hamiltonian is obtained by unitary transformation and projection, where the off-diagonal matrix elements between inter- multiplets become negligibly small, and compensating term is added in diagonal element for lowest- multiplet. We here introduce modified version of effective Hamiltonian as explained below.
First, we define a rotational operator which transforms the quantization axis to . With this operator, the Hamiltonian and (=ex, CF and Z) is transformed to:
| (27) |
| (28) | ||||
| (29) | ||||
| (30) | ||||
| (31) |
where , is the spherical tensor operator with rank for angular momentum Edomonds , and is a magnetic field tensor: and . is the Wigner’s function. Now we apply a unitary transformation (Schrieffer-Wolf transformation Schrieffer ) to ,
| (32) |
and introduce a projection operator , by which the space of the -multiplet is restricted to the lowest one. The operator is defined so as to remove the first-order off-diagonal matrix elements for in :
| (33) |
Apparently, . The second term of the right-hand-side of Eq. (32) has now a diagonal matrix with corrections to the diagonal elements in the original . The second and higher-order terms in are neglected. By inserting Eq. (33) to Eq. (32), we obtain
| (34) | ||||
| (35) | ||||
| (36) |
where and (=ex, CF and Z). We here classify analytical models depending on the approximation to the matrix element of for in Eq. (33) as follows:
-
•
model A: Lowest- multiplet without mixing as:
-
•
model B: Effective lowest- multiplet with mixing as:
-
•
model C: Modified effective lowest- multiplet with mixing (present study) as:.
where . The approximations are referred to as model A, B and C, hereafter. By using , Magnani . derived the effective lowest- multiplet Hamiltonian Magnani and Kuz’min had also derived an equivalent approximation for anisotropy constants Kuzminmix . In the latter work, it was pointed out that the approximations of the models A and B are not applicable to the Sm compounds due to relatively small . In the present study, we have modified to .
III.2.2 Approximation for Diagonal Matrix Element of
The energy levels for electron system are obtained by the exact diagonalization of in Eq. (6), and the diagonal matrix elements of can be expressed as:
| (37) |
through two unitary transformations by and . The first term in Eq. (37) can be obtained by using the relation and Wigner Eckert theorem Edomonds ,
| (38) |
where is the Stevens factor Stevens ; Hutchings . By using the model C with , the second term in Eq. (37) is approximated as,
| (39) |
where . Contributions from and are neglected in the second term of the square bracket. By using Wigner-Eckert theorem Edomonds and the relation for products of the matrix elements of the spherical tensor operators given by Eq. (5) in chapter 12. of Ref. Varshalovich , the diagonal matrix element is expressed as follows:
| (40) |
where . We here use the relation assuming as light rare-earth and and for Ce3+ and Sm3+, respectively, and in the other cases.
More explicit expression of depends on further approximations. So far two approximations have been adopted; one completely neglect the term , that is, Kuzminlinear , and the other is an approximation to neglect the second term in the square bracket in Eq. (39) which was adopted by Kuz’min Kuzminmix and Magnani Magnani . According to the model approximations of with A, B, and C, the quantities are denoted as with =A, B, and C. Clearly , and for =B and C,
| (41) |
with
| (42) |
where we formally set .
The energy levels for electron system, which consist of the lowest energy to the -th excited energy , are now expressed as,
| (43) |
(=A, B, and C) with to for the model A, B, and C.
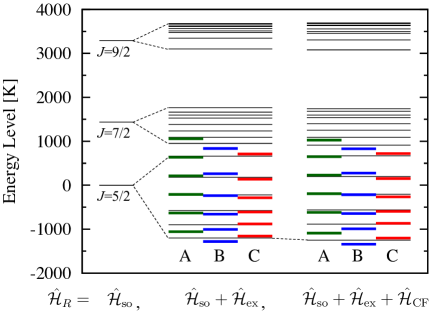
Fig. 3 shows the diagonal matrix element (=A, B, and C) of the effective lowest- multiplet Hamiltonian at in Eq. (43). Note that CF coefficients and exchange fields are determined by the first principles, and the same values are used for models A, B and C. The results are compared with the exact results. To distinguish the contribution from each , and in of Eq. (6), the original Hamiltonian is taken as , , or .
Let us first describe the characteristics for the result . In model A, the sixfold degeneracy of energy levels given by splits into equi-energy levels as . In model B, the equi-energy levels shift to lower energy states by -mixing term, In model C, the energy shifts, which was over-estimate by the -mixing term, are corrected.
The results obtained by show that the effect of CF potentials on the energy levels is weak, as expected, and they reproduce the results obtained by the numerical exact diagonalization method as shown in Fig. 3.
III.2.3 Finite Temperature Perturbation for Single Ion
We apply the first-order perturbation at finite temperature assuming . The unperturbed and perturbed Hamiltonians are and , respectively. Note that is effectively taken into account in the -multiplet formation of the ion. The approximated Gibbs free energy for - partial system on -th site up to first-order perturbation is formally expressed as , where , , and . More explicitly, it is given as,
| (44) |
by using in Eq. (43). It is noted that is model dependent because equals to , or , corresponding to the model adopted.
By using Helmholtz free energy for - partial system, the Gibbs free energy in the modified effective lowest- model is given as,
| (45) | ||||
| (46) |
with
| (47) | ||||
| (48) | ||||
| (49) |
Here , and the model dependence appears in , which is denoted as with =A, B or C. For =A, and for =B and C,
| (50) |
with
| (51) | ||||
| (52) |
where is the generalized Brillouin function Kuzminlinear defined by with for , where . The analytical expression of is given in Ref. Magnani and , and are linear combination of and , and , , and , respectively, as shown in Eq. (50).
Because of the first-order perturbation for , an analytical expression of the magnetic moment is obtained as with:
| (53) | ||||
| (54) |
where and are orbital and spin component of magnetic moment on the ion. It is noted that and are model dependent because of the model dependence of as shown above.
Within the finite temperature perturbation theory, the angular dependent part of single ion free energy in Eq. (47) with the tetragonal symmetry can be written by:
| (55) |
which is a truncated form of in Eq. (18). The is an angle independent constant. For example, the leading anisotropy constants for a trivalent magnetic light ion (Ce3+, Pr3+, Nd3+, Pm3+, and Sm3+) can be written as follows:
| (56) | ||||
| (57) |
All terms of MA constants in model A,B, and C are given by linear terms with respect to .
We may rewrite the approximations used and adopted in the present formalism by using in Eq. (50) as follows:
-
•
model A: Lowest- multiplet without mixing as or Kuzminlinear
- •
-
•
model C: Modified effective lowest- multiplet with mixing as (present study).
At , we have found a following simple relation holds between and as:
| (58) |
Because is independent of , relations among the models =A, B, and C on and can be generally expressed as follows:
| (59) | ||||
| (60) |
III.2.4 Thermodynamic Analysis
Finally we investigate the thermodynamical instability by using the thermodynamic relation between Gibbs and Helmholtz free energy, which explicitly contains the CF potentials and the exchange field determined by first principles. We have to note that above the room temperature the exchange contribution decreases with increasing temperature at a rate proportional to , so the energy hierarchy is changed and thermal fluctuation effects have to be considered as . Even in this case, the formulation derived here based on generalized Brillouin function holds as shown by Kuz’min in Refs. Kuzminmix ; Kuzminlimit . In this thermodynamic analysis, we use the model C.
By applying the finite temperature perturbation theory to the lowest- multiplet Hamiltonian, the approximated Gibbs free energy density for whole system can be expressed as:
| (61) | ||||
| (62) | ||||
| (63) |
where is Helmholtz free energy density for whole system with model C and and are corresponding energy for -shell and expectation value of magnetic moment on -th ion given in Eq. (47) and Eq. (46), respectively. The temperature dependence of can be expressed as the linear combination of the generalized Brillouin functions for ion and the temperature coefficient for ion in Eq. (12). The equilibrium condition is the same as Eq. (17), where becomes the direction of total magnetization in the equilibrium. We can also analyze the instability of magnetic metastable states, which are crucially important in permanent magnetic materials. The metastable condition is for given and with .
The MA constants in whole system are obtained by combining the contribution from sublattice in Eq. (55) with Fe sublattice same as Eqs. (21) and (22). can be substituted into the so called Krönmuller equation Kronmuller1 ; Kronmuller-text to obtain the coercive field
| (64) | ||||
| (65) |
where and are coercive and nucleation field, respectively. is microstructural parameter and is local effective demagnetization factor Kronmuller-text . The gives upper limit of .
IV Calculated Results for SmFe12
IV.1 Valence Mechanism of Magnetic Anisotropy
We first calculate the charge density distribution and Coulomb potential at 0 K on constituent atoms of SmFe12 lattice (Fig. 1) using the first principles. The calculated results determine the values of CF acting on electrons, the magnitude of the exchange field acting on the , and the magnitude of sublattice magnetization. These values are used for parameter values in the model Hamiltonian. The contribution to the CF from the charge density distribution inside (outside) the muffin-tine sphere radius is called ”valence (lattice) contribution” Hummler0 . If the CF is dominated by the former contribution, we call the mechanism of the MA ”valence mechanism” Tsuchiura1 .
The charge density distributions of single ion are approximately replaced with charge density on atomic orbitals of and states. To evaluated the valence contribution to CF parameters , we introduce distribution parameters Coehoorn ; Sakuma and defined as,
| (66) |
where is the solid angle and indicates the multiple orbitals for the quantum number (). The shape of the function in Eq. (66) is given in Fig. 5(c).
The particular cases are as follows:
| (67) | ||||
| (68) | ||||
| (69) |
where is the occupation number of the (, ) orbital. We note that . Valence contribution of and are determined as Richter1 ; Hummler0 ,
| (70) | ||||
| (71) |
with the Slater-Condon parameters:
| (72) |
where and . Via Eqs. (70) and (71), the distribution parameters determine . It may be noted that no and orbitals exist for .
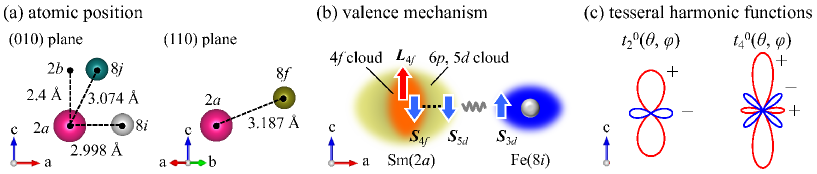
A simple explanation for the appearance of the uniaxial MA in a Sm ion surrounded by Fe atoms is given as follows. Fig. 5(a) shows the lattice strucutre of SmFe12 Hirayama2 ; Harashima . Left panel of Fig. 5(b) shows the location of Sm and Fe on (010) plane of the lattice. Because of the short atomic distance between Sm and the first nearest neighbor (n.n.) Fe() sites, the distribution of valence electrons on Sm extends within the plane as shown in Fig. 5(c). According to the negative sign of in Fig. 5(d), the distribution parameters defined by Eq. (66) in terms of electron numbers of and -orbitals are negative; , . Therefore, we obtain by Eq. (70) in agreement with the numerical value of shown in TABLE 1. As shown by Eq. (56) the main contribution of the MA constant is given by a product of and the positive value of Stevens factor , and becomes positive. This means that the because .
On the other hand, second neighbor Fe(8) and third neighbor Fe(8) atoms of Sm atom are situated obliquely upward as shown in Fig. 5(b). According to the negative sign of shown in Fig. 5(d), we obtained using Eq. (69), and from Eq. (71). Again the negative value is consistent with the numerical values of . The main contribution of MA constant comes from a product of and the positive value of , and results in .
Thus, the sign of MA constants and are determined by the configuration of Sm and Fe atoms in the lattice. In the following, we investigate the -mixing effect on single Sm magnetic properties at K.
IV.2 -Mixing Effect and Zero-Temperature Magnetic Properties of SmFe12 Compound
To clarify the -mixing effect on single-ion magnetic properties, we show the calculated results of the magnetic moments and the MA constants for model A, B, and C in TABLE 3. We used Eqs. (53) and (54) for and Eqs. (56) and (57) for , and the values of , , and in TABLE 1. As a reference, we also show the results obtained by the statistical method: in Eqs. (23) and (24) and defined in Eqs. (19) and (20). Both the analytical and statistical results give and for three models A, B, and C. The calculated results in model C (present model) agree best with the statistical ones.
We find that the absolute values of and in model B and C are larger than those in model A, which is attributed to inclusion of the -mixing effects. The model B proposed in the previous studies Kuzminmix ; Magnani over-estimated the -mixing effects by compared with model C, where in Eq. (58) for SmFe12 compound. Actually, values of and in TABLE 3 satisfy the relation in Eq. (59) and (60). The results in present study (=C) quantitatively agree well with statistical ones except for . The discrepancy in may be due to omitting the 2nd order terms of in Eq. (57), which have a positive contribution independent of the sign of Kuzmin2nd .
| model | A | B | C | statistics |
|---|---|---|---|---|
| 4.29 | 5.04 | 4.62 | 4.70 | |
| -3.57 | -5.08 | -4.24 | -4.39 | |
| 60.2 | 144.5 | 97.7 | 101.1 | |
| -14.0 | -74.6 | -40.9 | -23.5 |
IV.3 Finite Temperature Magnetic Properties
of SmFe12 Compound
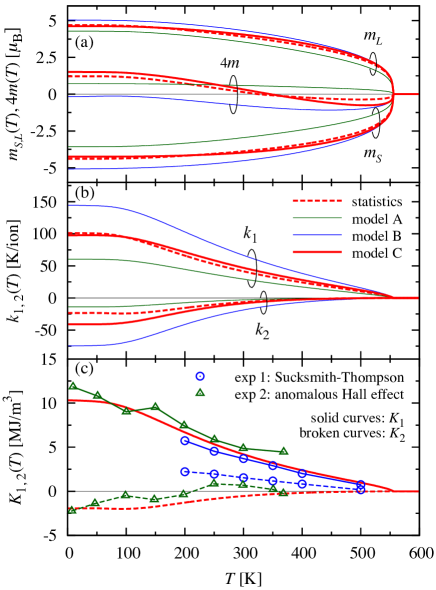
Calculated results of finite temperature magnetic properties for a single Sm ion in equilibrium at : the magnetic moment in Eqs. (53) and (54) and the MA constants in Eqs. (56) and (57) are shown in Fig. 6(a) and (b), respectively. The results show that the -mixing effect in model B increases the absolute values of both and . The over-estimation in model B is modified by the present model C in the whole temperature range. Obtained results of model C reproduce well the statistical results for in Eqs. (23) and (24) and for in Eqs. (19) and (20) as shown by broken lines in Fig. 6(a) and (b).
The physical meaning of the increment of the absolute value of and by -mixing may be given as follows. The expression of the free energy given by Eq. (48) includes the -mixing effect in the second term of the square bracket. The term decrease by , where . Because of the decrease in , the absolute value of the spin and orbital moments along are increased by . The tensor operators for even are also increased by , which contribute to increase in the absolute value of the MA constants .
The magnetic moment of Sm ion is reversed at around K in model C and calculation by Boltzmann statistics. The temperature is called compensation temperature. This phenomenon is observed also in other Sm compounds Adachi1 ; Adachi2 . Zhao pointed out that this phenomenon also appears at K in Sm2Fe17Nx using statistical method including similar parameter values with ours such as K and K Zhao . Their results are comparable with ours, however, the mechanism has not been surveyed. In the present model C, the magnetic moment of Sm ion can be written as . Because is proportional to and monotonically increasing with temperature below as shown in Fig. 4(a), the term compensates the at .
Fig. 6(c) shows the results of and obtained by statistical method in SmFe12 compound, which are compared with experimental ones denoted by exp 1 and exp 2 measured by the Sucksmith-Thompson method Hirayama2 and anomalous Hall effect Ogawa2 , respectively. At the whole temperature region the results of agree well with the experiments. Our statistical results qualitatively reproduce the experimental results below 200 K. The negative at low temperatures is origin of first-order magnetization process (FOMP) as discussed below.
IV.4 Thermodynamic Properties
of SmFe12 Compound
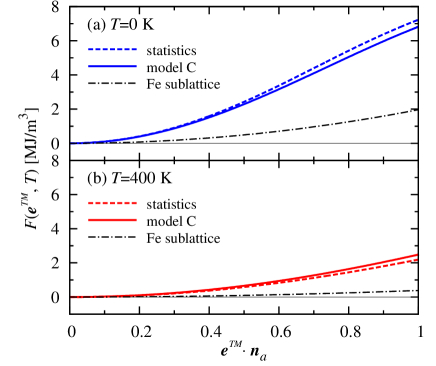
Fig. 7 shows calculated results of the Helmholtz free energy density given in Eq. (62) for model C as a function of with at K and K, where is unit vector parallel to -axis. The results are compared with statistical ones of in Eq. (14). When the direction of is changed, the free energy density on both Sm and Fe sublattice are increased. For the Sm sublattice, the energy increase originates from the CF, which can be expressed by the in Eq. (55), and for Fe sublattice, the energy increase can be written by: with and MJ/m3 at 0 and 400 K, respectively, which are much smaller than those of Sm sublattice and MJ/m3. The analytical results agree well with statistical ones.
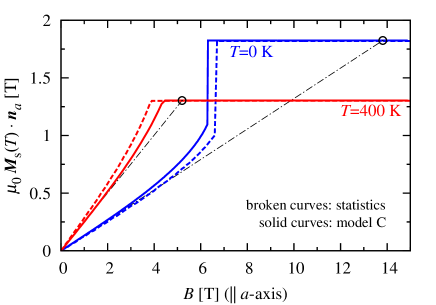
Fig. 8 shows calculated results of magnetization curves in the equilibrium states of SmFe12 at and 400 K, where the magnetic field is applied along -axis. Analytical results of the magnetization along the -axis are compared with statistical ones. We have confirmed that the results in model C well reproduce the statistical ones. At , we find characteristic behavior of an abrupt change in the magnetization at . The change is called first-order magnetization process (FOMP) and the is called as FOMP field. At =400 K, no FOMP appears in both analytical and statistical results and the magnetization saturates at the MA field . In SmFe12, the magnetization curve at low temperatures were not reported, however, in SmFe11Ti compound, FOMP observed at K and T Hu , which is qualitatively consistent with our results.
Let us consider the magnetization process along -axis and estimate nucleation field in the model C. The magnetization is first saturated as along -axis by an infinitesimal field. Then the direction of the magnetic field is reversed and the magnitude is increased as . The original state continues to exist as a quasi-stable state as far as the condition for a first-order variation is satisfied. The magnetization tends to decline when . The applied magnetic field at which the latter condition is satisfied is the nucleation field, which has been given as Kronmuller1 .
Because corresponds to the field at which the magnetization begins to decline with infinitesimally angle against -axis, the magnitude in realistic system can be estimated once the magnetization curve is obtained along a hard axis. Fig. 8 shows the magnetization curve along -axis calculated in the model C. is given by a crossing point of the magnetization curve in the saturated state and the tangential line of the magnetization curve at zero field . When the value of , the magnetic field coincides with defined in Eq. (65).
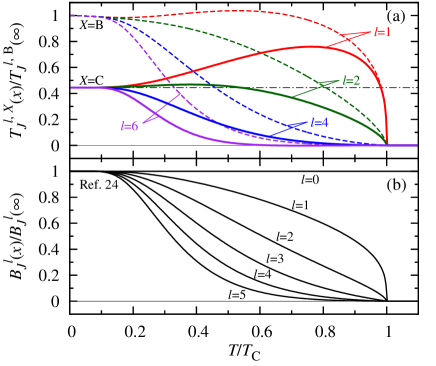
The magnetization curves along hard and easy-axis in the case of and can be characterized by the nucleation field , the FOMP field , and the MA field . These values are analytically expressed by using the ratio as,
| (73) | ||||
| (74) | ||||
| (75) | ||||
with
| (76) |
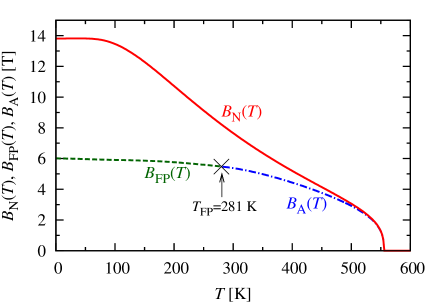
where we use the approximate free energy density: , in which the small contributions , are neglected. Details are shown in Appendix A. Calculated results of , , and are shown in Fig. 9. The condition of FOMP appearance in model C is given by between in Eq. (74). As for SmFe12 compound, the FOMP is realized below K , which is analytically obtained from the condition: . The curves of and are continuously connected at , which is called as FOMP temperature. When the magnetization direction is in-plane at .
V Summary
The temperature dependence of magnetic anisotropy (MA) constants and magnetization of SmFe12 were investigated by using two methods for the model Hamiltonian which combines quantum and phenomenological ones for rare-earth () and Fe subsystem, respectively. Parameter values of Hamiltonian were determined by the first-principles. First method adopts a numerical procedure with Boltzmann statistics for the Sm electrons. The other one is an analytical method which deals with the magnetic states of ions with strong mixing of states with different quantum number of angular momentum (-mixing). We have modified the previous analytical methods for Sm ions which have relatively small spin-orbit interaction, and clarified that they over-estimate the -mixing effects for Sm-transition metal compounds. It has been shown that the results of our analytical method agree with those obtained by statistical method. Our analytical method revealed that the increasing spin angular momentum with -mixing caused by strong exchange field, enhances the absolute value of orbital angular momentum and MA constants via spin-orbit interaction, and that these -mixing effects remain even above room temperature. The calculated results of MA constants show that and in SmFe12 in consistent with experiment.
The peculiar temperature dependence known as first-order magnetization process (FOMP) in SmFe12 has been attributed to the negative . It was also verified that the requirement for the appearance of FOMP is given as . The positive (negative) appears due to an increase in the crystal field parameter () caused by hybridization between -electrons of Fe on () site and and valence electrons on Sm. The mechanism of and in SmFe12 has been thus clarified by using the expressions of and obtained in the analytical method. Shortly, the sign of and in SmFe12 is attributed to the characteristic lattice structure around Sm ions, that is, crystallographic 2-sites on -axis adjacent to Sm are vacant. We also present results on the magnetization process and nucleation fields by calculating Gibbs free energy.
The present method will be applied to derive a general expression of the free energy to analyze MA of non-uniform systems such as disordered compounds, surfaces, and interfaces. The results will be reported in a forthcoming paper.
Acknowledgements.
This work is supported by ESICMM Grant Number 12016013 and ESICMM is funded by Ministry of Education, Culture, Sports, Science and Technology (MEXT). T. Y. was supported by JSPS KAKENHI Grant Numbers JP18K04678. P. N. was supported by the project Solid21.
Appendix A Magnetization Process in Condition
of and
To investigate the magnetization process in equilibrium along the -plane (e.g. -axis), we introduce the simplified model with magnetic anisotropy constants and , which can be expressed by the Gibbs free energy as:
| (77) | ||||
where with total magnetization and unit vector parallel to -axis . and () are temperature and applied magnetic field, respectively. The equilibrium condition is:
where gives minimum of . For , the magnetization is always tilted to the -axis direction due to . Otherwise, the magnetization curve is given by:
| (78) |
The first-order magnetization process (FOMP) appears, when has two values at certain , which is called as FOMP field .
To determine the for , we show the first and second derivative of with respect to as:
| (79) | ||||
| (80) |
A inflection point of for at fixed and is given by . Hereafter, we consider following two cases: and .
(i) The case of
is obtained from the condition for , because is always satisfied. The saturating point of magnetization is obtained from the condition as:
| (81) |
where . The is so-called anisotropy field.
(ii) The case of
is obtained from the condition
| (82) |
where is determined by the condition of local minium as: and . In the magnetization process, is continuously increased from zero with increasing according to for . At such that is satisfied, shows the abrupt jump and becomes saturated value of . The condition is rewritten as:
| (83) |
By solving the Eq. (83) for , two minimum points of with respect to are obtained at and
| (84) |
By using , the field at which the FOMP occurs is determined by:
| (85) |
As a result, for , the FOMP occurs between and .
References
- (1) T. Miyake, K. Terakura, Y. Harashima, H. Kino, and S. Ishibashi, J. Phys. Soc. Jpn. 83, 043702 (2014).
- (2) Y. Hirayama, Y. K. Takahashi, S. Hirosawa, K. Hono, Scr. Mater. 95, 70 (2015).
- (3) G. C. Hadjipanayis, A. M. Gabay, A. M. Schönhöbel, A. Martín-Cid,J. M. Barandiaran, and D. Niarchos, Engineering 6, 141 (2020).
- (4) K. Ohashi, Y. Yokoyama, R. Osugi, Y. Tawara, IEEE Trans. Magn. MAG-23, 3101 (1987).
- (5) K. Ohashi, Y. Tawara, R. Osugi, and M. Shimao, J. Appl. Phys. 64, 5714 (1988).
- (6) Bo-Ping Hu, Hong-Shuo Li, J. P. Gavigan, and J. M. D. Coey, J. Phys.: Condens. Matter 1, 755 (1989).
- (7) T. Kuno, S. Suzuki, K. Urushibara, K. Kobayashi, N. Sakuma, M. Yano, A. Kato, and A. Manabe, AIP Advances 6, 025221 (2016).
- (8) A. M. Schönhöbel, R. Madugundo, O. Yu. Vekilova, O. Eriksson, H. C. Herper, J. M. Barandiarán, G. C. Hadjipanayis, J. Alloys Compd. 786, 969 (2019).
- (9) H. Kato, T. Nomura, M. Ishizone, H. Kubota, and T. Miyazaki, J. Appl. Phys. 87, 6125 (2000).
- (10) Y. Hirayama, Y. K. Takahashi, S. Hirosawa, and K. Hono, Scr. Mater. 138, 62 (2017).
- (11) D. Ogawa, X. D. Xu, Y. K. Takahashi, T. Ohkubo, S. Hirosawa, and K. Hono, Scr. Mater. 164, 140 (2019).
- (12) D. Ogawa, T. Yoshioka, X. D. Xu, Y. K. Takahashi, H. Tsuchiura, T. Ohkubo, S. Hirosawa, and K. Hono, J. Magn. Magn. Mater. 497, 165965 (2020).
- (13) H. Sepehri-Amin, Y. Tamazawa, M. Kambayashi, G. Saito, Y. K. Takahashi, D. Ogawa, T. Ohkubo, S. Hirosawa, M. Doi, T. Shima, and K. Hono, Acta Materialia 194, 337-342 (2020).
- (14) R. F. L. Evans, W. J. Fan, P. Chureemart, and T. A. Ostler, and M. O. A. Ellis, and R. W. Chantrell, J. Phys.: Condens. Matter 26, 103202 (2014).
- (15) Y. Toga, M. Matsumoto, S. Miyashita, H. Akai, S. Doi, T. Miyake, and A. Sakuma, Phys. Rev. B 94, 174433 (2016).
- (16) M. Nishino, Y. Toga, S. Miyashita, H. Akai, A. Sakuma, and S. Hirosawa, Phys. Rev. B 95, 094429 (2017).
- (17) T. Miyake and H. Akai J. Phys. Soc. Jpn. 87, 041009 (2018).
- (18) T. Yoshioka and H. Tsuchiura, Appl. Phys. Lett. 112, 162405 (2018).
- (19) H. Tsuchiura, T. Yoshioka, and P. Novák, Scr. Mater. 154, 248 (2018).
- (20) M. Yamada, H. Kato, H. Yamamoto, and Y. Nakagawa, Phys. Rev. B 38, 620 (1988).
- (21) R. Sasaki, D. Miura, and A. Sakuma, Appl. Phys. Express 8, 043004 (2015).
- (22) D. Miura, R. Sasaki, and A. Sakuma, Appl. Phys. Express 8, 113003 (2015).
- (23) D. Miura and A. Sakuma, AIP Advances 8, 075114 (2018).
- (24) M. D. Kuz’min, Phys. Rev. B 46, 8219 (1992).
- (25) M. D. Kuz’min and J. M. D. Coey, Phys. Rev. B 50, 12533 (1994).
- (26) M. D. Kuz’min, Phys. Rev. B 51, 8904 (1995).
- (27) Y. Millev and M. Fähnle, Phys. Rev. B 52, 4336 (1995).
- (28) M. D. Kuz’min, J. Appl. Phys. 92, 6693 (2002).
- (29) N. Magnani, S. Carretta, E. Liviotti, and G. Amoretti, Phys. Rev. B 67, 144411 (2003).
- (30) Y. Harashima, K. Terakura, H. Kino, S. Ishibashi, and T. Miyake, JPS Conf. Proc. 5, 011021 (2015).
- (31) W. Körner, G. Krugel, and C. Elsasser, Sci. Rep. 6, 24686 (2016).
- (32) P. Delange, S. Biermann, T. Miyake, and L. Pourovskii, Phys. Rev. B 96, 155132 (2017).
- (33) J. H. Van Vleck, The Theory of Electric and Magnetic Susceptibilities (Oxford University Press, Oxford, 1932).
- (34) S. G. Sankar, V. U. S. Rao, E. Segal, W. E. Wallace, W. G. D. Frederick, and H. J. Garrett, Phys. Rev. B 11, 435 (1975).
- (35) H. W. de Wijn, A. M. van Diepen, and K. H. J. Buschow. phys. stat. sol. (b) 76, 11 (1976).
- (36) H. Sepehri-Amin, T. Ohkubo, T. Nishiguchi, S. Hirosawa, K. Hono, Scr. Matter 63, 1124 (2010).
- (37) H. Sepehri-Amin, T. Ohkubo, S. Nagashima, M. Yano, T. Shoji, A. Kato, T. Schrefl, and K. Hono, Acta Materialia 61, 6622-6634 (2013).
- (38) P. Blaha, K.Schwarz, G. Madsen, D. Kvasnicka, and J. Luitz, WIEN2k, An Augmented Pla ne Wave + Local Orbitals Program for Calculating Crystal Properties, Karlheinz Schwarz, TU Wien, Austria, 2001, ISBN 3-9501031-1-2.
- (39) M. Richter, P. M. Oppeneer, H. Eschrig, and B. Johansson Phys. Rev. B 46, 13919 (1992).
- (40) P. Novák, Phys. Stat. Sol. B 198, 729 (1996).
- (41) K. Hummler and M. Fähnle, Phys. Rev. B 53, 3272 (1996).
- (42) M. Richter, J. Phys. D 31, 1017 (1998).
- (43) M. Diviš, K. Schwarz, P. Blaha, G. Hilscher, H. Michor, and S. Khmelevskyi, Phys. Rev. B 62, 6774 (2000).
- (44) M. Diviš, J. Rusz, H. Michor, G. Hilscher, P. Blaha, and K. Schwarz, J. Alloys Compd. 403, 29 (2005).
- (45) M. Brooks, L. Nordström, and B. Johansson, J. Phys. Condens. Mater 3, 3393 (1991).
- (46) M. T. Hutchings, Solid State Phys. 16, 227 (1964).
- (47) R. J. Elliott, Magnetic Properties of Rare Earth Metals (Plenum, New York, 1972), Chap. 1.
- (48) M. D. Kuz’min, Phys. Rev. Lett. 94, 107204 (2005).
- (49) S. A. Nikitin, I. S. Tereshina, V. N. Verbetskiǐ, and A. A. Salamova, Phys. Solid State 40, 258 (1998).
- (50) A. R. Edomonds, Angular Momentum in Quantum Mechanics (Princeton University Press, Princeton, N. J., 1960)
- (51) D. A. Varshalovich, A. N. Moskalev, and V. K. Khersonskii, Quantum Theory of Angular Momentum (Wold Scientific, Singapore, 1988).
- (52) J. R. Schrieffer and P. A. Wolff, Phys. Rev. 149, 491 (1966).
- (53) K. Stevens, Proc. Phys. Soc. A65 209 (1952).
- (54) H. Kronmüller, K. D. Drust, and M. Sagawa, J. Magn. Magn. Mater. 69, 149 (1987).
- (55) H. Kronmüller and M. Fähnle, Micromagnetism and the Microstructure of Ferromagnetic Solids (Cambridge University Press, Cambridge, 2003)
- (56) H. Tsuchiura,T. Yoshioka, and P. Novák, IEEE Trans. Magn. 50, 2105004 (2014).
- (57) R. Coehoorn, K. H. J. Buschow, and M. W. Dirken, and R. C. Thiel, Phys. Rev. B 42, 4645 (1990).
- (58) A. Sakuma, J. Phys. Soc. Jpn. 61, 4119 (1992).
- (59) H. Adachi, H. Ino, and H. Miwa, Phys. Rev. B 56, 349 (1997).
- (60) H. Adachi, and H. Ino, Nature 401, 148 (1999).
- (61) T. S. Zhao, X. C. Kou, R. Grössinger, and H. R. Kirchmayr, Phys. Rev. B 44, 2846 (1991).