Statistical Model Checking of Common Attack Scenarios on Blockchain

Timed automaton specifies the behavior of atomic components. One can define an atomic component as the following elements:

• •

  set of ports for synchronization with other components

• •

  set of states of the component

• •

  set of variables for local data

• •

  set of transitions between states; the transition executes under certain boolean conditions.

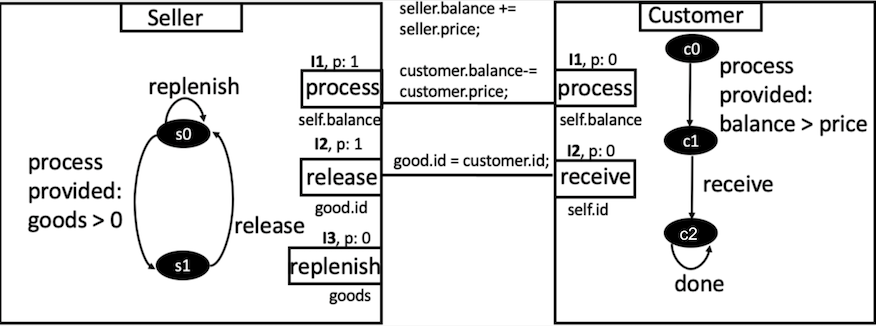
Fig. 1 illustrates a simplified purchasing model [8], adapted for the BIP framework. The atomic component Customer has 3 states c0, c1, and c2, variables balance, transfer, price and id. Also, the Customer component has two ports process and receive, and three transitions: process, receive and done. Interaction process executes only when the local variable balance $>$ price. The other atomic component explains the behavior of the seller with 2 states, s0, s1, internal variable balance and list of goods, and three transitions. The transition process executes only when the number of goods is greater than zero.

Atomic components can communicate with each other according to the logic in connectors. One can describe a connector as a sequence of ports that connect atomic components. SBIP 2.0 supports two types of interactions, timed and stochastic. Timed interactions take place only with time constraints that represent a lower and upper bound over clock valuations, as in timed automata. Stochastic interactions take place with a specific stochastic constraint, for example, a probability function.

Interaction I1 at Fig. 1 connects atomic component Customer through the port process. This port implements the money transfer from the Customer to the Seller atomic component. Variable balance on interaction I1 of the customer is reduced on the amount price, and the variable balance of the seller is incremented on the same amount. In interaction I2 the asset assigns to the customer. Thus, the connector from example at Fig. 1 is a set of ports: $p_{1}|p_{2}$, where $p_{1}$ - port of atomic component Customer and $p_{2}$ - port of external atomic component Seller.

Execution of priorities can proceed under certain conditions. If the condition holds, the priority of the considered connector is higher than another one. In the purchasing example from Fig. 1 a conflict can be between interactions I2 and I3 when the amount of good is non-zero. The interaction process executes first, as it has a higher priority.

Compound components are used for assembling a new component from the defined atomic components. Compound components include instances of atomic components and specify connectors between them. Fig. 1 illustrates a compound component that consists of two atomic components and two interactions.

Blockchain applications use peer-to-peer network architecture for communication between the network nodes. When a new client joins a blockchain for the first time, she discovers active peers using Domain Name System (DNS) for IP address resolution. This is a DNS bootstrapping process.

The DNS mechanism is susceptible to cache poisoning, hijacking, tunneling, man-in-the-middle, and other types of attack [24]. A vulnerability in DNS led to the famous 2016 cyberattack [5].

We consider a DNS cache poisoning attack performed with a co-called birthday attack [24] on Berkeley Internet Name Domain (BIND) software. A BIND server can send multiple simultaneous recursive queries for the same IP address so an adversary can predict the next transaction id. After guessing the next transaction id, the adversary provides extra information in a DNS reply packet. Thus, by simultaneously generating a flow of queries to the server and an equal number of forged replies one can get a collision of transaction id and change the proper domain address to the fake one. The probability of collision is $P=1-(1-\frac{1}{t})^{\frac{n*(n-1)}{2}}$ [24], where t is the total number of possible values in the master set, and n is the number of spoofed queries. The default number of possible values in the master set is $65535$.

We took a birthday attack because the probability of collision is much higher than in conventional spoofing. The collision probability quickly increases up to $1.0$ along for less than $1000$ requests [24].

Let us describe an SBIP model of the DNS cache poisoning birthday attack. Fig. 2 illustrates the model. Here and on the other models, transitions with the prefix l present local interactions. The blue line indicates a connection between two atomic components. Connectors apply to interactions with the same name. For example, the adversary’s atomic component can communicate with cache through external ports requests, reply, and daemon. The behavior of the atomic components is the following:

• •

  Adversary. Provides a set of requests and replies. After each request, he tries to guess a transaction ID. A random event here is the guess transition, described by a collision probability function [24]. If the guess is successful, the adversary runs a daemon through the external interaction and goes to the final state $a2$.

• •

  Cache. The cache server replies to DNS queries. In the case of collision, the interaction daemon works. The address in the DNS cache changes, and the user gets a spoofed address.

• •

  User. Requests the DNS address from the cache server, connects to the network, and transfers funds. In case of a spoofed address, the transfer proceeds to the wrong recipient.

• •

  Blockchain network. Awaits until the user connects to it and accomplishes transfer funds.

• •

  Spoofed network. The same functionality as a blockchain network, but with the spoofed address.

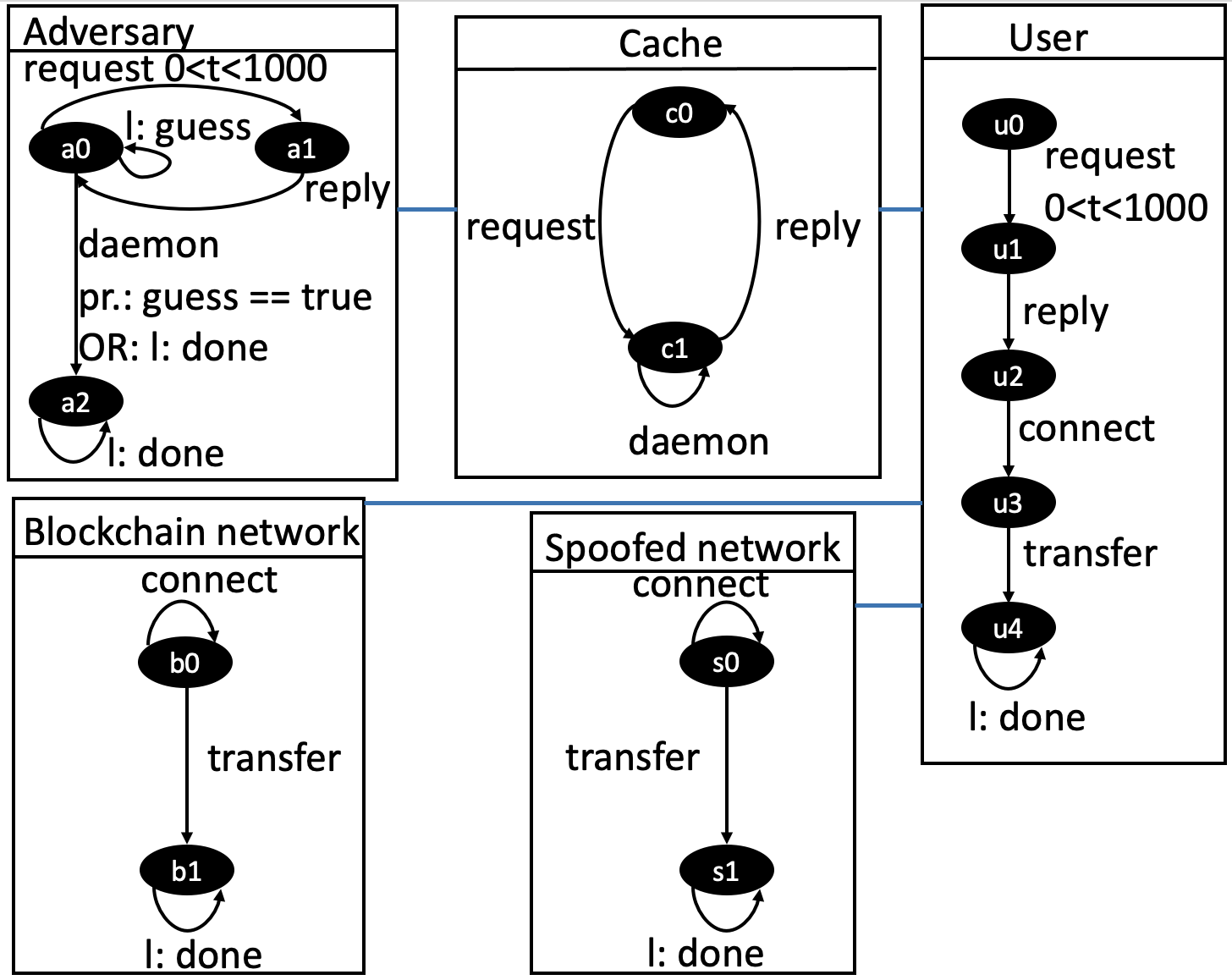
The scenario of the attack is the following. The adversary makes requests to change the DNS address. At the same time, the user makes a query to the server. The request from the user and the adversary are temporary interactions that accomplish in the time period [0, 1000]. The upper bound of the period is a parameter, and one can change it. With the received address the user connects to the network and transfers the money.

One can bound the probability of the birthday attack by a negligible function $\mu$ by using cryptographic encryption techniques, for example, DNSSEC with NSEC5 records bounds [11]. NSEC5 is a resource record that can be used to detect certain attacks on secure DNS requests. We restricted the probability of violation by the function $\mu=R*q_{s}*2^{-n}$ [11], where $R$ - the set of domain names, that equals 65535, $q_{s}$ - the number of adversary’s queries, $n$ - the length of the output of the hash function. Restriction applies on the transition daemon of the Cache atomic component.

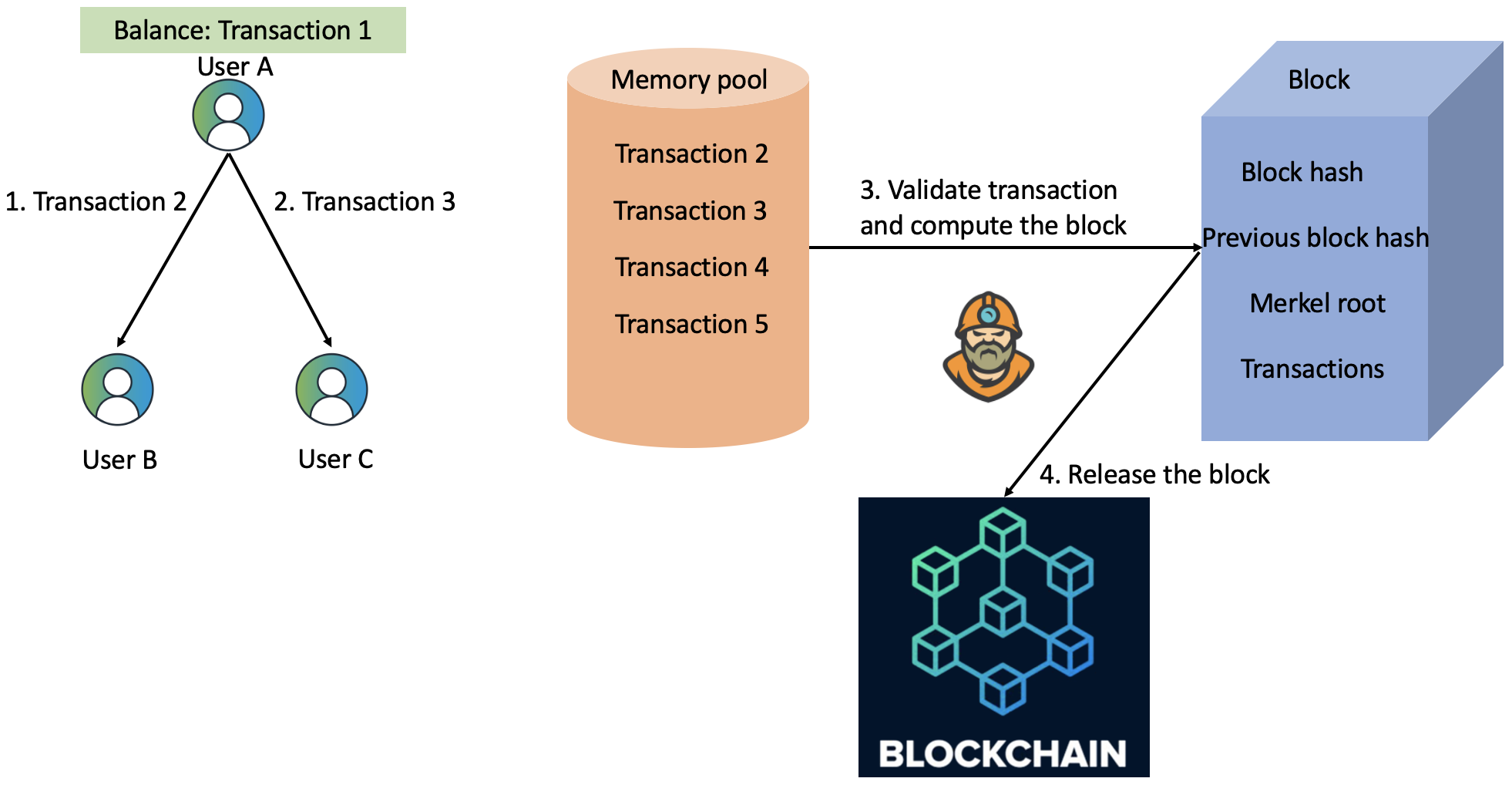
In a blockchain network, double-spending means applying the same transaction and its asset multiple times. Fig. 3 illustrates the process of double-spending. User A signs the transaction with a private key and sends it to user B. During the validation process, the recipient looks up the unspent transactions of the sender, verifies the sender’s signature, and waits for the transaction to be mined into a valid block. Releasing the transaction to the network takes a certain time, which depends on the network throughput, the size of the memory pool of unconfirmed transactions (mempool), the consensus protocol, and the priority factor of the transaction.

In the case of fast transactions, the receiver can release the asset to the sender before the transaction gets committed into the blockchain network. In a while, user A can send the same transaction to user C. In this case, only those transaction is valid which gets into the blockchain first, but the asset might have been released twice. Double spending is one of the most widespread attacks on the blockchain platforms [21]. We performed a model checking for different types of double-spending attacks.

An adversary can cause a delay for successful double-spending with a mempool flooding attack. Mempool flooding is a kind of DDoS attack carried out at the memory pools of the cryptocurrencies [21]. Mempool has substantial properties such as timeout for transactions and default size limit. Relying on these configurations, users can estimate it to prioritize transactions. A potential adversary can estimate a delay in the mempool queue and increase this delay by a DDoS attack.

The survey [15] proposes two approaches to avoid double-spending. First, to set up the listening period before delivering the asset to the adversary. That gives time to double-check the spoofed transaction if the adversary already sends it to another user. But this does not consider the worst-case scenario when the adversary sends the second transaction just before accepting the first one to the blockchain. The second approach implies insertion to the network additional ”observers” - nodes that would relay to the user all transactions that it receives. But observers entail additional upload to the network. Instead, we propose to set the time interval in which the blockchain participant can send one transaction to the network.

Model on Fig. 4 represents a simplified version of the mempool flooding scenario. We neglect the probability that one can send two transactions to the same miner by assuming that the blockchain network consists of a significant amount of participants. Also, in our model, there is no explicit mining fee for transactions. The historical data set considers the notion of the different fees for transactions implicitly. Below we explain atomic components.

• •

  Adversary. Sends a transaction from the same parent’s block to the different recipients. After that, the adversary waits for the release of the transaction’s assets.

• •

  Users A, B. Get the transaction from the sender, validate and locally verify it. Validation implies consistency with the blockchain’s history and verification examines the sender’s signature. After the verification phase, the user sends the transaction to the mempool and immediately releases the asset. The double-spending is successful if both assets were released to the sender.

• •

  Miners C, D. Take transactions from users and allocate them in the local mempool until the block will be mined. Mining time is a random variable with distribution from the historical dataset [2].

• •

  Proof-of-Work (PoW) Blockchain. We presented all other nodes as a PoW Blockchain atomic component. It takes the block from the miner, checks that the block does not contradict the history of committed transactions, and based on this either accepts or rejects the block.

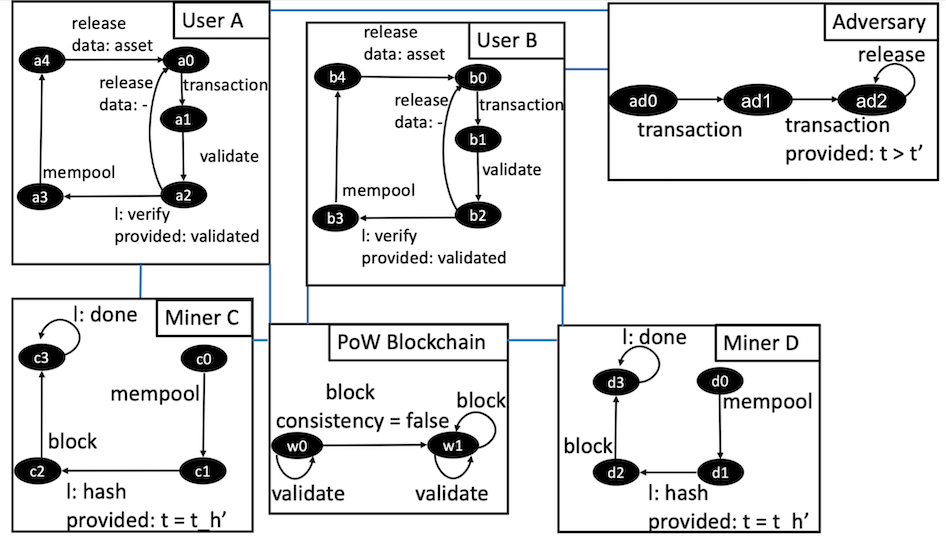
The adversary sends a transaction to user A. After some time, the model defines a lower bound as a $t^{\prime}$ parameter, the adversary generates a transaction with the same history as the first one and sends it to user B. When the user receives the transaction, she validates its consistency with the blockchain’s history. If the transaction is consistent, the user verifies the sender’s signature and sends it to the mempool. The user releases a product to the sender before transaction confirmation.

Another way to enlarge the accepting time of the transaction is a consensus delay attack [6]. While the memory pool increases the delay of a block because of the transactions queue, consensus delay appears because of the propagation time among the majority of users. When a new block is ready, the majority of blockchain’s participants should confirm it. From the example in Fig. 3, only one transaction gets acceptance which is the first to propagate among more the half of the whole nodes.

Fig. 5 illustrates the consensus delay model with the Proof-of-Work consensus protocol. The behavior of the adversary and users are the same as in the mempool flooding model. When a node gets transactions from the user, it builds them into the block and propagates this block among other nodes. Propagation takes some time and causes the delay. Ledger atomic component represents other nodes of the network.

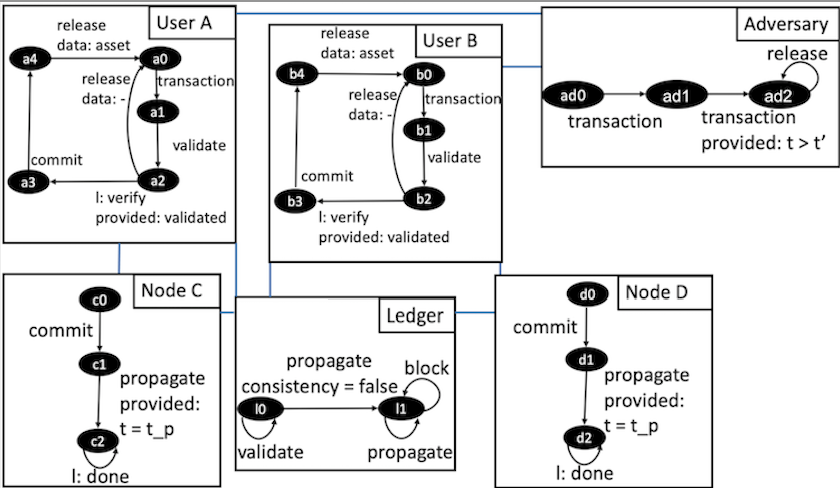
In the consensus delay model, the adversary sends two transactions at a time interval $t^{\prime}$. Users validate and verify transactions and send them to other nodes to propagate them. If the first transaction already got commitment by the network, the second benign user rejected the transaction on the validate transition. We fixed the time interval $t^{\prime}$, in which the adversary can send the spoofed transaction.

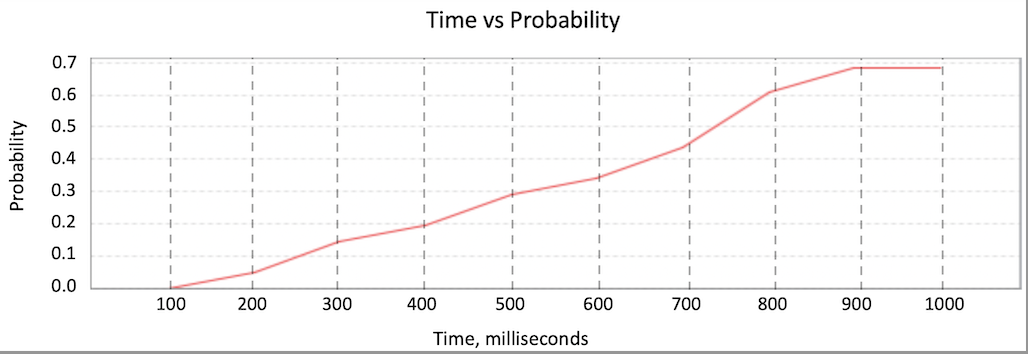
In this subsection, we provide the estimation of the adversary’s success probability for the DNS model. We calculated a discrete set of values of the probability collision function. According to the MTL specification, the balance of the spoofed network eventually becomes nonzero: $F[0,x]{spoofed.amount>0}$, where $x$ is a parameter of the time in the range [100, 1000].

Fig. 6 depicts a probability versus time plot. Time denotes the number of milliseconds from the start of the scenario. If we add the probabilistic interaction, that restricts the collision success, the probability of transfer to the wrong network decreases significantly. We checked the violation probability with the different hash functions with different lengths: SHA-1, SHA-224, SHA-256, SHA-384, SHA-512 [23]. The success of the daemon interaction depends on the probability function $\mu=R*q_{s}*2^{-n}$ [11], which we over-approximated by the uniform distribution.

Based on the Bitcoin data from 01/01/2016 till 01/05/2021 we provide the mining time [2] as a stochastic variable in our SBIP model. The stochastic variable $t_{h}$ is assigned to the value from the dataset uniformly and randomly.

The experiment aims to get a minimum time interval $t^{\prime}$ in which the same user can send two transactions with the negligible probability of double-spending. The specification here represents the success of getting assets from both users: $F[0,10^{12}]adversary.asset==2$. We took such an upper bound for the specification to over-approximate the mining time from the historical data set.

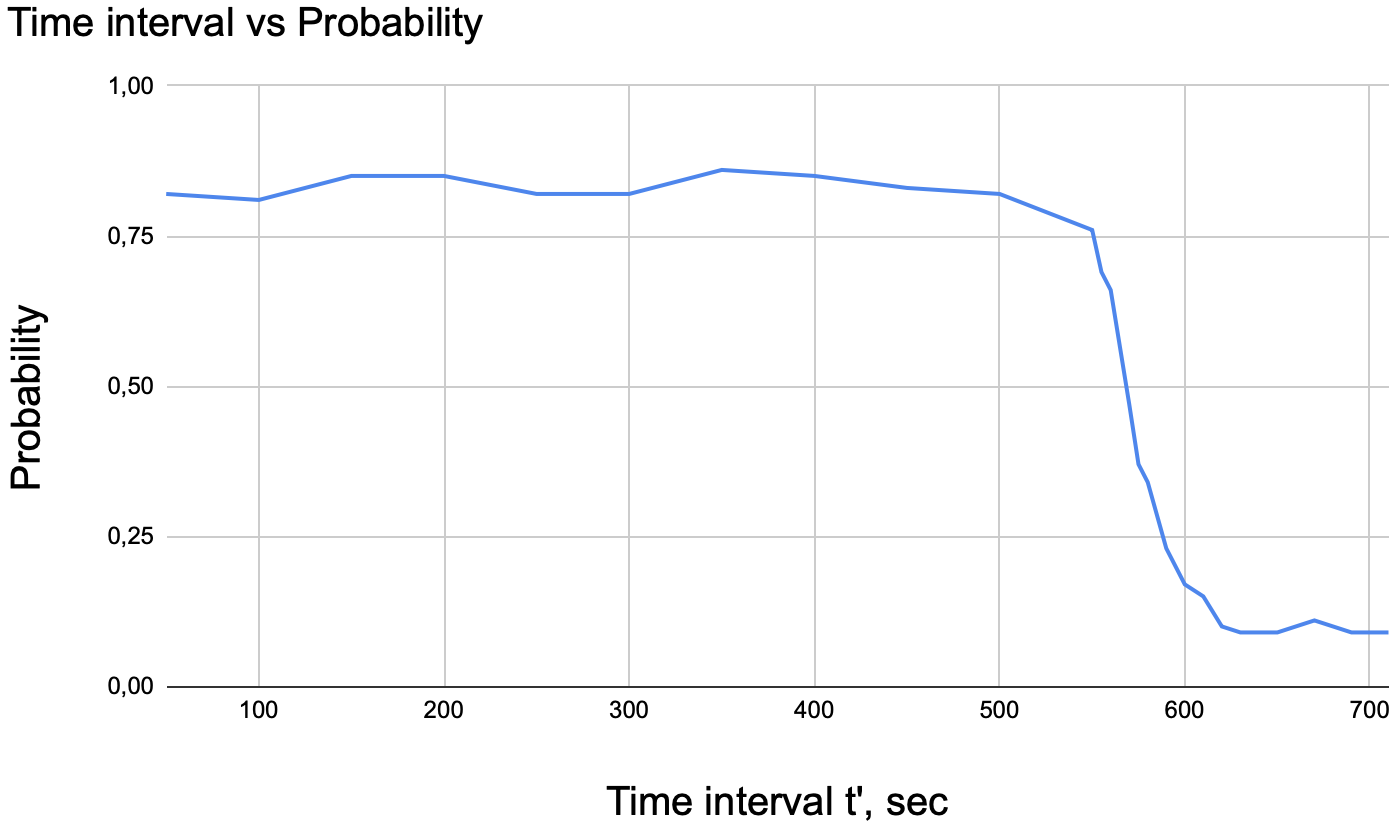
Fig. 7 illustrates the dependency of the double-spending probability on the time interval $t^{\prime}$. We estimated the double-spending success probability with the time step in 10 seconds for $t^{\prime}$ between 500 and 650. Between 0 and 500, we measured with the time step in 50 seconds, as the probability changes more slowly. For the time interval, $t^{\prime}$ between 0 and 500 milliseconds, the probability of the double-spending is around 0.8. The following characteristics of the experiment explain this value. First, the value of the precision and risk parameters in the experiment is $0.1$. Second, the adversary can send a transaction later than in $t^{\prime}$ seconds, as we provided the lower bound for the time interval.

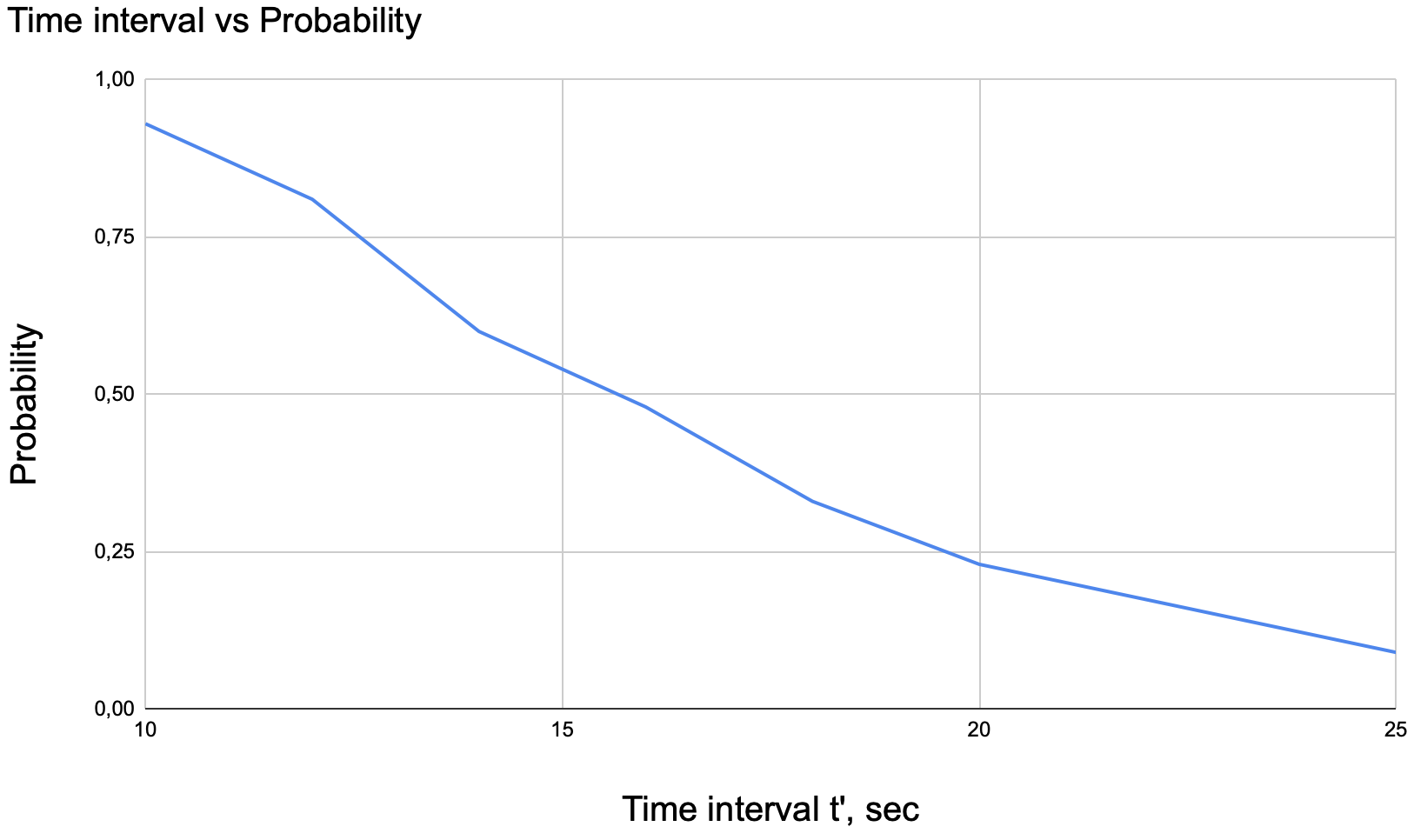
Similar to the mempool double-spending scenario, we used the data [3] of the block propagation time to get a stochastic variable value. The goal of the experiment is to get the time interval $t^{\prime}$ between the adversary’s transactions with which the double-spending probability is negligible. We took the historical data of propagation delay from 01/29/2016 till 01/05/2021 and assigned this data set to the random variable t’ of the atomic component Node.

The specification checks that the adversary got the double-spending of the same transaction:
$F[0,10^{12}$] $adversary.asset==2$. We accomplished measurements with the time step equals to 2 seconds. We over-approximated the propagation time in the specification to include all possible delays. Fig. 8 illustrates the dependency of the time interval $t^{\prime}$ from the double-spending probability.

As we have seen from the experiment, the probability of the connection to the wrong network grows with the number of requests from the adversary. The probability function illustrated in Fig. 6 is similar to the collision rate function [24]. That means that the experimental evaluation corresponds to the theory. One can see from the experiment that for hash functions with an output length of more than 20 bits, the collision probability equals zero. Thus, using any listed hash functions [23] prevents the adversary’s scenario.

For the mempool flooding model, we analyzed the impact of the time interval between two transactions on the double-spending success. The increment of the time interval $t^{\prime}$, in which the adversary can send a transaction, decreases the double-spending probability. After 570 seconds, the probability of successful double-spending becomes less than 0.5. After 610 seconds, the probability becomes around 0.1 and remains in this value asymptotically. That follows from the setting of experimental parameters $\delta$ and $\alpha$ to 0.1 value. Also, the average time in the mempool, which is around 600 seconds, corresponds to the measured time interval, with which the double-spending probability becomes negligible. The double-spending probability should decrease significantly around average mining time, as after this point the first transaction most probably releases from the mempool. According to the dependency illustrated in Fig.  7, by setting the restriction for sending one transaction from the same user in 650 seconds one can reduce the probability of the double-spending success significantly.

Justification of the time restriction on transactions from the same user depends on the application area. That makes sense in the networks, for which confirmation and release asset of the first transaction is more crucial than the second transaction processing.

Changing of probability versus time function in the consensus delay scenario, is smoother than in the mempool case, as there is a higher deviation in the data set. Fig. 5 illustrates this dependency. Taking into consideration the result of the mempool flooding experiment, we conclude that by restricting the time interval $t^{\prime}$ between two transactions from the same user in 650 seconds one can avoid both mempool flooding and consensus delay double-spending scenarios. To cover all factors that increase the double-spending success, one needs to make transaction fees and the mempool timeout as constants for all blockchain participants. The fixed transaction fee is possible to implement for the blockchain network [12]. One can fix the mempool timeout by assigning the same value for a timeout in memory pool configuration files for all blockchain participants and making these files immutable.

To sum up the experiment analysis, we specify security properties, that should hold for each system. In the case of a DNS attack, the system is safe if one uses any of the hash functions [23]. In the case of double-spending, one can put a time restriction for sending a transaction from one node. That bounds the successful attack probability by a negligible value and makes the system safe.