Steady gradient Ricci solitons with nonnegative curvature operator away from a compact set

By [14, Proposition 1.3], for any sequence $\{p_{i}\}\to\infty$, rescaled Ricci flows $(M,g_{p_{i}}(t);p_{i})$ converge subsequently to a splitting Ricci flow $(N\times\mathbb{R},\bar{g}(t);p_{\infty})$ in the Cheeger-Gromov sense, where $\bar{g}(t)=h(t)+dr^{2}$ as in (1.2). We assume that the ancient $\kappa$-solution $(N,h(t))$ is compact. Namely, there is a constant $C$ such that

Then we have the following curvature decay estimate.

By Lemma 2.2 and the normalization identity

we have

Moreover, by [9, Lemma 2.2] (or [6, Theorem 2.1]), $f$ satisfies

for two constants $c_{1}$ and $c_{2}$. Hence, the integral curve $\gamma(s)$ generated by $X=\nabla f$ extends to the infinity as $s\rightarrow\infty$.

Based on Lemma 2.1 and Lemma 2.2, by studying the level set geometry of $(M,g)$, we prove

In case that all split ancient $\kappa$-solution $(N,h(t))$ satisfies $(\ref{bound-h})$, we can classify $(N,h(t))$.

Compact ancient $\kappa$-solution of type I has been classified as follows (cf. [7, Theorem 7.34], [4], [12]).

To prove Proposition 2.4, we shall exclude the existence of ancient $\kappa$-solutions of type II. Actually, we prove the following diameter estimate for such ancient solutions.

Lemma 2.6 can be regarded as a higher dimensional version of [1, Lemma 2.2].

We use the argument by contradiction. On the contrary, we suppose that there exists a sequence of rescaled Ricci flows $(M,g_{q_{i}}(t);q_{i})$ ( $q_{i}\to\infty$), which converges to a limit Ricci flow $(N^{\prime}\times\mathbb{R},h^{\prime}(t)+ds^{2};q_{\infty})$, where $(N^{\prime},h^{\prime}(t))$ is a compact ancient $\kappa$-solution of type I. Then by Lemma 2.5, there exists a constant $C_{0}>0$ such that for any small $\epsilon>0$ it holds,

By Proposition 2.3, it follows

for all $q\in f^{-1}(f(q_{i}))$. We note that the constant $C$ is uniform by the classification result, Lemma 2.5, i.e., it is independent of the sequence of rescaled Ricci flows with a limit Ricci flow, which is a compact ancient $\kappa$-solution of type I.

On the other hand, for the sequence of $(M,g_{p_{i}}(t);p_{i})$ in Theorem 1.2, we can choose a point $p_{i_{0}}\in\{p_{i}\}$ such that

for all $i>i_{0}$. Let $\hat{X}=\frac{\nabla f}{|\nabla f|}$ and $\Gamma(s)$ be an integral curve of $\hat{X}$ starting from $p_{i_{0}}$, i.e., $\Gamma(0)=p_{i_{0}}$. We note that $\Gamma(s)$ tends to the infinity by (2.5) and (2.6), since Lemma 2.2 holds. Thus by $\eqref{type1-bound}$ and $\eqref{F_0}$, we can choose two sequences $\{p^{1}_{i}\}$ and $\{p^{2}_{i}\}$ of points in $\Gamma(s)$ to the infinity, which satisfy the following properties:

Thus there are $s^{1}_{i},s^{2}_{i},s_{i}$ with $s^{1}_{i}<s_{i}<s^{2}_{i}$ such that

where $q^{\prime}_{i}=\Gamma(s)\cap f^{-1}(f(q_{i}))$, see Figure 1.

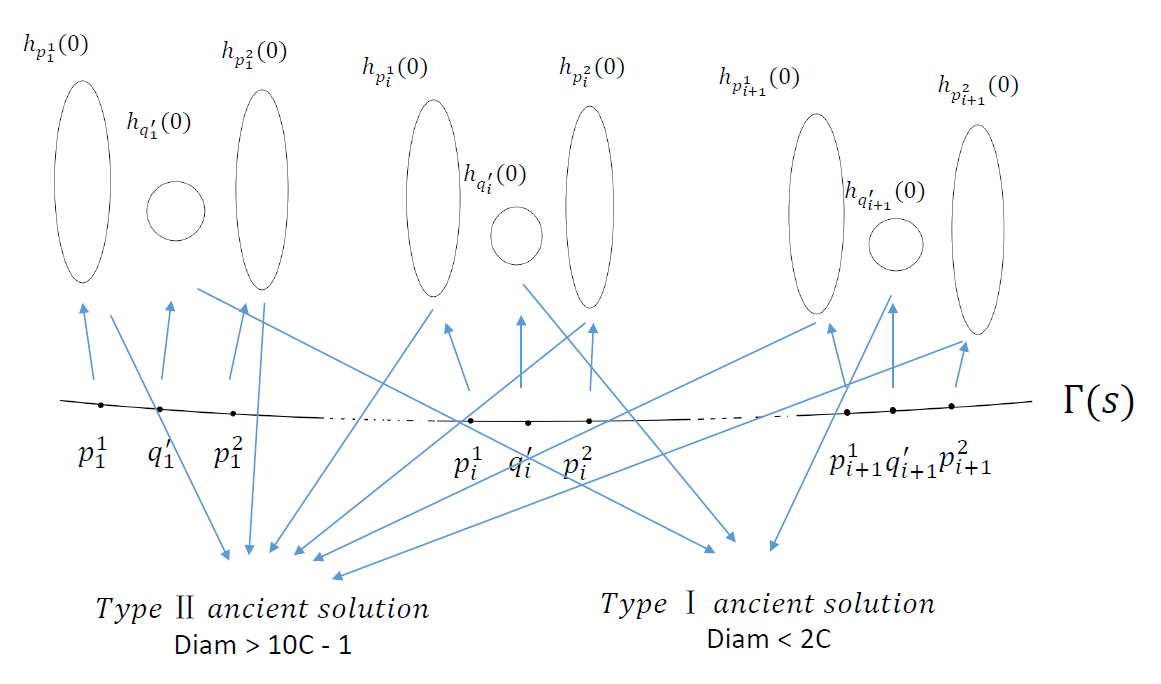
By [14, Proposition 1.3] and the relation 4) in (3.1), $(M,g_{p^{1}_{i}}(t);p^{1}_{i})$ converges subsequently to $(N_{1}\times\mathbb{R},h_{1}(t)+ds^{2};p^{1}_{\infty})$, where $h_{1}(t)$ satisfies

Thus, by $\eqref{type1-bound}$, we see that $h_{1}(t)$ must be a compact ancient $\kappa$-solution of type II. By Lemma 2.6, it follows

for any $t_{k}\to-\infty$. Hence, there exists a $k_{0}$ such that

We fix $t_{k_{0}}$ so that $\epsilon^{-1}>-10t_{k_{0}}$ as long as $\epsilon<<1$.

Next we claim there exists a constant $A>0$ such that

for all $i\gg 1$.

Suppose that the above claim is not true. Then by taking a subsequence, we may assume

Recall that $\left\{\phi_{t}\right\}_{t\in(-\infty,\infty)}$ is the flow of $-\nabla f$ with $\phi_{0}$ the identity and $(g(t),\Gamma(s))$ is isometric to $\left(g,\phi_{t}(\Gamma(s))\right)$. Then

Let $T_{k_{0},i}=t_{k_{0}}R(p_{i}^{1})^{-1}=t_{k_{0}}R\left(\Gamma\left(s^{1}_{i}\right)\right)^{-1}$ and

It follows

By combining (3.9) and (3.10), we see that $s^{\prime}_{i}\in[s^{1}_{i},s^{2}_{i}]$ for $i\gg 1$. Hence, by the relation 5) in (3.1), we obtain

By the isometry, we have

On the other hand, from the proof of [14, Proposition 3.6], we know that for each $\Gamma(s^{1}_{i})$, there exists a $(n-1)$-dimensional compact ancient $\kappa$-solution $h_{\Gamma(s^{1}_{i})}(t)$ such that

Since $R(\Gamma_{1}(s^{1}_{i}),T_{k_{0},i})\leq R(\Gamma(s^{1}_{i}))$ by the monotonicity of scalar curvature along $\Gamma(s)$, by (3.1), we get

Note that there are also another $(n-1)$-dimensional compact ancient $\kappa$-solutions $h_{\Gamma(s^{\prime}_{i})}(t)$ corresponding to the point $\Gamma(s^{\prime}_{i})$ as in (3.1) such that

Hence, combining $(\ref{s1-close1})$ and $(\ref{s1-close2})$, we derive

By the convergence, we have

It follows

where $R$ is the scalar curvature w.r.t. $h_{1}$. Thus by (3.1) and (3.7), we estimate

But this is impossible by (3.11). Hence, (3.8) must be true.

Now we can finish the proof of Theorem 1.2. By (3.8) and the relation 3) in (3.1), we have

where the last inequality follows from the monotonicity of $R$ along $\Gamma(s)$. Since $(M,g_{\Gamma(s_{i})}(t);\Gamma(s_{i}))$ converges subsequently to the limit flow $(N^{\prime}\times\mathbb{R},h^{\prime}(t)+ds^{2};q_{\infty})$, by the shrinking property of type I solution $(N^{\prime},h^{\prime}(t))$ in Lemma 2.5, we know

Then as in $(\ref{h-sequence-limit})$, we get

for some $t^{\prime}_{i}$, where $-t^{\prime}_{i}<2A$ by (3.20). Thus , combining $(\ref{type1-scaled-diameter})$ and (3.22) and by the convergence of $(M,g_{\Gamma(s_{i})}(t);\Gamma(s_{i}))$, we obtain

But this is impossible since by the relation 4) in (3.1) it holds

Therefore, we prove the theorem.