¹¹institutetext: Abigail Alvarez ²²institutetext: Facultad de Física, Universidad Veracruzana, 91000, Xalapa, VER., México
²²email: abialvarez@uv.mx
³³institutetext: Cuauhtemoc Campuzano ⁴⁴institutetext: Facultad de Física, Universidad Veracruzana, 91000, Xalapa, VER., México
⁴⁴email: ccampuzano@uv.mx
⁵⁵institutetext: Miguel Cruz ⁶⁶institutetext: Facultad de Física, Universidad Veracruzana, 91000, Xalapa, VER., México
⁶⁶email: miguelcruz02@uv.mx
⁷⁷institutetext: Efraín Rojas ⁸⁸institutetext: Facultad de Física, Universidad Veracruzana, 91000, Xalapa, VER., México
⁸⁸email: efrojas@uv.mx
⁹⁹institutetext: Joel Saavedra ¹⁰¹⁰institutetext: Instituto de Física, Pontificia Universidad Católica de Valparaíso, Casilla 4950, Valparaíso, Chile
¹⁰¹⁰email: joel.saavedra@ucv.cl

Stealths on $(1+1)$ -dimensional dilatonic gravity

Abigail Alvarez Cuauhtemoc Campuzano Miguel Cruz Efraín Rojas Joel Saavedra

Abstract

We study gravitational stealth configurations emerging on a charged dilatonic $(1+1)$ -D black hole spacetime. We accomplish this by considering the coupling of a non-minimally scalar field $\phi$ and a self-interacting scalar field $\Psi$ living in a $(1+1)$ -D charged black hole background. In addition, the self-interacting potential for $\Psi$ is obtained which exhibits transitions for some specific values of the non-minimal parameter. Atypically, we found that the solutions for these stealth scalar fields do not have a dependence on the temporal coordinate.

1 Introduction

The Einstein equations are one of the pillars of the General Relativity (GR) because they are quantifying the relationship between matter and the spacetime curvature. The conventional GR prescription says that the curvature of the spacetime is a manifestation of the presence of matter and this fact is encoded in the Einstein equations

\emph{G}_{\mu\nu}+\Lambda g_{\mu\nu}-\kappa T_{\mu\nu}=0,

(1)

where $T_{\mu\nu}$ is the energy-momentum tensor associated to the matter content. Needless to say that the finding physically interesting solutions to these equations is a difficult task due to their high nonlinearity.

Nevertheless, there are nontrivial configurations without back reaction on the geometry of the spacetime in which it has been shown the existence of a reverse reaction on the geometry of spacetime. These fields are called stealths, AyonBeato:2004ig . Such configurations are obtained from the Einstein equations when one impose the vanishing of them including customary matter, and for the other hand, the vanishing of an energy-momentum tensor associated to a non-minimally coupled scalar field, $\Psi$ , independently

0=\emph{G}_{\mu\nu}+\Lambda g_{\mu\nu}-\kappa T_{\mu\nu}=\kappa T_{\mu\nu}^{S}=0.

(2)

Originally it was shown the existence of these configurations in AyonBeato:2004ig for the well known $(2+1)$ -dimensional BTZ static black hole and later on in $(3+1)$ -dimensions for the Minkowski flat spacetime AyonBeato:2005tu . Thenceforth, this idea was implemented in several spacetimes: in an (A)dS spacetime AyonBeato:2005pr , and in the cosmology context Banerjee:2006pr ; Maeda:2012tu ; Ayon-Beato:2013bsa . Similarly, in $n$ dimensions, for higher-order gravity theories Gaete:2013ixa ; Hassaine:2013cma in the Lovelock gravity context Gaete:2013oda as well as in the non-relativistic version of the gauge/gravity correspondence in Lifshitz spacetime Ayon-Beato:2015qfa . Surprisingly, a stealth Schwarzschild solution arise in context of Galileons theory, in particular, on shift-symmetric part of Hordenski action, which is used to study no-hair theorems in a spherically symmetric spacetime Babichev:2013cya and its charged generalization Babichev:2015haa . In all these works, the stealth scalar field arises from the well known non-minimal coupling $\xi\Psi^{2}R$ in general relativity. In contrast with the ordinary matter, it is believed that the distinctive of these configurations is ability to be undetectable in the ambient spacetime which makes it an interesting phenomenon which could explain some current phenomena of the gravitation as in the case of dark matter/energy. The mechanism described above is quite general and can be applied for different spacetimes. Indeed, the current implementation of this idea on diverses geometries is under investigation in order to get a good understanding of the physical content behind the stealth setups. Despite the criticism on the instability of the stealth configurations, we believe that this framework should not be ruled out. In fact, it has recently emerged a strong interest in part because of the conformal symmetry properties and the potential cosmological implications that have this type of structures Ayon-Beato:2013bsa .

In this work we will merely present, but without giving any compelling physical conclusion, exact solutions for stealth configurations arising in the context of black hole physics for lower dimensions. Specifically, such configurations are realized by considering a non-minimally coupled scalar field, evolving in a two-dimensional charged dilatonic black hole background Frolov:1992xx . Inspired in the string theory, this black hole is very interesting in its own right due to their properties on the quantum effects in the black hole physics and by the their implications in the quantization of nonconformal fields, mainly. The solution for this geometry comes from string theory in two dimensions where its structure is equivalent to the planar symmetry of general relativity Lemos:1994fn . Due to the fact that the two-dimensional dilatonic black hole satisfy Einstein equations, then it is also considered as a genuine black hole in general relativity. When the exact solutions are obtained in this work, as a byproduct, one is able to identify the self-interacting potential for the stealth scalar field. At the moment there is no close relationship with any physical potential so it remains to be understood the role that such potential play.

This paper is organized as follows. In Sect. 2 we review briefly the coupling between a non-minimally scalar field with a $(1+1)$ -D charged dilatonic black hole. In Sect. 3 we obtain exact solutions for stealth configurations considering the two-dimensional charged dilatonic black holes. In addition, we discuss some interesting cases for $\xi\neq 0$ where stealth scalar field configurations appear. In all cases we were able to compute the accompanying self-interacting potentials. Finally, in Sect. 4 we give some conclusions.

2 $(1+1)$ -D charged dilatonic black hole coupled to a non-minimally a scalar field

In this Section we review briefly the $(1+1)-$ D gravity coupled with a dilaton field $\phi$ and a electromagnetic field besides and additional term involving a non-minimally coupled scalar field $\Psi$

$\displaystyle S$	$\displaystyle=$	$\displaystyle S_{\phi}+S_{\Psi},$	(3)
	$\displaystyle=$	$\displaystyle\frac{1}{2\kappa}\int d^{2}x\sqrt{-g}\,e^{-2\phi}\left[R+4\lambda^{2}+4(\nabla_{\alpha}\phi\nabla^{\alpha}\phi)\right]-\frac{1}{8\kappa}\int d^{2}x\sqrt{-g}e^{-2\phi}F_{\mu\nu}F^{\mu\nu}$
	$\displaystyle-$	$\displaystyle\int d^{2}x\sqrt{-g}\left[\frac{1}{2}\nabla_{\alpha}\Psi\nabla^{\alpha}\Psi+\frac{\xi}{2}R\Psi^{2}+U(\Psi)\right],$

where $R$ denotes the scalar curvature, $\lambda$ is a constant, $\xi$ is the non-minimal coupling parameter, $F_{\mu\nu}$ is the field strength of the Maxwell field $A_{\mu}$ and $U(\Psi)$ represents the self-interacting potential for the scalar field $\Psi$ . Note that the action can be splitted in two parts, $S_{\phi}$ and $S_{\Psi}$ , that is, the gravitational and the scalar field sectors, respectively. The first part corresponds to the $2D$ dilatonic gravity approach Grumiller:2002 which is the version of the Einstein-Hilbert theory in two dimensions with physical degrees of freedom and the second part corresponds to the non-minimal coupling of the scalar field $\Psi$ . Furthermore, besides the constant $\kappa$ , the quantity $e^{\phi}$ plays the role of a gravitational coupling constant Giddings:1992fp . Since we are interested in stealth configurations for the scalar field $\Psi$ , the quantity $e^{\phi}$ is not multiplying the second part of the action. In the stealth scalar field framework, these non-trivial configurations do not produce backreaction. These must be treated separately from the gravitational sector. The corresponding field equations are obtained from the variation of the action (3) with respect to the associated fields

	$\displaystyle\nabla_{\mu}\nabla_{\nu}\phi-g_{\mu\nu}\left(\Box\phi-\nabla_{\alpha}\phi\nabla^{\alpha}\phi+\lambda^{2}-\frac{1}{16}F_{\alpha\beta}F^{\alpha\beta}\right)$	(7)
$\displaystyle-$	$\displaystyle\frac{1}{4}F_{\mu}{}^{\alpha}F_{\alpha\nu}=\frac{\kappa}{2}e^{2\phi}T_{\mu\nu}^{{}\textit{S}},$
	$\displaystyle R+4\Box\phi-4\nabla_{\alpha}\phi\nabla^{\alpha}\phi+4\lambda^{2}-\frac{1}{4}F_{\alpha\beta}F^{\alpha\beta}=0,$
	$\displaystyle\Box\Psi-\xi R\Psi=\frac{dU(\Psi)}{d\Psi},$
	$\displaystyle\nabla_{\mu}(e^{-2\phi}F^{\mu\nu})=0.$

where the stealth’s energy-momentum tensor reads

T_{\mu\nu}^{S}=\nabla_{\mu}\Psi\nabla_{\nu}\Psi-g_{\mu\nu}\left(\frac{1}{2}\nabla_{\alpha}\Psi\nabla^{\alpha}\Psi+U(\Psi)\right)+\xi(g_{\mu\nu}\Box-\nabla_{\mu}\nabla_{\nu}+G_{\mu}{}_{\nu})\Psi^{2}.

(8)

This expression is the key point in the search for stealth configurations. We have to impose the vanishing condition of the l.h.s of the Eq. (7) as stated in Eq. (2) in order to obtain the stealth scalar field configurations.

2.1 $(1+1)$ -dimensional dilatonic dlack hole solution

In order to study the stealth scalar field configuration in lower dimensional black hole geometries, we adopt the following background

ds^{2}=-f_{q}(r)dt^{2}+\frac{dr^{2}}{f_{q}(r)}.

(9)

This corresponds to a $(1+1)$ -dimensional dilatonic black hole solution for the Einstein equations described by the vanishing of l.h.s. of Eq. (7). When some specific coordinates are chosen, the function $f_{q}$ is explicitly given by Frolov:1992xx ,

f_{q}(r)=1-\frac{2m}{Q}e^{-Qr}+\frac{q^{2}}{Q^{2}}e^{-2Qr},

(10)

where $m$ is a mass parameter, $q$ is proportional to the charge, $Q$ is a positive constant determined by the effective central charge $\lambda$ and the dilatonic field can be written in the simple form

\phi=Qr.

(11)

In this solution there is no contribution coming from a tachyon field and it was shown in Refs. McGuigan:1991qp ; Witten:1991yr that is the two dimensional version of the four dimensional Schwarzschild black hole solution.

It is worthy to note that when $m\geq q$ the expressions (10) and (11) describes a charged $(1+1)$ -dimensional black hole with charge $q$ . When $q>m$ , one gets a naked singularity and for the specific choice $m=1/2,Q=1/r_{0}$ and $q=0$ , the function $f_{q}(r)$ specializes to the well known uncharged case Witten:1991yr ; Sengupta ; Frolov:2000jh ,

f(r)=1-r_{0}e^{-\frac{r}{r_{0}}}\qquad\phi=\frac{r}{r_{0}},

(12)

where the parameter $r_{0}$ determines the position of the event horizon.

On the other hand, as mentioned previously, following AyonBeato:2004ig ; AyonBeato:2005tu the emerging of a stealth configuration is obtained by demanding the vanishing of the r.h.s. of Eq. (2), bearing in mind that both sides of this equation vanishes independently. Hence, we now turn to explore the conditions to obtain non-trivial stealth scalar field configurations in this $(1+1)$ -D charged black hole background.

3 Stealth configurations on a $(1+1)$ -D charged dilatonic black hole

To begin with, we proceed to obtain a nontrivial solution for the scalar field $\Psi$ . It will be useful to rewrite this field as follows

\displaystyle\Psi=\sigma^{\frac{2\xi}{4\xi-1}},

(13)

where $\sigma=\sigma(t,r)$ is a function depending on the coordinates and $\xi$ is the non-minimal coupling parameter satisfying $\xi\neq 1/4$ . Obviously, this ansatz tell us that the case $\xi=1/4$ must be discussed separately. Guided by the approach behind Eq. (2) all we need to do is to demand the vanishing of $T_{\mu\nu}^{{}\textit{S}}=0$ . By inserting (13) into (8), the off-diagonal component and the difference between the diagonal temporal and radial component of the energy-momentum tensor associated to $\Psi$ reads

	$\displaystyle T_{r}{}^{t}$	$\displaystyle=$	$\displaystyle-\frac{(2\xi)^{2}}{(4\xi-1)}\frac{\Psi^{2}}{\sigma}f_{q}^{3/2}\,\partial^{2}_{rt}(f_{q}^{-1/2}\sigma),$		(14)
	$\displaystyle T_{t}{}^{t}-T_{r}{}^{r}$	$\displaystyle=$	$\displaystyle\frac{4\xi^{2}}{(4\xi-1)}\frac{\Psi^{2}}{\sigma}(f_{q}^{2}\sigma_{rr}+\sigma_{tt}).$		(15)

The fulfillment of these equations guarantee that the nonlinear Klein-Gordon equation (7) is automatically satisfied. From the vanishing of Eq. (14) we must note that the solution for the sigma function can be recast as a sum of independent functions as follows

\sigma=\sqrt{f_{q}}T(t)+\alpha(r),

(16)

accompanied with the condition

\partial_{t}\left[\frac{\sigma(T_{t}{}^{t}-T_{r}{}^{r})}{\Psi^{2}}\right]=\frac{2\xi^{2}}{4\xi-1}\bigg{[}f_{q}\frac{d}{dr}\left(\frac{1}{\sqrt{f_{q}}}\frac{df_{q}}{dr}\right)\frac{dT}{dt}-2\frac{1}{\sqrt{f_{q}}}\frac{d^{3}T}{dt^{3}}\bigg{]}=0.

(17)

From Eqs. (15), (16) and (17) one is able to show that the function $T$ is a constant. This feature means that stealth scalar field does not evolve in time. Thus, for $\xi\neq 1/4$ and considering $\sigma=\sigma(r)$ from the Eq. (15) one arrives at

\Psi(r)=(\bar{A}r+\bar{B})^{\frac{2\xi}{4\xi-1}},

(18)

where $\bar{A}$ and $\bar{B}$ are integration constants. It is important to observe that this solution is determined independently of the metric function and this scalar field coincides with the stealth scalar field on the AdS background, as shown in AyonBeato:2005pr .

With this information we now attempt to find the self-interacting potential for the scalar field $\Psi$ . From the temporal-temporal component of the energy-momentum tensor and by using the solution for scalar field (18) and the metric function (12) we get the self-interaction potential for $\xi\neq 1/4$ in the form

	$\displaystyle U_{\xi}(\Psi)$	$\displaystyle=$	$\displaystyle\bar{A}\frac{2\xi^{2}\Psi^{\frac{1}{2\xi}}}{Q^{2}(1-4\xi)^{2}}\bigg{\{}\left[2(1-4\xi)Q+\bar{A}\Psi^{\frac{1-4\xi}{2\xi}}\right]q^{2}\exp\left[-2Q\left(\frac{\Psi^{\frac{4\xi-1}{2\xi}}-\bar{B}}{\bar{A}}\right)\right]$		(19)
		$\displaystyle-$	$\displaystyle 2Q\left[(1-4\xi)Q+\bar{A}\Psi^{\frac{1-4\xi}{2\xi}}\right]m\exp\left[-Q\left(\frac{\Psi^{\frac{4\xi-1}{2\xi}}-\bar{B}}{\bar{A}}\right)\right]+\bar{A}Q^{2}\Psi^{\frac{1-4\xi}{2\xi}}\,\bigg{\}}.\quad$		(19)

This potential allows the existence of stealth fields in $(1+1)$ -D from the metric (9). In Fig. (2), for the sake of illustration, we plot the expression (19) for the simple case $\xi=1/2$ with $\bar{A}$ just being a constant parameter. We can observe that the charged case exhibits an absolute minimum near to the origin. This is due to the fact that the first term dominates the behavior of the potential for small values of $\Psi$ .

3.1 Some interesting cases

3.1.1 The $\xi=1/4$ case

For this value, the solution (18) is not longer valid therefore we will focus on this specific case. By means of the redefinition of the scalar field as follows

\Psi(t,r)=Ce^{\sigma(t,r)},

(20)

and inserting this together with the value $\xi=1/4$ in Eq. (8) we obtain that the resulting equations can be reduced to

	$\displaystyle T_{r}{}^{t}$	$\displaystyle=$	$\displaystyle-\frac{1}{2}\Psi^{2}f_{q}^{3/2}\,\partial^{2}_{rt}(f_{q}^{-1/2}\sigma),$		(21)
	$\displaystyle T_{t}{}^{t}-T_{r}{}^{r}$	$\displaystyle=$	$\displaystyle\frac{1}{2}\Psi^{2}(f_{q}^{2}\sigma_{rr}+\sigma_{tt}).$		(22)

Following a similar procedure, it is straightforward to obtain the nontrivial solution given by

\Psi(r)=\bar{\Psi}_{0}e^{\bar{\beta}r},

(23)

where $\bar{\beta}$ and $\bar{\Psi}_{0}$ are integration constants. For this case the self-interacting potential reads

	$\displaystyle U_{1/4}(\Psi)$	$\displaystyle=$	$\displaystyle\frac{m\Psi_{0}^{2}(Q-2\bar{\beta})\bar{\beta}}{2Q}\left(\frac{\Psi}{\Psi_{0}}\right)^{-\frac{(Q-2\bar{\beta})}{\bar{\beta}}}-\frac{q^{2}\Psi_{0}^{2}(Q-\bar{\beta})\bar{\beta}}{2Q^{2}}\left(\frac{\Psi}{\Psi_{0}}\right)^{-\frac{2(Q-\bar{\beta})}{\bar{\beta}}}$		(24)
		$\displaystyle+$	$\displaystyle\frac{\bar{\beta}^{2}}{2}\Psi^{2}.$		(24)

The shape of the self-interaction potential (24) is depicted in Fig. (1). We infer that when $\Psi\rightarrow 0$ , then $U(\Psi)\rightarrow 0$ . In fact, we have two minimums. On the other hand, the potential grows as $\Psi$ is increased. In addition, we must note the appearance of a local maximum.

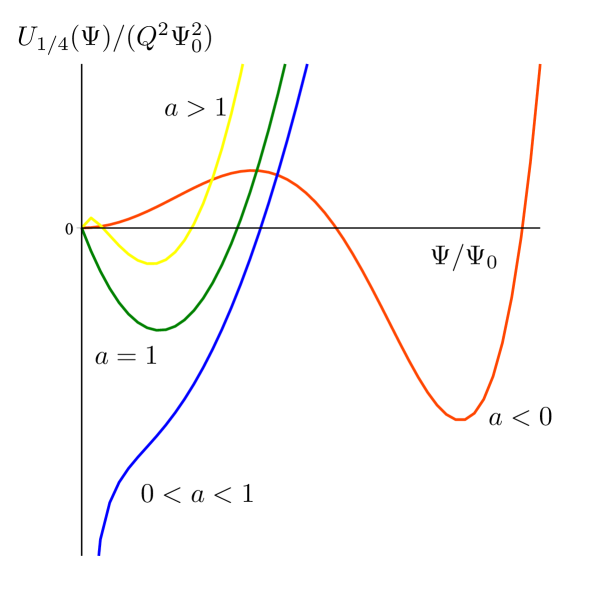
Refer to caption — Figure 1: This potential represents the self-interaction of the scalar field $\Psi$ for the value $\xi=1/4$ . Here we have considered $\bar{\beta}=aQ$ and $q=m=Q/2$ , where different values of $a$ has been taken, namely for the red line $a=-0.5$ , blue line $a=0.8$ , the green $a=1$ and the yellow $a=1.5$ .

3.1.2 The $\xi=1/2$ case

For this case the associated solution is given by

U_{1/2}=\frac{\bar{A}}{2Q^{2}}\left\{\left(\bar{A}-2Q\Psi\right)q^{2}e^{\left[-\frac{2Q}{\bar{A}}\left(\Psi-\bar{B}\right)\right]}-2Q\left(\bar{A}-Q\Psi\right)m\,e^{\left[-\frac{Q}{\bar{A}}\left(\Psi-\bar{B}\right)\right]}+\bar{A}Q^{2}\right\}.

(25)

From this expression we observe a linear dependence of the stealth field on the self-interacting potential. In addition, the solution (13) exhibits a linear dependence in the coordinate $r$ which leads to a weird behaviour because the stealth fiels will permeate the space as $r$ grows. This potential is plotted in (2).

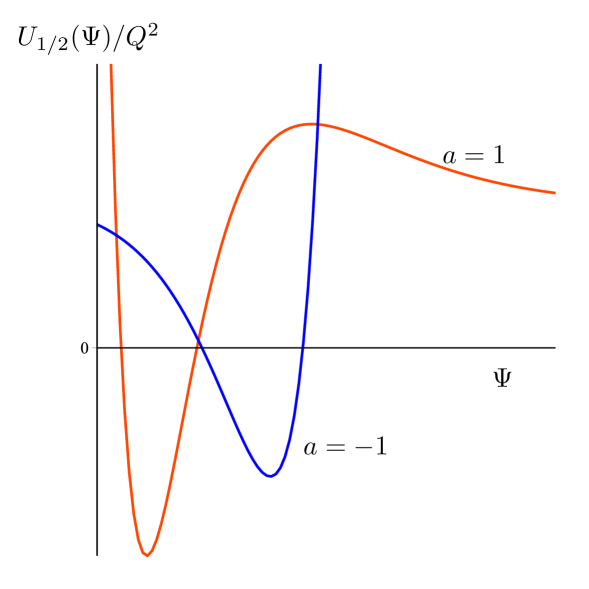
3.1.3 The uncharged case

When the electromagnetic field is switched off the nontrivial solutions found previously specialize to the uncharged case straightforwardly. In this case the equations of motion are modified slightly if we consider the vanishing of $F_{\mu\nu}$ besides $q=0$ in the geometric solution given by (12). Explicitly, the set of solutions are provided by the self-interacting potential

\displaystyle U_{\xi}(\Psi)={A}\frac{2\xi^{2}}{(1-4\xi)^{2}}\Big{\{}

\displaystyle-

\displaystyle\left[(1-4\xi)+Ar_{0}\Psi^{\frac{1-4\xi}{2\xi}}\right]\,e^{-\frac{\left(\Psi^{\frac{4\xi-1)}{2\xi}}-B\right)}{Ar_{0}}}+A\Psi^{\frac{1-4\xi}{2\xi}}\Big{\}}\Psi^{\frac{1}{2\xi}}.\qquad

(26)

Here, we have considered that $m=1/2$ , $Q=1/r_{0}$ where $A,B$ are constant parameters. For the sake of illustration, the self-interacting potential for the particular value $\xi=1/5$ is plotted in Fig. (3). We can observe that in this case the this potential exhibits a local minimum or a local maximum for different values of the parameter $a:=Ar_{0}$ .

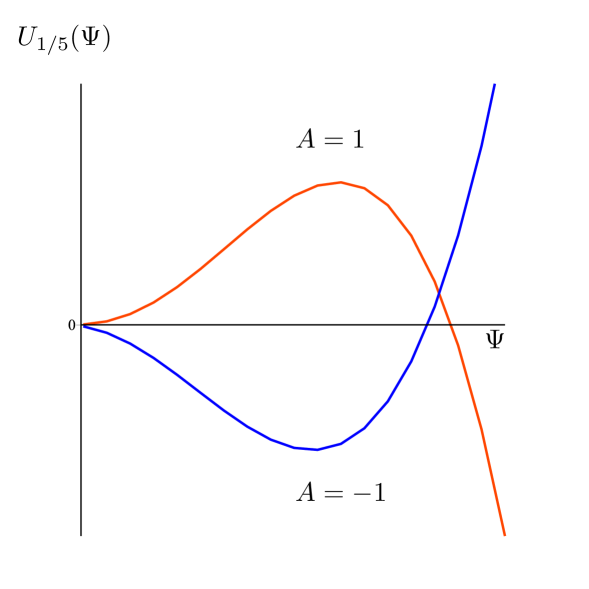
As in the charged configuration situation, there is a special value for the non-minimal coupling parameter, $\xi=1/4$ , namely. It is necessary a separate treatment in order to obtain a nontrivial solution. Since the mechanism already performed is quite general in such case the stealth solution reduces to

\Psi(r)=\Psi_{0}\,e^{\beta r},

(27)

where $\alpha$ and $\Psi_{0}$ are integration constants while its associated self-interacting potential reads

U_{1/4}=\frac{\beta}{4}\left[(1-2\beta r_{0})\left(\frac{\Psi}{\Psi_{0}}\right)^{-\frac{1}{\beta r_{0}}}+2\beta\right]\Psi^{2}.

(28)

4 Conclusions

In this work we have obtained the stealth scalar field configurations arising in a $(1+1)$ -dimensional dilatonic black hole spacetime. We found that the solutions for the stealth scalar field do not evolve in time. These solutions were obtained using the most general metric ansatz (9). It is worth noting that these solutions look similar to those obtained for the case of the stealth field on the AdS background, as shown in AyonBeato:2005pr . The simplicity of the mathematical manipulations in $(1+1)$ -dimensional spacetimes and the similarities that they possess with the four dimensional case, provide some hints to glimpse the properties of more complicated cases, in this sense, we expect a similar behavior for the stealth configurations that could appear if the Schwarzschild solution is used as background. Needless to say, a number of theoretical questions are still to be addressed. Most notably, it is no clear what degrees of freedom are represented by this scalar field. Work is in progress. For example, with regards the potential function, a more detailed analysis on the integration constants and the values of $\xi$ is mandatory in order to have an acceptable behaviour. In addition, the relationship of this potential with a known physical system does not exist yet.

On the other hand, the behavior of the stealth will depend strongly on the value of the exponent of $\Psi$ (see Eqs. (18) and (23)). For example, for the exponent $\Xi:=(4\xi-1)/(2\xi)$ in the range $1<\Xi<\infty$ the stealth has positive exponents of $r$ , and the behaviour seems like a typical polynomial function. As mentioned in the text, the particular value $\xi=1/2$ casts out a linear dependence of the stealth in the coordinate $r$ which leads to a unbounded behaviour because the stealth will permeate the space as $r$ grows . To end this discussion it is necessary to be cautious with the rational values of $\Xi$ in order to have a real value for $\Psi$ . This can be achieved with an acceptable choice of the integration constants $\bar{A}$ and $\bar{B}$ . Finally, we expect the existence of stealth solutions considering another type of non-minimal couplings, like $\xi G^{\mu\nu}\nabla_{\mu}\Psi\nabla_{\nu}\Psi$ Sushkov:2009 , by applying this procedure. It will be reported elsewhere.

Acknowledgements.

The authors acknowledge to Eloy Ayón-Beato for enlightening discussions. AA acknowledges pasrtial support by CONACyT Grant Estancias Posdoctorales Vinculadas al Fortalecimiento de Calidad del Posgrado Nacional 2016-1. AA, CC and ER acknowledges partial support by CONACyT Grant CB-2012-177519-F and grant PROMEP, CA-UV, Álgebra, Geometría and Gravitación. CC also acknowledges CONACyT Grant I0010-2014-02 Estancias Internacionales-233618-C. MC is being supported by CONACYT- México through grant Repatriaciones 2015-04. JS thank the hospitality of Facultad de Física Universidad Veracruzana. This work was partially supported by SNI (México).

References

(1) Ayon-Beato, E., Martínez, C., Zanelli, J.: Stealth scalar field overflying a $(2+1)$ black hole. Gen. Rel. Grav. 38, 145 (2006). arXiv: hep-th/0403228
(2) Ayon-Beato, E., Martínez, C., Troncoso, R., Zanelli, J.: Gravitational Cheshire effect: Nonminimally coupled scalar fields may not curve spacetime. Phys. Rev. D 71, 104037 (2005). arXiv: hep-th/0505086
(3) Ayon-Beato, E., Martínez, C., Troncoso, R., Zanelli, J.: Stealths on AdS. Private communication.
(4) Banerjee, N., Jain, R. K., Jatkar, P.: Non-Gravitating Scalar Field in the FRW Background. Gen. Rel. Grav. 40, 93 (2008). arXiv: hep-th/0610109
(5) Maeda, H., Maeda, K. I.: Creation of the universe with a stealth scalar field. Phys. Rev. D 86, 124045 (2012). arXiv:1208.5777 [gr-qc]
(6) Ayón-Beato, E., García, A. A., Ramírez-Baca, P. I., Terrero-Escalante, C. A.: Conformal stealth for any standard cosmology. Phys. Rev. D 88, 063523 (2013). arXiv:1307.6534 [gr-qc]
(7) Bravo-Gaete, M., Hassaine, M.: Topological black holes for Einstein-Gauss-Bonnet gravity with a nonminimal scalar field. Phys. Rev. D 88, 104011 (2013). arXiv:1308.3076 [hep-th]
(8) Hassaine, M.: Rotating AdS black hole stealth solution in $D=3$ dimensions. Phys. Rev. D 89, 044009 (2014). arXiv:1311.4623 [hep-th]
(9) Bravo-Gaete, M., Hassaine, M.: Planar AdS black holes in Lovelock gravity with a nonminimal scalar field. JHEP 1311, 177 (2013). arXiv:1309.3338 [hep-th]
(10) Ayón-Beato, E., Hassaine, M., Juárez-Aubry, M. M.: Stealths on Anisotropic Holographic Backgrounds. arXiv:1506.03545 [gr-qc]
(11) E. Babichev and C. Charmousis.: Dressing a black hole with a time-dependent Galileon. JHEP 1408, 106 (2014). arXiv:1312.3204 [gr-qc].
(12) E. Babichev, C. Charmousis and M. Hassaine.: Charged Galileon black holes. JCAP 1505, 031 (2015). arXiv:1503.02545 [gr-qc].
(13) Frolov, V. P.: Two-dimensional black hole physics. Phys. Rev. D 46, 5383 (1992).
(14) Lemos, J. P. S.: Two-dimensional black holes and planar general relativity. Class. Quant. Grav. 12, 1081 (1995). arXiv:gr-qc/9407024.
(15) Grumiller, D., Kummer, W., Vassilevich, D. V.: Dilaton gravity in two dimensions. Phys. Rep. 369, 327 (2002)
(16) Giddings, S. B.: Toy models for black hole evaporation. arXiv:hep-th/9209113
(17) McGuigan, M. D., Nappi, C. R., Yost, S. A.: Charged black holes in two-dimensional string theory. Nucl. Phys. B 375, 421 (1992). arXiv:hep-th/9111038
(18) Witten, E.: On string theory and black holes. Phys. Rev. D 44, 314 (1991)
(19) Mandal, G., Sengupta, A. M., Wadia, S. R.: Title. Mod. Phys. Lett. A 6, 1685 (1991)
(20) Frolov, V. P., Zelnikov, A.: Nonminimally coupled massive scalar field in a 2-D black hole: exactly solvable model. Phys. Rev. D 63, 125026 (2001). arXiv: hep-th/0012252
(21) Sushkov, S. V.: Charged black holes in two-dimensional string theory. Phys. Rev. D 80, 103505 (2009). arXiv:hep-th/9111038

Stealths on (1+1)(1+1)-dimensional dilatonic gravity