Stress clamp experiments on multicellular tumor spheroids

Cancer progression occurs in several stages. In the case of carcinomas, which are cancers of epithelial cells, the primary tumor grows locally, until some cells invade the neighboring tissue called the stroma which is essentially made of extracellular matrix, fibroblast cells, immune cells and capillary vessels. Three key elements control proliferation of the primary tumor: the accumulation of gene mutations and the tumor biochemical and mechanical micro-environments. It is difficult to isolate in vivo one of these factors to measure accurately its importance. Several recent works suggest that mechanical stress plays a role in tumor progression. A mechanical stress applied to genetically predisposed tissues or tumor spheroids grown in vitro induces signaling pathways that are characteristic of cancer invasion Whitehead et al. (2008); Demou (2010). It has also been shown that an increase of mechanical stress leads to a reduction in cancer cell proliferation in vitro, and drives apoptosis through the mitochondrial pathway Cheng et al. (2009); Roose et al. (2003); Helmlinger et al. (1997). In spite of these experimental evidences, the precise role of the micro-environment, and its interaction with the tumor, are poorly understood. Our group has developed a theoretical framework Basan et al. (2009); Ranft et al. (2010); Basan et al. (2011) to describe the influence of the balance between cell division and apoptosis on tumor growth under stress. The theory is based on the existence of a homeostatic state of a tissue. This is the steady state of the tissues where cell division balances cell death. The homeostatic stress is a function of the biochemical state of the tissue and depends on the local concentrations of nutrients, oxygen and growth factors as well as on the environment of the tissue. Signaling induced by the stroma can for example modify the homeostatic state. In the simple case where the biochemical state of the tissue can be maintained constant, the homeostatic stress is the stress that the tissue can exert at steady state on the walls of a confining chamber. It is a measure of mechanical forces that cells can sustain in this state. Indeed to grow against the surrounding tissue, cells have to exert mechanical stress on the neighboring cells.

In this paper we test experimentally the relevance of the homeostatic stress concept. We measure the effect of a known external stress on the growth of a cellular aggregate mimicking a tumor over timescales longer than the typical time scales of cell division or apoptosis. We use a new experimental strategy to exert a well defined mechanical stress on multicellular tumor spheroids for a period of time exceeding 20 days.

We prepare colon carcinoma cell spheroids derived from mouse CT26 cell lines (ATCC CRL-2638) using a classical agarose cushion protocol Mueller-klieser and Kunz-schughart (2010). The wells of a 48 wells plate are covered with agarose gel (Ultrapure agarose, Invitrogen Co, Carlsbad, CA) and cell suspensions are seeded on the gels at concentration of $20000$ cells per well. Cells self-assemble into spheroids in less than 24h. Cells are cultured under 95% air/ 5% CO₂ atmosphere in DMEM enriched with 10% calf serum (culture medium). Using confocal microscopy, we check that the shape of the spheroid is indeed close to a sphere. A constant stress is applied on the tissue over long time scales by imposing the osmotic pressure of a solution of the bio-compatible polymer Dextran ($M_{w}=100$kDa, Sigma-Aldrich Co, St Louis, Mo). This polymer is known to be neutral and is not metabolized by mammalians cells. We also confirmed that it is neither a growth or a death factor by plating cells for 3 days with Dextran and measuring cell concentration and viability.

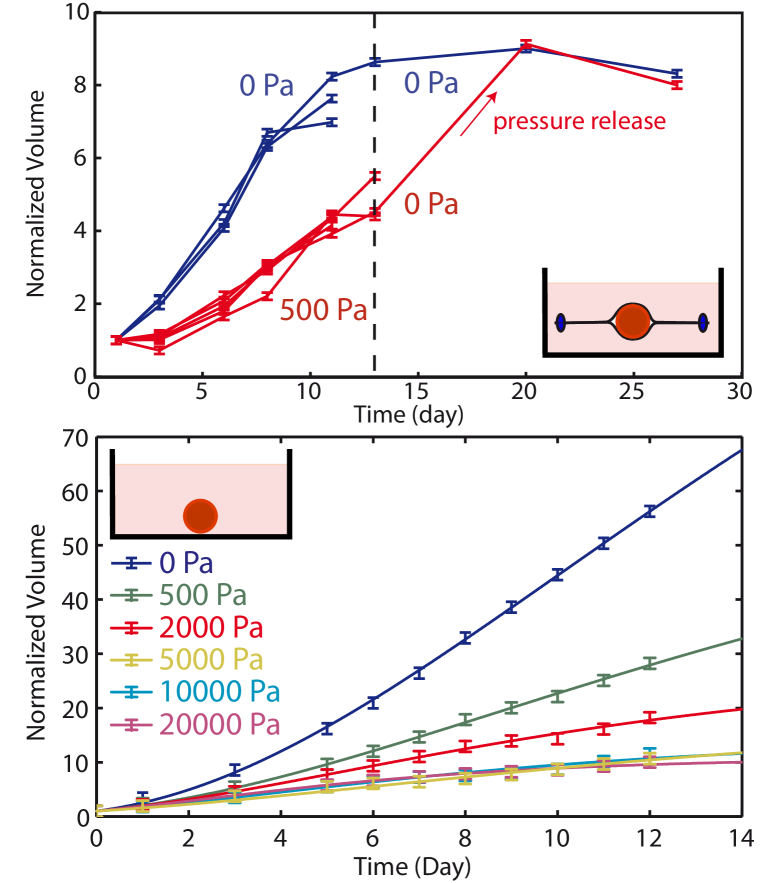
We first perform indirect stress measurements. A growing spheroid is positioned inside a closed dialysis bag (diameter 10 mm, Sigma-Aldrich) which is then placed in an external medium with added Dextran. The dialysis membrane was chosen so that its molecular weight cut-off (10 kDa) impedes the diffusion of Dextran. The osmotic stress induces a force on the dialysis membrane, which is transmitted in a quasi-static equilibrium to the spheroid and calibrated as in Bonnet-Gonnet et al. (1994); Bouchoux et al. (2009). The stress exerted on the cellular system can be seen as a network stress that tends to reduce the volume occupied by the spheroid. It acts directly on the cells, and not on the interstitial fluid. The volume $V(t)/V_{0}$, normalized by the initial volume of the spheroid $V_{0}$, is measured at successive times from a top view using differential interference contrast microscopy (Axiovert 100, Zeiss). In the absence of any applied stress, the spheroid reaches a steady state with a typical diameter 900 $\mu$m. When Dextran is added to the medium, a decrease of the growth rate $\frac{dV}{dt}$ and of the steady state volume are observed (Fig.1-Top). Interestingly, after a stress release, the growth of the spheroid resumes until it reaches the same steady state volume as in the absence of external pressure. This indicates that the effect of stress is fully reversible. Altogether these results show that an external applied stress modulates the growth of tumor spheroids.

We have also performed direct experiments where the osmotic stress is applied onto the spheroid in the absence of the dialysis membrane. In order to verify that Dextran cannot diffuse inside the spheroid, we have placed it in a medium supplemented with fluorescent FITC-Dextran at an osmotic stress $\Pi=1000$Pa. After 4 days of incubation, the first 70 $\mu$m of the spheroid were imaged using spinning disc microscopy. We measured that the amount of Dextran able to penetrate into the spheroid is negligible compared to the Dextran concentration in the medium. The osmotic stress is thus applied on the first layer of cells that plays the role of the dialysis membrane in the direct experiment and transmits the stress to the rest of the spheroid. The volume of the spheroid has also been measured as a function of time (Fig.1-Bottom). We observe a dependence of the growth rate and the steady state size on stress very similar to that observed in the indirect experiment, validating our approach. Interestingly, for a stress larger than $10kPa$ the effect of stress saturates and the growth curves are indistinguishable from each other.

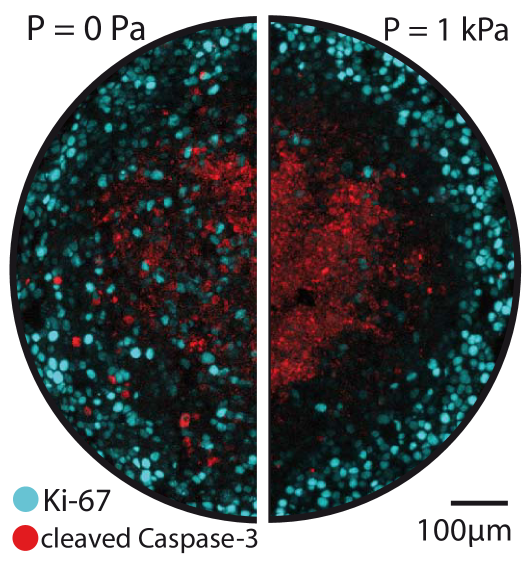
The direct experiment is based on the application of a mechanical stress on the surface of the spheroid through an osmotic shock. Osmotic stress is known to have direct effects on cell growth and apoptosis in particular through the mitogen activated protein kinase (MAPK) pathway Cowan (2003); Racz et al. (2007); Nielsen et al. (2008); Xie et al. (2007). However, in all these studies, the effect of an osmotic shock is only measured for an osmotic stress two orders of magnitude larger than the one applied in our experiments ($1MPa$ compared to $10kPa$). Moreover we do not observe any apoptosis at the surface of the spheroid where the osmotic stress is exerted (Fig. 2). In addition, it can be checked by balancing chemical potentials that the presence of Dextran outside the spheroid creates a negligible concentration gradient of all other solubles molecules. The concentration difference of a small soluble solute exchanged between the interior and the exterior of the spheroid can be estimated as $\Delta c_{s}/c_{s}=v\Pi/kT(1-\Theta_{s})<10^{-3}$ where $c_{s}$ and $\Theta_{s}$ are the concentration and the volume fraction of the solute, $v$ the molecular volume of the solvent and $\Pi$ the applied osmotic stress. In other words, the chemical potential of water in the cell is dominated by the small ions and it is only slightly modified by the presence of Dextran.

Finally we investigate experimentally the spatial dependence of cell division and apoptosis using cryo-sections and immuno-fluorescence. Spheroids of comparable diameters are embedded in a freezing medium, placed at $-80^{o}$C and cut in slices of 5 $\mu$m thickness at the level of their equatorial plane. Using a classical immuno-staining protocol, we then label fluorescently dividing cells (in cyan with an anti-Ki67 antibody) and apoptotic cells (in red with an anti -cleaved caspase3 antibody) (See Fig. 2). We observe that in the absence of external stress, cell division is distributed over all the spheroid with an increase at the periphery, whereas for an external stress of $1$kPa, it is greatly reduced in the center of the sections. As in previous studies Mueller-Klieser (1997); Mueller-klieser and Kunz-schughart (2010), we observe an accumulation of apoptotic cells in the center of the spheroid but with no measurable effect of stress on this localization.

In order to better understand this stress dependence of cell division and to interpret the generic trends of the experimental findings, we performed numerical simulations similar to those of Ref. Basan et al. (2011, 2009). We adapt these simulations to the geometry and setup of the experiments. In brief, in the simulations, a cell is represented by a pair of particles which repel each other and thus move apart. When a critical distance is reached, the cell divides. After division, each original particle constitutes, together with a newly inserted particle in its surrounding, a daughter cell. Particles belonging to different cells interact with all particles with a short range interaction: a constant attractive force describes cell-cell adhesion, while a repulsive short range potential ensures volume exclusion. The viscous drag between cells is taken into account by a “Dissipative Particle Dynamics“ -type thermostat. Finally a constant apoptosis rate provides cell removal. In order to mimic the experiments, tissue spheroids are grown in a container together with a ”passive liquid” under stress. This liquid interacts with the cell particles in a similar way as cell particles with each others and it transmits the stress on the spheroid.

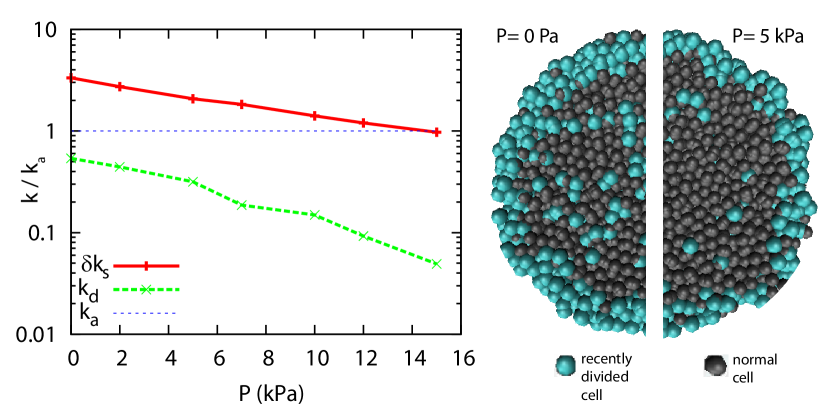
As in the experiments, we observe a steady state that depends on the applied stress. In the numerical simulations each division event can be traced and the spatial distribution of divisions can be measured to build virtual cryosections of the simulated spheroids. We observe a strong dependence of the division rate on the distance to the surface of the spheroids and a clear decrease of cell division anywhere in the section but stronger in the core (see Fig.3).

Based on the growth curves and cryosection observations, we present a simple two rate description of the spheroid growth in the absence or the presence of external stress: the core of the spheroid is mostly undergoing apoptosis whereas its periphery is proliferating. In this situation, the net growth rate is proportional to the area $(\propto r^{2})$ while the net death rate is proportional to the volume $(\propto r^{3})$. This surface growth effect leads to a stable steady state size. The surface localization of the proliferation can be obtained using purely mechanical considerations. A cell must deform its environment to grow. The deformation is facilitated if the cell is closer to the surface, and this implies that proliferation is favored at the surface. The increased number of cell divisions at the surface drives a flow from the surface of the spheroid toward its center. The flow is a possible explanation for the accumulation of the long lasting apoptotic markers in the center of the spheroid. A mechanical control of cell cycle entrance can also explain the growth of tumor spheroids in free suspension Drasdo and Höhme (2005). In this case nutrient depletion causes the formation of a necrotic core which generates death at the inner surface of the viable rim $(\propto r^{2})$ i.e. not proportional to the volume thereby not generating a steady state Drasdo and Höhme (2005); Schaller and Meyer-Hermann (2005). Using a fluorescently labelled growth factor (Alexa 555- EGF) we have verified that the transport of these molecules is not affected by stress. This result supports a direct mechanical effect on the division rate.

Our two rate model can be seen as a simplified version of the two rate model of Radszuweit et al. Radszuweit et al. (2009). The net bulk growth rate is $k=k_{d}-k_{a}$, where $k_{d}$ and $k_{a}$ are the division and apoptosis rates respectively. It is a function of stress. At the surface, the net growth rate $k_{d}-k_{a}+\delta k_{s}$ is larger and $\delta k_{s}$ has a different stress dependence. Taking into account surface and bulk growth, the growth equation reads :

Assuming a constant cell density and a constant thickness $\lambda$ of the region where the division rate increment is equal to $\delta k_{s}$, one can express for $R>\lambda$ the rate of volume increase as :

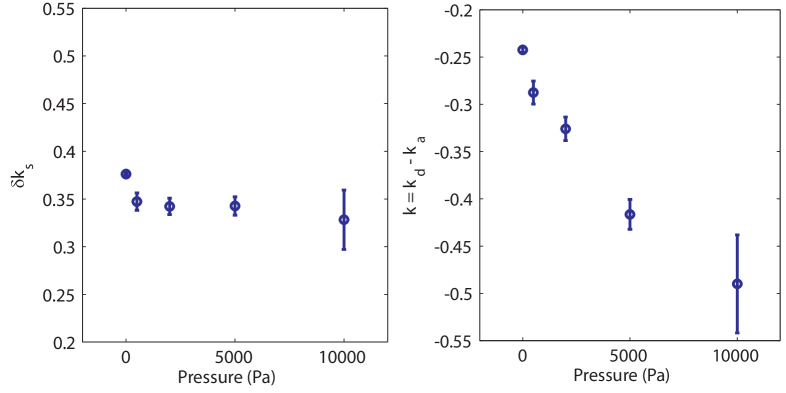
For small spheroids ($R<<\lambda$) the growth rate is positive and constant ($k_{d}+\delta k_{d}-k_{a}$), this leads to the previously described exponential growth Drasdo and Höhme (2005); Schaller and Meyer-Hermann (2005). In our case the growth curves can readily be fitted by Eq. 2 in the range of large spheroids Von Bertalanffy (1957). The variation with pressure of the parameters $k=k_{d}-k_{a}$ and $\delta k_{s}$ is given in Fig. 4. The surface growth rate $\delta k_{s}$ is less affected by stress than the bulk growth rate $k$. A similar fit can be performed on the simulations. The bulk and surface growth rates $k$ and $\delta k_{s}$ are represented on Fig. 3. Although both the surface and bulk growth rates depend exponentially on pressure, the decay constant of the surface rate is much smaller than that of the bulk rate. While the bulk rate decreases by more than one order of magnitude, the surface rate decreases by a factor 3. This supports the hypotheses of the simulations. In summary, cell division in the core of the spheroid is strongly affected by stress whereas cell division rate increment on the surface of the spheroid depends more weakly on stress.

In conclusion, we have shown by a direct measurement of the tissue response to an external stress that the application of an external stress drastically limits the growth of tumoral spheroids. Previous approaches Helmlinger et al. (1997); Fritsch et al. (2010) had used the elastic deformation of poro-elastic gels to measure the maximum stress that can be developed by spheroids. The measured stress in these experiments is in the same range as in our measurements. In a recent study a localized increase of mitochondrial apoptosis and a reduction of proliferation in presence of stress were also reported Cheng et al. (2009). This difference with our results may be due to the fact that in our case we are not controlling the rigidity of the surrounding substrate but the applied pressure. This may leads to a different response of the spheroid. Our results favors the idea that direct mechanical effects can have strong implications in cancer proliferation. This raises the question of the players in the crosstalk between stress and cellular response and in particular of the nature of the stress sensor.

We would like to thank F. Brochard, F. Graner, P. Nassoy, K. Alessandri and J. Kaes for useful discussions. F.M. and G.C. would like to thank Axa Research Fund and CNRS for funding. The group belongs to the CNRS consortium CellTiss.