Strong antiferromagnetic proximity coupling in a heterostructured superconductor Sr₂VO₃FeAs

Heterostructures of correlated electronic systems offer novel and versatile platforms for triggering various types of interactions and stabilizing exotic electronic orders Damascelli ; Chakalian ; Gozar ; Satapathy ; Driza ; FeSeSTO1 ; FeSeSTO2 ; FeSecharge ; FeAscharge . When one of the constituent layers hosts a superconducting state, the other blocking layer in-between serves as an active spacer that controls the dimensionality and also introduces additional proximity coupling. For example, in high-$T_{c}$ cuprates and iron-based superconductors (FeSCs), various types of blocking layers are used to tune the superconducting properties by changing doping levels, modifying the interlayer coupling, introducing lattice strain  Damascelli ; Chakalian ; Gozar ; Satapathy ; Driza , or inducing additional pairing interaction by interfacial phonons FeSeSTO1 ; FeSeSTO2 or charge transfer FeSecharge ; FeAscharge . Particularly, when the blocking layer is magnetic, additional magnetic interactions with localized spins may have substantial influence on the superconducting properties, but this issue has not been much explored.

Sr₂VO₃FeAs is a naturally-assembled heterostructure and has a unique position among FeSCs. In this compound, superconducting FeAs layers and insulating SrVO₃ layers are alternately stacked Zhu ; Ok (Fig. 1a), analogous to the superlattice of FeSe/SrTiO₃ choi1 ; choi2 , but with additional magnetic proximity coupling between Fe and V spins. The SrVO₃ layers have been identified to host the Mott-insulating state Nakamura2010b ; Qian2011a ; Kim2015 ; Ok ; Ok2 in the absence of a long-range magnetism of the V spins Ok . Instead, in the FeAs layers, various phase transitions occurs above the superconducting transition at $T_{c}\sim$ 30 K Zhu ; Ok ; Cao , including an intriguing $C_{4}$ symmetric transition at $T_{\rm HO}\sim$ 150 K Ok ; NMR ; SH1 ; SH2 without breaking any of the underlying translational, rotational, and time reversal symmetries, reminiscent of the so-called $hidden$ order transition YKKim . Such a transition has never been observed in other FeSCs, and magnetic proximity coupling that induces frustration between stripe-type Fe and Neel-type V antiferromagnetism Ok , has been suggested to be responsible for it. However, whether or not such a magnetic proximity coupling is strong enough, and if so, whether it is ferromagnetic (FM) or antiferromagnetic (AFM), have not been clarified yet.

In this Letter, we present experimental evidences for strong AFM exchange coupling of itinerant Fe spins to localized V spins, using the upper critical field $H_{c2}$ of Sr₂VO₃FeAs single crystal for both $H\parallel ab$ and $H\parallel c$, determined by magnetoresistance measurements up to 30 T and radio-frequency (RF) contactless measurements up to 65 T. A strongly convex $H_{c2}^{c}(T)$ for $H\parallel c$ is observed in contrast to a steep linear increase of $H_{c2}^{ab}(T)$ near $T_{c}$ for $H\parallel ab$. In comparison with other FeSCs, we found that the Jaccarino-Peter (JP) effect with an exchange field up to $\sim$ 20 T is responsible for this unusual behavior. Our observations confirm that magnetic proximity coupling can play a critical role for inducing unusual magnetic and superconducting properties of Sr₂VO₃FeAs.

Single crystals of Sr₂VO₃FeAs were grown using self flux techniques Ok . The typical size of each single crystal was 200$\times$200$\times$10 $\mu m^{3}$. High crystallinity and stoichiometry were confirmed by X-ray diffraction and energy-dispersive spectroscopy. The single crystals show a clear superconducting transition at $T_{c}^{onset}\sim$ 27 K, which is somewhat lower than a maximum $T_{c}^{onset}\sim$ 35 K in a polycrystalline sample Zhu . This difference may be attributed to a partial deficiency of oxygen SVOFA-O . Magnetotransport measurements were carried out using conventional six-probe method in a 14 T Physical Property Measurement System and a 33 T Bitter magnet at the National High Magnetic Field Lab., Tallahassee. RF contactless measurements up to 65 T were performed in the National High Magnetic Field Lab., Los Alamos.

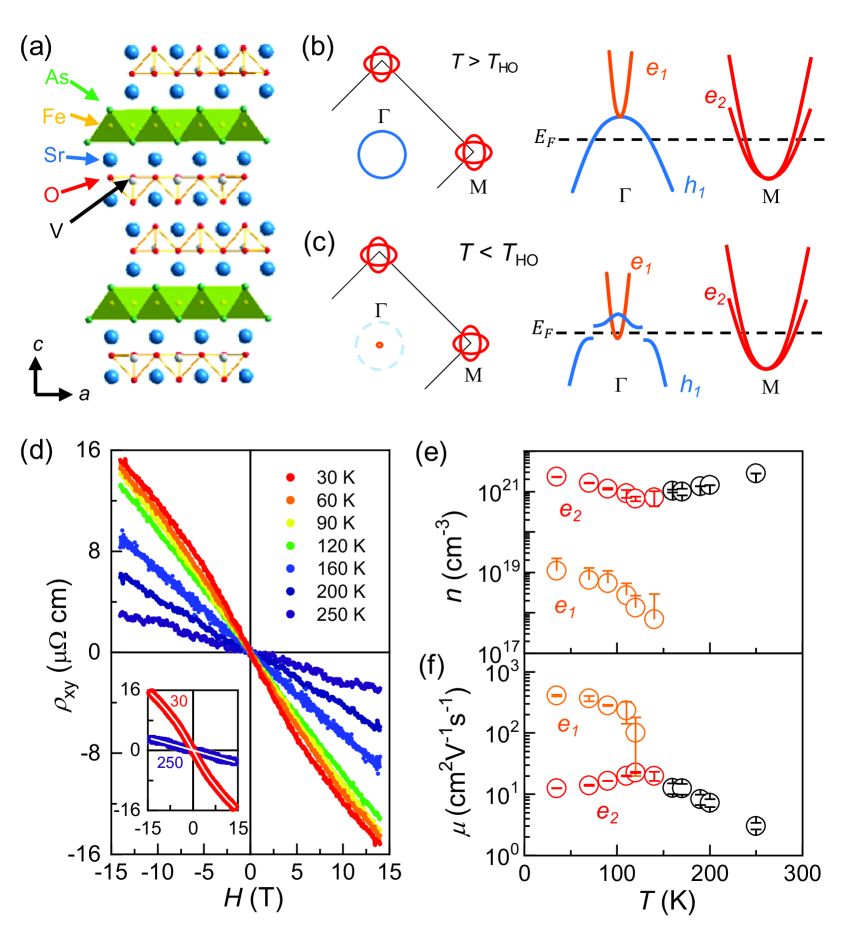
Before discussing the upper critical field $H_{c2}$ of Sr₂VO₃FeAs, we first consider the Fermi surface reconstruction across the $C_{4}$ symmetric transition $T_{\rm HO}$ $\approx$ 150 K. According to recent ARPES results on Sr₂VO₃FeAs in the wide range of temperature, the heavy hole FS centered at the $\Gamma$ point of Brillouin Zone (BZ), denoted $h_{1}$ in Figs. 1b and 1c, has a relatively strong $k_{z}$ dispersion and becomes fully gapped below $T_{\rm HO}$. In contrast, the two dimensional electron FS at the $M$ point ($e_{2}$ in Figs. 1b and 1c) remains gapless. Concomitantly the additional small electron FS ($e_{1}$ in Figs. 1b and 1c), which is absent in the calculated band structures of Sr₂VO₃FeAs YKKim , is introduced at the $\Gamma$ point, as illustrated in Figs. 1b and 1c. Because of this unusual band selective gap opening at $T_{\rm HO}$, low-energy electronic structures of Sr₂VO₃FeAs are significantly reconstructed to yield two separate electron FSs ($e_{1}$ and $e_{2}$) with strong mismatch in size(Supplementary Fig. S1) supp . These features are highly distinct from those of other FeSCs.

The FS reconstruction of Sr₂VO₃FeAs is also probed by the field dependent Hall resistivity $\rho_{xy}(H)$ of Sr₂VO₃FeAs at different temperatures under magnetic field up to 14 T (Fig. 1d). Above $T_{\rm HO}\sim 150$ K, a linear field dependence of $\rho_{xy}(H)$ with a negative slope is observed up to $H$ = 14 T, similar to the cases of other FeSCs, in which charge conduction is dominated by electron FSs with a high mobility hall1 . The contribution of the hole FSs usually appear in $\rho_{xy}(H)$ at low temperatures with a positive slope FeSehall ; ba122hall ; Hall112 ; Hall111 ; Hall122 ; Hall1111 ; supp , but is completely absent in Sr₂VO₃FeAs. Instead we found that a non-linear field dependence in $\rho_{xy}(H)$ suddenly appears below $T_{0}$, which is well reproduced by the two-band model with two distinct electron carriers. Using a constraint of $1/\rho_{xx}(T)=\sum n_{i}e\mu_{i}$, the fit to the two-band model gives us the temperature dependent carrier density ($n_{i}$) and carrier mobility ($\mu_{i}$) as shown in Figs. 1e and 1f. Clearly, additional electron carriers ($e_{1}$) with lower density but a higher mobility are induced on top of the high density electron carriers ($e_{2}$). The densities of the two electron carriers are estimated to be $\approx 1.1\times 10^{19}$ cm^-3 and $\approx$ 2.3$\times 10^{21}$ cm^-3, which are in good agreement with those of the $e_{1}$ FS at the $\Gamma$ ($\approx$ $2.0\times 10^{19}$ cm^-3) and the $e_{2}$ FS at the $X$ point ($\approx$ $1.1\times 10^{21}$), obtained by recent ARPES studies Kim2015 . This additional conduction channel of the small FS ($e_{1}$) with high mobility compensate for the loss of conduction from the gapped hole FS below $T_{\rm HO}$, which may explain a weak resistivity anomaly across $T_{\rm HO}$.

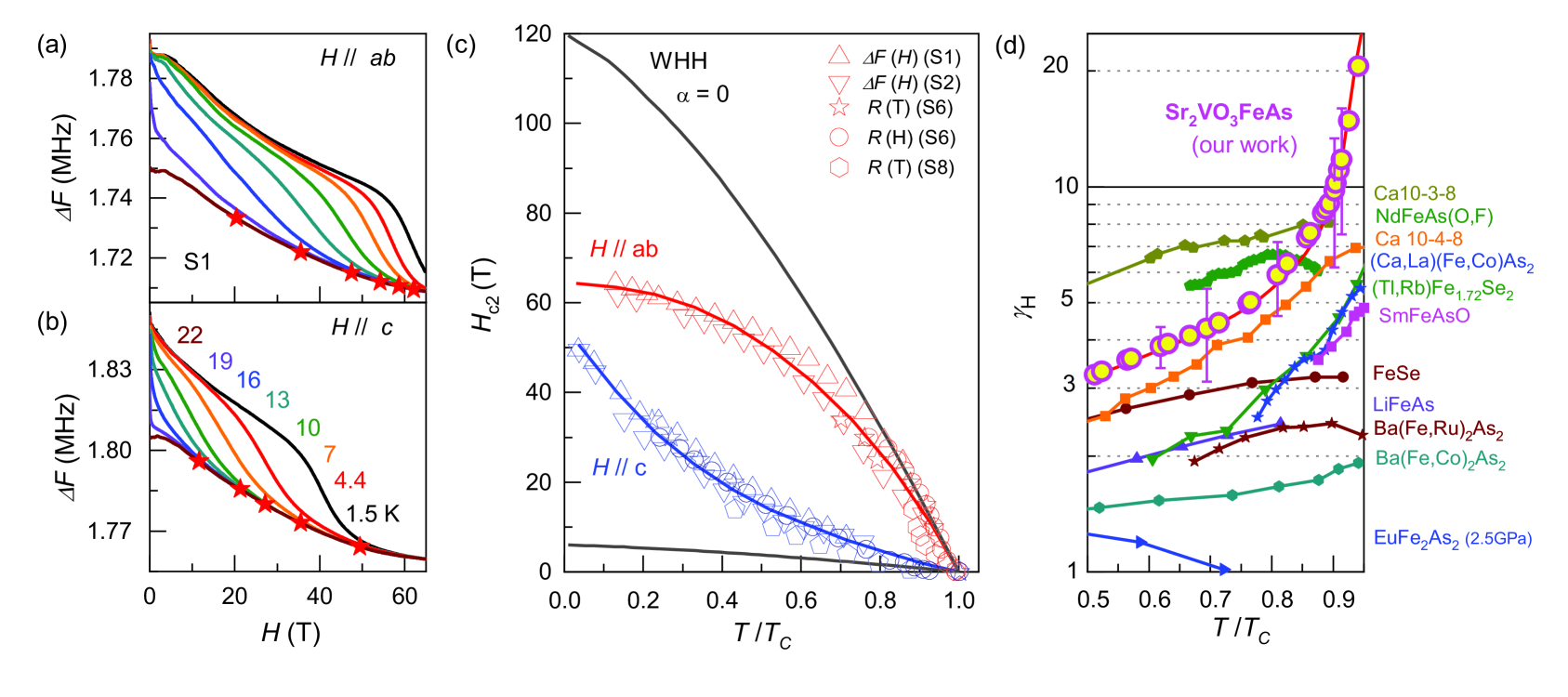
Now we focus on the upper critical field $H_{c2}$ of Sr₂VO₃FeAs single crystals, obtained from RF measurements and the resistivity (Fig. 2). The radio-frequency curves as a function of magnetic fields along $H\parallel ab$ and $H\parallel c$ yield $H_{c2}(T)$ at various temperatures (Figs. 2a and 2b). Here we determined $H_{c2}$ by taking the magnetic field at which the steepest slope of the radio-frequency intercepts the normal-state background. Temperature and magnetic field dependence of resistivity $\rho_{xx}$ were also used to determine $H_{c2}(T)$ under magnetic field up to 33 T (Supplementary Fig. S2) supp . Using the criterion of 50$\%$ of resistive transition, we obtained $H_{c2}(T)$, consistent with that from the RF contactless measurements. We note that using different criteria for $H_{c2}$ in the RF and the resistivity measurements obtained qualitatively the same $H_{c2}(T)$ behaviour(Supplementary Fig. S3) supp .

Figure 2 (c) shows $H_{c2}(T)$ curves as function of the normalized temperature ($t=T/T_{c}$) for $H\parallel ab$ and $H\parallel c$. We found that $H_{c2}(T)$ curves taken from different samples and different measurements are consistent with each other. Depending on the magnetic field orientations, $H_{c2}(T)$ exhibits different behaviors. For $H\parallel ab$, $H_{c2}^{ab}(T)$ shows a concave temperature dependence with saturation at low temperatures. This shape is typically observed in many FeSCs hc2 ; hc2review in which the Pauli limiting effect dominates over other pair-breaking mechanisms. In contrast, $H_{c2}^{c}(T)$ for $H\parallel c$ shows a strongly convex behaviour with a strong upward curvature. The similar convex behaviours of $H_{c2}(T)$ have been rarely observed, except in some FeSCs including Ba(Fe,Co)₂As₂ D122_3 , (Sr,Eu)(Fe,Co)₂As₂ D122_4 , LaFeAs(O,F) D1111_1 , and NdFeAs(O,F) gNd111 . However their upward curvature of $H_{c2}(T)$ is far less significant than found in Sr₂VO₂FeAs.

This strong anisotropic behavior of $H_{c2}$ in Sr₂VO₃FeAs can be quantified by the anisotropy factor $\gamma_{H}=H^{ab}_{c2}/H^{c}_{c2}$. We plot the temperature dependent $\gamma_{H}$ for Sr₂VO₃FeAs together with other FeSCs in Fig. 2(d). Near $T_{c}$, the slope of $H_{c2}(T)$ is estimated to be $dH_{c2}/dT|_{T_{c}}\simeq$ -7.4 T/K for $H\parallel ab$ and $\simeq$ -0.2 T/K for $H\parallel c$, in Sr₂VO₃FeAs, resulting in $\gamma_{H}\sim$ 20 at $T\approx T_{c}$. This is the highest $\gamma_{H}$ found in FeSCs. As shown in Fig. 2(d), the typical values of $\gamma_{H}$ are $\simeq$ 2-3 in the so-called 122 compounds and $\gamma_{H}\simeq$ 5-6 in the 1111 compounds. Usually, the thicker blocking layer between the superconducting layers induces the stronger anisotropy of $H_{c2}$ with a larger $\gamma_{H}$. The $\gamma_{H}$ values of various FeSCs with a different thickness ($d$) of the blocking layer follow an empirical relation $\gamma_{H}$/$d$ $\sim$ 0.65 $\rm\AA ^{-1}$ (Supplementary Fig. S4) supp . However, Sr₂VO₃FeAs has $\gamma_{H}$ $\approx$ 20, which is by a factor of two larger than what is expected. This observation indicates that the relatively thick blocking layer in Sr₂VO₃FeAs alone cannot explain the observed $\gamma_{H}$ and also its strong temperature dependence.

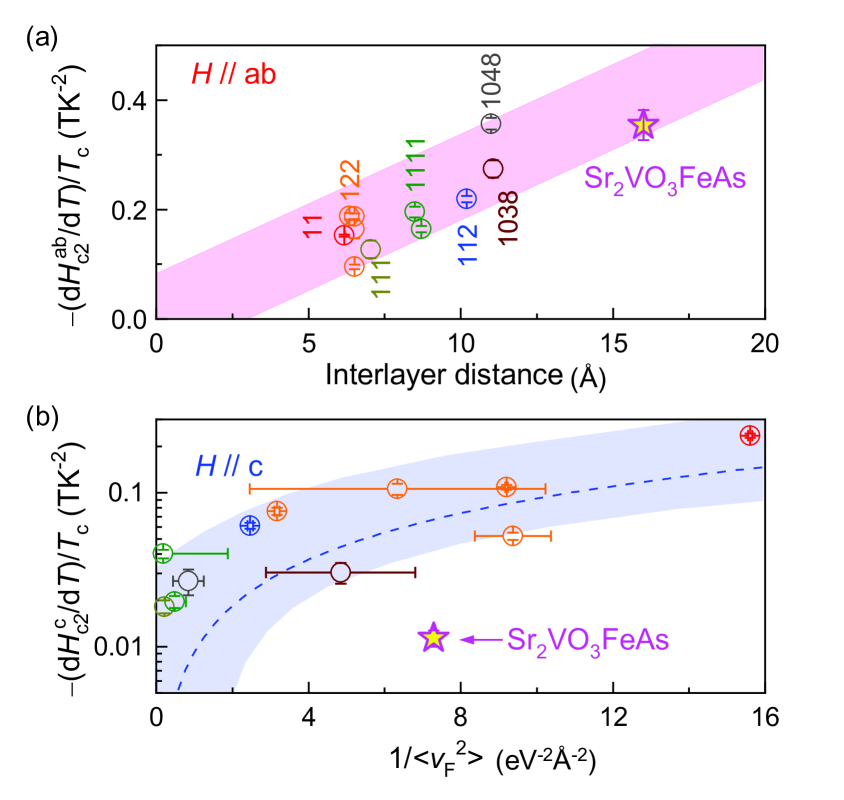
In comparison with other FeSCs, we found that the exceptionally small $dH_{c2}^{c}/dT$ near $T_{c}$ for $H\parallel c$ is crucial to the large $\gamma_{H}$ in Sr₂VO₃FeAs. In the case of $H\parallel ab$, the normalized slope of the upper critical field at $T_{c}$, $-(dH_{c2}^{ab}/dT)/T_{c}$ is closely related to the diffusivity along the $c$-axis and thus is sensitive to the interlayer distance. Sr₂VO₃FeAs nicely follows the linear trend of $-(dH_{c2}^{ab}/dT)/T_{c}$ as a function of the thickness of the blocking layer $d$ (Fig. 3a). The distinct behaviour of Sr₂VO₃FeAs is observed for $H\parallel c$. In the case of $H\parallel c$, $-(dH_{c2}^{c}/dT)/T_{c}$ is more sensitive to the electronic structure of the FeAs layer than to the interlayer distance. In conventional superconductors, $-(dH_{c2}^{c}/dT)/T_{c}$ is known to be proportional to $1/\langle v_{F}^{2}\rangle$ (Fig. 3b, blue dotted-line). The strong correlation between $-(dH_{c2}^{c}/dT)/T_{c}$ and $1/\langle v_{F}^{2}\rangle$ is confirmed in FeSCs (Fig. 3b). The data for Sr₂VO₃FeAs, however, clearly deviate from this trend and show the lowest $-(dH_{c2}^{c}/dT)/T_{c}$ value, leading to the largest $\gamma_{H}$ among the FeSCs.

For many FeSCs, temperature dependent $H_{c2}^{c}(T)$ has been understood using the two-band dirty-limit model multihc2 . In this model, the intra- and inter-band coupling ($\lambda_{11,22}$ and $\lambda_{12,21}$) and diffusivity of each band ($D_{1}$, $D_{2}$) determines $H_{c2}^{c}(T)$ (See Supplementary Fig. S5) supp . The two-band model can also reproduce the strongly convex behavior of $H_{c2}^{c}(T)$ of Sr₂VO₃FeAs, if we assume dominant interband coupling ($\lambda_{11}\lambda_{22}<\lambda_{12}\lambda_{21}$) and an unusually large $\eta=D_{1}^{ab}/D_{2}^{ab}\sim 30$ (Supplementary Figs. S5 and S6) supp . We note however that most of the FeSCs show a concave $H_{c2}^{c}(T)$, and even in a few cases, like Ba(Fe,Co)₂As₂ D122_3 , LaFeAs(O,F)  D1111_1 or NdFeAs(O,F) gNd111 , that show a convex $H_{c2}^{c}(T)$, the highest estimated $\eta$ is $\sim$ 10 hc2review , which is far less than the estimate $\eta\sim$ 30 for Sr₂VO₃FeAs. Furthermore, the hole FS ($h_{1}$) centered at the $\Gamma$ point of BZ is gapped out below $T_{\rm HO}$ (Figs. 1b and 1c), and therefore cannot participate in the interband superconducting pairing. The remaining interband coupling channel is between electron FSs ($e_{1}$ and $e_{2}$) centered at $\Gamma$ and $M$ points (Fig. 1c). However, considering their drastic size difference by two orders of magnitude, confirmed by ARPES and Hall resistivity results, they are unlikely to produce strong interband coupling. These observations suggest that the conventional multiband effect cannot be the origin of the observed $H_{c2}^{c}(T)$ of Sr₂VO₃FeAs.

Instead magnetic coupling between itinerant Fe and localized V spins can offer a natural explanation for a strongly convex behaviour of $H_{c2}^{c}(T)$. Recent high field magnetoresistance (MR) results reveal a strong negative MR with a clear kink at $\sim$ 38 T for $H\parallel c$, in contrast to the monotonic positive MR for $H\parallel ab$  YKKim . These results resemble the case of EuFe₂As₂ Eu122 and indicate a field-induced saturation of magnetic V moment for $H\parallel c$ but not for $H\parallel ab$. Strong exchange coupling $J$ of itinerant Fe electrons to localized V spins is then expected to introduce a net internal magnetic field $H_{J}$ = $J\left<S\right>/g_{m}\mu_{\rm B}$, which is referred to as the JP effect jacc . With AFM exchange interaction ($J<$0), a negative $H_{J}$ is produced by polarization of V spins along the external field, particularly for $H\parallel c$. For paramagnetic V spins, their susceptibility and thus $H_{J}$ increase with lowering temperatures. Therefore, $H_{J}$ compensates for the external field and enhances $H_{c2}(T)$ at low temperature with large external fields. This trend results in a convex $H_{c2}(T)$, as observed in Fig. 2(c).

In the JP model with multiple pair-breaking including the exchange field due to the localized moments jacc , $H_{c2}(T)$ can be described as

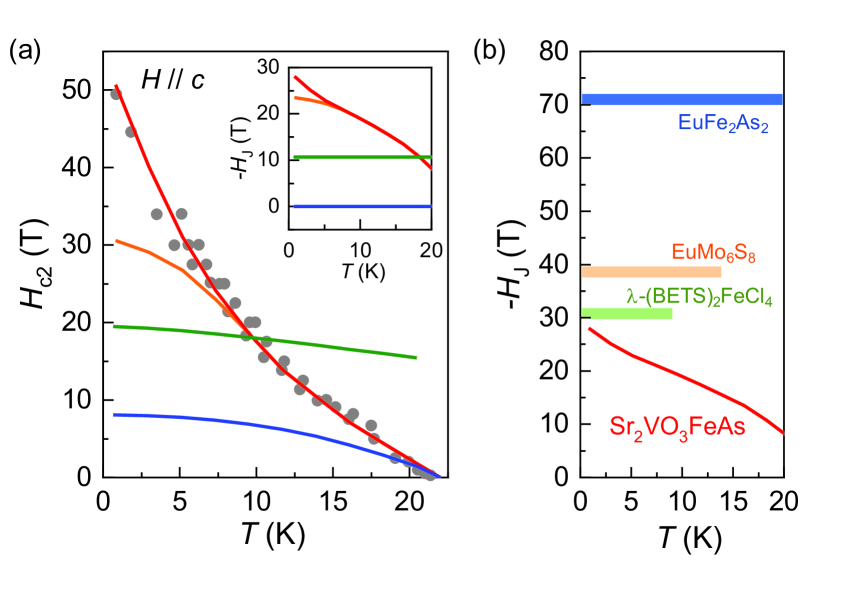
where $\gamma=[\alpha^{2}(h+h_{J})^{2}-\lambda_{SO}^{2}]^{\frac{1}{2}}$, $t=T/T_{c}$, $h=0.281H_{c2}/H_{c2}^{*}$, $h_{J}=0.281H_{J}/H_{c2}^{*}$, $H_{c2}^{*}$ is orbital critical field at $T$= 0 K, $\Psi$ is the digamma function, $\lambda_{SO}$ is spin-orbit scattering parameter and $\alpha$ is the Maki parameter. Using $\lambda_{SO}$ = 0.3 and $\alpha$ = 2.1, we successfully reproduced $H_{c2}(T)$ for $H$ $\parallel$ $c$ (Figs. 2c and 4a). We note that in the JP model, neither a temperature independent $H_{J}$ (green solid line) nor a saturating $H_{J}$ at low temperature (orange solid line) reproduces the observed upward curvature in $H_{c2}^{c}(T)$. The increasing $H_{J}$ at low temperatures (red solid line) is found to be crucial to reproduce the convex $H_{c2}(T)$, which is consistent with the paramagnetic state of V spins Ok . The best fit for $H$ $\parallel$ $c$ yields the negative exchange field $H_{J}$ increasing in magnitude up to $\sim$ 30 T with lowering temperature (red solid line in the inset of Fig. 4a). We also found that if the maximum $H_{J}$ is lower than $\sim$ 10 T, the calculated $H_{c2}(T)$ becomes similar to the WHH prediction. For $H$ $\parallel$ $ab$, therefore, the WHH-like behaviour can be explained by the upper bound of $H_{J}$ $\sim$ 10 T. This anisotropic $H_{J}$ may be due to the magnetic anisotropy of V spins, which is consistent with the anisotropic MR showing the conventional positive MR for $H\parallel{ab}$ and the negative MR for $H\parallel c$ below $T_{HO}$  YKKim .

The maximum $H_{J}$ of Sr₂VO₃FeAs, estimated for $H\parallel c$, is comparable with those of other superconductors that show the JP effect, including EuMo₆S₈ EuMoS1 ; EuMoS2 and $\lambda$-(BETS)FeCl₄ FeCl4_1 ; FeCl4_2 , and far less than $H_{J}$ $\sim$ 75 T of EuFe₂As₂ (Fig. 4b). However, considering the smaller $\left<S\right>$ = 1 of V spins with 3$d^{2}$ configurations than $\left<S\right>$ = 7/2 of Eu spins, the coupling constant $J$ $\sim$ 2.3 meV is comparable in EuFe₂As₂ and Sr₂VO₃FeAs, suggesting that they share the AFM interlayer exchange interaction. Despite the similarity, magnetism of Sr₂VO₃FeAs is highly distinct from that of EuFe₂As₂. In EuFe₂As₂, Eu magnetism is induced by RKKY interaction due to itinerant Fe electrons  Zapf . In contrast, the SrVO₃ layers in Sr₂VO₃FeAs have their own superexchange interaction ($J_{\rm S}$), competing with the RKKY interaction through the FeAs layers. The proximity coupling strength $J$ $\sim$ 2.3 meV is comparable with the superexchange interaction of V spins, $J_{\rm S}$ $\sim$ 1.6 meV, estimated from the Curie-Weiss temperature $\Theta_{\rm CW}\sim 100$ K Ok . Furthermore, it is AFM type, in contrast to the FM type expected in total energy calculations Ok ; Mazin . Such a significant AFM proximity coupling is effective to frustrate two distinct magnetic instabilities, Neel-type in V spins and stripe-type in Fe spins in Sr₂VO₃FeAs. This magnetic frustration has drastic effect on magnetism by destabilizing these conventional AFM orders in FeAs and SrVO₃ layers Ok , which precipitates a $C_{4}$ symmetric transition without long-range magnetic order.

In conclusion, based on the upper critical field $H_{c2}$ and Hall resistivity $\rho_{xy}$ results, we show that strong convex behavior of $H_{c2}(T)$ and the highly anisotropic $H_{c2}$ with the largest $\gamma_{H}\sim$ 20 among the FeSCs are due to magnetic proximity coupling with the neighboring localized V spins by the JP effect, rather than by the multi-band effect. These findings demonstrate that a heterostructured Sr₂VO₃FeAs is a unique example in which the exotic electronic order, triggered by the magnetic proximity coupling, significantly affects the low energy electronic structure and superconductivity. Our work highlights that correlated heterostructures with FeSCs offer novel and fertile grounds for studying the interplay between superconductivity and the hidden competing orders.

The authors thank Y. G. Bang for fruitful discussion. We also thank H. G. Kim in Pohang Accelerator Laboratory (PAL) for the technical support. This work was supported by the Institute for Basic Science (IBS) through the Center for Artificial Low Dimensional Electronic Systems (no. IBS-R014-D1) and by the National Research Foundation of Korea (NRF) through SRC (Grant No. 2018R1A5A6075964) and the Max Planck-POSTECH Center for Complex Phase Materials (Grant No. 2016K1A4A4A01922028). W.K. acknowledges the support by NRF (No. 2018R1D1A1B07050087, 2018R1A6A1A03025340), and Y.J.J. was supported by NRF (No. NRF-2019R1A2C1089017). A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement No. DMR-1644779 and the state of Florida.