Strong magnetic correlations to 900 K in single crystals of the trigonal antiferromagnetic insulators SrMn2As2 and CaMn2As2
Abstract
Crystallographic, electronic transport, thermal and magnetic properties are reported for and single crystals grown using Sn flux. Rietveld refinements of powder x-ray diffraction data show that the two compounds are isostructural and crystallize in the trigonal -type structure (space group ), in agreement with the literature. Electrical resistivity versus temperature measurements demonstrate insulating ground states for both compounds with activation energies of 85 meV for and 61 meV for . In a local-moment picture, the Mn+2 ions are expected to have high-spin with spectroscopic splitting factor . Magnetic susceptibility and heat capacity measurements versus reveal antiferromagnetic (AFM) transitions at K and 62(3) K for and , respectively. The anisotropic data indicate that the hexagonal axis is the hard axis and hence that the ordered Mn moments are aligned in the plane. The data for both compounds and the for show strong dynamic short-range AFM correlations from up to at least 900 K, likely associated with quasi-two-dimensional connectivity of strong AFM exchange interactions between the Mn spins within the corrugated honeycomb Mn layers parallel to the plane.
pacs:
75.50.Ee, 74.70.Xa, 75.40.-s, 72.15.EbI Introduction
The body-centered tetragonal ternary compounds ( = rare or alkaline earth, = transition metal, = Si, Ge, P, As, Sb) with the structureJust1996 have generated tremendous interest in the scientific community due to their novel electronic and magnetic properties. Prominent among these is the iron-arsenide family of parent compounds ( = Ca, Sr, Ba, Eu).Johnston2010 ; Stewart2011 ; Scalapino2012 ; Dagotto2013 ; Fernandes2014 ; Hosono2015 ; Dai2015 ; Inosov2016 ; Si2016 These materials are metallic and show nearly contiguous antiferromagnetic (AFM) spin-density wave and structural transitions at temperatures up to K. The suppression of these transitions by external pressure or chemical doping leads to superconductivity with bulk superconducting transition temperatures up to 56 K. It is believed that the FeAs layer as the conducting sheet in this structure plays a crucial role in the occurrence of superconductivity.Johnston2010 ; Stewart2011 ; Scalapino2012 ; Dagotto2013 ; Fernandes2014 ; Hosono2015 ; Dai2015 ; Inosov2016 ; Si2016 Hence, it is important to investigate other related materials with similar compositions and structures in the search for new superconductors and other novel phenomena. For example, SrNi2As2 ( K, Ref. Bauer2008, ) and BaNi2As2 ( K, Ref. Ronning2008, ) were both found to be superconductors.
On the other hand, SrCo2As2 (Refs. Pandey2013, ; Jayasekara2013, ; Wiecki2015, ) and BaCo2As2 (Refs. Sefat2009, ; Anand2014, ) are correlated metals with no structural, superconducting or long-range magnetic ordering transitions. From inelastic neutron scattering measurements, SrCo2As2 is found to exhibit strong AFM correlations at the same stripe wavevector as do the superconducting iron arsenides, which raises the interesting question of why SrCo2As2 is not a high- superconductor.Jayasekara2013 The reason has been suggested from NMR measurements to be that SrCo2As2 exhibits strong ferromagnetic (FM) spin correlations/fluctuations in addition to the AFM correlations and these compete with the AFM correlations that are the presumptive glue for superconductivity in these systems. Subsequent NMR studies indicated that the large range of observed within the FeAs-based systems may also arise from the competition between FM and AFM correlations.Wiecki2015b
Recently significant attention has focussed on Mn arsenides. Our studies of the properties of the parent and doped BaMn2As2 systems were originally motivated by their potential to be ThCr2Si2-type high- superconductors analogous to the cuprates. The semiconductor BaMn2As2 shows G-type (checkerboard-type) local-moment collinear AFM order below its high Néel temperature K with the ordered moments aligned along the tetragonal axis.Singh2009 ; Singh2009b ; Johnston2011 Thus magnetoelastic coupling does not cause a distortion of the crystal structure below , contrary to the orthorhombic distortion associated with AFM ordering in the compounds due to the collinear Fe ordered moments aligned in the plane. An optical gap of 48 meV was inferred for BaMn2As2 from the optical conductivity,Antel2012 consistent with results from the electrical resistivity versus temperature measurements in the plane.Singh2009 Furthermore, this optical studyAntel2012 found that BaMn2As2 is much more two-dimensional in its electronic properties than are the parent compounds.Singh2009 A neutron scattering study of isostructural found the same G-type AFM structure as in but with a lower K.Calder2014
Only 1.6% K substitution for Ba transforms BaMn2As2 into a local-moment AFM metal.Pandey2012 ; Yeninas2013 Higher doping levels lead to the onset of FM at % K-dopingBao2012 and half-metal FM behavior below the Curie temperature K at 40% K doping (Refs. Pandey2013b, ; Ueland2015, ) and at 60% Rb doping.Pandey2015 The FM is thus thought to be associated with FM ordering of the itinerant doped-hole spins and coexists with the G-type AFM order of the local Mn moments with K.Ueland2015 ; Lamsal2013
Unlike BaMn2As2 with the tetragonal structure, the compounds and both crystallize in the trigonal -type structureMewis1978 ; Brechtel1978 containing a corrugated honeycomb Mn sublattice which can be viewed as a triangular lattice bilayer. The possibility of geometrically-frustrated triangular-lattice exchange connectivity exists and such compounds often show novel physical behaviors associated with the geometric frustration.Ramirez1994 ; Moessner2006 ; Balents2010 Single crystals of were grown previously using Sn flux.Wang2011 These authors’ in-plane electrical resistivity measurements indicated that the ground state is insulating with activation energies of 0.29–0.64 eV depending on the range, and their magnetic susceptibility measurements indicated an AFM transition at K.Wang2011
Two neutron powder diffraction studiesRatcliff2009 ; Bridges2009 of the related -type revealed AFM ordering below K and 85 K, respectively, with an AFM propagation vector , i.e., the crystal and AFM unit cells are the same. In the former paper the AFM structure was deduced to be collinear, with the ordered moments aligned in the plane with a low- ordered moment of 2.8(1) /Mn, where is the Bohr magneton. In the latter paper, a model was favored with the ordered moments canted at with respect to the plane with an ordered moment of 3.38(6) /Mn.
Herein, we report the growth, crystal structure, , magnetization as a function of magnetic field , and heat capacity measurements of and single crystals. These studies were initiated because of the above-noted possibility that the Mn spin lattice might exhibit novel magnetic behaviors associated with the presence of geometric frustration within the triangular-lattice Mn layers. If the strongest AFM interactions are indeed within a triangular lattice layer, this should lead to a noncollinear AFM structure below . Instead, in a companion neutron diffraction study to the present work, the AFM structure of was found to be collinear with the ordered Mn moments aligned in the plane with magnitude 3.6 /Mn.Das2016 This magnetic structure is the same as one of the two AFM structures proposed for (Ref. Ratcliff2009, ) discussed above.
We discovered that the of and and the of above their respective Néel temperatures of 120 and 62 K exhibit behaviors characteristic of strong dynamic short-range AFM spin correlations up to at least 900 K, likely arising from quasi-two-dimensional connectivity of strong AFM Mn–Mn exchange interactions within the corrugated honeycomb Mn spin sublattice. This result is interesting because such strong AFM spin correlations up to high temperatures and the suppression of to much lower temperatures than expected from molecular field theory, due to AFM fluctuations associated with the low dimensionality of the exchange interaction connectivity, may give rise to novel physical properties upon doping the compounds into the metallic state.
II Experimental Details
Single crystals of and were grown using Sn flux. High-purity elements Sr (99.95%) from Sigma Aldrich, and Ca (99.95%), Co (99.998%), As (99.9999%) and Sn (99.999%) from Alfa Aesar were taken in the ratio (Sr,Ca):Mn:As:Sn = 1:2:2:20 and placed in an alumina crucible that was subsequently placed in a silica tube that was evacuated, partially refilled with high-purity argon (1/4 atm pressure) and then sealed. After preheating at 600∘C for 5 h, the assembly was heated to 1150 ∘C at the rate of 50 ∘C/h and held at this temperature for 20 h for homogenization. Then the furnace was slowly cooled at the rate of 5 ∘C/h to 700 ∘C. At this temperature the molten Sn flux was decanted using a centrifuge. Shiny hexagonal-shape single crystals of maximum dimensions were obtained.
Semiquantitative chemical analyses of the single crystals were performed using a JEOL scanning electron microscope (SEM) equipped with an EDX (energy-dispersive x-ray analysis) detector, where a counting time of 120 s was used. A room-temperature powder x-ray diffraction (XRD) pattern was recorded on crushed single crystals using a Rigaku Geigerflex powder diffractometer with Cu K radiation at diffraction angles 2 from 10∘ to 110∘ with a 0.02∘ step width. The data were analysed by Rietveld refinement using FullProf software.fullprof
measurements for and measurements for T were carried out using a Quantum Design, Inc., Magnetic Properties Measurement System (MPMS). The high-temperature for was measured using the vibrating sample magnetometer (VSM) option of a Quantum Design, Inc., Physical Properties Measurement System (PPMS). In this paper we exclusively use Gaussian cgs units for , and (see Sec. 3.5.1 of Ref. Johnston2010, ). In this system of units, the Tesla (T) is a unit of convenience for defined as 1 T = Oe, where Oe is the conventional cgs unit for .
data were obtained using a relaxation method with the heat capacity option of the PPMS. Four-probe data were obtained with an ac current amplitude at a frequency of 37.7 Hz using the ac transport option of the PPMS. Electrical contacts to a crystal were made by soldering 0.05 mm diameter Pt wire to a crystal using indium solder.
III Experimental Results
III.1 Crystal Structure
| Lattice parameters | ||
|---|---|---|
| (Å) | 4.2962(1) | 4.2376(1) |
| (Å) | 7.2997(2) | 7.0331(2) |
| 1.6991(1) | 1.6596(1) | |
| 116.682(6) | 109.372(6) | |
| Atomic coordinates | ||
| 0.6231(1) | 0.6248(4) | |
| 0.2667(2) | 0.2537(3) | |
| Refinement quality | ||
| 3.05 | 4.03 | |
| (%) | 10.3 | 12.7 |
| (%) | 13.6 | 16.4 |
| Shortest Mn–Mn | ||
| distances (Å) | ||
| 3.06306(8) | 3.0112(2) | |
| 4.29620(5) | 4.23760(5) | |
| 5.27633(7) | 5.1985(2) | |
| 6.0357(2) | 5.8171(4) | |
| 7.2997(2) | 7.0331(2) |
The crystal symmetry of several and crystals was checked by x-ray Laue back scattering which showed trigonal symmetry with well-defined diffraction spots which clearly indicated the good quality of the crystals. In this paper we use the hexagonal setting for the trigonal unit cell. The data also revealed that the and platelike crystals grow with the plate surface parallel to the hexagonal plane. SEM imaging and EDX analyses were performed to check the chemical composition and surface morphology of the crystals. The average elemental ratio of the samples was in agreement with the expected 1:2:2 stoichiometry of the compounds to within the errors. The amount of Sn incorporated into the crystal structure from the Sn flux is zero to within the experimental error. The present analyses did not show any other elements.
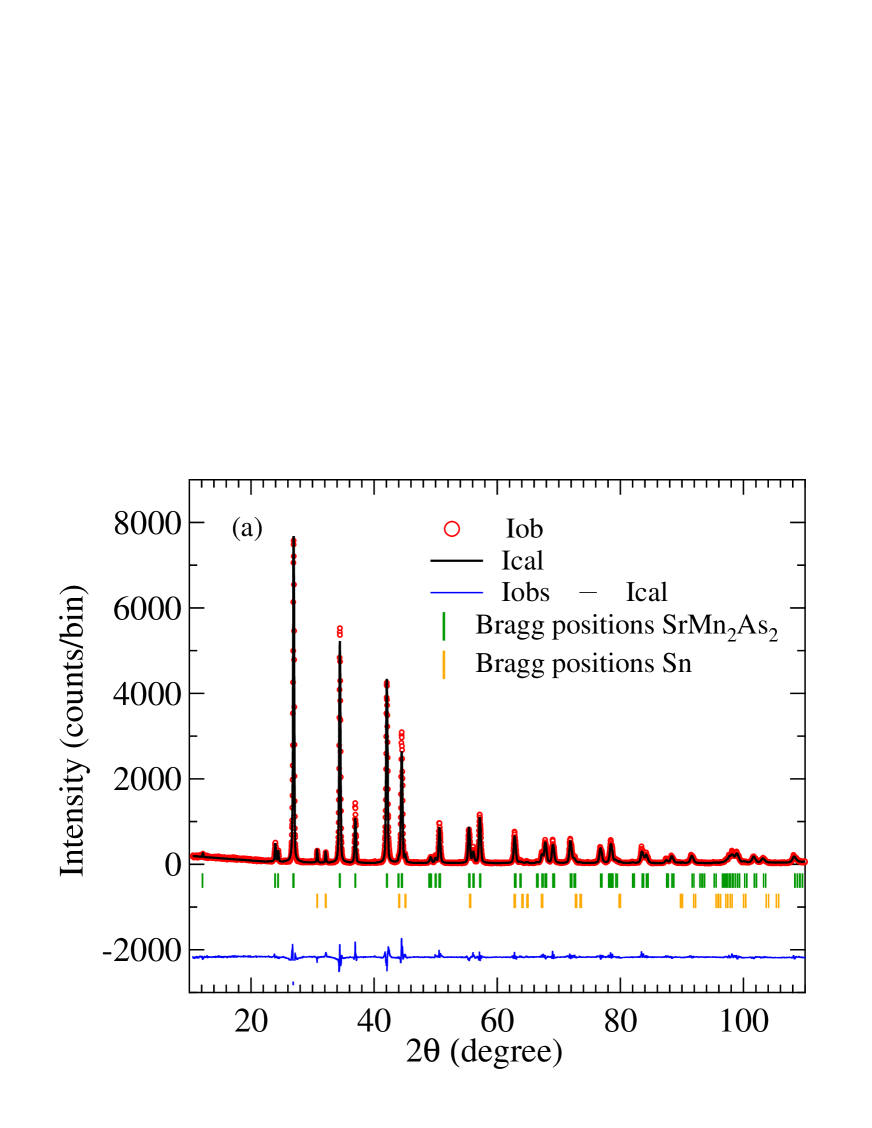
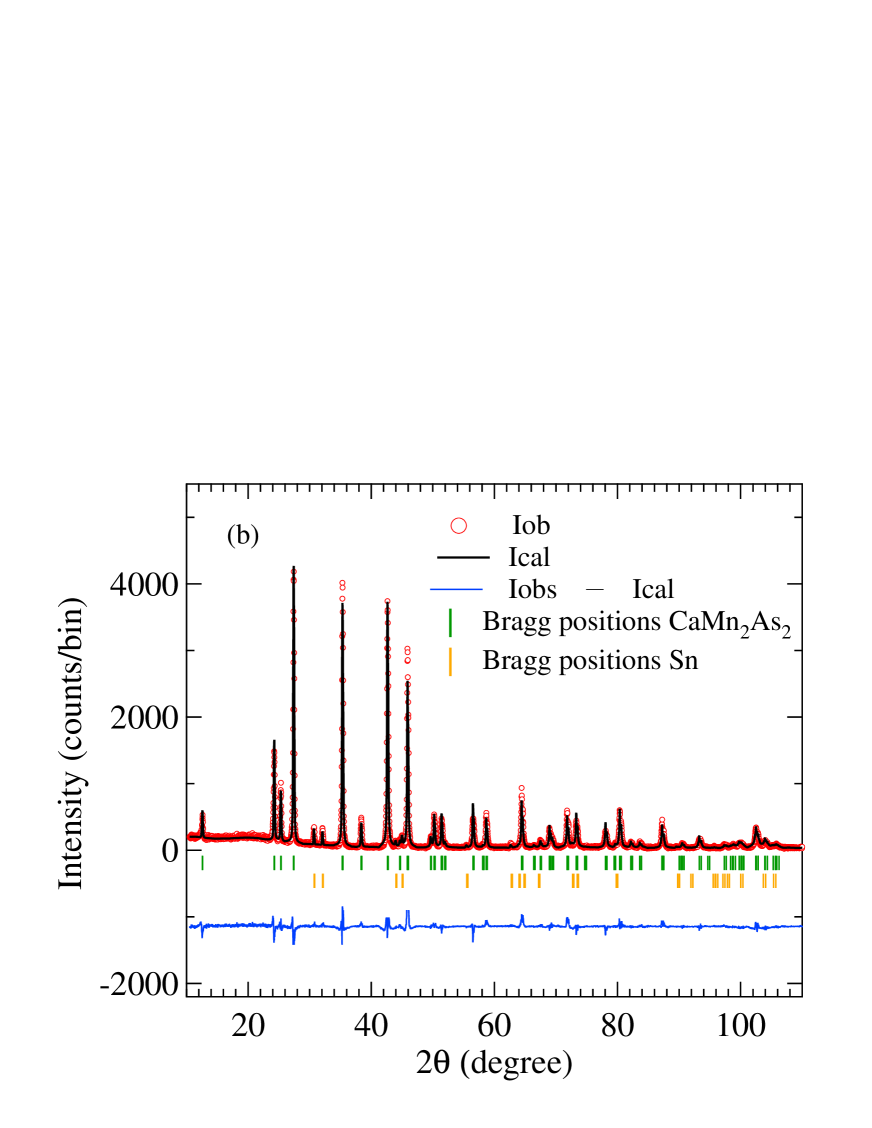
The phase purity of our and crystals was confirmed by powder XRD. Their XRD patterns at 300 K along with the results of Rietveld refinements are shown in Figs. 1(a) and 1(b), respectively. One sees the presence of adventitious elemental Sn flux, so two-phase Rietveld refinements were carried out. The refinement results confirm that the crystals have the trigonal -type structure with space group . The refinement and crystal parameters obtained are listed in Table 1. The crystal parameters are in good agreement with previously reported values.Mewis1978 ; Brechtel1978 ; Wang2011
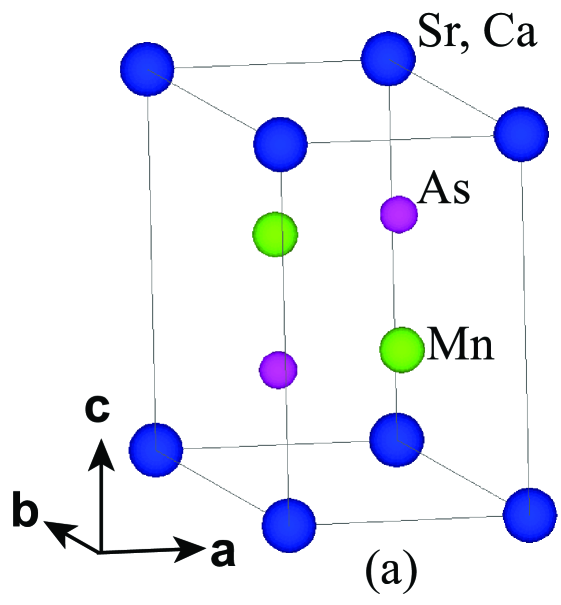
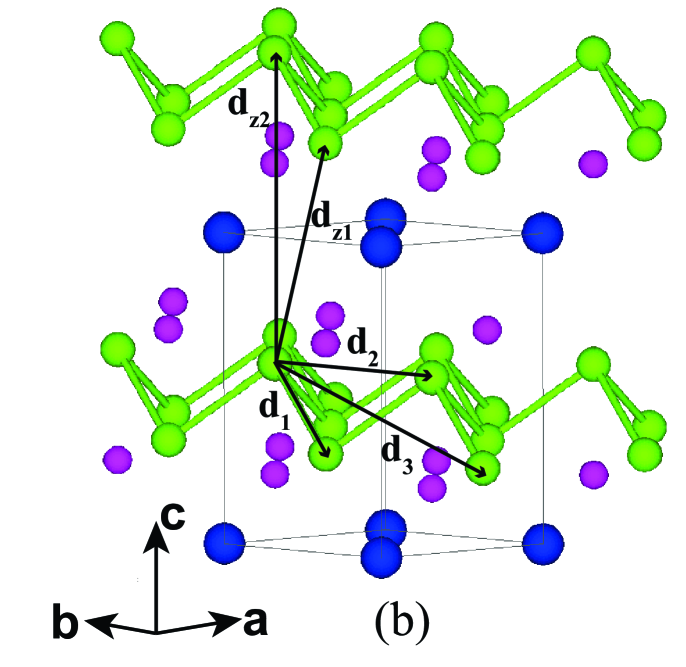
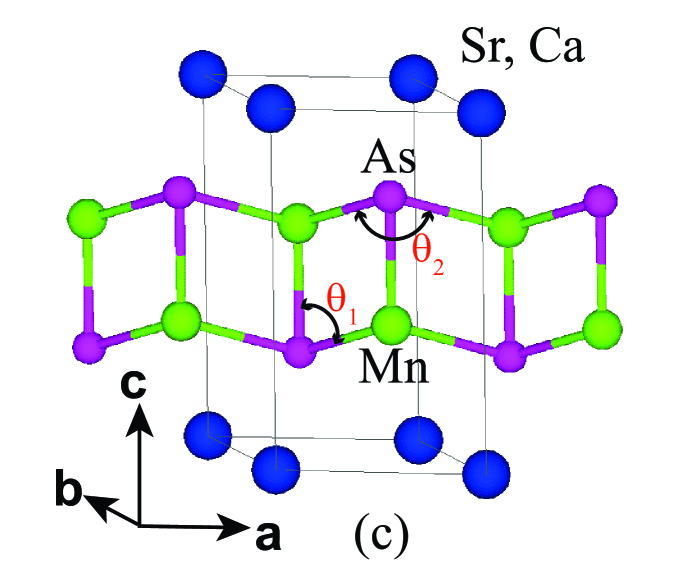
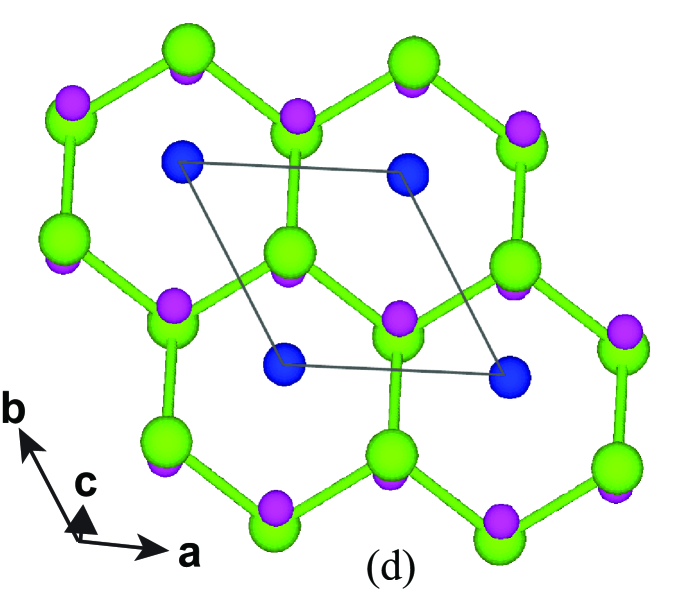
Figure 2(a) shows a unit cell of trigonal and in the hexagonal setting. As shown in Figs. 2(b) and 2(d), the structure consists of corrugated honeycomb layers that are stacked along the axis and separated by Sr+2 or Ca+2 cations, respectively. Alternatively, the Mn sublattice can be viewed as triangular double layers of Mn stacked along the axis and separated by Ca or Sr atoms. The three smallest Mn–Mn interatomic distances [see Fig. 2(b)] are within the corrugated Mn honeycomb layers and are listed in Table 1. The nearest-neighbor Mn–Mn distance () is between the two Mn atoms at different heights ( values) within a unit cell. The second-nearest-neighbor Mn-Mn distance () is between Mn atoms at the same height in adjacent unit cells along the plane forming a triangular-lattice layer, and the third-nearest-neighbor Mn–Mn distance () is between nearest-neighbor Mn atoms in adjacent unit cells in the plane. The nearest- and second-nearest-neighbor distances and between Mn atoms in adjacent layers in different unit cells along the axis are also listed in Table 1.
Since the minimum intralayer Mn–Mn distance Å is much shorter than the minimum interlayer Mn–Mn distance ( Å), and likely have a quasi-two-dimensional Mn–Mn exchange interaction connectivity. This large spatial anisotropy in the exchange interactions should be obvious from measurements, which is confirmed below. These exchange interactions could arise from direct Mn–Mn interactions and/or from indirect Mn–As–Mn superexchange interactions. The latter would likely occur via two main paths: (i) between first-nearest-neighbor Mn spins with Mn-As-Mn () = 72∘ and another between second-neighbor Mn spins with Mn-As-Mn () = 111∘ [see Fig. 2(c)]. It will be interesting to see which of these interactions are dominant within the unusual trigonal symmetry of the Mn spin lattice.
To summarize, the and trigonal structure is quite different from the body-centered tetragonal structure found for the parent compounds that is composed of metal-arsenide tetrahedra separated by alkaline earth layers. The primary difference between them is the geometry of the transition metal layers. In and , the Mn bilayer is a corrugated Mn honeycomb lattice where each Mn atom is coordinated by three other Mn atoms at like the corner of the cube as seen in Figs. 2(b) and 2(c), whereas in -type compounds such as BaMn2As2 or BaFe2As2, the Mn or Fe network is a simple square-planar lattice where each Mn or Fe is coordinated by four other Mn or Fe atoms, also at 90∘ angles between them. On the other hand, the AFM in is quasi-two-dimensional,Johnston2011 just as we find it to be in and from the data in Sec. III.3 below.
III.2 In-Plane Electrical Resistivity

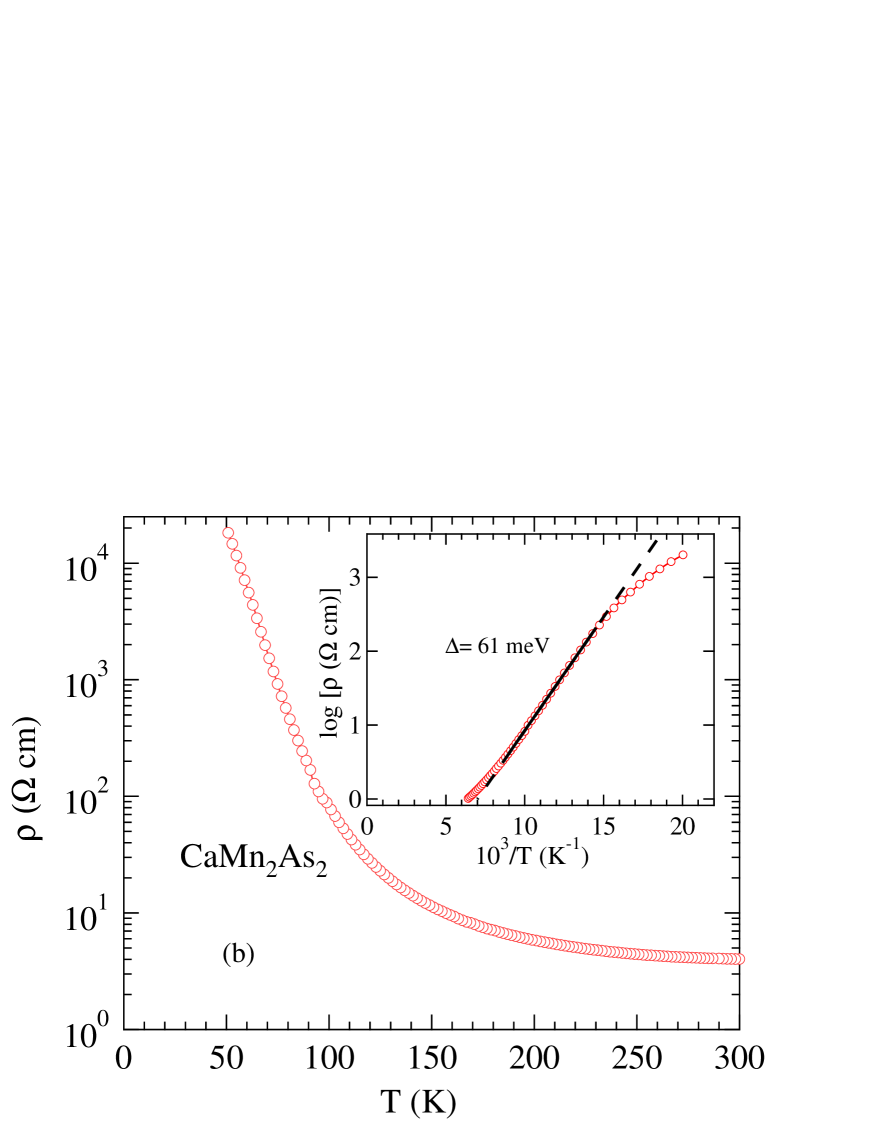
Figures 3(a) and 3(b) show of and , respectively, from to 300 K measured in the plane. The data show that both compounds are semiconductors with insulating intrinsic ground states. We fitted in the temperature region between 70 and 120 K by the expression , where is a constant, is Boltzmann’s constant and is the activation energy. The fits are shown as the solid straight lines through the data in the insets of Figs. 3(a) and 3(b), which give the activation energies meV for and meV for . These activation energies are of the same order as previously obtained from data for BaMn2As2.Singh2009 Our activation energy for SrMn2As2 is significantly smaller than the previously reported values and 0.64 eV, depending on the range, that were also obtained from single-crystal in-plane data.Wang2011
III.3 Magnetization and Magnetic Susceptibility


The zero-field-cooled (ZFC) magnetic susceptibility versus measured in T and T applied in the plane () and along the axis () for single crystals of and are shown in Figs. 4 and 5, respectively.
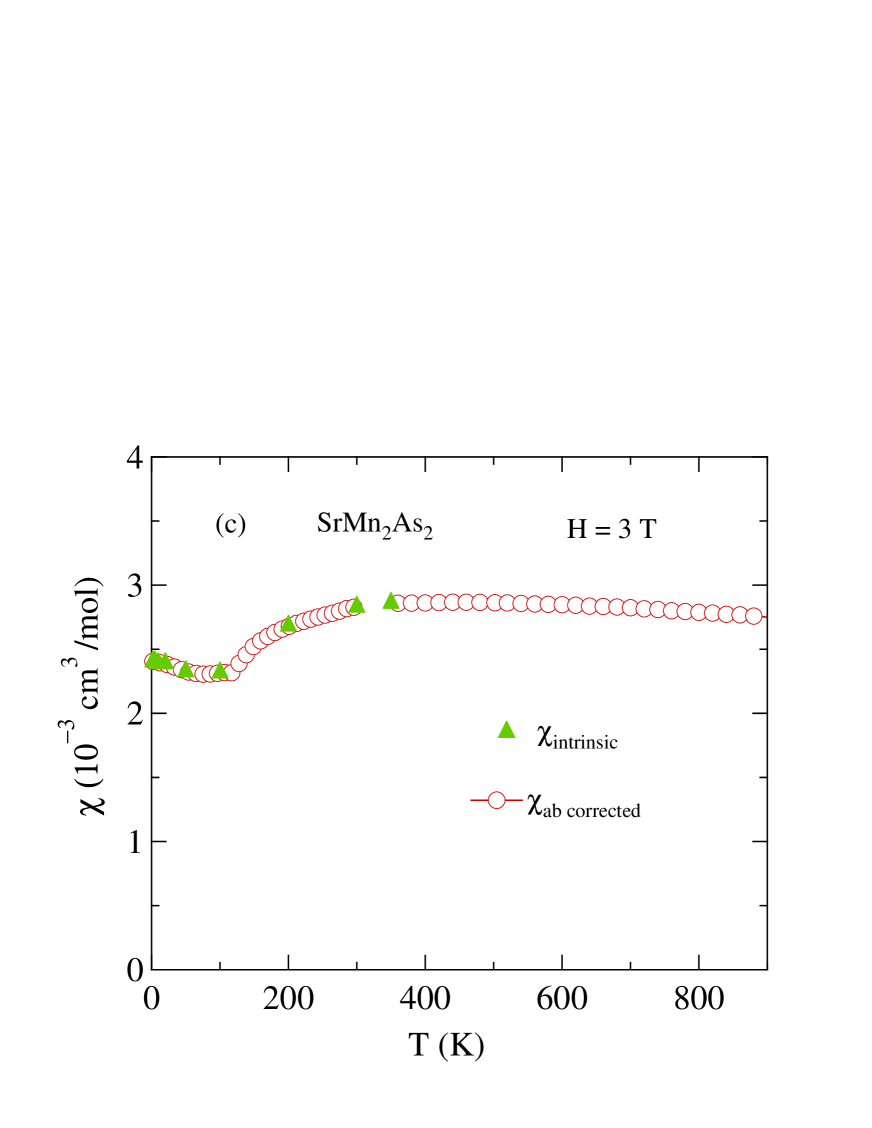
Clear AFM transitions are observed in at K for and K for , as indicated by vertical arrows in Figs. 4(a) and 5(a), respectively. We also performed FC (field-cooled) and ZFC measurements at T and T (not shown here). No hysteresis was observed between the ZFC and FC data, which is consistent with long-range AFM ordering of and below their respective Néel temperatures. The data in Figs. 4(a) and 5(a) for are nearly isotropic, as expected for Mn+2 with spin and .
From Figs. 4(a) and 5(a), the anisotropy in at indicates that the hard axis is the axis and the plane is the easy plane for both compounds. Furthermore, the nonzero limits of suggest that the AFM structure could be either a collinear AFM with multiple domains aligned within the plane or an intrinsic noncollinear structure with moments again aligned in the plane.Johnston2012 ; Johnston2015 ; Anand2015 ; Ryan2015 For collinear ordering, magnetic dipole interactions between the Mn moments favor -plane moment alignment over -axis alignment.Johnston2016 In [see Fig. 4(b)], the anisotropy in for is eliminated by a field of 3 T, which indicates a relatively small magnetocrystalline anisotropy compared to that in judging from Fig. 5(b). The small upturns in in Figs. 4 and 5 below K are believed due to trace amounts of paramagnetic local-moment impurities.
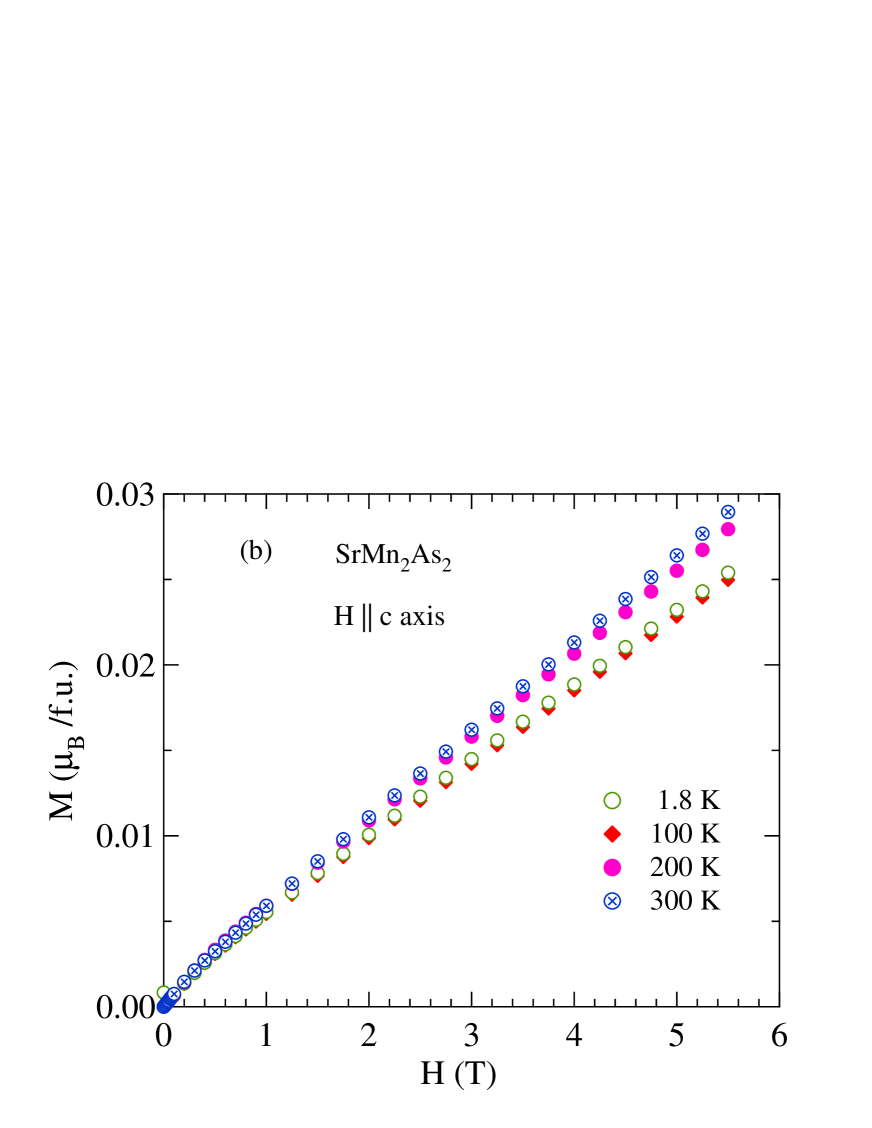
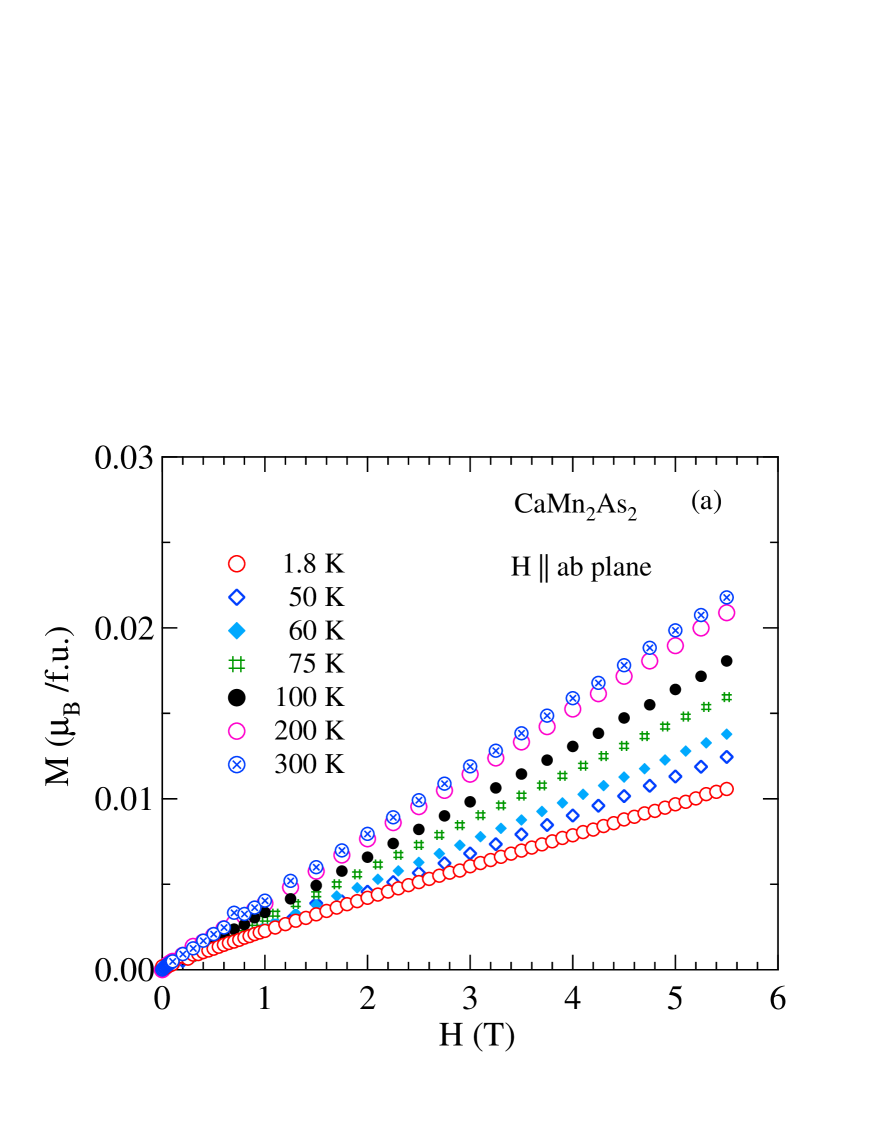
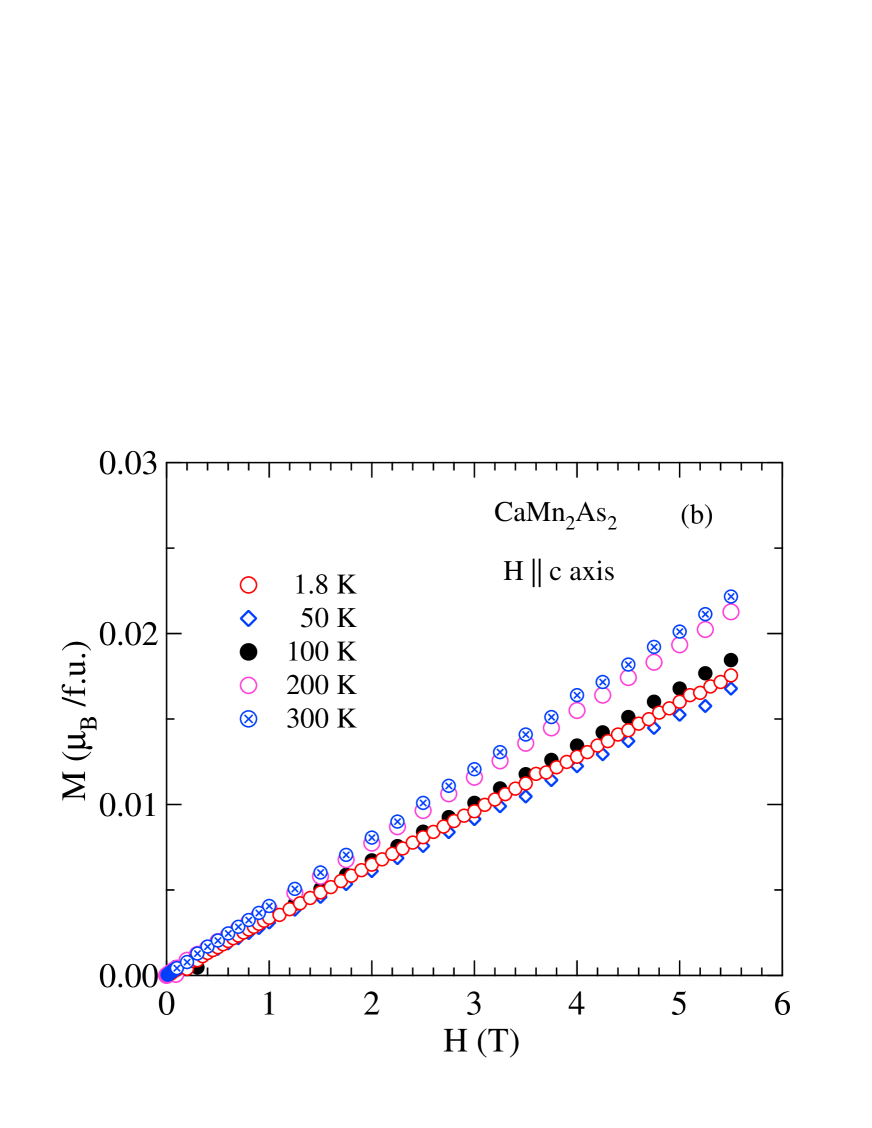
A small jump in is observed for in Fig. 4(b) on cooling below about 320 K. This is believed due to FM MnAs impurities with this Curie temperature that are present on the crystal surface and/or as an inclusion in the crystal, as previously observed for crystals.Singh2009 To extract the intrinsic magnetic behavior of , we carried out isotherm measurements at various temperatures. Figures 6 and 7 show isothermal data for and crystals, respectively, at different for plane () and axis (). The curves are almost linear at high fields, but for one sees nonlinearities at low fields (–2 T) for K, confirming the presence of saturable FM impurities.
To extract the intrinsic () we fitted the data in the high-field range –5.5 T by the linear relation
| (1) |
where is the saturation magnetization due to the FM impurities. The value of for is /f.u., which corresponds to 0.04 mol% of MnAs impurities using the saturation moment of /f.u. (Refs. Haneda1977, ; Saparov2012, ) for MnAs. The data in Figs. 4(b) and 5(b) were measured with T. Therefore, we obtained the intrinsic from the isotherm data according to
| (2) |
The data are shown by the filled green triangles in Figs. 4(b) and 5(b). It is seen that the data for match very well for both field directions with the data in Fig. 5(b), indicating a clean crystal without any detectable FM impurities.
In order to further clarify the magnetism in these systems we measured in the extended temperature range up to 900 K for and as shown in Figs. 4(c) and 5(c), respectively. One sees that exhibits very broad maxima at K for both compounds. This feature is a signature of a low-dimensional local-moment AFM system.Johnston2011 Thus and undergo a phase transition to a long-range ordered state below , preceeded by strong short-range AFM order at higher temperatures. Indeed, the Curie-Weiss temperature region of is not reached even at 900 K, indicating that strong AFM correlations survive to significantly higher temperatures.
From the Mn–Mn interatomic distances discussed in Sec. III.1, we inferred that the Mn–Mn exchange coupling along the axis between the corrugated honeycomb Mn layers in the plane is much smaller than within the layers. We confirm this here and in addition infer that the Mn–Mn exchange coupling within the corrugated honeycomb layers is dominantly antiferromagnetic.
III.4 Heat Capacity
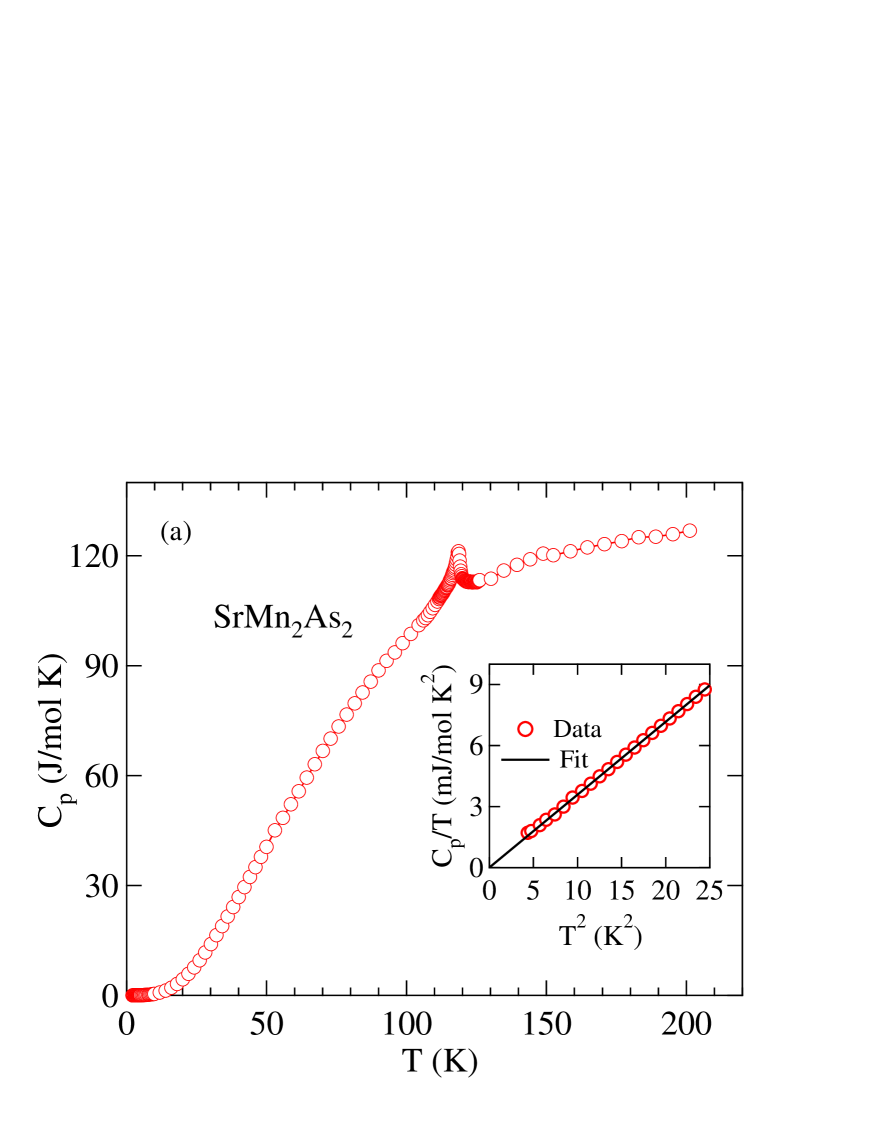
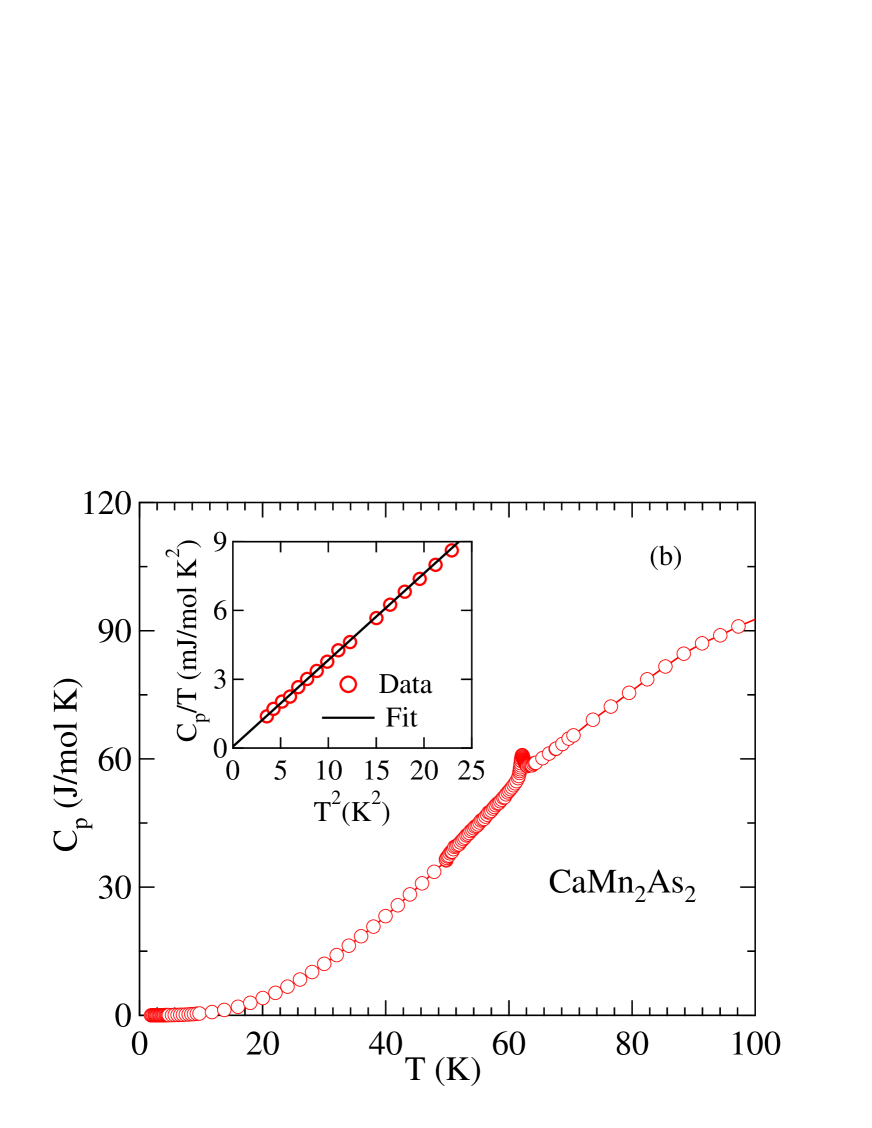
Figures 8(a) and 8(b) show zero-field data for and , respectively. The sharp anomalies in at 120(2) K in and at 62(3) K in are the respective Néel temperatures of the two compounds, which are in good agreement with values found above from the respective data.
III.4.1 Low-Temperature Behaviors
The insets of Figs. 8(a) and 8(b) show versus between 1.8 and 5 K. At low temperatures we model the data byKittel2005
| (3) |
where the coefficient is usually due to the electronic contribution (Sommerfeld coefficient) and is the coefficient of the Debye lattice contribution in the absence of three-dimensional AFM spin-wave contributions. The data were therefore fitted by the expression
| (4) |
From the fits of Eq. (6) to the data in the insets of Figs. 8(a) and 8(b) we obtain mJ/(mol K2) for and 0.05(7) mJ/(mol K2) for . The null values of are consistent with the insulating ground states found from the measurements in Sec. III.2.
The fitted values for are
| (5) |
and 0.37(1) mJ/(mol K for . We estimate the Debye temperatures for the two compounds from the Debye theory according toKittel2005
| (6) |
where is the molar gas constant and is the number of atoms per formula unit [ for and ]. We obtain
| (7a) | |||||
| (7b) | |||||
In the absence of anisotropy gaps in the AFM spin-wave spectrum, contributions to could arise from excitations of three-dimensional AFM spin waves at the low temperatures at which the values were extracted; hence the quoted values of are lower limits.
III.4.2 Magnetic Contributions to the Heat Capacity and Entropy of
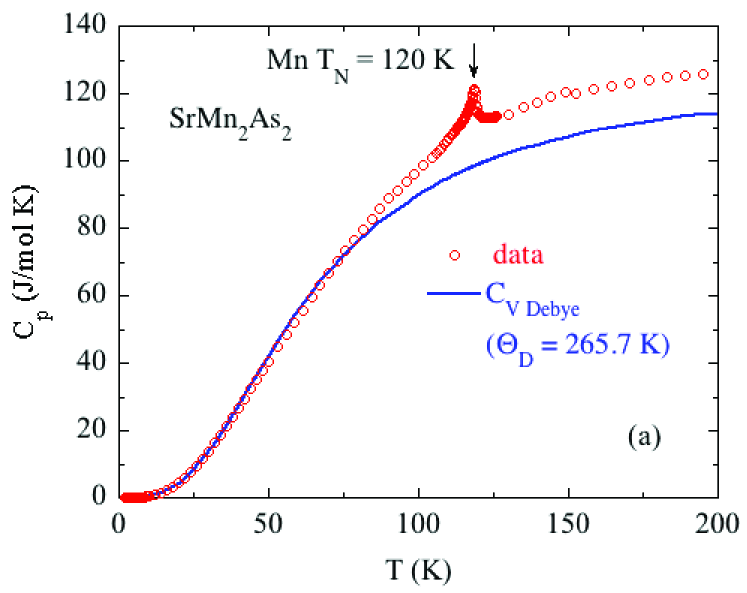
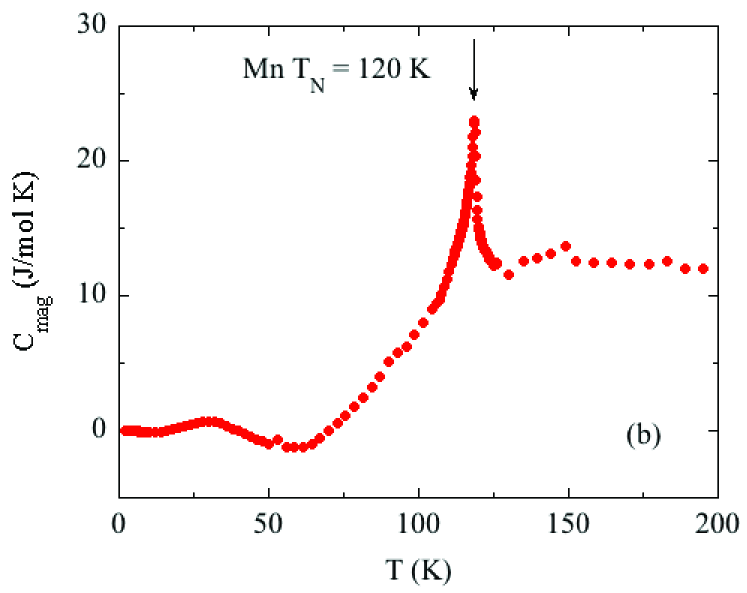
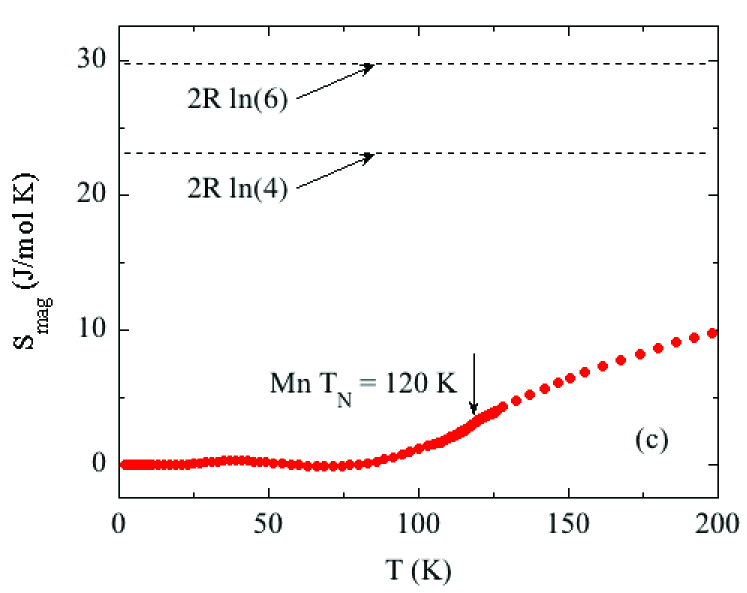
Here we extract estimates of the magnetic contribution to the measured heat capacity of and from that we obtain the magnetic contribution to the entropy over the temperature range from 1.8 to 200 K of the measurements. To accomplish this goal we first obtain an estimate of the lattice contribution to the measured . We use the expression
| (8a) | |||
| where is the Debye lattice heat capacity per mole of atoms given byKittel2005 | |||
| (8b) | |||
The representation of used here is an accurate analytic Padé approximant function of obtained by fitting numerical solutions of Eq. (8b) for a list of values.Goetsch2012 The fit of for in Fig. 9(a) by Eqs. (8) over the temperature range from 1.8 to 60 K and its extrapolation is shown by the blue curve in Fig. 9(a) using the fitted Debye temperature K. This value of is comparable with the value of 303 K obtained from the fit to the data for at low in Eq. (7a), especially considering that for a compound typically varies by % on cooling from 300 K to 2 K.Smart1966
The is calculated as the difference between the measured and the fitted in Fig. 9(a). The result in shown in Fig. 9(b), where a sharp peak at K is seen. The at shows that there is strong dynamic short-range AFM order above . The magnetic entropy is calculated from using
| (9) |
and the result is shown in Fig. 9(c). The entropy of completely disordered spins per mole of and is , which gives
| (10a) | |||||
| (10b) | |||||
as shown by the horizontal dashed black lines in Fig. 9(c). This range of spin values encompasses the known variations in the ordered moments of Mn spins in various materials similar to ours which can arise from quantum fluctuation and/or hybridization effects (see, e.g., Ref. Johnston2011, ). We find that in Fig. 9(c) is only % of the value for in Eqs. (10) and is still only % of the value for . Thus the strong short-range AFM order revealed in the and data above is consistent with the above conclusion from the data that strong short-range AFM order survives from up to at least 900 K.
IV Summary
We have shown that and are AFM insulators with Néel temperatures K and 62 K, respectively. The microscopic origin of this large difference in magnitude of the Néel temperatures together with the reason why the Sr compound has a higher than the Ca one, in spite of the smaller unit cell of the latter, remain to be explained.
The data at indicate that the hexagonal axis is a hard axis, with the ordered Mn spin-5/2 moments lying within the plane. Since a collinear AFM structure within the plane is inferred for from neutron diffraction measurements that were carried out in a companion study,Das2016 the nonzero limits of observed for this compound must arise from the three collinear AFM domains with their axes at to each other within the plane. If the populations of the three domains are equal, within molecular field theory one obtains , in approximate agreement with the data in Fig. 4(a). The prediction of the easy axis arising from the Mn–Mn magnetic dipole interactions in a collinear magnetic structure of obtained using the formalism of Ref. Johnston2016, and the experimental crystal structure is that the ordered moments should lie in the plane as inferred here from the data and also observedDas2016 in the neutron diffraction experiments.
Thus the potential geometric frustration for AFM ordering within the triangular-lattice bilayers parallel to the plane that originally motivated this work is apparently not important in and . In particular, if AFM Mn–Mn exchange interactions within a triangular sublattice layer were dominant, a noncollinear AFM structure would have resulted instead of the observedDas2016 collinear AFM structure.
Strong dynamic AFM short-range correlations up to at least 900 K as observed in our measurements, consistent with our data up to 200 K, are likely due to quasi-two-dimensional connectivity of strong AFM Mn–Mn exchange interactions within the corrugated honeycomb Mn layers. This in turn offers the possibility of novel electronic ground states arising upon doping these materials into the metallic state.
Acknowledgements.
We thank P. Das, A. Kreyssig and A. I. Goldman for helpful discussions. This research was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering. Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University under Contract No. DE-AC02-07CH11358.References
- (1) G. Just and P. Paufler, J. Alloys Compd. 232, 1 (1996).
- (2) D. C. Johnston, Adv. Phys. 59, 803 (2010).
- (3) G. R. Stewart, Rev. Mod. Phys. 83, 1589 (2011).
- (4) D. J. Scalapino, Rev. Mod. Phys. 84, 1383 (2012).
- (5) E. Dagotto, Rev. Mod. Phys. 85, 849 (1913).
- (6) R. M. Fernandes, A. V. Chubukov, and J. Schmalian, Nat. Phys. 10, 97 (2014).
- (7) H. Hosono and K. Kuroki, Physica C 514, 399 (2015).
- (8) P. Dai, Rev. Mod. Phys. 87, 855 (2015).
- (9) D. S. Inosov, Compt. Rend. Phys. 17, 60 (2016).
- (10) Q. Si, R. Yu, and E. Abrahams, Nat. Rev. Mater. 1, 1 (2016).
- (11) E. D. Bauer, F. Ronning, B. L. Scott, and J. D. Thompson, Phys. Rev. B 78, 172504 (2008).
- (12) F. Ronning, N. Kurita, E. D. Bauer, B. L. Scott, T. Park, T. Klimczuk, R. Movshovich, and J. D. Thompson, J. Phys.: Condens. Matter 20, 342203 (2008).
- (13) A. Pandey, D. G. Quirinale, W. Jayasekara, A. Sapkota, M. G. Kim, R. S. Dhaka, Y. Lee, T. W. Heitmann, P. W. Stephens, V. Ogloblichev, A. Kreyssig, R. J. McQueeney, A. I. Goldman, A. Kaminski, B. N. Harmon, Y. Furukawa, and D. C. Johnston, Phys. Rev. B 88, 014526 (2013).
- (14) W. Jayasekara, Y. Lee, A. Pandey, G. S. Tucker, A. Sapkota, J. Lamsal, S. Calder, D. L. Abernathy, J. L. Niedziela, B. N. Harmon, A. Kreyssig, D. Vaknin, D. C. Johnston, A. I. Goldman, and R. J. McQueeney, Phys. Rev. Lett. 111, 157001 (2013).
- (15) P. Wiecki, V. Ogloblichev, A. Pandey, D. C. Johnston, and Y. Furukawa, Phys. Rev. B 91, 220406(R) (2015).
- (16) A. S. Sefat, D. J. Singh, R. Jin, M. A. McGuire, B. C. Sales, and D. Mandrus, Phys. Rev. B 79, 024512 (2009).
- (17) V. K. Anand, D. G. Quirinale, Y. Lee, B. N. Harmon, Y. Furukawa, V. V. Ogloblichev, A. Huq, D. L. Abernathy, P. W. Stephens, R. J. McQueeney, A. Kreyssig, A. I. Goldman, and D. C. Johnston, Phys. Rev. B 90, 064517 (2014).
- (18) P. Wiecki, B. Roy, D. C. Johnston, S. L. Bud’ko, P. C. Canfield, and Y. Furukawa, Phys. Rev. Lett. 115, 137001 (2015).
- (19) Y. Singh, A. Ellern, and D. C. Johnston, Phys. Rev. B 79, 094519 (2009).
- (20) Y. Singh, M. A. Green, Q. Huang, A. Kreyssig, R. J. McQueeney, D. C. Johnston, and A. I. Goldman, Phys. Rev. B 80, 100403(R) (2009).
- (21) D. C. Johnston, R. J. McQueeney, B. Lake, A. Honecker, M. E. Zhitomirsky, R. Nath, Y. Furukawa, V. P. Antropov, and Y. Singh, Phys. Rev. B 84, 094445 (2011).
- (22) A. Antal, T. Knoblauch, Y. Singh, P. Gegenwart, D. Wu, and M. Dressel, Phys. Rev. B 86, 014506 (2012).
- (23) S Calder, B. Saparov, H. B. Cao, J. L. Niedziela, M. D. Lumsden, A. S. Sefat, and A. D. Christianson, Phys. Rev. B 89, 064417 (2014).
- (24) A. Pandey, R. S. Dhaka, J. Lamsal, Y. Lee, V. K. Anand, A. Kreyssig, T. W. Heitmann, R. J. McQueeney, A. I. Goldman, B. N. Harmon, A. Kaminski, and D. C. Johnston, Phys. Rev. Lett. 108, 087005 (2012).
- (25) S. Yeninas, A. Pandey, V. Ogloblichev, K. Mikhalev, D. C. Johnston, and Y. Furukawa, Phys. Rev. B 88, 241111(R) (2013).
- (26) J.-K. Bao, H. Jiang, Y.-L. Sun, W.-H. Jiao, C.-Y. Shen, H.-J. Guo, Y. Chen, C.-M. Feng, H.-Q. Yuan, Z.-A. Xu, G.-H. Cao, R. Sasaki, T. Tanaka, K. Matsubayashi, and Y. Uwatoko, Phys. Rev. B 85, 144523 (2012).
- (27) A. Pandey, B. G. Ueland, S. Yeninas, A. Kreyssig, A. Sapkota, Yang Zhao, J. S. Helton, J.W. Lynn, R. J. McQueeney, Y. Furukawa, A. I. Goldman, and D. C. Johnston, Phys. Rev. Lett. 111, 047001 (2013).
- (28) B. G. Ueland, A. Pandey, Y. Lee, A. Sapkota, Y. Choi, D. Haskel, R. A. Rosenberg, J. C. Lang, B. N. Harmon, D. C. Johnston, A. Kreyssig, and A. I. Goldman, Phys. Rev. Lett. 114, 217001 (2015).
- (29) A. Pandey and D. C. Johnston, Phys. Rev. B 92, 174401 (2015).
- (30) J. Lamsal, G. S. Tucker, T. W. Heitmann, A. Kreyssig, A. Jesche, A. Pandey, W. Tian, R. J. McQueeney, D. C. Johnston, and A. I. Goldman, Phys. Rev. B 87, 144418 (2013).
- (31) A. Mewis, Z. Naturforsch. 33b, 606 (1978).
- (32) E. Brechtel, G. Cordier, and H. Schäfer, Z. Naturforsch. 33b, 820 (1978).
- (33) A. P. Ramirez, Annu. Rev. Mater. Sci. 24, 453 (1994).
- (34) R. Moessner and A. P. Ramirez, Physics Today 59, 24 (2006).
- (35) L. Balents, Nature 464, 199 (2010).
- (36) Z.W. Wang, H.X. Yang, H.F. Tian, H.L. Shi, J.B. Lu, Y.B. Qin, Z. Wang, J.Q. Li , J. Phys. Chem. Solids 72, 457 (2011).
- (37) W. Ratcliff II, A. L. Lima Sharma, A. M. Gomes, J. L. Gonzalez, Q. Huang, and J. Singleton, J. Magn. Magn. Mater. 321, 2612 (2009).
- (38) C. A. Bridges, V. V. Krishnamurthy, S. Poulton, M. P. Paranthaman, B. C. Sales, C. Myers, and S. Bobev, J. Magn. Magn. Mater. 321, 2653 (2009).
- (39) P. Das, N. S. Sangeetha, A. Pandey, Z. A. Benson, T. W. Heitmann, D. C. Johnston, A. I. Goldman, and A. Kreyssig, arXiv:1605:02004.
- (40) J. Rodríguez-Carvajal, Phys. B: Condens. Matter 192, 55 (1993).
- (41) D. C. Johnston, Phys. Rev. Lett. 109, 077201 (2012).
- (42) D. C. Johnston, Phys. Rev. B 91, 064427 (2015).
- (43) V. K. Anand and D. C. Johnston, Phys. Rev. B 91, 184403 (2015).
- (44) D. H. Ryan, J. M. Cadogan, V. K. Anand, D. C. Johnston, and R. Flacau, J. Phys.: Condens. Matter 27, 206002 (2015).
- (45) D. C. Johnston, Phys. Rev. B 93, 014421 (2016).
- (46) S. Haneda, N. Kazama, Y. Yamaguchi, and H. Watanabe, J. Phys. Soc. Jpn. 42, 1201 (1977).
- (47) B. Saparov, J. E. Mitchell, and A. S. Sefat, Supercond. Sci. Technol. 25, 084016 (2012).
- (48) C. Kittel, Introduction to Solid State Physics (Wiley, Hoboken, NJ, 2005).
- (49) R. J. Goetsch, V. K. Anand, A. Pandey, and D. C. Johnston, Phys. Rev. B 85, 054517 (2012).
- (50) J. S. Smart, Effective Field Theories of Magnetism (Saunders, Philadelphia, 1966).