Strong Pseudoprimes to Twelve Prime Bases
Abstract.
Let be the smallest strong pseudoprime to the first prime bases. This value is known for . We extend this by finding and . We also present an algorithm to find all integers that are strong pseudoprimes to the first prime bases; with a reasonable heuristic assumption we can show that it takes at most time.
2010 Mathematics Subject Classification:
Primary 11Y16, 11Y16; Secondary 11A41, 68W40, 68W101. Introduction
Fermat’s Little Theorem states that if is prime and , then
A composite number for which this congruence holds is called a pseudoprime to the base . We can restate Fermat’s Little Theorem by algebraically factoring (repeatedly) the difference of squares that arises in . In which case, if is an odd prime, writing with odd, and , then either
or
for some integer with . If a composite satisfies the above, we call a strong pseudoprime to the base . Unlike Carmichael numbers, which are pseudoprimes to all bases, there do not exist composite numbers that are strong pseudoprimes to all bases. This fact forms the basis of the Miller-Rabin probabilistic primality test [13]. Define to be the smallest integer that is a strong pseudoprime to the first prime bases. (See A014233 at oeis.org.)
The problem of finding strong pseudoprimes has a long history. Pomerance, Selfridge, and Wagstaff [12] computed for and . Jaeschke [7] computed for and . By looking at a narrow class of numbers, Zhang [18] gave upper bounds on for . Recently, Jian and Deng [8] verified some of Zhang’s conjectures and computed for and . We continue in this effort with the following.
Theorem 1.1.
We also verified Jian and Deng’s work in finding . Note that the ERH implies , if exists [1].
The proof of our theorem relies primarily on running an improved algorithm for finding strong pseudoprimes:
Theorem 1.2.
Given a bound and an integer that grows with , there is an algorithm to find all integers that are products of exactly two primes and are strong pseudoprimes to the first prime bases using at most arithmetic operations.
We have a heuristic argument extending this running time bound to integers with an arbitrary number of prime divisors. This result is an improvement over a heuristic from [2]. Our algorithm uses the work of Jian and Deng as a starting point, and our specific improvements are these:
- •
- •
-
•
We used a simple table of linked-lists indexed by a hash function based on prime signatures. We used this to store small primes by signature for very fast lookup. See §2.4.
-
•
When it made sense to do so, we parallelized our code and made use of Big Dawg, Butler University’s cluster supercomputer.
Our changes imply that adding more prime bases for a pseudoprime search (that is, making larger) speeds up the algorithm.
The rest of this paper is organized as follows. Section 2 contains a description of the algorithm and its theoretical underpinnings. Section 3 contains the proof of the running time. Section 4 contains implementation details.
2. Algorithmic Theory and Overview
To find all that are strong pseudoprimes to the first prime bases, we use some well-known conditions to limit how many such integers we need to check. This is outlined in the first subsection below.
We construct all possibilities by generating in factored form, , where is the number of prime divisors of , and . It turns out that cannot be too big; we only had to test up to . So we wrote separate programs for each possible and the case dominates the running time.
Let . Our algorithms generate all candidate values, and then for each search for possible primes to match with , to form a strong pseudoprime candidate .
For the bound , we choose a cutoff value . For , we use a GCD computation to search for possible primes , if they exist. For , we use sieving to find possible primes . Again, we use separate programs for GCDs and for sieving.
Once each is formed, we perform a strong pseudoprime test for the first prime bases to see if we have, in fact, found what we are looking for.
2.1. Conditions on (Strong) Pseudoprimes
For the purposes of this paper, it suffices to check square-free odd integers. A computation by Dorais and Klyve [3] shows that a pseudoprime to the bases 2 and 3 must be square-free if it is less than . Since the values Zhang conjectured as candidates for and are less than , we restrict our search to square-free numbers.
In general, to rule out integers divisible by squares, it suffices to find all Wieferich primes , and for each such prime, perform appropriate tests. This can easily be done in well under time. See §3.6.1 in [2].
To each prime we associate a vector called its signature. Let for distinct positive integers. Then the signature of is
where denotes valuation with respect to and is the multiplicative order of modulo .
Example 2.1.
Let be the prime . Then if .
Theorem 2.2 (Proposition 1 in [7]).
Let with distinct primes, with different integers such that for all and . Then is a strong pseudoprime to each base in if and only if n is a pseudoprime to each base in and .
If , then this theorem greatly limits the number of candidate values we need to check. In the case the initial sub-product is just a single prime, so this theorem does not, at first, appear to help. However, it does play a role in sieving for . For the rest of this paper, we use as the vector containing the first or prime numbers.
2.2. Greatest Common Divisors
As above, let . We explain in this subsection how to find all possible choices for to form as a strong pseudoprime to the first prime bases using a simple GCD computation.
Let be one of the from . The pseudoprimality condition implies that
i.e., that divides . Considering multiple bases, we know that must divide
However, since we are concerned with strong pseudoprimes, we can consider only the relevant algebraic factor of . Following Bleichenbacher’s notation [2], let for odd and
Theorem 2.3 (Theorem 3.23 of [2]).
A necessary condition for an integer of the from , for a given with prime, to be a strong pseudprime to the bases is that divide .
This theorem allows us to construct the product of all possible values for a given by computing a GCD. To carry this out, we figure out which of the values would be the smallest, compute that, and then compute the next smallest value modulo the smallest, perform a GCD, and repeat until we get an answer , or use up all the base values.
Example 2.4.
Let , which is prime. We have
In this case, we would begin the computations with since it is the smallest. We then compute . This tells us that any of the form is not a strong pseudoprime to the vector .
These computations start off easy as is small and progressively get harder (in an essentially linear fashion) as grows. As a practical matter, these computations only need to be done once. As an example, [8] found
to be a strong pseudoprime to the first eight prime bases. When considering , they sieved (which we explain in the next section) for . It is reasonable to ask whether there is a larger prime that can be paired with that would form a strong pseudoprime to eight bases. In our computation we check by computing a GCD to answer “no.”
Algorithm 1: Using GCDs to rule out values
-
Input:
Integers and , where is the number of prime divisors and is the product of primes with matching signature, and the base vector containing the smallest primes.
-
1:
Let give the smallest estimated value for as defined above.
-
2:
If , let else let .
-
3:
Compute .
-
4:
Compute using modular exponentiation.
-
5:
Set ;
-
6:
while and do
-
7:
Set ; if set again.
-
8:
Compute .
-
9:
Set .
-
7:
-
10:
end while
-
11:
if then
-
12:
We can rule out .
-
12:
-
13:
else
-
14:
We factor and check each prime with to see if is a strong pseudoprime.
-
14:
-
15:
end if
Computing is the bottleneck of this algorithm. When using or higher, we never found anything to factor in the last step.
2.3. Sieving
As above, let and we try to construct by finding . In order to search up to a bound , we need to search primes in the interval . We combine two types of sieving to search this interval quickly. The first we call -sieving, and the second we call signature sieving. For each prime define
By the r-rank Artin Conjecture [11], we expect with very high probability that . Let . Since for any this means is a multiple of . So, . This tells us that lies in a specific residue class modulo , and we call searching for using this value -sieving.
We can further narrow down the residue classes that may lie in with respect to primes in . The following two propositions appeared originally in [7].
Proposition 2.5.
For primes and , if and then .
Proposition 2.6.
For primes and , if and then .
One may consider higher reciprocity laws, and Jaeschke did so [7]. We found quadratic reciprocity sufficient.
The authors of [8] consider searching for modulo . They considered residue classes modulo that arose from the propositions above. With the inclusion of each additional prime from , we effectively rule out half of the cases to consider, thereby doubling the speed of the sieving process.
Ideally, we would like to include every prime in for the best performance, but with normal sieving, the sieve modulus becomes quite large and requires we keep track of too many residue classes to be practical. Instead, we adapted the space-saving wheel datastructure [16, 15], which had been used successfully to sieve for pseudosquares. Sieving for primes with specified quadratic character modulo a list of small primes is the same algorithmic problem. This wheel sieve uses a data structure that takes space proportional to instead of space proportional to as used in traditional sieving. It does, however, produce candidate primes out of order. This is not an issue, so long as we make sure the sieve modulus does not exceed . In practice, we dynamically include primes from so that , and we favor the inclusion of smaller primes.
Algorithm 2: Sieving
-
Input:
in factored form as , for , search bound , and base vector of length .
-
1:
Compute .
-
2:
Set . Compute wheel modulus as follows:
-
3:
for do
-
4:
if then
-
5:
if does not divide then
-
6:
Set .
-
6:
-
7:
end if
-
5:
-
8:
end if
-
4:
-
9:
end for
-
10:
if divisible by 4 then
-
11:
Set
-
11:
-
12:
else
-
13:
Set and
-
14:
Set
-
13:
-
15:
end if
-
16:
Let be the signature of .
- 17:
-
18:
for each residue modulo generated by the wheel do
-
19:
Use the Chinese Remainder Theorem to compute such that and .
-
20:
Sieve for primes in the interval that are .
-
21:
For each such probable prime found, perform a strong pseudoprime test on .
-
19:
-
22:
end for
Note that if consists entirely of primes that are , then all primes found by the sieve, when using all of , will have the correct signature.
Example 2.7.
Consider . Now, (factorization is obtained via sieving). We may use signature information for the primes , , , , , , , and . However, since we may only use the first 4 primes in the signature before the combined modulus is too large. The signature information for 3 implies that however, the case need not be considered since we know (because of ) that . Given the signature information for the primes 5 and 13, we search in and . At this point we sieve for primes . To this we add the following 12 new congruence conditions and sieve for each individual condition.
-
(1)
Let .
-
(a)
Let .
-
(b)
Let .
-
(c)
Let .
-
(d)
Let .
-
(e)
Let .
-
(f)
Let .
-
(a)
-
(2)
Let .
-
(a)
Let .
-
(b)
Let .
-
(c)
Let .
-
(d)
Let .
-
(e)
Let .
-
(f)
Let .
-
(a)
2.4. Hash Table Datastructure
In order to compute GCDs or sieve as described above, it is necessary to construct integers in an efficient way, where all the primes have matching signatures. We do this by storing all small primes in a hash table datastructure that supports the following operations:
-
•
Insert the prime with its signature . We assume any prime being inserted is larger than all primes already stored in the datastructure. (That is, insertions are monotone increasing.) We also store with and its signature for use later, thereby avoiding the need to factor .
-
•
Fetch a list of all primes from the datastructure, in the form of a sorted array , whose signatures match . The fetch operation brings the values along as well.
We then use this algorithm to generate all candidate values for a given and :
Algorithm 3: Generating Values
-
Input:
, search bound , cutoff , base vector of length .
-
1:
Let denote our hash table datastructure
-
2:
Let denote the smallest prime not in .
-
3:
for each prime (with in factored form) do
-
4:
Compute from the factorization of ;
-
5:
.fetch(); List of primes with matching signature
-
6:
for .length do
-
7:
Form ;
-
8:
if then
-
9:
Use in a GCD computation to find matching values;
-
9:
-
10:
else
-
11:
Use for a sieving computation to find matching values;
-
11:
-
12:
end if
-
7:
-
13:
end for
-
14:
if then
-
15:
.insert(,,);
-
15:
-
16:
end if
-
4:
-
17:
end for
Note that the inner for-loop above is coded using nested for-loops in practice. This is partly why we wrote separate programs for each value of . To make this work as a single program that handles multiple values, one could use recursion on .
Also note that we split off the GCD and sieving computations into separate programs, so that the inner for-loop was coded to make sure we always had either or as appropriate.
We implemented this datastructure as an array or table of linked lists, and used a hash function on the prime signature to compute which linked list to use. The hash function computes its hash value from the signature as follows:
-
•
If , the all-zero vector, then , and we are done.
-
•
Otherwise, compute a modified copy of the signature, . If contains only 0s and 1s, then . If not, find the largest integer entry in , and entries in are 1 if the corresponding entry in matches the maximum, and 0 otherwise.
For example, if (our example from earlier), then .
-
•
is the value of viewed as an integer in binary.
So for our example, .
Computing a hash value takes time.
Each linked list is maintained in sorted order; since the insertions are monotone, we can simply append insertions to the end of the list, and so insertion time is dominated by the time to compute the hash value, time. Note that the signature and is stored with the prime for use by the fetch operation.
The fetch operation computes the hash value, and then scans the linked list, extracting primes (in order) with matching signature. If the signature to match is binary (which occurs roughly half the time), we expect about half of the primes in the list to match, so constructing the resulting array takes time linear in multiplied by the number of primes fetched. Note that values are brought along as well. Amortized over the full computation, fetch will average time that is linear in the size of the data returned. Also note that the average cost to compare signatures that don’t match is constant.
The total space used by the data structure is an array of length , plus one linked list node for each prime . Each linked list node holds the prime, its value, and its signature, for a total of bits, since each prime is bits.
2.5. Algorithm Outline
Now that all the pieces are in place, we can describe the algorithm as a whole.
Given an input bound , we compute the GCD/sieve cutoff (this is discussed in §3 below).
We then compute GCDs as discussed above using candidate values for . For some value of , we’ll discover that there are no candidate values with prime factors, at which point we are done with GCD computations.
Next we sieve as discussed above, using candidate values for . Again, for some value, we’ll discover there are no candidate values with prime factors, at which point we are done.
We wrote a total of eight programs; GCD programs for and sieving programs for . Also, we did not bother to use the wheel and signature sieving, relying only on sieving, for .
3. Algorithm Analysis
3.1. Model of Computation
We assume a RAM model, with potentially infinite memory. Arithmetic operations on integers of bits (single-precision) and basic array indexing and control operations all are unit cost. We assume fast, FFT-based algorithms for multiplication and division of large integers. For -bit inputs, multiplication and division cost operations [14]. From this, an FFT-based GCD algorithm takes operations; see, for example, [17].
3.2. Helpful Number Theory Results
Let our modulus so that ; each base is an odd prime with , except for with . We use our two propositions from §2.3, together with quadratic reciprocity to obtain a list of residue classes for each odd prime and two residue classes modulo . The total number of residue classes is . A prime we are searching for with a matching signature must lie in one of these residue classes.
Let us clarify that when we state in sums and elsewhere that a prime has signature equivalent to , we mean that the quadratic character is consistent with as stated in Propositions 2.5 and 2.6. We write to denote this consistency under quadratic character, which is weaker than .
Lemma 3.1.
Given a signature of length , and let as above. Let . If , then number of primes with is at most
Proof.
We will choose proportional to so that for some constant .
Lemma 3.2.
We have
This follows easily from Lemma 3.1 by partial summation. We could make this tighter by making use of Theorem 4 from [9], and observe that the constants (in their notation) cancel with one another in a nice fashion when summing over different residue classes modulo . See also section 6 of that paper.
Let denote the number of integers with exactly distinct prime divisors, each of which has signature equivalent to of length .
Lemma 3.3.
Proof.
Proof is by induction on . follows from Lemma 3.1.
Let denote the value of for the prime using a vector with the first prime bases. We need the following lemma from [10, Cor. 2.4]:
Lemma 3.4.
There exists a constant such that
Using this, we obtain the following.
Theorem 3.5.
Let . Then
Proof.
We have
Note that . ∎
3.3. A Conjecture
In order to prove our running time bound for , we make use of the conjecture below. Let be the set of integers with exactly distinct prime divisors each of which has signature matching . In other words, counts integers in bounded by .
Conjecture 3.6.
Let be as above. Then
Theorem 3.7.
Assuming Conjecture 3.6 is true, we have
3.4. Proof of Theorem 1.2
We now have the pieces we need to prove our running time bound.
As above, each pseudoprime candidate we construct will have the form , where is the product of distinct primes with matching signature. Again, is our base vector of small primes of length .
3.4.1.
In this case is prime.
GCD Computation. For each prime we perform a GCD computation as described in §2.2. The bottleneck of this computation is computing GCDs of -bit integers. This gives a running time proportional to
Sieving Computation. For each prime with , we sieve the interval for primes that are . We also employ signature sieving, but for the simplicity of analysis, we omit that for now. Using the methods from [15], we can sieve an arithmetic progression of length in operations. We do not need proof of primality here, so a fast probabilistic test works fine. This gives a running time proportional to
At this point we know and, to keep the GCD and sieving computations balanced, , say. This means Theorem 3.5 applies; we set and to obtain
assuming that with .
Minimizing implies and gives the desired running time of . This completes our proof. ∎.
3.4.2.
In this case is composite.
GCD Computation. For we construct integers for computing GCDs, with consisting of exactly prime divisors less than , with signatures matching . For each prime , we perform a hash table lookup and fetch the list of such primes; this is Step 5 of Algorithm 3. This overhead cost is . Summing this over all primes gives .
Next, for each prime we construct at most values for (Step 7 of Algorithm 3), and using Lemma 3.3 and multiplying by the cost of computing the GCD, this gives us
| (3.1) |
for the total running time.
Sieving Computation. Again, the main loop enumerates all choices for the second-largest prime . First, we construct all possible -values with , , and , so with all the and . We also have . This implies .
For a given , fetching the list of primes below with matching signatures takes time (Algorithm 3 Step 5). Summing over all , splitting the sum at , this takes time.
As above, we write . We claim that the total number of values is . Let be as above. There are at most values of for each . Again, splitting this at , we have
and
This covers work done at Step 7 of Algorithm 3.
Finally, the cost of sieving is at most
If we use Theorem 3.7, based on our conjecture, and using the lower bound , this leads to the bound
| (3.2) |
Without the conjecture, we use Lemma 3.2 together with the argument outlined in Hardy and Wright [5] in deriving (22.18.8), we obtain that
We then use
As above, this leads to the bound
| (3.3) |
To balance the cost of GCDs with sieving, we want to balance (3.1) with (3.2) or (3.3), depending on whether we wish to assume our conjecture or not. Simplifying a bit, this means balancing with either or . The optimal cutoff point is then either under the assumption of Conjecture 3.6, or unconditionally, for a total time of
with our conjecture, or
without. We have proven the following.
Theorem 3.8.
Assuming Conjecture 3.6, our algorithm takes time to find all integers that are strong pseudoprimes to the first prime bases, if with .
If we choose so that is a fractional power of , then Lemma 3.3 implies that there is a constant such that if , then there is no work to do. This explains why our computation did not need to go past . It also explains why, in practice, the case is the bottleneck of the computation, and is consistent with the implications of our conjecture that the work for each value of decreases as increases.
4. Implementation Details
In this final section, we conclude with some details from our algorithm implementation.
4.1. Strong Pseudoprimes Found
In addition to our main results for and , we discovered the following strong pseudoprimes. This first table contains pseudoprimes found while searching for
| Factorization | |
|---|---|
| 3825123056546413051 | 747451 149491 34233211 |
| 230245660726188031 | 787711 214831 1360591 |
| 360681321802296925566181 | 424665351661849330703321 |
| 164280218643672633986221 | 286600958341573201916681 |
| 318665857834031151167461 | 399165290221798330580441 |
| 7395010240794120709381 | 60807114061121614228121 |
| 164280218643672633986221 | 286600958341573201916681 |
This second table contains pseudoprimes found while verifying .
| Factorization | |
|---|---|
| 318665857834031151167461 | 399165290221798330580441 |
| 2995741773170734841812261 | 12238753558212447750711641 |
| 667636712015520329618581 | 5777701584611155540316921 |
| 3317044064679887385961981 | 12878361822612575672364521 |
| 3317044064679887385961981 | 12470503392612494100678521 |
| 552727880697763694556181 | 5257032816611051406563321 |
| 360681321802296925566181 | 424665351661849330703321 |
| 7395010240794120709381 | 60807114061121614228121 |
| 3404730287403079539471001 | 13047471570012609494314001 |
| 164280218643672633986221 | 286600958341573201916681 |
4.2. Hash Table Datastructure
It is natural to wonder how much time is needed to manage the hash table datastructure from §2.4. Specifically, we measured the time to create the table when inserting all primes up to a set bound. For this measurement, we used a vector with the first 8 prime bases. We also measured how long it took, for each prime up to the bound listed, to also perform the fetch operation, which returns a list of primes with matching signature with values.
| Largest Prime | Table Entries | Creation Time | Fetching Time |
|---|---|---|---|
| 78490 | 1.13 | 2.58 | |
| 664571 | 11.49 | 2:44.49 | |
| 5761447 | 1:56.22 | 3:30:50.2 |
The times are given in seconds, or minutes:seconds, or hours:minutes:seconds as appropriate.
We felt the data structure was a success, in that it was fast and small enough that it was not noticed in the larger computation.
4.3. Almost-Linear GCDs
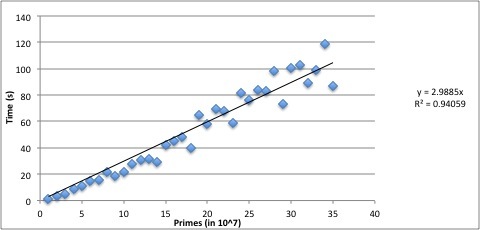
In Figure 1, we present the times to perform Algorithm 1 on selected prime values for (so this is for the case). The data points were obtained by averaging the time needed to carry out Algorithm 1 for the first ten primes exceeding for . Averaging was required because the size of the values is not uniformly increasing in . This explains the variance in the data; for example, the first ten primes after happened to have smaller values on average than the first ten primes after .
It should be clear from the data that our GMP algorithm for computing GCDs was using an essentially linear-time algorithm. Note that if we chose to extend the computation to large enough values, memory would become a concern and we would expect to see paging/thrashing degrade performance.
4.4. GCD/Sieving Crossover
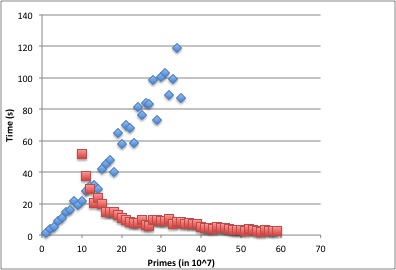
In Figure 2, we present a comparison of the timings for computing GCDs (Algorithm 1, diamonds on the graph) with signature sieving (Algorithm 2, squares on the graph). For this graph, we are looking at choosing the crossover point , and again, we are focusing on the case.
-
•
One would expect that the signature sieving curve should behave as an inverse quadratic; the time to sieve for one prime is proportional to
and we expect most of the time. However, utilizing signatures obscures this to some degree, since the algorithm cannot make use of all prime bases if they divide , hence the minor variations in the curve. Let us elaborate this here.
The data points for signature sieving in Figure 2 represent the average sieve time for the first 50 primes past for . There is a lot of variance in these timing because of the inclusion and exclusion of primes from the signature depending if they are relatively prime to . For example, has and therefore has few primes from the base set to use in signature sieving. The inability to add extra primes shows up in the timing data; a careful inspection of the data shows a strange jump when primes transition from to . The data points to a steady decrease, then an almost two fold increase in time followed by a steady decrease again. We believe this is because, on average, one less base prime may be used in signature sieving. Using one less base prime results in approximately twice as much work.
-
•
In the computation for , our actual crossover point was , even though the timing data would suggest the optimal crossover point is around . From a cost-efficiency point of view, we chose poorly. However, the choice was made with two considerations. One is that the program to compute GCDs (Algorithm 1) is simple to write, so that program was up and running quickly, and we let it run while we wrote the sieving code (Algorithm 2). Second is that, initially, we did not know which value we would ultimately be able to compute. Since the results from GCD computations apply to all larger values of , we opted to err in favor of computing more GCDs.
4.5. Signature Sieving
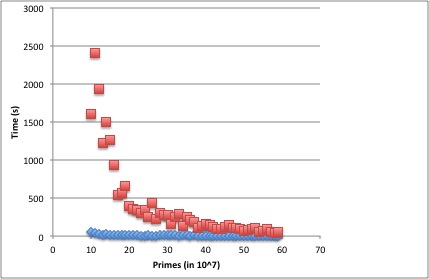
Figure 3 shows the impact that signature sieving makes. Here the squares in the graph give -sieving times with no signature information used, and the diamonds show the same -sieving work done while taking advantage of signature information using the space-saving wheel. Since there is relatively little variance involved in -sieving, each point represents the first prime after for . On the same interval signature sieving practically looks like it takes constant time compared to -sieving. If we had opted to not incorporate signature sieving in, then the expected crossover point given these timings would occur when the primes are around .
References
- [1] Eric Bach, Explicit bounds for primality testing and related problems, Math. Comp. 55 (1990), no. 191, 355–380. MR 1023756 (91m:11096)
- [2] Daniel Bleichenbacher, Efficiency and security of cryptosystems based on number theory, Ph.D. thesis, Swiss Federal Institute of Technology Zurich, 1996.
- [3] François G. Dorais and Dominic Klyve, A Wieferich prime search up to , J. Integer Seq. 14 (2011), no. 9, Article 11.9.2, 14. MR 2859986
- [4] Brian Dunten, Julie Jones, and Jonathan Sorenson, A space-efficient fast prime number sieve, Inform. Process. Lett. 59 (1996), no. 2, 79–84. MR 1409956 (97g:11141)
- [5] G. H. Hardy and E. M. Wright, An introduction to the theory of numbers, 5th ed., Oxford University Press, 1979.
- [6] Henryk. Iwaniec, On the Brun-Titchmarsh theorem, J. Math. Soc. Japan 34 (1982), no. 1, 95–123.
- [7] Gerhard Jaeschke, On strong pseudoprimes to several bases, Math. Comp. 61 (1993), no. 204, 915–926. MR 1192971 (94d:11004)
- [8] Yupeng Jiang and Yingpu Deng, Strong pseudoprimes to the first eight prime bases, Math. Comp. (2014), 1–10 (electronic).
- [9] A. Languasco and A. Zaccagnini, A note on Mertens’ formula for arithmetic progressions, Journal of Number Theory 127 (2007), no. 1, 37 – 46.
- [10] Francesco Pappalardi, On the order of finitely generated subgroups of q*(mod p) and divisors of p−1, Journal of Number Theory 57 (1996), no. 2, 207 – 222.
- [11] Francesco Pappalardi, On the -rank Artin conjecture, Math. Comp. 66 (1997), no. 218, 853–868. MR 1377664 (97f:11082)
- [12] Carl Pomerance, J. L. Selfridge, and Samuel S. Wagstaff, Jr., The pseudoprimes to , Math. Comp. 35 (1980), no. 151, 1003–1026. MR 572872 (82g:10030)
- [13] Michael O. Rabin, Probabilistic algorithm for testing primality, J. Number Theory 12 (1980), no. 1, 128–138. MR 566880 (81f:10003)
- [14] A. Schönhage and V. Strassen, Schnelle Multiplikation großer Zahlen, Computing (Arch. Elektron. Rechnen) 7 (1971), 281–292, MR 45 #1431. MR 45 #1431
- [15] Jonathan P. Sorenson, The pseudosquares prime sieve, Algorithmic number theory, Lecture Notes in Comput. Sci., vol. 4076, Springer, Berlin, 2006, pp. 193–207. MR 2282925 (2007m:11168)
- [16] Jonathan P. Sorenson, Sieving for pseudosquares and pseudocubes in parallel using doubly-focused enumeration and wheel datastructures, Proceedings of the 9th International Symposium on Algorithmic Number Theory (ANTS-IX) (Nancy, France) (Guillaume Hanrot, Francois Morain, and Emmanuel Thomé, eds.), Springer, July 2010, LNCS 6197, ISBN 978-3-642-14517-9, pp. 331–339.
- [17] Damien Stehlé and Paul Zimmermann, A binary recursive GCD algorithm, Sixth International Algorithmic Number Theory Symposium (Burlington, Vermont, USA) (Duncan Buell, ed.), Springer, June 2004, LNCS 3076, pp. 411–425. MR MR2138011 (2006e:11194)
- [18] Zhenxiang Zhang, Two kinds of strong pseudoprimes up to , Math. Comp. 76 (2007), no. 260, 2095–2107 (electronic). MR 2336285 (2008h:11114)