Structural Reductions and Stutter Sensitive Properties

[Word] A word over a finite alphabet $\Sigma$ is an infinite sequence of symbols in $\Sigma$. We canonically denote a word $r$ using one of the two forms:

• •

  (plain word) $r=a_{0}^{n_{0}}a_{1}^{n_{1}}a_{2}^{n_{2}}\ldots$ with for all $i\in{\rm Nature}$, $a_{i}\in\Sigma$, $n_{i}\in{\rm Nature}^{+}$ and $a_{i}\neq a_{i+1}$, or

• •

  ($\omega$-word) $r=a_{0}^{n_{0}}a_{1}^{n_{1}}\ldots a_{k}^{\omega}$ with $k\in{\rm Nature}$ and for all $0\leq i\leq k$, $a_{i}\in\Sigma$, and for $i<k$, $n_{i}\in{\rm Nature}^{+}$ and $a_{i}\neq a_{i+1}$. $a_{k}^{\omega}$ represents an infinite stutter on the final symbol $a_{k}$ of the word.

The set of all words over alphabet $\Sigma$ is denoted $\Sigma^{\omega}$.

These notations using a power notation for repetitions of a symbol in a word are introduced to highlight stuttering. We force the symbols to alternate to ensure we have a canonical representation: with $\sigma$ a suffix (not starting by symbol $b$), the word $aab\sigma$ must be represented as $a^{2}b^{1}\sigma$ and not $a^{1}a^{1}b^{1}\sigma$. To represent a word of the form $aabbcccccc\ldots$ we use an $\omega$-word: $a^{2}b^{2}c^{\omega}$.

[Shorter than] A plain word $r=a_{0}^{n_{0}}a_{1}^{n_{1}}a_{2}^{n_{2}}\ldots$ is shorter than a plain word $r^{\prime}=a_{0}^{n_{0}^{\prime}}a_{1}^{n_{1}^{\prime}}a_{2}^{n_{2}^{\prime}}\ldots$ if and only if for all $i\in{\rm Nature}$, $0<n_{i}\leq n_{i}^{\prime}$. For two $\omega$-words $r=a_{0}^{n_{0}}\ldots a_{k}^{\omega}$ and $r^{\prime}=a_{0}^{n_{0}^{\prime}}\ldots a_{k}^{\omega}$, $r$ is shorter than $r^{\prime}$ if and only if for all $i<k$, $n_{i}\leq n_{i}^{\prime}$.

We denote this relation on words as $r{\rm Phys.~Rev.~E}r^{\prime}$.

For instance, for any given suffix $\sigma$, $ab\sigma{\rm Phys.~Rev.~E}a^{2}b\sigma$. Note that $ab\sigma{\rm Phys.~Rev.~E}ab^{2}\sigma$ as well, but that $a^{2}b\sigma$ and $ab^{2}\sigma$ are incomparable. $\omega$-words are incomparable with plain words.

The ${\rm Phys.~Rev.~E}$ relation is a partial order on words.

[Stutter equivalence] A word $r$ is stutter equivalent to $r^{\prime}$, denoted as $r\sim r^{\prime}$ if and only if there exists a shorter word $r^{\prime\prime}$ such that $r^{\prime\prime}{\rm Phys.~Rev.~E}r\land r^{\prime\prime}{\rm Phys.~Rev.~E}r^{\prime}$. This relation $\sim$ is an equivalence relation thus partitioning words of $\Sigma^{\omega}$ into equivalence classes.

We denote $\hat{r}$ the equivalence class of a word $r$ and denote $\underaccent{\bar}{\hat{r}}$ the shortest word in that equivalence class.

For any given word $r=a_{0}^{n_{0}}a_{1}^{n_{1}}a_{2}^{n_{2}}\ldots$ there is a shortest representative in $\hat{r}$ that is the word $\underaccent{\bar}{\hat{r}}=a_{0}a_{1}a_{2}\ldots$ where no symbol is ever consecutively repeated more than once (until the $\omega$ for an $\omega$-word). By definition all words that are comparable to $\underaccent{\bar}{\hat{r}}$ are stutter equivalent to each other, since $\underaccent{\bar}{\hat{r}}$ can play the role of $r^{\prime\prime}$ in the definition of stutter equivalence, giving us an equivalence relation: it is reflexive, symmetric and transitive.

For instance, with $\sigma$ denoting a suffix, $\underaccent{\bar}{\hat{r}}=ab\sigma$ would be the shortest representative of any word of $\hat{r}$ of the form $a^{n_{0}}b^{n_{1}}\sigma$. We can see by this definition that, despite being incomparable, $a^{2}b\sigma\sim ab^{2}\sigma$ since $ab\sigma{\rm Phys.~Rev.~E}a^{2}b\sigma$ and $ab\sigma{\rm Phys.~Rev.~E}ab^{2}\sigma$.

[Language] A language $\mathscr{L}$ over a finite alphabet $\Sigma$ is a set of words over $\Sigma$, hence $\mathscr{L}\subseteq\Sigma^{\omega}$. We denote by $\bar{\mathscr{L}}=\Sigma^{\omega}\setminus\mathscr{L}$ the complement of a language $\mathscr{L}$.

In the literature, most studies that exploit a form of stuttering are focused on stutter insensitive languages [PPH96, Val90, Pel94, GW94, HP06]. In a stutter insensitive language $\mathscr{L}$, duplicating any letter (also called stuttering) or removing any duplicate letter from a word of $\mathscr{L}$ must produce another word of $\mathscr{L}$. In other words, all stutter equivalent words in a class $\hat{r}$ must be either in the language or outside it. Let us introduce weaker variants of this property, which were originally presented in [PPRT22].

[Shortening insensitive] A language $\mathscr{L}$ is shortening insensitive if and only if for any word $r$ it contains, all shorter words $r^{\prime}\in\Sigma^{\omega}$ such that $r^{\prime}{\rm Phys.~Rev.~E}r$ also belong to $\mathscr{L}$.

For instance, a shortening insensitive language $\mathscr{L}$ that contains the word $a^{3}b\sigma$ must also contain shorter words $a^{2}b\sigma$, and $ab\sigma$. If it contains $a^{2}b^{2}\sigma$ it also contains $a^{2}b\sigma$, $ab^{2}\sigma$ and $ab\sigma$.

[Lengthening insensitive] A language $\mathscr{L}$ is lengthening insensitive if and only if for any word $r$ it contains, all longer words $r^{\prime}\in\Sigma^{\omega}$ such that $r{\rm Phys.~Rev.~E}r^{\prime}$ also belong to $\mathscr{L}$.

For instance, a lengthening insensitive language $\mathscr{L}$ that contains the word $a^{2}b\sigma$ must also contain all longer words $a^{3}b\sigma$, $a^{2}b^{2}\sigma$ …, and more generally words of the form $a^{n}b^{n^{\prime}}\sigma$ with $n\geq 2$ and $n^{\prime}\geq 1$. If it contains $\underaccent{\bar}{\hat{r}}=ab\sigma$ the shortest representative of an equivalence class, it contains all words in the stutter equivalence class.

While stutter insensitive languages have been heavily studied, there is, to our knowledge, no study on what reductions are possible if only one direction holds, i.e. the language is shortening or lengthening insensitive, but not both. A shortening insensitive language is essentially asking for something to happen before a certain deadline or stuttering “too much”. A lengthening insensitive language is asking for something to happen at the earliest at a certain date or after having stuttered at least a certain number of times. Figure 2 represents these situations graphically.

A language is both shortening and lengthening insensitive if and only if it is stutter insensitive (see Fig. 2). This fact is already used in [MD15] to identify a stutter insensitive language using only its automaton. Furthermore since stutter equivalent classes of words are entirely inside or outside a stutter insensitive language, a language $\mathscr{L}$ is stutter insensitive if and only if the complement language $\bar{\mathscr{L}}$ is stutter insensitive.

However, if we look at sensitivity to length and how it interacts with the complement operation, we find a dual relationship where the complement of a shortening insensitive language is lengthening insensitive and vice versa.

A language $\mathscr{L}$ is shortening insensitive if and only if the complement language $\bar{\mathscr{L}}$ is lengthening insensitive.

If we look at Figure 2, the dual effect of complement on the sensitivity of the language to length is apparent: if gray and white are switched we can see that $\bar{\mathscr{L}_{b}}$ is lengthening insensitive and $\bar{\mathscr{L}_{c}}$ shortening insensitive.

[Reduction] Let $I$ be a reduction function $\Sigma^{\omega}\rightarrow\Sigma^{\omega}$ such that $I(r){\rm Phys.~Rev.~E}r$ for every $r$ in $\Sigma^{\omega}$. The reduction by $I$ of a language $\mathscr{L}$ is $\mathit{Red}_{I}(\mathscr{L})=\{I(r)\mid r\in\mathscr{L}\}$.

Note that the ${\rm Phys.~Rev.~E}$ partial order is not strict so that the image of a word may be the word itself, hence the identity function is a reduction function. In most cases however we expect the reduction function to map many words $r$ of the original language to a single shorter word $r^{\prime}$ of the reduced language. Note that given any two reduction functions $I$ and $I^{\prime}$, $I\circ I^{\prime}$ is also a reduction function, therefore $\mathit{Red}_{I}(\mathit{Red}_{I^{\prime}}(\mathscr{L}))=\mathit{Red}_{I\circ I^{\prime}}(\mathscr{L})$ is still a reduction of $\mathscr{L}$. Hence chaining reduction rules still produces a reduction. As we will discuss in Section 3.1 structural reductions of a specification such as Lipton’s transaction reduction [Lip75, Laa18] or Petri net agglomerations [Ber85, Thi20] (see also Section 3.6) induce a reduction at the language level. In Fig. 1 fusing statements into a single atomic step in the program induces a reduction of the language.

With this theorem original to this paper we now can build a semi-decision procedure that is able to prove some lengthening or disprove some shortening insensitive properties using a reduction of a system. In practice, the language $\mathscr{L}$ will be the language of the negation of a property, and $\mathscr{L}^{\prime}$ and $\mathit{Red}_{I}(\mathscr{L}^{\prime})$ will be respectively the language of a system and the language of its reduced version.

From the point of view of LTL verification with a state-based logic, executions of a system (also called runs) are seen as infinite words over the alphabet $\Sigma=2^{\mathrm{AP}}$, where $\mathrm{AP}$ is a set of atomic propositions that may be true or false in each state. So each symbol in a run gives the truth value of all of the atomic propositions in that state of the execution, and each time an action happens we progress in the run to the next symbol. Some actions of the system update the truth value of atomic propositions, but some actions can leave them unchanged, which corresponds to stuttering.

[Kripke Structure Syntax] Let $\mathrm{AP}$ designate a set of atomic propositions. A Kripke structure $\mathit{KS}_{\mathrm{AP}}=\langle S,R,\lambda,s_{0}\rangle$ over $\mathrm{AP}$ is a tuple where $S$ is the set of states, $R\subseteq S\times S$ is the transition relation, $\lambda:S\rightarrow 2^{\mathrm{AP}}$ is the state labeling function, and $s_{0}\in S$ is the initial state. {defi}[Kripke Structure Semantics] The language $\mathscr{L}(\mathit{KS}_{\mathrm{AP}})$ of a Kripke structure $\mathit{KS}_{\mathrm{AP}}$ is defined over the alphabet $2^{\mathrm{AP}}$. It contains all runs of the form $r=\lambda(s_{0})\lambda(s_{1})\lambda(s_{2})\ldots$ where $s_{0}$ is the initial state of $\mathit{KS}_{\mathrm{AP}}$ and $\forall i\in{\rm Nature}$, either $(s_{i},s_{i+1})\in R$, or if $s_{i}$ is a deadlock state such that $\forall s^{\prime}\in S,(s_{i},s^{\prime})\not\in R$ then $s_{i+1}=s_{i}$.

All system executions are considered maximal, so that they are represented by infinite runs. If the system can deadlock or terminate in some way, we can extend these finite words by an infinite stutter on the last symbol of the word to obtain a run.

Example. Subfigure (1) of Figure 1 depicts a program where each thread ($\alpha$ and $\beta$) has three reachable positions (we consider that each instruction is atomic). In this example we assume that the only observable atomic propositions are $p$ (true when $x=0$) and $q$ (true when $y=0$). The variable $z$ is not observed.

Subfigure (2) of Figure 1 depicts the reachable states of this system as a Kripke structure. Actions of thread $\beta$ (which do not modify the value of $p$ or $q$) are horizontal while actions of thread $\alpha$ are vertical. While each thread has 3 reachable positions, the emission of the message by $\beta$ must precede the reception by $\alpha$ so that some situations are unreachable. Based on Definition 3.1 we can compute the language $\mathscr{L}_{A}$ of this system. It consists of three words: when thread $\beta$ goes first $pq^{3}$ $\bar{p}q$ $\bar{p}\bar{q}^{\omega}$, with an interleaving $pq^{2}$ $\bar{p}q^{2}$ $\bar{p}\bar{q}^{\omega}$, and when thread $\alpha$ goes first $pq$ $\bar{p}q^{3}$ $\bar{p}\bar{q}^{\omega}$.

In subfigure (3) of Figure 1, the actions "$z=40;chan.send(z);$"of thread $\beta$ are fused into a single atomic operation. This is possible because action $z=40$ of thread $\beta$ is stuttering (it cannot affect either $p$ or $q$) and is non-interfering with other events (it neither enables nor disables any event other than subsequent instruction "chan.send(z)"). The language of this smaller KS is a reduction of the language of the original system. It contains two runs: thread $\alpha$ goes first $pq$ $\bar{p}q^{2}$ $\bar{p}\bar{q}^{\omega}$ and thread $\beta$ goes first $pq^{2}$ $\bar{p}q$ $\bar{p}\bar{q}^{\omega}$.

In subfigure (4) of Figure 1, the already fused action "$z=40;chan.send(z);$"of thread $\beta$ is further fused with the chan.recv(); action of thread $\alpha$. This leads to a smaller KS whose language is still a reduction of the original system now containing a single run: $pq$ $\bar{p}q$ $\bar{p}\bar{q}^{\omega}$. This simple example shows the power of structural reductions, when they are applicable, with a reduction of the initial language to a single word.

Let us consider the problem of model-checking of an $\omega$-regular property $\varphi$ (such as one described by an LTL formula) on a system using the automata-theoretic approach [Var07]. In this approach, we wish to answer the problem of language inclusion: do all runs of the system $\mathscr{L}(\mathit{KS})$ belong to the language of the property $\mathscr{L}(\varphi)$ ? To do this, when the property $\varphi$ is an $\omega$-regular language (e.g. an LTL or PSL formula), we first negate the property $\lnot\varphi$, then build a (variant of) a Büchi automaton $A_{\lnot\varphi}$ whose language¹¹1Because computing the complement $\bar{A}$ of a Büchi automaton $A$ is worse than exponential in the worst case [Yan08, SV12], syntactically negating $\varphi$ and producing an automaton $A_{\lnot\varphi}$ is preferable when $A$ is derived from e.g. an LTL formula. consists of all the runs that do not satisfy $\varphi$ i.e. $\mathscr{L}(A_{\lnot\varphi})=\Sigma^{\omega}\setminus\mathscr{L}(\varphi)$. We then perform a synchronized product between this Büchi automaton and the Kripke structure $\mathit{KS}$ corresponding to the system’s state space $A_{\lnot\varphi}\otimes\mathit{KS}$ (where $\otimes$ is defined to satisfy $\mathscr{L}(A\otimes B)=\mathscr{L}(A)\cap\mathscr{L}(B)$). Either the language of the product is empty $\mathscr{L}(A_{\lnot\varphi}\otimes\mathit{KS})=\emptyset$, and the property $\varphi$ is thus true of this system, or the product is non empty, and from any run in the language of the product we can build a counter-example to the property.

We will consider in the rest of the paper that the shortening or lengthening insensitive language of Definitions 2.2 and 2.2 is given as an omega-regular language or Büchi automaton typically obtained from the negation of an LTL property, and that the reduction of Definition 2.4 is applied to a language that corresponds to all runs in a Kripke structure typically capturing the state space of a system.

LTL verification with reductions. With Theorem 1, a shortening insensitive property shown to be true on the reduction (empty intersection with the language of the negation of the property) is also true of the original system. A lengthening insensitive property shown to be false on the reduction (non-empty intersection with the language of the negation of the property, hence counter-examples exist) is also false in the original system. Unfortunately, our procedure cannot prove using a reduction that a shortening insensitive property is false, or that a lengthening insensitive property is true. We offer a semi-decision procedure.

We now present a strategy to decide if a given property expressed as a Büchi automaton is shortening insensitive, lengthening insensitive, or both.

This section relies heavily on the operations introduced and discussed at length in [MD15]. The authors define two syntactic transformations $sl$ and $cl$ of a transition-based generalized Büchi automaton (TGBA) $A_{\varphi}$ that can be built from any LTL formula $\varphi$ to represent its language $\mathscr{L}(\varphi)=\mathscr{L}(A_{\varphi})$ [Cou99]. TGBA are a variant of Büchi automata where the acceptance conditions are placed on edges rather than states of the automaton.

The $cl$ closure operation decreases stutter, it adds to the language any word $r^{\prime}\in\Sigma^{\omega}$ that is shorter than a word $r$ in the language. Informally, the strategy consists in detecting when a sequence $q_{1}\xrightarrow{a}q_{2}\xrightarrow{a}q_{3}$ is possible and adding an edge $q_{1}\xrightarrow{a}q_{3}$, hence its name $cl$ for “closure”. The $sl$ self-loopization operation increases stutter, it adds to the language any run $r^{\prime}\in\Sigma^{\omega}$ that is longer than a run $r$ in the language. Informally, the strategy consists in adding a self-loop to any state so that we can always decide to repeat a letter (and stay in that state) rather than progress in the automaton, hence its name $sl$ for “self-loop”. More formally $\mathscr{L}(cl(A_{\varphi}))=\{r^{\prime}\mid\exists r\in\mathscr{L}(A_{\varphi}),r^{\prime}{\rm Phys.~Rev.~E}r\}$ and $\mathscr{L}(sl(A_{\varphi}))=\{r^{\prime}\mid\exists r\in\mathscr{L}(A_{\varphi}),r{\rm Phys.~Rev.~E}r^{\prime}\}$.

Using these operations [MD15] shows that there are several possible ways to test if an omega-regular language (encoded as a Büchi automaton) is stutter insensitive: essentially applying either of the operations $cl$ or $sl$ should leave the language unchanged. This allows one to recognize that a property is stutter insensitive even though it syntactically contains e.g. the neXt operator of LTL.

For instance $A_{\varphi}$ is stutter insensitive if and only if $\mathscr{L}(sl(cl(A_{\varphi}))\otimes A_{\lnot\varphi})=\emptyset$. The full test is thus simply reduced to a language emptiness check testing that both $sl$ and $cl$ operations leave the language of the automaton unchanged.

Indeed for stutter insensitive languages, all or none of the runs belonging to a given stutter equivalence class of runs $\hat{r}$ must belong to the language $\mathscr{L}(A_{\varphi})$. In other words, if shortening or lengthening a run can make it switch from belonging to $A_{\varphi}$ to belonging to $A_{\lnot\varphi}$, the language is stutter sensitive. This is apparent on Figure 2.

We want weaker conditions here, but we can reuse the $sl$ and $cl$ operations developed for testing stutter insensitivity. Indeed for an automaton $A$ encoding a shortening insensitive language, $\mathscr{L}(cl(A))=\mathscr{L}(A)$ should hold. Conversely if $A$ encodes a lengthening insensitive language, $\mathscr{L}(sl(A))=\mathscr{L}(A)$ should hold. We express these tests as emptiness checks on a product in the following way.

Thanks to property 2.3, and in the spirit of [MD15] we could also test the complement of a language for the dual property if that is more efficient, i.e. $\mathscr{L}(sl(\bar{A})\otimes A)=\emptyset$ if and only if $A$ defines a shortening insensitive language and similarly $\mathscr{L}(cl(\bar{A})\otimes A)=\emptyset$ iff $A$ is lengthening insensitive. We did not really investigate these alternatives as the complexity of the test was already negligible in all of our experiments.

Overall complexity of these tests is dominated by the complement operation on the automaton $A$ to compute $\bar{A}$; this operation is worst case exponential in the size of $A$. However, when the automaton $A_{\varphi}$ is obtained by translating a LTL formula $\varphi$, we can compute $A_{\lnot\varphi}$ the automaton for the negation of $\varphi$ instead of the complement $\bar{A_{\varphi}}$, avoiding this exponential. The $cl$ operation only introduces new edges, so $cl(A)$ is worst case quadratic in the number of states of $A$. The $sl$ operation unfortunately may require adding new states, to allow to stutter on the last seen valuation of the system (a valuation is in $2^{AP}$), hence is worst case exponential over the number of atomic propositions in $A$, but formulas in our experiments do not have more than 5 atomic propositions so this complexity does not dominate the procedure. The emptiness check computes the product of two automata and which is worst case linear to the product of the sizes of the two automata.

With these elements we can describe a semi decision procedure to verify a property $\varphi$ on a system represented by a Kripke structure $\mathit{KS}$.

1. (1)

   Decide if $\varphi$ is shortening insensitive or lengthening insensitive using Theorem 2. If neither is true, abort the procedure.

2. (2)

   Reduce the system $\mathit{KS}$ using the atomic propositions of $\varphi$ as observed alphabet $\mathit{KS}^{\prime}=\mathit{Reduce}(\mathit{KS},\varphi)$. Thus $\mathit{KS}^{\prime}$ is a reduction in the sense of Definition 2.4.

3. (3)

   Use a model-checker to verify whether the reduced system $\mathit{KS}^{\prime}$ satisfies $\varphi$, i.e. whether $\mathscr{L}(A_{\lnot\varphi}\otimes\mathit{KS}^{\prime})=\emptyset$.

4. (4)

   If $\mathit{KS}^{\prime}$ satisfies $\varphi$ and $\varphi$ is shortening insensitive or $\mathit{KS}^{\prime}$ does not satisfy $\varphi$ and $\varphi$ is lengthening insensitive, conclude.

5. (5)

   Otherwise abort the procedure, and run a model-checker using the original system and property.

Note that the complexity of this procedure is dominated by the model-checking step, since $\mathit{KS}$ is typically extremely large in front of $A_{\lnot\varphi}$. If the reduction is successful, $\mathit{KS}^{\prime}$ can be up to exponentially smaller than $\mathit{KS}$, but this depends on the size of the observed alphabet as well as on the system definition. The experiments presented in Section 4 confirm that in most cases verifying on the reduced system is much cheaper than doing model-checking on the original system.

Structural reductions are one of the possible strategies to reduce the complexity of analyzing a system. Depending on the input formalism the terminology used is different, but the main results remain stable.

In [Lip75] transaction reduction consists in fusing two adjacent actions of a thread (or even across threads in recent versions such as [Laa18] ). The first action must not modify atomic properties and must commutate with any action of other threads. Fusing these actions leads to shorter runs, where a stutter is lost. In the program of Fig. 1, "z=40" is enabled from the initial state and must happen before "chan.send(z)", but it commutes with instructions of thread $\alpha$ and is not observable. Hence the language $\mathscr{L}_{B}$ built with an atomicity assumption on "z=40;chan.send(z)" is indeed a reduction of $\mathscr{L}_{A}$.

Let us reason at the level of a Kripke structure. The goal of such reductions is to structurally detect the following situation in language $\mathscr{L}$: let $r=a_{0}^{n_{0}}a_{1}^{n_{1}}a_{2}^{n_{2}}\ldots$ designate a run (not necessarily in the language). Then there must exist two indexes $i$ and $j$ such that for any natural number $k$, $i\leq k\leq j$, $r_{k}=a_{0}^{n_{0}}\ldots a_{i}^{n_{i}}\ldots a_{k}^{n_{k}+1}\ldots a_{j}^{n_{j}}\ldots$ is in the language. In other words, the set of runs $\{r_{k}=a_{0}^{n_{0}}\ldots a_{i}^{n_{i}}\ldots a_{k}^{n_{k}+1}\ldots a_{j}^{n_{j}}\ldots\mid i\leq k\leq j\}$ must be included in the language. This corresponds to an event that does not impact the truth value of atomic propositions (it stutters) and can be freely commuted with any event that occurs between indexes $i$ and $j$ in the run. This event is simply constrained to occur at the earliest at index $i$ in the run and at the latest at index $j$. In Fig. 1 the event "z=40" can happen as early as in the initial state, and must occur before "chan.send(z)" and thus matches this definition.

Note that these runs are all stutter equivalent, but are incomparable by the shorter than relation (e.g. $aabc\sigma,abbc\sigma,abcc\sigma$ are incomparable). In this situation, a reduction can choose to only represent the run $r$ (e.g. $r=abc\sigma$ represents all these runs) instead of any of these runs. This run was not originally in the language in general, but it is indeed shorter than any of the $r_{k}$ runs so it matches definition 2.4 for a reduction. Note that the stutter-equivalent class $\hat{r}$ of $r$ does contain all these longer runs so that in a stutter insensitive context, examining $r$ is enough to conclude for any of the runs in $\hat{r}$. This is why usage of structural reductions is compatible with verification of a logic such as $LTL_{\setminus X}$ and has been proposed for that express purpose in the literature [PP00, HP06, Laa18].

Thus transaction reductions [Lip75, Laa18] as well as both pre-agglomeration and post-agglomeration of Petri nets [PP00, EHP05, HP06, Thi20] produce a system whose language is a reduction of the language of the original system.

A formal definition involves a) introducing the syntax of a formalism and b) its semantics in terms of language, then c) defining the reduction rule, and d) proving its effect is a reduction at the language level. The exercise is not particularly difficult, and the definition of reduction rules mostly fall into the category above, where a non observable event that happens at the earliest at point $i$ in the run and at the latest at point $j$ in the run is abstracted from the trace. As an example, we provide in Section 3.6 such a proof for structural agglomerations rules on Petri nets.

Our experimental Section 4.2 uses slightly extended versions of these rules (defined in [Thi20]) for (potentially partial) pre and post-agglomeration. That paper presents $22$ structural reductions rules from which we selected the rules valid in the context of LTL verification. Only one rule preserving stutter insensitive LTL was not compatible with our approach since it does not produce a reduction at the language level: rule $3$ “Redundant transitions” proposes that if two transitions $t_{1}$ and $t_{2}$ have the same combined effect as a transition $t$, and firing $t_{1}$ enables $t_{2}$, $t$ can be discarded from the net. This reduces the number of edges in the underlying $\mathit{KS}$ representing the state space, but does not affect reachability of states. However, it selects as representative a run involving both $t_{1}$ and $t_{2}$ that is longer than the one using $t$ in the original net, it is thus not legitimate to use it in our strategy (although it remains valid for $LTL_{\setminus X}$). Rules $14$ “Pre agglomeration” and $15$ “Post agglomeration” are the most powerful rules of [Thi20] that we are able to apply in our context. They are known to preserve $LTL_{\setminus X}$ (but not full LTL) and their effect is a reduction at the language level, hence we can use them when dealing with shortening/lengthening insensitive formulae.

This section presents agglomeration rules for Petri nets, and shows that this transformation of the structure of a net leads to a reduction of the associated language in the sense of Definition 2.4. All of this section is new content with respect to [PPRT22].

[Structure] A Petri net $N=\langle\mathcal{P},\mathcal{T},\mathcal{W}_{-},\mathcal{W}_{+},m_{0}\rangle$ is a tuple where $\mathcal{P}$ is the finite set of places, $\mathcal{T}$ is the finite set of transitions, $\mathcal{W}_{-}:\mathcal{P}\times\mathcal{T}\rightarrow{\rm Nature}$ and $\mathcal{W}_{+}:\mathcal{P}\times\mathcal{T}\rightarrow{\rm Nature}$ represent the pre and post incidence matrices, and $m_{0}:\mathcal{P}\rightarrow{\rm Nature}$ is the initial marking.

Notations. We use $p$ (resp. $t$) to designate a place (resp. transition) or its index dependent on the context. We represent markings $m$ as vectors of natural numbers with $|\mathcal{P}|$ entries. We also describe $\mathcal{W}_{-}(t)$ and $\mathcal{W}_{+}(t)$, for any given transition $t$, as vectors with $|\mathcal{P}|$ entries. In vector spaces, we use $v\geq v^{\prime}$ to denote $\forall i,v(i)\geq v^{\prime}(i)$, and we use sum $v+v^{\prime}$ with the usual element-wise definition. Since a Petri net is bipartite graph, we note $\bullet{n}$ (resp. ${n}\bullet$) the pre set (resp. post set) of a node $n$ (place or transition). For example, the pre set of place $p$ is $\bullet{p}=\{t\in\mathcal{T}{}\mid\mathcal{W}_{+}(p,t)>0\}$.

[Semantics] The semantics of a Petri net is given by the firing rule $\xrightarrow{t}$ that relates pairs of markings: in any marking $m\in{\rm Nature}^{|\mathcal{P}|}$, if $t\in\mathcal{T}$ satisfies $m\geq\mathcal{W}_{-}(t)$, then $m\xrightarrow{t}m^{\prime}$ with $m^{\prime}=m+\mathcal{W}_{+}(t)-\mathcal{W}_{-}(t)$. Given a set of atomic propositions $\mathrm{AP}$ and an evaluation function $\lambda:{\rm Nature}^{|\mathcal{P}|}\rightarrow 2^{\mathrm{AP}}$, we can associate to a net $N=\langle\mathcal{P},\mathcal{T},\mathcal{W}_{-},\mathcal{W}_{+},m_{0}\rangle$ the corresponding Kripke structure $\mathit{KS}_{\mathrm{AP}}=\langle{\rm Nature}^{|\mathcal{P}|},\{(m,m^{\prime})\mid\exists t\in\mathcal{T},m\xrightarrow{t}m^{\prime}\},\lambda,m_{0}\rangle$ over $\mathrm{AP}$.

An atomic proposition is a Boolean formula (using $\lor,\land,\lnot$) built from comparisons ($\bowtie\in\{<,\leq,=,\geq,>\}$) of arbitrary weighted sum of place markings to another sum or a constant, e.g. $\sum_{p\in\mathcal{P}}\alpha_{p}\cdot m(p)\bowtie k$, with $\alpha_{p}\in\mathds{Z}$ and $k\in\mathds{Z}$. The support of a property expressed over $\mathrm{AP}$ is the set of places whose marking is truly used in an atomic predicate, i.e. such that at least one comparison atom has a non zero $\alpha_{p}$ in a sum. The support $\mathit{Supp}\subseteq\mathcal{P}{}$ of the property defines the subset $\mathit{Inv}_{\mathrm{AP}}{}\subseteq\mathcal{T}$ of invisible or stuttering transitions $t$ satisfying $\forall p\in\mathit{Supp},\mathcal{W}_{-}(p,t)=\mathcal{W}_{+}(p,t)$. Hence, given a labeling function $\lambda:{\rm Nature}^{\mathcal{P}}{}\rightarrow 2^{\mathrm{AP}}$, we can guarantee that $\forall t\in\mathit{Inv}_{\mathrm{AP}}{}$ and any $m,m^{\prime}\in{\rm Nature}^{\mathcal{P}}{}$, if $m\xrightarrow{t}m^{\prime}$ then $\lambda(m)=\lambda(m^{\prime})$. With respect to stutter, the atomic propositions $\mathrm{AP}$ are only interested in the projection of reachable markings over the variables in the support, values of places in $\mathcal{P}{}\setminus\mathit{Supp}$ are not observable in markings. A small support means more potential reductions, as rules mostly cannot apply to observed places or their neighborhood.

Agglomeration in a place $p$ consists in discarding $p$ and its surrounding transitions (pre and post set of $p$) to build instead a transition for every element in the Cartesian product $\bullet{p}\times{p}\bullet$ that represents the effect of the sequence of firing a transition in $\bullet{p}$ then immediately a transition in ${p}\bullet$. This “acceleration” of tokens in $p$ reduces interleaving in the state space, but can preserve properties of interest if $p$ is chosen correctly. This type of reduction has been heavily studied [HP06, Laa18] as it forms a common ground between structural reductions, partial order reductions and techniques that stem from transaction reduction.

We present here two rules that can be used to safely decide if a place can be agglomerated. Figure 3 shows these rules graphically, using the classical graphical notation for Petri nets.

[Pre and Post Agglomeration] Let $N$ designate a Petri net and $\mathit{Supp}\subseteq\mathcal{P}{}$ be the support of a property on this net. Let $p\in\mathcal{P}$ be a place of $N$ satisfying:

Pre agglomeration in $p$ is possible if it also the case that:

Post agglomeration in $p$ is possible if it also the case that:

In either of these cases, we agglomerate place $p$ leading to a net where

• •

  we discard all transitions in $\bullet{p}\cup{p}\bullet$ and place $p$ from the net, and

• •

  $\forall h\in\bullet{p},\forall f\in{p}\bullet,$ we add a new transition $t$ such that $\mathcal{W}_{-}(t)=\mathcal{W}_{-}(h)+\mathcal{W}_{-}(f)$ and $\mathcal{W}_{+}(t)=\mathcal{W}_{+}(h)+\mathcal{W}_{+}(f)$

Pre agglomeration (see Fig. 3(a)) looks for a place $p$ such that all predecessor transitions $h\in\bullet{p}$ are stuttering, have $p$ as single output place, and once enabled cannot be disabled by firing any other transition (hence they commute freely with other transitions that do not consume in $p$). With these conditions, we can always “delay” the firing of $h$ until it becomes relevant to enable a transition that consumes from $p$. This will yield a Petri net whose language is a reduction of the original one.

Conversely, Post agglomeration (see Fig. 3(b)) looks for a place $p$ such that all successor transitions $f\in{p}\bullet$ are stuttering, and have $p$ as single input place. With these conditions, tokens that arrive in $p$ are always free to choose where they want to go, and nothing can prevent them from going there. Instead of waiting in $p$ until we take this decision, we can make this choice immediately after firing a transition $h$ that places a token in $p$. This again will yield a Petri net whose language is a reduction of the original one.

Let $N$ be a Petri net, and $p$ a place of this net satisfying one of the agglomeration criterion. The agglomeration in $p$ of $N$ produces a net whose language is a reduction of the language of $N$.

The pre and post agglomeration rules presented here are variants on the rules initially introduced by Berthelot [Ber85], and have been used in the context of stutter insensitive LTL model-checking [PP00, HP06].

This section provides an empirical study of the applicability of the techniques presented in this paper to LTL properties found in the literature. To achieve this we explored several LTL benchmarks [EH00, SB00, DAC98, HJM⁺21, KBG⁺21]. Some work [EH00, SB00] summarizes the typical properties that users express in LTL. The formulae of this benchmark have been extracted directly from the literature. Dwyer et al. [DAC98] propose property specification patterns, expressed in several logics including LTL. These patterns have been extracted by analysing 447 formulae coming from real world projects. The RERS challenge [HJM⁺21] presents generated formulae inspired from real world reactive systems. The MCC [KBG⁺21] benchmark establishes a huge database of $45152$ LTL formulae in the form of $1411$ Petri net models coming from $114$ sources with $32$ random LTL formulae for each one. These formulae use up to $5$ state-based atomic propositions (e.g. "$m(p0)+m(p1)>2$" or "$t1$ is fireable"), limit the nesting depth of temporal operators to $5$ and are filtered by the organizers in order to be non trivial. Since these formulae come with a concrete system we were able to use this benchmark to also provide performance results for our approach in Section 4.2. We retained $43989$ model/formula pairs from this benchmark; the missing $1163$ were rejected due to parse limitations of our tool when the model size is excessive ($>10^{7}$ transitions). This set of roughly $2200$ formulae exhibiting real patterns and $44,000$ random ones lets us evaluate if the fragment of LTL that we consider is common in practice. Table 1 summarizes, for each benchmark, the number and percentage of formulae that are either stuttering insensitive, lengthening insensitive, or shortening insensitive. The sum of both shortening and lengthening formulae represents more than one third (and up to 60 percent) of the formulae of these benchmarks.

Concerning the polarity, although lengthening insensitive formulae seem to appear more frequently, most of these benchmarks actually contain each formula in both positive and negative forms (we retained only one) so that the summed percentage might be more relevant as a metric since lengthening insensitivity of $\varphi$ is equivalent to shortening insensitivity of $\lnot\varphi$. Analysis of the human generated Dwyer patterns [DAC98] reveals that shortening/lengthening insensitive formulae mostly come from the patterns precedence chain, response chain and constrained chain. These properties specify causal relation between events, which are observable as causal relations between observably different states (that might be required to strictly follow each other), but this causality chain is not impacted by non observable events.

Benchmark Setup. Among the LTL benchmarks presented in Table 1, we opted for the MCC benchmark to evaluate the techniques presented in this paper. This benchmark seems relevant since (1) it contains both academic and industrial models, (2) it has a huge set of (random) formulae and (3) includes models so that we could measure the effect of the approach in a model-checking setting. The model-checking competition (MCC) is an annual event in its $10^{th}$ edition in 2021 where competing tools are evaluated on a large benchmark. We use the formulae and models from the latest $2021$ edition of the contest, where Tapaal [DJJ⁺12] was awarded the gold medal and ITS-Tools  [Thi15] was silver in the LTL category of the contest. We evaluate both of these tools in the following performance measures, showing that our strategy is agnostic to the back-end analysis engine. Our experimental setup consists in two steps.

1. (1)

   Parse the model and formula pair, and analyze the sensitivity of the formula. When the formula is shortening or lengthening insensitive (but not both) output two model/formula pairs: reduced and original. The “original” version does also benefit from structural simplification rules (e.g. removing redundant places and transitions, implicit places that are always sufficiently marked to fire related transitions…), but we apply only rules that are compatible with full LTL (in particular not enabling agglomeration rules). The “reduced” version additionally benefits from rules that are reductions at the language level, in the sense of Definition 2.4. These rules mainly include pre and post agglomeration, that also can enable even more structural simplification rules, since we iterate all applicable reduction rules to a fixed point. The original and reduced model/formula pairs that result from this procedure are then exported in the same format the contest uses. This step was implemented within ITS-tools.

2. (2)

   Run an MCC compatible tool on both the reduced and original versions of each model/formula pair and record the time performance and the verdict.

For the first step, using Spot [MD15], we detect that a formula is either shortening or lengthening insensitive for 99.81% of formulae in less than 1 second. After this analysis, we obtain 12 227 model/formula pairs where the formula is either shortening insensitive or lengthening insensitive (but not both). Among these pairs, in $3005$ cases (24.6%) none of the structural reduction rules we use were applicable. For more details on the precise structural reductions, see the companion artifact paper [TMRPAP24]. Since our strategy does not improve such cases, we retain the remaining 9 222 (75.4%) model/formula pairs in the performance plots of Figure 4. We measured that on average 34.19% of the places and 32.69% of the transitions of the models were discarded by reduction rules with respect to the “original” model, though the spread is high as there are models that are almost fully reducible and some that are barely so. Application of reduction rules is in complexity related to the size of the structure of the net and takes less than 20 seconds to compute in 95.5% of the models. We are able to treat $9222$ examples (21% of the original $43989$ model/formula pairs of the MCC) using reductions. All these formulae until now could not be handled using reduction techniques.

For the second step, we measured the solution time for both reduced and original model/formula pairs using the two best tools of the MCC’2021 contest. A full tool using our strategy might optimistically first run on the reduced model/formula pair hoping for a definitive answer, but we recommend the use of a portfolio approach where the first definitive answer is kept. In these experiments we neutrally measured the time for taking a semi-decision on the reduced model vs. the time for taking a (complete) decision on the original model. We then classify the results into two sets, decidable instances are shown on the left of Fig. 4 and instances that are not decidable (by our procedure) are on the right. On “decidable instances” our semi-decision procedure could have concluded reliably because the system satisfies the formula and the property is shortening insensitive, or the system does not satisfy the formula and the property is lengthening insensitive. Non decidable instances shown on the right are those where the verdict on the reduced model is not to be trusted (or both the original and reduced procedures timed out).

With this workflow we show that our approach is generic and can be easily implemented on top of any MCC compatible model-checking tool. All experiments were run with a 950 seconds timeout (close to 15 minutes, which is generous when the contest offers 1 hour for 16 properties). We used a heterogeneous cluster of machines with four cores allocated to each experiment, and ensured that experiments concerning reduced and original versions of a given model/formula are comparable (by running them on the same architecture). To help reproducibility of these experiments, a software artifact is presented in [TMRPAP24], and available from the CodeOcean platform https://doi.org/10.24433/CO.6846969.v1.

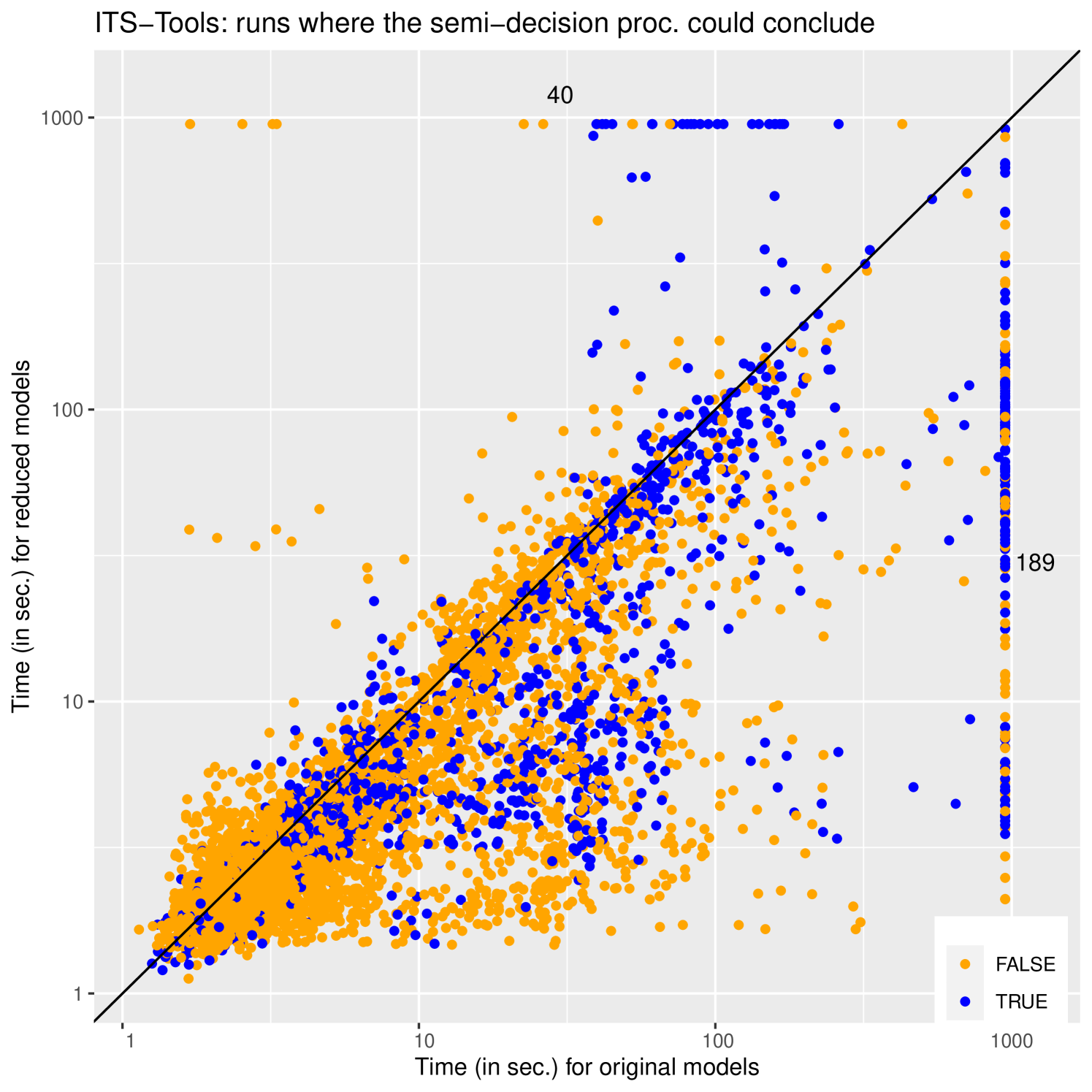
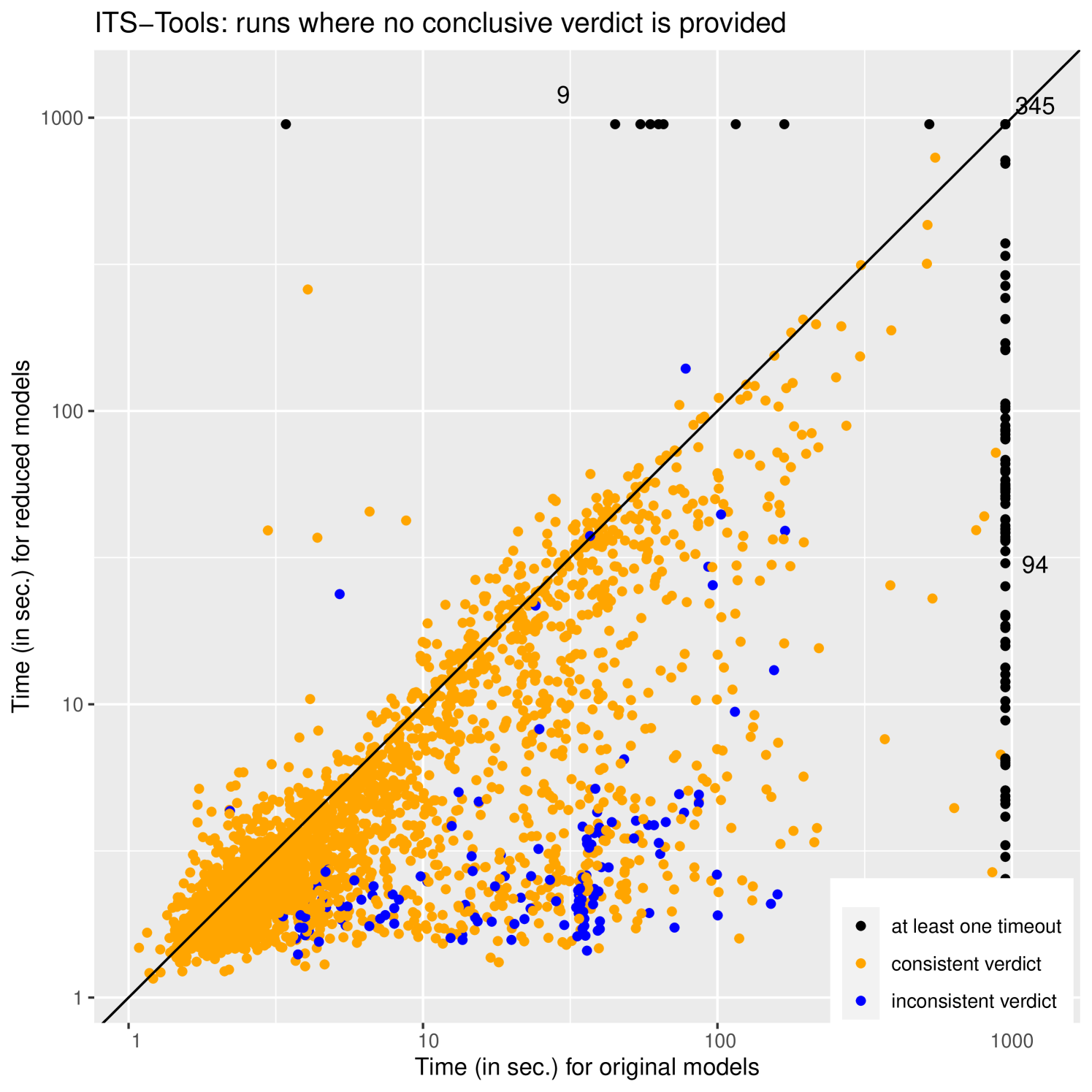
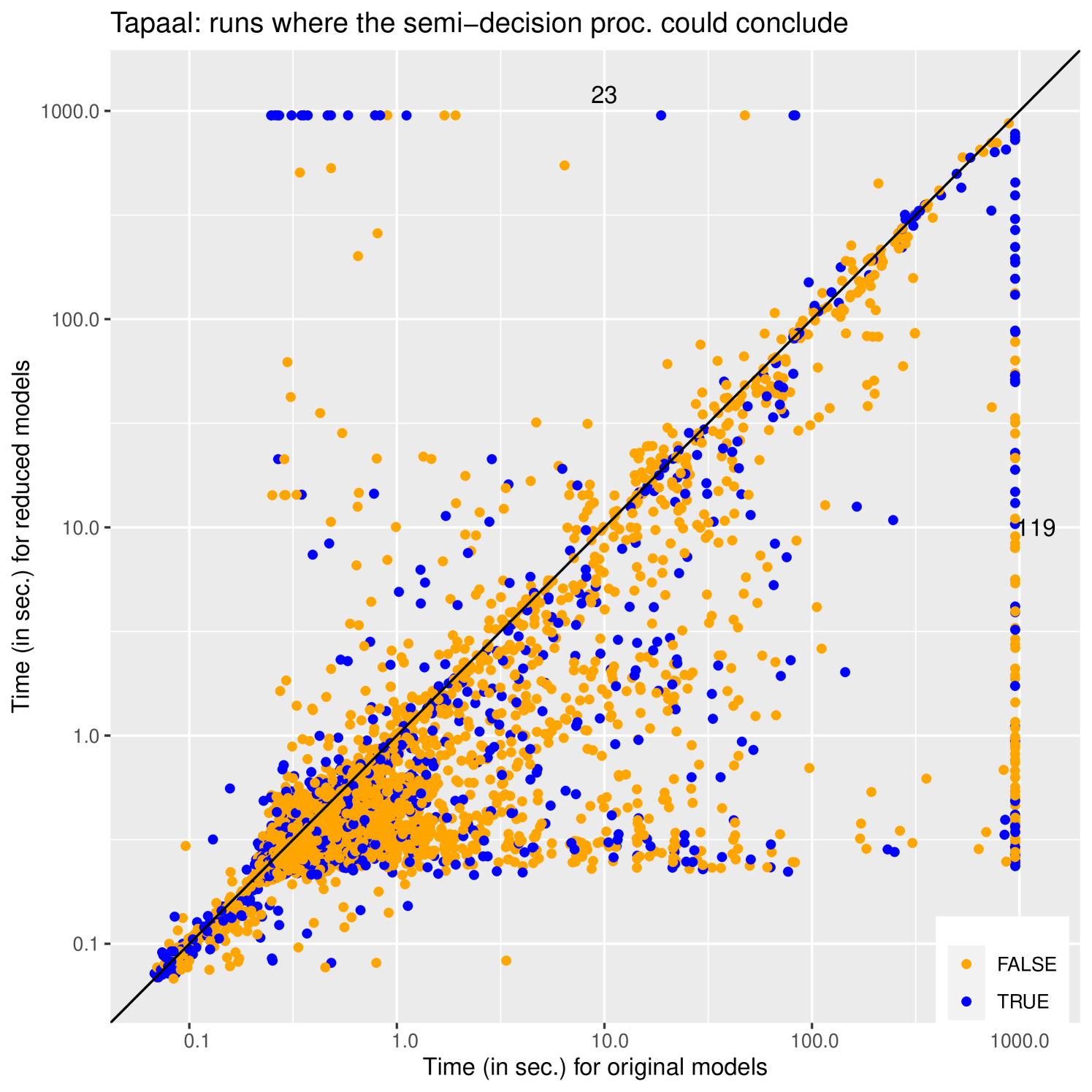
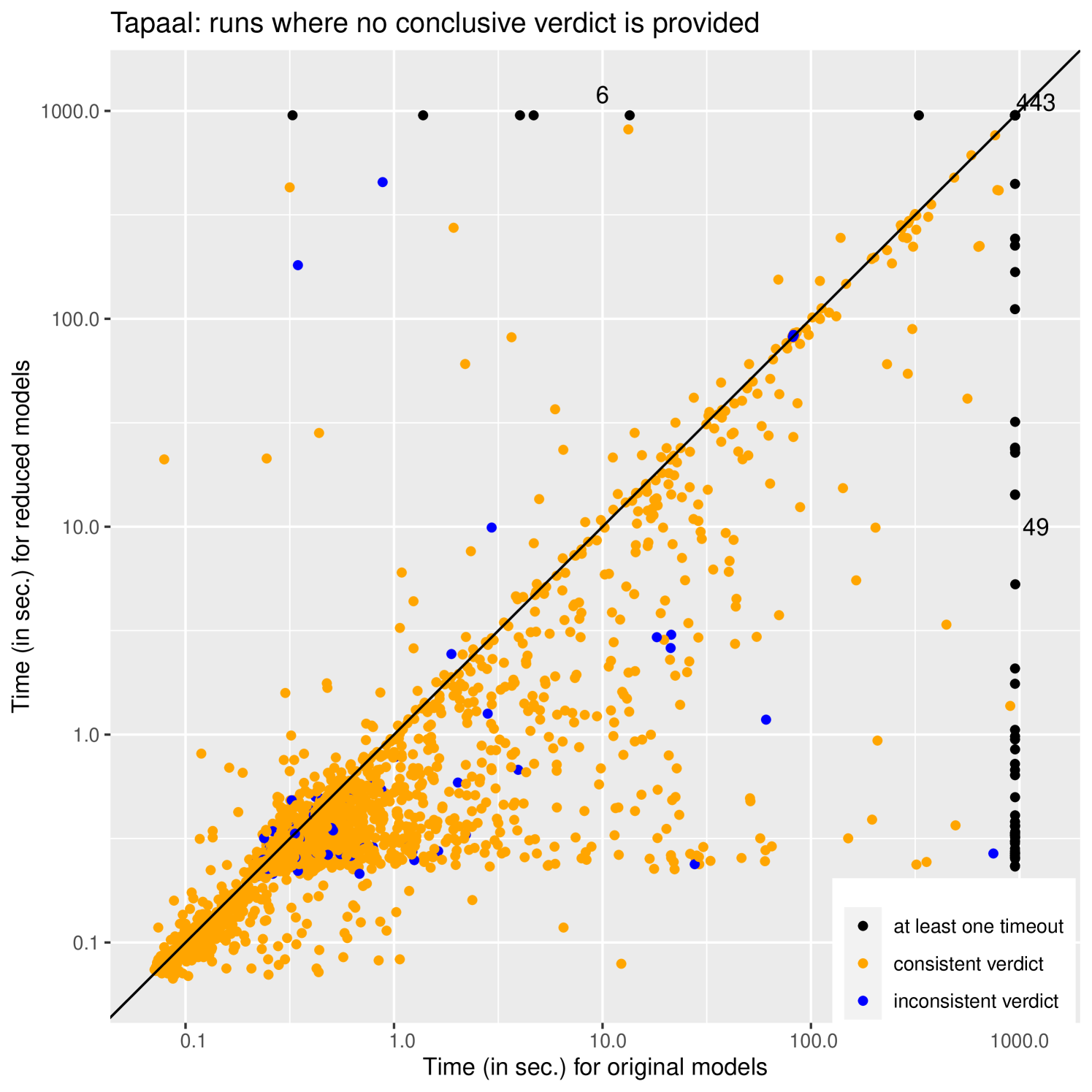
Figure 4 presents the results of these experiments. The results are all presented as log-log scatter plots opposing a run on the original to a run on the reduced model/formula pair. Each dot represents an experiment on a model/formula pair; a dot below the diagonal indicates that the reduced version was faster to solve, while a point above it indicates a case where the reduced model actually took longer to solve than the original (fortunately there are relatively few)²²2An example found in the benchmark is a formula requiring $XXXGp$, original system has no states satisfying $p$ 3 steps from initial state, but the reduced model does; and it takes a very long sequence of steps to reinvalidate $p$. Points that timeout for one (or both) of the approaches are plotted on the line at 950 seconds, we also indicate the number of points that are in this line (or corner) next to it.

The plots on the left (a) and (c) correspond to “decidable instances” while those on the right are not decidable by our procedure. The two plots on the top correspond to the performance of ITS-tools, while those on the bottom give the results with Tapaal. The general form of the results with both tools is quite similar confirming that our strategy is indeed responsible for the measured gains in performance and that they are reproducible. Reduced problems are generally easier to solve than the original. This gain is in the best case exponential as is visible through the existence of spread of points reaching out horizontally in this log-log space (particularly on the Tapaal plots).

The colors on the decidable instances reflect whether the verdict was true or false. For false properties a counter-example was found by both procedures interrupting the search, and while the search space of a reduced model is a priori smaller, heuristics and even luck can play a role in finding a counter-example early. True answers on the other hand generally require a full exploration of the state space so that the reductions should play a major role in reducing the complexity of model-checking. The existence of True answers where the reduction fails is surprising at first, but a smaller Kripke structure does not necessarily induce a smaller product as happens sometimes in this large benchmark (and in other reduction techniques such as stubborn sets [Val90]). On the other hand the points aligned to the right of the plots a) and c) (189 for ITS-tools and 119 for Tapaal) correspond to cases where our procedure improved these state of the art tools, allowing one to reach a conclusion when the original method fails.

The plots on the right use orange to denote cases where the verdict on the reduced and original models were the same; on these points the procedures had comparable behaviors (either exploring a whole state space or exhibiting a counter-example). The blue color denotes points where the two procedures disagree, with several blue points above the diagonal reflecting cases where the reduced procedure explored the whole state space and thought the property was true while the original procedure found a counter-example (this is the worst case). Surprisingly, even though on these non decidable plots b) and d) our procedure should not be trusted, it mostly agrees (in 95% of the cases) with the decision reached on the original.

Out of the 9222 experiments in total, for ITS-tools 5901 runs reached a trusted decision (64 %), 2927 instances reached an untrusted verdict (32 %), and the reduced procedure timed out in 394 instances (4 %). Tapaal reached a trusted decision in 5866 instances (64 %), 2884 instances reached an untrusted verdict (31 %), and the reduced procedure timed out in 472 instances (5 %). On this benchmark of formulae we thus reached a trusted decision in almost two thirds of the cases using the reduced procedure.

The idea is to partition the language of the (negation of the) property into four parts: the stutter insensitive part, the pure shortening insensitive part, the pure lengthening insensitive part, and the pure fully length sensitive part. This is a partition of the language, hence the “pure” qualifier indicates that there is no overlap, e.g. the pure shortening insensitive part does not contain any word of the stutter insensitive part of the original language.

Given this partition, we can use the most efficient available procedure to check emptiness of the product of the system with each part. For the first three parts in particular, we can work with a reduction of the system. The stutter insensitive part benefits from a full decision procedure when working with the reduction, and the partly length insensitive parts can use the semi-decision procedure of Theorem 1.

Length-sensitive partition of a language.

Given a language $\mathscr{L}$, we define:

• •

  The stutter insensitive part of $\mathscr{L}$ noted $SI^{\pm}(\mathscr{L})$ is defined as the largest subset of $\mathscr{L}$ that is stutter insensitive. More precisely $\forall r\in\mathscr{L}$,

  $$r\in SI^{\pm}(\mathscr{L})\Leftrightarrow(\forall r^{\prime}\in\Sigma^{\omega},r^{\prime}{\rm Phys.~Rev.~E}r\lor r{\rm Phys.~Rev.~E}r^{\prime}\Rightarrow r^{\prime}\in\mathscr{L})$$

• •

  The pure shortening insensitive part of $\mathscr{L}$ noted $SI^{-}(\mathscr{L})$ is the largest subset of $\mathscr{L}$ that is shortening insensitive but does not intersect with $SI^{\pm}(\mathscr{L})$. More precisely $\forall r\in\mathscr{L}$

  $$r\in SI^{-}(\mathscr{L})\Leftrightarrow\left\{\begin{array}[]{l}\forall r^{\prime}\in\Sigma^{\omega},r^{\prime}{\rm Phys.~Rev.~E}r\Rightarrow r^{\prime}\in\mathscr{L}\\ \exists r^{\prime\prime}\in\Sigma^{\omega}\setminus\mathscr{L},r{\rm Phys.~Rev.~E}r^{\prime\prime}\end{array}\right.$$

• •

  The pure lengthening insensitive part of $\mathscr{L}$ noted $SI^{+}(\mathscr{L})$ is the largest subset of $\mathscr{L}$ that is lengthening insensitive but does not intersect with $SI^{\pm}(\mathscr{L})$. More precisely $\forall r\in\mathscr{L}$

  $$r\in SI^{+}(\mathscr{L})\Leftrightarrow\left\{\begin{array}[]{l}\forall r^{\prime}\in\Sigma^{\omega},r{\rm Phys.~Rev.~E}r^{\prime}\Rightarrow r^{\prime}\in\mathscr{L}\\ \exists r^{\prime\prime}\in\Sigma^{\omega}\setminus\mathscr{L},r^{\prime\prime}{\rm Phys.~Rev.~E}r\end{array}\right.$$

• •

  The pure fully length sensitive part of $\mathscr{L}$ noted $SS(\mathscr{L})$ is the largest subset of $\mathscr{L}$ that is shortening and lengthening sensitive but does not intersect with the previous parts. More precisely $\forall r\in\mathscr{L}$

  $$r\in SS(\mathscr{L})\Leftrightarrow\left\{\begin{array}[]{l}\exists r^{\prime}\in\Sigma^{\omega}\setminus\mathscr{L},r{\rm Phys.~Rev.~E}r^{\prime}\\ \exists r^{\prime\prime}\in\Sigma^{\omega}\setminus\mathscr{L},r^{\prime\prime}{\rm Phys.~Rev.~E}r\end{array}\right.$$

To compute this partition when the language $\mathscr{L}$ is represented by a Buchi automaton $A$, we can reuse the closure ($cl$) and self-loopization ($sl$) syntactic transformations of an automaton introduced in Section 3.3.

Computing the length-sensitive partition of a language.

Let $A$ designate a Büchi automaton recognizing language $\mathscr{L}$.

• •

  Let $B=sl(cl(A))$, let $C=B\otimes\bar{A}$, let $D=sl(cl(C))$, then $SI^{\pm}(A)=A\otimes\overline{D}$

• •

  Let $A^{\prime}=A\otimes\overline{SI(A)}$,

  • –

    Let $B^{-}=cl(A^{\prime})$, let $C^{-}=B^{-}\otimes\overline{A^{\prime}}$, let $D^{-}=sl(C^{-})$, then $SI^{-}(A)=A^{\prime}\otimes\overline{D^{-}}$.

  • –

    Let $B^{+}=sl(A^{\prime})$, let $C^{+}=B^{+}\otimes\overline{A^{\prime}}$, let $D^{+}=cl(C^{+})$, then $SI^{+}(A)=A^{\prime}\otimes\overline{D^{+}}$.

• •

  Finally, $SS(A)=A\otimes\overline{SI(A)}\otimes\overline{SI^{-}(A)}\otimes\overline{SI^{+}(A)}$

The automaton produced in each case matches Definition 5.1, e.g. $\mathscr{L}(SI^{\pm}(A))=SI^{\pm}(\mathscr{L})$ when $A$ recognizes language $\mathscr{L}$. The reasoning behind these definitions is illustrated in Figure 5. For each equivalence class, we simply reason on three distinct but comparable words $r,r^{\prime}$ and $r^{\prime\prime}$ such that $r{\rm Phys.~Rev.~E}r^{\prime}{\rm Phys.~Rev.~E}r^{\prime\prime}$. The question for each of these words is whether they belong to the language of $A$ or not. This gives us $2^{3}=8$ cases to consider, but some cases are redundant, e.g. the case where $r$ and $r^{\prime}$ belong to $A$ but $r^{\prime\prime}$ doesn’t is homogeneous to the case where $r$ belongs to $A$ but neither $r^{\prime}$ nor $r^{\prime\prime}$ do. Figure 5 thus only represents the $6$ significantly different cases for a given equivalence class of runs.

It can be noted that it is quite easy to adapt the steps to compute less strict versions of these “partitions”, e.g. extracting the sublanguage $SI^{\pm}\cup SI^{-}$ can be done using equations for computing $SI^{-}$ (see Fig. 5) but substituting $A$ for $A^{\prime}$ in all equations. This involves fewer complement operations on automata.

Unfortunately, computing the complement of an automaton $A$ is worst case exponential in the size of $A$, and the procedure described here uses several complementations to implement set difference: $\mathscr{L}(A)\setminus\mathscr{L}(B)=\mathscr{L}(A\otimes\bar{B})$. At least when the automaton $A_{\varphi}$ comes from an LTL property, we can compute $A_{\lnot\varphi}$ instead of computing the complement $\bar{A_{\varphi}}$. The other complement operations in our procedure seem unavoidable at this stage however. Despite this high worst case complexity, the complexity of model-checking as a whole is usually dominated by the size of the Kripke structure, which can be substantially reduced by structural reductions. Hence a model-checking procedure using the partition and structural reductions where possible might still be competitive with the default procedure that cannot use structural reductions at all unless the property is fully stutter insensitive.

As preliminary experimentation we computed these partitions on the LTL formulae of Section 4.1 ³³3The total number of formulae in the MCC dataset do not match those in Table 1 since this experiment was run with a more recent version of ITS-Tools (release $2022-11$) that can parse more model/formula pairs of this benchmark ($44252$ up from $43989$ out of $45152$ model/formula pairs in the full MCC data set).. Results are presented in Table 2.