Structure and classification results for the $\infty$ -elastica problem

Roger Moser¹¹1Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK. E-mail: r.moser@bath.ac.uk

Abstract

Consider the following variational problem: among all curves in $\mathbb{R}^{n}$ of fixed length with prescribed end points and prescribed tangents at the end points, minimise the $L^{\infty}$ -norm of the curvature. We show that the solutions of this problem, and of a generalised version, are characterised by a system of differential equations. Furthermore, we have a lot of information about the structure of solutions, which allows a classification.

1 Introduction

Variational problems involving the curvature of a curve $\Gamma\subseteq\mathbb{R}^{n}$ have a long history. This is true especially for the Euler elastica problem, which is to minimise the quantity

\int_{\Gamma}\kappa^{2}\,ds,

where $\kappa$ is the curvature of $\Gamma$ . This functional may be regarded as a model for the stored elastic energy of a thin rod and its theory can be traced back to Jacob and Daniel Bernoulli and to Euler [9, 24], but the problem has also been studied in more modern times [6, 17, 18, 20]. An obvious generalisation is the $p$ -elastica problem for $p\in[1,\infty)$ , which corresponds to the quantity $\int_{\Gamma}\kappa^{p}\,ds$ . This functional has been proposed for applications in image processing [22] and has also been studied in its own right [11, 10].

While the step from elastica to $p$ -elastica amounts to replacing an $L^{2}$ -norm by an $L^{p}$ -norm, in this paper we consider curves minimising the $L^{\infty}$ -norm of the curvature. Thus, roughly speaking, we wish to minimise the maximum curvature. This quantity may not directly appear as the energy of a physical problem, but questions related to it are of fundamental geometric interest and may appear in design problems as well. In effect we ask, how much does a curve have to be bent in order to satisfy certain constraints? We consider constraints in the form of a fixed length combined with boundary conditions, but other types are conceivable as well and may admit a similar theory.

To my knowledge, the $\infty$ -elastica problem has not been studied before. The step from $p<\infty$ to $p=\infty$ changes the nature of the problem significantly. In particular, we have a functional that is not differentiable in any meaningful sense and the usual steps to find an Euler-Lagrange equation do no longer work. While we still have the notion of a minimiser, there is no obvious way to define critical points. In this paper, we propose another concept instead, derive a system of equations that can be thought of as Euler-Lagrange equations, and finally analyse and classify the solutions.

In addition to the standard $L^{\infty}$ -norm, the theory in this paper allows a weighted version as well. We therefore consider the following set-up of the problem. Let $n\in\mathbb{N}$ with $n\geq 2$ . We fix a number $\ell>0$ , which is the prescribed length of the curves considered. We also fix a weight function $\alpha\colon[0,\ell]\to(0,\infty)$ , which should be of bounded variation and such that $1/\alpha$ is bounded. We represent curves in $\mathbb{R}^{n}$ by parametrisations $\gamma\colon[0,\ell]\to\mathbb{R}^{n}$ by arc length for the moment, so we assume that $|\gamma^{\prime}|\equiv 1$ in $[0,\ell]$ . The curvature is then $\kappa=|\gamma^{\prime\prime}|$ . As we wish to consider its (weighted) $L^{\infty}$ -norm, we assume that $\gamma$ belongs to the Sobolev space $W^{2,\infty}((0,\ell);\mathbb{R}^{n})$ and we define the functional

\mathcal{K}_{\alpha}(\gamma)=\operatorname*{ess\,sup}_{[0,\ell]}\alpha|\gamma^{\prime\prime}|.

We consider a problem for curves with prescribed end points and prescribed tangent vectors at these end points. Thus for fixed $a_{1},a_{2}\in\mathbb{R}^{n}$ and fixed $T_{1},T_{2}\in S^{n-1}=\left\{x\in\mathbb{R}^{n}\colon|x|=1\right\}$ , we require that

\gamma(0)=a_{1},\quad\gamma(\ell)=a_{2},\quad\gamma^{\prime}(0)=T_{1},\quad\text{and}\quad\gamma^{\prime}(\ell)=T_{2}.

(1)

Let $\mathcal{G}$ denote the set of all $\gamma\in W^{2,\infty}((0,\ell);\mathbb{R}^{n})$ with $|\gamma^{\prime}|\equiv 1$ in $[0,\ell]$ satisfying (1). We are particularly interested in minimisers of $\mathcal{K}_{\alpha}$ in $\mathcal{G}$ , but the observations in this paper suggest to consider the following weaker notion as well.

Definition 1 ( $\infty$ -elastica).

Suppose that $\gamma\in\mathcal{G}$ . We say that $\gamma$ is an $\infty$ -elastica if there exists $M\in\mathbb{R}$ such that for every $\tilde{\gamma}\in\mathcal{G}$ , the inequality

\mathcal{K}_{\alpha}(\gamma)\leq\mathcal{K}_{\alpha}(\tilde{\gamma})+\frac{M}{2}\int_{0}^{\ell}|\tilde{\gamma}^{\prime}-\gamma^{\prime}|^{2}\,ds

holds true.

It turns out that this condition is equivalent to a system of differential equations. Connections between a variational problem and differential equations are of course quite common, but for a functional that is not differentiable, such a strong correspondence is surprising. In order to write down the system concisely, we introduce some notation: if $V,W\in\mathbb{R}^{n}$ , then $\operatorname{proj}_{V,W}^{\perp}$ denotes the orthogonal projection onto the orthogonal complement of the linear subspace of $\mathbb{R}^{n}$ spanned by $V$ and $W$ .

Theorem 2 (Characterisation by differential equations).

Suppose that $\gamma\in\mathcal{G}$ , and let $T=\gamma^{\prime}$ and $k=\mathcal{K}_{\alpha}(\gamma)$ . Then $\gamma$ is an $\infty$ -elastica if, and only if, there exist $\lambda\in S^{n-1}$ and $g\in W^{1,\infty}(0,\ell)\setminus\{0\}$ with $g\geq 0$ such that the equations

	$\displaystyle g((\alpha T^{\prime})^{\prime}+k^{2}T/\alpha)$	$\displaystyle=k^{2}\operatorname{proj}_{T,T^{\prime}}^{\perp}(\lambda),$		(2)
	$\displaystyle g^{\prime}$	$\displaystyle=\alpha\lambda\cdot T^{\prime}$		(3)

hold weakly in $(0,\ell)$ .

It is clear how to interpret weak solutions of (3). In order to make sense of (2), we use that fact that $g$ , being in $W^{1,\infty}(0,\ell)$ , has a weak derivative. Thus (2) is satisfied weakly if

\int_{0}^{\ell}\left(g\alpha T^{\prime}\cdot\xi^{\prime}+g^{\prime}\alpha T^{\prime}\cdot\xi-gk^{2}\alpha^{-1}T\cdot\xi+k^{2}\operatorname{proj}_{T,T^{\prime}}^{\perp}(\lambda)\cdot\xi\right)\,ds=0

for all $\xi\in C_{0}^{\infty}((0,\ell);\mathbb{R}^{n})$ .

If we add another condition, we obtain a criterion for minimisers of $\mathcal{K}_{\alpha}$ , too.

Theorem 3 (Sufficient condition for minimisers).

Let $\gamma\in\mathcal{G}$ and $T=\gamma^{\prime}$ . Suppose that there exist $\lambda\in S^{n-1}$ and $g\in W^{1,\infty}(0,\ell)\setminus\{0\}$ such that (2) and (3) are satisfied weakly in $(0,\ell)$ , and such that $0\leq g\leq-\alpha\lambda\cdot T$ in $[0,\ell]$ . Then $\gamma$ minimises $\mathcal{K}_{\alpha}$ subject to the boundary conditions (1).

This condition is sufficient but not necessary, as shown in Example 21 below.

It is worthwhile to consider the case $\alpha\equiv 1$ separately, as the system (2), (3) can then be written as a single equation, albeit with an additional parameter. This is because in this case, the right-hand side of (3) is the derivative of $\lambda\cdot T$ and the equation implies that there exists $\eta\in\mathbb{R}$ such that $g=\lambda\cdot T-\eta$ . Thus

T^{\prime\prime}+k^{2}T=\frac{k^{2}\operatorname{proj}_{T,T^{\prime}}^{\perp}(\lambda)}{\lambda\cdot T-\eta},

(4)

at least where $\lambda\cdot T\neq\eta$ . The left-hand side is a geometric quantity related to the torsion of the corresponding curve if $n=3$ . Indeed, it can be seen, with arguments as in Proposition 12 below, that the torsion is $\pm k^{-1}|T^{\prime\prime}+k^{2}T|$ .

Analysing the system (2), (3), we obtain good information about the structure of $\infty$ -elasticas as well, which allows a classification.

Theorem 4 (Structure and classification).

Suppose that $\gamma\in\mathcal{G}$ and let $T=\gamma^{\prime}$ and $k=\mathcal{K}_{\alpha}(\gamma)$ . Then $\gamma$ is an $\infty$ -elastica if, and only if, there exists $\lambda\in S^{n-1}$ such that at least one of the following statements holds true.

(i)
There exists a line $\mathcal{L}\subseteq\mathbb{R}^{n}$ parallel to $\lambda$ and there exist finitely many intervals $J_{1},\dotsc,J_{N}\subseteq[0,\ell]$ , pairwise disjoint and open relative to $[0,\ell]$ , such that $\gamma^{-1}(\mathcal{L})=[0,\ell]\setminus\bigcup_{i=1}^{N}J_{i}$ and such that for $i=1,\dotsc,N$ ,
- •
  
  $\gamma(\overline{J}_{i})\cup\mathcal{L}$ is contained in a plane,
- •
  
  $\alpha\gamma^{\prime\prime}$ is continuous with $\alpha|\gamma^{\prime\prime}|\equiv k$ in $J_{i}$ , and
- •
  
  for any $s_{0}\in\overline{I}_{i}\setminus I_{i}$ , there exists $\delta>0$ such that $\lambda\cdot\gamma^{\prime\prime}>0$ in $(s_{0},s_{0}+\delta)\cap I_{i}$ and $\lambda\cdot\gamma^{\prime\prime}<0$ in $(s_{0}-\delta,s_{0})\cap I_{i}$ .
(ii)

There is a three-dimensional affine subspace of $\mathbb{R}^{n}$ that contains $\gamma([0,\ell])$ . Furthermore, $\alpha\gamma^{\prime\prime}\in W^{1,\infty}((0,\ell);\mathbb{R}^{n})$ with $\alpha|\gamma^{\prime\prime}|\equiv k$ and there exists $g\in W^{2,\infty}(0,\ell)$ with $g>0$ such that (2) and (3) hold true almost everywhere.

To summarise, an $\infty$ -elastica is either a concatenation of two-dimensional curves or a single three-dimensional curve solving a certain system of differential equations. In the first case, we have additional conditions that determine the curves to a significant degree. For example, in the case $\alpha\equiv 1$ , it is readily seen that any planar $\infty$ -elastica comprises either

(a)

a circular arc, followed by several line segments and full circles of equal radius, followed by a circular arc (cf. Figure 1(a)), or
(b)

several circular arcs of equal length (apart from the first and the last) and radius but alternating sense of rotation (cf. Figure 1(b) and 1(c)).

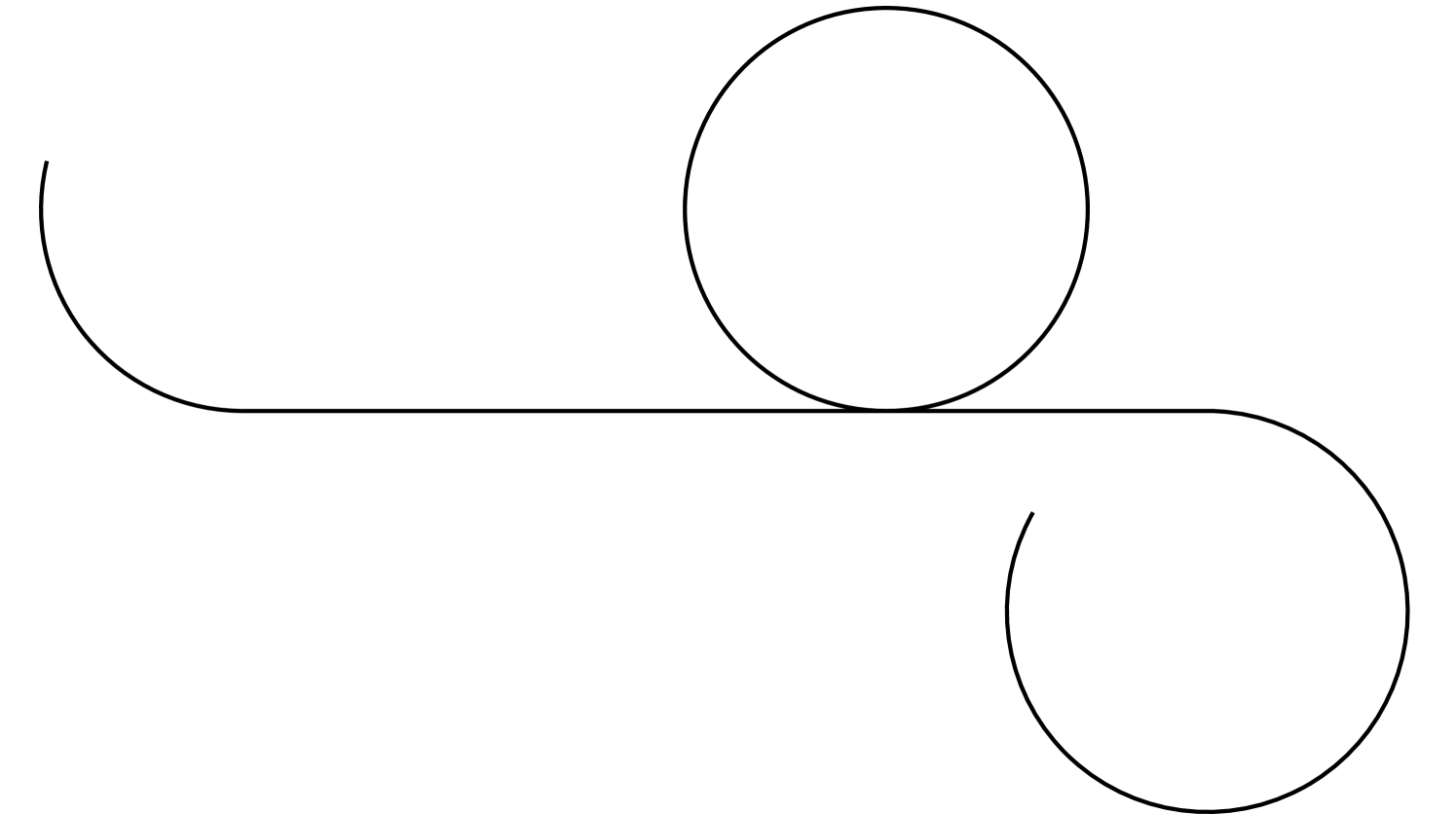
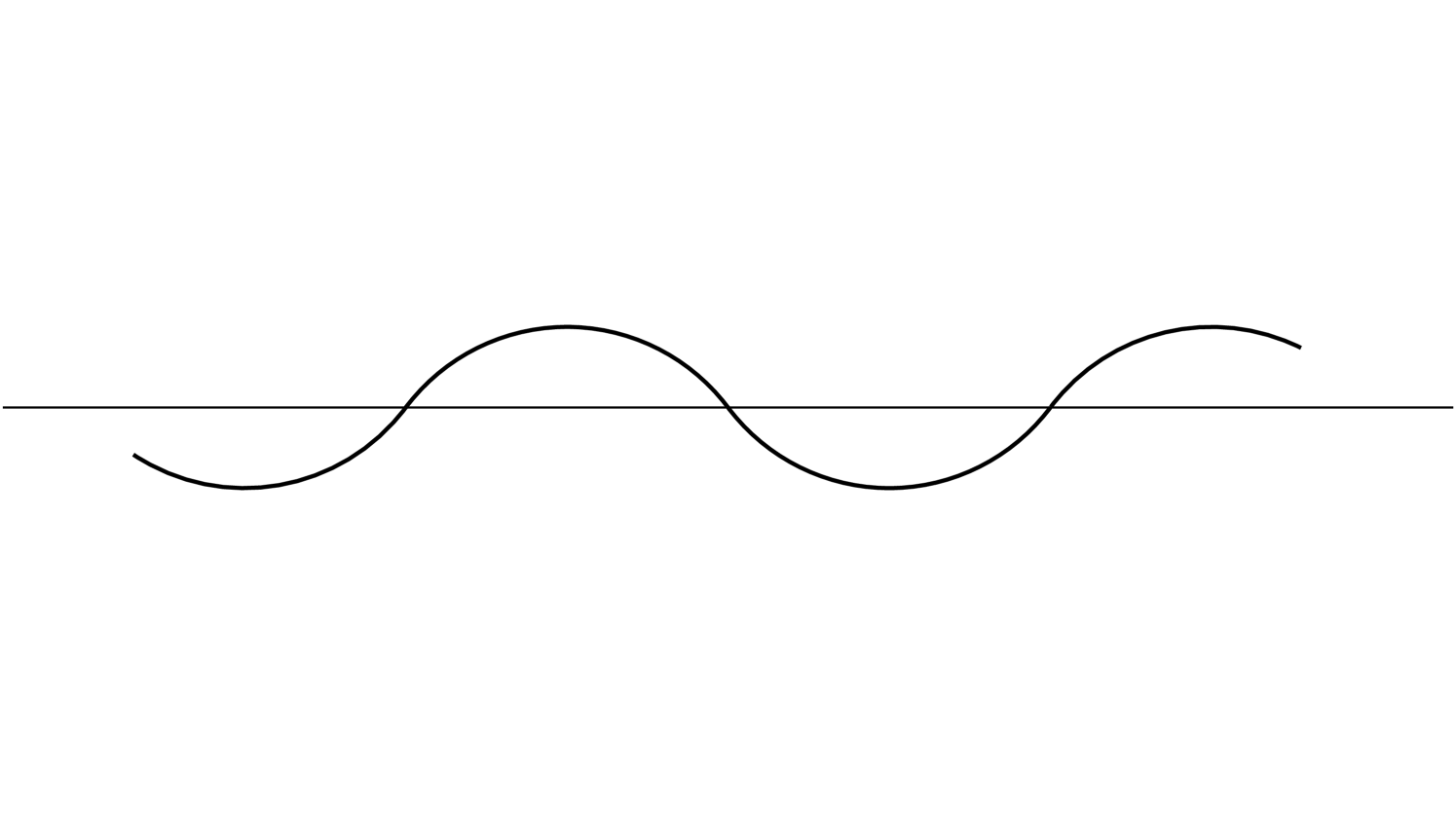
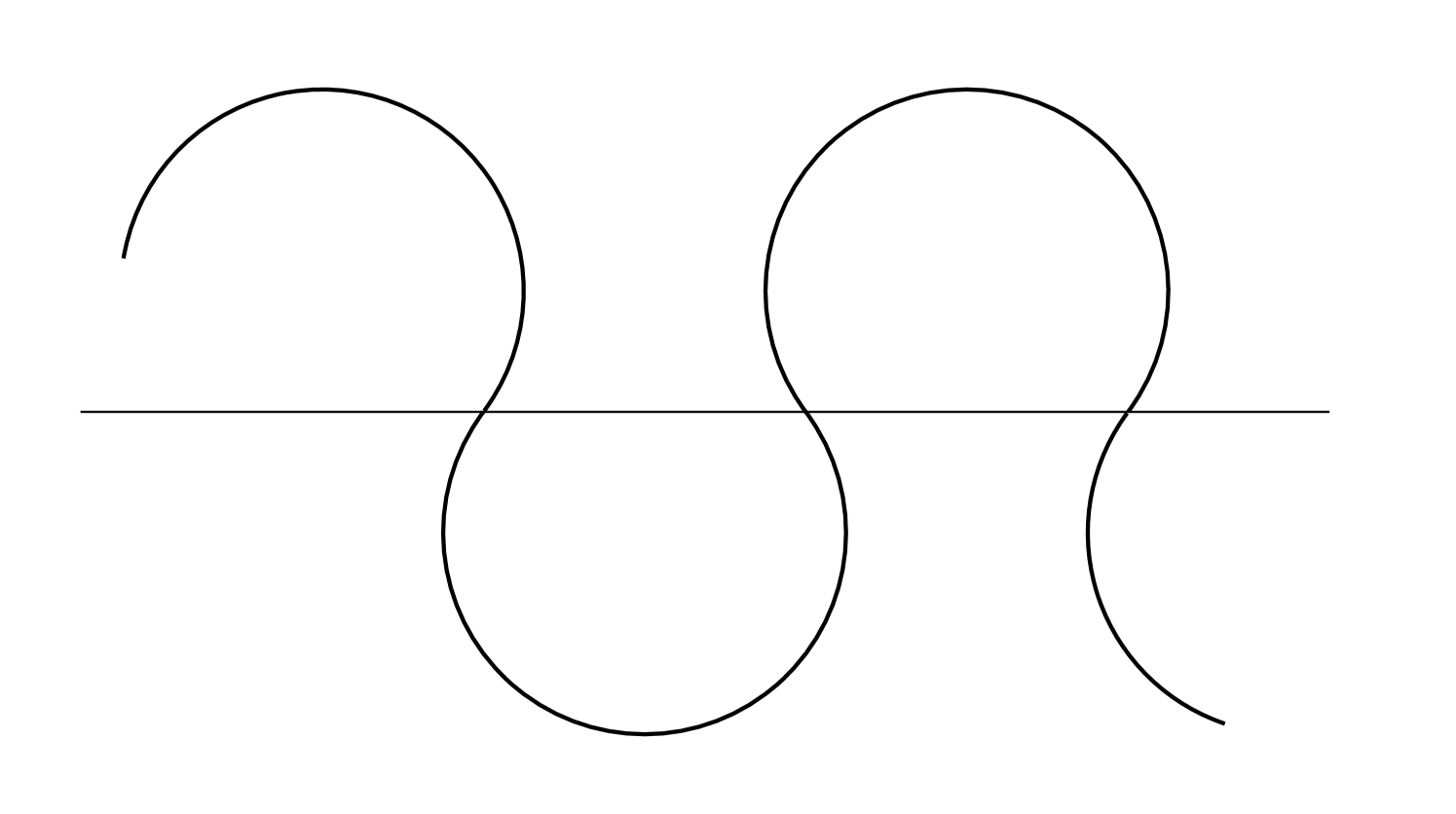
Curves of both types, with the additional restriction that they consist of at most three pieces, have been found by Dubins [8] as the solutions of a different variational problem: Dubins minimises the length of a planar curve subject to boundary conditions of the type (1) and subject to the constraint that the curvature should nowhere exceed a given number. This problem was previously considered by Markov [21] and is therefore known as the Markov-Dubins problem. Dubins calls the solutions $R$ -geodesics if $1/R$ is the maximum curvature permitted. A similar result has been proved by Sussmann [30] in dimension $n=3$ . Just as in Theorem 4, Sussmann finds two types of solutions: concatenations of circles and line segments on the one hand and three-dimensional curves, that he calls helicoidal arcs, on the other hand. The latter correspond to solutions of equation (4). Sussmann’s proof relies on a reformulation of the problem as an optimal control problem and on Pontryagin’s maximum principle. For the problem studied in this paper, such an approach seems to be unavailable.

It is no surprise that we obtain similar solutions, for the two problems are connected.

Proposition 5 ( $R$ -geodesics minimise $\mathcal{K}_{1}$ ).

Let $R>0$ . Suppose that $\gamma\colon[0,\ell]\to\mathbb{R}^{n}$ parametrises an $R$ -geodesic by arc length. Then $\gamma$ minimises $\mathcal{K}_{1}$ subject to its boundary data.

As a consequence, we obtain an alternative proof of Dubins’s and Sussmann’s main results. Theorem 4 will initially give less information in case i, but the proofs can then be completed with elementary arguments and some of Dubins’s lemmas. We give a sketch of these arguments in Section 7.

The Markov-Dubins problem, and variants thereof [25], have found applications in motion planning [19].

There is a connection to another classical problem. In 1925, Schmidt [27] studied open spacial curves of fixed length that minimise the length of the chord under the constraint that the curvature is bounded pointwise by a given function (that we identify with $1/\alpha$ ). He generalised a result of A. Schur [28], which in turn refines an unpublished result ascribed by both authors to Schwarz. Another proof of this result may be found in a book of Blaschke [5, §31], and a proof in English is given by S. S. Chern [7]. The solutions of this problem are obviously minimisers of $\mathcal{K}_{\alpha}$ , too, even under weaker boundary conditions. Schmidt concludes that any curve with shortest chord subject to his curvature constraint must be planar and convex. This can of course not be expected for the variational problem with boundary conditions (1) in general.

The strategy for the proofs of Theorem 2–4 is to first approximate the $L^{\infty}$ -norm of the curvature by $L^{p}$ -norms for $p<\infty$ and then let $p\to\infty$ . For $p<\infty$ , we obtain a similar variational problem, which gives rise to an Euler-Lagrange equation. When we pass to the limit $p\to\infty$ , the Euler-Lagrange equation is preserved in some form and eventually gives rise to the system (2), (3). We also obtain some information about the structure of solutions from the limit. A detailed analysis of the differential equations is also necessary for Theorem 4.

To my knowledge, this is the first study of the above variational problem in the literature, although, as already discussed, several related problems have been studied in significant detail. There is also extensive work on variational problems involving an $L^{\infty}$ -norm in general, going back to the work of Aronsson [1, 2, 3]. An introduction with many further references is given in a book by Katzourakis [12]. Higher order problems have been studied more recently as well [4, 23, 26, 15, 16, 13, 14], but there is a much smaller body of literature. An approximation by $L^{p}$ -norms, as in this paper, is common for variational problems in $L^{\infty}$ , but subsequently, most of the literature relies on methods and ideas quite different from what is used here. Nevertheless, our approach has previously been deployed, too [23, 26, 13, 14]. For comparison, the paper of Katzourakis and the author [13] studies functions $u\colon\Omega\to\mathbb{R}$ , for some domain $\Omega\subseteq\mathbb{R}^{n}$ , that minimise $\operatorname*{ess\,sup}_{x\in\Omega}|F(x,\Delta u(x))|$ for a given function $F$ under prescribed boundary data. The paper describes the structure of minimisers, derives a system of partial differential equations that characterises them, and proves that minimisers are unique.

For the problem studied here, it cannot be expected that minimisers are unique in general, and this is one of the reasons why the previous methods are insufficient. For example, if the boundary data are symmetric with respect to a reflection (for $n=2$ ) or rotation about a line (for $n>2$ ), but $\ell$ is too long to admit a straight line segment, then the symmetry of the problem automatically gives rise to multiple solutions. Therefore, if we use approximations to the variational problem, we will typically recover some solution in the limit, but not necessarily all possible solutions. We overcome this difficulty by adding another term that penalises the distance from a given solution. This is the main novelty in the first part of our analysis. The penalisation corresponds to the last term in the inequality of Definition 1, and thus, although initially introduced as a technical device, proves to be interesting in its own right, as it gives rise to a variational problem equivalent to the system of differential equations in Theorem 2.

The second part of our analysis, which leads to the proof of Theorem 4, is completely new. The underlying method may be restricted to this and similar problems, but our theory provides one of the first examples (the equally restrictive and more elementary theory of Katzourakis-Pryer [15, Section 8] being the only other example I am aware of), where a non-trivial second-order variational problem in $L^{\infty}$ can be solved exhaustively.

2 Reparametrisation and approximation

In this section, we prepare the ground for the proofs of Theorems 2–4. We first reformulate the problem by reparametrising the curves appropriately. Then we discuss an approximation of the $L^{\infty}$ -norm by $L^{p}$ -norms. We also add a penalisation term to the functionals, the purpose of which is to guarantee convergence to a given (rather than an arbitrary) solution of the problem as $p\to\infty$ . At the same time, we shift our main attention from a curve in $\mathbb{R}^{n}$ to its tangent vector field.

Recall that we previously considered parametrisations $\gamma\colon[0,\ell]\to\mathbb{R}^{n}$ by arc length satisfying the boundary conditions (1). From now on, a parametrisation with speed $\alpha$ is more convenient. Therefore, define

\psi(s)=\int_{0}^{s}\frac{d\sigma}{\alpha(\sigma)},\quad 0\leq s\leq\ell,

and $L=\psi(\ell)$ . Also consider the inverse $\phi=\psi^{-1}\colon[0,L]\to[0,\ell]$ and $\beta=\alpha\circ\phi$ . If $\gamma$ is a parametrisation by arc length, then the reparametrisation $c\colon[0,L]\to\mathbb{R}^{n}$ , given by $c(t)=\gamma(\phi(t))$ , satisfies $|c^{\prime}(t)|=\phi^{\prime}(t)=1/\psi^{\prime}(\phi(t))=\beta(t)$ .

We now consider the tangent vector field along $c$ , normalised to unit length. Thus let $\tau\colon[0,L]\to S^{n-1}$ be defined by $\tau(t)=c^{\prime}(t)/\beta(t)$ . (An equivalent definition is $\tau(t)=\gamma^{\prime}(\phi(t))$ .) Then (1) implies that

\tau(0)=T_{1}\quad\text{and}\quad\tau(L)=T_{2}.

(5)

Setting $a=a_{2}-a_{1}$ , we also obtain the condition

\int_{0}^{L}\beta(t)\tau(t)\,dt=a.

(6)

Conversely, if we have $\tau\in W^{1,\infty}((0,L);S^{n-1})$ satisfying (5) and (6), then $\gamma\in\mathcal{G}$ can be reconstructed from $\tau$ by

\gamma(s)=a_{1}+\int_{0}^{s}\tau(\psi(\sigma))\,d\sigma,\quad 0\leq s\leq\ell.

The functional $\mathcal{K}_{\alpha}$ can be written in terms of $\tau$ as follows:

\mathcal{K}_{\alpha}(\gamma)=\operatorname*{ess\,sup}|\tau^{\prime}|.

Hence in order to study the above problem, it suffices to consider $\tau$ and to study the functional

K_{\infty}(\tau)=\operatorname*{ess\,sup}|\tau^{\prime}|

under the boundary conditions (5) and the integral constraint (6). We note that $\gamma$ is an $\infty$ -elastica if, and only if, $\tau$ has the following property.

Definition 6.

Suppose that $\tau\in W^{1,\infty}((0,L);S^{n-1})$ satisfies the boundary conditions (5) and the constraint (6). We say that $\tau$ is a pseudo-minimiser of $K_{\infty}$ if there exists $m\in\mathbb{R}$ such that

K_{\infty}(\tau)\leq K_{\infty}(\tilde{\tau})+\frac{m}{2L}\int_{0}^{L}\beta|\tilde{\tau}-\tau|^{2}\,dt

for any other $\tilde{\tau}\in W^{1,\infty}((0,L);S^{n-1})$ satisfying (5) and (6).

One of the key tools for the proofs of Theorems 2–4 is an approximation of $K_{\infty}$ by

K_{p}(\tau)=\left(\frac{1}{L}\int_{0}^{L}|\tau^{\prime}|^{p}\,dt\right)^{1/p}

for $p\in[2,\infty)$ . We eventually consider the limit as $p\to\infty$ to recover $K_{\infty}$ . Furthermore, given $\tau_{0}\in W^{1,\infty}((0,L);S^{n-1})$ and $\mu\geq 0$ , we consider the functionals

J_{p}^{\mu}(\tau;\tau_{0})=K_{p}(\tau)+\frac{\mu}{2L}\int_{0}^{L}\beta|\tau-\tau_{0}|^{2}\,dt.

In the proofs of Theorems 2–4, we will assume that $\tau_{0}$ is a pseudo-minimiser of $K_{\infty}$ . Minimisers of $J_{p}^{\mu}({\mkern 2.0mu\cdot\mkern 2.0mu};\tau_{0})$ can then be found with the direct method, and the assumption will guarantee that they converge to $\tau_{0}$ as $p\to\infty$ . This will eventually allow some conclusions about $\tau_{0}$ . Indeed, the following preliminary observations are almost immediate from the structure of the variational problem.

Proposition 7.

Let $\mu>0$ and $\tau_{0}\in W^{1,\infty}((0,L);S^{n-1})$ be given. For every $p\in[2,\infty)$ , suppose that $\tau_{p}\in W^{1,p}((0,L);S^{n-1})$ is a minimiser of $J_{p}^{\mu}({\mkern 2.0mu\cdot\mkern 2.0mu};\tau_{0})$ subject to the constraints (5) and (6) and let $k_{p}=K_{p}(\tau_{p})$ .

Then there are Lagrange multipliers $\Lambda_{p}\in\mathbb{R}^{n}$ such that

\frac{d}{dt}\left(|\tau_{p}^{\prime}|^{p-2}\tau_{p}^{\prime}\right)+|\tau_{p}^{\prime}|^{p}\tau_{p}=k_{p}^{p-1}\beta\bigl{(}\Lambda_{p}-(\Lambda_{p}\cdot\tau_{p})\tau_{p}-\mu\tau_{0}+\mu(\tau_{0}\cdot\tau_{p})\tau_{p}\bigr{)}

(7)

weakly in $(0,L)$ .

2.

If $\tau_{0}$ satisfies (5) and (6) and is a pseudo-minimiser of $K_{\infty}$ , then there exists $\mu_{0}>0$ such that the following holds true. If $\mu\geq\mu_{0}$ , then $\tau_{p}\rightharpoonup\tau_{0}$ weakly in $W^{1,q}((0,L);\mathbb{R}^{n})$ for every $q<\infty$ and $k_{p}\to K_{\infty}(\tau_{0})$ as $p\to\infty$ .

Proof.

The Euler-Lagrange equation (7) is derived with standard computations. The only feature that is perhaps unusual is the constraint $\tau_{p}(t)\in S^{n-1}$ for $t\in[0,L]$ , but this sort of constraint is common in the theory of harmonic maps and it is explained, e.g., in a book by Simon [29] how to deal with it. We therefore omit the details in the proof of statement 1.

Next we note that by the choice of $\tau_{p}$ and by Hölder’s inequality, for any pair of numbers $p,q\in(1,\infty)$ with $p\leq q$ , we find the inequalities

J_{p}^{\mu}(\tau_{p};\tau_{0})\leq J_{p}^{\mu}(\tau_{q};\tau_{0})\leq J_{q}^{\mu}(\tau_{q};\tau_{0})\leq K_{q}(\tau_{0})\leq K_{\infty}(\tau_{0}).

(8)

So for any $q\in[2,\infty)$ , the one-parameter family $(\tau_{p})_{q\leq p<\infty}$ is bounded in $W^{1,q}((0,L);\mathbb{R}^{n})$ . Therefore, there exists a sequence $p_{i}\to\infty$ such that $\tau_{p_{i}}$ converges weakly in $W^{1,q}((0,L);\mathbb{R}^{n})$ , for every $q<\infty$ , to a limit

\tau_{\infty}\in\bigcap_{q<\infty}W^{1,q}((0,L);S^{n-1}).

Clearly $\tau_{\infty}$ will satisfy (5) and (6) again. By the lower semicontinuity of the $L^{q}$ -norm with respect to weak convergence and by (8),

J_{\infty}^{\mu}(\tau_{\infty};\tau_{0})=\lim_{q\to\infty}J_{q}^{\mu}(\tau_{\infty};\tau_{0})\leq\lim_{q\to\infty}\liminf_{i\to\infty}J_{q}^{\mu}(\tau_{p_{i}};\tau_{0})\leq K_{\infty}(\tau_{0}).

(9)

If there exists $m>0$ such that

K_{\infty}(\tau_{0})\leq K_{\infty}(\tau)+\frac{m}{2L}\int_{0}^{L}\beta|\tau-\tau_{0}|^{2}\,dt

for all $\tau\in W^{1,\infty}((0,L);S^{n-1})$ satisfying (5) and (6), then (9) implies that

J_{\infty}^{\mu}(\tau_{\infty};\tau_{0})\leq J_{\infty}^{m}(\tau_{\infty};\tau_{0}).

Thus

(\mu-m)\int_{0}^{L}\beta|\tau_{\infty}-\tau_{0}|^{2}\,dt\leq 0.

If we choose $\mu>m$ , this means that $\tau_{\infty}=\tau_{0}$ . In particular, the limit is then independent of the choice of the sequence $(p_{i})_{i\in\mathbb{N}}$ , and therefore we have in fact weak convergence of $\tau_{p}$ to $\tau_{\infty}=\tau_{0}$ in $W^{1,q}((0,L);\mathbb{R}^{n})$ for every $q<\infty$ .

The inequalities in (8) also imply that

\lim_{p\to\infty}J_{p}^{\mu}(\tau_{p};\tau_{0})\leq K_{\infty}(\tau_{0}),

in particular that the limit exists. On the other hand, as we now know that $\tau_{\infty}=\tau_{0}$ , we can go back to (9) and conclude that

K_{\infty}(\tau_{0})\leq\lim_{q\to\infty}\liminf_{i\to\infty}J_{q}^{\mu}(\tau_{p_{i}};\tau_{0})\leq\lim_{p\to\infty}J_{p}^{\mu}(\tau_{p};\tau_{0}).

Hence $K_{\infty}(\tau_{0})=\lim_{p\to\infty}J_{p}^{\mu}(\tau_{p};\tau_{0})$ . Since the weak convergence $\tau_{p}\rightharpoonup\tau_{0}$ in $W^{1,2}((0,L);\mathbb{R}^{n})$ implies strong convergence in $L^{2}((0,L);\mathbb{R}^{n})$ as well, it follows that $K_{\infty}(\tau_{0})=\lim_{p\to\infty}k_{p}$ . ∎

Eventually we will need a careful analysis of the Euler-Lagrange equation (7) for the proofs of Theorems 2–4. To this end, we need to know that the Lagrange multipliers $\Lambda_{p}$ do not grow too quickly as $p\to\infty$ . We prove the following.

Lemma 8.

Suppose that $\tau_{p}\in W^{1,p}((0,L);S^{n-1})$ and let $k_{p}=K_{p}(\tau_{p})$ . Suppose that $\limsup_{p\to\infty}k_{p}<\infty$ and there exist $\Lambda_{p}\in\mathbb{R}^{n}$ such that (7) holds weakly in $(0,L)$ for every $p\in[2,\infty)$ . Then either

\limsup_{p\to\infty}\left(p^{-6}|\Lambda_{p}|\right)<\infty

or there exists a sequence $p_{i}\to\infty$ such that $\tau_{p_{i}}$ converges uniformly to a constant vector as $i\to\infty$ .

Proof.

Suppose that no subsequence converges uniformly to a constant vector. Then it follows that for every sufficiently large $p$ , either $\Lambda_{p}=0$ or the angle $\omega_{p}$ between $\tau_{p}$ and $\Lambda_{p}$ satisfies

\sup_{t\in[0,L]}\omega_{p}(t)\geq\frac{1}{p}\quad\text{and}\quad\sup_{t\in[0,L]}(\pi-\omega_{p}(t))\geq\frac{1}{p}.

Note that

|\sin\omega_{p}|=\frac{|\Lambda_{p}-(\Lambda_{p}\cdot\tau_{p})\tau_{p}|}{|\Lambda_{p}|}

if $\Lambda_{p}\neq 0$ . Hence for every sufficiently large $p$ , there exists $t_{p}\in[0,L]$ such that

\left|\Lambda_{p}-(\Lambda_{p}\cdot\tau_{p}(t_{p}))\tau_{p}(t_{p})\right|\geq\frac{|\Lambda_{p}|}{2p}.

Because we have a uniform bound for $\|\tau_{p}^{\prime}\|_{L^{2}(0,L)}$ , the Sobolev embedding theorem gives a uniform bound for $\|\tau_{p}\|_{C^{0,1/2}([0,T])}$ as well. Hence there exists a number $\delta>0$ such that the inequality

\left|\Lambda_{p}-(\Lambda_{p}\cdot\tau_{p})\tau_{p}\right|\geq\frac{|\Lambda_{p}|}{3p}

holds in $[t_{p}-\delta/p^{2},t_{p}+\delta/p^{2}]\cap[0,L]$ for all sufficiently large values of $p$ . Choose $\eta\in C_{0}^{\infty}((t_{p}-\delta/p^{2},t_{p}+\delta/p^{2})\cap(0,L))$ such that $0\leq\eta\leq 1$ and

\int_{0}^{L}\eta\,ds\geq\frac{\delta}{2p^{2}},

but $|\eta^{\prime}|\leq 5p^{2}/\delta$ . Test (7) with $\eta\Lambda_{p}$ . This yields

\int_{0}^{L}\eta|\tau_{p}^{\prime}|^{p}\tau_{p}\cdot\Lambda_{p}\,dt-\int_{0}^{L}\eta^{\prime}|\tau_{p}^{\prime}|^{p-2}\tau_{p}^{\prime}\cdot\Lambda_{p}\,dt\\ =k_{p}^{p-1}\int_{0}^{L}\eta\beta\left|\Lambda_{p}-(\Lambda_{p}\cdot\tau_{p})\tau_{p}\right|^{2}\,dt-\mu k_{p}^{p-1}\int_{0}^{L}\eta\beta\left(\tau_{0}-(\tau_{0}\cdot\tau_{p})\tau_{p}\right)\cdot\Lambda_{p}\,dt.

By the choice of $\eta$ , we know that

\int_{0}^{L}\eta\beta\left|\Lambda_{p}-(\Lambda_{p}\cdot\tau_{p})\tau_{p}\right|^{2}\,dt\geq\frac{\delta|\Lambda_{p}|^{2}}{18p^{4}\|1/\alpha\|_{L^{\infty}(0,\ell)}}.

Moreover, we have the estimates

	$\displaystyle\int_{0}^{L}\eta\|\tau_{p}^{\prime}\|^{p}\tau_{p}\cdot\Lambda_{p}\,dt$	$\displaystyle\leq Lk_{p}^{p}\|\Lambda_{p}\|,$
	$\displaystyle-\int_{0}^{L}\eta^{\prime}\|\tau_{p}^{\prime}\|^{p-2}\tau_{p}^{\prime}\cdot\Lambda_{p}\,dt$	$\displaystyle\leq\frac{5p^{2}}{\delta}Lk_{p}^{p-1}\|\Lambda_{p}\|,$
	$\displaystyle\int_{0}^{L}\eta\beta\left(\tau_{0}-(\tau_{0}\cdot\tau_{p})\tau_{p}\right)\cdot\Lambda_{p}\,dt$	$\displaystyle\leq L\\|\alpha\\|_{L^{\infty}(0,\ell)}\|\Lambda_{p}\|.$

Hence

|\Lambda_{p}|\leq\frac{18Lp^{4}}{\delta}\|1/\alpha\|_{L^{\infty}(0,\ell)}\left(\frac{5p^{2}}{\delta}+\mu\|\alpha\|_{L^{\infty}(0,\ell)}+k_{p}\right),

and the desired inequality follows. ∎

3 Preliminary properties of $\infty$ -elasticas

The purpose of this section is to extract some information for pseudo-minimisers of $K_{\infty}$ , and therefore for $\infty$ -elasticas, from the Euler-Lagrange equation (7) by studying the limit $p\to\infty$ . The resulting statements are less strong than the main results in the introduction, but they will serve as a first step.

Proposition 9.

Suppose that $\tau\in W^{1,\infty}((0,L);S^{n-1})$ is a pseudo-minimiser of $K_{\infty}$ . Let $k=K_{\infty}(\tau)$ . Then there exist $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})\setminus\{0\}$ and $\lambda\in\mathbb{R}^{n}$ such that the equations

	$\displaystyle u^{\prime}+(u\cdot\tau^{\prime})\tau$	$\displaystyle=\beta(\lambda-(\lambda\cdot\tau)\tau),$		(10)
	$\displaystyle\|u\|\tau^{\prime}$	$\displaystyle=ku,$		(11)

hold almost everywhere in $(0,L)$ .

Proof.

The statements are obvious (for $u=1$ and $\lambda=0$ ) if $\tau$ is constant. We therefore assume that this is not the case.

Fix $\mu>0$ and consider the functionals $J_{p}^{\mu}({\mkern 2.0mu\cdot\mkern 2.0mu};\tau)$ . Minimisers $\tau_{p}$ of $J_{p}^{\mu}({\mkern 2.0mu\cdot\mkern 2.0mu};\tau)$ under the boundary conditions (5) and the constraint (6) can be constructed with the direct method. Let $k_{p}=K_{p}(\tau_{p})$ . We assume that $\mu>0$ is chosen so large that statement 2 in Proposition 7 applies.

We consider the Euler-Lagrange equation (7). The underlying idea for the next step is to regard it as an equation in $|\tau_{p}^{\prime}|^{p-2}\tau_{p}^{\prime}$ . But at the same time, we renormalise. Thus we introduce the functions

u_{p}=\frac{k_{p}^{1-p}|\tau_{p}^{\prime}|^{p-2}\tau_{p}^{\prime}}{1+|\Lambda_{p}|}.

We also define

\lambda_{p}=\frac{\Lambda_{p}}{1+|\Lambda_{p}|}\quad\text{and}\quad m_{p}=\frac{\mu}{1+|\Lambda_{p}|}.

Then we can write (7) (for $\tau_{0}=\tau$ ) in the form

u_{p}^{\prime}+(u_{p}\cdot\tau_{p}^{\prime})\tau_{p}=\beta(\lambda_{p}-(\lambda_{p}\cdot\tau_{p})\tau_{p}-m_{p}\tau+m_{p}(\tau\cdot\tau_{p})\tau_{p}).

(12)

Writing $p^{\prime}=p/(p-1)$ , we note that

\|u_{p}\|_{L^{p^{\prime}}(0,L)}=\frac{k_{p}^{p-1}}{1+|\Lambda_{p}|}\left(\int_{0}^{L}|\tau_{p}^{\prime}|^{p}\,dt\right)^{1/p^{\prime}}=\frac{L^{1/p^{\prime}}}{1+|\Lambda_{p}|}.

(13)

The right-hand side remains bounded as $p\to\infty$ . Moreover, we know that

\|\tau_{p}^{\prime}\|_{L^{p}(0,L)}=L^{1/p}k_{p}\to k

as $p\to\infty$ by Proposition 7. As $|\tau_{p}|\equiv 1$ , $|\lambda_{p}|\leq 1$ , and $0<m_{p}\leq\mu$ , equation (12) immediately gives a uniform bound for $\|u_{p}\|_{W^{1,1}(0,L)}$ . Thus we have a uniform bound in $L^{\infty}((0,L);\mathbb{R}^{n})$ as well, and using the equation again, we conclude that

\limsup_{p\to\infty}\|u_{p}^{\prime}\|_{L^{q}(0,L)}<\infty

for any $q<\infty$ . Thus we may choose a sequence $p_{i}\to\infty$ such that $u_{p_{i}}\rightharpoonup u$ , for some $u\in\bigcap_{q<\infty}W^{1,q}((0,L);\mathbb{R}^{n})$ , weakly in $W^{1,q}((0,L);\mathbb{R}^{n})$ for any $q<\infty$ as $i\to\infty$ . In particular $u_{p_{i}}\to u$ uniformly as $i\to\infty$ . Since $|\lambda_{p}|\leq 1$ and $0<m_{p}\leq\mu$ , we may assume that at the same time, we have the convergence $\lambda_{p_{i}}\to\lambda$ for some $\lambda\in\mathbb{R}^{n}$ and $m_{p_{i}}\to m$ for some $m\in[0,\mu]$ . By Proposition 7, we know that $\tau_{p}\to\tau$ weakly in $W^{1,q}((0,L);\mathbb{R}^{n})$ for any $q<\infty$ . Thus restricting (12) to $p_{i}$ and letting $i\to\infty$ , we derive equation (10) almost everywhere. Now (10) implies that $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})$ .

If $|\Lambda_{p_{i}}|\to\infty$ as $i\to\infty$ , then $\lambda\in S^{n-1}$ and (10) cannot be satisfied for $u\equiv 0$ (as we have assumed that $\tau$ is not constant). If $|\Lambda_{p_{i}}|\not\to\infty$ , then (13) implies that $\|u\|_{L^{1}(0,L)}\neq 0$ . In either case, we conclude that $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})\setminus\{0\}$ .

As $u$ is continuous, the set $\Omega=\left\{t\in[0,L]\colon u(t)\neq 0\right\}$ is open relative to $[0,L]$ . For any $t\in\Omega$ , there exist $\delta>0$ and $\epsilon>0$ such that $\delta\leq|u_{p_{i}}|\leq 1/\delta$ in $(t-\epsilon,t+\epsilon)\cap[0,L]$ for any $i$ large enough. Now note that

\tau_{p}^{\prime}=k_{p}(1+|\Lambda_{p}|)^{1/(p-1)}|u_{p}|^{1/(p-1)}\frac{u_{p}}{|u_{p}|}

wherever $u_{p}\neq 0$ by the definition of $u_{p}$ . As we have assumed that $\tau$ is not constant, we know that

(1+|\Lambda_{p}|)^{1/(p-1)}\to 1

as $p\to\infty$ by Lemma 8. We further know that

|u_{p_{i}}|^{1/(p_{i}-1)}\to 1\quad\text{and}\quad\frac{u_{p_{i}}}{|u_{p_{i}}|}\to\frac{u}{|u|}

uniformly in $(t-\epsilon,t+\epsilon)\cap[0,L]$ as $i\to\infty$ . Therefore, by the above identity,

\tau_{p_{i}}^{\prime}\to\tau^{\prime}=\frac{ku}{|u|}

locally uniformly in $\Omega$ . We therefore obtain equation (11). ∎

For planar curves, we can say more.

Lemma 10.

Let $\tau\in W^{1,\infty}((0,L);S^{n-1})$ and $\lambda\in\mathbb{R}^{n}\setminus\{0\}$ . Suppose that $\tau([0,L])$ is contained in a two-dimensional linear subspace $X\subseteq\mathbb{R}^{n}$ . Let

c(t)=a_{1}+\int_{0}^{t}\beta(\theta)\tau(\theta)\,d\theta

for $t\in[0,L]$ . Suppose that $k=K_{\infty}(\tau)\neq 0$ and consider a set $\Omega\subseteq[0,L]$ . Then the following statements are equivalent.

(i)

There exists $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})$ such that (10) and (11) hold true almost everywhere and $\Omega=\left\{t\in[0,L]\colon u(t)\neq 0\right\}$ .
(ii)

The vector $\lambda$ belongs to $X$ and there exists a line $\mathcal{L}\subseteq X+a_{1}$ parallel to $\lambda$ such that $\Omega=\left\{t\in[0,L]\colon c(t)\not\in\mathcal{L}\right\}$ . Moreover, $\tau^{\prime}$ is continuous with $|\tau^{\prime}|\equiv k$ in $\Omega$ . For any $t_{0}\in[0,L]\setminus\Omega$ , if there exists $\delta>0$ with $(t_{0}-\delta,t_{0})\subseteq\Omega$ , then there exists $\delta^{\prime}\in(0,\delta]$ such that $\lambda\cdot\tau^{\prime}(t)<0$ in $(t_{0}-\delta^{\prime},t_{0})$ ; and if there exists $\delta>0$ with $(t_{0},t_{0}+\delta)\subseteq\Omega$ , then there exists $\delta^{\prime}\in(0,\delta]$ such that $\lambda\cdot\tau^{\prime}(t)>0$ in $(t_{0},t_{0}+\delta^{\prime})$ .

Proof.

We may choose coordinates such that $X=\mathbb{R}^{2}\times\{0\}$ and then write

\tau=(\cos\omega,\sin\omega,0)

in $[0,L]$ for some function $\omega\colon[0,L]\to\mathbb{R}$ . Now for $x\in\mathbb{R}^{n}$ , write $x^{\perp}=(-x_{2},x_{1},x_{3},\dotsc,x_{n})$ . In particular $\tau^{\perp}=(-\sin\omega,\cos\omega,0)$ and $\tau^{\prime}=\omega^{\prime}\tau^{\perp}$ .

If i is satisfied, then (11) implies that $u(t)\in X$ for every $t\in[0,L]$ , and then (10) implies that $\lambda\in X$ . It is clear that $u/|u|$ is continuous in $\Omega$ . Thus equation (11) further implies that $\omega^{\prime}$ is continuous in $\Omega$ with $|\omega^{\prime}|\equiv k$ . Defining $f=|u|\omega^{\prime}/k$ , we compute $u=f\tau^{\perp}$ and

u^{\prime}+(u\cdot\tau^{\prime})\tau=f^{\prime}\tau^{\perp}.

(14)

Multiplying (10) with $\tau^{\perp}$ , we conclude that

f^{\prime}=\beta\lambda\cdot\tau^{\perp}

(15)

in $\Omega$ . Outside of $\Omega$ , we know that $f$ vanishes, and it follows that for any $t_{1},t_{2}\in[0,L]$ , we have the inequality $|f(t_{1})-f(t_{2})|\leq\|\beta\|_{L^{\infty}(0,L)}|\lambda||t_{1}-t_{2}|$ . So $f\in W^{1,\infty}(0,L)$ and (14), (15) hold true almost everywhere in $[0,L]$ .

Consider $c$ as defined above and note that $(c^{\prime})^{\perp}=\beta\tau^{\perp}$ . Hence $f^{\prime}=\lambda\cdot(c^{\prime})^{\perp}$ in $[0,L]$ . It follows that there exists some number $b\in\mathbb{R}$ such that

f^{-1}(\{0\})=\left\{t\in[0,L]\colon\lambda^{\perp}\cdot c(t)=b\right\}.

In other words, the line $\mathcal{L}=\left\{x\in X+a_{1}\colon\lambda^{\perp}\cdot x=b\right\}$ , which is parallel to $\lambda$ , has the property that $\Omega=\left\{t\in[0,L]\colon c(t)\not\in\mathcal{L}\right\}$ .

Now suppose that $t_{0}\in[0,L]\setminus\Omega$ such that there exists $\delta>0$ with $(t_{0}-\delta,t_{0})\subseteq\Omega$ . Recall that $|\omega^{\prime}|\equiv k$ in $(t_{0}-\delta,t_{0})$ while the sign of $\omega^{\prime}$ is constant. So $\omega^{\prime}=\sigma k$ in $(t_{0}-\delta,t_{0})$ for some $\sigma\in\{-1,1\}$ . Hence

\tau(t)=\cos(k(t-t_{0}))\tau(t_{0})+\sigma\sin(k(t-t_{0}))\tau^{\perp}(t_{0})

(16)

and

\tau^{\prime}(t)=-k\sin(k(t-t_{0}))\tau(t_{0})+\sigma k\cos(k(t-t_{0}))\tau^{\perp}(t_{0})

in $(t_{0}-\delta,t_{0})$ . Moreover, identity (15) implies that

f^{\prime}(t)=-\sigma\beta(t)\sin(k(t-t_{0}))\lambda\cdot\tau(t_{0})+\beta(t)\cos(k(t-t_{0}))\lambda\cdot\tau^{\perp}(t_{0})

(17)

in $(t_{0}-\delta,t_{0})$ . As $f(t_{0})=0$ and as $f$ has the same sign as $\omega^{\prime}$ in $(t_{0}-\delta,t_{0})$ , we immediately conclude that $\sigma\lambda\cdot\tau^{\perp}(t_{0})\leq 0$ ; and in the case of equality, we further conclude that $\lambda\cdot\tau(t_{0})<0$ . But then, as

\lambda\cdot\tau^{\prime}(t)=-k\sin(k(t-t_{0}))\lambda\cdot\tau(t_{0})+\sigma k\cos(k(t-t_{0}))\lambda\cdot\tau^{\perp}(t_{0}),

this implies that $\lambda\cdot\tau^{\prime}(t)<0$ in $(t_{0}-\delta^{\prime},t_{0})$ for some $\delta^{\prime}>0$ . If there exists $\delta>0$ such that $(t_{0},t_{0}+\delta)\subseteq\Omega$ , then we can draw similar conclusions with the same arguments. Hence ii is satisfied.

Conversely, suppose that ii holds true. If $c([0,L])\subseteq\mathcal{L}$ , set $u=0$ . Otherwise, set

f(t)=\lambda\cdot c^{\perp}(t)+b,

where $b\in\mathbb{R}$ is chosen such that $\Omega=f^{-1}(\{0\})$ . Then $f\in W^{1,\infty}(0,L)$ and (15) is satisfied. If $(t_{0},t_{1})\subseteq\Omega$ is any connected component of $\Omega$ , then $\omega^{\prime}=\sigma k$ in $(t_{0},t_{1})$ for some fixed $\sigma\in\{-1,1\}$ . Hence we can write $\tau$ in the form (16) and it follows that $f^{\prime}$ satisfies (17) in $(t_{0},t_{1})$ . The condition on the sign of $\lambda\cdot\tau^{\prime}$ near $t_{0}$ implies that $\sigma\lambda\cdot\tau^{\perp}(t_{0})\geq 0$ ; and in the case of equality, it also implies that $\lambda\cdot\tau(t_{0})<0$ . Therefore, the function $f$ has the same sign as $\omega^{\prime}$ in $(t_{0},t_{1})$ . Similar conclusions hold if we have connected components of $\Omega$ of the form $[0,t_{1})$ or $(t_{0},L]$ . Hence $f$ and $\omega^{\prime}$ have the same sign everywhere in $\Omega$ .

Now we set $u=f\tau^{\perp}$ . Then (11) is obvious and (10) can be verified by computing (14) again and observing that

\beta(\lambda-(\lambda\cdot\tau)\tau)=\beta(\lambda\cdot\tau^{\perp})\tau^{\perp}=(\lambda\cdot(c^{\prime})^{\perp})\tau^{\perp}=f^{\prime}\tau^{\perp}.

This concludes the proof. ∎

4 Analysis of the differential equations

In this section we study the system (10), (11) and its relationship to the variational problem in more detail. Furthermore, we show that it is equivalent to (2), (3) up to the reparametrisation introduced in Section 2.

Proposition 11.

Suppose that $\tau\in W^{1,\infty}((0,L);S^{n-1})$ satisfies (5) and (6). If there exist $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})\setminus\{0\}$ and $\lambda\in\mathbb{R}^{n}$ such that (10) and (11) hold almost everywhere in $(0,L)$ , then $\tau$ is a pseudo-minimiser of $K_{\infty}$ . If in addition $k|u|+\beta\lambda\cdot\tau\leq 0$ in $[0,L]$ , then $\tau$ is a minimiser of $K_{\infty}$ under the constraints (5) and (6).

Proof.

Suppose that equations (10) and (11) hold true. Let $\Sigma=u^{-1}(\{0\})$ . We claim that $\tau^{\prime}=0$ almost everywhere on $\Sigma$ . Indeed, if $\lambda=0$ , then it follows from (10) that $\left|\frac{d}{dt}|u|\right|\leq|u|\|\tau^{\prime}\|_{L^{\infty}(0,L)}$ . As it is assumed that $u\not\equiv 0$ , this inequality implies that $u\neq 0$ throughout $[0,L]$ . If $\lambda\neq 0$ , then at almost every point $t\in\Sigma$ , either $u^{\prime}(t)\neq 0$ (so $t$ is an isolated point of $\Sigma$ ) or $\tau(t)=\pm\lambda/|\lambda|$ . As $\tau\in W^{1,\infty}((0,L);S^{n-1})$ , it has a derivative almost everywhere and we conclude that $\tau^{\prime}=0$ almost everywhere in $\Sigma$ .

Now consider a competitor $\tilde{\tau}\colon[0,L]\to S^{n-1}$ satisfying (5) and (6). Let $\sigma=\tilde{\tau}-\tau$ and note that

1=|\tau+\sigma|^{2}=1+2\tau\cdot\sigma+|\sigma|^{2}

in $[0,L]$ . Hence

\tau\cdot\sigma=-\frac{|\sigma|^{2}}{2}.

Furthermore, the definition of $\sigma$ guarantees that $\sigma(0)=\sigma(L)=0$ and

\int_{0}^{L}\beta\sigma\,dt=0.

Observing that $u\cdot\tau^{\prime}=k|u|$ because of (11), we now use (10) to compute

\begin{split}\int_{0}^{L}\sigma^{\prime}\cdot u\,dt&=-\int_{0}^{L}\sigma\cdot u^{\prime}\,dt\\ &=\int_{0}^{L}\left((k|u|+\beta\lambda\cdot\tau)\tau\cdot\sigma-\beta\lambda\cdot\sigma\right)\,dt\\ &=-\frac{1}{2}\int_{0}^{L}(k|u|/\beta+\lambda\cdot\tau)\beta|\sigma|^{2}\,dt\\ &\geq-\frac{1}{2}\left(k\|u/\beta\|_{L^{\infty}(0,L)}+|\lambda|\right)\bigl{\|}\sqrt{\beta}\sigma\bigr{\|}_{L^{2}(0,L)}^{2}.\end{split}

(18)

Set

M=\frac{k\|u/\beta\|_{L^{\infty}(0,L)}+|\lambda|}{2\|u\|_{L^{1}(0,L)}}.

Then there exists a set $A\subseteq[0,L]$ of positive measure such that $\sigma^{\prime}\cdot u\geq-M\|\sqrt{\beta}\sigma\|_{L^{2}(0,L)}^{2}|u|$ and $u\neq 0$ in $A$ . (Otherwise, we would conclude that

\begin{split}\int_{0}^{L}\sigma^{\prime}\cdot u\,dt&=\int_{(0,L)\setminus\Sigma}\sigma^{\prime}\cdot u\,dt\\ &<-M\bigl{\|}\sqrt{\beta}\sigma\bigr{\|}_{L^{2}(0,L)}^{2}\int_{(0,L)\setminus\Sigma}|u|\,dt\\ &=-M\bigl{\|}\sqrt{\beta}\sigma\bigr{\|}_{L^{2}(0,L)}^{2}\int_{0}^{L}|u|\,dt\\ &=-\frac{1}{2}\left(k\|u/\beta\|_{L^{\infty}(0,L)}+|\lambda|\right)\bigl{\|}\sqrt{\beta}\sigma\bigr{\|}_{L^{2}(0,L)}^{2},\end{split}

in contradiction to (18).) Hence

\sigma^{\prime}\cdot\tau^{\prime}=\sigma^{\prime}\cdot\frac{ku}{|u|}\geq-kM\bigl{\|}\sqrt{\beta}\sigma\bigr{\|}_{L^{2}(0,L)}^{2}

almost everywhere in $A$ . As $|\tau^{\prime}|=k$ almost everywhere in $A$ , it follows that

\begin{split}|\tilde{\tau}^{\prime}|&=\sqrt{|\tau^{\prime}|^{2}+2\tau^{\prime}\cdot\sigma^{\prime}+|\sigma^{\prime}|^{2}}\\ &\geq\sqrt{k^{2}-2kM\bigl{\|}\sqrt{\beta}\sigma\bigr{\|}_{L^{2}(0,L)}^{2}}\\ &\geq k-2M\bigl{\|}\sqrt{\beta}\sigma\bigr{\|}_{L^{2}(0,L)}^{2}\end{split}

almost everywhere in $A$ (unless the right-hand side is negative, in which case the intermediate expression should be replaced by $0$ ). In particular,

K_{\infty}(\tilde{\tau})\geq K_{\infty}(\tau)-2M\int_{0}^{L}\beta|\tilde{\tau}-\tau^{\prime}|^{2}\,dt.

That is, we have shown that $\tau$ is a pseudo-minimiser.

Finally, if $k|u|+\beta\lambda\cdot\tau\leq 0$ , we can improve (18) and conclude that

\int_{0}^{L}\sigma^{\prime}\cdot u\,dt\geq 0.

So there exists a set of positive measure $A\subseteq[0,L]$ where $u\neq 0$ and $\sigma^{\prime}\cdot\tau^{\prime}\geq 0$ . Thus $|\tilde{\tau}^{\prime}|^{2}\geq|\tau^{\prime}|^{2}=k^{2}$ almost everywhere in $A$ , and it follows immediately that $K_{\infty}(\tau)\leq K_{\infty}(\tilde{\tau})$ . ∎

Next we reformulate the system (10), (11). We obtain the system (19), (20) below, which corresponds to (2), (3) up to the reparametrisation from Section 2.

Proposition 12.

Suppose that $\tau\in W^{1,\infty}((0,L);S^{n-1})$ . Let $\lambda\in\mathbb{R}^{n}$ and $k\geq 0$ .

Suppose that $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})\setminus\{0\}$ satisfies (10) and (11) almost everywhere in $(0,L)$ . Then there exists $f\in W^{1,\infty}(0,L)\setminus\{0\}$ with $f\geq 0$ such that

	$\displaystyle f(\tau^{\prime\prime}+k^{2}\tau)$	$\displaystyle=\beta k^{2}\operatorname{proj}_{\tau,\tau^{\prime}}^{\perp}(\lambda),$		(19)
	$\displaystyle f^{\prime}$	$\displaystyle=\beta\lambda\cdot\tau^{\prime},$		(20)

weakly in $(0,L)$ . If $k>0$ , then $f=k|u|$ has this property.

2.

Suppose that there exists $f\in W^{1,\infty}(0,L)\setminus\{0\}$ with $f\geq 0$ satisfying (19) and (20) weakly in $(0,L)$ . Then there exists $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})\setminus\{0\}$ such that (10) and (11) hold almost everywhere; and if $k>0$ , such that also $f=k|u|$ .
3.

If there exists $f\in W^{1,\infty}(0,L)\setminus\{0\}$ with $f\geq 0$ such that (19) and (20) hold weakly and $f+\beta\lambda\cdot\tau\leq 0$ in $(0,L)$ , then $\tau$ minimises $K_{\infty}$ subject to the constraints (5) and (6).

Proof.

Suppose first that we have a weak solution of (10) and (11) for some $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})\setminus\{0\}$ . Let $\Omega=\left\{t\in[0,L]\colon u(t)\neq 0\right\}$ .

If $k=0$ , then $\tau^{\prime}=0$ in $\Omega$ by (11). With the same arguments as in the proof of Proposition 11, we show that $\tau^{\prime}=0$ almost everywhere in $[0,L]\setminus\Omega$ . Hence (19), (20) automatically hold true for any constant function $f$ .

If $k>0$ , then we consider the function $f=k|u|$ . Equation (11) then implies that $u=f\tau^{\prime}/k^{2}$ almost everywhere. We conclude that $\tau^{\prime}=k^{2}u/f$ in $\Omega$ , so $\tau\in W_{\mathrm{loc}}^{2,\infty}(\Omega)$ . Hence from (10) we derive the equation

f(\tau^{\prime\prime}+|\tau^{\prime}|^{2}\tau)+f^{\prime}\tau^{\prime}=k^{2}\beta(\lambda-(\lambda\cdot\tau)\tau)

(21)

almost everywhere in $\Omega$ . Taking the inner product with $\tau^{\prime}$ and observing that $\tau\cdot\tau^{\prime}=0$ (because $|\tau|\equiv 1$ ) and $\tau^{\prime\prime}\cdot\tau^{\prime}=0$ (because $|\tau^{\prime}|\equiv k$ in $\Omega$ ), we see that

k^{2}f^{\prime}=k^{2}\beta\lambda\cdot\tau^{\prime}.

This amounts to equation (20). Of course $f\geq 0$ by the definition of $f$ .

Differentiating the equation $\tau\cdot\tau^{\prime}=0$ , we see that $\tau\cdot\tau^{\prime\prime}+|\tau^{\prime}|^{2}=0$ . Recalling that $\tau^{\prime}\cdot\tau^{\prime\prime}=0$ , we conclude that

\operatorname{proj}_{\tau,\tau^{\prime}}^{\perp}(\tau^{\prime\prime})=\tau^{\prime\prime}-(\tau\cdot\tau^{\prime\prime})\tau=\tau^{\prime\prime}+k^{2}\tau

in $\Omega$ . Applying $\operatorname{proj}_{\tau,\tau^{\prime}}^{\perp}$ to both sides of (21), we see that (19) holds almost everywhere in $\Omega$ . Also note that the function $f\tau^{\prime}=k^{2}u$ is continuous. Thus if $(t_{1},t_{2})$ is any connected component of $\Omega$ , then for any $\xi\in C_{0}^{\infty}((0,L);\mathbb{R}^{n})$ ,

\int_{t_{1}}^{t_{2}}\left(f(\tau^{\prime}\cdot\xi^{\prime}-k^{2}\tau\cdot\xi)+f^{\prime}\tau^{\prime}\cdot\xi+k^{2}\beta\operatorname{proj}_{\tau,\tau^{\prime}}^{\perp}(\lambda)\cdot\xi\right)\,dt\\ =k^{2}u(t_{2})\cdot\xi(t_{2})-k^{2}u(t_{1})\cdot\xi(t_{1})=0.

A similar conclusion holds if $[0,t_{2})$ or $(t_{1},L]$ is a connected component of $\Omega$ . Away from $\Omega$ , we know that $u=0$ and therefore either $\lambda=0$ or $\tau=\pm\lambda/|\lambda|$ almost everywhere in $[0,L]\setminus\Omega$ by (10). Hence (19) holds weakly in all of $(0,L)$ .

Conversely, suppose that we have a weak solution of (19), (20) for $f\in W^{1,\infty}(0,L)\setminus\{0\}$ with $f\geq 0$ . Consider the open set $\Omega=\left\{t\in[0,L]\colon f(t)\neq 0\right\}$ . Here we can use (19) to conclude that $\tau\in W_{\mathrm{loc}}^{2,\infty}(\Omega)$ . We differentiate the equation $|\tau|^{2}=1$ twice and we obtain $\tau^{\prime\prime}\cdot\tau+|\tau^{\prime}|^{2}=0$ almost everywhere in $\Omega$ . On the other hand, multiplying both sides of (19) with $\tau$ , we find that $\tau^{\prime\prime}\cdot\tau+k^{2}=0$ in $\Omega$ . Hence $|\tau^{\prime}|\equiv k$ in $\Omega$ .

If $k=0$ , then $\tau^{\prime}\equiv 0$ in $\Omega$ and (20) implies that $f$ is locally constant in $\Omega$ . So in this case, it follows that $\Omega=[0,L]$ and (11) is automatically satisfied. Moreover, it is then easy to find $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})\setminus\{0\}$ that solves (10).

If $k>0$ , then we claim that (21) is satisfied in $\Omega$ . In order to see why, we split the equation into three parts by projecting orthogonally onto the spaces $\mathbb{R}\tau(t)$ and $\mathbb{R}\tau^{\prime}(t)$ and onto the orthogonal complement of $\mathbb{R}\tau(t)\oplus\mathbb{R}\tau^{\prime}(t)$ at almost every $t\in\Omega$ . The projection onto $\mathbb{R}\tau(t)$ is trivial. The projection onto $\mathbb{R}\tau^{\prime}(t)$ amounts to (20), and applying $\operatorname{proj}_{\tau(t),\tau^{\prime}(t)}^{\perp}$ gives (19). Thus we have a solution of (21) in $\Omega$ .

Setting $u=f\tau^{\prime}/k^{2}$ , we can then verify (10) and (11) in $\Omega$ . Outside of $\Omega$ , we know that $f=0$ and $u=0$ . Hence (20) implies that $\lambda\cdot\tau^{\prime}=0$ almost everywhere outside of $\Omega$ . Moreover, (19) implies that $\operatorname{proj}_{\tau,\tau^{\prime}}^{\perp}(\lambda)=0$ almost everywhere in $[0,L]\setminus\Omega$ . That is, $\lambda$ is a multiple of $\tau$ and (10), (11) are satisfied almost everywhere in $[0,L]\setminus\Omega$ as well.

Furthermore, if $f+\beta\lambda\cdot\tau\leq 0$ , then $k|u|+\beta\lambda\cdot\tau\leq 0$ , and the last statement follows from Proposition 11. ∎

As mentioned previously, the new system of differential equations (19), (20) corresponds to (2), (3) up to the reparametrisation from Section 2. But Proposition 12 requires only that $\lambda\in\mathbb{R}^{n}$ , whereas $\lambda\in S^{n-1}$ in Theorem 2. For this reason, the following observation is useful.

Lemma 13.

Let $\tau\in W^{1,\infty}((0,L);S^{n-1})$ , $\lambda\in\mathbb{R}^{n}$ , and $f\in W^{1,\infty}(0,L)\setminus\{0\}$ with $f\geq 0$ such that (19), (20) hold weakly. Then there exist $\tilde{f}\in W^{1,\infty}(0,L)\setminus\{0\}$ with $\tilde{f}\geq 0$ and $\tilde{\lambda}\in S^{n-1}$ such that (19), (20) hold weakly for $\tilde{f}$ instead of $f$ and for $\tilde{\lambda}$ instead of $\lambda$ as well.

Proof.

If $\lambda\neq 0$ , then it suffices to define $\tilde{f}=f/|\lambda|$ and $\tilde{\lambda}=\lambda/|\lambda|$ and check that both equations are still satisfied. If $\lambda=0$ , then $f$ is constant and positive. Hence $\tau^{\prime\prime}+k^{2}\tau=0$ in $(0,L)$ . With the same arguments as in the proof of Proposition 12, we see that $|\tau^{\prime}|\equiv k$ . The resulting equation $\tau^{\prime\prime}+|\tau^{\prime}|^{2}\tau=0$ means that $\tau$ follows a geodesic, i.e., a great circle on $S^{n-1}$ . This implies that $\tau(t)$ and $\tau^{\prime}(t)$ span the same two-dimensional subspace of $\mathbb{R}^{n}$ everywhere, and any $\tilde{\lambda}$ in this subspace will satisfy $\operatorname{proj}_{\tau,\tau^{\prime}}^{\perp}(\tilde{\lambda})=0$ . Now we choose $\tilde{f}$ such that (20) holds true (for $\tilde{\lambda}$ instead of $\lambda$ ) and at the same time $\tilde{f}>0$ in $[0,L]$ . Then both equations are satisfied. ∎

We now have all the tools for the proofs of the first two results in the introduction.

Proofs of Theorem 2 and Theorem 3.

With the reparametrisation from Section 2, an $\infty$ -elastica gives rise to a pseudo-minimiser of $K_{\infty}$ and vice versa. According to Proposition 9 and Proposition 11, pseudo-minimisers of $K_{\infty}$ correspond to solutions of (10), (11), which is equivalent to (19), (20) by Proposition 12. Lemma 13 shows that it suffices to consider this system for $\lambda\in S^{n-1}$ . Now we check that the system corresponds to (2), (3) for the original parametrisation, and this proves Theorem 2. Theorem 3 follows from the last statement of Proposition 12. ∎

5 Preparation for the proof of Theorem 4

The system of ordinary differential equations (19), (20) becomes degenerate at points where $f$ vanishes. It turns out, however, that $f$ remains positive for generic solutions as described in the following result. This information will be crucial for statement ii in Theorem 4.

Lemma 14.

Let $\lambda,\tau_{0}\in S^{n-1}$ and $\tau_{1}\in\mathbb{R}^{n}$ such that $\tau_{0}\perp\tau_{1}$ , and let $f_{0}>0$ and $t_{0}\in[0,L]$ . If the vectors $\tau_{0}$ , $\tau_{1}$ , and $\lambda$ are linearly independent, then the initial value problem

$\displaystyle\tau^{\prime\prime}+\|\tau^{\prime}\|^{2}\tau$	$\displaystyle=\beta f^{-1}\|\tau^{\prime}\|^{2}\operatorname{proj}_{\tau,\tau^{\prime}}^{\perp}(\lambda),$	(22)
$\displaystyle f^{\prime}$	$\displaystyle=\beta\lambda\cdot\tau^{\prime},$
$\displaystyle\tau(t_{0})$	$\displaystyle=\tau_{0},\quad\tau^{\prime}(t_{0})=\tau_{1},\quad f(t_{0})=f_{0},$

has a unique global solution, consisting of $\tau\colon[0,L]\to S^{n-1}$ and $f\colon[0,L]\to(0,\infty)$ . For all $t\in[0,L]$ , this solution satisfies $|\tau^{\prime}(t)|=|\tau_{1}|$ and $\lambda\cdot\tau(t)\neq\pm 1$ , and $\tau(t)$ remains in the linear subspace of $\mathbb{R}^{n}$ spanned by $\tau_{0}$ , $\tau_{1}$ , and $\lambda$ .

Proof.

Under these assumptions, we clearly have a unique solution of the initial value problem in a certain interval $(t_{1},t_{2})\cap[0,L]$ such that $\lambda\cdot\tau\neq\pm 1$ and $f>0$ in that interval. Multiplying (22) with $\tau$ , we see that $\frac{d}{dt}(\tau\cdot\tau^{\prime})=0$ . Hence the solution will continue to take values on the sphere $S^{2}$ . Multiplying the equation with $\tau^{\prime}$ , we further see that $\frac{d}{dt}|\tau^{\prime}|^{2}=0$ . Setting $k=|\tau_{1}|$ , we conclude that $|\tau^{\prime}|=k$ in $(t_{1},t_{2})\cap[0,L]$ . Moreover, if $V\in\mathbb{R}^{n}$ is any vector perpendicular to $\tau_{0}$ , $\tau_{1}$ , and $\lambda$ , then the function $h=V\cdot\tau$ satisfies

h^{\prime\prime}+|\tau^{\prime}|^{2}h=-\beta f^{-1}\left(|\tau^{\prime}|^{2}(\lambda\cdot\tau)h+(\lambda\cdot\tau^{\prime})h^{\prime}\right)

in $(t_{1},t_{2})\cap[0,L]$ and $h(t_{0})=h^{\prime}(t_{0})=0$ . Hence $h\equiv 0$ , and the solution $\tau$ will remain in the linear subspace spanned by $\tau_{0}$ , $\tau_{1}$ , and $\lambda$ in $(t_{1},t_{2})\cap[0,L]$ . So we may assume that $n=3$ without loss of generality. We may further choose coordinates such that $\lambda=(0,0,1)$ .

It now suffices to show that $\liminf_{t\searrow t_{1}}f(t)>0$ and $\limsup_{t\searrow t_{1}}|\lambda\cdot\tau(t)|<1$ (unless $t_{1}<0$ ) and that $\liminf_{t\nearrow t_{2}}f(t)>0$ and $\limsup_{t\nearrow t_{2}}|\lambda\cdot\tau(t)|<1$ (unless $t_{2}>L$ ). The standard theory for ordinary differential equations will then imply the result.

We use spherical coordinates on $S^{2}$ and we write

\tau=(\cos\varphi\sin\vartheta,\sin\varphi\sin\vartheta,\cos\vartheta)

for $\varphi,\vartheta\colon(t_{1},t_{2})\cap[0,L]\to\mathbb{R}$ with $\vartheta(t)\in(0,\pi)$ for all $t\in(t_{1},t_{2})$ . Writing also

e_{1}=(-\sin\varphi,\cos\varphi,0)\quad\text{and}\quad e_{2}=(\cos\varphi\cos\vartheta,\sin\varphi\cos\vartheta,-\sin\vartheta),

we obtain an orthonormal basis $(\tau(t),e_{1}(t),e_{2}(t))$ of $\mathbb{R}^{3}$ such that $e_{1}(t)$ and $e_{2}(t)$ span the tangent space of $S^{2}$ at $\tau(t)$ for every $t\in(t_{1},t_{2})\cap[0,L]$ . We compute

\tau^{\prime}=\varphi^{\prime}\sin\vartheta\,e_{1}+\vartheta^{\prime}\,e_{2}

and

\tau^{\prime\prime}+|\tau^{\prime}|^{2}\tau=\left(\varphi^{\prime\prime}\sin\vartheta+2\varphi^{\prime}\vartheta^{\prime}\cos\vartheta\right)e_{1}+\left(\vartheta^{\prime\prime}-(\varphi^{\prime})^{2}\sin\vartheta\cos\vartheta\right)e_{2}.

Define $Z=-\vartheta^{\prime}\,e_{1}+\varphi^{\prime}\sin\vartheta\,e_{2}$ , so that $|Z|=|\tau^{\prime}|$ and $Z\perp\tau^{\prime}$ . Then

|\tau^{\prime}|^{2}\operatorname{proj}_{\tau,\tau^{\prime}}^{\perp}(\lambda)=(\lambda\cdot Z)Z=\varphi^{\prime}\vartheta^{\prime}\sin^{2}\vartheta\,e_{1}-(\varphi^{\prime})^{2}\sin^{3}\vartheta\,e_{2}.

Therefore, we obtain the equations

	$\displaystyle\varphi^{\prime\prime}\sin\vartheta+2\varphi^{\prime}\vartheta^{\prime}\cos\vartheta$	$\displaystyle=\beta f^{-1}\varphi^{\prime}\vartheta^{\prime}\sin^{2}\vartheta,$		(23)
	$\displaystyle\vartheta^{\prime\prime}-(\varphi^{\prime})^{2}\sin\vartheta\cos\vartheta$	$\displaystyle=-\beta f^{-1}(\varphi^{\prime})^{2}\sin^{3}\vartheta,$		(24)

and furthermore

f^{\prime}=-\beta\vartheta^{\prime}\sin\vartheta.

(25)

For the rest of the proof, it suffices to consider (23) and (25).

We first claim that $\varphi^{\prime}$ does not vanish anywhere in $(t_{1},t_{2})\cap[0,L]$ . Otherwise, equation (23) would imply that it remains $0$ throughout $(t_{1},t_{2})\cap[0,L]$ , and $\tau$ would parametrise a piece of a great circle through $(0,0,1)$ . This, however, is impossible under the assumption that $\tau_{0}$ , $\tau_{1}$ , and $\lambda$ are linearly independent.

Thus we may divide by $\varphi^{\prime}\sin\vartheta$ in (23) and we find that

\frac{\varphi^{\prime\prime}}{\varphi^{\prime}}=-\frac{f^{\prime}}{f}-\frac{2\vartheta^{\prime}\cos\vartheta}{\sin\vartheta}.

Integrating, we see that there exists $b\in\mathbb{R}$ such that

\log|\varphi^{\prime}|=-\log f-2\log\sin\vartheta+b.

Set $B=e^{b}$ . Then

|\varphi^{\prime}|=\frac{B}{f\sin^{2}\vartheta}.

The equation $(\varphi^{\prime})^{2}\sin^{2}\vartheta+(\vartheta^{\prime})^{2}=|\tau^{\prime}|^{2}=k^{2}$ then implies that

\frac{B^{2}}{f^{2}\sin^{2}\vartheta}\leq k^{2}.

It follows immediately that $f$ and $\sin\vartheta$ stay away from $0$ and this concludes the proof. ∎

The following technical lemma is also required for the proof of Theorem 4.

Lemma 15.

Suppose that $(b_{i})_{i\in\mathbb{N}}$ is a sequence of positive numbers such that

\sum_{i=1}^{\infty}\left|1-\frac{b_{i+1}}{b_{i}}\right|<\infty.

Then $\sum_{i=1}^{\infty}b_{i}=\infty$ .

Proof.

Ignoring finitely many terms if necessary, we may assume that

\sum_{i=1}^{\infty}\left|1-\frac{b_{i+1}}{b_{i}}\right|\leq\frac{1}{2}.

Fix $I\in\mathbb{N}$ . Let $q_{i}=b_{i+1}/b_{i}$ for $i=1,\dotsc,I-1$ . Choose a permutation $S\colon\{1,\dots,I-1\}\to\{1,\dots,I-1\}$ such that $q_{S(1)}\leq\dotsb\leq q_{S(I-1)}$ and define $q_{i}^{\prime}=\min\{q_{S(i)},1\}$ . Also define $b_{1}^{\prime},\dotsc,b_{I}^{\prime}>0$ by $b_{1}^{\prime}=b_{1}$ and

b_{i+1}^{\prime}=q_{i}^{\prime}b_{i}^{\prime},\quad i=1,\dotsc,I-1.

Then

\sum_{i=1}^{I-1}(1-q_{i}^{\prime})\leq\sum_{i=1}^{I-1}|1-q_{i}|\leq\frac{1}{2}

(26)

and $b_{i}^{\prime}\leq b_{i}$ for all $i=1,\dots,I$ .

As $q_{i}^{\prime}$ is non-decreasing in $i$ , inequality (26) implies that

1-q_{i}^{\prime}\leq\frac{1}{2i}\leq\frac{1}{i+1}

for $i=1,\dots,I-1$ . Define $B_{i}=1/i$ for $i=1,\dotsc,I$ . Then

\frac{b_{i+1}^{\prime}}{b_{i}^{\prime}}=q_{i}^{\prime}\geq\frac{i}{i+1}=\frac{B_{i+1}}{B_{i}}.

Hence

b_{i}^{\prime}=\frac{b_{i}^{\prime}}{b_{i-1}^{\prime}}\dotsb\frac{b_{2}^{\prime}}{b_{1}^{\prime}}b_{1}\geq\frac{B_{i}}{B_{i-1}}\dotsb\frac{B_{2}}{B_{1}}b_{1}=\frac{B_{i}}{B_{1}}b_{1}=\frac{b_{1}}{i}.

It follows that

\sum_{i=1}^{I}b_{i}\geq\sum_{i=1}^{I}b_{i}^{\prime}\geq b_{1}\sum_{i=1}^{I}\frac{1}{i}.

Letting $I\to\infty$ , we obtain the desired result. ∎

6 Proof of Theorem 4

Now we consider the situation of Theorem 4. Suppose first that $\gamma\in\mathcal{G}$ is an $\infty$ -elastica and let $k=\mathcal{K}_{\alpha}(\gamma)$ . If $k=0$ , then $\gamma^{\prime\prime}=0$ almost everywhere and $\gamma$ parametrises a line segment. Then clearly statement i in Theorem 4 is satisfied. Therefore, we assume that $k>0$ henceforth.

Consider the reparametrised tangent vector field $\tau\colon[0,L]\to S^{n-1}$ with $\tau(t)=\gamma^{\prime}(\phi(t))$ for $t\in[0,L]$ as in Section 2. Then $\tau$ is a pseudo-minimiser of $K_{\infty}$ . Hence by Proposition 9, there exist $\lambda\in\mathbb{R}^{n}$ and $u\in W^{1,\infty}((0,L);\mathbb{R}^{n})\setminus\{0\}$ such that (10) and (11) hold true almost everywhere. According to Proposition 12, the function $f=k|u|$ satisfies (19) and (20) weakly, and by Lemma 13 we may assume that $\lambda\in S^{n-1}$ .

Let $\Omega=\left\{t\in[0,L]\colon f(t)>0\right\}$ . Then (11) implies that $\tau^{\prime}$ is continuous in $\Omega$ with $|\tau^{\prime}|\equiv k$ . It follows from (19) that $\tau\in W_{\mathrm{loc}}^{2,\infty}(\Omega)$ . Moreover, by standard theory for ordinary differential equations, both $\tau$ and $f$ are locally uniquely determined by their initial conditions $\tau(t_{0})$ , $\tau^{\prime}(t_{0})$ , and $f(t_{0})$ for any $t_{0}\in\Omega$ .

If $\tau$ , $\tau^{\prime}$ , and $\lambda$ are linearly independent anywhere in $\Omega$ , then Lemma 14 implies that $\Omega=[0,L]$ and that $\tau$ takes values in a three-dimensional subspace of $\mathbb{R}^{n}$ , and (19) and (20) are satisfied almost everywhere. Equations (2) and (3) now arise when we reverse the reparametrisation from Section 2. The observation that $\alpha\gamma^{\prime\prime}=\tau^{\prime}\circ\psi$ implies that $\alpha\gamma^{\prime\prime}\in W^{1,\infty}((0,\ell);\mathbb{R}^{n})$ and that $\alpha|\gamma^{\prime\prime}|\equiv k$ . Equation (3) then implies that $g\in W^{2,\infty}(0,\ell)$ . Hence statement ii in Theorem 4 holds true.

This leaves the case when $\tau$ , $\tau^{\prime}$ , and $\lambda$ are linearly dependent everywhere in $\Omega$ . We assume this from now on. Then we can say more about the behaviour of $\tau$ in $\Omega$ .

Lemma 16.

If $(t_{1},t_{2})\subseteq\Omega$ , then the restriction of $\tau$ to $(t_{1},t_{2})$ follows a great circle in $S^{n-1}$ through $\lambda$ with constant speed $k$ . Furthermore, if $(t_{1},t_{2})$ is a connected component of $\Omega$ , then there exists $t_{0}\in(t_{1},t_{2})$ such that $\tau(t_{0})=\pm\lambda$ .

Proof.

We know that $\tau\cdot\tau^{\prime}=0$ everywhere, and $\tau^{\prime}$ is continuous with $|\tau^{\prime}|\equiv k$ in $\Omega$ . As $\tau(t)$ , $\tau^{\prime}(t)$ , and $\lambda$ are linearly dependent, we further know that $\tau^{\prime}(t)$ is in the space spanned by $\tau(t)$ and $\lambda$ for every $t\in\Omega$ with $\tau(t)\neq\pm\lambda$ . Hence $\tau$ follows a great circle on $S^{n-1}$ through $\lambda$ with speed $k$ ; indeed, by the continuity of $\tau^{\prime}$ , this is true throughout $(t_{1},t_{2})$ even if there are any points where $\tau(t)=\pm\lambda$ . If $(t_{1},t_{2})$ is a connected component of $\Omega$ , then $f(t_{1})=0=f(t_{2})$ . By (20), this means that $\lambda\cdot\tau^{\prime}$ must change sign somewhere in $(t_{1},t_{2})$ . Given what we know about $\tau$ so far, there must exists $t_{0}\in(t_{1},t_{2})$ such that $\tau(t_{0})=\pm\lambda$ . ∎

Next consider the set $\Omega^{\prime}=\left\{t\in[0,L]\colon\tau(t)\neq\pm\lambda\right\}\cup\Omega$ . This is an open set relative to $[0,L]$ as well.

Lemma 17.

The set $\Omega^{\prime}\setminus\Omega$ is discrete.

Proof.

As $f=0$ in $[0,L]\setminus\Omega$ , we know that $f^{\prime}=0$ almost everywhere in this set. Using (20), we conclude that $\tau^{\prime}\cdot\lambda=0$ almost everywhere, and (19) implies that $\lambda$ is in the subspace spanned by $\tau$ and $\tau^{\prime}$ almost everywhere in $[0,L]\setminus\Omega$ . Hence $\tau=\pm\lambda$ almost everywhere in $[0,L]\setminus\Omega$ . It follows that $\Omega^{\prime}\setminus\Omega$ is a null set, and so is $\Omega^{\prime}\setminus\overline{\Omega}$ . As the latter is an open set, it must be empty. So $\Omega^{\prime}\subseteq\overline{\Omega}$ .

For any $t_{0}\in\Omega^{\prime}\setminus\Omega$ , we may choose $\epsilon>0$ such that $\tau\neq\pm\lambda$ in $(t_{0}-\epsilon,t_{0}+\epsilon)\cap[0,L]$ by the continuity of $\tau$ . Let $J=(t_{0}-\epsilon,t_{0}+\epsilon)\cap(0,L)$ . Then $J$ cannot contain any connected components of $\Omega$ by Lemma 16. Therefore, the open set $J\cap\Omega$ consists of at most two intervals extending to one of the end points of $J$ . But we know that $J\subseteq\overline{\Omega}$ . Hence $J\cap\Omega=J\setminus\{t_{0}\}$ . We conclude that $t_{0}$ is an isolated point of $\Omega^{\prime}\setminus\Omega$ . That is, the set $\Omega^{\prime}\setminus\Omega$ is discrete. ∎

Lemma 18.

If $I$ is any connected component of $\Omega^{\prime}$ , then the restriction of $\tau$ to $I$ takes values in a great circle on $S^{n-1}$ through $\lambda$ .

Proof.

In view of Lemma 16 and Lemma 17, it suffices to examine what happens near a point $t_{0}\in I\setminus\Omega$ . There exists $\epsilon>0$ such that the restriction of $\tau$ to $(t_{0}-\epsilon,t_{0})$ follows a great circle through $\lambda$ , and the same statement applies to $(t_{0},t_{0}+\epsilon)$ . But as $t_{0}\in I\subseteq\Omega^{\prime}$ and $t_{0}\not\in\Omega$ , it is clear that $\tau(t_{0})\neq\pm\lambda$ . So we have the same great circle on both sides of $t_{0}$ , and the claim follows. ∎

We can now improve Lemma 17. This is the only place in the paper where we use the assumption that $\alpha$ is of bounded variation rather than just bounded.

Lemma 19.

If $I\subseteq\Omega^{\prime}$ is a connected component of $\Omega^{\prime}$ , then $I\setminus\Omega$ is finite.

Proof.

We argue by contradiction here, so we assume that $I\setminus\Omega$ is not finite. Then by Lemma 17, either $\inf I$ or $\sup I$ is an accumulation point of $I\setminus\Omega$ , and we assume for simplicity that this is true for $\sup I$ . (The arguments are similar if it is $\inf I$ .) Then there is a sequence $(t_{i})_{i\in\mathbb{N}}$ in $I\setminus\Omega$ such that $t_{i+1}>t_{i}$ and $(t_{i},t_{i+1})\subseteq\Omega$ for all $i\in\mathbb{N}$ . So $f(t_{i})=0$ for all $i\in\mathbb{N}$ . By Lemma 16, we know that $\tau$ follows a great circle through $\lambda$ with speed $k$ in the interval $(t_{i},t_{i+1})$ and there exists a point $\rho_{i}\in(t_{i},t_{i+1})$ such that $\tau(\rho_{i})=\pm\lambda$ for every $i\in\mathbb{N}$ . If $\tau(\rho_{i})=\lambda$ and $\tau(\rho_{i+1})=-\lambda$ or vice versa, then $\rho_{i+1}-\rho_{i}\geq\pi/k$ ; so this can happen at most a finite number of times. Dropping finitely many members of the sequence, we may assume that $\rho_{i+1}-\rho_{i}<\pi/k$ for every $i$ ; then $\tau(\rho_{i})$ has always the same sign and for simplicity we assume that $\tau(\rho_{i})=\lambda$ for every $i\in\mathbb{N}$ . Then

\lambda\cdot\tau(t)=\cos(k(t-\rho_{i}))

in $(t_{i},t_{i+1})$ for all $i\in\mathbb{N}$ .

It follows immediately that $\rho_{i+1}-t_{i+1}=t_{i+1}-\rho_{i}$ for every $i\in\mathbb{N}$ . Furthermore, equation (20) implies that

0=\int_{t_{i}}^{t_{i+1}}f^{\prime}(t)\,dt=-k\int_{t_{i}}^{t_{i+1}}\beta(t)\sin(k(t-\rho_{i}))\,dt.

Hence

k\int_{t_{i}}^{\rho_{i}}\beta(t)\left|\sin(k(t-\rho_{i}))\right|\,dt=k\int_{\rho_{i}}^{t_{i+1}}\beta(t)\left|\sin(k(t-\rho_{i}))\right|\,dt.

Define

b_{i}=k\int_{t_{i}}^{\rho_{i}}\left|\sin(k(t-\rho_{i}))\right|\,dt=1-\cos(k(\rho_{i}-t_{i}))

and

b_{i}^{\prime}=k\int_{\rho_{i}}^{t_{i+1}}\left|\sin(k(t-\rho_{i}))\right|\,dt=1-\cos(k(t_{i+1}-\rho_{i})).

If $b_{i}^{\prime}\leq b_{i}$ , then we may choose $\omega_{i}\in[t_{i},\rho_{i}]$ and $\omega_{i}^{\prime}\in[\rho_{i},t_{i+1}]$ such that

k\int_{t_{i}}^{\rho_{i}}\beta(t)\left|\sin(k(t-\rho_{i}))\right|\,dt\geq b_{i}\beta(\omega_{i})

and

k\int_{\rho_{i}}^{t_{i+1}}\beta(t)\left|\sin(k(t-\rho_{i}))\right|\,dt\leq b_{i}^{\prime}\beta(\omega_{i}^{\prime});

then

\frac{b_{i}^{\prime}}{b_{i}}\geq\frac{\beta(\omega_{i})}{\beta(\omega_{i}^{\prime})}.

If $b_{i}<b_{i}^{\prime}$ , then instead we choose $\omega_{i}\in[t_{i},\rho_{i}]$ and $\omega_{i}^{\prime}\in[\rho_{i},t_{i+1}]$ such that

k\int_{t_{i}}^{\rho_{i}}\beta(t)\left|\sin(k(t-\rho_{i}))\right|\,dt\leq b_{i}\beta(\omega_{i})

and

k\int_{\rho_{i}}^{t_{i+1}}\beta(t)\left|\sin(k(t-\rho_{i}))\right|\,dt\geq b_{i}^{\prime}\beta(\omega_{i}^{\prime});

then

\frac{b_{i}^{\prime}}{b_{i}}\leq\frac{\beta(\omega_{i})}{\beta(\omega_{i}^{\prime})}.

In both cases,

\left|1-\frac{b_{i}^{\prime}}{b_{i}}\right|\leq\left|1-\frac{\beta(\omega_{i})}{\beta(\omega_{i}^{\prime})}\right|=\frac{|\beta(\omega_{i}^{\prime})-\beta(\omega_{i})|}{|\beta(\omega_{i}^{\prime})|}\leq|\beta(\omega_{i}^{\prime})-\beta(\omega_{i})|\,\sup_{[0,\ell]}\frac{1}{\alpha}.

Hence

\sum_{i=1}^{\infty}\left|1-\frac{b_{i}^{\prime}}{b_{i}}\right|\leq\sup\biggl{\{}\sum_{j=1}^{J}|\alpha(s_{j})-\alpha(s_{j-1})|\colon 0\leq s_{0}\leq\dotsb\leq s_{J}\leq\ell\biggr{\}}\,\sup_{[0,\ell]}\frac{1}{\alpha}.

The right-hand side is finite, because $\alpha$ is assumed to be of bounded variation and $1/\alpha$ is bounded.

We have already seen that $t_{i+1}-\rho_{i}=\rho_{i+1}-t_{i+1}$ for every $i\in\mathbb{N}$ . This means that $b_{i}^{\prime}=b_{i+1}$ . We now apply Lemma 15 to the sequence $(b_{1},b_{1}^{\prime},b_{2},b_{2}^{\prime},\dotsc)$ . We infer that

\sum_{i=1}^{\infty}(b_{i}+b_{i}^{\prime})=\infty.

(27)

But clearly

\sum_{i=1}^{\infty}(\rho_{i}-t_{i})+\sum_{i=1}^{\infty}(t_{i+1}-\rho_{i})\leq L,

as this is the sum of the lengths of pairwise disjoint intervals in $(0,L)$ . Hence there exists $i_{0}\in\mathbb{N}$ such that

\rho_{i}-t_{i}\leq\frac{2}{k^{2}}\quad\text{and}\quad t_{i+1}-\rho_{i}\leq\frac{2}{k^{2}}

for all $i\geq i_{0}$ , which implies that

b_{i}=1-\cos(k(\rho_{i}-t_{i}))\leq\rho_{i}-t_{i}

and

b_{i}^{\prime}=1-\cos(k(t_{i+1}-\rho_{i}))\leq t_{i+1}-\rho_{i}.

Now we have a contradiction to (27). ∎

Lemma 20.

The set $\Omega^{\prime}$ has finitely many connected components.

Proof.

We can ignore any connected components of the form $[0,t_{2})$ or $(t_{1},L]$ . Thus we fix another connected component $I=(t_{1},t_{2})$ . Then $f(t_{1})=0$ and $\tau(t_{1})=\pm\lambda$ , and also $f(t_{2})=0$ and $\tau(t_{2})=\pm\lambda$ . Furthermore, by Lemma 19, there exists $t_{3}\in(t_{1},t_{2}]$ such that $f(t_{3})=0$ and $(t_{1},t_{3})\subseteq\Omega$ . According to Lemma 16, this implies that there exists $t_{4}\in(t_{1},t_{3})$ with $\tau(t_{4})=\pm\lambda$ . We further know that $\tau$ follows a great circle with speed $k$ in $(t_{1},t_{4})$ , and therefore $t_{4}-t_{1}\geq\pi/k$ . So there can only be finitely many connected components. ∎

Now we can complete the proof of Theorem 4 as follows.

By Lemma 20, we can partition $\Omega^{\prime}$ into finitely many connected components $I_{1},\dotsc,I_{M}$ . Let $t_{i}=\inf I_{i}$ and $t_{i}^{\prime}=\sup I_{i}$ for $i=1,\dotsc,M$ . Setting $A=[0,L]\setminus\bigcup_{i=1}^{M}I_{i}$ , we observe that $f=0$ and $\tau=\pm\lambda$ on $A$ .

The set $\tau(\overline{I}_{i})$ is contained in a two-dimensional subspace $X_{i}\subseteq\mathbb{R}^{n}$ with $\lambda\in X_{i}$ for every $i=1,\dotsc,M$ by Lemma 18. Hence Lemma 10 may be applied to the restriction of $\tau$ to $\overline{I}_{i}$ . Consequently, there exists a line $\mathcal{L}_{i}\subseteq X_{i}+c(t_{i})$ for every $i=1,\dotsc,M$ such that $\left\{t\in\overline{I}_{i}\colon f(t)=0\right\}=\left\{t\in\overline{I}_{i}\colon c(t)\in\mathcal{L}_{i}\right\}$ , where $c=\gamma\circ\phi$ . But we know that $f(t_{i})=0$ , except possibly for $i=1$ if $t_{1}=0$ , and that $f(t_{i}^{\prime})=0$ , except possibly for $i=M$ if $t_{M}^{\prime}=L$ . Moreover, each $\mathcal{L}_{i}$ is parallel to $\lambda$ . As $\tau=\pm\lambda$ on $A$ , we also conclude that $c([t_{i}^{\prime},t_{i+1}])$ is a line segment parallel to $\lambda$ for $i=1,\dotsc,M-1$ , and the same applies to $c([0,t_{1}])$ if $t_{1}>0$ and to $c([t_{M}^{\prime},L])$ if $t_{M}^{\prime}<L$ . Hence the lines $\mathcal{L}_{i}$ all coincide with a single line $\mathcal{L}\subseteq\mathbb{R}^{n}$ and $c(A)\subseteq\mathcal{L}$ .

If there are any points $t\in I_{i}\setminus\Omega$ , then we further subdivide $I_{i}$ . According to Lemma 19, there are only finitely many such points. Thus we obtain pairwise disjoint, relatively open intervals $I_{1}^{*},\ldots,I_{N}^{*}\subseteq[0,L]$ such that $c(t)\not\in\mathcal{L}$ for all $t\in I_{i}^{*}$ for $i=1,\dotsc,N$ but $c(t)\in\mathcal{L}$ for all $t\in[0,L]\setminus\bigcup_{i=1}^{N}I_{i}^{*}$ . Lemma 10 then further implies that $\tau^{\prime}$ is continuous with $|\tau^{\prime}|\equiv k$ in $I_{i}^{*}$ , and that there exists $\delta>0$ such that for any $t_{0}\in\overline{I_{i}^{*}}\setminus I_{i}^{*}$ , the inequality $\lambda\cdot\tau^{\prime}>0$ is satisfied in $(t_{0},t_{0}+\delta)\cap I_{i}^{*}$ and $\lambda\cdot\tau^{\prime}<0$ in $(t_{0}-\delta,t_{0})\cap I_{i}^{*}$ for all $i=1,\dotsc,N$ .

Reversing the reparametrisation from Section 2 and setting $J_{i}=\phi(I_{i}^{*})$ , we therefore find the situation described in statement i of Theorem 4.

Finally, we want to prove that every curve satisfying one of the conditions in Theorem 4 is indeed an $\infty$ -elastica. This is clear if $\gamma([0,L])$ is contained in a line, so we assume otherwise.

In the case of condition ii, the claim follows immediately from Proposition 12 and Proposition 11. If condition i is satisfied, we use Lemma 10 for any piece of $\gamma$ restricted to $\overline{J}_{i}$ . In order to work with the usual reparametrisation, we set $I_{i}=\psi(J_{i})$ and let $t_{i}=\inf I_{i}$ and $t_{i}^{\prime}=\sup I_{i}$ . Then Lemma 10 gives rise to $u_{i}\colon\overline{I}_{i}\to\mathbb{R}^{n}$ satisfying (10), (11) in $I_{i}$ with $u_{i}(t_{i})=0$ (unless $t_{i}=0$ ) and $u_{i}(t_{i}^{\prime})=0$ (unless $t_{i}^{\prime}=L$ ), but $u_{i}\neq 0$ in $I_{i}$ . Hence we define $u\colon[0,L]\to\mathbb{R}^{n}$ by

u(t)=\begin{cases}u_{i}(t)&\text{if }t\in I_{i},\ i=1,\dotsc,N,\\ 0&\text{else}.\end{cases}

Then (10) and (11) are satisfied almost everywhere in $(0,L)$ . Proposition 11 now completes the proof.

7 The Markov-Dubins problem

In this section, we first prove Proposition 5, thus establishing the connection to the Markov-Dubins problem of minimising length subject to curvature constraints. Then we show how to recover some of the main results of Dubins [8, Theorem I] and Sussmann [30, Theorem 1] from Theorem 4.

Proof of Proposition 5.

Suppose that $\gamma\in\mathcal{G}$ does not minimise $\mathcal{K}_{1}$ under the boundary conditions (1). We want to show that the curve parametrised by $\gamma$ is not an $R$ -geodesic. For $R>1/\mathcal{K}_{1}(\gamma)$ , this is obvious, as $\gamma$ does not satisfy the required curvature constraint. Thus we assume that $R\leq 1/\mathcal{K}_{1}(\gamma)$ .

We may assume without loss of generality that $a_{1},a_{2}\in\{0\}^{n-1}\times\mathbb{R}$ . In the following, we write $x=(x^{\prime},x_{n})$ for a generic point $x=(x_{1},\dotsc,x_{n})\in\mathbb{R}^{n}$ , where $x^{\prime}=(x_{1},\dotsc,x_{n-1})$ . Let $\epsilon>0$ and consider the map $\Phi_{\epsilon}\colon\mathbb{R}^{n}\to\mathbb{R}^{n}$ defined by

\Phi_{\epsilon}(x)=\left(\frac{x^{\prime}}{1+\epsilon|x^{\prime}|^{2}},x_{n}\right).

This has the derivative $d\Phi_{\epsilon}(0,x_{n})=\mathrm{id}_{\mathbb{R}^{n}}$ for any $x_{n}\in\mathbb{R}$ . We have the convergence $\Phi_{\epsilon}\to\mathrm{id}_{\mathbb{R}^{n}}$ in $C^{2}(C;\mathbb{R}^{n})$ for any compact set $C\subseteq\mathbb{R}^{n}$ as $\epsilon\to 0$ . Moreover, for any $x,V\in\mathbb{R}^{n}$ , unless $x^{\prime}=0$ or $V^{\prime}=0$ , we find that $|d\Phi_{\epsilon}(x)V|<|V|$ . Now choose $\hat{\gamma}\in\mathcal{G}$ with $\mathcal{K}_{1}(\hat{\gamma})<\mathcal{K}_{1}(\gamma)$ . Consider $\hat{\gamma}_{\epsilon}=\Phi_{\epsilon}\circ\hat{\gamma}$ for some $\epsilon>0$ that remains to be determined. Then $\hat{\gamma}_{\epsilon}$ still satisfies the boundary conditions (1).

As $\gamma$ does not minimise $\mathcal{K}_{1}$ by the above assumption, we conclude that $\gamma([0,\ell])\not\subseteq\{0\}^{n-1}\times\mathbb{R}$ . Hence $|a_{2}-a_{1}|<\ell$ and $\hat{\gamma}([0,\ell])$ is not contained in $\{0\}^{n-1}\times\mathbb{R}$ either. Therefore, the length of $\hat{\gamma}_{\epsilon}$ is strictly less than $\ell$ . But $\hat{\gamma}_{\epsilon}\to\hat{\gamma}$ in $C^{2}([0,\ell])$ as $\epsilon\to 0$ . Hence for some $\epsilon>0$ small enough, we conclude that the curvature $\hat{\kappa}_{\epsilon}$ of $\hat{\gamma}_{\epsilon}$ satisfies $\|\hat{\kappa}_{\epsilon}\|_{L^{\infty}(0,\ell)}\leq\mathcal{K}_{1}(\gamma)\leq 1/R$ . Hence we have found a shorter curve with the same boundary data satisfying the required curvature constraint. ∎

Now suppose that $n=2$ . We wish to give an alternative proof of Dubins’s main result [8, Theorem I] based on Theorem 4. Let $k>0$ and consider a $1/k$ -geodesic parametrised by $\gamma\in\mathcal{G}$ . Then Proposition 5 and Theorem 4 imply that $\gamma$ is consistent with one of the descriptions a or b in the introduction.

In the case a, it is clear that any minimiser of the length will not contain any full circles, so the curve will at most consist of a circular arc, followed by a line segment, followed by another circular arc. This is one of the solutions described by Dubins.

In the case b, we have a sequence of several circular arcs. If there were more than four pieces, then it is also easy to see that a piece of the curve could be replaced by a line segment, thus reducing the length. This is of course impossible for a minimiser of the length, hence we have four or fewer pieces. In order to see that four consecutive circular arcs are also impossible, we still need Dubins’s Lemma 2. Almost all of Dubins’s other arguments, however, have been bypassed.

Sussmann’s results for $n=3$ [30, Theorem 1] follow in a similar way from Theorem 4 and again one of Dubins’s lemmas. If we have a solution as in statement i, then we first distinguish the following two cases. If the entire curve is planar, we apply the above reasoning. (Sussmann’s theorem contains another statement in this case, which is a consequence of a result of Dubins [8, Sublemma].) Otherwise, we note that the curve must meet the line $\mathcal{L}$ tangentially. Then we may have a circular arc at either end of the curve and we may have some intermediate pieces. But if one of these intermediate pieces is not a segment of $\mathcal{L}$ , it is clear that it must be a full circle. This clearly cannot happen for a solution of the Markov-Dubins problem, so in fact we have (at most) a concatenation of a circular arc, a line, and another circular arc. A solution as in statement ii, on the other hand, is a helicoidal arc in Sussmann’s terminology.

8 Examples

We finally examine a few examples of minimisers and $\infty$ -elasticas, which highlight some features and some limitations of the theory. Throughout this section, we assume that $\alpha\equiv 1$ .

Example 21 (Circular arc).

We first consider a circular arc parametrised by $\gamma\colon[0,\ell]\to\mathbb{R}^{2}$ with $\gamma(s)=r(\cos(s/r),\sin(s/r))$ and with tangent vector $T(s)=(-\sin(s/r),\cos(s/r))$ and constant curvature $k=1/r$ . This is an $\infty$ -elastica by Theorem 4. If we want to check equations (2) and (3) directly, then we first compute $T^{\prime\prime}+k^{2}T=0$ . Moreover, the vectors $T$ and $T^{\prime}$ span $\mathbb{R}^{2}$ everywhere, so $\operatorname{proj}_{T,T^{\prime}}^{\perp}(\lambda)=0$ regardless of the value of $\lambda$ . Thus we only need to consider equation (3), which gives $g^{\prime}(s)=-\frac{1}{r}(\lambda_{1}\cos(s/r)+\lambda_{2}\sin(s/r))$ . This is satisfied for $g(s)=\lambda_{2}\cos(s/r)-\lambda_{1}\sin(s/r)+h=\lambda\cdot T(s)+h$ for any $h\in\mathbb{R}$ . Clearly we can choose $h$ such that $g\geq 0$ in $[0,\ell]$ .

Now suppose that we wish to apply Theorem 3. We have a minimiser of $\mathcal{K}_{1}$ if the inequalities $0\leq\lambda\cdot T+h\leq-\lambda\cdot T$ are satisfied simultaneously. They give rise to the conditions

\frac{h}{2}\leq\min_{[0,\ell]}(-\lambda\cdot T)\leq\max_{[0,\ell]}(-\lambda\cdot T)\leq h.

It is possible to satisfy these if, and only if, $\ell\leq 2\pi r/3$ , in which case we can choose $\lambda=(\sqrt{3}/2,-1/2)$ and $h=1$ . Thus a circular arc of radius $r$ minimises $\mathcal{K}_{1}$ if its length does not exceed $2\pi r/3$ .

The example shows that the condition of Theorem 3 is sufficient but not necessary, for the above circular arc is still a minimiser as long as $\ell\leq 2\pi r$ by the results of Schmidt [27].

Next we consider the question whether the notion of an $\infty$ -elastica is genuinely more general than that of a minimiser of $\mathcal{K}_{\alpha}$ . The answer is yes, and the following example gives a one-parameter family of $\infty$ -elasticas that are not minimisers and not even local minimisers with respect to the $W^{1,2}$ -topology.

Example 22 (Non-minimising $\infty$ -elastica).

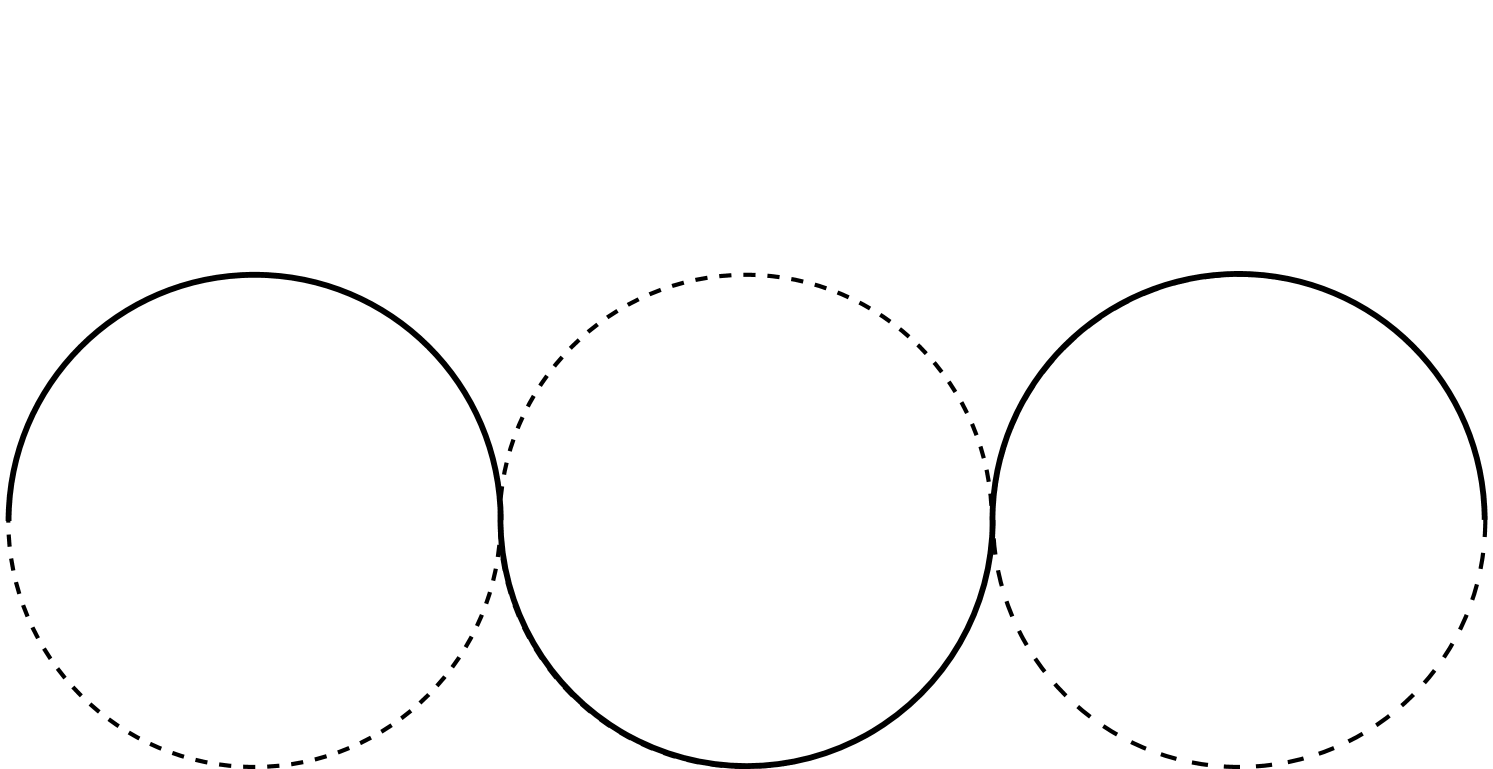
Consider curves with end points $a_{1}=(-1,0)$ and $a_{2}=(1,0)$ and tangent vectors $T_{1}=(0,1)$ and $T_{2}=(0,-1)$ . If $\ell=\pi$ , then there is one candidate that consists of three semicircles of radius $1/3$ ; this is illustrated in Figure 2(a). It is an $\infty$ -elastica by Theorem 4.

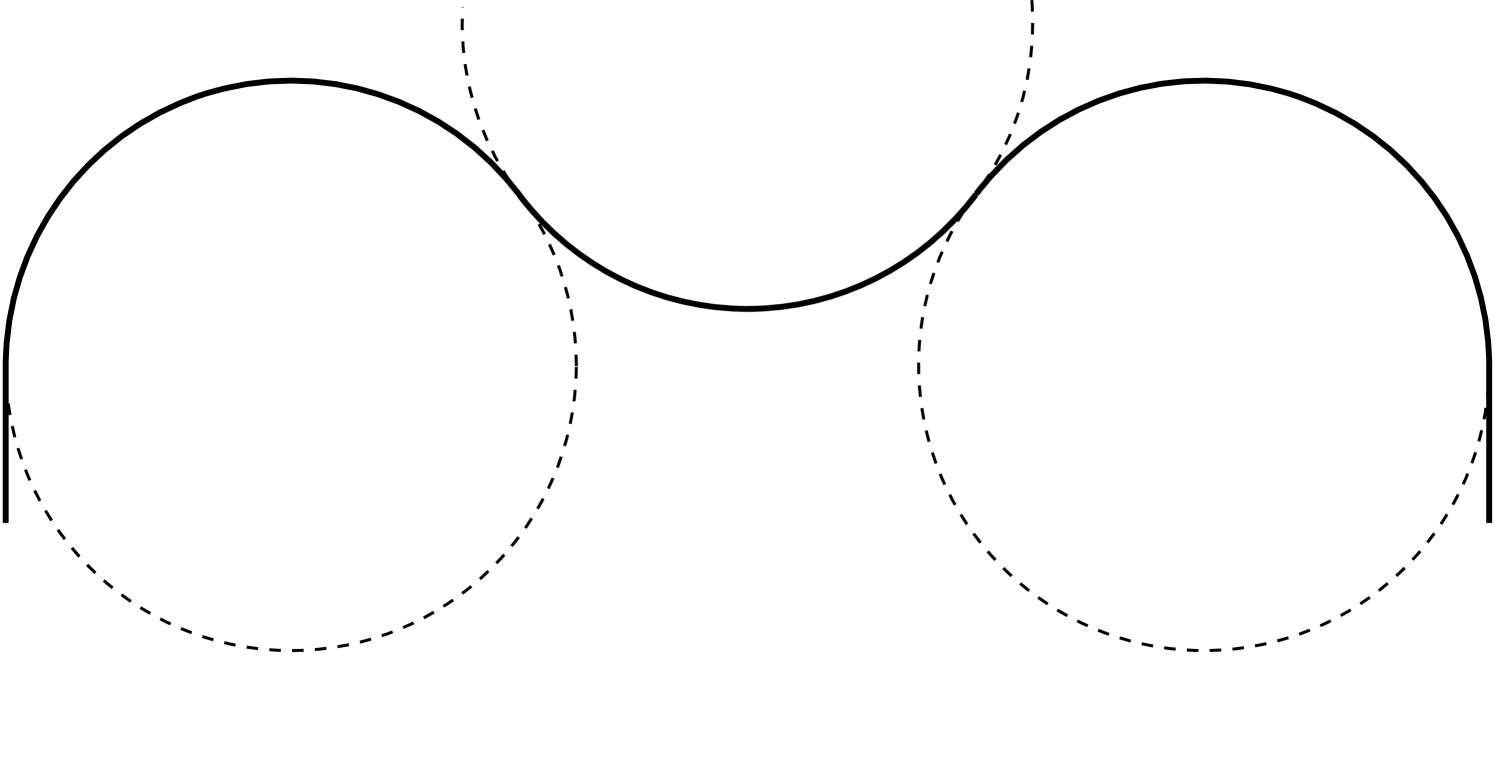
For $r\in[1/3,1)$ , we also construct some comparison curves including three circular arcs of radius $r$ . To this end, define $\omega(r)=\arccos((1-r)/2r)$ . For $h\in\mathbb{R}$ , there is a curve comprising three circular arcs of radius $r$ , with centres

(r-1,h),\quad(0,h+2r\sin\omega(r)),\quad(1-r,h),

that connects the points $(-1,h)$ and $(1,h)$ . The length of this curve is $\tilde{\ell}(r)=r(3\pi-4\omega(r))$ . We compute $\tilde{\ell}(1/3)=\pi=\tilde{\ell}(1)$ and

\tilde{\ell}^{\prime\prime}(r)=\frac{4(1-r)}{r(3r^{2}+2r-1)^{3/2}}>0

in $(1/3,1)$ . Hence $\tilde{\ell}(r)<\pi$ for all $r\in(1/3,1)$ . If we choose $h=(\pi-\tilde{\ell}(r))/2$ , we can attach a line segment to each end and thereby construct a comparison curve of length $\pi$ that satisfies the required boundary conditions (see Figure 2(b)). But the value of $\mathcal{K}_{1}$ is $1/r<3$ .

Finally we have an example of a three-dimensional $\infty$ -elastica, showing that both cases in Theorem 4 can indeed occur.

Example 23 (Helical arc).

Consider $\gamma\colon[0,\ell]\to\mathbb{R}^{3}$ given by

\gamma(s)=(r\cos\omega\cos(s/r),r\cos\omega\sin(s/r),s\sin\omega)

for some $\omega\in(0,\pi/2)$ . The curvature of this curve is $k=r^{-1}\cos\omega$ . For $T=\gamma^{\prime}$ , we compute

T^{\prime\prime}+k^{2}T=\frac{\sin\omega\cos\omega}{r^{2}}(\sin\omega\sin(s/r),-\sin\omega\cos(s/r),\cos\omega).

Now let $\lambda=(0,0,1)$ . Then $\lambda\cdot T=\sin\omega$ . In order to find $\operatorname{proj}_{T,T^{\prime}}^{\perp}(\lambda)$ , we first compute

N=\frac{r}{\cos\omega}T\times T^{\prime}=(\sin\omega\sin(s/r),-\sin\omega\cos(s/r),\cos\omega)

and note that $N$ is a unit vector perpendicular to $T$ and $T^{\prime}$ . Hence

\operatorname{proj}_{T,T^{\prime}}(\lambda)=(\lambda\cdot N)N=\cos\omega(\sin\omega\sin(s/r),-\sin\omega\cos(s/r),\cos\omega).

Choosing $\eta=\sin\omega-\cos\omega\cot\omega$ , we see that equation (4) is satisfied. Hence $\gamma$ is an $\infty$ -elastica.

References

[1] G. Aronsson, Minimization problems for the functional ${\rm sup}_{x}\,F(x,\,f(x),\,f^{\prime}(x))$ , Ark. Mat. 6 (1965), 33–53.
[2] , Minimization problems for the functional ${\rm sup}_{x}\,F(x,f(x),f^{\prime}(x))$ . II, Ark. Mat. 6 (1966), 409–431.
[3] , Extension of functions satisfying Lipschitz conditions, Ark. Mat. 6 (1967), 551–561.
[4] , On certain minimax problems and Pontryagin’s maximum principle, Calc. Var. Partial Differential Equations 37 (2010), no. 1-2, 99–109.
[5] W. Blaschke, Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Band I. Elementare Differentialgeometrie, Dover Publications, New York, N. Y., 1945, 3d ed.
[6] R. Bryant and P. Griffiths, Reduction for constrained variational problems and $\int{1\over 2}k^{2}\,ds$ , Amer. J. Math. 108 (1986), no. 3, 525–570.
[7] S. S. Chern, Curves and surfaces in Euclidean space, Studies in Global Geometry and Analysis, Math. Assoc. Amer. (distributed by Prentice-Hall, Englewood Cliffs, N.J.), 1967, pp. 16–56.
[8] L. E. Dubins, On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents, Amer. J. Math. 79 (1957), 497–516.
[9] L. Euler, Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti, Marc-MichelBousquet & Co., Lausanne–Geneva, 1744.
[10] V. Ferone, B. Kawohl, and C. Nitsch, Generalized elastica problems under area constraint, Math. Res. Lett. 25 (2018), no. 2, 521–533.
[11] R. Huang, A note on the $p$ -elastica in a constant sectional curvature manifold, J. Geom. Phys. 49 (2004), no. 3-4, 343–349.
[12] N. Katzourakis, An introduction to viscosity solutions for fully nonlinear PDE with applications to calculus of variations in $L^{\infty}$ , SpringerBriefs in Mathematics, Springer, Cham, 2015.
[13] N. Katzourakis and R. Moser, Existence, uniqueness and structure of second order absolute minimisers, Arch. Ration. Mech. Anal. 231 (2019), no. 3, 1615–1634.
[14] N. Katzourakis and E. Parini, The eigenvalue problem for the $\infty$ -Bilaplacian, NoDEA Nonlinear Differential Equations Appl. 24 (2017), no. 6, Art. 68, 25.
[15] N. Katzourakis and T. Pryer, Second-order $L^{\infty}$ variational problems and the $\infty$ -polylaplacian, Adv. Calc. Var. (Ahead of Print) (2018), DOI:10.1515/acv-2016-0052.
[16] , On the numerical approximation of $p$ -biharmonic and $\infty$ -biharmonic functions, Numer. Methods Partial Differential Equations 35 (2019), no. 1, 155–180.
[17] J. Langer and D. A. Singer, Knotted elastic curves in ${\bf R}^{3}$ , J. London Math. Soc. (2) 30 (1984), no. 3, 512–520.
[18] , The total squared curvature of closed curves, J. Differential Geom. 20 (1984), no. 1, 1–22.
[19] J. Laumond, S. Sekhavat, and F. Lamiraux, Guidelines in nonholonomic motion planning for mobile robots, Robot Motion Planning and Control, Lecture Notes in Control and Information Sciences, vol. 229, Springer-Verlag, Berlin–Heidelberg, 1998, pp. 1–53.
[20] A. Linnér, Explicit elastic curves, Ann. Global Anal. Geom. 16 (1998), no. 5, 445–475.
[21] A. A. Markov, Some examples of the solution of a special kind of problem on greatest and least quantities, Soobshch. Kharkovsk. Mat. Obshch. 1 (1887), 250–276, in Russian.
[22] S. Masnou and J.-M. Morel, Level lines based disocclusion, Proceedings 1998 IEEE International Conference on Image Processing, 1998, pp. 259–263.
[23] R. Moser and H. Schwetlick, Minimizers of a weighted maximum of the Gauss curvature, Ann. Global Anal. Geom. 41 (2012), no. 2, 199–207.
[24] W. A Oldfather, C. A. Ellis, and D. M. Brown, Leonhard Euler’s elastic curves, Isis 20 (1933), 72–160.
[25] J. A. Reeds and L. A. Shepp, Optimal paths for a car that goes both forwards and backwards, Pacific J. Math. 145 (1990), no. 2, 367–393.
[26] Z. N. Sakellaris, Minimization of scalar curvature in conformal geometry, Ann. Global Anal. Geom. 51 (2017), no. 1, 73–89.
[27] E. Schmidt, Über das Extremum der Bogenlänge einer Raumkurve bei vergeschriebenen Einschränkungen ihrer Krümmung, Sitzungsberichte preuss. Akad. Wissenschaften Berlin 1925 (1925), 485–490.
[28] A. Schur, Über die Schwarzsche Extremaleigenschaft des Kreises unter den Kurven konstanter Krümmung, Math. Ann. 83 (1921), 143–148.
[29] L. Simon, Theorems on regularity and singularity of energy minimizing maps, Lectures in Math. ETH Zürich, Birkhäuser, Basel, 1996.
[30] H. J. Sussmann, Shortest 3-dimensional paths with a prescribed curvature bound, Proceedings of 1995 34th IEEE Conference on Decision and Control, vol. 4, 1995, pp. 3306–3312.

	$\displaystyle\int_{0}^{L}\eta\|\tau_{p}^{\prime}\|^{p}\tau_{p}\cdot\Lambda_{p}\,dt$	$\displaystyle\leq Lk_{p}^{p}\|\Lambda_{p}\|,$
	$\displaystyle-\int_{0}^{L}\eta^{\prime}\|\tau_{p}^{\prime}\|^{p-2}\tau_{p}^{\prime}\cdot\Lambda_{p}\,dt$	$\displaystyle\leq\frac{5p^{2}}{\delta}Lk_{p}^{p-1}\|\Lambda_{p}\|,$
	$\displaystyle\int_{0}^{L}\eta\beta\left(\tau_{0}-(\tau_{0}\cdot\tau_{p})\tau_{p}\right)\cdot\Lambda_{p}\,dt$	$\displaystyle\leq L\\|\alpha\\|_{L^{\infty}(0,\ell)}\|\Lambda_{p}\|.$

Structure and classification results for the ∞\infty-elastica problem

Abstract

1 Introduction

Definition 1 (∞\infty-elastica).

Theorem 2 (Characterisation by differential equations).

Theorem 3 (Sufficient condition for minimisers).

Theorem 4 (Structure and classification).

Proposition 5 (RR-geodesics minimise 𝒦1\mathcal{K}_{1}).

2 Reparametrisation and approximation

Definition 6.

Proposition 7.

Proof.

Lemma 8.

Proof.

3 Preliminary properties of ∞\infty-elasticas

Proposition 9.

Proof.

Lemma 10.

Proof.

4 Analysis of the differential equations

Proposition 11.

Proof.

Proposition 12.

Proof.

Lemma 13.

Proof.

Proofs of Theorem 2 and Theorem 3.

5 Preparation for the proof of Theorem 4

Lemma 14.

Proof.

Lemma 15.

Proof.

6 Proof of Theorem 4

Lemma 16.

Proof.

Lemma 17.

Proof.

Lemma 18.

Proof.

Lemma 19.

Proof.

Lemma 20.

Proof.

7 The Markov-Dubins problem

Proof of Proposition 5.

8 Examples

Example 21 (Circular arc).

Example 22 (Non-minimising ∞\infty-elastica).

Example 23 (Helical arc).

References

Structure and classification results for the $\infty$ -elastica problem

Definition 1 ( $\infty$ -elastica).

Proposition 5 ( $R$ -geodesics minimise $\mathcal{K}_{1}$ ).

3 Preliminary properties of $\infty$ -elasticas

Example 22 (Non-minimising $\infty$ -elastica).