Structure of ${}^{13}\mathrm{C}$ in the Cluster Shell Model

To obtain the single-particle energy levels, we define

$\displaystyle H\;=\;T+V(\vec{r})+V_{\rm so}(\vec{r})+\frac{1}{2}(1+\tau_{3})V_{\rm C}(\vec{r})~{},$

(1)

i.e. the sum of the kinetic energy, a central potential obtained by convoluting the density

	$\displaystyle\rho(\vec{r})=$	$\displaystyle\left(\frac{\alpha}{\pi}\right)^{3/2}\sum_{i=1}^{k}\exp\left[-\alpha\left(\vec{r}-\vec{r}_{i}\right)^{2}\right]$
	$\displaystyle=$	$\displaystyle\left(\frac{\alpha}{\pi}\right)^{3/2}\mbox{e}^{-\alpha(r^{2}+\beta^{2})}\,4\pi\,\sum_{\lambda\mu}i_{\lambda}(2\alpha\beta r)\,Y_{\lambda\mu}(\theta,\phi)\sum_{i=1}^{k}Y_{\lambda\mu}^{\ast}(\theta_{i},\phi_{i})~{},$		(2)

with the interaction between the $\alpha$-particle and the nucleon, a spin-orbit interaction, and a Coulomb potential for an odd proton. In equation 1, $\vec{r}_{i}=(r_{i},\theta_{i},\phi_{i})$ represent the coordinates of the $\alpha$-particles with respect to the center-of-mass of the cluster structure. The case of ¹³C belongs to $k=3$ with an equilateral triangular configuration, whose coordinates are given by $(\beta,\frac{\pi}{2},0)$, $(\beta,\frac{\pi}{2},\frac{2\pi}{3})$ and $(\beta,\frac{\pi}{2},\frac{4\pi}{3})$. The deformation parameter (from spherical symmetry) is $\beta$, which is the distance of each of the alpha particles to the center of mass of the cluster structure. The resulting potentials are

	$\displaystyle V\left(\vec{r}\right)$	$\displaystyle=-V_{0}\sum_{\lambda\mu}f_{\lambda}\left(r\right)Y_{\lambda\mu}\left(\theta,\phi\right)\sum_{i=1}^{k}Y_{\lambda\mu}^{*}\left(\theta_{i},\phi_{i}\right),$		(3)
	$\displaystyle V_{so}\left(\vec{r}\right)$	$\displaystyle=V_{0,so}\frac{1}{2}\left[\frac{1}{r}\frac{\partial V\left(\vec{r}\right)}{\partial r}\left(\vec{s}\cdot\vec{l}\right)+\left(\vec{s}\cdot\vec{l}\right)\frac{1}{r}\frac{\partial V\left(\vec{r}\right)}{\partial r}\right],$		(4)
	$\displaystyle f_{\lambda}\left(r\right)$	$\displaystyle=e^{-\alpha\left(r^{2}+\beta^{2}\right)}4\pi i_{\lambda}\left(2\alpha\beta r\right).$		(5)

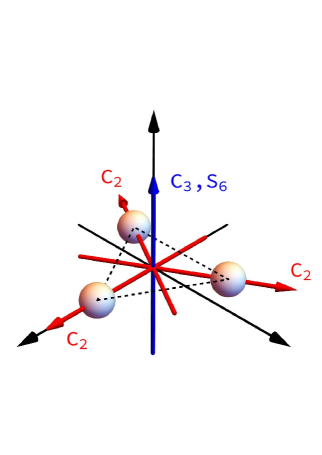
To construct a complete wave function we need to understand in more detail the ${\cal D}^{\prime}_{3h}$ symmetry. The objective is to construct a symmetry-adapted basis for ${\cal D}^{\prime}_{3h}$ symmetry instead of a spherical basis[17, 18]. In the case of triangular symmetry the eigenstates of equation 1 can be classified according to the doubly degenerate spinor representations of the double point group ${\cal D}^{\prime}_{3h}$ [19, 20]: $\Omega=E_{1/2}$, $E_{5/2}$ and $E_{3/2}$, or in the notation of Ref. [17] $\Omega=E_{1/2}^{(+)}$, $E_{1/2}^{(-)}$ and $E_{3/2}$, respectively. From similar work in molecular physics, to differentiate between the degenerate states, one finds all rotations of the structure of study; the case in question is shown in figure 1. Then improper rotations are used (in this case the $S_{6}$) to identify the intrinsic states of the doubly degenerate spinor representations. The resulting labels are $\gamma=\pm 5/2$ for $\Omega=E_{5/2}$, $\gamma=\pm 1/2$ for $E_{1/2}$ and $\gamma=\pm 3/2$ for $E_{3/2}$. The Hamiltonian of the CSM is solved in the body-fixed system, using the harmonic oscillator basis $|nljm\rangle$.

$\displaystyle\phi_{\Omega\gamma}=$

$\displaystyle\sum_{nljm}C^{\Omega\gamma}_{nljm}\left|nljm\right>$

(6)

The rotational states can be labeled by the angular momentum $I$, parity $P$, and its projection $K$ on the symmetry axis, $|I^{P}K\rangle$. Both $I$ and $K$ are half integers. Then the allowed values of $K^{P}$ for each one of the spinor representations, along with their $\gamma$ labels are given by [17, 18]

$\displaystyle\begin{array}[]{lcl}\Omega=E_{1/2},\;\gamma=\pm\frac{1}{2}&:&K^{P}=\pm\frac{1}{2}^{+},\mp\frac{5}{2}^{-},\pm\frac{7}{2}^{-},\ldots\\ \Omega=E_{5/2},\;\gamma=\pm\frac{5}{2}&:&K^{P}=\mp\frac{1}{2}^{-},\pm\frac{5}{2}^{+},\mp\frac{7}{2}^{+},\ldots\\ \Omega=E_{3/2},\;\gamma=\pm\frac{3}{2}&:&K^{P}=\pm\frac{3}{2}^{+},\mp\frac{3}{2}^{-},\mp\frac{9}{2}^{+},\ldots\end{array}$

(10)

with $I=|K|$, $|K|+1$, $\ldots$. A schematic view can be seen in figure 2. The complete wave function is defined then by [18]

$\displaystyle\left|\Omega\gamma;I^{P}MK\right>=\sqrt{\frac{2I+1}{16\pi^{2}}}\psi_{v}\left(1+{\cal S}_{i}^{-1}{\cal S}_{e}\right)\phi_{\Omega\gamma}D_{MK}^{I}(\omega)$

(11)

where $\psi_{v}$ is the vibrational wave function, $\phi_{\Omega\gamma}$ the intrinsic wave function and $D_{MK}^{I}(\omega)$ the rotational wave function. The wave function is invariant under the transformation ${\cal S}_{i}^{-1}{\cal S}_{e}$ where the operator ${\cal S}$ is the product of a rotation about $\pi$ followed by a parity transformation [18]. The operator ${\cal S}_{i}^{-1}$ acts on the intrinsic wave function and ${\cal S}_{e}$ on the rotational wave function.

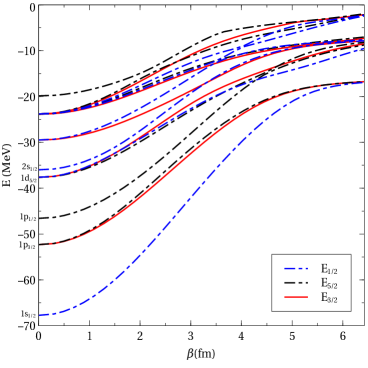
Previous work on the splitting of single-particle levels is shown in [13, 21]. The splitting of the single-particle energy levels is seen in figure 3. Two simple observations that are illustrated in the figure are that at a value of $\beta=0$ the spherical symmetry is recovered, and at max value, we have 3-fold degeneracy of the spherical symmetry. In other words, at the max value we obtain the view of a particle in a field formed by three separate (not bound in a nucleus) alpha particles, which is unlike the Nilsson model where in the case of max deformation one obtains the splitting for an ”infinite cigar”. From the elastic form factors, one obtains the value for $\beta$ and then comes back to figures 3 and 2 and obtains the base rotational band proposed for ¹³C. Foreshadowing the subsequent section, the value obtained for $\beta$ is 1.71 fm, which in turn gives the ground state rotational band as $\Omega=E_{5/2}$, and the ground state with $I^{P}=\frac{1}{2}^{-}$.

The charge distribution is taken to be section 2.1, plus a point-like distribution for the extra nucleon

$\displaystyle\rho(\vec{r})=\frac{(Ze)_{\rm c}}{3}\left(\frac{\alpha}{\pi}\right)^{3/2}\sum_{i=1}^{3}\exp\left[-\alpha\left(\vec{r}-\vec{r}_{i}\right)^{2}\right]+\tilde{e}\delta(\vec{r}-\vec{r}_{\rm sp}),$

(12)

$(Ze)_{\rm c}$ is the electric charge of the $3\alpha$ core nucleus, and $\tilde{e}$ the effective charge of the extra nucleon, which for the case of ¹³C is taken to be zero. Making a Fourier transformation of equation 12, and then summing over final and averaged over initial states, we obtain the multipoles of the longitudinal (Coulomb) form factor;

$\displaystyle F_{C\lambda}\left(q;\Omega^{\prime}\gamma^{\prime},I^{\prime}K^{\prime}\rightarrow\Omega\gamma,IK\right)$

$\displaystyle=\frac{\sqrt{4\pi}}{\left(Ze\right)_{\mathrm{odd}}}\langle I^{\prime},K^{\prime},\lambda,K-K^{\prime}\left|I,K\right\rangle\delta_{\Omega\Omega^{\prime}}\delta_{\gamma\gamma^{\prime}}G_{vv^{\prime}}^{\mathrm{c}}\left(q\right),$

(13)

where $(Ze)_{\rm odd}$ denotes the electric charge of the odd nucleus. For the vibrationally elastic case with $v=v^{\prime}=0$ the collective part is given by

$\displaystyle G^{\rm c}_{00}(q;\lambda,K-K^{\prime})$

$\displaystyle=(Ze)_{\rm c}\,j_{\lambda}(q\beta)\,\mbox{e}^{-q^{2}/4\alpha}\,Y_{\lambda,K-K^{\prime}}(\frac{\pi}{2},0)\,\delta_{K-K^{\prime},3\kappa}$

(14)

A final remark arises when calculating form factors with diagonal intrinsic states. In that case, branching ratios are found between different form factors with the same multipole.

$\displaystyle\frac{\left|F_{C\lambda}(q;\Omega\gamma,I^{\prime}K^{\prime}\rightarrow\Omega\gamma,I_{1}K_{1})\right|^{2}}{\left|F_{C\lambda}(q;\Omega\gamma,I^{\prime}K^{\prime}\rightarrow\Omega\gamma,I_{2}K_{2})\right|^{2}}=\frac{\left<I^{\prime},K^{\prime},\lambda,K_{1}-K^{\prime}|I_{1},K_{1}\right>^{2}}{\left<I^{\prime},K^{\prime},\lambda,K_{2}-K^{\prime}|I_{2},K_{2}\right>^{2}}.$

(15)

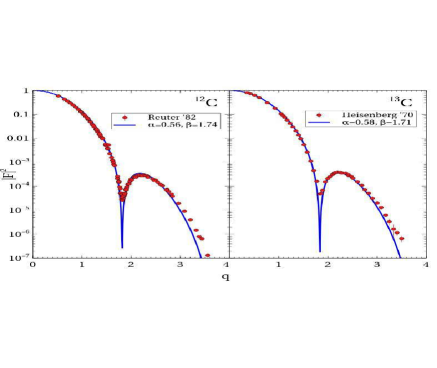
Finally one sees that the single particle element for Coulomb form factors doesn’t give any contribution to the total value, thus we expect that for both ¹²C and ¹³C to have the same q dependence. The results are illustrated in figures 4 and 5.

Just as previously done for the Coulomb form factors, the transverse form factors are obtained from a Fourier transform of the current $\vec{J}$ and magnetization operator $\vec{\mu}$, with a little more algebra involved to obtain the final expressions. The main assumption we do from the CSM is that the only contributor to both is the extra nucleon

	$\displaystyle\vec{J}$	$\displaystyle=0$		(16)
	$\displaystyle\vec{\mu}$	$\displaystyle=\delta\left(\vec{r_{i}}-\vec{x}\right)\mu_{i}\frac{\vec{\sigma}\left(i\right)}{2M_{i}},$		(17)

where $\mu_{i}$ is the magnetic moment (in nuclear magnetons) of the nucleon involved, in this case for the free neutron is $\mu_{n}=-1.91$ and $M_{i}$ is the mass. The multipoles for the transverse form factor are then given by

	$\displaystyle F_{E\lambda/M\lambda}(q;\Omega^{\prime}\gamma^{\prime},I^{\prime}K^{\prime}$	$\displaystyle=\left<I^{\prime},K^{\prime},\lambda,K-K^{\prime}|I,K\right>\delta_{vv^{\prime}}G_{\Omega\gamma,\Omega^{\prime}\gamma^{\prime}}^{{\rm sp}}(q)$
		$\displaystyle+P(-1)^{I+K}\left<I^{\prime},K^{\prime},\lambda,-K-K^{\prime}|I,-K\right>\delta_{vv^{\prime}}H_{\Omega\gamma,\Omega^{\prime}\gamma^{\prime}}^{{\rm sp}}(q),$		(18)

where $G_{\Omega\gamma,\Omega^{\prime}\gamma^{\prime}}^{{\rm sp}}(q)$ and $H_{\Omega\gamma,\Omega^{\prime}\gamma^{\prime}}^{{\rm sp}}(q)$ will have the form

	$\displaystyle G^{\rm sp}_{\Omega\gamma,\Omega^{\prime}\gamma^{\prime}}(q)$	$\displaystyle=\sum_{nljm}\sum_{n^{\prime}l^{\prime}j^{\prime}m^{\prime}}C^{\Omega\gamma}_{nljm}C^{\Omega^{\prime}\gamma^{\prime}}_{n^{\prime}l^{\prime}j^{\prime}m^{\prime}}\left<nljm\left|\hat{T}_{\lambda\mu}^{\zeta}\left(q,\vec{r}\,\right)\right|n^{\prime}l^{\prime}j^{\prime}m^{\prime}\right>$		(19a)
	$\displaystyle H^{\rm sp}_{\Omega\gamma,\Omega^{\prime}\gamma^{\prime}}(q)$	$\displaystyle=\sum_{nljm}\sum_{n^{\prime}l^{\prime}j^{\prime}m^{\prime}}C^{\Omega\gamma}_{nljm}C^{\Omega^{\prime}\gamma^{\prime}}_{n^{\prime}l^{\prime}j^{\prime}m^{\prime}}(-1)^{n+j+m}\left<nlj,-m\left|\hat{T}_{\lambda\mu}^{\zeta}\left(q,\vec{r}\,\right)\right|n^{\prime}l^{\prime}j^{\prime}m^{\prime}\right>$		(19b)

and $\hat{T}_{\lambda\mu}^{\zeta}\left(q,\vec{r}\,\right)$ are the electric/magnectic transverse form factor operators

	$\displaystyle\hat{T}_{\lambda\mu}^{E}\left(q,\vec{r}\,\right)$	$\displaystyle=q\frac{\mu_{i}}{2M_{N}}\vec{M}_{\lambda,\lambda}^{\mu}(\vec{r_{i}})\cdot\vec{\sigma}(i)$
	$\displaystyle\hat{T}_{\lambda\mu}^{M}\left(q,\vec{r}\,\right)$	$\displaystyle=iq\frac{\mu_{i}}{2M_{N}}\left(-\sqrt{\frac{\lambda}{2\lambda+1}}\vec{M}_{\lambda,\lambda+1}^{\mu}(\vec{r_{i}})+\sqrt{\frac{\lambda+1}{2\lambda+1}}\vec{M}_{\lambda,\lambda-1}^{\mu}(\vec{r_{i}})\right)\cdot\vec{\sigma}(i)$
	$\displaystyle\vec{M}_{\lambda_{1},\lambda_{2}}^{\mu}\left(\vec{r}\,\right)$	$\displaystyle=j_{\lambda_{2}}(qr)\vec{Y}_{\lambda_{1}\lambda_{2}1}^{\mu}(\theta,\phi).$		(20)

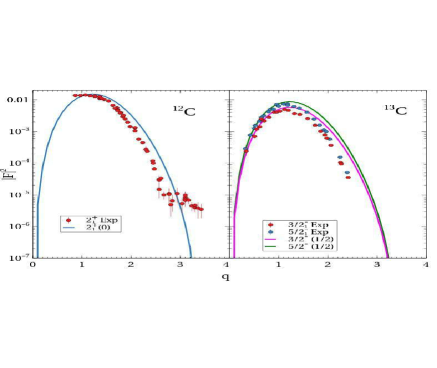
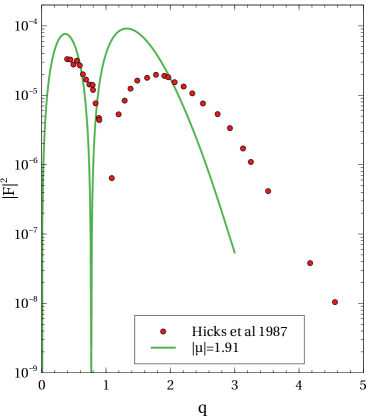
The results are showed in figure 6.