Structure of the and the reaction
Abstract
The resonance production reaction is investigated within the framework of the coupled-channels Alt-Grassberger-Sandhas (AGS) equations. We perform full three-body calculations for the - amplitudes on the physical real energy axis and investigate how the signature of the appears in the cross sections of the reactions, also in view of the planned E31 experiment at J-PARC. Two types of meson-baryon interaction models are considered: an energy-dependent interaction based on chiral effective field theory, and an energy-independent version that has been used repeatedly in phenomenological approaches. These two models have different off-shell properties that imply correspondingly different behavior in the three-body system. We investigate how these features show up in differential cross sections of reactions. Characteristic patterns distinguishing between the two models are found in the invariant mass spectrum of the final state. The reaction, with different ( and ) charge combinations in the final state, is thus demonstrated to be a useful tool for investigating the subthreshold behavior of the interaction.
pacs:
14.20.Pt, 13.75.Jz, 21.85.+d, 25.80.NvI Introduction
Understanding the structure of the is a long-standing issue in hadron physics. The nominal location of the mass, 27 MeV below the threshold, deviates prominently from the expected naive quark model pattern and indicates a more complex structure. Following early work by Dalitz et al. more than half a century ago Dalitz and Tuan (1959, 1960), the began to be considered as a quasi-bound state embedded in the continuum. Motivated by such a picture, phenomenological potential models were designed to reproduce the mass together with two-body scattering data Akaishi and Yamazaki (2002); Shevchenko (2012).
A more systematic framework emerged with developments of meson-baryon effective field theory based on the spontaneous breaking of chiral symmetry in low-energy QCD. In this theory the kaon is part of the pseudoscalar octet of Nambu-Goldstone bosons, but with an important explicit chiral symmetry breaking term introduced by its mass, GeV, that reflects the relatively large mass of the strange quark, GeV. Over the years, chiral dynamics, as the synthesis of chiral effective field theory and coupled channels methods Kaiser et al. (1995); Oset and Ramos (1998); Oller and Meissner (2001); Hyodo and Jido (2012), has turned out to be a highly successful approach to deal with interactions and the .
Even though the phenomenological and the chiral SU(3) interactions produce comparable results at and above threshold, they differ significantly in their extrapolations to subthreshold energies Hyodo and Weise (2008). The phenomenological interactions are constructed to describe the as a single pole of the scattering amplitude around 1405 MeV, corresponding to a quasi-bound state of the system with a binding energy of about 30 MeV. On the other hand, the - coupled-channels amplitude resulting from chiral SU(3) dynamics has two poles, one of which is located around 1420 MeV Oller and Meissner (2001); Jido et al. (2003) while the other pole represents a broad structure above the threshold. The pole at 1420 (rather than 1405) MeV corresponds to a quasi-bound system with a binding energy of 15 MeV, about half the binding produced with the purely phenomenological potentials. These differences in the pole structures come from different off-shell properties. The interaction based on chiral SU(3) dynamics is necessarily energy-dependent: the Nambu-Goldstone boson nature of the dictates that the leading-order -wave interaction is proportional to the time derivative of the antikaon field and thus varies linearly with the energy. Consequently, as one extrapolates deeper into the subthreshold region, the attraction generated by this interaction becomes progressively weaker than the one proposed by the energy-independent phenomenological potentials. At the same time, corresponding differences occur in the strong channel couplings.
Hence the binding energies predicted by interactions based on chiral dynamics are systematically smaller than those suggested by the phenomenological models. These differences are further enhanced in the so-called few-body kaonic nuclei, such as the strange dibaryon resonance under discussion in the - coupled system Yamazaki and Akaishi (2002); Shevchenko et al. (2007a); Ikeda and Sato (2007); Shevchenko et al. (2007b); Yamazaki and Akaishi (2007); Dote et al. (2008, 2009); Wycech and Green (2009); Ikeda and Sato (2009); Ikeda et al. (2010); Barnea et al. (2012). How a possible signature of this strange dibaryon resonance shows up in a suitable production reaction is of great interest as it reflects the two-body dynamics in the channel Ohnishi et al. (2013).
Exploring the structure of the requires a precise determination of the - interaction. The data base available to constrain these interactions includes the old scattering cross sections Humphrey and Ross (1962); Sakitt et al. (1965); Kim (1965); Kittel et al. (1966); Evans et al. (1983), the threshold branching ratios Tovee et al. (1971); Nowak et al. (1978), and the kaonic hydrogen measurements Iwasaki et al. (1997); Ito et al. (1998); Beer et al. (2005) with special emphasis on more recent accurate SIDDHARTA data Bazzi et al. (2011, 2012). These latter data strongly constrain the input, as shown by the systematic study of chiral SU(3) dynamics using next-to-leading order driving interactions Ikeda et al. (2011, 2012). The experimental data just mentioned are collected at and above the threshold. Since elastic scattering cannot be performed, the subthreshold energy region is only accessible by measuring mass spectra of decay products in reactions producing the . The relevant spectra have recently been measured in photoproduction reactions by the LEPS Collaboration at SPring-8 Ahn (2003); Niiyama et al. (2008) and by the CLAS Collaboration at JLab Moriya et al. (2013a, b), and in collisions by the HADES Collaboration at GSI Agakishiev et al. (2013). The importance of accurately determined spectra as constraints for the subthreshold interaction has also been emphasized in Refs. Roca and Oset (2013a, b); Guo and Oller (2013); Mai and Meissner (2015).
Yet another process of prime interest is the reaction. It was studied long ago by Braun Braun et al. (1977) in a bubble-chamber experiment at momenta between 686 and 844 MeV. A new experiment is ongoing at J-PARC (E31 Noumi et al. (2009)) with a 1 GeV beam 111In this paper, we focus on the in-flight reactions with relatively energetic incident kaons. The same process at lower energy has been studied in Ref. Tan (1973). For theoretical studies with this kinematics, see Refs. Jido et al. (2011); Revai (2013).. In the E31 experiment, the production cross sections will be measured separately for all combinations of charges, i.e., , , and . It is therefore important to establish a theoretical framework for a detailed analysis of this reaction. Theoretical investigations of with comparable kinematics have previously been performed in simplified models assuming a two-step process Jido et al. (2009); Miyagawa and Haidenbauer (2012); Jido et al. (2013); Yamagata-Sekihara et al. (2013). To extract the information of the subthreshold interaction from the experimental spectrum, an improved framework for the reaction mechanism is called for.
In this work a full three-body calculation of the - amplitude is performed employing the coupled-channels Alt-Grassberger-Sandhas (AGS) equations. We investigate how the resonance manifests itself in the differential cross section of the reaction. At J-PARC it is planned to observe the in the mass spectrum measured by detecting the forward kicked-out neutron Noumi et al. (2009). Our calculation focuses on this observable. One of the aims is to study the role of different off-shell properties of the underlying interactions as they are realized in chiral dynamics versus phenomenological potential models. We thus employ two different types of - interactions, i.e., energy-dependent (E-dep.) and energy-independent (E-indep.), and examine how the different off-shell properties of these interactions show up in the three-body dynamics.
In Sec. II, we introduce the AGS equations for the three-body - system and derive the cross section for the reaction. The two-body interactions used in this work are summarized in Sec. III. The numerically computed differential cross sections are presented and discussed in Sec. IV. A summary follows in Sec. V.
II Three-Body Equations
II.1 Alt-Grassberger-Sandhas equations for the reaction
We begin by constructing the three-body amplitudes relevant to the reaction. Throughout this paper it is assumed that the three-body processes take place via separable two-body interactions given by the following forms in the two-body center-of-mass (c.m.) frame:
| (1) |
where is a vertex (cutoff) factor of the two-body channel with relative momentum and isospin . The interaction matrix is a function of the total energy in the two-body system. In the three-body system, we define the two-body energy as with the three-body energy and the spectator particle energy , where is the relative momentum of the spectator particle . The explicit forms of the relevant two-body interactions are presented in detail in Sec. III.
| Isobar | Allowed isospin(s) | Spectator particle | Three-body Fock space |
|---|---|---|---|
| 0, 1 | |||
| (0), 1 | |||
| 0 | |||
| 1/2, (3/2) | |||
| 1/2, (3/2) |
The ansatz (1) specifies strongly interacting two-body subsystems in the three-body processes. We refer to these meson-baryon or dibaryon subsystems conveniently as “isobars”. The three-body dynamics can then be described as quasi-two-body scattering of an isobar and a spectator particle in all possible coupled isobar-spectator channels. The quasi-two-body amplitudes, , are determined by solving the AGS equations Amado (1963); Alt et al. (1967),
| (2) |
Here, and denote two-particle subsystems forming “isobars” with isospins and , respectively; the subscripts represent the spectator particles which include, respectively, , , , , or . The notations for the isobars are summarized in Table 1. As pointed out in Sec. III, in this work we include only the partial wave for the interaction, thus only the isospin state appears for the subsystem (the isobar denoted ). For later purposes the partial wave projections of the amplitudes of Eq. (2) are needed. They are given as:
| (3) |
with and the notation . Here, is the Legendre polynomial with orbital angular momentum between isobar and spectator particle. After the partial wave projections the AGS equations (2) are written as:
| (4) |
The driving term describes a particle-exchange interaction process connecting two-body channels, , and corresponding spectators as illustrated in Fig. 1(a). It is given by:
| (5) |
where and are the energies of the spectator particles and , respectively; with is the energy of the exchanged particle ; () is the relative momentum between the exchange-particle and the spectator-particle (). Using relativistic kinematics we have () and is defined as
| (6) | ||||
| (7) |
The isobar amplitudes, as illustrated in Fig. 1 (b), are determined by solving the Lippmann-Schwinger equations with the two-body interaction (1),
| (8) |
Here, is the energy of the interacting pair (), .
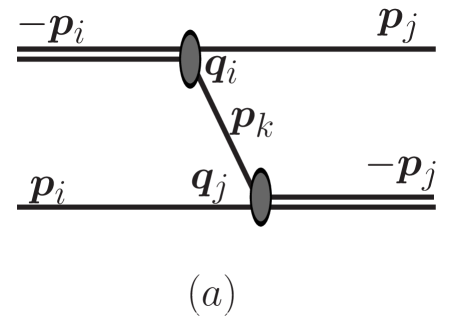

After antisymmetrization of the two-nucleon states in the three-body system, the coupled-channels AGS matrix integral equations (4) are written formally and symbolically (suppressing sums, integrals and all indices other than the isobar assignments) as:
| (9) |
II.2 Cross sections for
In this subsection, following Ref. Ohnishi et al. (2013), we present formulas for computing cross sections of the two-body-to-three-body reaction, . By using the anti-symmetrized AGS amplitudes (9), the breakup amplitudes for are given as
| (10) |
Here
is the residue of the two-body propagator,
at the deuteron pole, with its proper binding
energy, i.e.,
normalizes the initial state deuteron wave function.
Note again that all two-body subsystems listed in Table 1,
including both hyperons and , contribute to when permitted by selection rules.
The following notations
are used for the expressions appearing in Eq. (10):
: plane wave state of the three-body system;
:
three-body system in the coupling scheme, with , , , and being the isobar
quantum number,
the total quantum number,
the isospin of the isobar and its angular momentum relative to the spectator,
respectively.
The projection involves the product of spherical harmonics and spin-isospin Clebsch-Gordan coefficients. The matrix calculated in the isospin basis is then decomposed into the , , and final states using isospin CG coefficients. The momenta and are related to the momenta and by a Lorentz boost
| (11) | ||||
| (12) |
With the matrix Eq. (10) the cross sections of interest are derived as
| (13) |
with the initial relative velocity , the invariant/missing mass , and the total energy . In the second line of Eq. (13), the momenta and are the on-shell momenta for given energies and . Angular integrations are denoted by . The differential cross sections are
| (14) | ||||
| (15) |
where
| (16) |
The symbol stands as usual for averaging of initial states and sum of final states subject to conservation laws.
III Two-Body Interactions
| (MeV) | (MeV) | (MeV) | (MeV) | (MeV) | |
|---|---|---|---|---|---|
| E-dep. | 1100 | 1100 | 800 | 800 | 800 |
| E-indep. | 1160 | 1100 | 1100 | 850 | 1250 |
We refer back to Eq. (1) and explain the explicit forms of the meson-baryon interactions (Sec. III.1) and baryon-baryon interactions (Sec. III.3) used in this work. In this section spectator indices are suppressed for simplicity.
III.1 Meson-baryon interaction
Two models for the -wave meson-baryon interactions used in Refs. Ikeda and Sato (2007, 2009); Ikeda et al. (2010); Ohnishi et al. (2013) are employed in this work. Both are derived from the leading order chiral Lagrangian (the Weinberg-Tomozawa term Weinberg (1966); Tomozawa (1966)) but have different off-shell behavior. One of them is referred to as the energy dependent (E-dep.) model Ikeda et al. (2010),
| (17) |
Here, is the meson energy of the channel , , ; is the meson (baryon) mass; MeV is the pion decay constant; the coupling coefficients are determined by the flavor SU(3) structure constant (see Ref. Ohnishi et al. (2013)). The vertex factors are chosen as dipole form factors with cutoff scales ,
The characteristic energy dependence of the meson-baryon interaction (17) is dictated by spontaneously broken chiral symmetry. The corresponding Nambu-Goldstone bosons are identified with the pseudoscalar meson octet, and their leading -wave couplings involve the time derivatives of the meson fields.
The other model, referred to here as the energy independent (E-indep.) model Ikeda and Sato (2007, 2009), is obtained by fixing the two-body energy at each threshold energy, :
| (18) |
While this restricted model with constant couplings is not consistent with Goldstone’s theorem for low-energy pseudoscalar meson interactions, it is nonetheless a prototype of phenomenological potentials that have been used in the literature, and so we discuss it here for comparison with the energy-dependent approach based on chiral meson-baryon effective field theory.
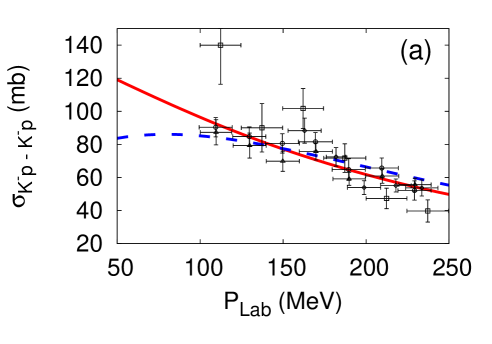
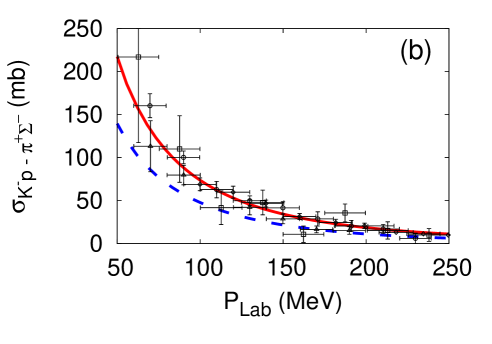
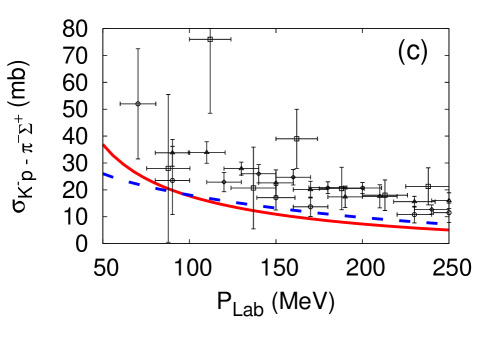
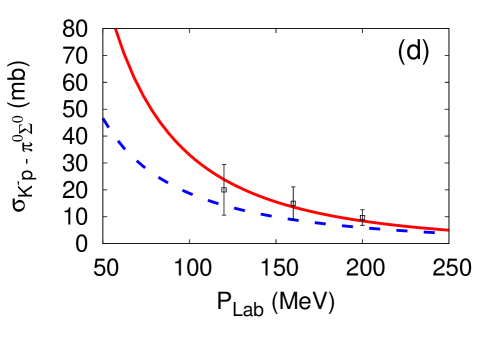
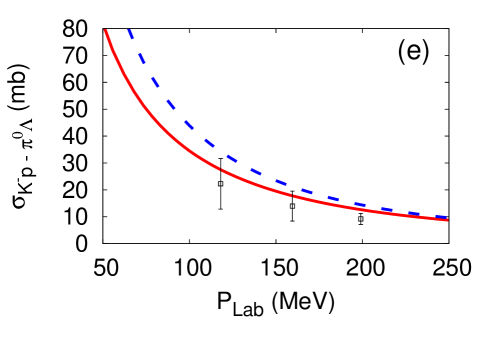
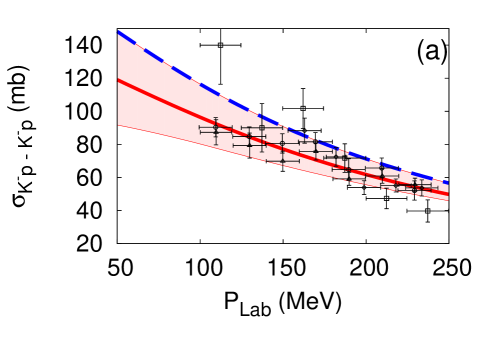
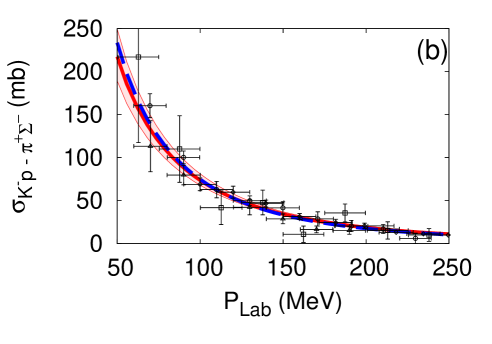
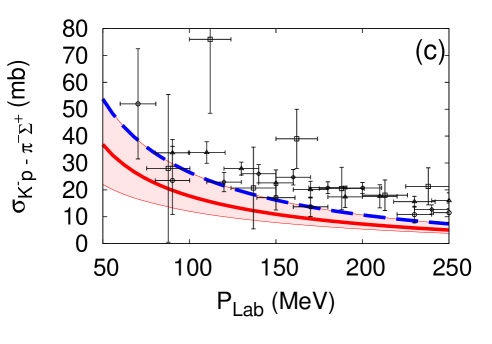
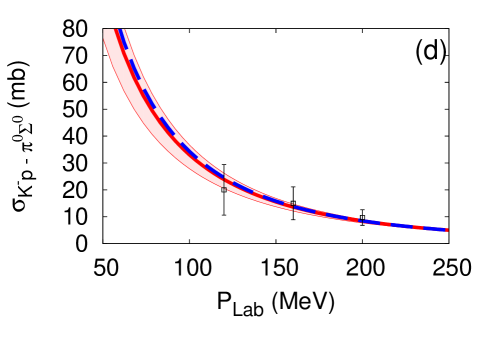
The cutoff parameters for the -- systems are determined by fitting the scattering cross sections Humphrey and Ross (1962); Sakitt et al. (1965); Kim (1965); Kittel et al. (1966); Evans et al. (1983). Results of the fit for the E-dep. and E-indep. models are presented in Fig. 2. The fitted cutoff values are listed in Table 2.
|
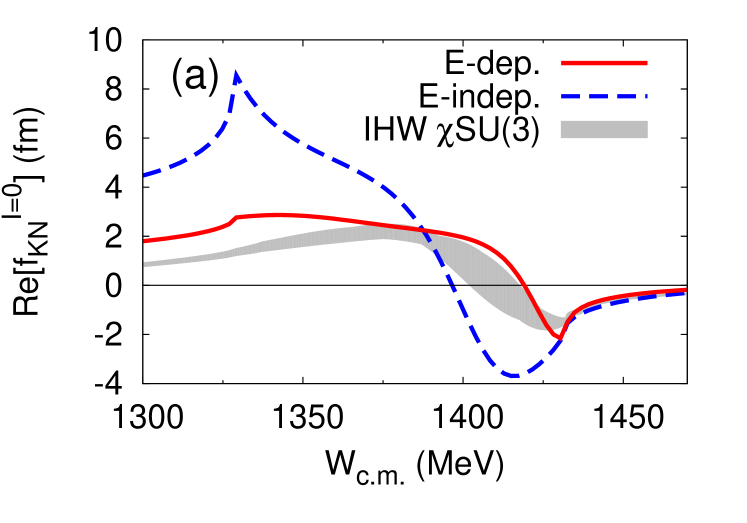
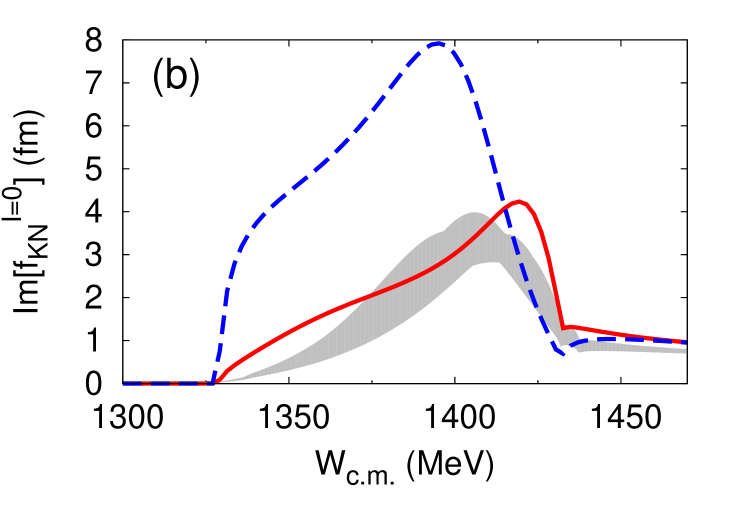
The different off-shell behaviors of the two types of models leads to different analytic structure of the amplitudes. We find that the E-dep. model has two poles on the physical and unphysical sheet. The behavior of the subthreshold amplitudes is similar to that obtained with the chiral SU(3) dynamics Ikeda et al. (2011, 2012) (see Fig. 3), and the scattering length is consistent with SIDDHARTA measurement in the E-dep. model. On the other hand, the E-indep. model has a single pole corresponding to . It shares this property with other phenomenological potential models. The behavior below threshold of the amplitudes in the E-indep. model is very different compared with that obtained from chiral SU(3) dynamics (Fig. 3). In the E-indep. model, it is difficult to reproduce the scattering length in comparison with SIDDHARTA measurements although the cross sections are reproduced within experimental errors.
Table 3 lists the pole energies of the -wave scattering amplitudes in the complex energy plane between the and threshold energies and the scattering length. The primary purpose of this study is to clarify the influence of the subthreshold behavior of the interaction in the spectrum.
| (MeV) | (fm) | |
|---|---|---|
| E-dep. model | ||
| E-indep. model | ||
| SIDDHARTA |
As for the cutoff parameters of interactions, we have determined them by fitting the and scattering lengths Schroder et al. (1999). The resulting values are MeV for both the E-dep. and E-indep. models.
III.2 Cutoff parameter dependence
| (MeV) | (MeV) | (MeV) | (MeV) | (MeV) | |
|---|---|---|---|---|---|
| E-dep. | 1070-1170 | 1070-1170 | 790-900 | 790-900 | 790-900 |
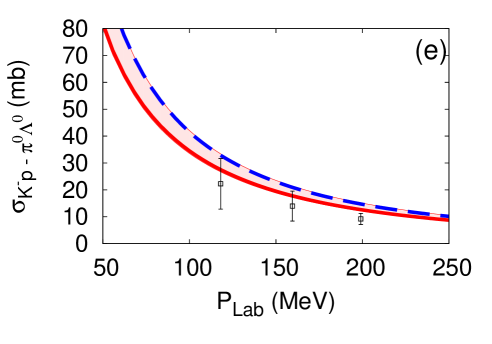
Parameters of the two-body potential are the cutoffs , determined by fitting the reaction cross sections within experimental errors. Acceptable variations of these cutoffs are examined for the E-dep. model. The ranges of cutoff scales compatible with experimental errors are listed in Table 4 and the corresponding fits to data are presented in Fig. 4. The resulting scattering length including uncertainties is fm, consistent with the scattering length deduced from the SIDDHARTA kaonic hydrogen measurements.
As seen in Fig. 4 one might have the impression that the cross section is not optimally reproduced. On the other hand, this is a relatively small cross section with limited weight in the overall fitting procedure. By examining the dashed curves in Fig. 4, we have checked that optimizing the fit to this selected cross section does not have a significant influence on the other cross sections within uncertainties.
III.3 Baryon-baryon interactions
| (MeV) | (MeV) | (MeV fm3) | (MeV fm3) |
|---|---|---|---|
| 1350 | 321 | 1.41 |
| 1.51 | 0.40 | 1.08 |
The following baryon-baryon interactions are commonly used for the E-dep. and E-indep. meson-baryon models. As for the interaction in , we take the following Yamaguchi-type two-term separable form:
| (19) |
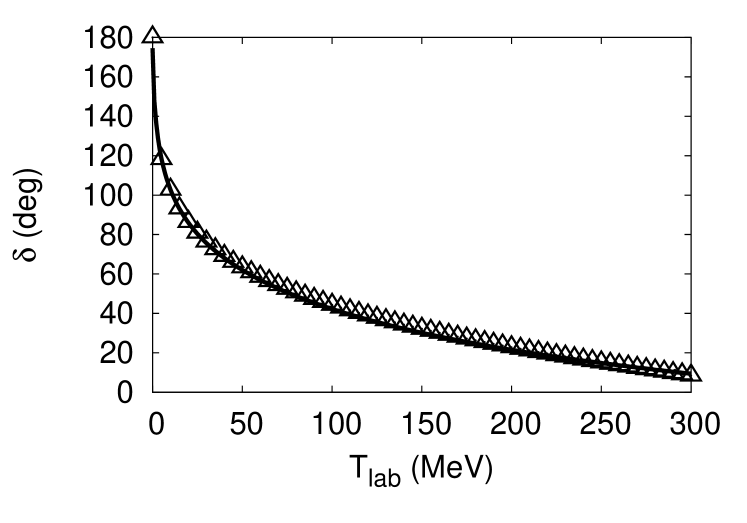
Here, () is the coupling strength of the repulsive (attractive) potential. The form factors are defined by , with being the cutoff parameters of the interactions. The coupling strengths and the cutoff parameters are determined by fitting the phase shifts of the Nijmegen 93 model Stoks et al. (1994) (see Fig. 5 for the result of the fit). The resulting values of the parameters are summarized in Table 5. The obtained deuteron binding energy is MeV.
As for the -wave interactions, we follow the form given in Ref. Torres et al. (1986):
| (20) |
Here, is the reduced mass of the system; the form factor is defined as . The coupling constants and the cutoff parameters are determined by fitting the phase shifts of the Jülich’04 model Haidenbauer and Meissner (2005). The resulting values of the coupling constants are summarized in Table 6. The cutoff parameters are MeV, MeV, and MeV.
IV Results and Discussion
|
IV.1 Differential cross section of the reaction
|
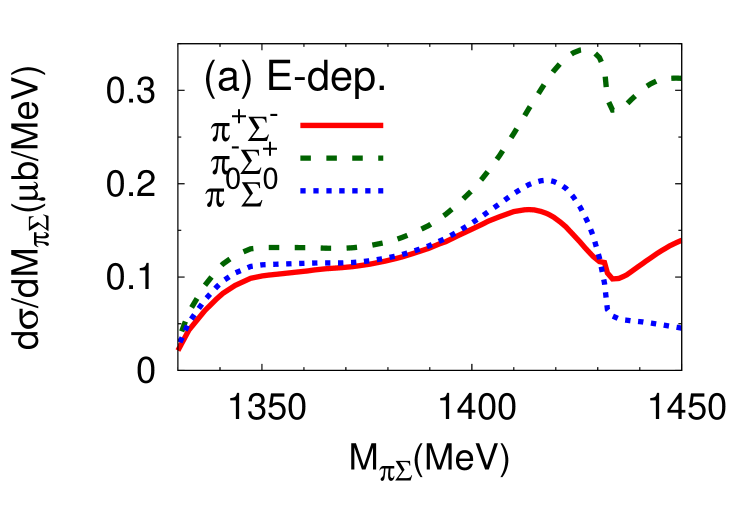
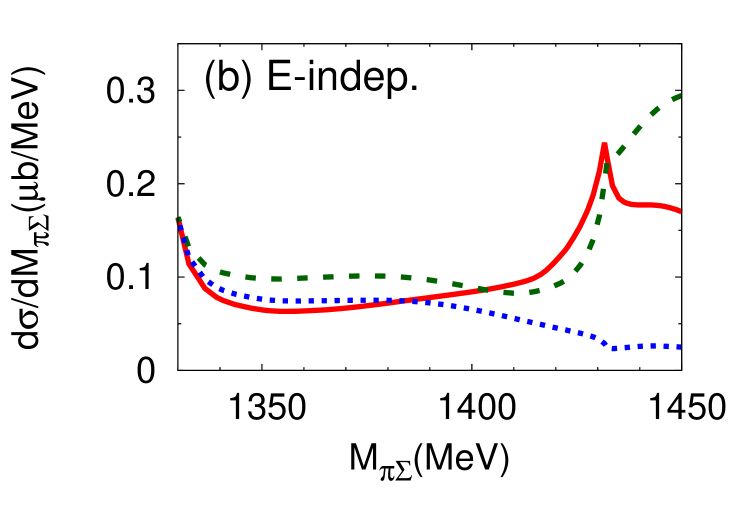
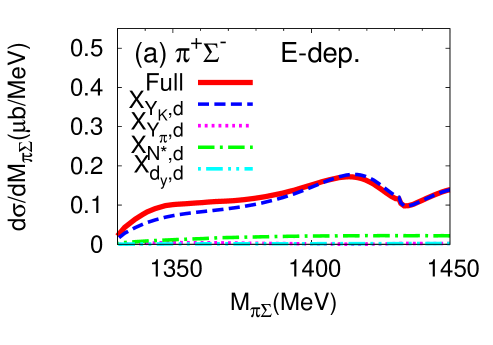
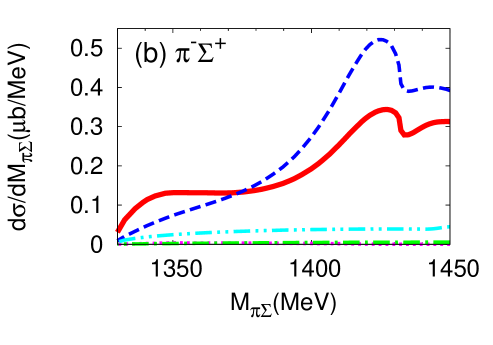
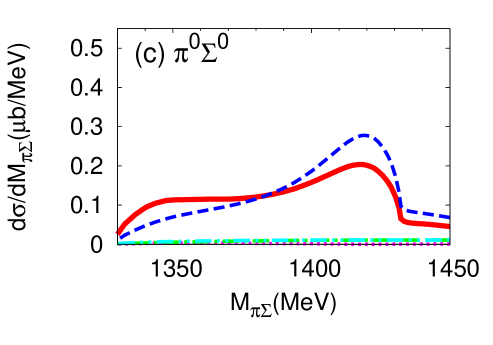
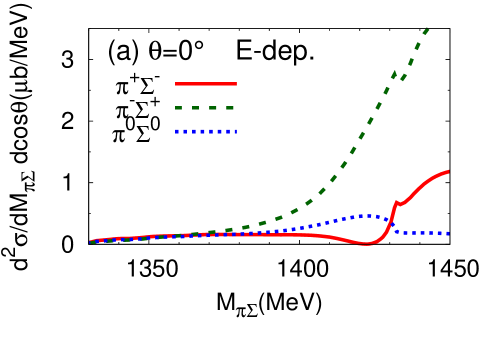
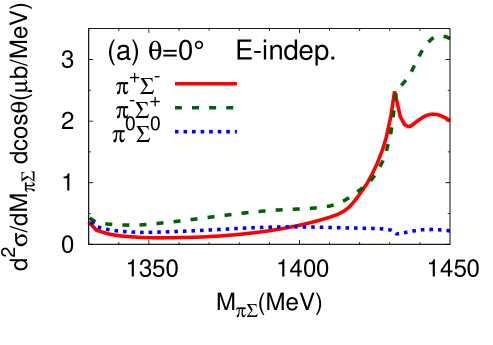
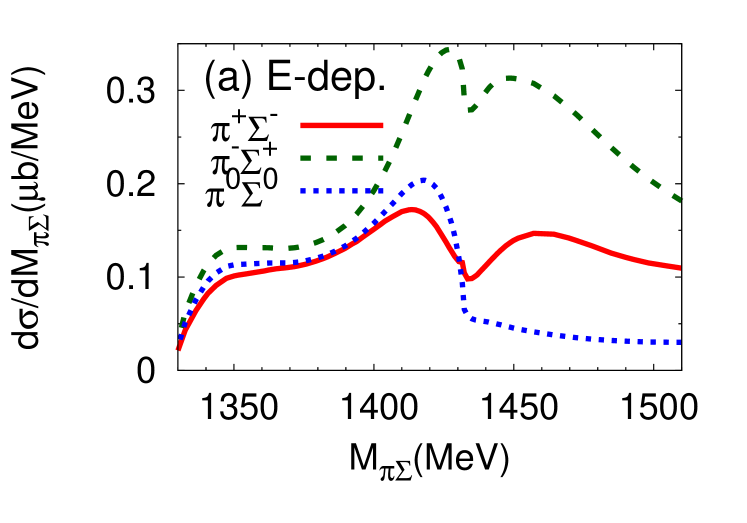
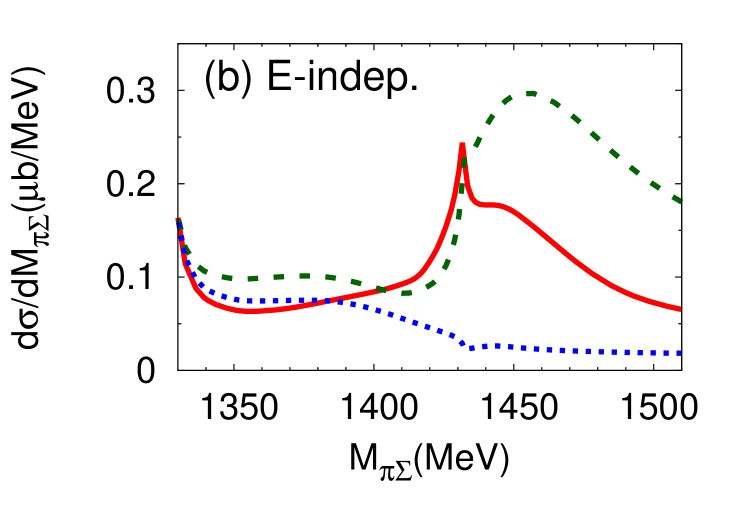
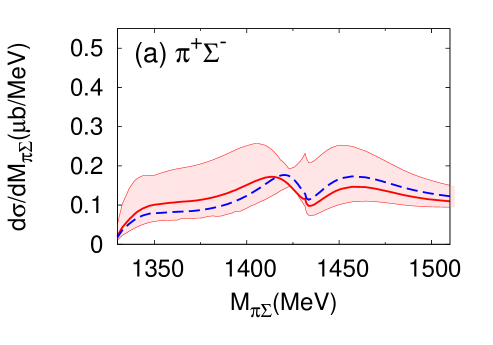
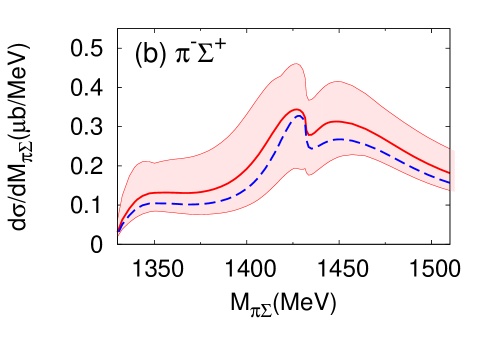
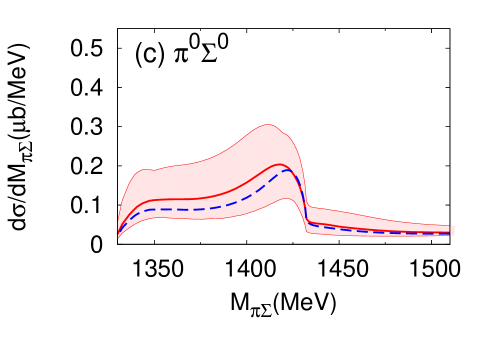
We proceed now to investigate the dependence of the differential cross section, of Eq. (15), as a function of the invariant mass of the final state. Results for the different charge combinations, , , and are shown in Fig. 6 (a) and (b) for the E-dep. and E-indep. models, respectively, whereby the isospin basis states have been decomposed into charge basis states using Clebsch-Gordan coefficients. In view of the planned J-PARC experiment, the initial momentum is chosen as GeV/, corresponding to the total energy MeV.
The differential cross section is an order of magnitude smaller than that calculated by assuming a two-step process Jido et al. (2009); Miyagawa and Haidenbauer (2012); Jido et al. (2013); Yamagata-Sekihara et al. (2013). Well-defined maxima are found at - MeV for the E-dep. model in all charge combinations of in the final state 222The difference among the spectra in the charge basis is due to the interference effect with the amplitude Nacher et al. (1999).. The positions of the peak structures are close to the calculated quasi bound pole position ( MeV). In the E-dep. model, the second pole with its large width, MeV, barely affects the differential cross section. On the other hand, no resonance structure is seen for the E-indep. model. The magnitude of the differential cross section and the interference patterns with backgrounds are evidently different for the E-dep. and E-indep. models. This suggests that the reaction can indeed provide significant information on the - subsystem.
Next, we show the contributions of each reaction process to the differential cross section (Fig. 7). As can be seen in Eq. (10), the reaction dynamics involves the quasi-two-body processes characterized by the amplitudes , , , and . The amplitude which contains the final state interaction turns out to be the dominant contribution to the cross section. The contribution from modifies the cross section for and final states, while its influence is small for the final state. This is because the component has Clebsch-Gordan coefficients which cancel for final state.
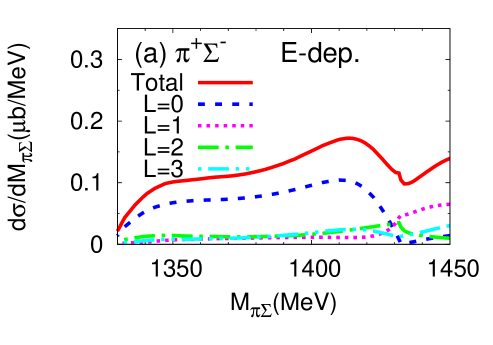
IV.2 Partial waves and angular dependence of the reaction
|
|
|
Consider now the contributions from each partial wave component with orbital angular momentum to the differential cross section for E-dep. model. The solid curve in Fig. 8 show the results with the total orbital angular momentum summed up to , which correspond to those shown in Fig. 6 (a), respectively. The decomposition into angular momentum contributions with , and displayed in this figure demonstrates the convergence of the partial wave expansion. The large incident energy implies that there are sizable contributions with . The - and -wave components dominate in the region below threshold. Around the threshold the -wave component also becomes important for the and channels.
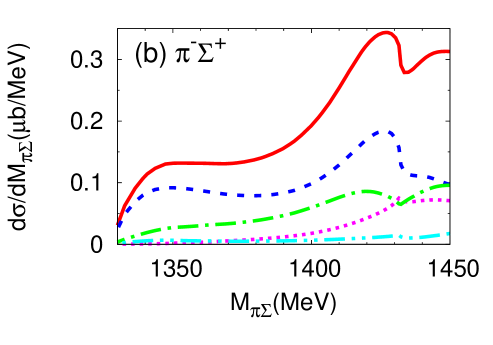
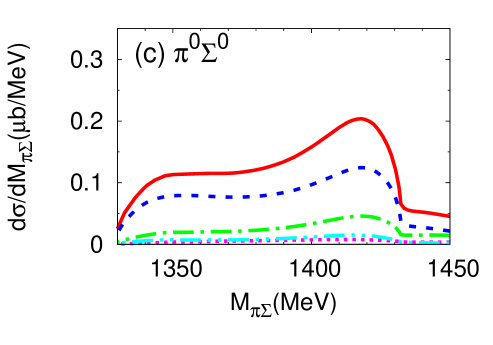
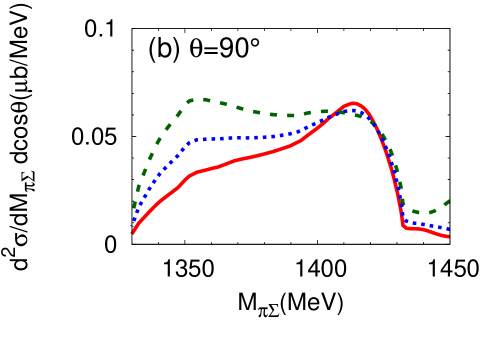
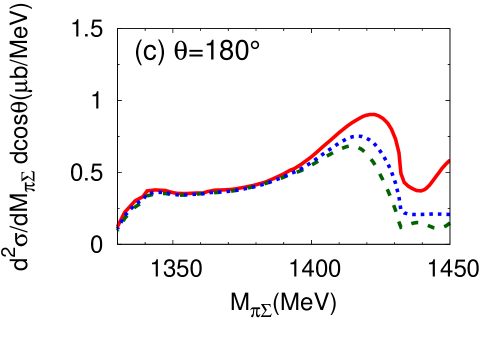
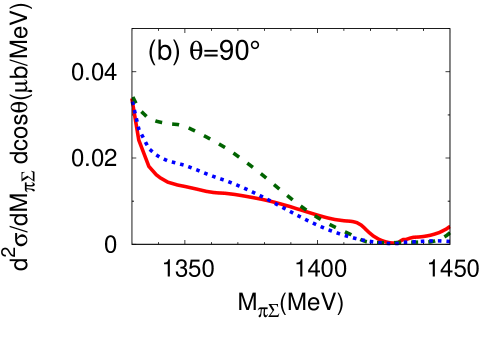
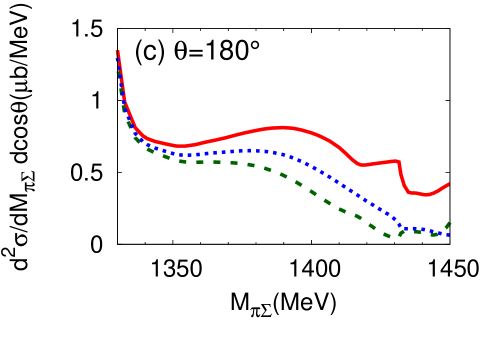
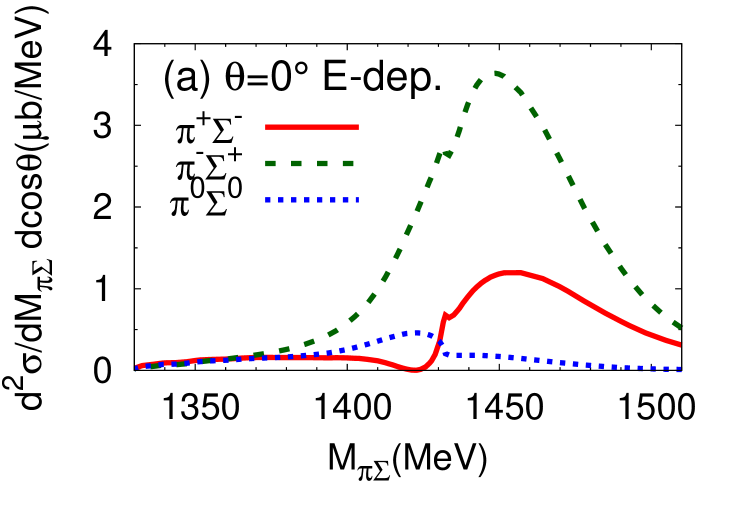
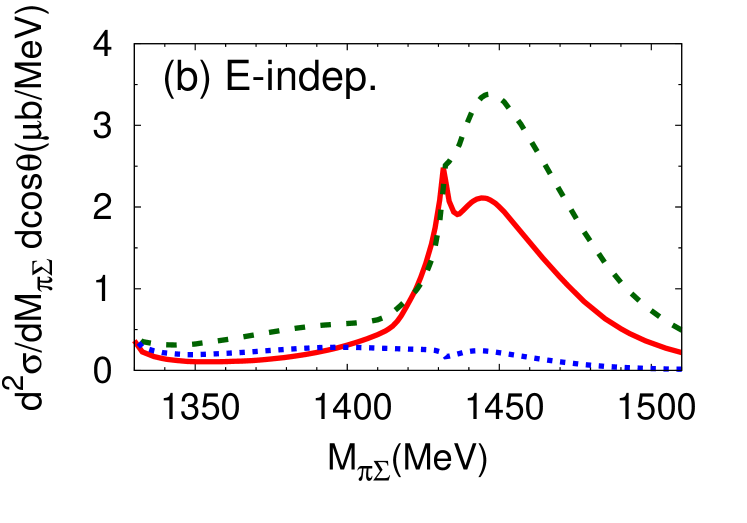
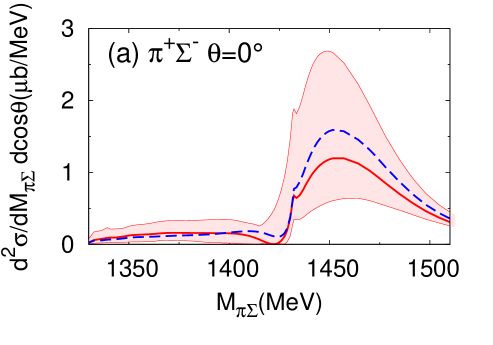
It is instructive to investigate the angular dependence of the double differential cross section, defined in Eq. (14). In Fig. 9 (Fig. 10), we present the double differential cross section for neutron scattering angles (a) , (b) , and (c) for E-dep. model (E-indep. model). Here is the neutron scattering angle in the center-of-mass frame. At one finds a strong dependence on the final state. The threshold cusp effect is enhanced in the and channels. The detailed channel dependence is closely related to the interference of the isospin and components of the in the final state. The forward reaction thus provides information on the - interaction not only in the but also in channel.
At the differential cross section is strongly suppressed in both the E-dep. and E-indep. models. It remains relatively flat at . Clearly, the interesting physics information is expected to be observable primarily with neutrons produced in forward direction. In the actual experiment the neutron will be detected in a forward cone around . We have checked that the differential cross section integrated over an angle interval from to does not change much from the pattern seen at .
IV.3 Cross sections above the threshold energy and cutoff dependence
|
|
|
|
While the primary focus in this study is on the subthreshold region and the two-body - dynamics governing the formation in the three-body system, it is also instructive to explore invariant mass spectra above threshold in . In fact our calculation (see Fig. 11) yields pronounced structures, especially for the charged channels ( and ), in the angle-integrated differential cross section. These structures are qualitatively different in the E-dep. and E-indep. approaches.
The double differential cross section with the neutron emitted in forward direction is of special interest (see Fig. 12). Our three-body calculations predict a strongly developed maximum around GeV for both the E-dep. and the E-indep. models, a feature that should be well observable. A less pronounced effect is seen in the channel which requires both charge exchange and strangeness exchange mechanisms.
The appearance of the prominent maximum in around GeV can be traced to a combination of subtle three-body mechanisms in the coupled - system: the nucleon exchange process between the incident and the deuteron, with a propagating pair and a spectator nucleon, and subsequent exchange leading to the final and neutron. The momentum matching between these two basic processes in the three-body system produces the pronounced enhancement in the channel about 20 MeV above threshold.
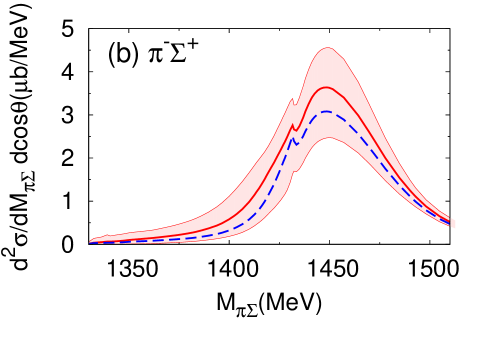
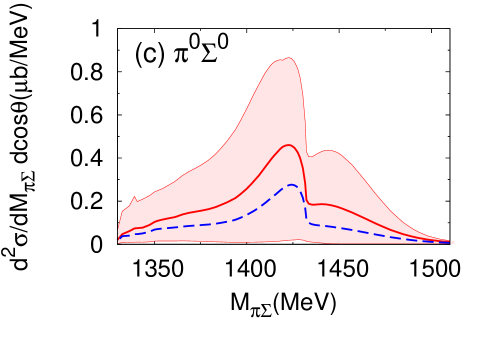
The appearance of such a structure in raises of course the question of model dependence and sensitivity to cutoff variations in the two-body amplitudes. This cutoff dependence turns out indeed to be stronger in the three-body system with its off-shell dynamics, as compared to the two-body subsystems. In order to examine this issue, we have performed calculations of the differential cross sections using the acceptable range of cutoff scales at the two-body vertices discussed previously and listed in Table 4. This leads to the theoretical uncertainty bands displayed in Fig. 13 for and in Fig. 14 for the double differential cross section with forward-emitted neutron, both taken at an incident momentum GeV. In particular, we have examined the influence of using the optimized cross section for while maintaining the other cross sections well reproduced within uncertainties (compare the solid and dashed curves in Figs. 13 and 14). While the absolute magnitudes of the differential cross sections are indeed subject to uncertainties, the structural patterns of the forward double differential cross sections for and final states remains quite stable with respect to cutoff variations, with the exception of the neutral () combination for which no prediction is possible.
At the same time as this genuine three-body dynamical structure in the final state appears around MeV, it is quite remarkable that with forward neutrons does not display a signal any more (whereas it is still visible in the angle-integrated for ). This is a consequence of interferences of three-body mechanisms in and amplitudes which screen the pole contribution.
V Summary
Within the framework of the coupled-channels AGS equations, we have investigated how the signature of the appears in differential cross sections of reactions. Two types of meson-baryon interactions, the E-dep. and E-indep. models, have been considered to illustrate how the difference of the subthreshold behaviors translates into the spectra. The E-dep. approach is generally favored because of its foundation in chiral SU(3) effective field theory.
Characteristic structures reflecting the formation and dynamics of the in the - three-body system are found in differential cross section as a function of the invariant mass. By comparison of results using E-dep. and E-indep. models, it may be possible to discriminate between these two approaches, especially in comparison with separately measured and invariant mass spectra. Of particular interest in this context are double differential cross sections with detection of the emitted neutron in forward directions, to be measured in a forthcoming experiment at J-PARC. Detailed final state channel dependence originates from the interference of and components of the final states, providing important information not only on the but also the - interactions.
Three-body dynamics in the coupled - system is predicted to generate a pronounced maximum in the double-differential cross section with a forward-emitted neutron at a invariant mass GeV. Further detailed studies exploring this structure are under way.
Acknowledgements.
The authors thank H. Noumi and A. Hosaka for helpful comments and discussions. The numerical calculation has been performed on a supercomputer (NEC SX8R) at the Research Center for Nuclear Physics, Osaka University. This work was partly supported by the Grants-in-Aid for Scientific Research on Innovative Areas from MEXT (Grant No. 2404:24105008), by RIKEN Junior Research Associate Program, by RIKEN iTHES Project, by the Yukawa International Program for Quark-Hadron Sciences (YIPQS), by JSPS KAKENHI Grants Nos. 23224006, 24740152 and 25800170, and by DFG through CRC 110.References
- Dalitz and Tuan (1959) R. Dalitz and S. Tuan, Phys. Rev. Lett. 2, 425 (1959).
- Dalitz and Tuan (1960) R. Dalitz and S. Tuan, Ann. Phys. (NY) 10, 307 (1960).
- Akaishi and Yamazaki (2002) Y. Akaishi and T. Yamazaki, Phys. Rev. C65, 044005 (2002).
- Shevchenko (2012) N. V. Shevchenko, Phys. Rev. C85, 034001 (2012), arXiv:1103.4974 [nucl-th] .
- Kaiser et al. (1995) N. Kaiser, P. Siegel, and W. Weise, Nucl. Phys. A594, 325 (1995), arXiv:nucl-th/9505043 [nucl-th] .
- Oset and Ramos (1998) E. Oset and A. Ramos, Nucl. Phys. A635, 99 (1998), arXiv:nucl-th/9711022 [nucl-th] .
- Oller and Meissner (2001) J. Oller and U. G. Meissner, Phys. Lett. B500, 263 (2001), arXiv:hep-ph/0011146 [hep-ph] .
- Hyodo and Jido (2012) T. Hyodo and D. Jido, Prog. Part. Nucl. Phys. 67, 55 (2012), arXiv:1104.4474 [nucl-th] .
- Hyodo and Weise (2008) T. Hyodo and W. Weise, Phys. Rev. C77, 035204 (2008), arXiv:0712.1613 [nucl-th] .
- Jido et al. (2003) D. Jido, J. Oller, E. Oset, A. Ramos, and U. Meissner, Nucl. Phys. A725, 181 (2003), arXiv:nucl-th/0303062 [nucl-th] .
- Yamazaki and Akaishi (2002) T. Yamazaki and Y. Akaishi, Phys. Lett. B535, 70 (2002).
- Shevchenko et al. (2007a) N. V. Shevchenko, A. Gal, and J. Mares, Phys. Rev. Lett. 98, 082301 (2007a), arXiv:nucl-th/0610022 [nucl-th] .
- Ikeda and Sato (2007) Y. Ikeda and T. Sato, Phys. Rev. C76, 035203 (2007), arXiv:0704.1978 [nucl-th] .
- Shevchenko et al. (2007b) N. V. Shevchenko, A. Gal, J. Mares, and J. Revai, Phys. Rev. C76, 044004 (2007b), arXiv:0706.4393 [nucl-th] .
- Yamazaki and Akaishi (2007) T. Yamazaki and Y. Akaishi, Phys. Rev. C76, 045201 (2007), arXiv:0709.0630 [nucl-th] .
- Dote et al. (2008) A. Dote, T. Hyodo, and W. Weise, Nucl. Phys. A804, 197 (2008), arXiv:0802.0238 [nucl-th] .
- Dote et al. (2009) A. Dote, T. Hyodo, and W. Weise, Phys. Rev. C79, 014003 (2009), arXiv:0806.4917 [nucl-th] .
- Wycech and Green (2009) S. Wycech and A. M. Green, Phys. Rev. C79, 014001 (2009), arXiv:0808.3329 [nucl-th] .
- Ikeda and Sato (2009) Y. Ikeda and T. Sato, Phys. Rev. C79, 035201 (2009), arXiv:0809.1285 [nucl-th] .
- Ikeda et al. (2010) Y. Ikeda, H. Kamano, and T. Sato, Prog. Theor. Phys. 124, 533 (2010), arXiv:1004.4877 [nucl-th] .
- Barnea et al. (2012) N. Barnea, A. Gal, and E. Liverts, Phys. Lett. B712, 132 (2012), arXiv:1203.5234 [nucl-th] .
- Ohnishi et al. (2013) S. Ohnishi, Y. Ikeda, H. Kamano, and T. Sato, Phys. Rev. C88, 025204 (2013), arXiv:1302.2301 [nucl-th] .
- Humphrey and Ross (1962) W. E. Humphrey and R. R. Ross, Phys.Rev. 127, 1305 (1962).
- Sakitt et al. (1965) M. Sakitt, T. Day, R. Glasser, N. Seeman, J. Friedman, et al., Phys.Rev. 139, B719 (1965).
- Kim (1965) J. Kim, Phys.Rev.Lett. 14, 29 (1965).
- Kittel et al. (1966) W. Kittel, G. Otter, and I. Wacek, Phys.Lett. 21, 349 (1966).
- Evans et al. (1983) D. Evans, J. Major, E. Rondio, J. A. Zakrzewski, J. Conboy, et al., J.Phys. G9, 885 (1983).
- Tovee et al. (1971) D. Tovee, D. Davis, J. Simonovic, G. Bohm, J. Klabuhn, et al., Nucl.Phys. B33, 493 (1971).
- Nowak et al. (1978) R. Nowak, J. Armstrong, D. Davis, D. Miller, D. Tovee, et al., Nucl.Phys. B139, 61 (1978).
- Iwasaki et al. (1997) M. Iwasaki, R. Hayano, T. Ito, S. Nakamura, T. Terada, et al., Phys.Rev.Lett. 78, 3067 (1997).
- Ito et al. (1998) T. Ito, R. Hayano, S. Nakamura, T. Terada, M. Iwasaki, et al., Phys.Rev. C58, 2366 (1998).
- Beer et al. (2005) G. Beer et al. (DEAR Collaboration), Phys.Rev.Lett. 94, 212302 (2005).
- Bazzi et al. (2011) M. Bazzi, G. Beer, L. Bombelli, A. Bragadireanu, M. Cargnelli, et al., Phys. Lett. B704, 113 (2011), arXiv:1105.3090 [nucl-ex] .
- Bazzi et al. (2012) M. Bazzi, G. Beer, L. Bombelli, A. Bragadireanu, M. Cargnelli, et al., Nucl.Phys. A881, 88 (2012), arXiv:1201.4635 [nucl-ex] .
- Ikeda et al. (2011) Y. Ikeda, T. Hyodo, and W. Weise, Phys. Lett. B706, 63 (2011), arXiv:1109.3005 [nucl-th] .
- Ikeda et al. (2012) Y. Ikeda, T. Hyodo, and W. Weise, Nucl. Phys. A881, 98 (2012), arXiv:1201.6549 [nucl-th] .
- Ahn (2003) J. Ahn (LEPS Collaboration), Nucl.Phys. A721, 715 (2003).
- Niiyama et al. (2008) M. Niiyama, H. Fujimura, D. Ahn, J. Ahn, S. Ajimura, et al., Phys. Rev. C78, 035202 (2008), arXiv:0805.4051 [hep-ex] .
- Moriya et al. (2013a) K. Moriya et al. (CLAS Collaboration), Phys. Rev. C87, 035206 (2013a), arXiv:1301.5000 [nucl-ex] .
- Moriya et al. (2013b) K. Moriya et al. (CLAS Collaboration), Phys. Rev. C88, 045201 (2013b), arXiv:1305.6776 [nucl-ex] .
- Agakishiev et al. (2013) G. Agakishiev et al. (HADES Collaboration), Phys.Rev. C87, 025201 (2013), arXiv:1208.0205 [nucl-ex] .
- Roca and Oset (2013a) L. Roca and E. Oset, Phys. Rev. C87, 055201 (2013a), arXiv:1301.5741 [nucl-th] .
- Roca and Oset (2013b) L. Roca and E. Oset, Phys. Rev. C88, 055206 (2013b), arXiv:1307.5752 [nucl-th] .
- Guo and Oller (2013) Z.-H. Guo and J. A. Oller, Phys. Rev. C87, 035202 (2013), arXiv:1210.3485 [hep-ph] .
- Mai and Meissner (2015) M. Mai and U.-G. Meissner, Eur. Phys. J. A51, 30 (2015), arXiv:1411.7884 [hep-ph] .
- Braun et al. (1977) O. Braun, H. Grimm, V. Hepp, H. Strobele, C. Thol, et al., Nucl. Phys. B129, 1 (1977).
- Noumi et al. (2009) H. Noumi et al., J-PARC proposal E31, (2009) .
- Jido et al. (2009) D. Jido, E. Oset, and T. Sekihara, Eur. Phys. J. A42, 257 (2009), arXiv:0904.3410 [nucl-th] .
- Miyagawa and Haidenbauer (2012) K. Miyagawa and J. Haidenbauer, Phys. Rev. C85, 065201 (2012), arXiv:1202.4272 [nucl-th] .
- Jido et al. (2013) D. Jido, E. Oset, and T. Sekihara, Eur. Phys. J. A49, 95 (2013), arXiv:1207.5350 [nucl-th] .
- Yamagata-Sekihara et al. (2013) J. Yamagata-Sekihara, T. Sekihara, and D. Jido, Prog. Theor. Exp. Phys. 2013, 043D02 (2013), arXiv:1210.6108 [nucl-th] .
- Amado (1963) R. D. Amado, Phys. Rev. 132, 485 (1963).
- Alt et al. (1967) E. Alt, P. Grassberger, and W. Sandhas, Nucl.Phys. B2, 167 (1967).
- Weinberg (1966) S. Weinberg, Phys. Rev. Lett. 17, 616 (1966).
- Tomozawa (1966) Y. Tomozawa, Nuovo Cimento A46, 707 (1966).
- Meissner et al. (2004) U. G. Meissner, U. Raha, and A. Rusetsky, Eur. Phys. J. C35, 349 (2004), arXiv:hep-ph/0402261 [hep-ph] .
- Schroder et al. (1999) H. Schroder, A. Badertscher, P. Goudsmit, M. Janousch, H. Leisi, et al., Phys.Lett. B469, 25 (1999).
- Stoks et al. (1994) V. G. J. Stoks, R. A. M. Klomp, C. P. F. Terheggen, and J. J. de Swart, Phys.Rev. C49, 2950 (1994), arXiv:nucl-th/9406039 [nucl-th] .
- Torres et al. (1986) M. Torres, R. Dalitz, and A. Deloff, Phys.Lett. B174, 213 (1986).
- Haidenbauer and Meissner (2005) J. Haidenbauer and Ulf.-G. Meissner, Phys. Rev. C72, 044005 (2005), arXiv:nucl-th/0506019 [nucl-th] .
- Tan (1973) T. H. Tan, Phys. Rev. D7, 600 (1973).
- Jido et al. (2011) D. Jido, E. Oset, and T. Sekihara, Eur. Phys. J. A47, 42 (2011), arXiv:1008.4423 [nucl-th] .
- Revai (2013) J. Revai, Few Body Syst. 54, 1865 (2013), arXiv:1203.1813 [nucl-th] .
- Nacher et al. (1999) J. Nacher, E. Oset, H. Toki, and A. Ramos, Phys.Lett. B455, 55 (1999), arXiv:nucl-th/9812055 [nucl-th] .