Structures and finite-temperature abundances of defects in In2O3-II from first-principles calculations
Abstract
We have studied intrinsic defect complexes in \ceIn2O3 using ab initio random structure searching (AIRSS). Our first-principles density-functional-theory calculations predict the thermodynamic stability of several novel defect structures. We combine the static lattice energy and harmonic vibrational energy with the often-neglected configurational entropy to construct the free energy, which is minimised to predict defect abundances at finite temperatures. We predict that some of our new defect structures – in particular our {In,2VO} and {2In,3VO} defects – can exist in significant abundances at finite temperatures, and their densities of electronic states indicate that they could play an important role in the unexpectedly high density of n-type charge carriers observed in .
The thermodynamically most stable crystalline form of indium oxide () is a transparent semiconducting oxide (TCO) that adopts the bixbyite structure. TCOs are relatively uncommon materials, but they are of significant technological interest. They combine the usually mutually exclusive properties of optical transparency in the visible range with high electrical conductivity. It has been observed that nominally undoped exhibits intrinsic n-type conductivity, which has been associated with the presence of both oxygen vacancy defects Curreli et al. (2005); Bierwagen (2015) and hydrogen impurities Galazka et al. (2013). The aim of this work is to study the energetics and structures of low-energy defects in undoped .
Undoped exhibits n-type conductivity with carrier concentrations of up to De Wit et al. (1977), even when grown in exceptionally pure environments Bierwagen (2015). This phenomenon is known as unintentional doping (UID). The UID in was originally attributed to oxygen vacancies acting effectively as donors De Wit et al. (1977); consistently with this, is a non-stoichiometric material with an excess of In relative to O De Wit et al. (1977). However, studies have been inconsistent on whether such vacancies are sufficiently shallow in energy to explain the effect Limpijumnong et al. (2009); Bierwagen and Speck (2012). Other candidates which have been put forward to explain the unexpectedly high carrier density of include indium self-interstitials Tang et al. (2010) and hydrogen impurities King et al. (2009). Experimentally, the carrier density of depends strongly on the temperature at which it is manufactured Galazka et al. (2013). A great deal of research has been focused on optoelectronic applications of TCOs created by doping with tin Agoston et al. (2009), which has been used in energy-efficient windows Hamberg and Granqvist (1986) and as an anode in OLEDs (organic light-emitting diodes) Park et al. (2002). Undoped also finds technological applications in gas sensors Xu et al. (2013), and nanotubes Shen et al. (2005) have applications in arrays of nanotubes for biosensing Curreli et al. (2005).
Density-functional theory (DFT) has previously been used to elucidate the optical properties of that give rise to its transparency Walsh et al. (2008) and to calculate formation energies of intrinsic point defects Ágoston et al. (2009); Agoston et al. (2009). In this work we go beyond previous studies by predicting the structures of defect complexes from first principles, which has allowed us to identify many new defects. We have used the ab initio random structure searching method (AIRSS) Pickard and Needs (2011) to discover low energy defect structures. We have also incorporated finite-temperature effects in calculating their energetic stability. Previously AIRSS has been used to study phases of materials at high pressures Pickard and Needs (2006), to determine structures of point defect complexes formed by impurities in silicon Morris et al. (2011, 2009, 2013), to investigate zirconolite as a material for nuclear waste encapsulation Mulroue et al. (2011, 2013), and to map out the sequence of phase transitions in the lithiation and sodiation of phosphorus anodes in batteries Mayo et al. (2016).
Our calculations provide the static lattice energies, the configurational entropy accounting properly for the symmetries of defects, and the contribution of the phonons to the free energy. Each of these contributions can have a large impact on the defect abundances at ambient conditions. All DFT calculations reported in this letter were performed using the castep plane-wave code Clark et al. (2005); the methodological details are provided in the Supplemental Material.
The bixbyite structure Karazhanov et al. (2007) of symmetry, also known as \ceIn2O3-II, is thermodynamically stable at ambient conditions. The structure contains two inequivalent types of In atom on the and Wyckoff sites. All oxygen atoms are equivalent and are on the site.
In AIRSS a large number of random structures are generated using DFT methods and relaxed to the nearest local minimum of the energy landscape Pickard and Needs (2011). The structures that are particularly low in energy can then be singled out for further examination. The structure searching computations were performed using the 40-atom primitive cell of -II, and more accurate calculations on the most promising defects were performed in a 160-atom supercell.
The initial structures for the AIRSS searches were created by selecting a sphere of radius centred on a random position within the unit cell, and then removing atoms within the sphere at random and inserting In or O atoms. The atomic coordinates of all atoms within the sphere were randomised, making sure that they were not unphysically close to one another.
We adopt throughout a notation in which defects are indicated by listing their contents within braces; we also use to refer to a vacancy of element x so that, for example, {In, } constitutes an indium substitutional. Metastable defects are indicated using asterisks; for example, the lowest-energy oxygen vacancy would be denoted using {}, the second-lowest as {}*, and the third-lowest as {}**.
Because empirically exhibits a deficit of oxygen relative to its ideal bulk stoichiometry, we searched for defects formed by a mixture of oxygen vacancies and indium interstitials. These searches generated a total of 632 defect structures (although many of them are duplicates). To our knowledge, none of the ‘nontrivial’ defects found here – i.e., anything but single-atom interstitials, vacancies, and substitutionals – has been reported previously in the literature.
Defect abundances at finite temperatures are calculated by constructing the free energy and minimising it with respect to the abundances. Our expression for the free energy takes into account contributions from the static-lattice formation energies, phonons, and the configurational entropy associated with the defects:
| (1) | ||||
where the are the number of defects of type , is the total number of lattice sites, is the configurational degeneracy per lattice site, is the temperature-dependent vibrational free energy, and is the formation energy of the -th defect.
The vibrational free energy is given within the harmonic approximation by Al-Mushadani and Needs (2003) , where is the phonon density of states of the -th defect. We calculate the configurational degeneracies of the defects by applying each symmetry operator of the space group of bulk and counting the number of differently oriented versions of the same defect that are thereby generated. (In the calculation of the , we count defects which differ only by a translation as the same, since the entropy associated with placing a defect on different lattice sites is already included in Eq. 1.) The logarithm of the degeneracy then gives the orientational configurational entropy per lattice site (divided by ), as described in Ref. Morris et al., 2008. Along with a contribution from the combinatorics of assigning the defects to particular lattice sites, this forms the third term of Eq. 1. The defect abundances are computed by minimising Eq. 1 with respect to the at some particular temperature, .
The formation energy of a defect is defined as Freysoldt et al. (2014)
| (2) |
In the above, is the number of defect atoms of species ; the are the associated chemical potentials; is the total energy of the defective unit cell; and is the total energy of the bulk unit cell.
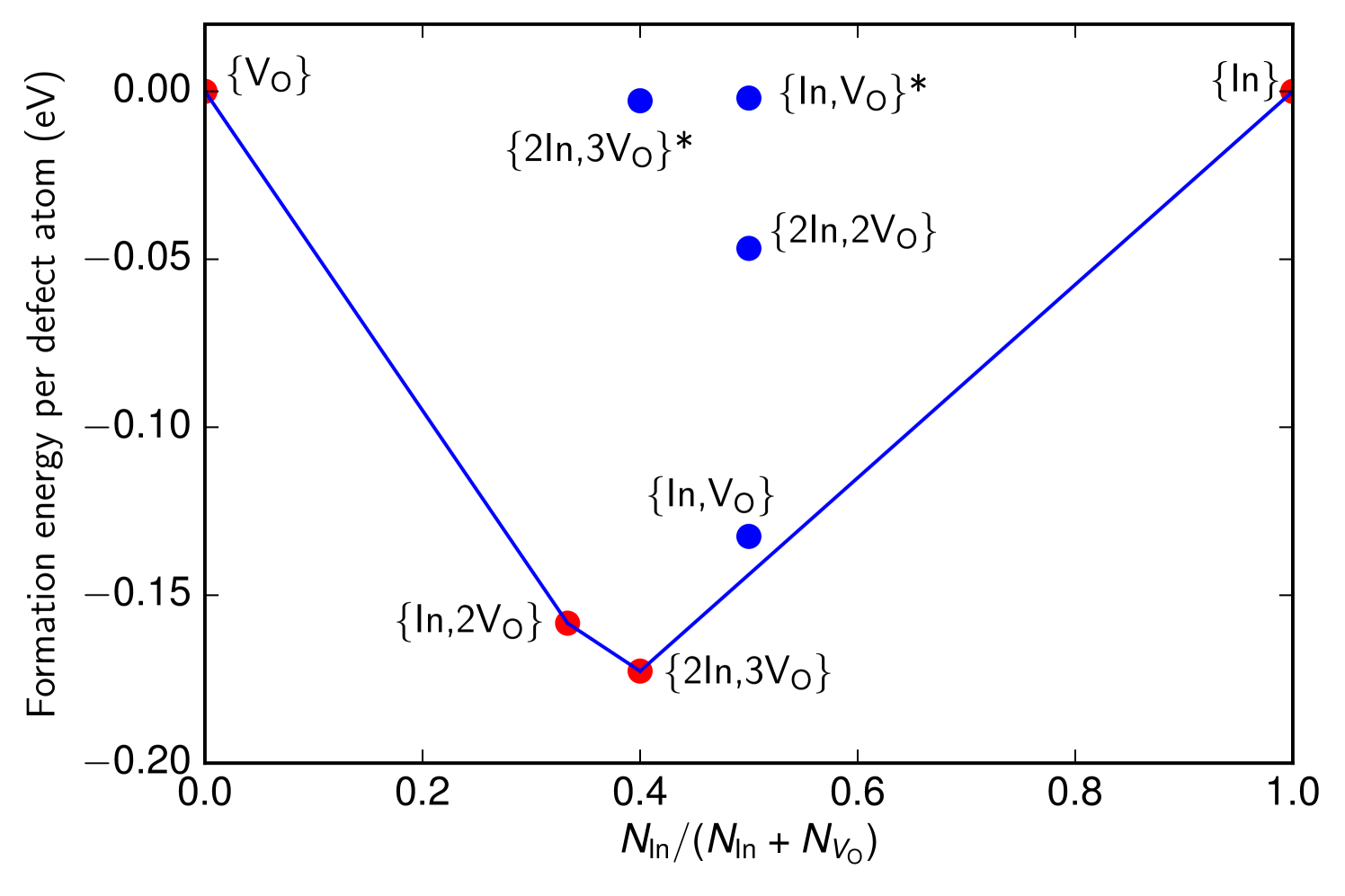
To visualise the energetics of the binary defects generated by the structure searching, we use the Maxwell construction, which has previously been applied to defects in Ref. Morris et al., 2011. The Maxwell construction is obtained by plotting the formation energy per atom of each defect against its composition. At , only those defects lying on the convex hull of the resulting scatter plot are thermodynamically stable.
The Maxwell construction for the most energetically favorable defects after re-optimisation in the larger 160-atom unit cell is shown in Fig. 1. Note that we treat vacancies just as we would atoms, so that in Fig. 1, the -axis runs from the case where there are oxygen vacancies but no indium interstitials to the case where there are indium interstitials but no oxygen vacancies. Fig. 1 shows how the two types of defect bind as a function of their concentrations relative to each other. The chemical potentials for and In were calculated using the oxygen vacancy and indium interstitial defects, with . (We note that the convex hull ceases to be meaningful at , since Eq. 1 shows that the entropy is a nonlinear function of the defect concentrations.)
We now survey the structures of the defects whose energies are reported in Fig. 1. The lowest-energy indium interstitial was found to be the -site defect previously reported in Ref. Agoston et al., 2009. Since all oxygen atoms in occupy the same Wyckoff site, there is only one way to remove an oxygen atom, leading to a single possible O vacancy defect (barring significant disruption to the lattice in its vicinity, which we find to be energetically unfavorable).
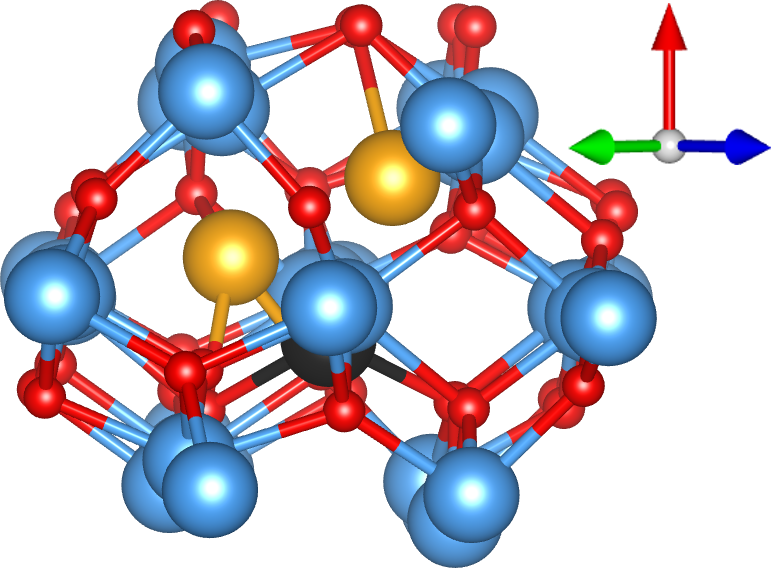
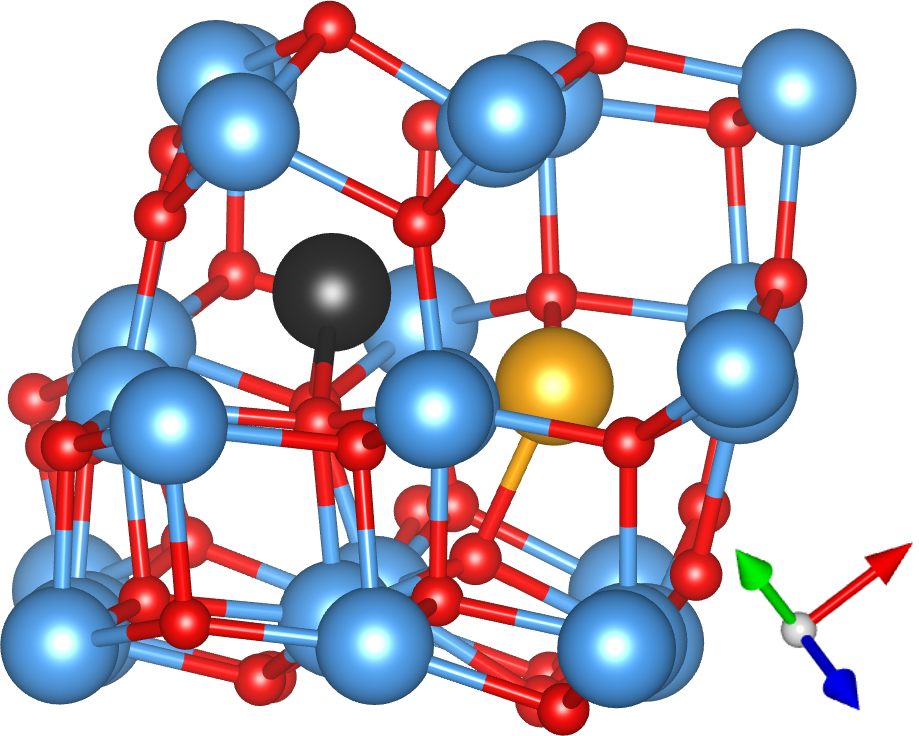
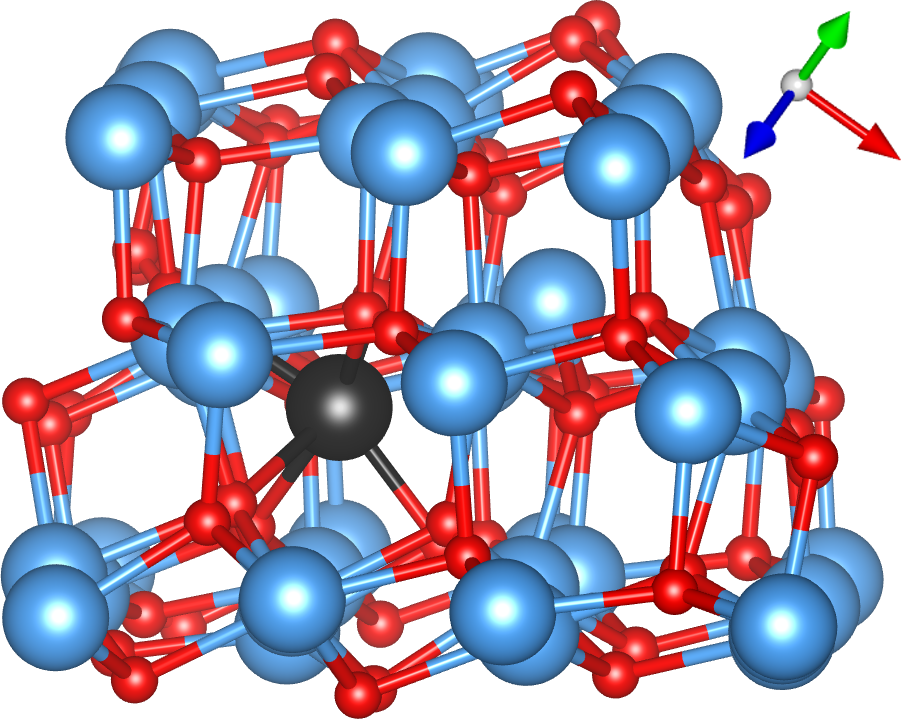
The defect with the lowest formation energy was found to be {2In,3VO}, which is shown in Fig. 2(a). In this defect, two In atoms (orange) sit either side of an In site as in a split interstitial. This is accommodated by the removal of 3 O atoms and the significant displacement of another In atom (black) away from the defect. The {In,2VO} defect shown in Fig. 2(b) is also on the convex hull and consists of an interstitial indium atom (black) with partially ionic bonds to two nearby oxygen atoms, which significantly displace a nearby indium atom (orange, to its lower-right). The {In,VO} defect, consisting of an In substitutional as shown in Fig. 2(c), is close enough to the hull to become potentially relevant at finite temperatures, given the intrinsic errors in DFT calculations. In this defect, an In atom (black) substitutes for an O atom, which significantly displaces the closest In atom, which is visible to its top-right in Fig. 2(c). To our knowledge, these defect structures have not been reported previously in the literature except for the indium interstitial and oxygen vacancy at the endpoints of the convex hull from which the chemical potentials were taken. The metastable {2In,2VO}, {In,VO}*, and {2In,3VO}* defects shown in Fig. 1 are described in the Supplemental Material.
Having identified the structures of defect complexes formed from oxygen vacancies and indium interstitials, their capacity to act as shallow donors was studied by calculating their densities of electronic states (DOS); if any of the defects identified create occupied states close to the conduction band, they are potentially implicated in the intrinsic n-type doping that is observed in . We investigated the DOS of each defect lying close to the convex hull, and obtained the results shown in Fig. 3, given alongside the bulk DOS for reference. This was done for each defect lying close to the convex hull. The densities of states were calculated using castep and the adaptive broadening functionality Yates et al. (2007) of the OptaDOS Morris et al. (2014) code.
As is typical, the PBE functional significantly underestimates the band gap of ; our calculations produce a gap of , compared to an experimental value of around . It is therefore possible, in principle, that the presence of occupied defect levels near the bottom of the valence band is simply the result of the inaccurately small gap predicted by the PBE functional. We tested this by recalculating the DOS for the oxygen vacancy using the HSE06 Krukau et al. (2006) screened exchange functional which gives larger and more accurate band gaps than PBE. By comparing the densities of states with the PBE and HSE06 functionals, we find that using an accurate band gap shifts the defect levels shift upwards with the conduction band rather than being fixed with respect to the valence band. This dispels concerns that the shallowness of the defect levels relative to the valence band may be an artifact of the unphysically small PBE band gap. (The two densities of states are shown in the Supplemental Material.)
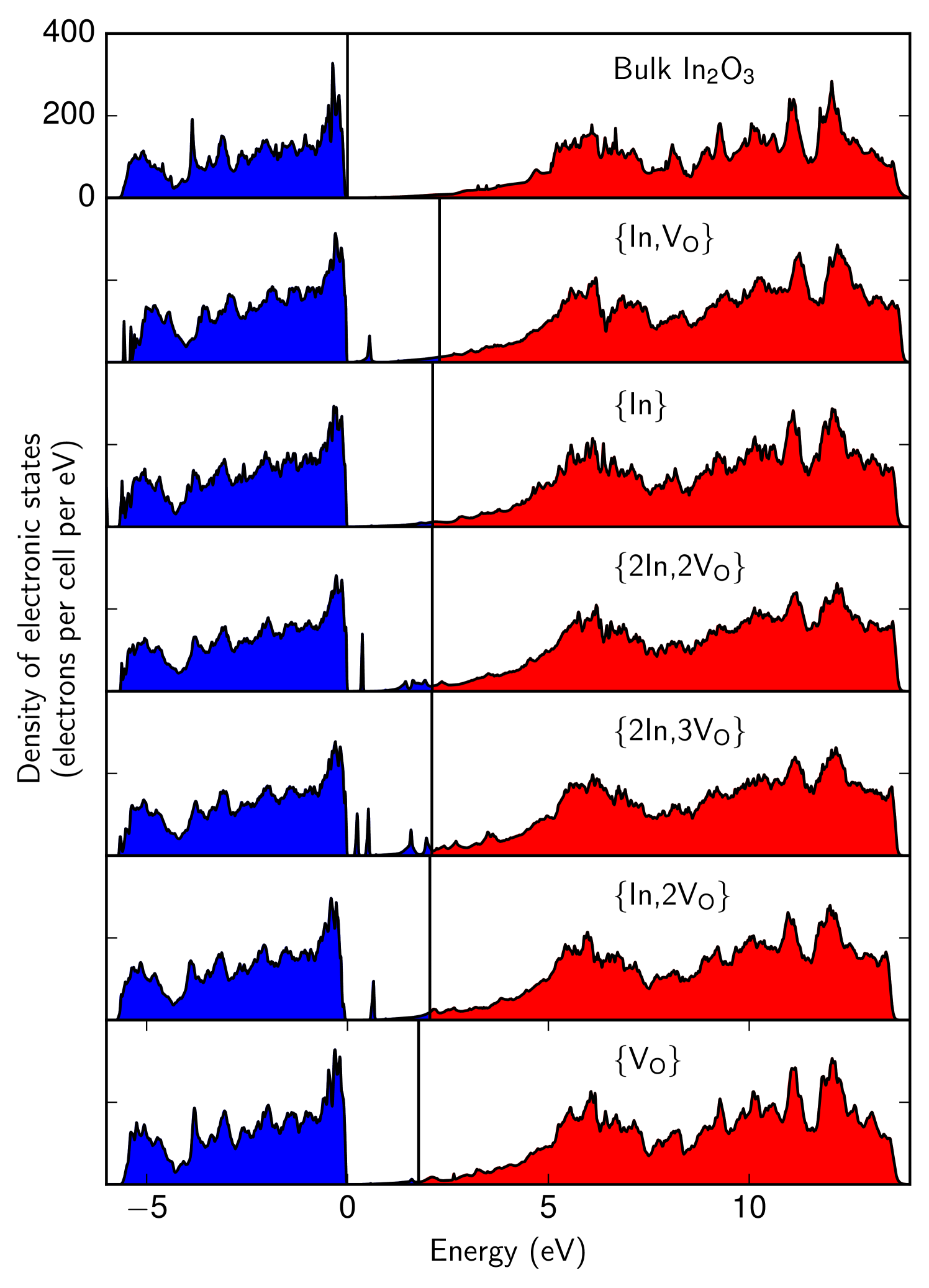
After predicting the defects and their structures, we next predicted their abundances at finite temperatures using the methods described previously. Harmonic phonon calculations were performed for all of the 160-atom defect cells and the free energy was constructed and minimised using Eq. 1. Such calculations were repeated for a range of temperatures and stoichiometries, giving the defect abundances as a function of temperature and stoichiometry. This allows the construction of the phase diagram shown in Fig. 4 in which the -axis gives the relative concentration of oxygen vacancies and indium interstitials as in Fig. 1.
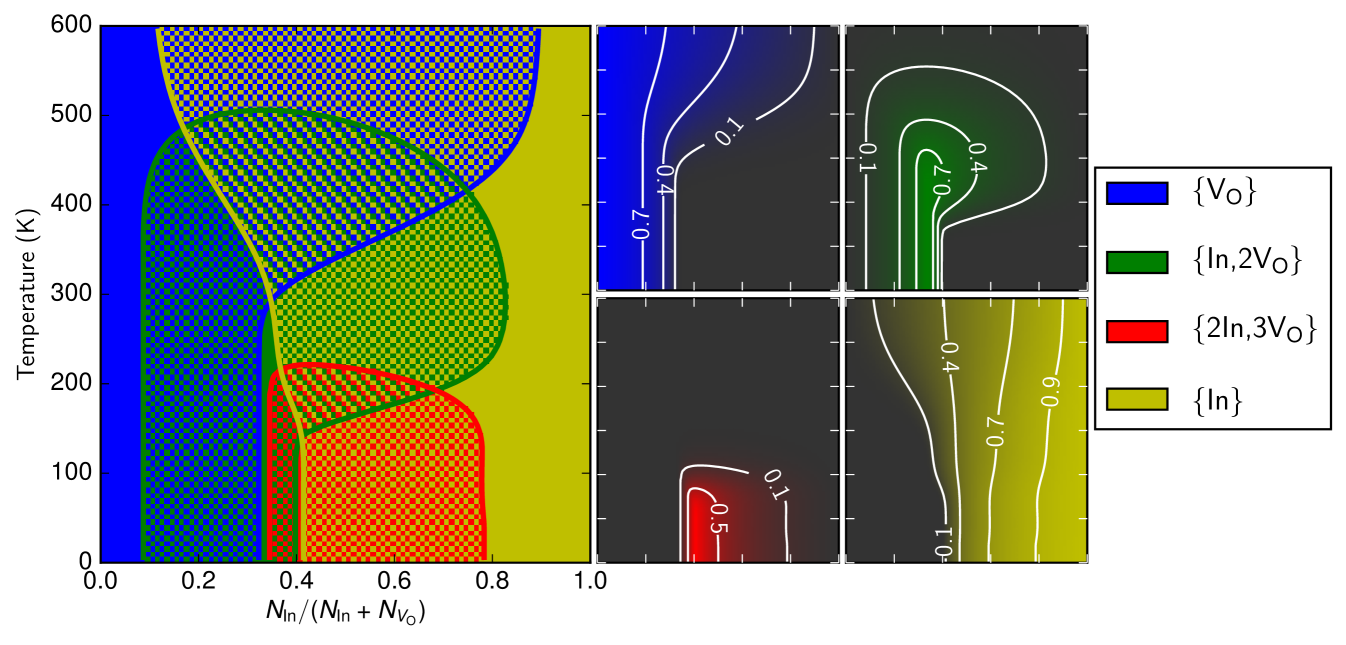
The phase diagram indicates that finite temperature effects are highly significant, with the {2In,3VO} defect dissociating almost entirely above room temperature. This is because the configurational entropy is maximised by breaking composite defects into multiple smaller defects. This entropically driven dissociation leads, once the {2In,3VO} defects have largely dissociated, to the formation of a higher number of {In,2VO} defects over certain temperature ranges, until the temperature increases still further and entropy maximisation dominates over energy minimisation so that the defect complexes break up completely and the {VO} and {In} point defects no longer bind to each other. (We have also recomputed the phase diagram using only those defects which had appeared in the literature prior to this paper, and the results confirm that our new defects significantly alter the predicted interaction between oxygen vacancies and indium interstitials; the recomputed phase diagram is shown in the Supplemental Material.)
We find the impact of the orientational degeneracy term to be very significant: by recomputing the phase diagram with translational entropy included but orientational entropy ignored, we calculate that the inclusion of the orientational degeneracy term pushes the temperature above which the {In,2VO} defect constitutes under 10% of all defects from down to the shown in Fig. 4. This can be understood once again as an entropically driven destabilisation of larger defect complexes such as {In,2VO} relative to their dissociation into smaller defects. We note that the magnitude of this change – a full shift in the transition temperature at which {In,2VO} dissociates – demonstrates the importance of capturing the effects of orientational entropy, as we have done here using our group theory scheme. (The recalculated phase diagram without orientational entropy included is also shown in the Supplemental Material.)
The defect structures, formation energies, degeneracies, and sources (AIRSS or literature) are summarised in Table 1. Note that the large number of defects with a degeneracy of 24 arises because the primitive cell of has 24 symmetry operators, and most of the defects break all of the symmetries of the bulk.
In conclusion, we have implemented a general methodology for first-principles predictions of defect abundances in crystalline materials at finite temperature. This methodology has been applied to bixbyite . Vibrational corrections and defect degeneracies are included in the free energies, which has led to the prediction of novel defect complexes from first principles. Using a group theory method, we have calculated the important but often-neglected contribution of the orientational degeneracy to the defect free energies, which has allowed us to provide a more accurate prediction of the abundances of the defects than has been possible to obtain before.
Studies of the intrinsic doping of have focused on the oxygen vacancy and indium interstitial defects as possible causes, but the results of our structure searches suggest that these point defects in fact tend to bind to each other to form composite defects whose structures we have described here for the first time; moreover, our finite-temperature calculations suggest that they remain bound at ambient conditions. By calculating the electronic DOS of these defects, we have also shown that they have the potential to act as shallow donors, which provide a source of charge carriers. These results could have significant implications for the question of the cause of intrinsic doping in , whose origin has been the subject of ongoing controversy. Given experimental findings that the conductivity of varies significantly with its annealing temperature, our calculations could also offer greater insight into the underlying defect physics affecting the manufacturing process.
| Defect | /atom | Degeneracy | Origin |
|---|---|---|---|
| {In,2VO} | -0.16 | 24 | AIRSS |
| {In,VO} | -0.13 | 24 | Known Agoston et al. (2009) |
| {In,VO}* | 0.00 | 24 | AIRSS |
| {2In,2VO} | -0.05 | 24 | AIRSS |
| {In} | 0.00 | 4 | Known Tomita et al. (2005) |
| {2In,3VO}* | 0.00 | 24 | AIRSS |
| {VO} | 0.00 | 24 | Known Tanaka et al. (1997) |
| {2In,3VO} | -0.17 | 24 | AIRSS |
Acknowledgements.
R. J. N. acknowledges financial support from the Engineering and Physical Sciences Research Council (EPSRC) of the U.K. [EP/J017639/1]. This work was performed using the Darwin Supercomputer of the University of Cambridge High Performance Computing Service (http://www.hpc.cam.ac.uk/), provided by Dell Inc. using Strategic Research Infrastructure Funding from the Higher Education Funding Council for England and funding from the Science and Technology Facilities Council. R. J. N. and A. J. M. acknowledge use of the Archer facilities of the U.K.’s national high-performance computing service (for which access was obtained via the UKCP consortium EP/K014560/1). J. M. W. acknowledges the support of the EPSRC Centre for Doctoral Training in Computational Methods for Materials Science. A. J. M. acknowledges support from the Winton Programme for the Physics of Sustainability. Data used in this work are available via the Cambridge data repository at dx.doi.org/10.17863/CAM.4396. We are grateful to Chris G. Van De Walle for fruitful discussions.References
- Curreli et al. (2005) M. Curreli, C. Li, Y. Sun, B. Lei, M. A. Gundersen, M. E. Thompson, and C. Zhou, Journal of the American Chemical Society 127, 6922 (2005).
- Bierwagen (2015) O. Bierwagen, Semiconductor Science and Technology 30, 24001 (2015).
- Galazka et al. (2013) Z. Galazka, K. Irmscher, M. Pietsch, T. Schulz, R. Uecker, D. Klimm, and R. Fornari, Cryst. Eng. Comm. 15, 2220 (2013).
- De Wit et al. (1977) J. H. W. De Wit, G. Van Unen, and M. Lahey, Journal of Physics and Chemistry of Solids 38, 819 (1977).
- Limpijumnong et al. (2009) S. Limpijumnong, P. Reunchan, A. Janotti, and C. G. Van De Walle, Physical Review B - Condensed Matter and Materials Physics 80, 193202 (2009).
- Bierwagen and Speck (2012) O. Bierwagen and J. S. Speck, Appl. Phys. Lett. 101, 102107 (2012).
- Tang et al. (2010) L.-M. Tang, L.-L. Wang, D. Wang, J.-Z. Liu, and K.-Q. Chen, Journal of Applied Physics 107, 83704 (2010).
- King et al. (2009) P. D. C. King, R. L. Lichti, Y. G. Celebi, J. M. Gil, R. C. Vilao, H. V. Alberto, J. Piroto Duarte, D. J. Payne, R. G. Egdell, I. McKenzie, C. F. McConville, S. F. J. Cox, and T. D. Veal, Physical Review B - Condensed Matter and Materials Physics 80, 081201 (2009).
- Agoston et al. (2009) P. Agoston, P. Erhart, A. Klein, and K. Albe, Journal of Physics: Condensed Matter 21, 455801 (2009).
- Hamberg and Granqvist (1986) I. Hamberg and C. G. Granqvist, Journal of Applied Physics 60, R123 (1986).
- Park et al. (2002) N. G. Park, M. Y. Kwak, B. O. Kim, O. K. Kwon, Y. K. Kim, B. You, T. W. Kim, and Y. S. Kim, Jpn. J. Appl. Phys. 41, 1523 (2002).
- Xu et al. (2013) X. Xu, D. Wang, J. Liu, P. Sun, Y. Guan, H. Zhang, Y. Sun, F. Liu, X. Liang, Y. Gao, and E. al., Sensors and Actuators B: Chemical 185, 32 (2013).
- Shen et al. (2005) X.-P. Shen, H.-J. Liu, X. Fan, Y. Jiang, J.-M. Hong, and Z. Xu, Journal of Crystal Growth 276, 471 (2005).
- Walsh et al. (2008) A. Walsh, J. L. F. Da Silva, S.-H. Wei, C. Körber, A. Klein, L. F. J. Piper, A. DeMasi, K. E. Smith, G. Panaccione, and P. Torelli, Physical Review Letters 100, 167402 (2008).
- Ágoston et al. (2009) P. Ágoston, K. Albe, R. M. Nieminen, and M. J. Puska, Phys. Rev. Lett. 103, 245501 (2009).
- Pickard and Needs (2011) C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter 23, 53201 (2011).
- Pickard and Needs (2006) C. J. Pickard and R. J. Needs, Physical Review Letters 97, 045504 (2006).
- Morris et al. (2011) A. J. Morris, C. P. Grey, R. J. Needs, and C. J. Pickard, Phys. Rev. B 84, 224106 (2011).
- Morris et al. (2009) A. J. Morris, C. J. Pickard, and R. J. Needs, Phys. Rev. B 80, 144112 (2009).
- Morris et al. (2013) A. J. Morris, R. J. Needs, E. Salager, C. P. Grey, and C. J. Pickard, Phys. Rev. B 87, 174108 (2013).
- Mulroue et al. (2011) J. Mulroue, A. J. Morris, and D. M. Duffy, Phys. Rev. B 84, 094118 (2011).
- Mulroue et al. (2013) J. Mulroue, M. Watkins, A. J. Morris, and D. M. Duffy, Journal of Nuclear Materials 437, 261 (2013).
- Mayo et al. (2016) M. Mayo, K. J. Griffith, C. J. Pickard, and A. J. Morris, Chemistry of Materials 28, 2011 (2016), arXiv:1510.03248 .
- Clark et al. (2005) S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson, and M. C. Payne, Zeitschrift fur Kristallographie 220, 567 (2005).
- Karazhanov et al. (2007) S. Z. Karazhanov, P. Ravindran, P. Vajeeston, A. Ulyashin, T. G. Finstad, and H. Fjellvåg, Phys. Rev. B 76, 075129 (2007).
- Al-Mushadani and Needs (2003) O. K. Al-Mushadani and R. J. Needs, Phys. Rev. B 68, 235205 (2003).
- Morris et al. (2008) A. J. Morris, C. J. Pickard, and R. J. Needs, Physical Review B 78, 184102 (2008).
- Freysoldt et al. (2014) C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti, and C. G. Van De Walle, Reviews of Modern Physics 86, 253 (2014).
- Yates et al. (2007) J. R. Yates, X. Wang, D. Vanderbilt, and I. Souza, Physical Review B 75, 195121 (2007).
- Morris et al. (2014) A. J. Morris, R. J. Nicholls, C. J. Pickard, and J. R. Yates, Computer Physics Communications 185, 1477 (2014).
- Krukau et al. (2006) A. V. Krukau, O. A. Vydrov, A. F. Izmaylov, and G. E. Scuseria, The Journal of Chemical Physics 125, 224106 (2006).
- Tomita et al. (2005) T. Tomita, K. Yamashita, Y. Hayafuji, and H. Adachi, Applied Physics Letters 87, 051911 (2005).
- Tanaka et al. (1997) I. Tanaka, M. Mizuno, and H. Adachi, Physical Review B 56, 3536 (1997).