Study of the $D_{s}^{+}\to a_{0}(980)\rho$ and $a_{0}(980)\omega$ decays

The two-body $D_{s}^{+}\to PP,PV$ decays with $P(V)$ denoting the strangeless pesudoscalar (vector) meson have no configurations from the $W$-boson emission processes because $\bar{s}$ in $D_{s}^{+}$ cannot be eliminated, as drawn in Fig. 1 for the topological diagrams T and C. Interestingly, it leads to a specific exploration for the annihilation mechanism applied to $D_{s}^{+}\to\pi^{+}\pi^{0},\pi^{+}\rho^{0},\pi^{+}\omega$ Fajfer:2003ag ; Bhattacharya:2009ps ; Cheng:2010ry ; Fusheng:2011tw ; Cheng:2019ggx ; Li:2013xsa .

In the short-distance $W$-boson annihilation (WA) $D_{s}^{+}(c\bar{s})\to W^{+}\to u\bar{d}$ process, $u\bar{d}$ can be seen to move in the opposite directions in the $D_{s}^{+}$ rest frame, such that there exists no orbital angular momentum between them. It indicates that $G(u\bar{d})=G(\pi^{+})=+1$ with $G$ denoting the $G$-parity symmetry Cheng:2010ry . Since $G$-parity is a multiplicative quantum number, one obtains $G(\pi^{+}\rho^{0},\pi^{+}\pi^{0})=(+1,-1)$. Consequently, the WA $D_{s}^{+}\to\pi^{+}\rho^{0}(\pi^{+}\pi^{0})$ decay due to $G(u\bar{d})=G(\pi^{+}\rho^{0})[=-G(\pi^{+}\pi^{0})]$ is a $G$-parity conserved (violated) process, which corresponds to the experimental result ${\cal B}(D_{s}^{+}\to\pi^{+}\rho^{0})=(1.9\pm 1.2)\times 10^{-4}$ $[{\cal B}(D_{s}^{+}\to\pi^{+}\pi^{0})<3.4\times 10^{-4}]$ pdg . By contrast, although the WA $D_{s}^{+}\to\pi^{+}\omega$ decay violates the $G$-parity symmetry, ${\cal B}(D_{s}^{+}\to\pi^{+}\omega)=(1.9\pm 0.3)\times 10^{-3}$ shows no suppression pdg . It is hence considered to receive the long-distance annihilation contribution Fajfer:2003ag ; Cheng:2010ry .

The $D_{s}^{+}\to SP,SV$ decays can help to investigate the short and long-distance annihilation mechanisms Cheng:2010vk ; Hsiao:2019ait ; Ling:2021qzl , where $S$ stands for a non-strange scalar meson. For example, the WA process for $D_{s}^{+}\to a_{0}^{0(+)}\pi^{+(0)}$ violates $G$-parity Achasov:2017edm ; Hsiao:2019ait , such that its branching fraction is expected as small as ${\cal B}(D_{s}^{+}\to\pi^{+}\pi^{0})$. Nonetheless, one measures that ${\cal B}(D_{s}^{+}\to a_{0}^{0(+)}\pi^{+(0)})\simeq 100{\cal B}(D_{s}^{+}\to\pi^{+}\rho^{0})$ BESIII:2019jjr ; pdg . Clearly, it indicates the main contribution from the long-distance annihilation process Hsiao:2019ait . Explicitly, the long-distance annihilation process for $D_{s}^{+}\to a_{0}^{0(+)}\pi^{+(0)}$ starts with the $D_{s}^{+}\to\eta^{(\prime)}\rho^{+}$ weak decay, followed by the $\eta^{(\prime)}$ and $\rho^{+}$ rescattering. With the $\pi^{+(0)}$ exchange, $\eta^{(\prime)}$ and $\pi^{+}$ are turned into $a_{0}^{+(0)}$ and $\pi^{0(+)}$, respectively. Since BESIII has recently reported the first observation of the branching fractions of $D_{s}^{+}\to SV,S\to PP$ as BESIII:2021qfo ; BESIII:2021aza

	$\displaystyle{\cal B}_{+}(D_{s}^{+}\to a_{0}^{+}\rho^{0},a_{0}^{+}\to\pi^{+}\eta)$	$\displaystyle=$	$\displaystyle(2.1\pm 0.8\pm 0.5)\times 10^{-3}\,,$
	$\displaystyle{\cal B}_{0}(D_{s}^{+}\to a_{0}^{0}\rho^{+},a_{0}^{0}\to K^{+}K^{-})$	$\displaystyle=$	$\displaystyle(0.7\pm 0.2\pm 0.1)\times 10^{-3}\,,$		(1)

we are wondering which of the short and long-distance annihilation processes can be the dominant contribution. Hence, we propose to study $D_{s}^{+}\to a_{0}^{+(0)}\rho^{0(+)}$, $D_{s}^{+}\to a_{0}^{+}\omega$, and the resonant three-body $D_{s}^{+}\to a_{0}^{+(0)}\rho^{0(+)},a_{0}^{+(0)}\to[\eta\pi^{+(0)},K^{+}\bar{K}^{0}(K^{+}K^{-})]$ decays, in order to analyze the data in Eq. (I). We will also test if ${\cal B}(D_{s}^{+}\to a_{0}^{+}\rho^{0},a_{0}^{+}\rho^{0})$ have nearly equal sizes as ${\cal B}(D_{s}^{+}\to a_{0}^{+}\pi^{0})\simeq{\cal B}(D_{s}^{+}\to a_{0}^{0}\pi^{+})$ that respects the isospin symmetry.

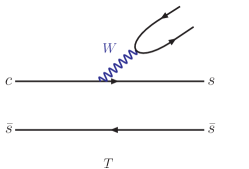
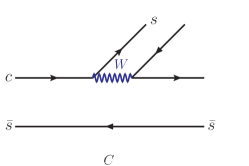
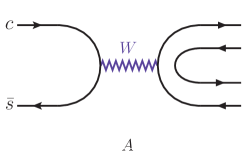
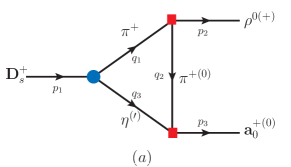
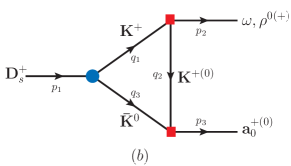
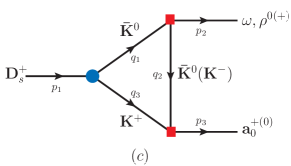
Considering the short-distance WA processes, $D_{s}^{+}\to PP(PV)$ and $D_{s}^{+}\to SP(SV)$ both get an $A$ term as the annihilation amplitude in Fig. 1. According to ${\cal B}(D_{s}^{+}\to\pi^{+}\rho^{0})\simeq 10^{-4}$ that receives the short-distance WA contribution pdg , one regards $A$ to give ${\cal B}(D_{s}^{+}\to a_{0}^{+(0)}\rho^{0(+)})$ not larger than $10^{-4}$. However, ${\cal B}_{+}$ in Eq. (I) suggests ${\cal B}(D_{s}^{+}\to a_{0}^{+}\rho^{0})\simeq 10^{-3}$. This strongly suggests that the main contribution to $D_{s}^{+}\to a_{0}^{+(0)}\rho^{0(+)}$ is from the long-distance annihilation process. For $D_{s}^{+}\to a_{0}^{+}\omega$, the WA contribution is suppressed with the $G$-parity violation, such that $A\simeq 0$. Therefore, we start with the triangle rescattering processes for $D_{s}^{+}\to a_{0}^{+(0)}\rho^{0(+)}$ and $D_{s}^{+}\to a_{0}^{+}\omega$ as the most possible main contributions.

See Fig. 2, the rescattering processes for $D_{s}^{+}\to a_{0}^{+(0)}\rho^{0(+)}$ include both the weak and strong decays. In our case, the weak decays come from $D^{+}_{s}\to\pi^{+}\eta^{(\prime)},K^{+}\bar{K}^{0}$, and the amplitudes are given by Cheng:2010ry ; Cheng:2019ggx ; Fusheng:2011tw ; Bhattacharya:2009ps

	$\displaystyle{\cal M}_{\eta}(D^{+}_{s}\to\pi^{+}\eta)$	$\displaystyle=$	$\displaystyle\frac{G_{F}}{\sqrt{2}}V^{*}_{cs}V_{ud}(\sqrt{2}A\cos\phi-T\sin\phi)\,,$
	$\displaystyle{\cal M}_{\eta^{\prime}}(D^{+}_{s}\to\pi^{+}\eta^{\prime})$	$\displaystyle=$	$\displaystyle\frac{G_{F}}{\sqrt{2}}V^{*}_{cs}V_{ud}(\sqrt{2}A\sin\phi+T\cos\phi)\,,$
	$\displaystyle{\cal M}_{K}(D^{+}_{s}\to K^{+}\bar{K}^{0})$	$\displaystyle=$	$\displaystyle\frac{G_{F}}{\sqrt{2}}V^{*}_{cs}V_{ud}(C+A)\,,$		(2)

where $G_{F}$ is the Fermi constant, $V^{*}_{cs}V_{ud}$ the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements, and $V^{*}_{cs}V_{ud}\simeq 1$ presents the Cabibbo-allowed decay modes. In addition, $(T,C,A)$ are the topological amplitudes, along with the mixing angle $\phi=43.5^{\circ}$ from the $\eta-\eta^{\prime}$ mixing matrix FKS ; FKS2 :

$\displaystyle\left(\begin{array}[]{c}\eta\\ \eta^{\prime}\end{array}\right)=\left(\begin{array}[]{cc}\cos\phi&-\sin\phi\\ \sin\phi&\cos\phi\end{array}\right)\left(\begin{array}[]{c}\sqrt{1/2}(u\bar{u}+d\bar{d})\\ s\bar{s}\end{array}\right)\,.$

(9)

For the strong decays $V,S\to PP$, the amplitudes are given by Hsiao:2019ait

	$\displaystyle{\cal M}_{\rho^{0(+)}\to\pi^{+(0)}\pi^{-(+)}}=g_{\rho}\epsilon\cdot(q_{1}-q_{2}),\,$
	$\displaystyle{\cal M}_{a_{0}^{+}\to\eta^{(\prime)}\pi^{+},K^{+}\bar{K}^{0}}=g_{\eta^{(\prime)}},g_{K}\,,$		(10)

where $\epsilon_{\mu}$ is the polarization four vector of the $\rho$ meson, and $q_{1,2}^{\mu}$ are the four momenta of $\pi^{+}\pi^{-}(\pi^{0}\pi^{+})$, respectively. The $SU(3)$ flavor symmetry is able to relate different $V(S)\to PP$ decay channels Tornqvist:1979hx ; Fayyazuddin:2012qfa , such that we obtain $g_{\rho}/2$ for ${\cal M}_{\rho^{0}\to K^{+}K^{-},\bar{K}^{0}K^{0}}$, $g_{\rho}/\sqrt{2}$ for ${\cal M}_{\rho^{+}\to K^{+}\bar{K}^{0}}$, and $(-)g_{K}/\sqrt{2}$ for ${\cal M}_{a^{0}_{0}\to K^{+}K^{-}(\bar{K}^{0}K^{0})}$, together with $(-)g_{\rho}/2$ for ${\cal M}_{\omega\to K^{+}K^{-}(\bar{K}^{0}K^{0})}$.

By assembling the weak and strong couplings in the rescattering processes, we derive that

	$\displaystyle{\cal M}(D_{s}^{+}\to\rho^{0(+)}a^{+(0)}_{0})$	$\displaystyle=$	$\displaystyle{\cal M}_{a}+{\cal M}_{a}^{\prime}+{\cal M}_{b}+{\cal M}_{c}\,,$
	$\displaystyle{\cal M}(D_{s}^{+}\to\omega a^{+}_{0})$	$\displaystyle=$	$\displaystyle\hat{\cal M}_{b}+\hat{\cal M}_{c}\,,$		(11)

with $M_{a}^{(\prime)}$ and $M_{b(c)}[\hat{M}_{b(c)}]$ for Fig. 2a and Fig. 2b(c), respectively. More explicitly, ${\cal M}_{a,b,c}$ are given by Hsiao:2019ait ; Yu:2020vlt ; Hsiao:2021tyq

	$\displaystyle{\cal M}_{a}$	$\displaystyle=$	$\displaystyle\int\frac{d^{4}{q}_{1}}{(2\pi)^{4}}\frac{{\cal M}_{\eta}{\cal M}_{\rho^{0(+)}\to\pi^{+}\pi^{-(0)}}{\cal M}_{a^{+(0)}_{0}\to\eta\pi^{+(0)}}F_{\pi}(q_{2}^{2})}{(q_{1}^{2}-m_{\pi}^{2}+i\epsilon)[(q_{1}-p_{2})^{2}-m_{\pi}^{2}+i\epsilon][(q_{1}-p_{1})^{2}-m_{\eta}^{2}+i\epsilon]}\,,$
	$\displaystyle{\cal M}_{b}$	$\displaystyle=$	$\displaystyle\int\frac{d^{4}{q}_{1}}{(2\pi)^{4}}\frac{{\cal M}_{K}{\cal M}_{\rho^{0(+)}\to K^{+}K^{-}(K^{+}\bar{K}^{0})}{\cal M}_{a_{0}^{+(0)}\to\bar{K}^{0}K^{+(0)}}F_{K}(q_{2}^{2})}{(q_{1}^{2}-m_{K}^{2}+i\epsilon)[(q_{1}-p_{2})^{2}-m_{K}^{2}+i\epsilon][(q_{1}-p_{1})^{2}-m_{K}^{2}+i\epsilon]}\,,$
	$\displaystyle{\cal M}_{c}$	$\displaystyle=$	$\displaystyle\int\frac{d^{4}{q}_{1}}{(2\pi)^{4}}\frac{{\cal M}_{K}{\cal M}_{\rho^{0(+)}\to\bar{K}^{0}K^{0(+)}}{\cal M}_{a_{0}^{+(0)}\to\bar{K}^{0}K^{+(0)}}F_{K}(q_{2}^{2})}{(q_{1}^{2}-m_{K}^{2}+i\epsilon)[(q_{1}-p_{2})^{2}-m_{K}^{2}+i\epsilon][(q_{1}-p_{1})^{2}-m_{K}^{2}+i\epsilon]}\,,$		(12)

with $q_{2}=q_{1}-p_{2}$ and $q_{3}=q_{1}-p_{1}$ following the momentum flows in Fig. 2. The form factor $F_{M}(q_{2}^{2})\equiv(\Lambda_{M}^{2}-m^{2}_{M})/(\Lambda_{M}^{2}-q^{2}_{2})$ with the cutoff parameter $\Lambda_{M}$ [$M=(\pi,K)$] is to avoid the overestimation with $q_{2}$ to $\pm\infty$ Du:2021zdg . Substituting $\eta^{\prime}$ and $\omega$ for $\eta$ in ${\cal M}_{a}$ and $\rho^{0}$ in ${\cal M}_{b(c)}$ leads to ${\cal M}_{a}^{\prime}$ and $\hat{\cal M}_{b(c)}$, respectively.

As a consequence, we find that

	$\displaystyle{\cal M}(D_{s}^{+}\to\rho^{0}a^{+}_{0})$	$\displaystyle=$	$\displaystyle{\cal M}(D_{s}^{+}\to\rho^{+}a^{0}_{0})\,,$
	$\displaystyle{\cal M}(D_{s}^{+}\to\omega a^{+}_{0})$	$\displaystyle=$	$\displaystyle 0\,,$		(13)

where the first relation respects the isospin symmetry, whereas $\hat{\cal M}_{b}=-\hat{\cal M}_{c}$ due to ${\cal M}_{\omega\to K^{+}K^{-}}=-{\cal M}_{\omega\to\bar{K}^{0}K^{0}}$ cancels the rescattering contributions to $D_{s}^{+}\to\omega a^{+}_{0}$, which causes ${\cal M}(D_{s}^{+}\to\omega a^{+}_{0})=0$.

To deal with the triangle loops in Eq. (II), the equation in Refs. tHooft:1978jhc ; Hahn:1998yk ; Denner:2005nn ; Passarino:1978jh can be useful, given by

	$\displaystyle\int\frac{d^{4}q_{1}}{i\pi^{2}}\frac{q_{1}^{\mu}}{(q_{1}^{2}-m_{1}^{2}+i\epsilon)[(q_{1}-p_{2})^{2}-m_{2}^{2}+i\epsilon][(q_{1}-p_{1})^{2}-m_{3}^{2}+i\epsilon]}$
	$\displaystyle=-p_{\rho}^{\mu}C_{1}(p_{a_{0}}^{2},m_{\rho}^{2},m_{D_{s}}^{2},m_{1}^{2},m_{2}^{2},m_{3}^{2})-p_{D_{s}}^{\mu}C_{2}(p_{a_{0}}^{2},m_{\rho}^{2},m_{D_{s}}^{2},m_{1}^{2},m_{2}^{2},m_{3}^{2})\,.$		(14)

By calculating the triangle rescattering processes, we obtain

	$\displaystyle\Gamma(D_{s}^{+}\to\rho^{0{+}}a^{+(0)}_{0})=\frac{|\vec{p}_{2}|^{3}}{8\pi m_{\rho}^{2}}|H|^{2}\,,$
	$\displaystyle H=\frac{1}{8\pi^{2}}\bigg{(}g_{\rho}g_{\eta}{\cal M}_{\eta}C_{\eta}+g_{\rho}g_{\eta^{\prime}}{\cal M}_{\eta^{\prime}}C_{\eta^{\prime}}+g_{\rho}g_{K}{\cal M}_{K}C_{K}\bigg{)}\,,$		(15)

with $C_{\eta^{(\prime)}}=C_{2,\eta^{(\prime)}}-C_{2,\eta^{(\prime)}}^{*}$ and $C_{K}=C_{2,K}-C_{2,K}^{*}$ as the integrated results of the $C_{2}$ terms in Eq. (II), where $C_{2,M}^{(*)}$ are defined by

	$\displaystyle C_{2,\eta}^{(*)}$	$\displaystyle=$	$\displaystyle C_{2}(m_{\pi},m_{\pi}(\Lambda_{\pi}),m_{\eta})\,,$
	$\displaystyle C_{2,\eta^{\prime}}^{(*)}$	$\displaystyle=$	$\displaystyle C_{2}(m_{\pi},m_{\pi}(\Lambda_{\pi}),m_{\eta^{\prime}})\,,$
	$\displaystyle C_{2,K}^{(*)}$	$\displaystyle=$	$\displaystyle C_{2}(m_{K},m_{K}(\Lambda_{K}),m_{K})\,.$		(16)

However, the $C_{1}$ terms have been disappearing due to $p_{\rho}\cdot\epsilon=0$ in the amplitudes.

For the three-body decays $D_{s}^{+}\to\rho^{0(+)}(a^{+(0)}_{0}\to)\eta\pi^{+(0)},K^{+}\bar{K}^{0}(K^{+}K^{-})$, we present pdg

	$\displaystyle\Gamma(D_{s}^{+}\to\rho a_{0},a_{0}\to\eta\pi(KK))$
	$\displaystyle=\int\int\frac{1}{(2\pi)^{3}}\frac{|\vec{p}_{2}|^{2}}{32m_{D_{s}}m_{\rho}^{2}}|H|^{2}\frac{g_{\eta(K)}^{2}}{\mid D_{a_{0}}(s)\mid^{2}}dsdt\,,$		(17)

with $s=(p_{\eta(K)}+p_{\pi(K)})^{2}$ and $t=(p_{\rho}+p_{\pi(K)})^{2}$, such that the theoretical results can be compared to the data in Eq. (I). In the above equation, $1/D_{a_{0}}(s)$ presents the propagator for $a_{0}$, and we define Achasov:2004uq

$\displaystyle D_{a_{0}}(s)=s-m_{a_{0}}^{2}-\sum\limits_{\alpha\beta}{\bigg{[}\text{Re}\Pi^{\alpha\beta}_{a_{0}}(m^{2}_{a_{0}})-\Pi^{\alpha\beta}_{a_{0}}(s)\bigg{]}}\,,$

(18)

where

	$\displaystyle\Pi^{\alpha\beta}_{a_{0}}(x)$	$\displaystyle=$	$\displaystyle\frac{G^{2}_{\alpha\beta}}{16\pi}\bigg{\{}\frac{m_{\alpha\beta}^{+}m_{\alpha\beta}^{-}}{\pi x}\log\bigg{[}\frac{m_{\beta}}{m_{\alpha}}\bigg{]}-\theta[x-(m_{\alpha\beta}^{+})^{2}]$
		$\displaystyle\times$	$\displaystyle\rho_{\alpha\beta}\bigg{(}i+\frac{1}{\pi}\log\bigg{[}\frac{\sqrt{x-(m_{\alpha\beta}^{+})^{2}}+\sqrt{x-(m_{\alpha\beta}^{-})^{2}}}{\sqrt{x-(m_{\alpha\beta}^{-})^{2}}-\sqrt{x-(m_{\alpha\beta}^{+})^{2}}}\bigg{]}\bigg{)}$
		$\displaystyle-$	$\displaystyle\rho_{\alpha\beta}\bigg{(}1-\frac{2}{\pi}\arctan\bigg{[}\frac{\sqrt{-x+(m_{\alpha\beta}^{+})^{2}}}{\sqrt{x-(m_{\alpha\beta}^{-})^{2}}}\bigg{]}\bigg{)}(\theta[x-(m_{\alpha\beta}^{-})^{2}]-\theta[x-(m_{\alpha\beta}^{+})^{2}])$
		$\displaystyle+$	$\displaystyle\rho_{\alpha\beta}\frac{1}{\pi}\log\bigg{[}\frac{\sqrt{(m_{\alpha\beta}^{+})^{2}-x}+\sqrt{(m_{\alpha\beta}^{-})^{2}-x}}{\sqrt{(m_{\alpha\beta}^{-})^{2}-x}-\sqrt{(m_{\alpha\beta}^{+})^{2}-x}}\bigg{]}\theta[(m_{\alpha\beta}^{-})^{2}-x]\bigg{\}}\,,$
	$\displaystyle\rho_{\alpha\beta}$	$\displaystyle\equiv$	$\displaystyle\left|\sqrt{x-(m_{\alpha\beta}^{+})^{2}}\sqrt{x-(m_{\alpha\beta}^{-})^{2}}\right|/x\,,$		(19)

with $G_{\alpha\beta}=(g_{\eta^{(\prime)}},g_{K})$ for $\alpha\beta={(\eta^{(\prime)}\pi,K\bar{K})}$ and $m_{\alpha\beta}^{\pm}=m_{\alpha}\pm m_{\beta}$.

In the numerical analysis, we adopt $V_{cs}=V_{ud}=1-\lambda^{2}/2$ with $\lambda=0.22453\pm 0.00044$ in the Wolfenstein parameterization pdg , along with $m_{a_{0}^{0}}=0.987$ GeV Kornicer:2016axs ; Bugg:2008ig . The topological parameters $(T,C,A)$ have been extracted as Cheng:2019ggx

	$\displaystyle(|T|,|C|,|A|)=(0.363\pm 0.001,0.323\pm 0.030,0.064\pm 0.004)~{}\mbox{GeV}^{3}~{}\,,$
	$\displaystyle(\delta_{C},\delta_{A})=(-151.3\pm 0.3,23.0^{+\;\;7.0}_{-10.0})^{\circ}\,,$		(20)

where $\delta_{C,A}$ are the relative strong phases. According to the extraction, we obtain ${\cal B}(D_{s}^{+}\to\pi^{+}\eta,\pi^{+}\eta^{\prime},K^{+}\bar{K}^{0})=(1.8\pm 0.2,4.2\pm 0.5,3.1\pm 0.5)\times 10^{-2}$, consistent with the experimental values of $(1.68\pm 0.10,3.94\pm 0.25,2.95\pm 0.14)\times 10^{-2}$, respectively pdg . For $V,S\to PP$, the strong coupling constants read Bugg:2008ig ; Kornicer:2016axs ; pdg

$\displaystyle g_{\rho}=6.0\,,(g_{\eta},g_{\eta^{\prime}},g_{K})=(2.87\pm 0.09,-2.52\pm 0.08,2.94\pm 0.13)~{}\text{GeV}\,.$

(21)

Empirically, $\Lambda_{M}$ of ${\cal O}(1.0~{}\text{GeV})$ is commonly used to explain the data Tornqvist:1993ng ; Li:1996yn ; Wu:2019vbk ; besides, it is obtained that $\Lambda_{K}-\Lambda_{\pi}=m_{K}-m_{\pi}$ Cheng:2004ru . Therefore, we are allowed to use $(\Lambda_{\pi},\Lambda_{K})=(1.25\pm 0.25,1.60\pm 0.25)$ GeV, which result in

	$\displaystyle C_{\eta}$	$\displaystyle=$	$\displaystyle[(0.57\pm 0.08)+i(0.17\pm 0.09)]~{}\text{GeV}^{-2}\,,$
	$\displaystyle C_{\eta^{\prime}}$	$\displaystyle=$	$\displaystyle[(0.34\pm 0.03)-i(0.27\pm 0.07)]~{}\text{GeV}^{-2}\,,$
	$\displaystyle C_{K}$	$\displaystyle=$	$\displaystyle[(0.85\pm 0.03)-i(0.45\pm 0.08)]~{}\text{GeV}^{-2}\,,$		(22)

with $p_{a_{0}}^{2}=m_{a_{0}}^{2}$. Subsequently, we predict

	$\displaystyle{\cal B}(D_{s}^{+}\to\rho^{0(+)}a^{+(0)}_{0})=(3.0\pm 0.3\pm 1.0)\times 10^{-3}\,,$
	$\displaystyle{\cal B}(D_{s}^{+}\to\omega a^{+}_{0})=0\,,$		(23)

where the first error in ${\cal B}(D_{s}^{+}\to\rho^{0(+)}a^{+(0)}_{0})$ takes into account the uncertainties from $\Lambda_{\pi}$ and $\Lambda_{K}$, and the second one combines those from $V_{cs}^{*}$, $V_{ud}$, $(T,C,A)$, and the strong coupling constants. For the resonant three-body decays, we obtain

	$\displaystyle{\cal B}(D_{s}^{+}\to\rho^{0(+)}(a^{+(0)}_{0}\to)\eta\pi^{+(0)})$	$\displaystyle=$	$\displaystyle(1.6^{+0.2}_{-0.3}\pm 0.6)\times 10^{-3}\,,$
	$\displaystyle{\cal B}(D_{s}^{+}\to\rho^{+}(a^{0}_{0}\to)K^{+}K^{-},K^{0}\bar{K}^{0})$	$\displaystyle=$	$\displaystyle(0.9^{+0.1}_{-0.1}\pm 0.4,0.7^{+0.1}_{-0.1}\pm 0.3)\times 10^{-4}\,,$
	$\displaystyle{\cal B}(D_{s}^{+}\to\rho^{0}(a^{+}_{0}\to)K^{+}\bar{K}^{0})$	$\displaystyle=$	$\displaystyle(1.5^{+0.2}_{-0.3}\pm 0.6)\times 10^{-4}\,,$		(24)

where the sources of the two errors are the same as those in Eq. (III).

In the triangle loop, when the momentum flow approaches the mass shell for one of the three propagators, the integration with $i\epsilon\simeq im\Gamma$ gives rise to the imaginary parts in Eq. (III), where $\Gamma$ is a very tiny decay width for $\pi$, $\eta^{(\prime)}$ or $K$. The off-shell integrations are responsible for the real parts in Eq. (III), for which we take ${\cal M}_{a}$ as our description. In principle, the integration allows a momentum flow from $-\infty$ to $+\infty$. However, when the exchange particle proceeds with $q_{2}^{2}$ around several GeV², instead of the infinity, the integration with $q_{2}^{2}\sim\pm\infty$ causes an overestimation Du:2021zdg . We have accordingly introduced the form factor $F_{\pi}$ in Eq. (II) to cut off the contribution from $q_{2}^{2}\sim\pm\infty$. While $q_{1}^{2}$, $q_{2}^{2}$ and $q_{3}^{2}$ have been associated in the loop, $F_{\pi}$ also works to cut off the contributions from the propagators of the rescattering particles $\pi^{+}$ and $\eta^{(\prime)}$. Note that the single cutoff form factor has also been commonly used elsewhere Wu:2021udi ; Wu:2019rog ; Li:2014pfa  ¹¹1Please also consult Refs. Cheng:2021nal , where one considers three cutoff form factors..

The smallness of the WA $D_{s}^{+}\to MM$ decay can be traced back to its amplitude, given by Hsiao:2019wyd ; Hsiao:2014zza ; Huang:2021qld

	$\displaystyle{\cal M}_{WA}(D_{s}^{+}\to MM)\propto f_{D_{s}}q^{\mu}\langle MM|\bar{u}\gamma_{\mu}(1-\gamma_{5})d|0\rangle$
	$\displaystyle\simeq(m_{u}+m_{d})\langle MM|\bar{u}\gamma_{5}d|0\rangle\,,$		(25)

where $q^{\mu}\langle MM|u\gamma_{\mu}d|0\rangle=0$ corresponds to the conservation of the vector current (CVC); most importantly, $m_{u(d)}\simeq 0$ causes the chiral suppression of the WA $D_{s}^{+}\to MM$ decay. According to the data, ${\cal B}(D_{s}^{+}\to\pi^{+}\rho^{0})=(1.9\pm 1.2)\times 10^{-4}$ indicates that ${\cal B}_{WA}(D_{s}^{+}\to MM)$ should be around $10^{-4}$. In addition, ${\cal B}(D_{s}^{+}\to\pi^{+}\pi^{0})<3.4\times 10^{-4}$ suggests that the G-parity violation suppresses the WA process even more. Therefore, since $D_{s}^{+}\to\rho a_{0},\rho\pi$ are both the G-parity conserved processes, it is reasonable to present that ${\cal B}_{WA}(D_{s}^{+}\to\rho a_{0})\simeq{\cal B}_{WA}(D_{s}^{+}\to\rho\pi)\sim 10^{-4}$. As a theoretical support, we present

			$\displaystyle{\cal B}_{WA}(D_{s}^{+}(c\bar{s})\to\rho a_{0})$		(26)
		$\displaystyle=$	$\displaystyle R_{f}\frac{(V_{cs}^{*}V_{ud}f_{D_{s}})^{2}\tau_{D_{s}}}{(V_{cb}V_{ud}^{*}f_{B_{c}})^{2}\tau_{B_{c}}}{\cal B}_{WA}(B_{c}^{+}(c\bar{b})\to\rho a_{0})\sim 10^{-4}\,,$

in agreement with our estimation, where $R_{f}=3.1\times 10^{-2}$ is mostly from the phase space factors, and ${\cal B}_{WA}(B_{c}^{+}\to\rho a_{0})\simeq 1.0\times 10^{-5}$ is adopted from Ref. Liu:2010kq .

Disregarding the WA contributions, we predict ${\cal B}(D_{s}^{+}\to\rho^{0(+)}a^{+(0)}_{0})=3.0\times 10^{-3}$ in Eq. (III). It is found that the $\eta\pi,\eta^{\prime}\pi,K^{+}\bar{K}^{0}$ rescatterings and their interferences give 6%, 7%, 30% and 59% of ${\cal B}(D_{s}^{+}\to a_{0}^{+(0)}\rho^{0(+)})$, respectively. By contrast, the $\rho\eta^{(\prime)}$ rescatterings from $D_{s}^{+}\to\rho\eta^{(\prime)}$ dominantly contribute to $D_{s}^{+}\to a_{0}^{+(0)}\pi^{0(+)}$, instead of $D_{s}^{+}\to K^{*}K$ Hsiao:2019ait . Since $D_{s}^{+}\to\omega a^{+}_{0}$ has no rescattering effects; besides, the WA contribution is suppressed by the $G$-parity violation, we anticipate that ${\cal B}(D_{s}^{+}\to\omega a^{+}_{0})\simeq{\cal B}(D_{s}^{+}\to\pi^{+}\pi^{0})<3.4\times 10^{-4}$ pdg .

In Eq. (III), ${\cal B}(D_{s}^{+}\to\rho^{0}(a^{+}_{0}\to)\eta\pi^{+})=(1.6^{+0.2}_{-0.3}\pm 0.6)\times 10^{-3}$ is able to explain the data [see Eq. (I)], demonstrating the sufficient long-distance annihilation contribution. It is confusing that ${\cal B}(D_{s}^{+}\to a_{0}^{0}\rho^{+},a_{0}^{0}\to K^{+}K^{-})$ is 10 times smaller than ${\cal B}_{0}$ in Eq. (I). For clarification, we take the approximate form of the resonant branching fraction: ${\cal B}(D_{s}^{+}\to SV,S\to PP)\simeq{\cal B}(D_{s}^{+}\to SV){\cal B}(S\to PP)$, together with the isospin relation: ${\cal B}(D_{s}^{+}\to\rho^{0}a^{+}_{0})\simeq{\cal B}(D_{s}^{+}\to\rho^{+}a^{0}_{0})$, such that ${\cal B}_{0}/{\cal B}_{+}$ is reduced as ${\cal B}(a_{0}^{0}\to K^{+}K^{-})/{\cal B}(a_{0}^{+}\to\eta\pi^{+})\simeq 1/3$, disagreeing with ${\cal B}(a_{0}^{0}\to K^{+}K^{-})/{\cal B}(a_{0}^{+}\to\eta\pi^{+})=1/10$ from the experimental extraction Cheng:2010vk . Therefore, we conclude that there exists a possible contradiction between the observations in Eq. (I).

In our reasoning, the contradiction might be caused by $D_{s}^{+}\to\rho^{+}f_{0},f_{0}\to K^{+}K^{-}$ with $f_{0}\equiv f_{0}(980)$, which can be mistaken as $D_{s}^{+}\to\rho^{+}a_{0}^{0},a_{0}^{0}\to K^{+}K^{-}$ PC . First, since $D_{s}^{+}\to\rho^{+}f_{0}$ is an external $W$-boson emission process, its branching fraction can be of order $10^{-3}$. Second, $a_{0}$ and $f_{0}$ are both scalar mesons, and have nearly the same masses and overlapped decay widths. As a result, it is possible that one cannot distinguish between the resonant signals of $D_{s}^{+}\to\rho^{+}(f_{0},a_{0}),(f_{0},a_{0})\to K^{+}K^{-}$ in the $K^{+}K^{-}$ invariant mass spectrum. For a careful examination, we suggest a measurement of ${\cal B}(D_{s}^{+}\to\rho^{0}(a^{+}_{0}\to)K^{+}\bar{K}^{0})/{\cal B}(D_{s}^{+}\to\rho^{+}(a^{0}_{0}\to)K^{+}K^{-})$, which will be observed around 2 if there exists no resonant $f_{0}\to K^{+}K^{-}$ decay to be involved in ${\cal B}(D_{s}^{+}\to\rho^{+}K^{+}K^{-})$.