Studying Radiative Baryon Decays with the SU(3) Flavor Symmetry
Abstract
The weak and electromagnetic radiative baryon decays of octet , decuplet , single charmed anti-triplet and sextet , single heavy bottomed anti-triplet and sextet are investigated by using SU(3) flavor symmetry irreducible representation approach. We analyze the contributions from a single quark transition and exchange transitions, and find that the amplitudes could be easily related by SU(3) flavor symmetry in the weak radiative decays, weak radiative decays, weak decays, weak decays and electromagnetic decays. Nevertheless, the amplitude relations are a little complex in the and weak decays due to quark antisymmetry in and exchange contributions. Predictions for branching ratios of , , , , , , , , and are given. The results in this work can be used to test SU(3) flavor symmetry approach in the radiative baryon decays by the future experiments at BESIII, LHCb and Belle-II.
I INTRODUCTION
Radiative weak decays have attracted a lot of attention for a long time in both theory and experiment, since they could give us a chance to study the interplay of the electromagnetic, weak and strong interactions, to test the standard model and to probe new physics. A large number of bottomed baryons, charmed baryon and hyperons are produced at the LHC Cerri:2018ypt ; Aaij:2017ddf ; Junior:2018odx , significant experimental progresses about baryon rare decays have been achieved recently at LHCb, and one of them is that radiative decay has been observed with a branching ratio of for the first time Aaij:2019hhx . Furthermore, many radiative weak decays of strange baryons have been measured PDG2020 , and there are longstanding theoretical difficulties to explain the experimental data Lach:1995we ; Donoghue:1985rk . Now the sensitivity for measurements of hyperon decays is in the range of at the BESIII Li:2016tlt ; Bigi:2017eni ; Asner:2008nq ; Ablikim:2018zay . Therefore, more baryon radiative decays will be detected by the experiments in the near future, so it’s feasible to explore these decays now.
Theoretically, due to our poor understanding of QCD at low energy regions, theoretical calculations of decay amplitudes are not well understood. SU(3) flavor symmetry has attracted a lot of attentions. The SU(3) flavor symmetry approach, which is independent of the detailed dynamics, offers an opportunity to relate different decay modes. Nevertheless, it cannot determine the size of the amplitudes by itself. However, if experimental data are enough, one may use the data to extract the amplitudes, which can be viewed as predictions based on symmetry. There are two popular ways of the SU(3) flavor symmetry. One is to construct the SU(3) irreducible representation amplitude by decomposing effective Hamiltonian. Another way is topological diagram approach, where decay amplitudes are represented by connecting quark line flows in different ways and then relate them by the SU(3) symmetry. The SU(3) irreducible representation approach (IRA) shows a convenient connection with the SU(3) symmetry, the topological diagram approach gives a better understanding of dynamics in the different amplitudes. The SU(3) flavor symmetry works well in bottomed hadron decays Dery:2020lbc ; He:1998rq ; He:2000ys ; Fu:2003fy ; Hsiao:2015iiu ; He:2015fwa ; He:2015fsa ; Deshpande:1994ii ; Gronau:1994rj ; Gronau:1995hm ; Shivashankara:2015cta ; Zhou:2016jkv ; Cheng:2014rfa ; Singer:1995is , charmed hadron decays Grossman:2012ry ; Pirtskhalava:2011va ; Cheng:2012xb ; Savage:1989qr ; Savage:1991wu ; Altarelli:1975ye ; Lu:2016ogy ; Geng:2017esc ; Geng:2018plk ; Geng:2017mxn ; Geng:2019bfz ; Wang:2017azm ; Wang:2019dls ; Wang:2017gxe ; Muller:2015lua and hyperon decays Xu:2020jfr ; Wang:2019alu ; Chang:2014iba ; Zenczykowski:2005cs ; Zenczykowski:2006se .
Many weak radiative decays have been studied by chiral perturbation theory Bos:1996ig , perturbative QCD He:2006ud , quark model approach Singer:1996xh , Bethe-Salpeter equation approach Liu:2019rpm , relativistic quark model Faustov:2017ous , light-cone sum-rule Aliev:2004ju , single universal extra dimension scenario Colangelo:2007jy and effective Lagrangian approach Cheng:1994kp , etc. And some electromagnetic radiative baryon decays have been also studied in Refs. Ramalho:2020tnn ; Junker:2019vvy . In this work, we will study the weak radiative baryon decays with a single quark transitions (, , , ) and corresponding exchange transitions as well as the electromagnetic radiative decays of by using the SU(3) IRA. We will firstly construct the SU(3) irreducible representation amplitudes for different kinds of radiative baryon decays, secondly obtain the decay amplitude relations between different decay modes, then use the available data to extract the SU(3) irreducible amplitudes, and finally predict the not-yet-measured modes for further tests in experiments.
This paper is organized as follows. In Sec. II, we will collect the representations for the baryon multiplets and the branching ratio expressions of the radiative baryon decays. In Sec. III, we will analyze the weak radiative decays of , and as well as the electromagnetic radiative decays . Our conclusions are given in Sec. IV.
II Theoretical Frame for
II.1 Baryon multiplets
The light baryons octet and decuplet under the SU(3) flavor symmetry of quarks can be written as
| (4) | |||||
| (14) |
The single charmed anti-triplet and sextet can be written as
| (18) |
The anti-triplet and sextet with a heavy b quark have a similar form to and , respectively,
| (22) |
II.2 Decay branching ratio of
In the standard model, the weak radiative baryon decays with transition can proceed via loop Feynman diagrams as shown in Fig. 1. The effective Hamiltonian for transition shown in Fig. 1 can be written as Buchalla:1995vs
| (23) |
where , with , is the polarization vectors of photon, and the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements for , , , , respectively.
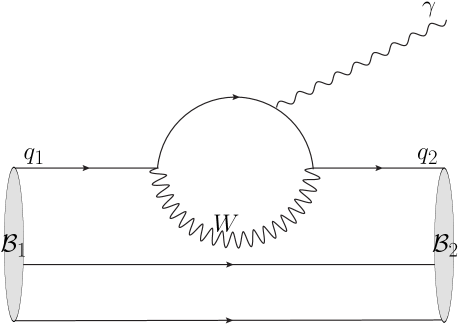
Then the decay amplitudes can be written as
| (24) | |||||
The baryon matrix elements can be parameterized by the form factors, but not all relevant form factors have been calculated and there is no very reliable method to calculate some form factors at present. Nevertheless, the baryon matrix elements also can be obtained by the SU(3) IRA. In terms of the SU(3) flavor symmetry, baryon states and quark operators can be parameterized into SU(3) tensor forms, while the polarization vectors are invariant under SU(3) flavor symmetry. The decay amplitudes in terms of the SU(3) IRA are given in later Tab. 1, Tab. 3, Tab. 4 and Tab. 5 for , , and weak decays, respectively.
The branching ratios of the weak decays can be obtained by the decay amplitudes
| (25) |
After extracting the masses, the Wilson Coefficients, etc, from , the branching ratios of the and weak decays are Faustov:2017wbh ; Gutsche:2013pp
| (26) |
where may be given by the form factors as with for the weak decays and for the weak decays. As for the weak decays, the branching ratios are Mannel:2011xg
| (27) |
For the electromagnetic decays, the expressions of their branching ratios are different from Eq. (26), and the following relations will be used to obtain the results Junker:2019vvy
| (28) |
In addition, according to Refs. Verma:1988gf ; Lach:1995we ; Azimov:1996uf , other three kinds of Feynman diagrams might contribute to the weak baryon decays. The example for is displayed in Fig. 2. Fig. 2 (a-b) are two-quark and three-quark transitions with the exchange, which have been discussed, for examples, in Refs. Verma:1988gf ; Dubovik:2007qg . Since Fig. 2 (c) is suppressed by the two propagators, and its contribution can be safely neglected. We will consider the W-exchange contributions in Fig. 2 (a-b) in later analysis of SU(3) flavor symmetry.
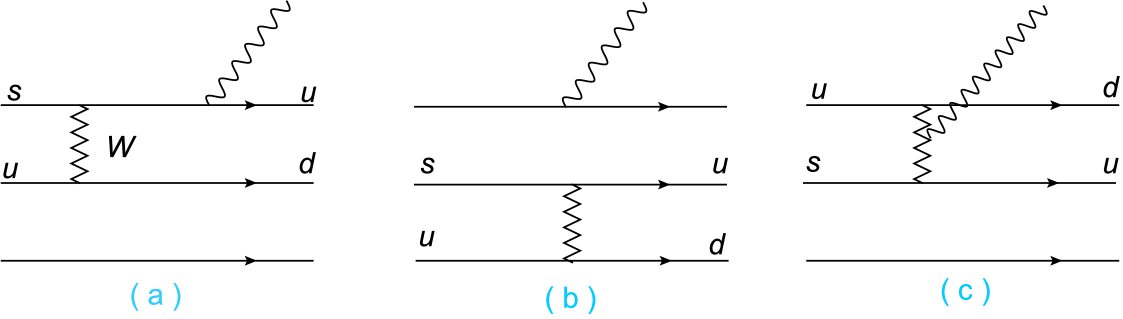
III Results and Analysis
The theoretical input parameters and the experimental data within the errors from Particle Data Group PDG2020 will be used in our numerical results.
III.1 weak radiative decays
The SU(3) flavor structure of the relevant Hamiltonian can been found, for instance, in Refs. Zeppenfeld:1980ex ; Savage:1989ub ; Deshpande:1994ii . The SU(3) IRA decay amplitudes for decays via can be parameterized as
| (29) | |||||
| (30) | |||||
| (31) |
with , which denotes the transition operators with . The coefficients , which contain information about QCD dynamics, include the single quark emission contributions in Fig. 1 and and ( are the set of all ) long distance contributions Dery:2020lbc ; Deshpande:1994cn (the similar in following in Eqs. (36-47)), nevertheless, the long distance contributions in the b-sector are small and under control Golowich:1994zr ; Deshpande:1994cn . Noted that (and later weak decays are not allowed by the quark symmetry. The SU(3) IRA amplitudes of and weak decays are given in Tab. 1. And the information of relevant CKM matrix elements ( ) for () transition is not shown in Tab. 1.
| Decay modes | |
| via the transition: | |
| via the transition: | |
| via the transition: | |
| via the transition: | |
| via the transition: | |
| via the transition: | |
| Observables | Experimental data PDG2020 | Our SU(3) IRA predictions | Other predictions |
| Wang:2008sm | |||
| Liu:2019rpm ; Faustov:2020thr | |||
| Decay modes | |
| : | |
| : | |
| : | |
| : | |
Now, we discuss the weak decays. Decays , , and (, , and ) proceed via the () flavor changing neutral current transition. From Tab. 1, one can see that the 7 decay amplitudes of can be related by one parameter . Noted that our via the transitions are consistent with ones of in Ref. Fayyazuddin:2017sxq and ones of the CKM-leading part results in Ref. Dery:2020lbc . Among these 7 decay modes, only has been measured at present, which is listed in the second column of Tab. 3. Using data of and the expression of in Eq. (26) to get , and then other 6 branching ratios are obtained, which are given in the third column of Tab. 3. Previous predictions for in the light-cone sum rules and for in the relativistic quark model and in the Bethe-Salpeter equation approach are listed in the last column of Tab. 3. Our SU(3) IRA prediction of agrees with ones in the relativistic quark model or in the Bethe-Salpeter equation approach Liu:2019rpm ; Faustov:2020thr . More experimental data about the decays in the further could test the SU(3) flavor symmetry approach.
As given in Tab. 1, the decay amplitudes of the and weak decays can be parameterized by only one parameter and , respectively. And our via the transition are consistent with ones of in Ref. Fayyazuddin:2017sxq . Unfortunately, none of the and weak decays has been measured at present. Any measurement of the () will give us chance to predict other 10 (11) decay modes.
In addition, baryons also can decay to by only exchange Cheng:1994kp . The SU(3) IRA decay amplitudes for the decays are
| (32) | |||||
| (33) | |||||
| (34) | |||||
| (35) |
Since the CKM matrix element occur for all processes, we will absorb it in the coefficients as well as , and only keep and representing the Cabbibo angle PDG2020 . The SU(3) IRA amplitudes of weak decays are summarized in Tab. 3, in which we keep and information for comparing conveniently, and we may easily see the amplitude relations in this table. Just none of these decays has been measured yet.
III.2 weak radiative decays
via transition are similar to the via transition. Nevertheless, the short distance contributions from could be negligible, and the dominant contributions in charmed baryon decays mainly from the W-exchange contributions similar as Fig. 2 (a-b) Singer:1995is . The SU(3) flavor structure of the relevant Hamiltonian can been found, for instance, in Refs. Zeppenfeld:1980ex ; Savage:1989ub ; Deshpande:1994ii . The SU(3) IRA amplitudes of the baryon weak decays are
| (36) | |||||
| (37) | |||||
| (38) |
with which denotes the transition operators with . The terms denote the contributions from shown in Fig.1 and the long distance contribution from the real intermediate state , and . The terms denote the exchange contributions similar as Fig. 2. Noted that () related to operator is antisymmetric (symmetric) in upper indices. The non-vanish and for transitions can be found in Ref. Wang:2017azm . Using antisymmetric in and symmetric in , we have
| (39) |
Since none of the down-type quarks are heavy, the Glashow-Iliuopoulos-Maiani (GIM) mechanism suppression is obvious in the charm sector. The terms related to the short and long distance contributions of transition are strongly suppressed by the GIM mechanism. As for the exchange transition, there are three kinds of charm quark decays into light quarks
| (40) |
which are related to , , and are proportional to , (), and , respectively. The relevant CKM matrix elements can be written by the Wolfenstein parameterization PDG2020
| (41) |
So three kinds of charm quark decays in Eq. (40) are called Cabibbo allowed, singly Cabibbo suppressed, and doubly Cabibbo suppressed decays, respectively.
The SU(3) IRA amplitudes of and weak decays are given in the second column of Tab. 4. For well understanding, we also show the relevant CKM matrix information in Tab. 4, too. In addition, the contribution of to the decay branching ratio can be about 5.5 times larger than one of due to Wilson Coefficient suppressed, for examples, see Geng:2017esc ; Geng:2018plk . If ignoring the GIM strongly suppressed transition contributions and the Wilson Coefficient suppressed term contributions, the decay amplitudes of , and are related by only one parameter , and , respectively. The simplifications resulting are listed in the last column of Tab. 4. Just all baryon weak radiative decays of baryons have not been measured yet.
| Decay modes | approximative | |
| Cabibbo allowed : | ||
| singly Cabibbo suppressed : | ||
| doubly Cabibbo suppressed : | ||
| Cabibbo allowed : | ||
| singly Cabibbo suppressed : | ||
| doubly Cabibbo suppressed : | ||
| 0 | ||
| Cabibbo allowed : | ||
| singly Cabibbo suppressed : | ||
| doubly Cabibbo suppressed : | ||
III.3 weak radiative decays
The SU(3) flavor structure of the relevant Hamiltonian can be found in Ref. Wang:2019alu . The decay amplitudes of the and weak radiative decays can be parameterized as
| (42) | |||||
| (43) | |||||
| (44) | |||||
| (45) |
where for quark, related to the transition operator , and related to operator is symmetric in upper indices Wang:2019alu . In Eqs. (42-45), the terms denote the contributions from shown in Fig.1 and the long distance contribution from and Singer:1995is (for weak radiative decays, the long distance contributions may be significantly larger than the short distance ones), the terms denote the exchange contributions shown in Fig. 2 (a-b), and the internal radiation contributions in Fig. 2 (c) are neglected in this work.
The SU(3) IRA amplitudes of the weak decays are summarized in Tab. 5, in which the information of the same CKM matrix elements is not shown.
| Decay modes | |
| weak decays: | |
| weak decays: | |
| weak decays: | |
| weak decays: | |
From Tab. 5, one can see that the amplitudes of , , , , , , , only contain coefficients , which means that the exchange transitions don’t contribute to these decays since the initial baryons don’t contain quark. Otherwise, the exchange contributions are canceled in and decays. So above decays could be used to explore the short distance and long distance contributions. Other decay amplitudes contained both and could proceed from the short distance contributions, long distance contributions and W-exchange contributions.
| Observables | Experimental data PDG2020 | Our predictions in | Our predictions in |
| : | |||
For the weak decays, all decay modes expect for have been measured and paid a lot of attentions, experimental data are listed in the second column of Tab. 6, and there are longstanding theoretical difficulties to explain the experimental data of the weak decays. In the weak decays, they may decay via the single quark emission, corresponding long distance effects and the -exchange transition. Since the quarks are antisymmetric in both the initial states and the final states , there are more independent parameters than ones in weak decays. The relevant SU(3) flavor parameters could be complex, and we set is real and add relative phases , , for , and , respectively. And then 7 independent parameters given by
| (46) |
Two cases for the weak decays will be considered in our analysis. In case , we will only consider the single quark emission and long distance effects, , set . In case , we will consider all effects.
In case , there are 3 independent parameters and . Firstly, we use three data of , and to constrain the parameters as well as obtain that , and , and noted that is slightly larger than . Then, we use the obtained , and to predict other three branching ratios, and the results are given in the third column of Tab. 6. One can see that the predictions of and in are not inconsistent with their data. In case , since , , and , one have that , which are far away from the experimental one . In addition, the SU(3) IRA prediction of is about 2.6 times larger than its data. So it’s necessary to considering the exchange contributions.
In case , we use all five data of the branching ratios to constrain seven parameters. We obtain that , , , , , and . One can see that, after satisfying all present data within , three phases are almost unlimited, and the , and terms give the same magnitude contributions. lies in , and its contribution might be similar to (or smaller than) ones of , and .
In both and cases, the branching ratio of is too small to see in the experiments, and this weak decay completely overwhelmed by the simpler electromagnetic decay .
For the baryon decuplet radiative weak decays, only baryon has a sufficiently long lifetime, is’s accessible to experimental study. Using the experimental upper limit , we obtain that and . The upper limits of the two branching ratios are very tiny since have very short lifetime, so the and decays are difficult to be measured in the experiments.
III.4 electromagnetic radiative decays
In addition, the baryon decuplet also can decay only through electromagnetic interactions by the transition at the quark level. The SU(3) IRA amplitudes of the electromagnetic decays can be parameterized as
| (47) |
Three cases are considered in calculating the electromagnetic decay amplitudes. : assuming all three quarks in baryon can emit photon, : assuming and quarks in baryon can emit photon, and : assuming the heaviest quark in baryon can emit photon. The SU(3) IRA amplitudes of electromagnetic decays in three cases are listed in Tab. 7.
| Decay modes | in | in | in |
For electromagnetic decays, and have been measured, and have been upper limited, and the relevant experimental data are listed in the second column of Tab. 8. Comparing the amplitudes in three cases with the data, the and cases are eliminated, and we will use the IRA amplitudes in case in the following analysis.
Using Eq. (28), the branching ratios will be obtained by , and the results are listed in the last column of Tab. 8. The SU(3) IRA predictions for and are quite consistent with present data. Noted that the estimated result from PDG PDG2020 , which is covered by our prediction. The branching ratio predictions are at the order of , and they might be measured at the BESIII or LHC experiments in near future. So these electromagnetic decays could be used to test the SU(3) flavor symmetry.
| Observables | Experimental data PDG2020 | Our predictions |
IV Conclusions
Baryon radiative decays give us a chance to study the interplay of the electromagnetic, weak and strong interactions. Some baryon radiative decay modes have been measured and some others could be studied at BESIII, LHCb and Belle-II experiments. In this work, we have analyzed baryon radiative decays of the octet , decuplet , single charmed anti-triplet , single charmed sextet , single bottomed anti-triplet and single bottomed sextet by using the irreducible representation approach to test the SU(3) flavor symmetry. Our main results are given in order:
-
•
weak radiative decays:
Each kind of the decay amplitudes can be related by only one parameter in the , and weak decays via as well as the , , and via the exchange transitions. Using the only measured , we have predicted other six decay branching ratios of weak decays, and they might be measured by the experiments in near future. Unfortunately, none of and weak decays has been measured at present. Any measurement of will give us chance to predict many other decay branching ratios. -
•
weak radiative decays:
weak radiative decays are quite different from weak radiative decays, they may receive the contributions of both the and the exchange transitions. After ignoring the GIM strongly suppressed transition contributions and the Wilson Coefficient suppressed term contributions, the decay amplitudes of , and are also related by only one parameter , and , respectively. Just none of weak radiative decays has been measured at present. -
•
weak radiative decays:
As for weak radiative decays, some decays only receive the short distance and long distance transition contributions, other decays could receive both the transition and the W-exchange transition contributions. For the weak decays, all decay modes expect for have been measured, and we have found that only considering the short and long distance transition contributions can not explain all current data by SU(3) IRA. Present all data could be explained by considering both the transition contributions and the exchange contributions. has been predicted, just this branching ratio is very tiny. For the weak decays, we have used the upper limit of to obtain the upper limit predictions of and , just both upper limit predictions are tiny. -
•
electromagnetic radiative decays:
All decay amplitudes of electromagnetic radiative decays could be related by only one parameter , the SU(3) IRA predictions for and are quite consistent with present data. Other branching ratio predictions are at the order of , and they might be measured by the experiments in near future.
Flavor SU(3) symmetry could provide us very useful information about the decays. According to our predictions, some branching ratios are accessible to the experiments at BESIII, LHCb and Belle-II. Our results in this work can be used to test SU(3) flavor symmetry approach in the radiative baryon decays by the future experiments.
ACKNOWLEDGEMENTS
The work was supported by the National Natural Science Foundation of China (Contract No. 11675137) and the Key Scientific Research Projects of Colleges and Universities in Henan Province (Contract No. 18A140029).
References
References
- (1) A. Cerri et al., CERN Yellow Rep. Monogr. 7, 867 (2019) [arXiv:1812.07638 [hep-ph]].
- (2) R. Aaij et al. (LHCb Collaboration), Phys. Rev. Lett. 120, no. 22, 221803 (2018) [arXiv:1712.08606 [hep-ex]].
- (3) A. A. Alves Junior et al., JHEP 1905, 048 (2019), [arXiv:1808.03477 [hep-ex]].
- (4) R. Aaij et al. (LHCb Collaboration), Phys. Rev. Lett. 123, no. 3, 031801 (2019) [arXiv:1904.06697 [hep-ex]].
- (5) P.A. Zyla et al. (Particle Data Group), to be published in Prog. Theor. Exp. Phys. 2020, 083C01 (2020).
- (6) J. Lach and P. Zenczykowski, Int. J. Mod. Phys. A 10, 3817 (1995).
- (7) J. F. Donoghue, E. Golowich and B. R. Holstein, Phys. Rept. 131, 319 (1986).
- (8) M. Ablikim et al. (BESIII Collaboration), Nature Phys. 15, 631 (2019) [arXiv:1808.08917 [hep-ex]].
- (9) H. B. Li, Front. Phys. (Beijing) 12, no. 5, 121301 (2017) [arXiv:1612.01775 [hep-ex]].
- (10) I. I. Bigi, X. W. Kang and H. B. Li, Chin. Phys. C 42, no. 1, 013101 (2018) [arXiv:1704.04708 [hep-ph]].
- (11) D. M. Asner et al., Int. J. Mod. Phys. A 24, S1 (2009) [arXiv:0809.1869 [hep-ex]].
- (12) A. Dery, M. Ghosh, Y. Grossman and S. Schacht, JHEP 2003, 165 (2020) [arXiv:2001.05397 [hep-ph]].
- (13) X. G. He, Eur. Phys. J. C 9, 443 (1999) [hep-ph/9810397].
- (14) X. G. He, Y. K. Hsiao, J. Q. Shi, Y. L. Wu and Y. F. Zhou, Phys. Rev. D 64, 034002 (2001) [hep-ph/0011337].
- (15) H. K. Fu, X. G. He and Y. K. Hsiao, Phys. Rev. D 69, 074002 (2004) [hep-ph/0304242].
- (16) Y. K. Hsiao, C. F. Chang and X. G. He, Phys. Rev. D 93, no. 11, 114002 (2016) [arXiv:1512.09223 [hep-ph]].
- (17) X. G. He and G. N. Li, Phys. Lett. B 750, 82 (2015) [arXiv:1501.00646 [hep-ph]].
- (18) M. Gronau, O. F. Hernandez, D. London and J. L. Rosner, Phys. Rev. D 50, 4529 (1994) [hep-ph/9404283].
- (19) M. Gronau, O. F. Hernandez, D. London and J. L. Rosner, Phys. Rev. D 52, 6356 (1995) [hep-ph/9504326].
- (20) S. H. Zhou, Q. A. Zhang, W. R. Lyu and C. D. L , Eur. Phys. J. C 77, no. 2, 125 (2017) [arXiv:1608.02819 [hep-ph]].
- (21) H. Y. Cheng, C. W. Chiang and A. L. Kuo, Phys. Rev. D 91, no. 1, 014011 (2015) [arXiv:1409.5026 [hep-ph]].
- (22) M. He, X. G. He and G. N. Li, Phys. Rev. D 92, no. 3, 036010 (2015) [arXiv:1507.07990 [hep-ph]].
- (23) N. G. Deshpande and X. G. He, Phys. Rev. Lett. 75, 1703 (1995) [hep-ph/9412393].
- (24) S. Shivashankara, W. Wu and A. Datta, Phys. Rev. D 91, 115003 (2015) [arXiv:1502.07230 [hep-ph]].
- (25) P. Singer, Nucl. Phys. Proc. Suppl. 50 (1996) 202 [hep-ph/9512308].
- (26) Y. Grossman and D. J. Robinson, JHEP 1304, 067 (2013) [arXiv:1211.3361 [hep-ph]].
- (27) D. Pirtskhalava and P. Uttayarat, Phys. Lett. B 712, 81 (2012) [arXiv:1112.5451 [hep-ph]].
- (28) H. Y. Cheng and C. W. Chiang, Phys. Rev. D 86, 014014 (2012) [arXiv:1205.0580 [hep-ph]].
- (29) M. J. Savage and R. P. Springer, Phys. Rev. D 42, 1527 (1990).
- (30) M. J. Savage, Phys. Lett. B 257, 414 (1991).
- (31) G. Altarelli, N. Cabibbo and L. Maiani, Phys. Lett. 57B, 277 (1975).
- (32) C. D. Lü, W. Wang and F. S. Yu, Phys. Rev. D 93, no. 5, 056008 (2016) [arXiv:1601.04241 [hep-ph]].
- (33) C. Q. Geng, Y. K. Hsiao, Y. H. Lin and L. L. Liu, Phys. Lett. B 776, 265 (2018) [arXiv:1708.02460 [hep-ph]].
- (34) C. Q. Geng, Y. K. Hsiao, C. W. Liu and T. H. Tsai, Phys. Rev. D 97, no. 7, 073006 (2018) [arXiv:1801.03276 [hep-ph]].
- (35) C. Q. Geng, Y. K. Hsiao, C. W. Liu and T. H. Tsai, JHEP 1711, 147 (2017) [arXiv:1709.00808 [hep-ph]].
- (36) C. Q. Geng, C. W. Liu, T. H. Tsai and S. W. Yeh, Phys. Lett. B 792, 214 (2019) [arXiv:1901.05610 [hep-ph]].
- (37) W. Wang, Z. P. Xing and J. Xu, Eur. Phys. J. C 77, no. 11, 800 (2017) [arXiv:1707.06570 [hep-ph]].
- (38) D. Wang, Eur. Phys. J. C 79, no. 5, 429 (2019) [arXiv:1901.01776 [hep-ph]].
- (39) D. Wang, P. F. Guo, W. H. Long and F. S. Yu, JHEP 1803, 066 (2018) [arXiv:1709.09873 [hep-ph]].
- (40) S. Müller, U. Nierste and S. Schacht, Phys. Rev. D 92, no. 1, 014004 (2015) [arXiv:1503.06759 [hep-ph]].
- (41) Y. G. Xu, X. D. Cheng, J. L. Zhang and R. M. Wang, J. Phys. G 47, no. 8, 085005 (2020) [arXiv:2001.06907 [hep-ph]].
- (42) R. M. Wang, M. Z. Yang, H. B. Li and X. D. Cheng, Phys. Rev. D 100, no. 7, 076008 (2019) [arXiv:1906.08413 [hep-ph]].
- (43) H. M. Chang, M. G. Alonso and J. M. Camalich, Phys. Rev. Lett. 114, no. 16, 161802 (2015) [arXiv:1412.8484 [hep-ph]].
- (44) P. Zenczykowski, Phys. Rev. D 73, 076005 (2006) [hep-ph/0512122].
- (45) P. Zenczykowski, Nucl. Phys. Proc. Suppl. 167, 54 (2007) [hep-ph/0610191].
- (46) J. W. Bos, D. Chang, S. C. Lee, Y. C. Lin and H. H. Shih, Phys. Rev. D 54, 3321 (1996) [hep-ph/9601299].
- (47) X. G. He, T. Li, X. Q. Li and Y. M. Wang, Phys. Rev. D 74, 034026 (2006) [hep-ph/0606025].
- (48) P. Singer and D. X. Zhang, Phys. Lett. B 383, 351 (1996) [hep-ph/9606343].
- (49) L. L. Liu, C. Wang, X. W. Kang and X. H. Guo, Eur. Phys. J. C 80, no. 3, 193 (2020) [arXiv:1912.12622 [hep-ph]].
- (50) R. N. Faustov and V. O. Galkin, Mod. Phys. Lett. A 32, 1750125 (2017) [arXiv:1706.01379 [hep-ph]].
- (51) T. M. Aliev and A. Ozpineci, Nucl. Phys. B 732, 291 (2006) [hep-ph/0406331].
- (52) P. Colangelo, F. De Fazio, R. Ferrandes and T. N. Pham, Phys. Rev. D 77, 055019 (2008) [arXiv:0709.2817 [hep-ph]].
- (53) H. Y. Cheng, C. Y. Cheung, G. L. Lin, Y. C. Lin, T. M. Yan and H. L. Yu, Phys. Rev. D 51, 1199 (1995) [hep-ph/9407303].
- (54) G. Ramalho, arXiv:2002.07280 [hep-ph].
- (55) O. Junker, S. Leupold, E. Perotti and T. Vitos, Phys. Rev. C 101, no. 1, 015206 (2020) [arXiv:1910.07396 [hep-ph]].
- (56) G. Buchalla, A. J. Buras and M. E. Lautenbacher, Rev. Mod. Phys. 68, 1125 (1996) [hep-ph/9512380].
- (57) R. N. Faustov and V. O. Galkin, Phys. Rev. D 96, no. 5, 053006 (2017) [arXiv:1705.07741 [hep-ph]].
- (58) T. Gutsche, M. A. Ivanov, J. G. Korner, V. E. Lyubovitskij and P. Santorelli, Phys. Rev. D 87, 074031 (2013) [arXiv:1301.3737 [hep-ph]].
- (59) T. Mannel and Y. M. Wang, JHEP 1112, 067 (2011) [arXiv:1111.1849 [hep-ph]].
- (60) R. C. Verma and A. Sharma, Phys. Rev. D 38, 1443 (1988).
- (61) Y. I. Azimov, Z. Phys. A 359, 75 (1997) [hep-ph/9611315].
- (62) E. N. Dubovik, V. S. Zamiralov and S. N. Lepshokov, AIP Conf. Proc. 964, no. 1, 71 (2007) [hep-ph/0701141].
- (63) D. Zeppenfeld, Z. Phys. C 8, 77 (1981).
- (64) M. J. Savage and M. B. Wise, Phys. Rev. D 39, 3346 (1989) Erratum: [Phys. Rev. D 40, 3127 (1989)].
- (65) N. G. Deshpande, X. G. He and J. Trampetic, Phys. Lett. B 367, 362 (1996) [hep-ph/9412222].
- (66) E. Golowich and S. Pakvasa, Phys. Rev. D 51, 1215 (1995) [hep-ph/9408370].
- (67) Fayyazuddin and M. J. Aslam, Phys. Rev. D 95, no. 11, 113002 (2017) [arXiv:1705.05106 [hep-ph]].
- (68) R. N. Faustov and V. O. Galkin, Particles 3, no. 1, 208 (2020).
- (69) Y. m. Wang, Y. Li and C. D. Lu, Eur. Phys. J. C 59, 861 (2009) [arXiv:0804.0648 [hep-ph]].