Suboptimality analysis of receding horizon quadratic control with unknown linear systems and its applications in learning-based control
Abstract
This work analyzes how the trade-off between the modeling error, the terminal value function error, and the prediction horizon affects the performance of a nominal receding-horizon linear quadratic (LQ) controller. By developing a novel perturbation result of the Riccati difference equation, a novel performance upper bound is obtained and suggests that for many cases, the prediction horizon can be either or to improve the control performance, depending on the relative difference between the modeling error and the terminal value function error. The result also shows that when an infinite horizon is desired, a finite prediction horizon that is larger than the controllability index can be sufficient for achieving a near-optimal performance, revealing a close relation between the prediction horizon and controllability. The obtained suboptimality performance bound is applied to provide novel sample complexity and regret guarantees for nominal receding-horizon LQ controllers in a learning-based setting. We show that an adaptive prediction horizon that increases as a logarithmic function of time is beneficial for regret minimization.
Receding horizon control, model predictive control, learning-based control.
1 Introduction
Receding-horizon control (RHC), also called model predictive control (MPC) interchangeably, has been applied to various applications, such as process control, building climate control, and robotics control [1, 2]. It has important advantages such as using optimization based on a model of the system to improve the control performance and the ability to handle constraints and multivariate systems. Due to the importance of RHC in applications, extensive efforts have been devoted to its performance analysis in [3, 4, 5, 6] and references therein, such as stability, constraint satisfaction, and suboptimality analysis. These analyses can help understand the behavior of RHC and motivate novel RHC approaches.
While the majority of works focus on stability and constraint satisfaction [3], this work considers the suboptimality analysis of the closed-loop control performance. We briefly illustrate our problem via a generic RHC scheme. Given a discrete-time system , where , and are the state and input, respectively, we consider the setting where is unknown, but we have access to an approximate prediction model instead. At time step , a generic RHC controller has the following form:
| (1) | ||||
where is the prediction horizon, is a stage cost function, and denotes the predicted state vector at time step , obtained by applying the input sequence to the prediction model starting from . In (1), a terminal value function is incorporated. At time step , only the computed input from (1) is applied as the control input to the system.
In (1), a modeling error may be present, i.e., deviates from the unknown real system , which may result from system identification, linearization, or model reduction. While the modeling error can be explicitly considered in the robust controller design[3], the nominal controller (1) is considered in this work, as it is more fundamental and commonly used in practice. The terminal value function avoids the short-sightedness of the finite-horizon prediction and thus improves the control performance and guarantees stability. It is standard in RHC [4, 6] and also advocated in reinforcement learning (RL) to merge RL and RHC for performance improvement [7], where is trained offline, e.g., by the value iteration [8]. While the optimal value function is ideal for achieving stability and the optimal infinite-horizon control performance simultaneously, it is typically intractable to compute it exactly [9]. Therefore, considering an approximation of is a practical choice.
The suboptimality analysis of (1) is an open and challenging problem, due to the interplay between and the error sources. Particularly, when the prediction model is exact, it is well-known that increasing improves the closed-loop control performance [4, 9]. However, if a modeling error is present, increasing also propagates the prediction error. On the other hand, having a closer to the optimal value function can also improve the control performance. Therefore, the control performance is affected by the complex tradeoff between the error of the terminal value function, the modeling error , and the prediction horizon , where the norm will be defined later for the setting of this work.
This work provides a novel suboptimality analysis of (1) under the joint effect of the modeling error, the prediction horizon, and the terminal value function. We consider the probably most fundamental setting, where the system is linear and the stage cost is a quadratic function, i.e., the nominal receding-horizon LQ controller [10]. As shown in our work, the analysis in this setting is already highly challenging.
Moreover, we apply our analysis to the performance analysis of learning-based RHC controllers. In this case, the model is estimated from data, leading to an inevitable modeling error. Our suboptimality analysis can incorporate this modeling error to provide performance guarantees.
Related work: When the model is exact, the suboptimality analysis of RHC controllers, with constraints or economic cost, has been studied extensively in [4, 5, 6] and references therein. However, performance analysis in a setting where the system model is uncertain or unknown is rare. The suboptimality analysis of RHC for linear systems with a structured parametric uncertainty is considered in [11]; however, the impact of the approximation in the terminal value function is not investigated. Other relevant works can be found in the performance analysis of learning-based RHC [12, 13, 14], where the controller actively explores the state space of the unknown system and the model is recursively updated. There, a control performance metric called regret is concerned, which measures the accumulative performance difference over a finite time window between the controller and the ideal optimal controller. The impact of the modeling error has been investigated in the above analysis; however, the effect of the prediction horizon and the terminal value function on the control performance is not considered [14, 13, 12].
As we consider the LQ setting, the performance analysis of LQ regulator (LQR) for unknown systems is relevant, which has received renewed attention from the perspective of learning-based control [15, 16, 17]. The suboptimality analysis of LQR with a modeling error has been considered in [18, 19, 20]. This analysis is essential for deriving performance guarantees for learning-based LQR. It typically relies on the perturbation analysis of the Riccati equation [19, 20], which characterizes the solution of the Riccati equation under a modeling error. However, since LQR concerns an infinite prediction horizon, the above analysis does not consider the effect of the prediction horizon and the terminal value function.
Contribution: In this work, the main results are developed for controllable systems and then generalized to stabilizable systems. The contributions of this work are summarized here:
-
1.
As an essential step for achieving performance analysis with unknown systems, the performance analysis in the simpler setting, where the model is exact, is considered first. A novel performance bound for the receding-horizon LQ controller is obtained, which reveals a novel relation between the control performance and controllability.
-
2.
To achieve the suboptimality analysis with a modeling error, a core technical result is first established, i.e., a novel convergence rate of the Riccati difference equation when a modeling error is present. This result generalizes the perturbation results of the discrete Riccati equation [19, 20]. While the analyses in [19, 20] address the modeling error only, the incorporation of the prediction horizon and the terminal value function error in this work leads to major technical challenges, which require analyzing the convergence of the Riccati difference equation under a modeling error, instead of the fixed point of the Riccati equation as in [19, 20].
-
3.
Based on the above perturbation analysis, a novel performance upper bound for the nominal receding-horizon LQ controller with an inexact model is derived. The derived performance upper bound shows how the control performance may vary with changes in the modeling error, the terminal value function error, and the prediction horizon. Particularly, it suggests that for many cases, the prediction horizon can be either or to achieve a better performance, depending on the relative difference between the modeling error and the terminal value function error. Moreover, when is desired, the result suggests that for controllable systems, a finite that is larger than the controllability index is sufficient for achieving a near-optimal performance.
-
4.
The performance bound is utilized to derive a novel suboptimality bound for the nominal receding-horizon LQ controller, where the unknown system is estimated offline from data. The bound reveals how the control performance depends on the number of data samples. Moreover, a novel regret bound is derived for an adaptive RHC controller. This controller extends the state-of-the-art adaptive LQR controller with -greedy exploration [20, 17] from the infinite prediction horizon to an arbitrary finite prediction horizon. We show a novel regret upper bound for a fixed , where is a constant and denotes the total number of time steps for the closed-loop operation, and a regret bound for an adaptive being a logarithmic function of time.
Outline: This paper is structured as follows. Preliminaries are introduced in Section 2. For controllable systems, the suboptimality analysis is developed in Section 3 for an exact model and is generalized in Section 4 to incorporate the modeling error. The above results are extended in Section 5 to stabilizable systems and applied to learning-based control in Section 6. All proofs are presented in the Appendix.
Notation: Let denote the set of symmetric matrices of dimension , and let , denote the subsets of positive semi-definite and positive-definite symmetric matrices, respectively. Given , , denotes . Moreover, denotes the set of non-negative integers. Let denote the identity function, and denotes the composition of two functions. The symbol denotes the spectral norm of a matrix and the norm of a vector. Given any real sequence , we define for the special case . Given a real matrix and a real square matrix , and denote the maximum and the minimum singular values, respectively, and denotes the spectral radius. Note that . The symbol denotes the uniform distribution over the interval , denotes the expected value, and denotes the floor function. Given , and two non-negative functions and , we write (as , ) if for any , . If and depend on only, (as ) indicates for some [21].
2 Preliminaries and problem formulation
2.1 Preliminaries
We consider the discrete-time linear system
| (2) |
where is a white noise signal with , , , and . The initial state is a zero-mean random vector with and , and it is uncorrelated with the noise.
In this work, the true system is unknown, and we have access to an approximate model that satisfies and for some . This approximate model and its error bound can be obtained, e.g., from linear system identification [22, 23].
In the above setting, we consider the nominal receding-horizon LQ controller [10]. At time step , is measured, and the RHC controller solves the following optimization problem:
| (3a) | |||
| (3b) | |||
where , , and , . Then is the control input at time step .
We will first consider controllable systems. The extension to stabilizable systems is in Section 5. To this end, we define for and introduce the following assumptions:
Assumption 1
There exists such that has full rank, and the minimum is denoted by , called the controllability index.
Assumption 2
, , , and hold111Requiring to be positive-definite leads to a loss of generality. This assumption, however, is commonly imposed to obtain quantitative bounds[20]. Given , and can be achieved without losing generality by scaling them simultaneously. Letting is not restrictive and ensures that is invertible for technical simplicity..
For some intermediate technical results, we will relax the controllability requirement whenever possible for generality.
Assumption 3
System is stabilizable.
This RHC controller can be further characterized by the Riccati equation as follows. Given any , we define
| (4) |
and the Riccati mapping as
| (5) | ||||
where the last equality holds by the Woodbury matrix identity. To apply the Riccati mapping recursively, we define the Riccati iteration via recursion: For any integer ,
We consider the expected average infinite-horizon performance of , applied to the true system (2). Given any controller gain with , we denote its expected average infinite-horizon performance as
Under a stabilizing , the closed-loop system satisfies
| (7) |
for some that satisfies the Lyapunov equation:
Under Assumption 2, the optimal controller gain , which achieves the minimum , is the LQR controller gain:
| (8) |
where is the unique positive-definite solution of the discrete-time Riccati equation (DARE) [24]:
| (9) |
We further define the closed-loop matrix under as
| (10) |
It is well-known that is Schur stable, and its decay rate can be characterized by the standard Lyapunov analysis:
The proof of this result is presented in Appendix for completeness. If Assumption 1 holds additionally, then is controllable, which implies that is controllable, and thus there exists a real number such that
| (12) |
2.2 Problem formulation
In this work, we analyze the performance gap between the RHC controller and the ideal LQR controller.
Problem 1
Given a prediction horizon , an approximate model with and a terminal matrix with for some , find a non-trivial error bound such that
In Problem 1, a non-zero reflects how the errors , , and the finite prediction horizon of lead to a performance deviation from , which is an ideal controller with an infinite prediction horizon and the correct model. Choosing the infinite-horizon optimal controller as a baseline for performance comparison is standard in studies on learning-based control [19, 20] and MPC[4].
In the special case of a known system and , we have and for any . However, in the case of , which happens when the system is unknown or a numerical error is present for the computed even if the system is known, we can increase the prediction horizon to achieve a smaller . In the more complex situation where there is a modeling error, a larger leads to the propagation of the modeling error and thus may enlarge the performance gap. Our target is to characterize the above complex tradeoff among , , and .
In this work, the obtained bounds hold regardless of whether and are coupled. The presence of coupling, e.g., for some function , can be easily incorporated by plugging function into the bound . In addition, the error bounds obtained will also depend on the system matrices and . To simplify the algebraic expressions of the bounds, we upper bound the system matrices as
where is a real constant. Note that there always exists a sufficiently large such that the above holds.
Remark 1
Regarding the bound in Problem 1, its rate of change as the variables of interest change, i.e., , , and , will be the primary interest. The other constants involved in the bound will often be simplified for interpretability, and they typically depend on system parameters to reveal the relation between control performance and system properties. Therefore, the derived bound is more suitable for convergence analysis and qualitative insights instead of being used as a practical error bound.
Remark 2
We also note that is a worst-case bound that holds for any . Therefore, it can also be conservative for a particular instance.
3 Suboptimality analysis with known model
As the first step, we consider the simpler setting where . The goal is to analyze the joint effect of the prediction horizon and the approximation in the terminal value function on the control performance. To obtain the final performance bound in Section 3.3, we first develop two technical results in Sections 3.1 and 3.2.
Case 1
It holds that .
3.1 Preparatory performance analysis
We first characterize the performance gap between the LQR controller and a general linear controller that has a similar structure to the RHC controller (6). Given any , we define function as
| (13) |
Then given the controller gain for any , the following result characterizes its performance gap based on the difference .
Lemma 2
Lemma 2 directly follows from Lemma 4, which is presented later, as a special case of a known model. These results extend [19, Thm. 1] and [20, Prop. 7] by incorporating the terminal value function error. Lemma 2 shows that if is sufficiently close to , the controller gain can stabilize the system with a near-optimal performance.
3.2 Convergence rate of Riccati iterations
It is a classical result that converges to exponentially as increases [25]. Different convergence analyses have been investigated in the literature, leading to different convergence rates. The rates in [26] and [27, Thm. 14.4.1] are complex functions of the system parameters, characterized by the Thompson metric in [26] and a norm weighted by a special matrix in [27, Thm. 14.4.1]. These convergence rates are hard to interpret because of the specific metric and norm. On the other hand, the rates in [25, Ch. 4.4] and [28] utilize the standard matrix 2-norm and thus are easy to interpret; however, [25, Ch. 4.4] does not exploit controllability, leading to a slower convergence rate than [28]. To the best of our knowledge, [28] provides the most recent state-of-the-art analysis of convergence rates for controllable systems. Therefore, we develop our results based on [28]. While the result in [28] considers only a single convergence rate, we generalize it to incorporate two distinct convergence rates depending on the range of . We also compute the rates as a function of and thus of . The explicit dependency of the convergence rates on will facilitate the subsequent perturbation analysis in Section 4, where the effect of the modeling error on will be exploited.
To this end, we first define several new notations and functions. Recall defined in (4), and we define the function as
| (15) |
which denotes the closed-loop matrix under the controller gain , and thus . In addition, for any integers , define
| (16) |
where is a shorthand notation for . The definition shows . Note that is a state-transition matrix of a time-varying linear system, whose asymptotic stability is reflected by the convergence of to as [29].
The state-transition matrix is helpful for characterizing for any [28]:
| (17) |
which can be verified by applying Lemma 7(a) recursively. Recall that is Schur stable, satisfying . Therefore, (17) shows that as , the convergence of to is governed by the convergence of . Furthermore, exploiting the exponential decay of can further contribute to the convergence of .
Overall, we can characterize the rate of convergence of to as follows:
Lemma 3
Since , we have . Therefore, as increases, Lemma 3 shows a slower decay rate222Given and with and , , , we say is a faster decay rate than to indicate decays faster than as increases. for and a faster rate for . Recall in (16) and (17). Intuitively, the case is when the state-transition matrix is affected by the initial matrix and the consequent transient behaviors, which is evident from the dependency of on . Then, if , the time-varying closed-loop systems in (16) get closer to , leading to a faster convergence rate.
The technical challenge in developing Lemma 3 is the derivation of the two distinct decay rates. Given controllability, the faster rate for is established from the full rank property of by exploiting Lemma 1 and [28, Lem. 4.1]. Since is not of full rank for , the slower rate is established from stabilizability. The analysis is achieved by utilizing the stability analysis of linear time-varying systems [29], introduced in Lemma 9, and further deriving the decay rate as an explicit function of . Note that if , we obtain the rate in both cases of (18), recovering the square of the rate in (11).
3.3 Performance bound with a known model
Theorem 1
In Theorem 1, the upper bound on means that should be sufficiently large or should be sufficiently small, such that the RHC controller can stabilize the system with a suboptimal performance. Moreover, the performance gap satisfies
| (20) |
The above captures the tradeoff between the error and the prediction horizon : The performance gap decays quadratically in and exponentially in . The exponential decay obtained here is analogous to the exponential decay rate in [30] for linear RHC with estimated additive disturbances over the prediction horizon and in [6] for nonlinear RHC, while we have a novel characterization with two distinct decay rates.
The case in (20) has a faster decay rate than the rate for , which indicates the advantage of choosing a horizon333In this work, the control horizon and the prediction horizon are equal. larger than the controllability index, e.g., larger than the state dimension for general controllable systems. Selecting a horizon larger than the state dimension is also suggested in [31]. This also suggests that we may choose a smaller horizon for controlling fully-actuated systems, with and , compared to under-actuated systems.
4 Suboptimality analysis with unknown model
In this section, the results in Section 3 are generalized to consider the joint performance effect of the modeling error, terminal matrix error, and prediction horizon. To obtain the final performance bound in Section 4.3, we first develop several technical results in Sections 4.1 and 4.2.
4.1 Preparatory performance analysis
Given any and a general controller gain in (13), formulated on the approximate model, the following result characterizes the performance gap between and the optimal controller gain :
Lemma 4
4.2 Perturbation analysis of Riccati difference equation
As the RHC controller (6) is a special case of with , Lemma 4 can be exploited to analyze the suboptimality of the RHC controller. Particularly, Lemma 4 shows that can be upper bounded by a function of the modeling error bound and satisfying
| (21) |
Therefore, the main challenge is to characterize by investigating the Riccati iterations using the approximate model.
The above problem has been studied in the classical perturbation analysis of the Riccati difference equation [32]; however, the final bound in [32] does not explicitly show the dependence on , , and . In this work, we provide a novel upper bound as in (21) that captures this dependence.
To this end, due to the approximate model, we first define a state-transition matrix similar to (16):
| (22) |
where
with the functions and defined on :
Recall the closed-loop matrix in (15), and thus, we can interpret as a perturbed : If there is no modeling error, we have due to and . Therefore, can also be interpreted as a perturbed version of the state-transition matrix due to the approximate model.
Then, as an extension of (17) to the approximate model, the following lemma can be obtained:
Lemma 5
For any , and , define and . It holds that
| (23a) | |||
| (23b) | |||
where is a function on :
Equation (23) is closely related to (17): While (17) concerns the state-transition matrix of the true system, (23a) contains the perturbed state-transition matrix and the state-transition matrix of the approximate model; moreover, (23b) contains an extra term caused by the modeling error.
To upper bound , we exploit (23) with and . This motivates us to analyze the spectral norm of the perturbed state-transition matrices in (23). The analysis of these state-transition matrices is analogous to the stability analysis of the corresponding time-varying systems.
Then we establish the following results for the two perturbed state-transition matrices.
Lemma 6
To analyze in (23), we limit the modeling error by introducing the following technical assumptions:
Assumption 4
Assumption 5
The true system satisfies , where is a constant matrix formulated on the true system and is defined in (62).
Assumption 4 limits the modeling error, and Assumption 5 is related to the controllability of the real system, see more details in Remark 12 of Appendix 10. Assumption 4(a) ensures the stabilizability of any and is used to establish a slower decay rate of for , analogous to the slower rate in (18). Moreover, Assumption 4(b) ensures the controllability444Even if Assumption 4(b) also implies stabilizability, the upper bound for in Assumption 4(a) is still needed for computing the decay rates. of . Then, by combining Assumption 4(b) with Assumptions 4(c) and 5, we can exploit controllability to establish a faster decay rate for , analogous to the faster rate in (18). Note that in Assumptions 4(b), 4(c) and 5, the constants , , and depend on the true system only and are independent of the errors and under study. See more details in Appendix 10.
With the above assumptions, we have the following result:
Proposition 1
Proposition 1 shows that if the modeling error is sufficiently small, the approximate state-transition matrix, formulated on any , is guaranteed to converge to zero. The two distinct decay rates in (26) satisfy , analogous to the two decay rates in Lemma 3. Proposition 1 can also be of independent interest, e.g., for the stability analysis of finite-horizon LQR or the Kalman filter with modeling errors.
Remark 3
In the rest of this work, we will omit the dependence of , , and on and for the simplicity of notation. With Lemmas 5, 6 and Proposition 1, we can now characterize in (21) as a function of , and in the following result:
Theorem 2
Note that exists iff is sufficiently small, as in Assumption 4, such that , and thus the approximate Riccati iterations, formulated on any , will converge. In this case, the upper bound (27) characterizes the convergence behavior of the Riccati iterations under the modeling error. As the iteration number increases, the term in (27) decreases and drives closer to ; however, the remaining term increases and drives away from , which reflects the propagation of the modeling error. The above two terms capture the trade-off between the prediction horizon and the modeling error in the convergence of the approximate Riccati iterations.
4.3 Performance bound with a modeling error
Based on (6), Theorem 2 and Lemma 4, the tradeoff between the prediction horizon, the modeling error, and the terminal matrix error can be reflected in the performance of the RHC controller as follows.
Lemma 7
In Lemma 7, depends on because of in (6). Moreover, the upper bound for limits the joint effect of , , and , such that the resulting nominal RHC controller can stabilize the unknown system with a suboptimality guarantee. When the modeling error is significantly large, the nominal controller may fail to stabilize the unknown system. In this case, a more accurate terminal value function can be considered, or a robust controller can be used to explicitly address the error in the controller design [3].
In addition, as in (14) increases as increases, a larger input dimension or state dimension may lead to a larger and thus a larger performance gap in (29). Deriving the exact growth rate of when the state or input dimension increases is a subject of future work.
In the bound , due to the tradeoff in the term , increasing has a complex impact on the control performance due to the propagation of the modeling error. Then natural questions are whether an optimal prediction horizon can be found to minimize the performance upper bound , and how varies when the errors and change.
Example 1
To address the above questions, consider the case as an example. Then, we can rewrite (27) into
| (30) |
Note that in (30), the term
| (31) |
can be interpreted as a measure of the relative difference between and , due to and thus . Then (30) suggests that if the prediction horizon increases, the overall change of and depend on the sign of (31). More specifically, if is relatively smaller than , i.e., (31) is negative, then is attained at ; otherwise, is attained at the largest possible, i.e., in this example.
The observation in Example 1 can be generalized beyond the case . To state the formal result, the following terms are relevant, and their relation can be established:
| (32) |
which follows from . Similar to (31), the above terms represent three quantitative measures of the difference between the two errors and . Their signs decide the optimal prediction horizon , as shown in the following result:
Theorem 3
In the setting of Lemma 7, let , and consider the performance upper bound in (29).
-
(a)
If , then and is strictly decreasing as increases;
-
(b)
If , then with , and if holds additionally, is strictly increasing as increases;
-
(c)
If , is strictly increasing as increases and strictly decreasing as increases. Moreover,
-
•
with if additionally
-
•
otherwise;
-
•
-
(d)
If , is a constant as varies,
where and are defined in Proposition 1, is defined in (25), and is defined in (54) satisfying .
Theorem 3 shows that in (29), the performance upper bound of the RHC controller achieves its infimum either when or when , depending on the relative difference between and , quantified by the terms in (32). More specifically, Theorem 3(a) shows that if is relatively larger than in the sense of (31) being positive, achieves the infimum of . On the other hand, Theorem 3(b) shows that if is relatively larger than , i.e., when , is minimized by choosing . Note that is exponential in based on (27) and (30). In addition, given the errors, is a monotonic function of in Theorem 3(a) and (b), but it shows a more complex behavior in (c).
Remark 4
Depending on the relative difference between and , Theorem 3 indicates that choosing or could achieve a better control performance. However, even if is desired, a finite can be sufficient to make close to its infimum, based on its exponential dependence on . Considering additionally the faster decay rate in (28) when , it can be beneficial to choose a finite satisfying , where we recall that is the controllability index.
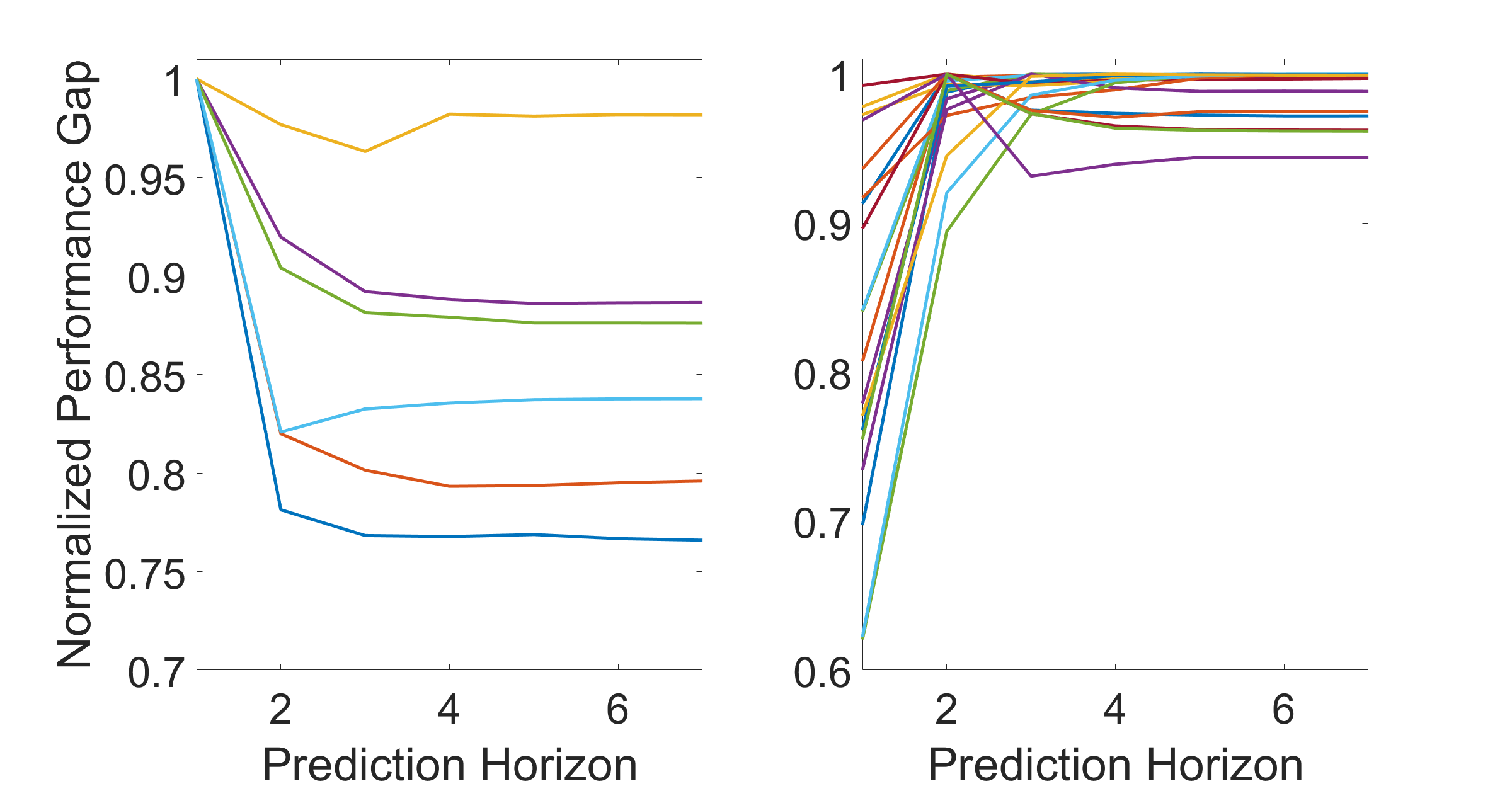
The above observation depends on the performance upper bound in (29) and thus may not reflect the actual behavior of . However, the observation can indeed be seen in extensive simulations in Fig. 1. In this simulation study, random real systems , with and , are generated, where each entry in and is sampled from and , respectively. All systems have controllability index . Moreover, each and the corresponding are perturbed by random matrices555For , a random matrix is multiplied by its transpose to generate a positive semi-definite matrix perturbation., whose entries are sampled from . This is repeated for times for each real system, leading to approximate and nominal RHC controllers. For each controller, we vary its prediction horizon and compute the normalized performance gap as .
The results are shown in Fig. 1. The performance gaps have initial transient behaviors but converge fast as increases. Most controllers indeed obtain their optimal control performance by choosing or the largest until convergence. Moreover, all of them converge after . This shows the potential benefit of choosing a finite satisfying , even if is desired. This is particularly important when the computational aspect is taken into account, as a larger also leads to a higher computational cost.
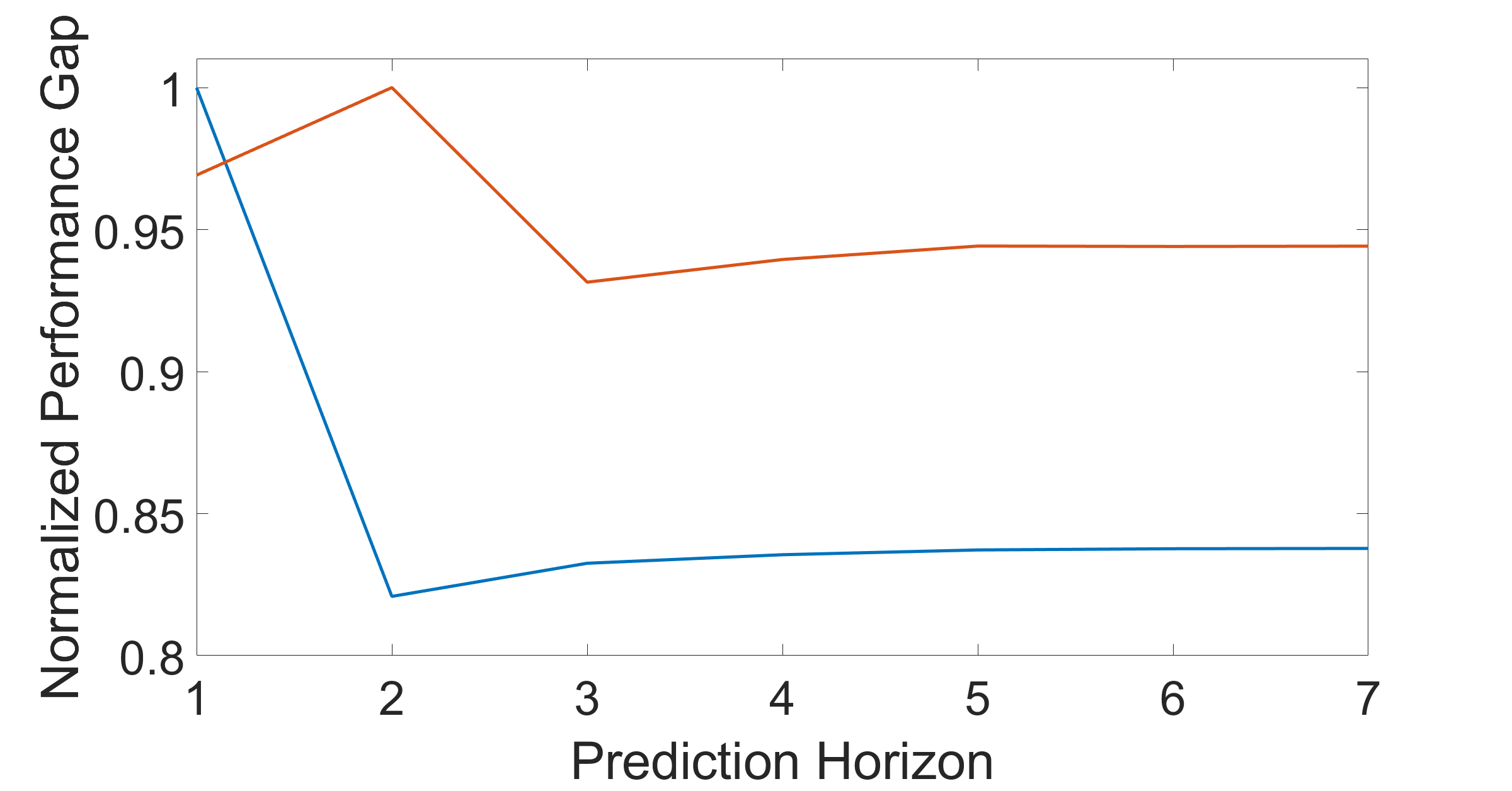
However, there are a few cases where the optimal is finite but greater than . Two examples are shown in Fig. 2, where and achieve the optimal performance, respectively. However, the performance difference between the optimal performance and the performance upon convergence is not significant. These examples show that the upper bound may not reflect the actual behavior of .
Remark 5
Lemma 7 is established under a tight condition, i.e., the bound on the errors can be small. This is a common limitation of analytical error bounds [19, 20]. Despite this limitation, we can still obtain a non-trivial result in Theorem 3, and this result can be observed when going beyond the tight condition, e.g., the modeling errors of the simulation in Fig. 1 are actually greater than .
To better interpret Theorem 3, we also consider the practical case where in the RHC controller (3). Then we have the following result.
Corollary 1
The above result shows that for the RHC controller with zero terminal function, using a large prediction horizon, ideally the nominal LQR controller, is beneficial. This is because the other choice leads to , which will never stabilize the system if the system is open-loop unstable.
5 Extensions to stabilizable systems
We generalize the previous results for controllable systems to stabilizable systems. Without controllability to establish the fast decay rates in (18) and in (26) for , we only establish a single decay rate for all . These results for stabilizable systems are formalized in Appendix 11. The single decay rate greatly simplifies the analysis, which leads to a variant of Theorem 2 for stabilizable systems:
Theorem 4
Similarly to (29), (33) also leads to an error bound
| (34) |
Equation (33) can be rewritten as (30). Therefore, the observation from Theorem 3 that the performance upper bound achieves its infimum at or remains valid for stabilizble systems, now depending on the sign of (31) only.
By observing (17), we note that for stabilizable systems, the faster rate in (18) can also be established by letting be sufficiently large, e.g. larger than a constant , such that the closed-loop matrices in become close to in (10). However, can be large and also does not have a clear interpretation, unlike the controllability index in (18). Therefore, this technical extension is not pursued here.
6 Applications in learning-based control
Besides the obtained theoretical insights, our suboptimality analysis can also be used to analyze the performance of learning-based controllers. Results in this section generalize the results in [19, 18, 20] for learning-based LQR controllers with an infinite horizon to RHC controllers with an arbitrary prediction horizon. We will compare our performance bounds analytically with the above existing results, as is done in similar studies on regret analysis [19, 20].
6.1 Offline identification and control
In this subsection, we first obtain an estimate offline from measured data of the unknown real system (2), and then synthesize a controller (3) with zero terminal matrix . This is the classical receding-horizon LQ controller [10].
There are many recent studies on linear system identification and its finite-sample error bounds [22, 23, 18]. For interpretability, we consider a relatively simple estimator from [18]. Assume that the white noise is Gaussian, and we conduct independent experiments on the unknown real system (2) by injecting independent Gaussian noise, i.e., with , where each experiment starts from and lasts for time steps. This leads to the measured data , , which is independent over the experiment index . To avoid the dependence among the data for establishing the estimation error, we use one data sample from each independent experiment, and then an estimate is obtained from the least-squares (LS) estimator [18]:
| (35) |
An error bound can be obtained [18, Prop. 1] such that with high probability and for some constant that depends on system parameters,
| (36) |
Consider the nominal controller (3) with and from (35). We can provide an end-to-end control performance guarantee by combining the LS estimation error bound (36) and our performance bound (34). We consider (34) here for generality as it needs more relaxed assumptions than (29). To this end, we first simplify (34) for interpretability.
Proposition 2
Combining Proposition 2 with the estimation error bound (36) from [18] directly leads to the following end-to-end performance guarantee:
Corollary 2
Corollary 2 reveals the effect of the prediction horizon and the number of data samples on the control performance. The performance gap is if , i.e., when the nominal LQR controller is considered. This growth rate agrees with the recent study [19] of the LQR controller. When is finite, an additional error exists and decreases as increases. When , the estimated model converges to the real system with high probability, leading to performance gap , i.e., the performance of the controller converges exponentially to the optimal one as increases, which matches our observation in (20). Note that controllability in Assumption 1 is introduced in Corollary 2, required by the estimation error bound [18]. Moreover, Assumption 4(a) is absent, as it is satisfied by a sufficiently large .
6.2 Online learning control with regret bound
In this subsection, we consider the adaptive LQR controller algorithm in [20], which has a state-of-the-art regret guarantee with greedy exploration. While there are other exploration strategies [17], the more fundamental greedy exploration is chosen to demonstrate the application of our analysis.
The nominal LQR controller within the adaptive control scheme in [20] is replaced by the receding-horizon LQ controller (3) with . Other cost matrices and are fixed throughout the close-loop operation. To match the setting in [20], in this subsection, we assume that is Gaussian with and the initial condition is . Following [20], we assume that a stabilizing but possibly suboptimal controller gain for the unknown true system is given a priori.
We briefly introduce the main idea of [20, Algorithm 1], and the details can be found in [20]. Starting from and a random input , the control algorithm utilizes a fixed controller gain within each time step period , where and is the period index. In the first few periods, the gain with a Gaussian perturbation is used, i.e., with and , to stabilize the unknown system. The perturbation ensures the informativity of the data for estimating the system later.
After collecting sufficient data at time step for some period , the controller conducts the following steps for every period . A new model is re-estimated at the initial time step of period . It is obtained from the LS estimator using the data from the last period , where , as
| (37) |
Then, for , the algorithm employs a new RHC controller gain , formulated based on666In [20], the estimated model, if not accurate, is further modified via projection. These details are presented in [20]. This projection step is redundant if the estimated model is sufficiently accurate. Moreover, it relies on a conservative error bound, leading to practical issues as discussed in Section 6.3. Therefore, the projection step is ignored later in the simulations of Section 6.3. via either the implicit form (3) or the explicit form (6), with a random perturbation, i.e., , where determines the size of the perturbation and decays as increases.
In this case, let denote the total number of time steps that have passed, and let denote the final period index. Let denote the above adaptive controller, and its performance is typically characterized by regret [22, 33]:
which measures the accumulative error of a particular realization under the controller. Ideally, we would like to have a sublinear regret, such that as , converges to zero with high probability, i.e., the average performance of the adaptive controller is optimal.
As shown in [20, Sect. 5.1] and [20, Appendix G.2], the following holds for the considered adaptive controller with high probability:
Combining the above equation with Proposition 2 leads to
| (38) |
where we have used the fact that the estimated model, obtained at , has error with high probability, based on [20, Lem. 5.4].
The regret upper bound (38) provides some interesting information. Firstly, note that for some constant . Therefore, if we have an infinite prediction horizon , i.e., when the nominal LQR is considered, then , which matches the rate of the adaptive LQR controllers in [19, 20].
If we have a finite , (38) shows with high probability,
| (39) |
where the regret is linear in . This observation matches the result in [34], where the regret of a linear unconstrained RHC controller, with a fixed prediction horizon and an exact system model, is linear in . This linear regret is caused by the fact that even if the model is perfectly identified, the RHC controller still deviates from the optimal LQR controller due to its finite prediction horizon.
To achieve a sublinear regret, (39) suggests that an adaptive prediction horizon is preferred. As also suggested in [34] but for the case of a known system, we can update via
e.g., updating , when the model is re-estimated, which again leads to a sublinear regret according to (38). Note that this is the optimal rate for the regret [20]. The intuition of this choice is that, with a more refined model due to re-estimation, the prediction horizon can be increased adaptively to improve the control performance.
6.3 Simulations of adaptive RHC
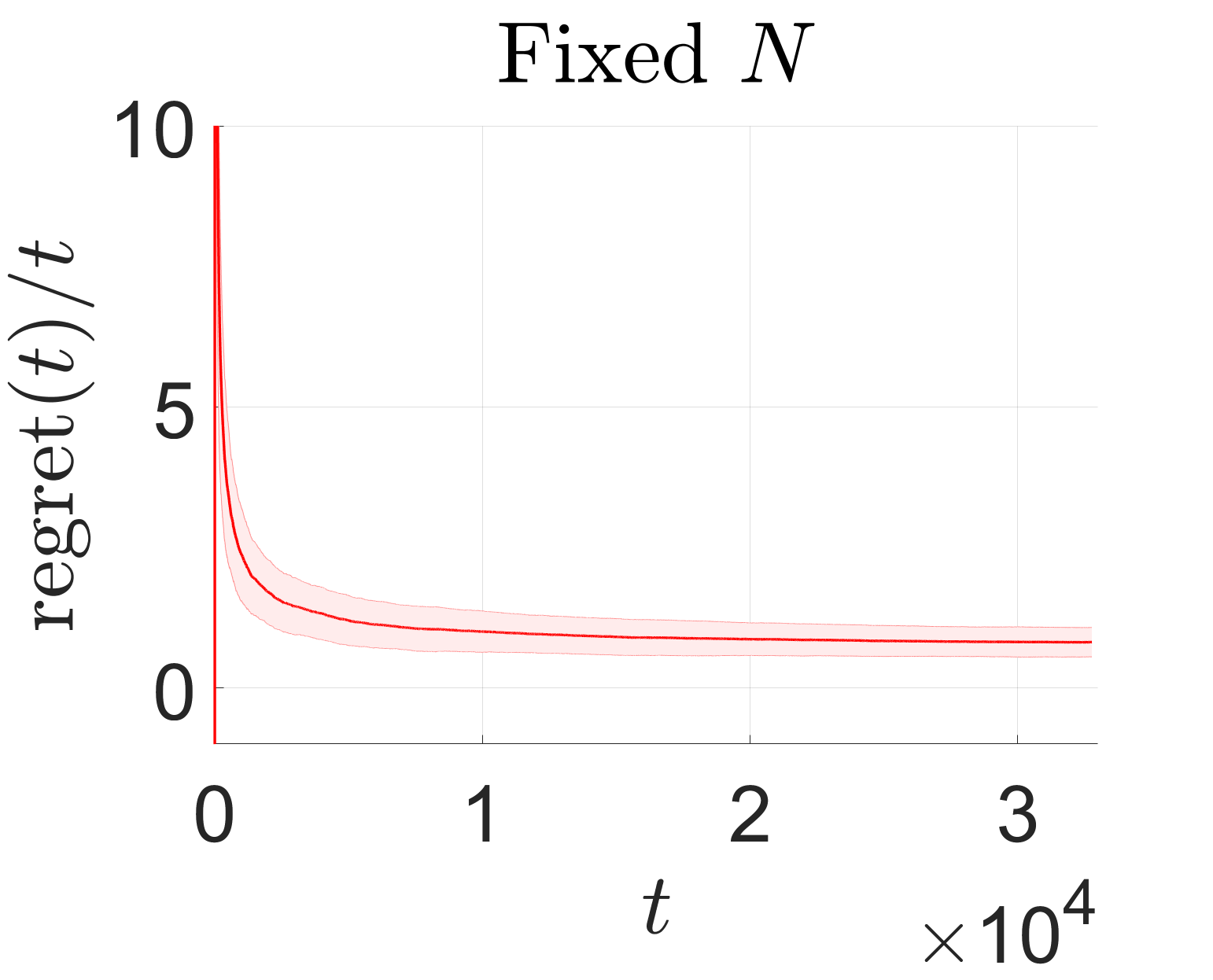
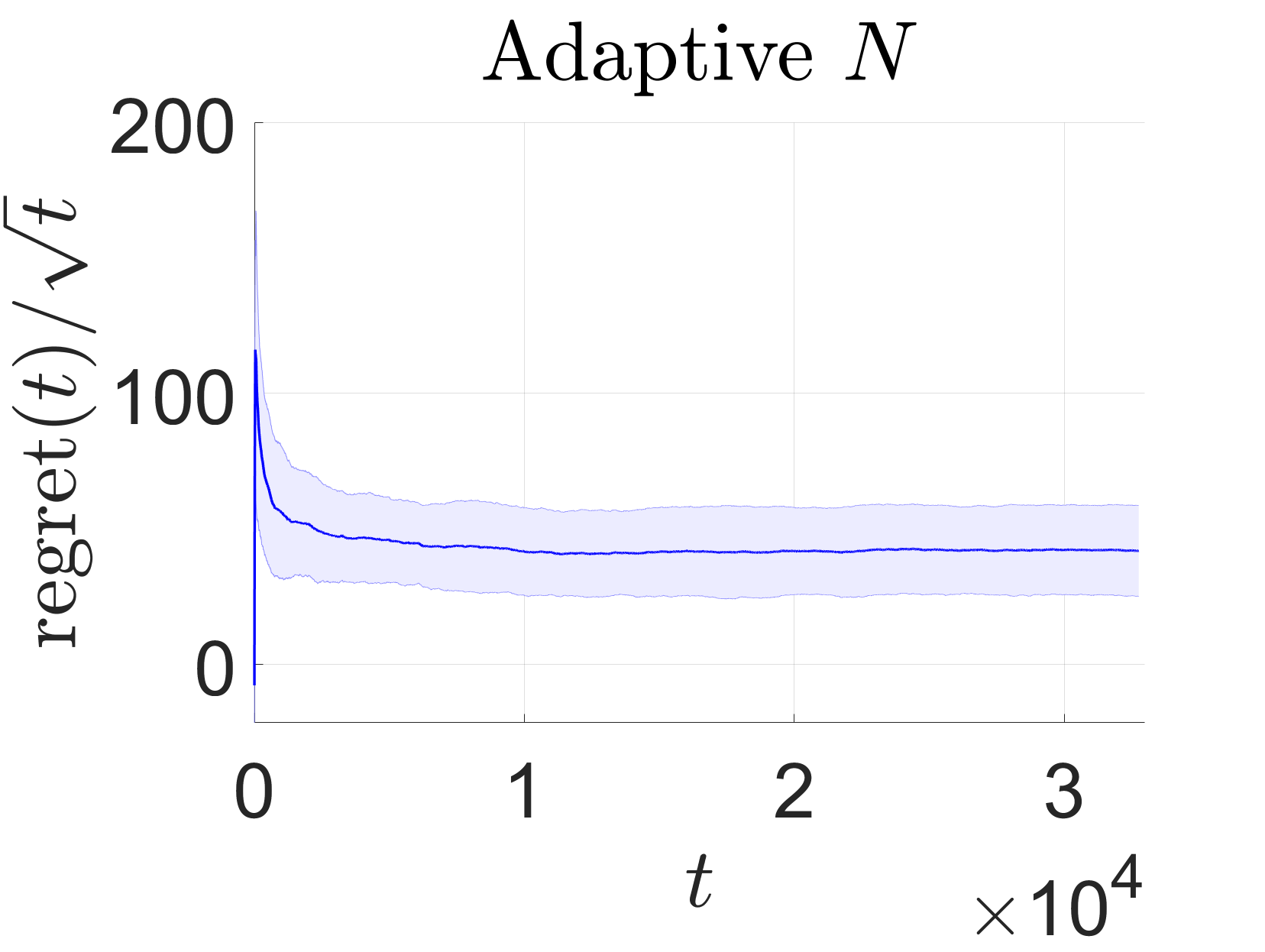
We use simulations to demonstrate the main theoretical insights from Section 6.2: For the adaptive RHC algorithm, while a fixed prediction horizon leads to a linear regret growth rate , an adaptive horizon, being a logarithmic function of time, leads to a more desired sublinear rate .
While the algorithm based on [20] in Section 6.2 has a regret guarantee, a conservative analytical modeling error bound , analogous to (36), is utilized in [20]. This conservatism causes practical issues, e.g., despite the actual modeling error being small, the if condition for some function in the algorithm is hardly met as the bound is too large. Therefore, by introducing tuning parameters, we slightly modify the algorithm in Section 6.2 to avoid analytical error bounds. The resulting algorithm is more practical and suffices to demonstrate the theoretical insight. We summarize the modifications here:
-
(i)
The key period index in Section 6.2 is chosen to be the first period such that holds, where is a tuning parameter.
-
(ii)
The LS estimator (37) uses data from all the previous periods, instead of only the last period.
-
(iii)
We let , where is a tuning parameter instead of being computed via an analytical formula as in [20].
In the above, (i) ensures that the collected data is informative to obtain an accurate LS estimate of the model. Point (ii) ensures the updated estimate is not worse than the previous one, as more data is used for estimation. With point (iii), the exploration effort decays as the period index increases.
We use the modified algorithm to control the unknown system with the following true system matrices:
Starting from , we compare the regret growth of the adaptive RHC controller with a fixed prediction horizon and the controller with an adaptive prediction horizon , where is updated when the controller is updated. Other parameters are , , , , , , and is the LQR controller gain for stabilization. Note that although the true system and its LQR controller are unknown, we choose the LQR controller to be the initial controller for simplicity. The choice of , if stabilizing, does not affect our illustration of the regret growth.
As the regret is a random variable due to the disturbance , we conduct simulations for each controller. The regret growth over time, normalized by or , is shown in Fig. 3. It shows that the regret grows linearly in under the fixed but in the order of under the adaptive . This illustrates the advantage of the adaptive prediction horizon for regret minimization.
While the modified algorithm does not preserve the theoretical guarantee in Section 6.2, it remains useful to demonstrate the impact of the adaptive prediction horizon on regret growth. Moreover, this algorithm has a structure similar to that of existing algorithms with regret guarantees, e.g., the adaptive LQ Gaussian (LQG) controller in [35]. Our future work will investigate the possibility of extending existing analyses to the modified algorithm.
7 Conclusions
This work analyzes the suboptimality of RHC under the joint effect of the modeling error, the terminal value function error, and the prediction horizon in the LQ setting. By deriving a novel perturbation analysis of the Riccati difference equation, we have obtained a novel performance upper bound of the controller. The bound suggests that letting the prediction horizon be or can potentially be beneficial, depending on the relative difference between the modeling error and the terminal matrix error. Moreover, when an infinite horizon is desired, a prediction horizon larger than the controllability index can be sufficient for achieving a near-optimal performance. Besides the above insight, this obtained performance bound has also been shown to be useful for analyzing the performance of learning-based receding-horizon LQ controllers.
Future work includes the derivation of tighter performance bounds to capture the non-trivial optimal horizon, which is finite but larger than . Moreover, the extension of the obtained results to more general settings, e.g., constrained RHC controllers with possibly nonlinear dynamics or output feedback, is an important direction. The analysis of computational efficiency is not considered in this work, as the controller in the current setting has a closed-form expression. Analyzing computational efficiency is also an important direction for the more general settings.
8 Technical tools
Technical tools from the literature are collected here.
Lemma 8
Given and any positive integer , we have
Proof 8.1.
This result is obtained by applying formula .
Lemma 5.
([19, Lem. 7]) Given and , it holds that .
Lemma 6.
([19, Lem. 5]) Consider , , such that for any . For any and , holds.
Lemma 7.
If , for any , , and ,
-
(a)
-
(b)
;
-
(c)
;
-
(d)
with defined in (41).
In addition, the following perturbation analysis of the Riccati equation from [20, Prop. 6] and [20, Lem. B.5, B.8] is useful for deriving the results of this work.
Lemma 8.
Another tool is the stability analysis of time-varying systems, directly implied by the proof of [29, Thm. 23.3].
Lemma 9.
Consider a system with and for integers . If there exists a matrix sequence satisfying for
for some positive constants , , and , then with .
9
9.1 Proof of Lemma 1
9.2 Proof of Lemma 3
We first define the following Gramian matrix: for
| (41) |
where , , and recall that is a shorthand notation for .
The proof for the case is achieved based on Lemma 3 and [28, Lem. 4.1]. We highlight the key steps for completeness. If , matrix has full rank due to Assumption 1. Lemma 7(d) shows for . Then based on Assumption 2 and [28, Lem. 4.1], is non-singular for , and moreover, its inverse is uniformly upper bounded for any and any . Combining (17) and the above shows for , which together with (11) concludes the proof for , with
| (42) |
When , the rank of the controllability matrix is less than , and thus is not guaranteed to be of full rank. Then directly exploiting (17) leads to
| (43) |
A naive approach is to upper bound by a constant. However, due to , can also be shown to be exponentially decay as increases, even without the controllability property. This result in (74) is exploited here and proved later in Appendix 11. Combining (11), (43), and (74) proves this case, with
| (44) |
derived from (74) using . The case holds trivially due to .
9.3 Proof of Lemma 4
The result is based on the following lemma:
Proof 9.1.
Then Lemma 4 can be proved as follows. Firstly, based on (45) and the assumption, we have . Then given Assumption 2, we have based on [20, Lem. B.5]777Note that in this work, the noise has a covariance matrix instead of as in [20]; however, the results in [20] extends to this work trivially.. Therefore, implies , which further shows that is Schur stable, according to [20, Lem. B.12]. Then given a stabilizing and based on [19, Lem. 3], we have
where the second inequality holds due to under according to [20, Lem. B.12]. Then combining the above result and Lemma 10 concludes the proof.
9.4 Proof of Lemma 5
Define the shorthand notations and . We prove this result by induction. The equality holds trivially when . Assume it holds for , then
| (46a) | ||||
| (46b) | ||||
| (46c) | ||||
9.5 Proof of Lemma 6
The matrix in (22) is reformulated as
| (51) |
where . To upper bound the norm of , we first upper bound : where the first identity follows form the matrix inverse lemma, and the final step follows from due to Assumption 2. Due to , letting leads to
| (52) |
| (53) | |||
where we have used from Lemma 8 in the second inequality. Based on (11) and , applying Lemma 6 concludes the proof.
9.6 Proof of Theorem 2
9.7 Proof of Lemma 7
9.8 Proof of Theorem 3
Equation (27) can be written more compactly as
| (57) |
Moreover, we can quantify the change from to by computing
The above equation and from (26) show that
| (58) |
The statement (a) follows from (30), (32), (57), and (58). For statement (b), if , then (30), (32), and (57) show that and are strictly increasing as increases, and they are also strictly increasing as increases. For the transition of the two regions of , consider
where the first inequality follows from Lemma 8. The above shows . Moreover, under the additional condition , the last part of statement (b) is proved by observing (58).
For statement (c), if , (30) and (57) show that is increasing as increases and decreasing as increases. This means that equals either or depending on the sign of
which can be proved to be in the interval as follows. The upper bound of this interval is proved by showing and thus , and the lower bound can be proved similarly. The above proves statement (c). Statement (d) follows trivially from (30) and (57).
9.9 Proof of Corollary 1
9.10 Proof of Proposition 2
Since , we let . In addition, holds under the assumption, which leads to
| (60) |
and thus . Therefore, we have
| (61) |
Given the upper bound on , in (54) satisfies for some constant independent of and , and can also be upper bounded by some constant . This shows Combining the above inequality with (29) concludes the proof.
10 Proof of Proposition 1
To prove this result, the dual Riccati mapping is relevant:
| (62) |
and its fixed point is denoted by . Let be a fixed point of (62) with replaced by . Let be the closed-loop system for under the corresponding LQR controller.
We will prove this result by considering the case and the case separately. When , the overall proof strategy is as follows. Due to , Lemma 7(d) shows for . Moreover, [28, Lem. 4.1] shows that if is positive definite, we have
| (63) |
Then the proof consists of the following analysis:
-
•
Perturbation analysis of the closed-loop system ;
-
•
Perturbation analysis of the Gramian matrix: Show that is invertible for and provides an upper bound on ;
-
•
Perturbation analysis of .
All perturbation bounds resulting from the above analysis will be expressed as functions of and .
The decay rate of the perturbed closed-loop system can be obtained as follows. Given , combining (11) and Lemma 8 leads to
| (64) |
The remaining analysis is presented as follows.
10.1 Perturbation analysis of the Gramian matrix
If , then and
The Gramian matrix is a perturbed version of . Based on Lemma 8, we can upper bound the perturbation of as
| (65) |
which satisfies
| (66) |
Under Assumption 1, recall from (12). This together with (11), (65), and [19, Lem. 6] show
with
| (67) | ||||
where is defined in (65), and the second equality follows from (66). Given in Assumption 4, is of full rank, and we have . Moreover, some algebraic manipulations show , which leads to
| (68a) | |||
| (68b) | |||
where (68b) follows from the fact that the RHS of (68a) approaches a constant as .
10.2 Perturbation analysis of the dual Riccati equation
Given under Assumption 2, let denote the symmetric positive-definite square root of . We further define
| (69) |
As is Schur stable, let represent its decay rate such that for some and for any . Then applying [19, Prop. 2] leads to the following:
Proof 10.1.
10.3 Final step when
10.4 Situation where
11 Proof of Theorem 4
11.1 Exponential decay of state transition matrix
Based on Lemma 5, an essential step to prove Theorem 4 is establishing the convergence rate of the state-transition matrix for stabilizable systems. The stability analysis of time-varying systems in Lemma 9, originally from [29], is a fundamental tool. To exploit it, we first provide a uniform upper bound on the Riccati iterations as an explicit function of .
Proof 11.1.
Lemma 14.
Proof 11.2.
As is a positive-definite matrix sequence when and satisfies , we first focus on this case where . Then for and from Lemma 7(b), is a time-varying Lyapunov function, satisfying , for the time-varying nominal system . Note that this nominal system admits the state-transition matrix of interest, i.e., . Then when , we have based on (73). Applying Lemma 9 shows
| (76) |
11.2 Proof of Theorem 4
References
- [1] M. Schwenzer, M. Ay, T. Bergs, and D. Abel, “Review on model predictive control: An engineering perspective,” Int. J. Adv. Manuf. Technol., vol. 117, no. 5-6, pp. 1327–1349, 2021.
- [2] S. Katayama, M. Murooka, and Y. Tazaki, “Model predictive control of legged and humanoid robots: models and algorithms,” Adv. Robot., vol. 37, no. 5, pp. 298–315, 2023.
- [3] D. Q. Mayne, “Model predictive control: Recent developments and future promise,” Automatica, vol. 50, no. 12, pp. 2967–2986, 2014.
- [4] L. Grüne and J. Pannek, Nonlinear Model Predictive Control: Theory and Algorithms. Springer, 2011.
- [5] L. Grüne and S. Pirkelmann, “Economic model predictive control for time-varying system: Performance and stability results,” Optim. Control Appl. Methods, vol. 41, no. 1, pp. 42–64, 2020.
- [6] J. Köhler, M. Zeilinger, and L. Grüne, “Stability and performance analysis of NMPC: Detectable stage costs and general terminal costs,” IEEE Trans. Autom. Control, vol. 68, no. 10, pp. 6114–6129, 2023.
- [7] D. Bertsekas, “Newton’s method for reinforcement learning and model predictive control,” Results Control Optim., vol. 7, p. 100121, 2022.
- [8] F. Moreno-Mora, L. Beckenbach, and S. Streif, “Predictive control with learning-based terminal costs using approximate value iteration,” IFAC-PapersOnLine, vol. 56, no. 2, pp. 3874–3879, 2023.
- [9] D. Bertsekas, Reinforcement Learning and Optimal Control. Athena Scientific, 2019.
- [10] R. R. Bitmead and M. Gevers, “Riccati difference and differential equations: Convergence, monotonicity and stability,” in The Riccati Equation. Springer, 1991, pp. 263–291.
- [11] F. Moreno-Mora, L. Beckenbach, and S. Streif, “Performance bounds of adaptive MPC with bounded parameter uncertainties,” Eur. J. Control, vol. 68, p. 100688, 2022.
- [12] D. Muthirayan, J. Yuan, D. Kalathil, and P. P. Khargonekar, “Online learning for predictive control with provable regret guarantees,” in Proc. 61st IEEE Conf. Decis. Control, 2022, pp. 6666–6671.
- [13] S. Lale, K. Azizzadenesheli, B. Hassibi, and A. Anandkumar, “Model learning predictive control in nonlinear dynamical systems,” in Proc. 60th IEEE Conf. Decis. Control, 2021, pp. 757–762.
- [14] I. Dogan, Z.-J. M. Shen, and A. Aswani, “Regret analysis of learning-based MPC with partially-unknown cost function,” IEEE Trans. Autom. Control, vol. 69, no. 5, pp. 3246–3253, 2024.
- [15] B. Recht, “A tour of reinforcement learning: The view from continuous control,” Annu. Rev. Control Robot. Auton. Syst., vol. 2, pp. 253–279, 2019.
- [16] N. Matni, A. Proutiere, A. Rantzer, and S. Tu, “From self-tuning regulators to reinforcement learning and back again,” in Proc. 58th IEEE Conf. Decis. Control, 2019, pp. 3724–3740.
- [17] A. Tsiamis, I. Ziemann, N. Matni, and G. J. Pappas, “Statistical learning theory for control: A finite-sample perspective,” IEEE Control Syst, vol. 43, no. 6, pp. 67–97, 2023.
- [18] S. Dean, H. Mania, N. Matni, B. Recht, and S. Tu, “On the sample complexity of the linear quadratic regulator,” Found. Comput. Math., vol. 20, no. 4, pp. 633–679, 2020.
- [19] H. Mania, S. Tu, and B. Recht, “Certainty equivalence is efficient for linear quadratic control,” in Proc. 33rd Adv. Neural Inf. Process. Syst., 2019, pp. 10 154–10 164.
- [20] M. Simchowitz and D. Foster, “Naive exploration is optimal for online LQR,” in Proc. 37th Int. Conf. Mach. Learn., 2020, pp. 8937–8948.
- [21] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein, Introduction to Algorithms. MIT press, 2022.
- [22] M. Simchowitz, H. Mania, S. Tu, M. I. Jordan, and B. Recht, “Learning without mixing: Towards a sharp analysis of linear system identification,” in Prof. 31st Conference on Learning Theory, 2018, pp. 439–473.
- [23] T. Sarkar and A. Rakhlin, “Near optimal finite time identification of arbitrary linear dynamical systems,” in Proc. 36th Int. Conf. Mach. Learn., 2019, pp. 5610–5618.
- [24] D. Bertsekas, Dynamic Programming and Optimal Control: Volume I. Athena scientific, 2012.
- [25] B. Anderson and J. B. Moore, Optimal Filtering. Prentice-Hall, 1979.
- [26] J. Lawson and Y. Lim, “A Birkhoff contraction formula with applications to Riccati equations,” SIAM J. Control Optim., vol. 46, no. 3, pp. 930–951, 2007.
- [27] B. Hassibi, A. H. Sayed, and T. Kailath, Indefinite-Quadratic Estimation and Control: A Unified Approach to and Theories. SIAM, 1999.
- [28] P. Del Moral and E. Horton, “A note on Riccati matrix difference equations,” SIAM J. Control Optim., vol. 60, no. 3, pp. 1393–1409, 2022.
- [29] W. J. Rugh, Linear System Theory. Prentice-Hall, 1996.
- [30] R. Zhang, Y. Li, and N. Li, “On the regret analysis of online LQR control with predictions,” in Proc. 2021 Am. Control Conf., 2021, pp. 697–703.
- [31] B. De Schutter and T. Van Den Boom, “Model predictive control for max-plus-linear discrete event systems,” Automatica, vol. 37, no. 7, pp. 1049–1056, 2001.
- [32] M. Konstantinov, I. Poptech, and V. Angelova, “Conditioning and sensitivity of the difference matrix Riccati equation,” in Proc. 1995 Am. Control Conf., 1995, pp. 466–466.
- [33] S. Lale, K. Azizzadenesheli, B. Hassibi, and A. Anandkumar, “Reinforcement learning with fast stabilization in linear dynamical systems,” in Proc. 25th Int. Conf. Artif. Intell. Stat., 2022, pp. 5354–5390.
- [34] C. Yu, G. Shi, S. J. Chung, Y. Yue, and A. Wierman, “The power of predictions in online control,” in Proc. 34th Adv. Neural Inf. Process. Syst., 2020, pp. 1994–2004.
- [35] A. Athrey, O. Mazhar, M. Guo, B. De Schutter, and S. Shi, “Regret analysis of learning-based linear quadratic Gaussian control with additive exploration,” in Proc. 22nd European Control Conference, 2024, pp. 1795–1801.
- [36] B. D. O. Anderson et al., Stability of Adaptive Systems: Passivity and Averaging Analysis. MIT Press, 1986.