Corresponding Author: ]leishu@fudan.edu.cn

Superconducting Properties of La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂: A $\rm\mu$ SR Study

Qiong Wu Kaiwen Chen Zihao Zhu Cheng Tan Yanxing Yang Xin Li State Key Laboratory of Surface Physics, Department of Physics, Fudan University, Shanghai 200438, People’s Republic of China Toni Shiroka Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institute, CH-5232 Villigen PSI, Switzerland Laboratorium für Festkörperphysik, ETH Zürich, CH-8093 Zürich, Switzerland Xu Chen Jiangang Guo Xiaolong Chen Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, P. O. Box 603, Beijing 100190, China Lei Shu [ State Key Laboratory of Surface Physics, Department of Physics, Fudan University, Shanghai 200438, People’s Republic of China Collaborative Innovation Center of Advanced Microstructures, Nanjing 210093, People’s Republic of China Shanghai Research Center for Quantum Sciences, Shanghai 201315, People’s Republic of China

Abstract

We report the results of muon spin rotation and relaxation ( $\rm\mu$ SR) measurements on the recently discovered layered Cu-based superconducting material La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.40, 0.45). Transverse-field $\rm\mu$ SR experiments on both samples show that the temperature dependence of superfluid density is best described by a two-band model. The absolute values of zero-temperature magnetic penetration depth $\lambda_{\rm ab}(0)$ were found to be 427(1.7) nm and 422(1.5) nm for $x=$ 0.40 and 0.45, respectively. Both compounds are located between the unconventional and the standard BCS superconductors in the Uemura plot. No evidence of time-reversal symmetry (TRS) breaking in the superconducting state is suggested by zero-field $\rm\mu$ SR measurements.

I Introduction

The relation between magnetism and superconductivity is one of the most prominent issues in condensed matter physics [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. Since the discovery of cuprate high transition temperature ( $T_{\rm c}$ ) superconductors, considerable efforts have been made to investigate the role of in-plane impurities in them. It is now well established that, in copper oxide superconductors, nonmagnetic Zn ions suppress $T_{c}$ even more strongly than magnetic Ni ions [11, 12, 13, 14]. Such behavior is in sharp contrast to that of conventional BCS superconductors, in which magnetic impurities can act as pairing-breaking agents, rapidly suppressing superconductivity [15, 16]. Another interesting behavior of unconventional superconducting systems such as the heavy-fermion, high $T_{c}$ cuprate, and iron-pnictide superconductors is the dome shape of the chemical doping dependence of $T_{\rm c}$ [17, 18, 19, 20].

Recently, the first Cu-As superconductor was discovered in the layered La₂Cu₅As₃O₂ with $T_{\rm c}=0.63$ K [21]. When Cu²⁺ is replaced by Ni²⁺, also in La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂, the $T_{\rm c}$ exhibits a dome-like structure. Remarkably, while the superconductivity in cuprate- and iron-based superconductors is completely suppressed when the substitution ratio of Cu or Fe exceeds 20% [22, 23], superconductivity in La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ persists until the substitution ratio exceeds 60% [21]. In this case, the robustness of superconductivity reveals the unexpected effect of impurities on inducing and enhancing superconductivity. Hence, La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ provides a broader platform for studying the doping effect in the superconducting phase diagram.

Specific heat measurements have revealed that the optimally doped La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.40) sample shows a sharp superconducting transition at $T_{\rm c}=$ 2.05 K, with a dimensionless jump $C_{\rm e}/\gamma_{\rm s}T_{\rm c}=1.42$ [21], consistent with the BCS weak-coupling limit (1.43). In the superconducting state, the temperature dependence of the specific heat coefficient is described by a fully-gapped model $C_{\rm e}/T\propto e^{-\Delta/k_{\rm B}T}$ after subtracting the upturn of $C_{\rm e}/T$ below $T<0.5$ K, which is attributed to the Schottky effect. These results suggest that La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.40) is a conventional BCS superconductor with a fully developed energy gap. However, the fit yields $2\Delta/k_{\rm B}T_{\rm c}=2.58$ [21], much smaller than the BCS weak coupling limit.

$\rm\mu$ SR experiments have been widely utilized to probe superconductivity in type-II superconductors at the microscopic level [24], and they are free from the influence of the Schottky effect. Transverse-field (TF) $\rm\mu$ SR measures the absolute value of the magnetic penetration depth $\lambda$ , which is related to the density of superconducting carriers. The temperature dependence of $\lambda$ is sensitive to the lowest-lying superconducting excitations and provides information on the symmetry of superconducting pairing [25, 26, 27, 28, 29, 30]. In addition, zero-field (ZF) $\rm\mu$ SR is a powerful method to detect small spontaneous internal magnetic fields due to the possible breaking of time-reversal symmetry (TRS) at the superconducting transition. These can be as small as 10 $\mu$ T, corresponding to about $10^{-2}$ of Bohr magneton $\rm{\mu_{B}}$ [31, 32, 33, 25, 34, 24].

Here, in order to study the doping effect on superconductivity, we perform $\rm\mu$ SR measurements on the polycrystalline samples of La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ for $x=0.40$ (optimal doping) and $x=0.45$ (overdoped). The temperature dependence of superfluid density determined from TF- $\rm\mu$ SR is best described by a two-band superconductivity model. $d$ -wave superconductivity possibly exists in one of the bands, with the fraction of $d$ -wave smaller in the overdoped sample than that in the optimally doped one. The superconducting energy gap is larger for optimal doping, suggesting that the coupling strength decreases with the increase of doping. Both compounds are located between the unconventional and the standard BCS superconductors in the Uemura plot. Meanwhile, no evidence of TRS breaking is suggested by ZF- $\rm\mu$ SR measurements.

II Experimental Details

Solid-state reactions were used to produce polycrystalline samples of La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x$ = 0.40, 0.45) [21]. The performed X-ray diffraction (XRD) studies and the density functional theory (DFT) calculation shows the band structures of La₂Cu₅As₃O₂, indicating that this newly synthesized sample is a layered superconducting compound, with the superconducting atomic layers consisting of the $[\rm{Cu_{5}As_{3}}]^{2-}$ cage-like structure [21].

$\rm\mu$ SR experiments were carried out using nearly 100% spin-polarized positive muons ( $\mu^{+}$ ) on the M15 beam line at TRIUMF, Vancouver, Canada for $x=0.40$ , and the DOLLY spectrometer of the S $\mu$ S muon source at Paul Scherrer Institute (PSI), Switzerland for $x=0.45$ , respectively. The samples were mounted on a silver sample holder at TRIUMF and a copper sample holder at PSI, respectively. Only a very limited amount of muons stopped in the extremely thin copper sample holder. In TF- $\rm\mu$ SR measurements, where the external field is applied perpendicular to the initial muon spin polarization, muons are implanted one at a time into a sample which is cooled (from above $T_{c}$ ) in an external magnetic field. Muon spins precesses around the local field at the implantation site, and the functional form of the muon spin polarization depends on the field distribution of the vortex state, including the magnetic penetration depth, the vortex core radius, and the structure of the flux-line lattice. For ZF- $\rm\mu$ SR measurements, the ambient magnetic field was actively compensated to better than 1 $\mu$ T. $\rm\mu$ SR data were analyzed using the musrfit software package [35].

III RESULTS

III.1 Transverse-field $\rm\mu$ SR experiments

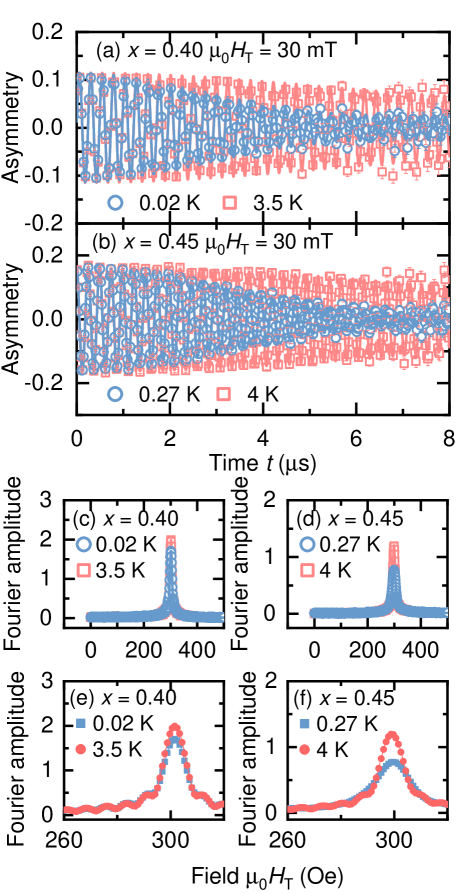
The $\rm\mu$ SR asymmetry spectrum usually consists of a signal from muons that stop in the sample and a slowly relaxing background signal from muons that miss the sample for example, stop in the sample holder. Fig. 1 (a) (b) show the typical TF- $\rm\mu$ SR muon spin precession signals at an applied field of $\mu_{\rm{0}}H=$ 30 mT in the normal (red squares) and superconducting states (blue circles) for La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.40 and 0.45) after subtracting the background signal. The superconducting volume fractions are estimated to be 60 $\%$ and 70 $\%$ from the TF $\rm\mu$ SR asymmetry at long times for x = 0.40 and 0.45, respectively. Fig. 1 (c) (d) show the Fourier transformations (FFT) of the total TF- $\rm\mu$ SR asymmetry. It can be inferred from the figure that vortex states are constructed in both samples at low temperatures [36]. Fig. 1 (e) (f) show the details of the FFT spectra. As shown in the figure, the magnetic fields in the superconducting state and the normal state are relatively close to each other. This is common in anisotropic powder superconducting samples [37, 38].

Refer to caption — Figure 1: (a)-(b) Representative TF- $\rm\mu$ SR asymmetry spectra $A(t)$ for La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.40 (panel (a)) and 0.45 (panel (b))) in the normal (red squares) and superconducting (blue circles) states with an external magnetic field of $\rm{\mu_{0}}H=$ 30 mT after subtracting the background signal. Solid curves: fits to the data using Eq. (1). (c)-(f) Fourier transformation of the total TF- $\rm\mu$ SR time spectra. (e)-(f) show the details of the FFT spectra.

The TF- $\rm\mu$ SR time spectra after subtracting the background signal can be well fitted by the function

A(t)=A_{0}\exp(-\frac{1}{2}{\sigma_{\rm TF}^{2}t}^{2})\cos(\gamma_{\rm\mu}B_{\rm s}t+\varphi_{s}),

(1)

where A₀ is the initial asymmetry of the muon spin in the sample. The Gaussian relaxation rate $\sigma_{\rm TF}$ due to the nuclear dipolar fields in the normal state is enhanced in the superconducting state due to the field broadening generated by the emergence of the flux-line lattice (FLL). $\gamma_{\rm\mu}=8.516$ $\times$ 10⁸ s^-1T^-1 is the gyromagnetic ratio of the muon, and $B_{\rm s}$ is the magnetic field at muon stopping sites.

Figure 2 shows the temperature dependence of $\sigma_{\rm TF}$ obtained from the fits using Eq. (1) for La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.40 and 0.45). There are noticeable upturns in $\sigma_{\rm TF}$ that develop below $T_{c}=2.2$ K and 1.8 K, respectively. The internal field distribution in the vortex state is the convolution of the FLL field distribution and the nuclear dipolar field distribution of the host material:

\sigma_{\rm TF}=\begin{cases}\sqrt{\sigma_{\rm FLL}^{2}+\sigma_{\rm dip}^{2}}&(T\leqslant T_{c})\\ \sigma_{\rm dip}&(T>T_{c})\end{cases}.

(2)

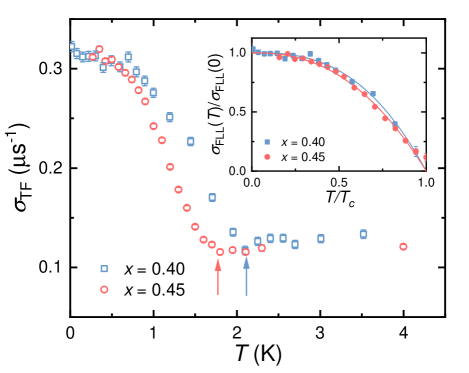
Above $T_{\rm c}$ , $\sigma_{\rm TF}=\sigma_{\rm dip}$ generated from the nuclear dipolar fields is roughly independent of temperature. Therefore, it was fixed to the average value (0.1179(11) $\rm{\mu s^{-1}}$ for $x=0.45$ and 0.127(2) $\rm{\mu s^{-1}}$ for $x=0.40$ ). The value of $\sigma_{\rm dip}$ is smaller for larger $x$ , consistent with the fact that the nuclear magnetic moment of nickel is smaller than that of copper [39].

In the inset of Fig. 2, the normalized FLL relaxation rate $\sigma_{\rm FLL}(T)/\sigma_{\rm FLL}(0)$ is plotted vs. the reduced temperature $T/T_{\rm c}$ for $x=$ 0.40 and 0.45. The data can be fitted with the phenomenological two-fluid model [40, 41]

\sigma_{\rm FLL}(T)=\sigma_{\rm FLL}(0)[1-(T/T_{\rm c})^{N}]\quad(T\leqslant T_{\rm c}).

(3)

The fitting parameters are listed in Table 1. There are several common predictions for the value of $N$ . For traditional BCS superconductors, $N\sim 4$ . However, both values of $N$ for $x=$ 0.40 and 0.45 are much lower than 4. The dirty-limit $d$ -wave model predicts a value of $N=2$ [42, 43]. However, in the La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ system, the upper critical field $H_{\rm c2}(0)$ is estimated to be 3 T [21], giving an estimated value of the Ginzburg-Landau coherence length $\xi(0)=[\Phi_{0}/2\pi H_{c2}(0)]^{1/2}=10.47$ nm, where $\Phi_{0}=2.07\times{10}^{-3}$ Tm² represents the magnetic flux quantum. Given the metallic behavior, the mean free path can be estimated by $l_{e}=\hbar k_{\rm F}/\rho_{0}ne^{2}$ [44], with residual resistivity $\rho_{0}=$ 0.34 $\rm{m\Omega cm}$ [21], yielding $l_{e}$ = 15 nm for $x=0.40$ . Thus, La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ may be a relatively clean superconductor with $\xi/l_{e}\approx 1$ . The predicted clean-limit $d$ -wave model $N$ value is $N=1$ [45]. As a result, our system may include both $s$ and $d$ waves.

Table 1: Parameters from fits to TF-

\rm\mu

SR data using the phenomenological two-fluid model for La

{}_{2}(

Cu_1-xNi_x)₅As₃O₂.

Parameters	$x=0.40$	$x=0.45$
$\sigma_{\rm FLL}(0)~{}(\rm{\mu s^{-1}})$	$0.287(2)$	$0.300(4)$
$T_{c}~{}(\rm{K})$	$2.08(4)$	$1.70(2)$
$N$	$2.72(17)$	$2.38(13)$
$\lambda_{\rm eff}(0)~{}(\rm nm)$	$559.4(1.9)$	$547(3)$
$\lambda_{\rm ab}(0)~{}(\rm nm)$	$427.02(1.49)$	$418(3)$
$\sigma_{\rm dip}~{}(\rm{\mu s^{-1}})$	$0.127(2)$	$0.1179(11)$
Adj. R²	0.98443	0.99172

For powder superconductor samples with $0.13/\kappa^{2}\ll H/H_{\rm c2}\ll 1$ ( $\kappa=\lambda/\xi$ is the Ginzburg-Laudau parameter, $H$ is the applied field), the Gaussian depolarization rate $\sigma_{\rm FLL}$ is directly related to the magnetic penetration depth $\lambda_{\rm eff}$ by [46, 47]

\displaystyle\frac{\sigma_{\rm FLL}}{\gamma_{\mu}}=\frac{0.172(1-b)[1+1.21(1-\sqrt{b})^{3}]\Phi_{0}}{2\pi\lambda_{\rm eff}^{2}},

(4)

where $b$ is the reduced applied field $b=H/H_{\rm c2}=0.01\ll 1$ . Therefore, the absolute values of effective magnetic penetration depth $\lambda_{\rm eff}(0)$ can be obtained and listed in Table 1. In addition, for layered superconductors, the in-plane magnetic penetration depth $\lambda_{\rm ab}(0)$ is also estimated by the relation $\lambda_{\rm eff}(0)=3^{1/4}\lambda_{ab}(0)$ [48, 49, 27].

The effective magnetic penetration depth $\lambda_{\rm eff}$ for isotropic superconductors is related to the density $n_{\rm s}$ of superconducting carriers and $m^{*}$ by the general London equation [40]

\lambda_{\rm{eff}}^{2}=\frac{m^{*}}{\mu_{0}e^{2}n_{\rm s}},

(5)

where $\mu_{0}$ is the magnetic constant, $m^{*}$ is the effective electron mass, and $e$ is the elementary charge. Therefore, the FLL relaxation rate $\sigma_{\rm FLL}$ is directly related to the superfluid density through $\sigma_{\rm FLL}\propto\lambda_{\rm{eff}}^{-2}\propto n_{\rm s}$ . Then we can use microscopic models to investigate the gap symmetry of La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ in more detail, as shown in Fig. 3.

Table 2: Parameters from the fits to the single-gap and two-gap models from TF-

\rm\mu

SR data. The weighting factor of phenomenological two-gap

\alpha

model

f_{\Delta_{1}}

, zero-temperature superconducting gap

\Delta(0)

, zero-temperature magnetic penetration depth

\lambda_{ab}(0)

, and reduced

\rm\chi_{red}^{2}

from fits of Eq. (6) and Eq. (9).

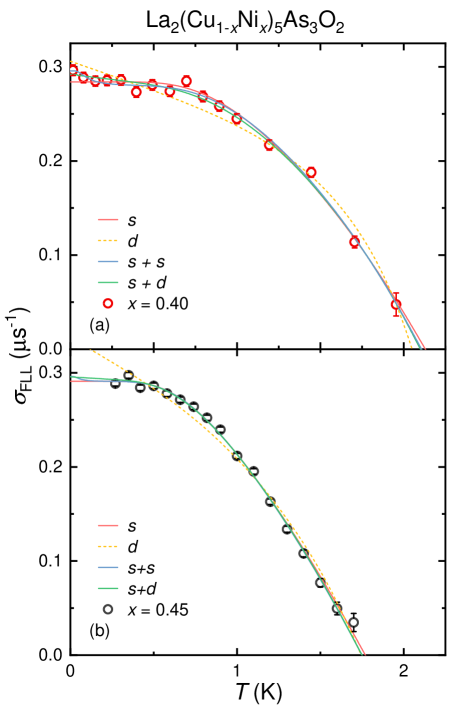
Ni doping	Model	$f_{\Delta_{1}}$	2 $\Delta_{1}/k_{B}T_{c}$	2 $\Delta_{2}/k_{B}T_{c}$	$\lambda_{ab}(0)$ (nm)	$\rm\chi^{2}_{red}$
	$s$	1	3.69(17)		427.4(1.8)	1.74
	$d$	1	6.68(37)		411(3)	4.46
0.40	$s+s$	0.95(3)	3.86(17)	0.20(13)	419(5)	1.31
	$s+d$	0.70(12)	4.03(21)	5.62(7)	422(3)	1.50
	$s$	1	3.34(7)		421.5(1.7)	2.19
	$d$	1	5.09(26)		392(5)	12.9
0.45	$s+s$	0.988(154)	3.42(2)	0.262(2)	420(31)	2.06
	$s+d$	0.976(114)	3.43(3)	4.15(3)	422(5)	2.09

The single-gap model is defined within the local London approximation [50]:

\frac{\sigma_{\rm FLL}(T)}{\sigma_{\rm FLL}(0)}=1+\frac{1}{\pi}\int_{0}^{2\pi}\int_{\Delta(T,\varphi)}^{\infty}\frac{\partial f(E)}{\partial E}\frac{E\ \mathrm{d}E\ \rm{d}\varphi}{\sqrt{E^{2}-\Delta^{2}(T,\varphi)}},

(6)

\Delta(T,\varphi)=\Delta_{0}\delta\left(T/T_{\rm c}\right)g(\varphi),

(7)

\delta\left(T/T_{\rm c}\right)=\tanh\left\{1.82\left[1.018\left(T_{\rm c}/T-1\right)\right]^{0.51}\right\},

(8)

where $\sigma_{\rm FLL}(0)$ is the FLL relaxation rate at zero temperature, $f(E)$ is the Fermi-Dirac distribution function, $\varphi$ is the angle along the Fermi surface, and $\Delta_{0}$ is the maximum superconducting gap value at $T=0$ . $g\left(\varphi\right)$ in Eq. (7) describes the angular dependence of the superconducting gap. Here $g\left(\varphi\right)=1$ and $|\cos(2\varphi)|$ refers to the $s$ -wave and $d$ -wave model, respectively.

The fitting parameters are listed in Table 2. It is clear from Fig. 3 that the $d$ -wave model (the dashed yellow lines) does not fit the data, also evidenced by the largest $\chi^{2}_{\rm red}$ in Table 2. The solid red curves in Fig. 3 representing the $s$ -wave model seem to fit the data well giving the reduced chi-square $\rm\chi^{2}_{red}$ 1.74 and 2.19 for $x$ = 0.40 and 0.45, respectively. Thus our results preliminarily suggest the $s$ -wave pairing for both overdoped and underdoped samples for La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x$ = 0.45, 0.40). $\Delta(0)$ is larger for the optimal doping sample, suggesting the coupling strength decreases with the increase of doping concentration.

However, we notice that the superfluid density of $x=$ 0.40 has a minor upturn at low temperatures. This may be due to nodal or multiband superconductivity. As a result, in addition to single-gap functions, we also employ the phenomenological two-gap $\alpha$ model with a weighting factor $f_{\Delta_{1}}$ [51, 52, 53],

\frac{\sigma_{\rm FLL}(T)}{\sigma_{\rm FLL}(0)}=f_{\Delta_{1}}\frac{\sigma_{\rm FLL,\Delta_{1}}(T)}{\sigma_{\rm FLL,\Delta_{1}}(0)}+(1-f_{\Delta_{1}})\frac{\sigma_{\rm FLL,\Delta_{2}}(T)}{\sigma_{\rm FLL,\Delta_{2}}(0)},

(9)

where ${\sigma_{\rm FLL,\Delta_{i}}^{-2}(T)}/{\sigma_{\rm FLL,\Delta_{i}}^{-2}(0)}~{}(i=1,~{}2)$ is the superfluid density contribution of one of the gaps.

While the smallest $\chi^{2}_{\rm red}$ in both compounds suggests that the $s+s$ model may be the best model, the resulting values of 2 $\Delta_{2}/k_{B}T_{c}$ is unreasonably small. The $s+d$ model is also better than the $s$ -wave model according to the $\chi^{2}_{\rm red}$ values. Moreover, the gap-to- $T_{c}$ ratios 2 $\Delta_{1,2}/k_{B}T_{c}$ determined from the $s+d$ model are also close to the BCS theoretical predictions (2 $\Delta_{s}/k_{B}T_{c}=$ 3.43(3) for $s$ -wave, and 2 $\Delta_{d}/k_{B}T_{c}=$ 4.15(3) for $d$ -wave, respectively) for $x$ = 0.45. Both $s+s$ and $s+d$ models can well deal with the upwarping phenomenon of superfluid density at low temperatures in $x$ = 0.40. However, we also notice that the relaxation rate of $x$ = 0.45 does not show obvious upwarping at the current lowest temperature of 0.27 K. And also the obtained $f_{\Delta_{d}}$ values for both compounds are extremely small. More studies are needed to determine whether $d$ -wave superconductivity exists in one of the bands.

III.2 Uemura Plot

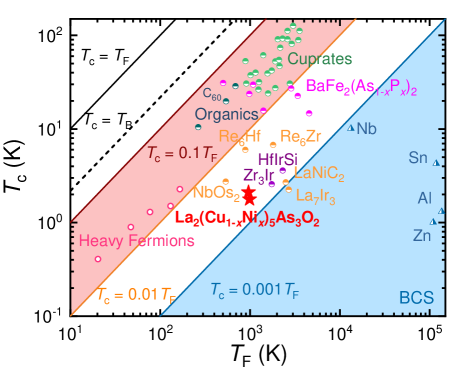
An Uemura plot [54, 55, 56] is shown in Fig. 4, including elemental superconductors (such as Nb, Al, Sn, and Zn), cuprates, alkali-doped C₆₀ (K₃C₆₀ and Rb₃C₆₀), heavy-fermion superconductors, and La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂. In this classification, unconventional superconductors usually lie in the orange area for $1/100\leqslant T_{\rm c}/T_{\rm F}\leqslant 1/10$ , conventional BCS superconductors fall in the blue region for $T_{\rm c}/T_{\rm F}\leqslant 1/1000$ , where $T_{\rm F}$ is the Fermi temperature [40, 55].

For the quasi-2D systems, $T_{\rm F}$ can be estimated by the following relation [40, 58],

k_{\mathrm{B}}T_{\mathrm{F}}=\frac{\pi\hbar^{2}n_{\rm 2D}^{s}}{m^{\ast}},

(10)

where $n_{\rm{2D}}^{s}$ is the two dimensional superfluid density within the superconducting planes derived from the in-plane superfluid density via $n_{\rm{2D}}^{s}=n_{\rm{ab}}^{s}d$ , where $d$ represents the interplanar distance. According to the general London equation Eq. (5), we can get the in-plane superfluid density through $n_{\rm{ab}}^{s}=\frac{m^{*}}{\mu_{0}e^{2}\lambda_{\rm{ab}}^{2}}$ .

Correspondingly,

T_{\rm F}=\frac{\pi\hbar^{2}\lambda_{\rm{ab}}^{-2}d}{k_{\rm B}\mu_{0}e^{2}},

(11)

therefore, $T_{\rm F}$ of La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.45 and 0.40) are estimated, and the results are listed in Table 3. As shown in Fig. 4, La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.40 and 0.45) fall in the crossover between the unconventional superconducting area and the conventional BCS region. The fact that $T_{\rm c}/T_{\rm F}$ is larger in $x=$ 0.40 than 0.45 may suggest a stronger pairing interaction in $x=0.40$ .

Table 3: Uemura plot parameters for La

{}_{2}(

Cu_1-xNi_x)₅As₃O₂

$x$	$\lambda_{\rm{ab}}(0)$ (nm)	$d$ ( $\rm{\AA}$ )	$T_{\rm F}(\rm{K})$	$T_{\rm c}(\rm{K})$	$T_{\rm c}/T_{\rm F}$
0.40	427	22.44	964	2.11	$\sim$ 1/457
0.45	422	22.43	990	1.77	$\sim$ 1/560

III.3 ZF- $\rm\mu$ SR

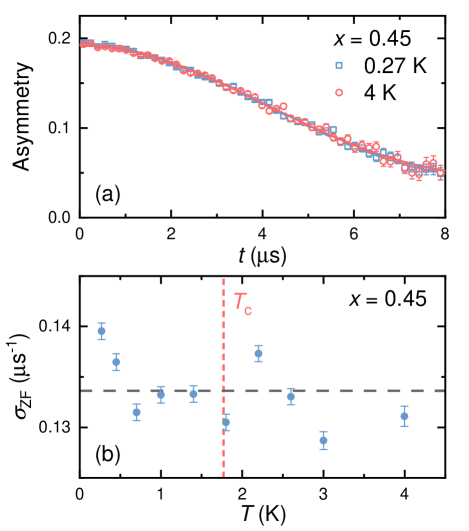
To further investigate the superconductivity in La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂, ZF- $\rm\mu$ SR experiments were performed. Fig. 5 (a) shows the time evolution of the decay positron count asymmetry, which is proportional to the muon spin polarization, at temperatures above and below $T_{c}$ in $x=$ 0.45. There is no noticeable difference between the superconducting and the normal state, suggesting the absence of a spontaneous magnetic field below $T_{c}$ . Therefore, TRS is conserved below the superconducting transition. Over the entire temperature range, the ZF- $\rm\mu$ SR spectra can be well described by the following function,

\frac{A\left(t\right)}{A(0)}=(1-f_{\rm bg})G_{\rm KT}(t)+f_{\rm bg}G_{\rm bg}(t),

(12)

where the two relaxing terms are the signals of the sample and the background. $A(0)$ is the initial total asymmetry at time $t=$ 0, and $f_{\rm bg}$ is the proportion of the background signal, which has the same value as the one in the TF- $\rm\mu$ SR experiments. $G_{\rm KT}(t)$ is the static Gaussian Kubo-Toyabe (KT) function [31]

G_{\rm KT}(\sigma_{\rm ZF},t)=\frac{1}{3}+\frac{2}{3}\left(1-\sigma^{2}_{\rm ZF}t^{2}\right)\exp\left(-\frac{1}{2}\sigma^{2}_{\rm ZF}t^{2}\right),

(13)

where $\sigma_{\rm ZF}$ is the Gaussian KT relaxation rate which corresponds to the relaxation due to static, randomly oriented local fields associated with the nuclear moments at the muon site. Fig. 5 (b) shows that there is no significant change in relaxation rate $\sigma_{\rm ZF}$ down to base temperature $T=0.27$ K. The average value of $\sigma_{\rm ZF}$ is 0.1336 $\mu s^{-1}$ , consistent with the typical nuclear dipolar moments of Ni and Cu [59, 60, 61].

IV DISCUSSION

Low-temperature investigations are crucial for determining the superconducting pairing mechanism. Our TF- $\rm\mu$ SR measurements were performed down to 20 mK, and the temperature dependence of superfluid density suggests that the two-band model best fits the data for both measured samples, one of which is dominated by the $s$ wave and the other in such a small proportion that we cannot confirm whether it is the $s$ wave or the $d$ wave under the current data conditions. The two-band superconductivity scenario is also supported by the density functional theory (DFT) calculations showing that two bands crossing the Fermi energy contribute to the Fermi surface in La₂Cu₅As₃O₂ [21]. Furthermore, the temperature dependence of the upper critical field $H_{c2}(T)$ of La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ exhibits a upward curvature [21], significantly different from the Werthamer-Helfand-Hohenberg relation [62], which may also proposes multi-band superconductivity [63].

BCS superconductivity and Bose-Einstein condensation (BEC) are two asymptotic limits of a fermionic superfluid. Systems with a small $T_{\rm c}/T_{\rm F}$ < 0.001 are usually considered to be BCS-like, while large $T_{\rm c}/T_{\rm F}$ values are expected only in the BEC-like picture and are considered to be a hallmark feature of unconventional superconductivity [54, 64, 40]. As shown in Fig. 4, La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ falls in the crossover area between BCS and exotic superconductors regions, like many other superconductors such as TRS breaking superconductors La₇Ir₃ and LaNiC₂ [60, 65, 57], and multi-band iron-based superconductors BaFe₂(As_1-xP_x)₂ [66]. In the Uemura plot classification scheme, these superconductors may not be traditional electron-phonon coupled BCS superconductors but more like exotic unconventional superconductors.

More experimental evidence is required to investigate whether $d$ -wave superconductivity exists in one of the bands. Table 2 shows that the proportion of $d$ -wave decreases as Ni concentration increases if it does exist. Such a behavior is rare but was observed in layered cuprates La_2-xCe_xCuO_4-y and Pr_2-xCe_xCuO_4-y, where a transition from $d$ - to $s$ -wave pairing occurs near the optimal doping [67]. Also in LaFeAs_1-xP_xO [68], the superconducting order parameter evolves from nodal to nodeless as the doping concentration exceeds 50%. Moreover, a crossover from a nodal to nodeless superconducting energy gap was also suggested in skutterudite PrPt₄Ge₁₂ through Ce substitution [69, 70], although the possibility of a transition from multi-band to single-band superconductivity can not be excluded. In addition, a molecular pairing scenario [45] was proposed to explain the transition from nodal to nodeless superconductivity in Yb-substituted CeCoIn₅ [71]. The Yb doping increases the chemical potential and drives a Lifshitz transition of the nodal Fermi surface, forming a fully gapped molecular superfluid of composite pairs. For La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂, the Fermi pocket around the $\Gamma$ point is relatively small according to the DFT calculations [21], and detailed electronic structure study is required to investigate whether the molecular pairing scenario can be applied.

V Conclusions

In summary, we performed ZF and TF - $\rm\mu$ SR measurements on the recently discovered layered superconductor La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ ( $x=$ 0.40, 0.45). The preservation of TRS is suggested by the ZF- $\rm\mu$ SR measurements. In combination with the $H_{c2}(T)$ data and DFT calculations [21], the temperature dependence of the superfluid density of La ${}_{2}($ Cu_1-xNi_x)₅As₃O₂ measured by TF- $\rm\mu$ SR is best described by the two-band model with the dominant $s$ wave superconducting energy gap larger for optimal doping, suggesting the coupling strength decreases with the increase of doping concentration. Both samples are classified between unusual superconductors and traditional BCS superconductors in the Uemura plot. More experimental evidence is required to investigate whether $d$ -wave superconductivity exists in one of the bands.

Acknowledgements.

This work is based on experiments performed at the Swiss Muon Source S

\mu

S, Paul Scherrer Institute, Villigen, Switzerland, and TRIUMF, Vancouver, Canada. The research performed in this work was supported by the National Key Research and Development Program of China, No. 2022YFA1402203, the National Natural Science Foundations of China, No. 12174065 and No.51922105, and the Shanghai Municipal Science and Technology (Major Project Grant No. 2019SHZDZX01 and No. 20ZR1405300).

References

Luke et al. [1993] G. M. Luke, A. Keren, L. P. Le, W. D. Wu, Y. J. Uemura, D. A. Bonn, L. Taillefer, and J. D. Garrett, Muon spin relaxation in $\mathrm{UPt}_{3}$ , Phys. Rev. Lett. 71, 1466 (1993).
Tsuei and Kirtley [2000] C. C. Tsuei and J. R. Kirtley, Pairing symmetry in cuprate superconductors, Rev. Mod. Phys. 72, 969 (2000).
Kivelson et al. [2003] S. A. Kivelson, I. P. Bindloss, E. Fradkin, V. Oganesyan, J. M. Tranquada, A. Kapitulnik, and C. Howald, How to detect fluctuating stripes in the high-temperature superconductors, Rev. Mod. Phys. 75, 1201 (2003).
Balatsky et al. [2006] A. V. Balatsky, I. Vekhter, and J.-X. Zhu, Impurity-induced states in conventional and unconventional superconductors, Rev. Mod. Phys. 78, 373 (2006).
Onari and Kontani [2009] S. Onari and H. Kontani, Violation of Anderson’s theorem for the sign-reversing $s$ -wave state of iron-pnictide superconductors, Phys. Rev. Lett. 103, 177001 (2009).
Hanaguri et al. [2010] T. Hanaguri, S. Niitaka, K. Kuroki, and H. Takagi, Unconventional $s$ -wave superconductivity in Fe(Se,Te), Science 328, 474 (2010).
Wu et al. [2011] T. Wu, H. Mayaffre, S. Krämer, M. Horvatić, C. Berthier, W. N. Hardy, R. Liang, D. A. Bonn, and M.-H. Julien, Magnetic-field-induced charge-stripe order in the high-temperature superconductor $\mathrm{YBa}_{2}\mathrm{Cu}_{3}\mathrm{O}_{y}$ , Nature 477, 191 (2011).
Guguchia et al. [2014] Z. Guguchia, R. Khasanov, M. Bendele, E. Pomjakushina, K. Conder, A. Shengelaya, and H. Keller, Negative oxygen isotope effect on the static spin stripe order in superconducting ${\mathrm{La}}_{2-x}{\mathrm{Ba}}_{x}{\mathrm{CuO}}_{4}(x=1/8)$ observed by muon-spin rotation, Phys. Rev. Lett. 113, 057002 (2014).
Sarkar et al. [2020] T. Sarkar, D. S. Wei, J. Zhang, N. R. Poniatowski, P. R. Mandal, A. Kapitulnik, and R. L. Greene, Ferromagnetic order beyond the superconducting dome in a cuprate superconductor, Science 368, 532 (2020).
Hayes et al. [2021] I. M. Hayes, D. S. Wei, T. Metz, J. Zhang, Y. S. Eo, S. Ran, S. R. Saha, J. Collini, N. P. Butch, D. F. Agterberg, A. Kapitulnik, and J. Paglione, Multicomponent superconducting order parameter in UTe₂, Science 373, 797 (2021).
Nachumi et al. [1996] B. Nachumi, A. Keren, K. Kojima, M. Larkin, G. M. Luke, J. Merrin, O. Tchernyshöv, Y. J. Uemura, N. Ichikawa, M. Goto, and S. Uchida, Muon spin relaxation studies of Zn-substitution effects in high- ${T}_{\mathit{c}}$ cuprate superconductors, Phys. Rev. Lett. 77, 5421 (1996).
Smith et al. [2001] C. M. Smith, A. H. Castro Neto, and A. V. Balatsky, ${T}_{c}$ suppression in Co-doped striped cuprates, Phys. Rev. Lett. 87, 177010 (2001).
Yang et al. [2013] H. Yang, Z. Wang, D. Fang, Q. Deng, Q. H. Wang, Y. Y. Xiang, Y. Yang, and H. H. Wen, In-gap quasiparticle excitations induced by non-magnetic Cu impurities in Na(Fe(0.96)Co(0.03)Cu(0.01))As revealed by scanning tunnelling spectroscopy, Nat. Commun. 4, 2749 (2013).
Guguchia et al. [2017] Z. Guguchia, B. Roessli, R. Khasanov, A. Amato, E. Pomjakushina, K. Conder, Y. J. Uemura, J. M. Tranquada, H. Keller, and A. Shengelaya, Complementary response of static spin-stripe order and superconductivity to nonmagnetic impurities in cuprates, Phys. Rev. Lett. 119, 087002 (2017).
Suhl and Matthias [1959] H. Suhl and B. T. Matthias, Impurity scattering in superconductors, Phys. Rev. 114, 977 (1959).
Anderson [1959] P. Anderson, Theory of dirty superconductors, J. Phys. Chem. Solids 11, 26 (1959).
Li et al. [2009] L. J. Li, Y. K. Luo, Q. B. Wang, H. Chen, Z. Ren, Q. Tao, Y. K. Li, X. Lin, M. He, Z. W. Zhu, G. H. Cao, and Z. A. Xu, Superconductivity induced by Ni doping in BaFe₂As₂ single crystals, New J. Phys. 11, 025008 (2009).
Stewart [2011] G. R. Stewart, Superconductivity in iron compounds, Rev. Mod. Phys. 83, 1589 (2011).
Ideta et al. [2013] S. Ideta, T. Yoshida, I. Nishi, A. Fujimori, Y. Kotani, K. Ono, Y. Nakashima, S. Yamaichi, T. Sasagawa, M. Nakajima, K. Kihou, Y. Tomioka, C. H. Lee, A. Iyo, H. Eisaki, T. Ito, S. Uchida, and R. Arita, Dependence of carrier doping on the impurity potential in transition-metal-substituted FeAs-based superconductors, Phys. Rev. Lett. 110, 107007 (2013).
Dai [2015] P. Dai, Antiferromagnetic order and spin dynamics in iron-based superconductors, Rev. Mod. Phys. 87, 855 (2015).
Chen et al. [2019] X. Chen, J. Guo, C. Gong, E. Cheng, C. Le, N. Liu, T. Ying, Q. Zhang, J. Hu, S. Li, and X. Chen, Anomalous dome-like superconductivity in RE₂(Cu_1-xNi_x)₅As₃O₂ (RE = La, Pr, Nd), iScience 14, 171 (2019).
Wu et al. [1996] X. Wu, S. Jiang, F. Pan, J. Lin, N. Xu, Mao Zhiqiang, Xu Gaoji, and Zhang Yuheng, Microstructures of La_1.85Sr_0.15CuO₄ doped with Ni at high doping level, Physica C Supercond. 271, 331 (1996).
Itoh et al. [2002] Y. Itoh, S. Adachi, T. Machi, Y. Ohashi, and N. Koshizuka, Ni-substituted sites and the effect on Cu electron spin dynamics of ${\mathrm{YBa}}_{2}{\mathrm{Cu}}_{3-x}{\mathrm{Ni}}_{x}{\mathrm{O}}_{7-\delta}$ , Phys. Rev. B 66, 134511 (2002).
Hillier et al. [2022] A. D. Hillier, S. J. Blundell, I. McKenzie, I. Umegaki, L. Shu, J. A. Wright, T. Prokscha, F. Bert, K. Shimomura, A. Berlie, H. Alberto, and I. Watanabe, Muon spin spectroscopy, Nat. Rev. Methods Primers 2, 5 (2022).
Alain Yaouanc [2010] P. D. d. R. Alain Yaouanc, Muon spin rotation, relaxation and resonance, Oxford University Press (2010).
Sonier et al. [2011] J. E. Sonier, W. Huang, C. V. Kaiser, C. Cochrane, V. Pacradouni, S. A. Sabok-Sayr, M. D. Lumsden, B. C. Sales, M. A. McGuire, A. S. Sefat, and D. Mandrus, Magnetism and disorder effects on muon spin rotation measurements of the magnetic penetration depth in iron-arsenic superconductors, Phys. Rev. Lett. 106, 127002 (2011).
Zhang et al. [2016] J. Zhang, K. Huang, Z. F. Ding, D. E. MacLaughlin, O. O. Bernal, P.-C. Ho, C. Tan, X. Liu, D. Yazici, M. B. Maple, and L. Shu, Superconducting gap structure in ambient-pressure-grown ${\mathrm{LaO}}_{0.5}{\mathrm{F}}_{0.5}{\mathrm{BiS}}_{2}$ , Phys. Rev. B 94, 224502 (2016).
Zhang et al. [2018] J. Zhang, Z. Ding, C. Tan, K. Huang, O. O. Bernal, P.-C. Ho, G. D. Morris, A. D. Hillier, P. K. Biswas, S. P. Cottrell, H. Xiang, X. Yao, D. E. MacLaughlin, and L. Shu, Discovery of slow magnetic fluctuations and critical slowing down in the pseudogap phase of YBa₂Cu₃O_y, Sci. Adv. 4, eaao5235 (2018).
Tan et al. [2018] C. Tan, T. P. Ying, Z. F. Ding, J. Zhang, D. E. MacLaughlin, O. O. Bernal, P. C. Ho, K. Huang, I. Watanabe, S. Y. Li, and L. Shu, Nodal superconductivity coexists with low-moment static magnetism in single-crystalline tetragonal FeS: A muon spin relaxation and rotation study, Phys. Rev. B 97, 174524 (2018).
Zhu et al. [2022] Z. H. Zhu, C. Tan, J. Zhang, P. K. Biswas, A. D. Hillier, M. X. Wang, Y. X. Yang, C. S. Chen, Z. F. Ding, S. Y. Li, and L. Shu, Muon spin rotation and relaxation study on topological noncentrosymmetric superconductor PbTaSe₂, New J. Phys. 24, 023002 (2022).
Hayano et al. [1979] R. S. Hayano, Y. J. Uemura, J. Imazato, N. Nishida, T. Yamazaki, and R. Kubo, Zero-and low-field spin relaxation studied by positive muons, Phys. Rev. B 20, 850 (1979).
Amato [1997] A. Amato, Heavy-fermion systems studied by $\mu$ SR technique, Rev. Mod. Phys. 69, 1119 (1997).
Aoki et al. [2003] Y. Aoki, A. Tsuchiya, T. Kanayama, S. R. Saha, H. Sugawara, H. Sato, W. Higemoto, A. Koda, K. Ohishi, K. Nishiyama, and R. Kadono, Time-reversal symmetry-breaking superconductivity in heavy-fermion ${\mathrm{P}\mathrm{r}\mathrm{O}\mathrm{s}}_{4}{\mathrm{S}\mathrm{b}}_{12}$ detected by muon-spin relaxation, Phys. Rev. Lett. 91, 067003 (2003).
Neha et al. [2019] P. Neha, P. K. Biswas, T. Das, and S. Patnaik, Time-reversal symmetry breaking in topological superconductor ${\mathrm{Sr}}_{0.1}{\mathrm{Bi}}_{2}{\mathrm{Se}}_{3}$ , Phys. Rev. Materials 3, 074201 (2019).
Suter and Wojek [2012] A. Suter and B. Wojek, Musrfit: A free platform-independent framework for $\mu$ SR data analysis, Physics Procedia 30, 69 (2012), 12th International Conference on Muon Spin Rotation, Relaxation and Resonance ( $\mu$ SR2011).
Karl et al. [2019] R. Karl, F. Burri, A. Amato, M. Donegà, S. Gvasaliya, H. Luetkens, E. Morenzoni, and R. Khasanov, Muon spin rotation study of type-I superconductivity: Elemental $\beta$ -Sn, Phys. Rev. B 99, 184515 (2019).
Weber et al. [1993] M. Weber, A. Amato, F. N. Gygax, A. Schenck, H. Maletta, V. N. Duginov, V. G. Grebinnik, A. B. Lazarev, V. G. Olshevsky, V. Y. Pomjakushin, S. N. Shilov, V. A. Zhukov, B. F. Kirillov, A. V. Pirogov, A. N. Ponomarev, V. G. Storchak, S. Kapusta, and J. Bock, Magnetic-flux distribution and the magnetic penetration depth in superconducting polycrystalline ${\mathrm{Bi}}_{2}$ ${\mathrm{Sr}}_{2}$ ${\mathrm{Ca}}_{1\mathrm{-}\mathit{x}}$ ${\mathrm{Y}}_{\mathit{x}}$ ${\mathrm{Cu}}_{2}$ ${\mathrm{O}}_{8+\mathrm{\delta}}$ and ${\mathrm{Bi}}_{2\mathrm{-}\mathit{x}}$ ${\mathrm{Pb}}_{\mathit{x}}$ ${\mathrm{Sr}}_{2}$ ${\mathrm{CaCu}}_{2}$ ${\mathrm{O}}_{8+\mathrm{\delta}}$ , Phys. Rev. B 48, 13022 (1993).
Maisuradze et al. [2009a] A. Maisuradze, R. Khasanov, A. Shengelaya, and H. Keller, Comparison of different methods for analyzing $\mu$ SR line shapes in the vortex state of type-II superconductors, Journal of Physics: Condensed Matter 21, 075701 (2009a).
N.W.Ashcroft [1976] N. M. N.W.Ashcroft, Solid state physics (Saunders College Publishing, 1976) pp. 657–658.
Hillier and Cywinski [1997] A. D. Hillier and R. Cywinski, The classification of superconductors using muon spin rotation, Appl. Magn. Reson. 13, 95 (1997).
Ding et al. [2019] Z. F. Ding, J. Zhang, C. Tan, K. Huang, Q. Y. Chen, I. Lum, O. O. Bernal, P.-C. Ho, D. E. MacLaughlin, M. B. Maple, and L. Shu, Renormalizations in unconventional superconducting states of ${\mathrm{Ce}}_{1-x}{\mathrm{Yb}}_{x}{\mathrm{CoIn}}_{5}$ , Phys. Rev. B 99, 035136 (2019).
Luetkens et al. [2008] H. Luetkens, H.-H. Klauss, R. Khasanov, A. Amato, R. Klingeler, I. Hellmann, N. Leps, A. Kondrat, C. Hess, A. Köhler, G. Behr, J. Werner, and B. Büchner, Field and temperature dependence of the superfluid density in ${\mathrm{LaFeAsO}}_{1-x}{\mathrm{F}}_{x}$ superconductors: A muon spin relaxation study, Phys. Rev. Lett. 101, 097009 (2008).
Hirschfeld et al. [1994] P. J. Hirschfeld, W. O. Putikka, and D. J. Scalapino, $d$ -wave model for microwave response of high- ${T}_{c}$ superconductors, Phys. Rev. B 50, 10250 (1994).
Wang et al. [2022] Y. Wang, M. Li, C. Pei, L. Gao, K. Bu, D. Wang, X. Liu, L. Yan, J. Qu, N. Li, B. Wang, Y. Fang, Y. Qi, and W. Yang, Critical current density and vortex phase diagram in the superconductor ${\mathrm{Sn}}_{0.55}{\mathrm{In}}_{0.45}\mathrm{Te}$ , Phys. Rev. B 106, 054506 (2022).
Erten et al. [2015] O. Erten, R. Flint, and P. Coleman, Molecular pairing and fully gapped superconductivity in Yb-doped ${\mathrm{CeCoIn}}_{5}$ , Phys. Rev. Lett. 114, 027002 (2015).
Brandt [1988] E. H. Brandt, Flux distribution and penetration depth measured by muon spin rotation in high- ${T}_{c}$ superconductors, Phys. Rev. B 37, 2349 (1988).
Brandt [2003] E. H. Brandt, Properties of the ideal Ginzburg-Landau vortex lattice, Phys. Rev. B 68, 10.1103/PhysRevB.68.054506 (2003).
Barford and Gunn [1988] W. Barford and J. Gunn, The theory of the measurement of the London penetration depth in uniaxial type II superconductors by muon spin rotation, Physica C Supercond. 156, 515 (1988).
Fesenko et al. [1991] V. Fesenko, V. Gorbunov, and V. Smilga, Analytical properties of muon polarization spectra in type-II superconductors and experimental data interpretation for mono- and polycrystalline HTSCs, Physica C Supercond. 176, 551 (1991).
Si et al. [2010] W. Si, Q. Jie, L. Wu, J. Zhou, G. Gu, P. D. Johnson, and Q. Li, Superconductivity in epitaxial thin films of Fe_1.08Te:O_x, Phys. Rev. B 81, 092506 (2010).
Padamsee et al. [1973] H. Padamsee, J. E. Neighbor, and C. A. Shiffman, Quasiparticle phenomenology for thermodynamics of strong-coupling superconductors, J. Low Temp. Phys. 12, 387 (1973).
Carrington and Manzano [2003] A. Carrington and F. Manzano, Magnetic penetration depth of MgB₂, Physica C Supercond. 385, 205 (2003).
Khasanov et al. [2007] R. Khasanov, A. Shengelaya, A. Maisuradze, F. L. Mattina, A. Bussmann-Holder, H. Keller, and K. A. Müller, Experimental evidence for two gaps in the high-temperature La_1.83Sr_0.17CuO₄ superconductor, Phys. Rev. Lett. 98, 057007 (2007).
Uemura et al. [1989] Y. J. Uemura, G. M. Luke, B. J. Sternlieb, J. H. Brewer, J. F. Carolan, W. N. Hardy, R. Kadono, J. R. Kempton, R. F. Kiefl, S. R. Kreitzman, P. Mulhern, T. M. Riseman, D. L. Williams, B. X. Yang, S. Uchida, H. Takagi, J. Gopalakrishnan, A. W. Sleight, M. A. Subramanian, C. L. Chien, M. Z. Cieplak, G. Xiao, V. Y. Lee, B. W. Statt, C. E. Stronach, W. J. Kossler, and X. H. Yu, Universal correlations between ${T}_{c}$ and $\frac{{n}_{s}}{{m}^{*}}$ (carrier density over effective mass) in high- ${T}_{c}$ cuprate superconductors, Phys. Rev. Lett. 62, 2317 (1989).
Uemura [2004] Y. J. Uemura, Condensation, excitation, pairing, and superfluid density in high- ${T}_{c}$ superconductors: the magnetic resonance mode as a roton analogue and a possible spin-mediated pairing, J. Phys. Condens. Matter 16, S4515 (2004).
Nakagawa et al. [2021] Y. Nakagawa, Y. Kasahara, T. Nomoto, R. Arita, T. Nojima, and Y. Iwasa, Gate-controlled BCS-BEC crossover in a two-dimensional superconductor, Science 372, 190 (2021).
Barker et al. [2018] J. A. T. Barker, B. D. Breen, R. Hanson, A. D. Hillier, M. R. Lees, G. Balakrishnan, D. M. Paul, and R. P. Singh, Superconducting and normal-state properties of the noncentrosymmetric superconductor $\mathrm{Re}_{3}\mathrm{Ta}$ , Phys. Rev. B 98, 104506 (2018).
Benfatto et al. [2001] L. Benfatto, S. Caprara, C. Castellani, A. Paramekanti, and M. Randeria, Phase fluctuations, dissipation, and superfluid stiffness in $d$ -wave superconductors, Phys. Rev. B 63, 174513 (2001).
Luke et al. [1991] G. M. Luke, J. H. Brewer, S. R. Kreitzman, D. R. Noakes, M. Celio, R. Kadono, and E. J. Ansaldo, Muon diffusion and spin dynamics in copper, Phys. Rev. B 43, 3284 (1991).
Hillier et al. [2009] A. D. Hillier, J. Quintanilla, and R. Cywinski, Evidence for time-reversal symmetry breaking in the noncentrosymmetric superconductor ${\mathrm{LaNiC}}_{2}$ , Phys. Rev. Lett. 102, 117007 (2009).
K. P. et al. [2020] S. K. P., D. Singh, A. D. Hillier, and R. P. Singh, Probing nodeless superconductivity in $\mathrm{La}{M}\mathrm{Si}$ ( ${M}=\mathrm{Ni}$ , Pt) using muon-spin rotation and relaxation, Phys. Rev. B 102, 094515 (2020).
Werthamer et al. [1966] N. R. Werthamer, E. Helfand, and P. C. Hohenberg, Temperature and purity dependence of the superconducting critical field, ${H}_{c2}$ . III. Electron spin and spin-orbit effects, Phys. Rev. 147, 295 (1966).
Hunte et al. [2008] F. Hunte, J. Jaroszynski, A. Gurevich, D. C. Larbalestier, R. Jin, A. S. Sefat, M. A. McGuire, B. C. Sales, D. K. Christen, and D. Mandrus, Two-band superconductivity in LaFeAsO_0.89F_0.11 at very high magnetic fields, Nature 453, 903 (2008).
Uemura et al. [1991] Y. J. Uemura, L. P. Le, G. M. Luke, B. J. Sternlieb, W. D. Wu, J. H. Brewer, T. M. Riseman, C. L. Seaman, M. B. Maple, M. Ishikawa, D. G. Hinks, J. D. Jorgensen, G. Saito, and H. Yamochi, Basic similarities among cuprate, bismuthate, organic, chevrel-phase, and heavy-fermion superconductors shown by penetration-depth measurements, Phys. Rev. Lett. 66, 2665 (1991).
Barker et al. [2015] J. A. T. Barker, D. Singh, A. Thamizhavel, A. D. Hillier, M. R. Lees, G. Balakrishnan, D. M. Paul, and R. P. Singh, Unconventional superconductivity in La₇Ir₃ revealed by muon spin relaxation: Introducing a new family of noncentrosymmetric superconductor that breaks time-reversal symmetry, Phys. Rev. Lett. 115, 267001 (2015).
Hashimoto et al. [2012] K. Hashimoto, K. Cho, T. Shibauchi, S. Kasahara, Y. Mizukami, R. Katsumata, Y. Tsuruhara, T. Terashima, H. Ikeda, M. A. Tanatar, H. Kitano, N. Salovich, R. W. Giannetta, P. Walmsley, A. Carrington, R. Prozorov, and Y. Matsuda, A sharp peak of the zero-temperature penetration depth at optimal composition in BaFe₂(As_1-xP_x)₂, Science 336, 1554 (2012).
Skinta et al. [2002] J. A. Skinta, M.-S. Kim, T. R. Lemberger, T. Greibe, and M. Naito, Evidence for a transition in the pairing symmetry of the electron-doped cuprates La_2-xCe_xCuO_4-y and Pr_2-xCe_xCuO_4-y, Phys. Rev. Lett. 88, 207005 (2002).
Shiroka et al. [2018] T. Shiroka, N. Barbero, R. Khasanov, N. D. Zhigadlo, H. R. Ott, and J. Mesot, Nodal-to-nodeless superconducting order parameter in LaFeAs_1-xP_xO synthesized under high pressure, npj Quant Mater 3, 25 (2018).
Maisuradze et al. [2009b] A. Maisuradze, M. Nicklas, R. Gumeniuk, C. Baines, W. Schnelle, H. Rosner, A. Leithe-Jasper, Y. Grin, and R. Khasanov, Superfluid density and energy gap function of superconducting $\mathrm{PrPt}_{4}\mathrm{Ge}_{12}$ , Phys. Rev. Lett. 103, 147002 (2009b).
Huang et al. [2014] K. Huang, L. Shu, I. K. Lum, B. D. White, M. Janoschek, D. Yazici, J. J. Hamlin, D. A. Zocco, P.-C. Ho, R. E. Baumbach, and M. B. Maple, Probing the superconductivity of $\mathrm{PrPt}_{4}\mathrm{Ge}_{12}$ through Ce substitution, Phys. Rev. B 89, 035145 (2014).
Kim et al. [2015] H. Kim, M. A. Tanatar, R. Flint, C. Petrovic, R. Hu, B. D. White, I. K. Lum, M. B. Maple, and R. Prozorov, Nodal to nodeless superconducting energy-gap structure change concomitant with fermi-surface reconstruction in the heavy-fermion compound $\mathrm{CeCoIn}_{5}$ , Phys. Rev. Lett. 114, 027003 (2015).

Superconducting Properties of La(2{}_{2}(Cu1-xNix)5As3O2: A μ\rm\muSR Study