Superfluid transition temperature of bond bipolarons with Coulomb interaction
Abstract
Utilizing an exactly sign-problem-free quantum Monte Carlo method, we explore the influence of long-range Coulomb interaction on the superfluid transition temperature of bipolarons in a two dimensional square lattice. The model studied here is the bond Su-Schrieffer-Heeger model with phonon-modulated electron hopping. Previously, in the absence of long-range Coulomb interaction, this model demonstrated the emergence of small-size, light-mass bipolarons that undergo a superfluid transition at high values of the transition temperature [Physical Review X 13, 011010, (2023)]. Our findings indicate that with the long-range Coulomb interaction, remains relatively high, even in the deep adiabatic regime where the phonon frequency and the Coulomb interaction . This result suggests a relatively high superfluid transition temperature for bond bipolarons with long range Coulomb interaction in the low-density regime, which could provide a new insights for the future experiments on dilute superconductors.
I Introduction
Electron-phonon coupling is a fundamental interaction within condensed matter physics, giving rise to a variety of intriguing phenomena. This coupling reflects the intricate relationship between the dynamic behavior of electrons, which are the charge carriers, and the vibrational modes of the crystal lattice, known as phonons. The consequences of this interaction lead to significant modifications in electronic properties, such as the formation of polaron and bipolaron Landau (1933); H. Fröhlich and Zienau (1950); Feynman (1955); Schultz (1959); Holstein (1959); Alexandrov and Kornilovitch (1999); Holstein (2000), changes in the effective mass of charge carriers Chakraverty et al. (1998); Bonča et al. (2000); Macridin et al. (2004), and variations in charge carrier mobility and scattering Prodanović and Vukmirović (2019). The polaron, formed through electron-phonon coupling, is particularly significant due to its connection to the mechanism of high-temperature superconductivity in the dilute-density regime. Under low-density conditions, electron-phonon interactions can pair two electrons into a single bipolaron, akin to the formation of a Bose-Einstein condensate-like superconductor. For such a superconducting state to occur, specific conditions must be met, including the presence of a bipolaron with a light effective mass, compact size, and a strong phonon-mediated pairing potential Zhang et al. (2023a); Sous et al. (2023).
Depending on whether the phonon vibrations are coupled to the electron density or the hopping motion of the electron, two primary types of electron-phonon coupling exist: the Holstein and bond Su-Schrieffer-Heeger (SSH) models. Extensive prior research has revealed that in the Holstein model, where phonons couple to electrons through density, the effective mass of both polaron and bipolaron grows exponentially at higher electron-phonon coupling strengths Kornilovitch and Pike (1997); Marchand et al. (2010); Bonča et al. (2000); Macridin et al. (2004). In stark contrast, the scenario changes significantly when considering the bond SSH model, where phonons couple to electrons through the hopping of electrons. Recent investigations into bond SSH polarons have garnered substantial interest, chiefly due to the remarkable characteristic of a relatively light effective mass even in strong coupling regimes, resulting in a lightweight polaron Marchand et al. (2010); Zhang et al. (2021); Carbone et al. (2021); Sous et al. (2018); Kim et al. (2024). Moreover, the bond SSH type of electron-phonon coupling holds significant promise for bipolaronic superconductivity because, for a single polaron, the effective mass remains light even in the presence of Holstein-type electron-phonon coupling Zhang (2024) and with dispersive phonons Zhang (2023), which are more relevant to real materials. The light effective mass of the polaron in the strong electron-phonon coupling regime suggests the possibility of a light effective mass bipolaron, which could lead to the formation of a Bose-Einstein condensate-like superconductor in the low-density limit.
References Zhang et al. (2023a); Sous et al. (2023) investigate the Bose-Einstein condensation of bipolarons using the bond SSH model. In the absence of long-range Coulomb repulsion, this model has recently been shown to form small-size, light-mass bipolarons that undergo a superfluid transition at high values of the critical transition temperature Zhang et al. (2023a) in two dimensions. Reference Sous et al. (2023) demonstrates that in three dimensions, even with the inclusion of long-range Coulomb repulsion, remains significantly higher than that of Holstein bipolaron and can be on the order of, or greater than, the typical upper bounds for phonon-mediated based on McMillan approximations. However, it raises the question of the extent to which the high for bond bipolaron persists in two dimensions with long-range Coulomb interaction. Additionally, it is important to know the adiabatic regimes in which this high could exist and the strength of the Coulomb interaction that can be tolerated while maintaining a high . These considerations are crucial for understanding the bond SSH bipolaron model as a mechanism for high-temperature superconductivity in low-dimensional systems for real materials since in real materials, the Coulomb interaction between electrons can not be neglected.
In this paper, we investigate the effects of long-range Coulomb interaction on the superfluid transition temperature of the bond SSH bipolaron model in two dimensions using a newly developed Quantum Monte Carlo method. Our approach is based on the path-integral formulation of the particle sector combined with real space diagrammatic techniques for the phonon sector Zhang et al. (2022). The results show that, in general, the long-range Coulomb interaction reduces . Despite this reduction, remains relatively high at and with . The combination of light mass and relatively small size of bipolarons, even in the presence of long-range Coulomb repulsion, accounts for the robustness of this mechanism and the relatively high values of observed.
The rest of this paper is organized as follows. In Sec. II, we present the Hamiltonian of the bond SSH model. In Sec. III, we introduce the method and the properties measured for the bipolaron. In Sec. IV, we present the expression for the superfluid transition temperature of the bipolaron model. In Sec. V, we discuss the results, and Sec. VI concludes the paper.
II Hamiltonian
We consider a bond SSH electron-phonon coupling on a two-dimensional square lattice. In this model, the electronic hopping between two sites is modulated by a single oscillator centered on the bond connecting these two sites. The model is described by the Hamiltonian Su et al. (1979); Barišić et al. (1970); Barišić (1972a, b):
| (1) | ||||
with the hopping amplitude of the electron. denotes the nearest neighbor sites. () is the electron creation (annihilation) operators on site with spin , and () is the phonon creation (annihilation) operators on bond connected site and site . is the on-site Hubbard repulsion and if not mentioned specifically, is fixed. is the nearest neighbor repulsion, and the long-range repulsive . and at site , and is the lattice constant. is the phonon frequency and is the electron-phonon coupling strength of the bond SSH type. is the oscillator associated with the bond connecting site and .
The properties of the bond SSH polaron and bipolaron is controlled by two parameters: (i) the effective coupling with the dimensionality of the system and , is a dimensionless parameter, and (ii) the adiabaticity ratio . The most interesting adiabatic regime is , where the phonon degree of freedom is considered comparable or slow with respect to the electron motion. We analyze the model’s behavior for two values of and 1.0 which are significantly smaller than the bare electronic bandwidth in 2D. Simulating values of smaller than 0.5, as well as larger Coulomb interaction poses a computational challenge since with this lower phonon frequency or larger Coulomb interaction, the bipolaron effective masses are found to be extremely large and hard to determine reliably. In the following, we focus on results for and 1.0. Without specific explanation, we choose based on the findings in Ref. Zhang et al. (2023a), which demonstrates that exhibits a dome-like dependence on . For a given electron-phonon coupling , peaks around the value of , which shows minimal variation with in two dimensions. Additionally, represents a regime where there is strong competition between the on-site Hubbard repulsion and the electronic kinetic energy.
III Method
By employing a Quantum Monte Carlo (QMC) approach based on a path-integral formulation for the electronic sector and utilizing a real-space diagrammatic representation for the phonon sector Zhang et al. (2022), we investigate the singlet bipolaron formation in the two-electron sector of the model 1. The study of this specific bipolaron model is free from the sign problem, allowing us to achieve numerically exact results with minimal statistical errors on large lattices, even in the challenging regime where . We simulate the model on a two-dimensional square lattice with a linear size of sites and open boundary conditions. This system size is sufficient to reach the thermodynamic limit and eliminate boundary effects.
The bipolaron energy at momentum and its typical size can be extracted from the pair Green’s function
| (2) |
where and are the center of mass and relative distance between the two electrons, respectively. In the asymptotic limit, the Green’s function is projected to the ground state in the corresponding momentum sector, as follows from the spectral Lehman representation. For the stable (non-decaying) quasiparticle state, we have
| (3) |
In this paper, we measure the properties of the bipolaron like the binding energy, effective mass, and bipolaron size.
Binding energy: the binding energy is defined as with the single polaron energy.
Effective mass: the bipolaron effective mass is defined as at momentum .
Mean-square radius: the bipolaron mean-square radius is defined as with the bipolaron ground-state wave function. To get the structure of the bound state, in simulations, we simply collect statistics for finding two electrons at a distance in the middle of the large- pair trajectory. The bipolaron mean squared-radius is then defined as , where is the probability of finding two electrons at a given distance in the ground state.
IV Superfluid transition temperature of bipolarons
A dilute system of electrons, at strong enough electron-phonon coupling, is unstable to the formation of bipolaron, leading to the formation of a gas of interacting bosons. These interacting bosons undergo a superfluid transition at the critical temperature . Remarkably, when only the short-range/onsite interactions between bipolarons are considered, this temperature dependence exhibits a weak double-logarithmic relationship with the effective bipolaron-bipolaron interactions Fisher and Hohenberg (1988); Prokof’ev et al. (2001); Pilati et al. (2008). In the presence of long-range Coulomb interaction, the value of is reduced by around Zhang et al. (2023b). Hence, unless competing instabilities such as phase separation or Wigner crystallization are present (based on previous research, these instabilities are improbable), we can safely assume a reduction in when considering the Coulomb interaction between bipolarons.
With these considerations in mind, our focus shifts to analyzing the superfluidity of a gas comprising hard-core bipolarons with long-range Coulomb interactions in a two-dimensional lattice. Here, the critical temperature is approximated by the expression
| (4) |
where represents the density of bipolarons and denotes the effective mass of the bipolaron. The coefficient accounts for the reduction in due to the long-range Coulomb interaction between bipolarons Zhang et al. (2023b). This formula holds true across a wide density range, provided that bipolarons do not overlap.
The maximum achievable through this mechanism occurs when the density corresponds to a bosonic liquid with an interparticle spacing approximately equal to the radial size of the bipolaron , which, post lattice regularization, must be at least unity. Thus, can be estimated as . From this, we derive an estimate for the maximum of the Berezinskii-Kosterlitz-Thouless (BKT) transition of the bipolaronic liquid, dependent solely on bipolaron properties by
| (5) |
with when the bipolarons are interacting with the long-range Coulomb interaction and 1 without long-range Coulomb interaction. The factor is choosen to be consistent with the results in Ref Zhang et al. (2023a). We henceforth refer to this optimized simply as in subsequent discussions and figures.
In summary, bipolarons experience a superfluid transition at a temperature determined by the properties of a single bipolaron, with the bipolaron size and effective mass calculated using the QMC method in section III. When considering the long-range Coulomb interaction between bipolarons, the superfluid transition temperature is reduced by a factor of Zhang et al. (2023b).
V Results and discussion
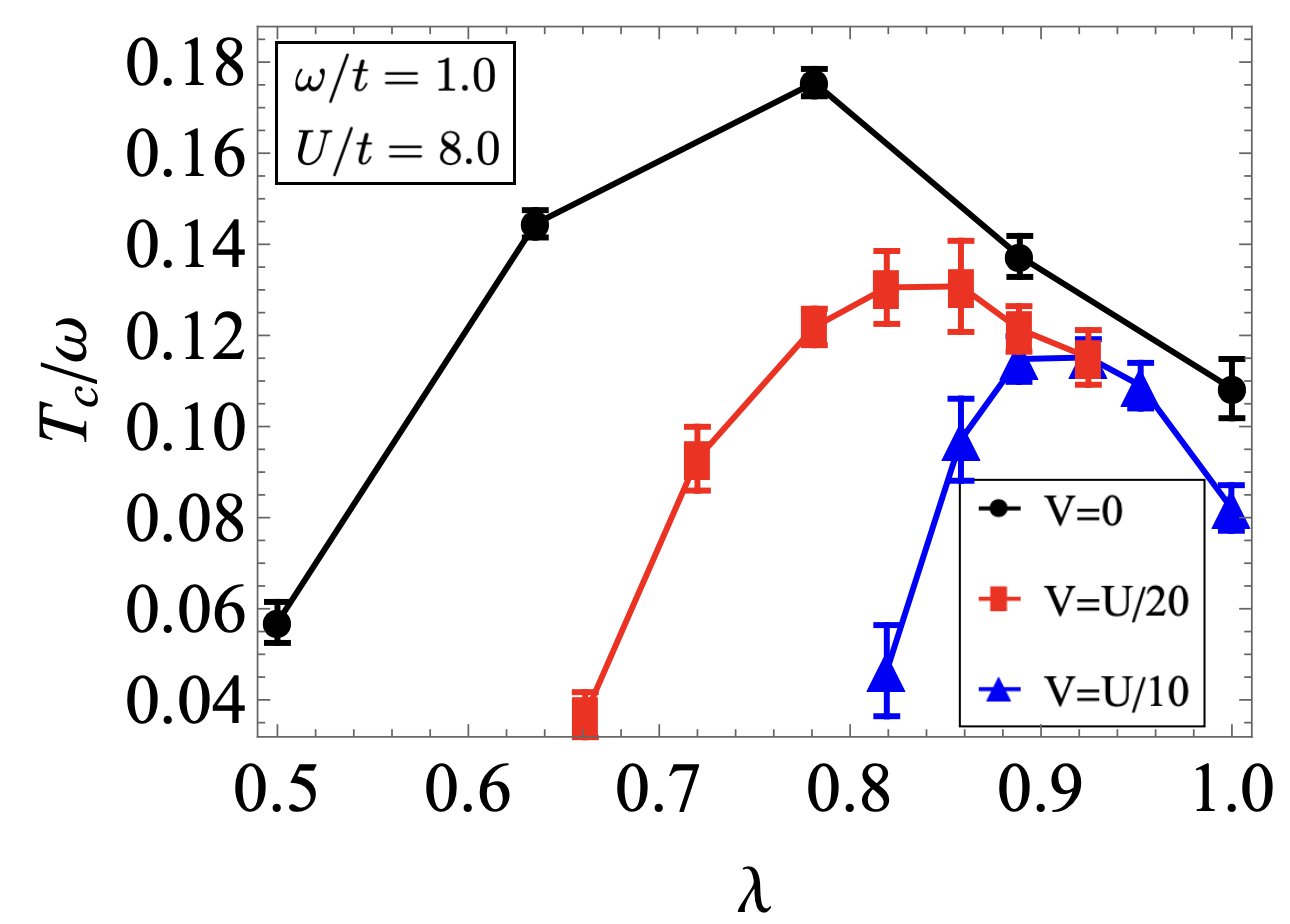
Figure 1 shows the superfluid transition temperature, denoted as in units of the phonon frequency , for the bond bipolaron model as a function of at phonon frequency and an on-site Hubbard repulsion , with various Coulomb interactions , , and . The dome shape of the optimal (an initial increase followed by a decrease in with increasing ) is clearly shown in Fig. 1, as observed in Ref. Zhang et al. (2023a); Sous et al. (2023). The optimal for decreases by about compared to the case without Coulomb interaction. With , which represents a relatively large Coulomb interaction, the optimal is reduced by around . Despite the reduction of the Coulomb interaction on the BKT transition temperature, the values of for the bond bipolaron appear to be greater than the upper bound of 0.05 predicted by McMillan’s phenomenological approach to Migdal-Eliashberg theory in the adiabatic limit for moderate values of . McMillan’s formula is
| (6) |
where represents the Coulomb pseudo-potential commonly found in many materials, predicts an upper bound of at . The findings in Fig.1 demonstrate that the values of do not decrease significantly at optimized electron-phonon coupling , despite the presence of strong Coulomb repulsion. The bipolaronic superconductivity remains relatively high under strong, poorly screened Coulomb repulsion. This is significant because in other models, like the Holstein model, strong Coulomb repulsion typically destroy . However, in the bond model, the bipolarons manage to maintain relatively high values even when .
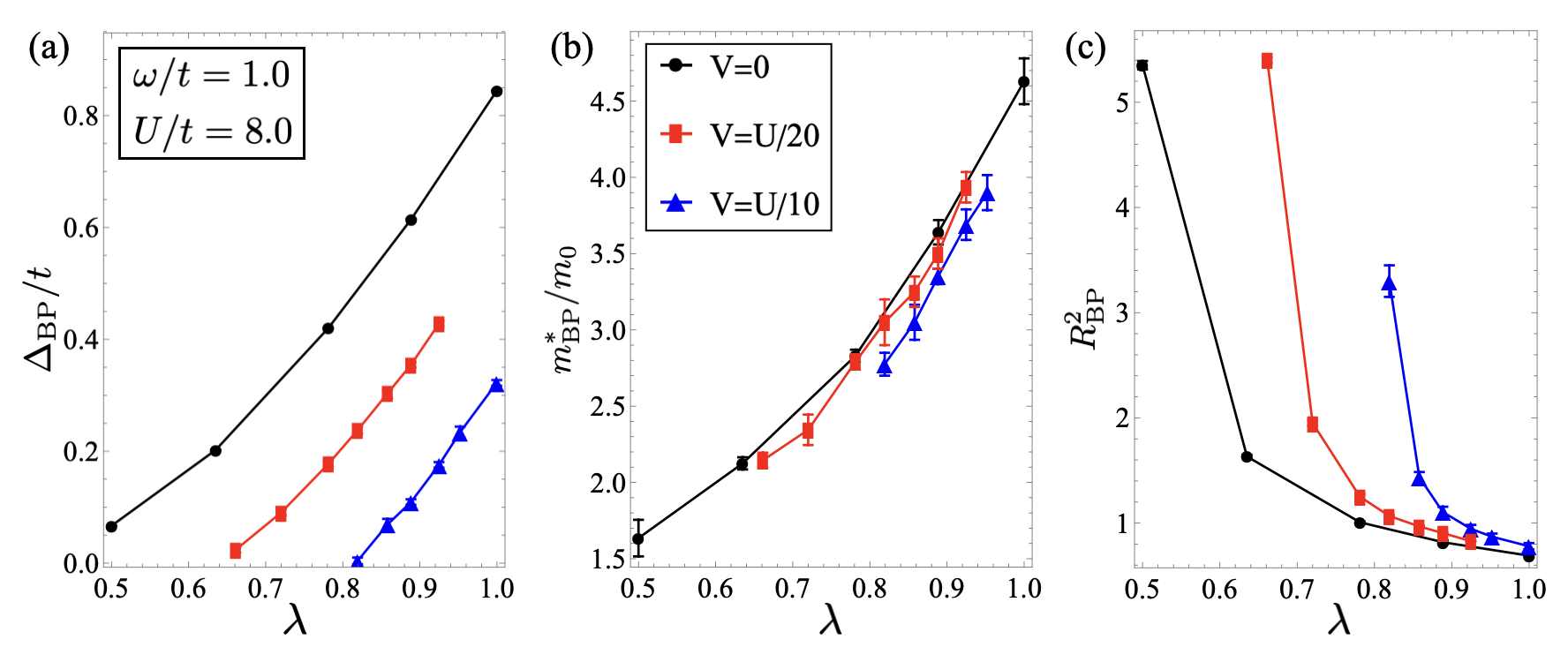
Figure 2 presents the features of bond bipolaron, specifically the binding energy (a), bipolaron effective mass (b), and bipolaron mean-square radius (c), in the presence of long-range Coulomb repulsion with values , , and with phonon frequency and an on-site Hubbard repulsion . From the binding energy required to form a bipolaron, as shown in Fig.2(a), it is evident that the coupling strength needed to form a bipolaron increases with the Coulomb interaction. This indicates that stronger electron-phonon coupling is necessary to overcome the repulsive Coulomb interaction to form a stable bipolaron. Furthermore, Fig.2(b) demonstrates that at the same coupling strength, the effective mass of the bipolaron decreases as the Coulomb repulsion increases. This decrease in effective mass suggests that the bipolaron becomes lighter with stronger Coulomb repulsion at the same coupling strength . Conversely, the size of the bipolaron, depicted in Fig.2(c), increases as increases at the same coupling strength , indicating that the spatial extent of the bipolaron expands under stronger Coulomb interaction.
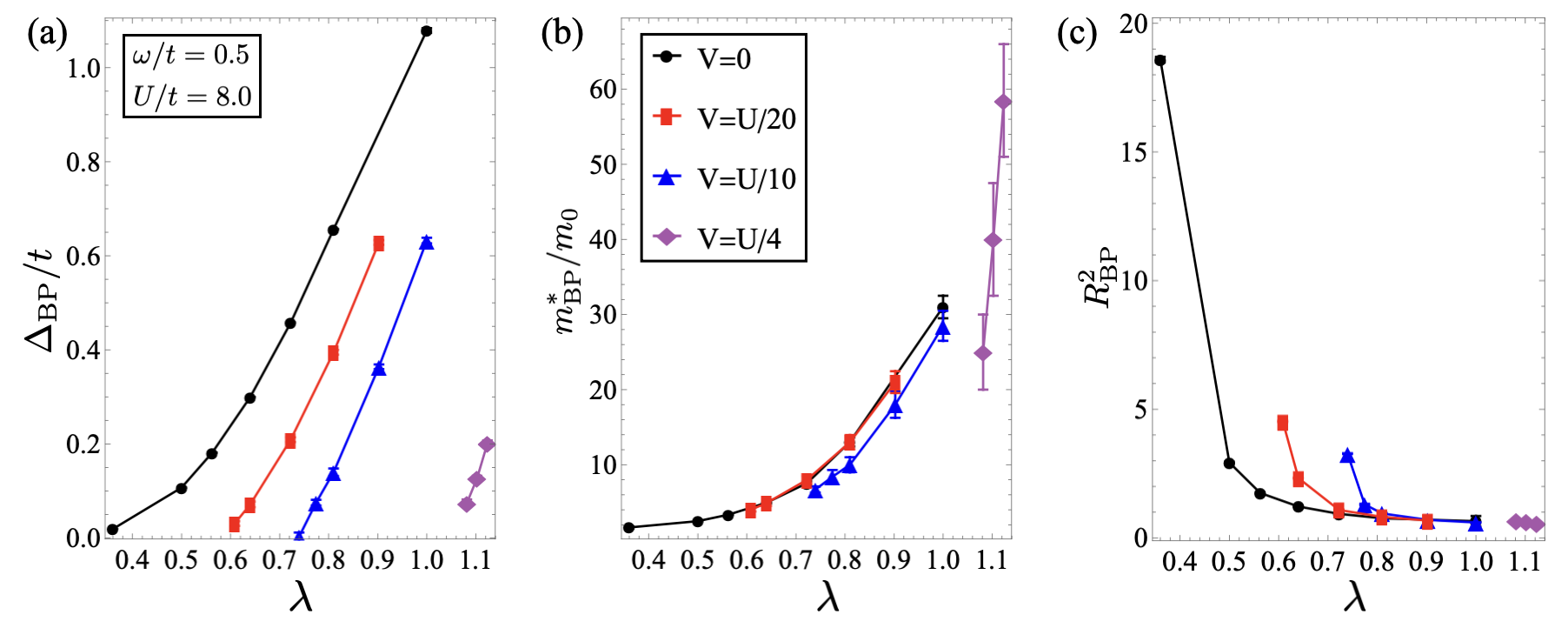
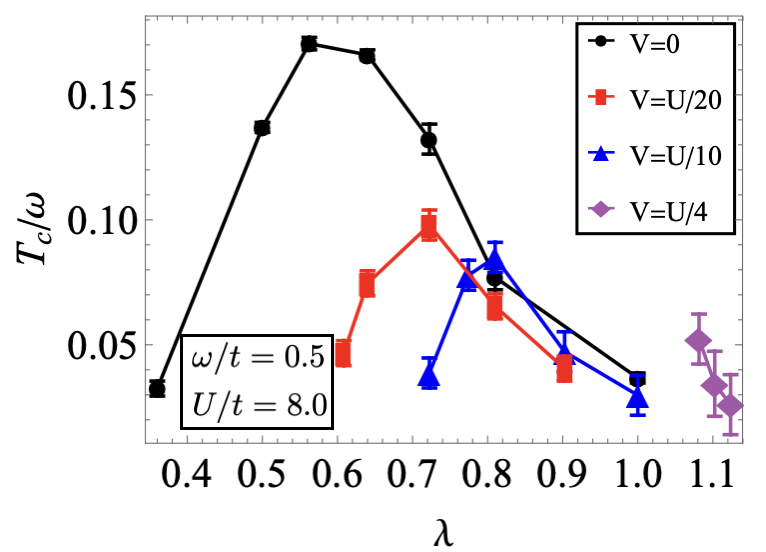
Figure 3 illustrates the superfluid transition temperature, denoted as , for the bond bipolaron model as a function of with , , with various Coulomb interactions , , , and . Even with , the values of for the bond bipolaron model appear to be comparable to or greater than the upper bound of 0.05 predicted by McMillan’s phenomenological approach to Migdal-Eliashberg theory in the adiabatic limit for (see previous discussion). In other words, our calculation predicts values higher than typical experimental findings in superconductors. Notably, as increases to , there is no peak of , and the value is less than 0.05. This is because, at such a large Coulomb interaction, the bipolaron forms a strongly bound state. Once formed, the effective mass increases abruptly, and the bipolaron size is confined within one lattice space since the two electrons are tightly bound together, as shown in Fig.4. Consequently, is ultimately suppressed by Coulomb interaction at with Coulomb interaction .
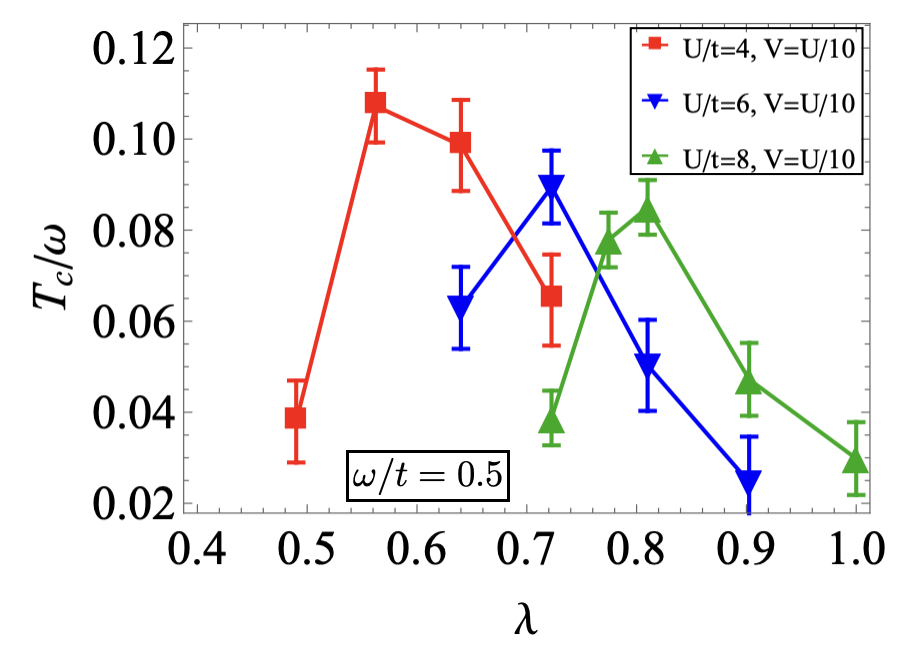
From a previous study Zhang et al. (2023a), it was demonstrated that, in the presence of only the on-site Hubbard repulsion , the optimal superfluid transition temperature, , for the bond bipolaron model, with an adiabatic ratio and electron-phonon coupling (same definition) reaches a maximum when . This result indicates that the on-site repulsive interaction can enhance in two-dimensional model. Here, we study the effect of long-range Coulomb interaction on this model. Specifically, we examine the effect of Coulomb interaction, fixed at , on the superfluid transition temperature for different values of (4.0, 6.0, and 8.0) while keeping the phonon frequency , as shown in Fig. 5. The results indicate that, although the on-site Hubbard repulsion can initially enhance the transition temperature, the introduction of long-range Coulomb interaction (here ) leads to a reduction in the peak value of as increases. This decline suggests that the influence of Coulomb interactions becomes dominant at higher , ultimately having a suppressive effect on compared to the enhancement provided by the Hubbard interaction alone.
VI Conclusion
In summary, we investigated the superfluid transition temperature, , of bond bipolaron model within a two-dimensional square lattice, with a focus on the influence of long-range Coulomb interaction. Our results demonstrate that, in general, the inclusion of long-range Coulomb repulsion reduces the BKT transition temperature. However, despite this reduction, remains relatively high for phonon frequency and , even with Coulomb interactions set at . This persistence of a relatively high transition temperature can be attributed to the combination of light effective mass and compact size of the bipolaron, which is maintained even in the presence of long-range Coulomb repulsion. These features underscore the robustness of the bipolaron mechanism, allowing for a relatively large to be observed, even with the long range Coulomb interaction. Moreover, our findings emphasize the significance of the Coulomb interaction at and suggest that the influence of Coulomb interactions becomes dominant at higher (see Fig. 5), having a suppressive effect on compared to the enhancement provided by the on-site Hubbard repulsion alone. This study offers key insights into the interplay between electron-phonon coupling and long-range Coulomb interaction, providing a framework for better understanding and manipulating these interactions in advanced materials and quantum systems, with potential implications for future research in high-temperature superconductivity.
Acknowledgements.
This work is supported by the National Natural Science Foundation of China (NSFC) under Grants No. 12204173 and 12275002, and the University Annual Scientific Research Plan of Anhui Province under Grant No 2022AH010013.References
- Landau (1933) L. D. Landau, “The movement of electrons in the crystal lattice,” Physikalische Zeitschrift der Sowjetunion 3, 664 (1933).
- H. Fröhlich and Zienau (1950) H. Pelzer H. Fröhlich and S. Zienau, “Xx. properties of slow electrons in polar materials,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 41, 221–242 (1950).
- Feynman (1955) R. P. Feynman, “Electron motion in crystal lattices,” Phys. Rev. 97, 660–665 (1955).
- Schultz (1959) T. D. Schultz, “Slow electrons in polar crystals: Self-energy, mass, and mobility,” Phys. Rev. 116, 526–543 (1959).
- Holstein (1959) T Holstein, “Studies of polaron motion: Part i. the molecular-crystal model,” Annals of Physics 8, 325–342 (1959).
- Alexandrov and Kornilovitch (1999) A. S. Alexandrov and P. E. Kornilovitch, “Mobile small polaron,” Phys. Rev. Lett. 82, 807–810 (1999).
- Holstein (2000) T. Holstein, “Studies of polaron motion: Part ii. the “small” polaron,” Annals of Physics 281, 725–773 (2000).
- Chakraverty et al. (1998) B. K. Chakraverty, J. Ranninger, and D. Feinberg, “Experimental and theoretical constraints of bipolaronic superconductivity in high materials: An impossibility,” Phys. Rev. Lett. 81, 433–436 (1998).
- Bonča et al. (2000) J. Bonča, T. Katrašnik, and S. A. Trugman, “Mobile bipolaron,” Phys. Rev. Lett. 84, 3153–3156 (2000).
- Macridin et al. (2004) A. Macridin, G. A. Sawatzky, and M. Jarrell, “Two-dimensional hubbard-holstein bipolaron,” Phys. Rev. B 69, 245111 (2004).
- Prodanović and Vukmirović (2019) N. Prodanović and N. Vukmirović, “Charge carrier mobility in systems with local electron-phonon interaction,” Phys. Rev. B 99, 104304 (2019).
- Zhang et al. (2023a) C. Zhang, J. Sous, D. R. Reichman, M. Berciu, A. J. Millis, N. V. Prokof’ev, and B. V. Svistunov, “Bipolaronic high-temperature superconductivity,” Phys. Rev. X 13, 011010 (2023a).
- Sous et al. (2023) J. Sous, C. Zhang, M. Berciu, D. R. Reichman, B. V. Svistunov, N. V. Prokof’ev, and A. J. Millis, “Bipolaronic superconductivity out of a coulomb gas,” Phys. Rev. B 108, L220502 (2023).
- Kornilovitch and Pike (1997) P. E. Kornilovitch and E. R. Pike, “Polaron effective mass from monte carlo simulations,” Phys. Rev. B 55, R8634–R8637 (1997).
- Marchand et al. (2010) D. J. J. Marchand, G. De Filippis, V. Cataudella, M. Berciu, N. Nagaosa, N. V. Prokof’ev, A. S. Mishchenko, and P. C. E. Stamp, “Sharp transition for single polarons in the one-dimensional su-schrieffer-heeger model,” Phys. Rev. Lett. 105, 266605 (2010).
- Zhang et al. (2021) C. Zhang, N. V. Prokof’ev, and B. V. Svistunov, “Peierls/su-schrieffer-heeger polarons in two dimensions,” Phys. Rev. B 104, 035143 (2021).
- Carbone et al. (2021) M. R. Carbone, A. J. Millis, D. R. Reichman, and J. Sous, “Bond-peierls polaron: Moderate mass enhancement and current-carrying ground state,” Phys. Rev. B 104, L140307 (2021).
- Sous et al. (2018) John Sous, Monodeep Chakraborty, Roman V. Krems, and Mona Berciu, “Light bipolarons stabilized by peierls electron-phonon coupling,” Phys. Rev. Lett. 121, 247001 (2018).
- Kim et al. (2024) Kyung-Su Kim, Zhaoyu Han, and John Sous, “Semiclassical theory of bipolaronic superconductivity in a bond-modulated electron-phonon model,” Phys. Rev. B 109, L220502 (2024).
- Zhang (2024) C. Zhang, “Light polarons with electron-phonon coupling,” Phys. Rev. B 109, 165119 (2024).
- Zhang (2023) C. Zhang, “Effect of dispersive optical phonons on the properties of the bond su-schrieffer-heeger polaron,” Phys. Rev. B 108, 075156 (2023).
- Zhang et al. (2022) C. Zhang, N. V. Prokof’ev, and B. V. Svistunov, “Bond bipolarons: Sign-free monte carlo approach,” Phys. Rev. B 105, L020501 (2022).
- Su et al. (1979) W. P. Su, J. R. Schrieffer, and A. J. Heeger, “Solitons in polyacetylene,” Phys. Rev. Lett. 42, 1698–1701 (1979).
- Barišić et al. (1970) S. Barišić, J. Labbé, and J. Friedel, “Tight binding and transition-metal superconductivity,” Phys. Rev. Lett. 25, 919–922 (1970).
- Barišić (1972a) S. Barišić, “Rigid-atom electron-phonon coupling in the tight-binding approximation.i,” Phys. Rev. B 5, 932–941 (1972a).
- Barišić (1972b) S. Barišić, “Self-consistent electron-phonon coupling in the tight-binding approximation. ii,” Phys. Rev. B 5, 941–951 (1972b).
- Fisher and Hohenberg (1988) Daniel S. Fisher and P. C. Hohenberg, “Dilute bose gas in two dimensions,” Phys. Rev. B 37, 4936–4943 (1988).
- Prokof’ev et al. (2001) N. Prokof’ev, O. Ruebenacker, and B. Svistunov, “Critical point of a weakly interacting two-dimensional bose gas,” Phys. Rev. Lett. 87, 270402 (2001).
- Pilati et al. (2008) S. Pilati, S. Giorgini, and N. Prokof’ev, “Critical temperature of interacting bose gases in two and three dimensions,” Phys. Rev. Lett. 100, 140405 (2008).
- Zhang et al. (2023b) C. Zhang, B. Capogrosso-Sansone, M. Boninsegni, N. V. Prokof’ev, and B. V. Svistunov, “Superconducting transition temperature of the bose one-component plasma,” Phys. Rev. Lett. 130, 236001 (2023b).