Superior dark-state cooling via nonreciprocal couplings in trapped atoms
Abstract
Cooling the trapped atoms toward their motional ground states is key to applications of quantum simulation and quantum computation. By utilizing nonreciprocal couplings between constituent atoms, we present an intriguing dark-state cooling scheme in -type three-level structure, which is shown superior than the conventional electromagnetically-induced-transparency cooling in a single atom. The effective nonreciprocal couplings can be facilitated either by an atom-waveguide interface or a free-space photonic quantum link. By tailoring system parameters allowed in dark-state cooling, we identify the parameter regions of better cooling performance with an enhanced cooling rate. We further demonstrate a mapping to the dark-state sideband cooling under asymmetric laser driving fields, which shows a distinct heat transfer and promises an outperforming dark-state sideband cooling assisted by collective spin-exchange interactions.
I Introduction
Cooling the trapped atoms toward their motional ground states engages a series of improving laser cooling techniques from Doppler to Sisyphus and subrecoil cooling schemes [1]. Upon approaching the motional ground state of atoms, the linewidth or the spontaneous decay rate of the transition puts a limit on the temperature that these cooling schemes can achieve. Their ultimate performance depends on the balance between cooling and heating mechanisms, where the fluctuations of spontaneously emitted and rescattered photons give rise to the constraint that forbids further cooling. In one of the subrecoil cooling platforms, the resolved sideband cooling [2, 3, 4, 5, 6] in the Lamb-Dicke regime suppresses the carrier transition and specifically excites the transition with one phononic quanta less. Effectively, it moves the atoms toward the zero-phonon state via spontaneous emissions, and essentially, the steady-state phonon occupation is determined by a squared ratio of the spontaneous emission rate over the trapping frequency, which can be much smaller than one.
Alternatively, the dark-state sideband cooling [7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22] utilizes -type three-level structure of atoms with two laser fields operating on two different hyperfine ground states and one common excited state. This leads to an effective dark-state picture owing to quantum interference between two ground states and forms an asymmetric absorption profile under the two-photon resonance condition with a large detuning. This profile allows a narrow transition in the resolved sideband to cool down the atoms by removing one phonon, similar to the sideband cooling scheme with a two-level structure. In contrast to the two-level structure, the effective laser drivings and decay rates in dark-state sideband cooling can be tunable, which makes it a flexible and widely-used cooling scheme in ultracold atoms.
Recently, a novel scheme of using nonreciprocal couplings in optomechanical systems [23, 24] manifests motional refrigeration, which gives insights in heat transfer by utilizing unequal decay channels. This coupling can be facilitated as well in a nanophotonics platform of atom-waveguide interface [25, 26, 27] which allows quantum state engineering via mediating collective nonreciprocal couplings between atoms [28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 27, 45, 46, 47]. In this quantum interface, a strong coupling regime in light-matter interaction can be reached by coupling atoms with evanescent fields at the waveguide surface, where the directionality of light exchange processes can be further manipulated and tailored by external magnetic fields [34]. This gives rise to exotic phenomena of collective radiation behaviors [38, 39, 40] and a new topological waveguide-QED platform that can host photonic bound states [48].
In this work, we theoretically investigate the dark-state sideband cooling scheme in trapped atoms with nonreciprocal couplings, as shown in Fig. 1. The nonreciprocal couplings can be facilitated in an atom-waveguide interface or via a photonic quantum link in free space [49], which leads to collective spin-phonon correlations [18, 50] and distinct heat exchanges. Here we present a superior dark-state cooling compared to the conventional single atom results by utilizing the nonreciprocal couplings between atoms. We explore various tunable parameter regimes which are allowed in dark-state cooling and identify the parameter region that gives better cooling performance without compromising its cooling rate. We further obtain an analytical form of the phonon occupation for the target atom under the asymmetric driving conditions. Our results demonstrate a distinct heat transfer within the atoms, which leads to a superior dark-state sideband cooling assisted by collective spin-exchange interactions. This opens new avenues in surpassing the cooling obstacle [51, 52, 18], which is crucial in scalable quantum computation [53, 54, 51, 55], quantum simulations [56, 57], and preparations of large ensemble of ultracold atoms [21, 58] or molecules [59]. This paper is organized as follows. We present the theoretical model of dark-state cooling with nonreciprocal couplings in Sec. II. We then identify the parameter regimes that demonstrate superior cooling behaviors and their cooling dynamics in Sec. III. In Sec. IV, we further show the analytical prediction of the steady-state phonon occupation of the target atom and confirm its validity under dark-state mapping. Finally we conclude in Sec. V.
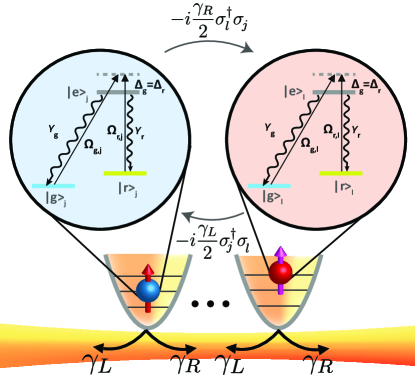
II Theoretical model
We start with a conventional EIT cooling scheme [7] with nonreciprocal couplings between constituent trapped atoms, as shown in Fig. 1. Each atom involves -type three-level atomic structure, where two hyperfine ground states and for th atom couple to their common excited state with laser fields of Rabi frequencies and , respectively. The intrinsic decay rates from the excited state are and . With the nonreciprocal couplings introduced as and , the dynamics of a density matrix for atoms with mass can be expressed as ()
| (1) |
where for the EIT cooling in the Lamb-Dicke (LD) regime (in the first order of LD parameter ) reads
| (2) | |||||
with the common laser detuning as required in EIT cooling scheme, i.e. the same difference between the th-site laser central frequencies () and the atomic transition frequencies ( and ). Projection angles of the laser fields to the motional direction are denoted as . The harmonic trap frequency is with a creation (annihilation) operator () in the quantized phononic states , and LD parameters are with . The coherent and dissipative nonreciprocal couplings in the zeroth order of are [35]
| (3) |
and
| (4) |
respectively, where denotes the wave vector in the guided mode that mediates nonreciprocal couplings , and quantifies the light-induced dipole-dipole interactions between the relative positions of trap centers and .
In terms of the eigenstates with only atomic spin degrees of freedom in Eq. (2), we can further diagonalize the EIT Hamiltonian [60] in a single-particle limit, where three eigenstates are
| (5) |
with , and the corresponding eigenenergies are
| (6) |
The angles and are defined as and , respectively. Under the EIT cooling condition of [7, 6], a red sideband transition between becomes resonant, and we can safely ignore the influences of off-resonant state and blue sideband transition between .
The effective Hamiltonian within the subspace and can then be obtained from Eq. (2), which reads in an interaction picture [6, 22],
| (7) |
with , , , and . The associated nonreciprocal coupling terms as in Eqs. (3) and (4) reduce to
| (8) | |||||
| (9) | |||||
where
| (10) | |||||
| (11) |
with and . We note that in general, unless , which would otherwise be assured in quantum systems with collective and pairwise dipole-dipole interactions [35]. This inequality arises owing to the mapping to the reduced Hilbert space, where different and determined by external laser fields can further allow extra and tunable degrees of freedom for cooling mechanism.
The above dark-state mapping sustains when the state can be detuned significantly from the subspace and , which leads to the requirement of for the th atom based on the condition of , the EIT cooling condition , and the usual assumption of a weak probe field . The resultant effective dark-state sideband cooling should also be legitimate by fulfilling the sideband cooling condition of and . This can be guaranteed when and are made small enough, which can easily be achieved by choosing large enough control fields and so are . In the setting of EIT cooling with nonreciprocal couplings, it is these tunable excitation parameters and the controllable directionality of spin-exchange couplings that give rise to distinct cooling behaviors we explore in the following section.
III Superior dark-state cooling
Here we consider a setting of two atoms with -type three-level configurations with nonreciprocal couplings, which represents the building block for a large-scale atomic array. In this basic unit under EIT cooling with collective spin-exchange interactions, we numerically obtain the steady-state phonon occupations tr from Eq. (1), under the Hilbert space with and . This truncation of phonon numbers is valid when the composite two-atom system is close to their motional ground state, that is when .
As a comparison to the single atom result () without nonreciprocal spin exchange interactions, we calculate the ratio to account for the superior or inferior cooling regime when is less or more than . In Fig. 2, we explore various parameter regimes of , , , , and look for superior cooling regions in the allowable parameters under EIT cooling conditions. In all plots, we investigate an asymmetric setup of driving fields in two atoms, where we focus on the cooling behavior of the target atom (), or otherwise we always observe heating effect. In Fig. 2(a), we find a superior cooling regime for the target atom when with a minimum at for a smaller probe-to-control field ratio . This presents the essential effect of nonreciprocal couplings, which leads to surpassing cooling behaviors owing to distinct heat transfer from collective spin-exchange interactions. The heating effect from symmetric EIT settings can be seen in Fig. 2(b), where at becomes larger than the respective single atom cases when . We note that at the unidirectional coupling when , the reaches the single atom limit as if the atom experiences one-way decay channel without the back action from the other atom. The asymmetric setting is favored for superior cooling and evidenced in Fig. 2(b) when .
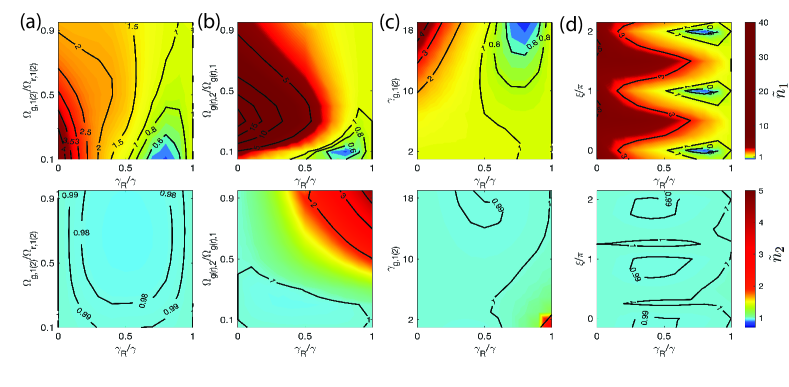
Furthermore in Fig. 2(c), we explore the effect of decay channels in the probe field and control field transitions. As increases along with a finite nonreciprocal coupling , a superior cooling region emerges and allows an impressive performance of almost twofold improvement () compared to the case without spin-exchange interactions. Finally in Fig. 2(d), we find the optimal operations of EIT cooling at or , which also reflects the optimal interparticle distances that permit superior EIT cooling. For of the residual atom in all lower panels, we find no significant cooling or even heating behaviors under asymmetric EIT driving conditions. This shows the essential role of the residual atom that hosts spin-exchange couplings to remove extra heat from the target atom. We note that throughout the paper, we consider the same ratio of nonreciprocal couplings between the left- and the right-propagating channels in either or for simplicity.
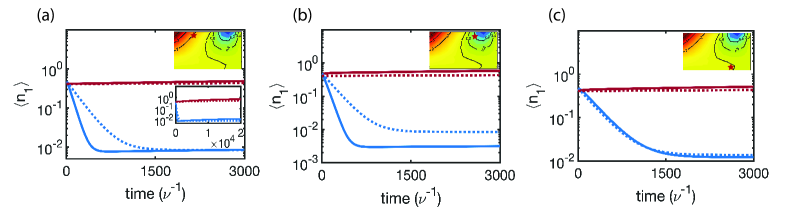
Next we numerically simulate the time dynamics of two-atom system in Fig. 3. To genuinely simulate the time evolutions in Eq. (1), we postulate the system in a thermal state initially [6, 61],
| (12) |
where is an average phonon number for both atoms. We assume and make a sufficient truncation on the finite motional states to guarantee the convergence in numerical simulations. As shown in Fig. 3, we select three contrasted regimes for heating, cooling, and neutral time dynamics. The characteristic times to reach the steady-states are shown shorter in cooling dynamics in Figs. 3(b). This presents an enhancement in cooling rate compared to the EIT cooling scheme in a single atom, in addition to the outperforming cooling behaviors in the steady-state phonon occupations. By contrast, the time dynamics in the heating regime shows a longer time behavior than the single atom case, while the neutral regime has a similar characteristic timescale. We attribute the enhanced cooling rate or prolonged time dynamics in heating to the collective spin-phonon couplings between the atoms.
IV Dark-state sideband cooling under asymmetric drivings
In Eqs. (7-9), we have demonstrated the mapping from EIT cooling with three-level structures to the effective dark-state sideband cooling scheme. Within , the mapping has reduced the Hilbert space dimensions in two atoms from to with coupled linear equations. We follow the wisdom in sideband cooling with chiral couplings by considering asymmetric driving conditions when [62]. In this way, we are able to perform a partial trace on the motional degree of freedom () and focus on the target atom behavior , which further diminishes the dimension of the Hilbert space to . The dynamics of this two-atom system can then be determined by the reduced density matrix .
The steady-state solutions for the density matrix elements of can further be simplified by taking advantage of the fact that is when and are much smaller than one. Therefore, we can neglect those whose leading terms are higher than the second order. Setting and keeping the terms of , , , , , we obtain
| (13) |
along with three other relationships,
| (14) | ||||
Solving the above equations leads to the solutions of density matrix elements expressed in terms of . Finally we obtain the steady-state phonon occupation for the target atom as ()
| (15) | |||||
where the approximate form assumes , and the first two terms are exactly the steady-state phonon occupation for a single atom under the sideband cooling [6]. The remaining terms are the modifications originating from the nonreciprocal couplings. At unidirectional coupling , Eq. (15) again reduces to the single atom result, which is also shown in Figs. 2(a) and 2(b) when or .
In the LD regime as , we can estimate Eq. (15) as
| (16) |
where the phonon occupation of the target atom is no longer limited by the effective spontaneous emission rate as in the single atom result of . If we assume and , by comparing to the single atom result, we obtain
| (17) |
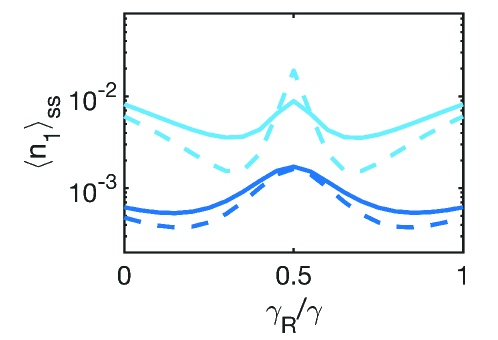
The above shows the minimum of when . This coincides with the predictions of the target ion under chiral-coupling-assisted sideband cooling [62] when an extreme LD regime as is applied. Furthermore in this extreme regime as in an infinite mass limit, a reciprocal coupling emerges to host the heat removal in the target atom from the mechanism of collective spin-exchange interaction. The values of at the minimum of would shift to nonreciprocal coupling regimes of when finite corrections of in Eq. (15) are retrieved, where two minimums arise from a quartic dependence of in Eq. (15). In Fig. 4, we show the superior dark-state sideband cooling under nonreciprocal couplings, where two lowest minimums can be identified as superior cooling compared to the single atom results at . We compare the exact results from EIT cooling scheme with three-level atomic structures and the predictions from the effective dark-state sideband cooling, which are well described by an analytical form in Eq. (15) under asymmetric driving conditions. This confirms the validity of dark-state mapping when large enough two-photon detunings are applied.
V Conclusion
In summary, we have shown theoretically that a superior EIT cooling behavior can be feasible when nonreciprocal couplings between constituent atoms are introduced. This provides a way to get around the cooling bottleneck [52, 18, 51] that an atom-based quantum computer or other applications of quantum technology may encounter. The conventional EIT cooling in a single atom is limited by the steady-state phonon occupation [22], while the corresponding dark-state sideband cooling is by . By utilizing nonreciprocal couplings between constituent atoms, an intriguing dark-state cooling scheme in -type three-level structure manifests a distinct heat transfer to further cool the target atom surpassing its single atom limit. We explore the allowable system parameters especially under asymmetric driving conditions and identify the regions for superior cooling performance with an enhanced cooling rate. Our results unravel the mechanism of collective spin-exchange interactions between trapped atoms, which enable new possibilities in driving the atoms toward their motional ground states. Future work will consider a multiatom platform, where more complex spin-phonon correlations may arise to further enhance the performance of the EIT cooling scheme.
ACKNOWLEDGMENTS
We acknowledge support from the Ministry of Science and Technology (MOST), Taiwan, under Grant No. MOST-109-2112-M-001-035-MY3. We are also grateful for support from TG 1.2 and TG 3.2 of NCTS.
References
- [1] C. Cohen-Tannoudji and D. Guéry-Odelin, Advances in Atomic Physics: An Overview (World Scientific, 2011).
- [2] F. Diedrich, J. C. Bergquist, W. M. Itano, and D. J. Wineland, Phys. Rev. Lett. 62, 403 (1989).
- [3] J. I. Cirac, R. Blatt, P. Zoller, and W. D. Phillips, Phys. Rev. A 46, 2668 (1992).
- [4] C. Monroe, D. M. Meekhof, B. E. King, S. R. Jefferts, W. M. Itano, D. J. Wineland, and P. Gould, Phys. Rev. Lett. 75, 4011 (1995).
- [5] C. Roos, T. Zeiger, H. Rohde, H. C. Nägerl, J. Eschner, D. Leibfried, F. Schmidt-Kaler, and R. Blatt, Phys. Rev. Lett. 83, 4713 (1999).
- [6] S. Zhang, J.-Q. Zhang, W. Wu, W.-S. Bao, and C. Guo, New J. Phys. 23, 023018 (2021).
- [7] G. Morigi, J. Eschner, and C. H. Keitel, Phys. Rev. Lett. 85, 4458 (2000).
- [8] C. F. Roos, D. Leibfried, A. Mundt, F. Schmidt-Kaler, J. Eschner, and R. Blatt, Phys. Rev. Lett. 85, 5547 (2000).
- [9] G. Morigi, Phys. Rev. A 67, 033402 (2003).
- [10] A. Retzker and M. B. Plenio, New. J. Phys. 9, 279 (2007).
- [11] J. Cerrillo, A. Retzker, and M. B. Plenio, Phys. Rev. Lett. 104, 043003 (2010).
- [12] A. Albrecht, A. Retzker, C. Wunderlich, and M. B. Plenio, New J. Phys. 13, 033009 (2011).
- [13] S. Zhang, C.-W. Wu, and P.-X. Chen, Phys. Rev. A 85, 053420 (2012).
- [14] S. Zhang, Q.-H. Duan, C. Guo, C.-W. Wu, W. Wu, and P.-X. Chen, Phys. Rev. A 89, 013402 (2014).
- [15] T. Kampschulte, W. Alt, S. Manz, M. Martinez-Dorantes, R. Reimann, S. Yoon, D. Meschede, M. Bienert, and G. Morigi, Phys. Rev. A 89, 033404 (2014).
- [16] R. Lechner, C. Maier, C. Hempel, P. Jurcevic, B. P. Lanyon, T. Monz, M. Brownnutt, R. Blatt, and C. F. Roos, Phys. Rev. A 93, 053401 (2016).
- [17] N. Scharnhorst, J. Cerrillo, J. Kramer, I. D. Leroux, J. B. Wübbena, A. Retzker, and P. O. Schmidt, Phys. Rev. A 98, 023424 (2018).
- [18] E. Jordan, K. A. Gilmore, A. Shankar, A. Safavi-Naini, J. G. Bohnet, M. J. Holland, and J. J. Bollinger, Phys. Rev. Lett. 122, 053603 (2019).
- [19] L. Feng, W. L. Tan, A. De, A. Menon, A. Chu, G. Pagano, and C. Monroe, Phys. Rev. Lett. 125, 053001 (2020).
- [20] M. Qiao, Y. Wang, Z. Cai, B. Du, P. Wang, C. Luan, W. Chen, H.-R. Noh, and K. Kim, Phys. Rev. Lett. 126, 023604 (2021).
- [21] C. Huang, S. Chai, and S.-Y. Lan, Phys. Rev. A 103, 013305 (2021).
- [22] S. Zhang, T.-C. Tian, Z.-Y. Wu, Z.-S. Zhang, X.-H. Wang, W. Wu, W.-S. Bao, and C. Guo, Phys. Rev. A 104, 013117 (2021).
- [23] H. Xu, L. Jiang, A. A. Clerk, and J. G. E. Harris, Nature 568, 65 (2019).
- [24] D.-G. Lai, J.-F. Huang, X.-L. Yin, B.-P. Hou, W. Li, D. Vitali, F. Nori, and J.-Q. Liao, Phys. Rev. A 102, 011502(R) (2020).
- [25] D. E. Chang, J. S. Douglas, A. González-Tudela, C.-L. Hung, H. J. Kimble, Rev. Mod. Phys. 90, 031002 (2018).
- [26] N. V. Corzo, J. Raskop, A. Chandra, A. S. Sheremet, B. Gouraud, and J. Laurat, Nature 566, 359 (2019).
- [27] A. S. Sheremet, M. I. Petrov, I. V. Iorsh, A. V. Poshakinskiy, A. N. Poddubny, arXiv:2103.06824.
- [28] C. W. Gardiner, Phys. Rev. Lett. 70 2269 (1993).
- [29] H. J. Carmichael, Phys. Rev. Lett. 70 2273 (1993).
- [30] K. Stannigel, P. Rabl, and P. Zoller, New J. Phys. 14, 063014 (2012).
- [31] I. J. Luxmoore, N. A. Wasley, A. J. Ramsay, A. C. T. Thijssen, R. Oulton, M. Hugues, S. Kasture, V. G. Achanta, A. M. Fox, and M. S. Skolnick, Phys. Rev. Lett. 110, 037402 (2013).
- [32] T. Ramos, H. Pichler, A. J. Daley, and P. Zoller, Phys. Rev. Lett. 113, 237203 (2014).
- [33] M. Arcari, I. Söllner, A. Javadi, S. Lindskov Hansen, S. Mahmoodian, J. Liu, H. Thyrrestrup, E. H. Lee, J. D. Song, S. Stobbe, and P. Lodahl, Phys. Rev. Lett. 113, 093603 (2014).
- [34] R. Mitsch, C. Sayrin, B. Albrecht, P. Schneeweiss, and A. Rauschenbeutel, Nat. Commun. 5, 5713 (2014).
- [35] H. Pichler, T. Ramos, A. J. Daley, and P. Zoller, Phys. Rev. A 91, 042116 (2015).
- [36] I. Söllner, S. Mahmoodian, S. L. Hansen, L. Midolo, A. Javadi, G. Kiršanskė, T. Pregnolato, H. El-Ella, E. H. Lee, J. D. Song, et al., Nat. Nanotechnol. 10, 775 (2015).
- [37] B. Vermersch, T. Ramos, P. Hauke, and P. Zoller, Phys. Rev. A 93, 063830 (2016).
- [38] P. Lodahl, S. Mahmoodian, S. Stobbe, A. Rauschenbeutel, P. Schneeweiss, J. Volz, H. Pichler, and P. Zoller, Nature 541, 473 (2017).
- [39] A. Albrecht, L. Henriet, A. Asenjo-Garcia, P. B Dieterle, O. Painter, and D. E. Chang, New J. Phys. 21, 025003 (2019).
- [40] H. H. Jen, M.-S. Chang, G.-D. Lin, and Y.-C. Chen, Phys. Rev. A 101, 023830 (2020).
- [41] H. H. Jen, Phys. Rev. Research 2, 013097 (2020).
- [42] H. H. Jen, Phys. Rev. A 102, 043525 (2020).
- [43] H. H. Jen, Phys. Rev. A 103, 063711 (2021).
- [44] M. Zanner, T. Orell, C. M. F. Schneider, R. Albert, S. Oleschko, M. L. Juan, M. Silveri, and G. Kirchmair, Nat. Phys. 18, 538 (2022).
- [45] R. Pennetta, M. Blaha, A. Johnson, D. Lechner, P. Schneeweiss, J. Volz, and A. Rauschenbeutel, Phys. Rev. Lett. 128, 073601 (2022).
- [46] H. H. Jen, Phys. Rev. A 105, 023717 (2022).
- [47] R. Pennetta, D. Lechner, M. Blaha , A. Rauschenbeutel, P. Schneeweiss, and J. Volz, Phys. Rev. Lett. 128, 203601 (2022).
- [48] E. Kim, X. Zhang, V. S. Ferreira, J. Banker, J. K. Iverson, A. Sipahigil, M. Bello, A. González-Tudela, M. Mirhosseini, and O. Painter, Phys. Rev. X 11, 011015 (2021).
- [49] A. Grankin, P. O. Guimond, D. V. Vasilyev, B. Vermersch, and P. Zoller, Phys. Rev. A 98, 043825 (2018).
- [50] A. Shankar, E. Jordan, K. A. Gilmore, A. Safavi-Naini, J. J. Bollinger, and M. J. Holland, Phys. Rev. A 99, 023409 (2019).
- [51] J. M. Pino, J. M. Dreiling, C. Figgatt, J. P. Gaebler, S. A. Moses, M. S. Allman, C. H. Baldwin, M. Foss-Feig, D. Hayes, K. Mayer, et al., Nature 592, 209 (2021).
- [52] D. Leibfried, R. Blatt, C. Monroe, and D. Wineland, Rev. Mod. Phys. 75, 281 (2003).
- [53] J. I. Cirac and P. Zoller, Phys. Rev. Lett. 74, 4091 (1995).
- [54] D. Kielpinski, C. Monroe, and D. J. Wineland, Nature 417, 709 (2002).
- [55] Y.-C. Shen and G.-D. Lin, New J. Phys. 22, 053032 (2020).
- [56] I. Buluta and F. Nori, Science 326, 108 (2009).
- [57] B. P. Lanyon, C. Hempel, D. Nigg, M. Müller, R. Gerritsma, F. Zähringer, P. Schindler, J. T. Barreiro, M. Rambach, G. Kirchmair, et al., Science 334, 57 (2011).
- [58] Y.-F. Hsiao, Y.-J. Lin, and Y.-C. Chen, Phys. Rev. A 98, 033419 (2018).
- [59] L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, L. W. Cheuk, W. Ketterle, and J. M. Doyle, Nat. Phys. 14, 890 (2018).
- [60] M. Fleischhauer, A. Imamoglu, and J. P. Marangos, Rev. Mod. Phys. 77, 633 (2005).
- [61] C. Roos, Controlling the quantum state of trapped ions, PhD thesis (University of Innsbruck, 2000).
- [62] C.-C. Chen, Y.-C. Wang, C.-C. Wang, and H. H. Jen, arXiv:2203.00877.