Supersolidity and crystallization of a dipolar Bose gas in an infinite tube

We consider an ultra-dilute gas of highly magnetic bosonic atoms confined in a tube potential (transverse harmonic confinement) of the form

$\displaystyle V(\bm{\rho})=\tfrac{1}{2}m(\omega_{x}^{2}x^{2}+\omega_{y}^{2}y^{2}),$

(1)

where $\omega_{x,y}$ are the angular trap frequencies, and $\bm{\rho}=(x,y)$. The eGPE energy functional for this system is given by $E=\int d\mathbf{x}\,E(\mathbf{x})$ where

$\displaystyle E(\mathbf{x})$

$\displaystyle=\psi^{*}[h_{\mathrm{sp}}+\tfrac{1}{2}g_{s}|\psi|^{2}+\tfrac{1}{2}\Phi_{\mathrm{dd}}(\mathbf{x})+\tfrac{2}{5}\gamma_{\mathrm{QF}}|\psi|^{3}]\psi,$

(2)

and $h_{\mathrm{sp}}=-\frac{\hbar^{2}}{2m}\nabla^{2}+V(\bm{\rho})$ is the single particle Hamiltonian. The short ranged interactions are governed by the coupling constant $g_{s}=4\pi\hbar^{2}a_{s}/m$ where $a_{s}$ is the $s$-wave scattering length. The long-ranged DDIs are described by the potential

$\displaystyle\Phi_{\mathrm{dd}}(\mathbf{x})=\int d\mathbf{x}^{\prime}\,U_{\mathrm{dd}}(\mathbf{x}-\mathbf{x}^{\prime})|\psi(\mathbf{x}^{\prime})|^{2},$

(3)

where the atoms are polarized along $y$

$\displaystyle U_{\mathrm{dd}}(\mathbf{r})=\frac{3g_{\mathrm{dd}}}{4\pi r^{3}}\left(1-\frac{3y^{2}}{r^{2}}\right),$

(4)

and $g_{\mathrm{dd}}=4\pi\hbar^{2}a_{\mathrm{dd}}/m$, with $a_{\mathrm{dd}}=m\mu_{0}\mu_{m}^{2}/12\pi\hbar^{2}$ being the dipolar length, and $\mu_{m}$ the magnetic moment. The effects of quantum fluctuations are described by the quintic nonlinearity with coefficient $\gamma_{\mathrm{QF}}=\frac{32}{3}g_{s}\sqrt{a_{s}^{3}/\pi}\mathcal{Q}_{5}(\epsilon_{\mathrm{dd}})$ where $\mathcal{Q}_{5}(x)=\operatorname{Re}\{\int_{0}^{1}du[1+x(3u^{2}-1)]^{5/2}\}$ [28] and $\epsilon_{\mathrm{dd}}\equiv a_{\mathrm{dd}}/a_{s}$.

We consider the gas to be constrained to have an average linear density of $n$, and hence the state $\psi$ is non-normalizable and the energy $E$ is infinite. For this reason it is necessary to minimize the energy per particle $\mathcal{E}$ to determine the system ground state. We can categorise such ground states into two types. (i) Uniform states that exhibit a continuous translational invariance and have the form $\psi(\mathbf{x})=\sqrt{n}\chi(\bm{\rho})$. (ii) Crystalline states that break translational symmetry and vary periodically along $z$ with period $L$. Our main aim in this work is to understand where and how the system transitions between these two states as the linear density and short range interactions vary.

It is useful to reduce the system to a unit cell (uc) of length $L$ along $z$ that periodically repeats along this direction, i.e. we take the uc to be $z\in[-L/2,L/2)$, with $x$ and $y$ over all space, and $\psi(\mathbf{x})=\psi(\mathbf{x}+L\hat{\mathbf{z}})$. The average density constraint enforces that $\int_{\mathrm{uc}}d\mathbf{x}|\psi|^{2}=nL$ atoms are in the uc. The energy per particle is given by

$\displaystyle\mathcal{E}=\frac{1}{nL}\int_{\mathrm{uc}}d\mathbf{x}\,E(\mathbf{x}).$

(5)

For the case of a uniform state, $\mathcal{E}$ is independent of $L$ (i.e. the uc is arbitrary), whereas for a crystalline state a particular $L$ will minimise $\mathcal{E}$ and the uc is well defined.¹¹1We note that due to periodicity in this case $\mathcal{E}$ will also be an equivalent minimum for $2L,3L,\ldots$ We also note that the integration in (5) is restricted to the uc whereas the DDI term $\Phi_{\mathrm{dd}}$ given by (3) involves an integral over all space.

For a fixed uc the energy of the system can be reduced by adjusting the wavefunction along the steepest descent direction, i.e. by making a change in $\psi$ proportional to $\delta\psi=\frac{\delta\mathcal{E}}{\delta\psi^{*}}=\frac{1}{nL}\mathcal{L}_{\mathrm{GP}}\psi,$ where

$\displaystyle\mathcal{L}_{\mathrm{GP}}=h_{\mathrm{sp}}+g_{s}|\psi|^{2}+\Phi_{\mathrm{dd}}(\mathbf{x})+\gamma_{\mathrm{QF}}|\psi|^{3},$

(6)

is the eGPE operator. Stationary states of the energy functional will satisfy the time-dependent eGPE equation $\mathcal{L}_{\mathrm{GP}}\psi=\mu\psi$, where $\mu$ is the chemical potential. Here we primarily use a gradient flow method (also known as the imaginary time method) to find stationary states. We do not describe this method here, but we follow a similar scheme to that described in Ref. [29] (also see [30]). However, after a fixed number of gradient flow steps we use a Newton-Krylov approach [31]. The Newton-Krylov approach is particularly beneficial in accelerating convergence of $\psi$ near the transition region where the landscape of the energy functional can be flat.

We represent the uc wavefunction using a planewave (or Fourier) spectral representation. This is discretized using an equally spaced 3D grid on the rectangular cuboid with dimensions $L_{\rho}\times L_{\rho}\times L$ and centered on the origin. Here the transverse discretization range $L_{\rho}$ is chosen sufficiently large that the wavefunction amplitude decays to a negligible value well-before the transverse boundary. The number of points in each direction is chosen so that the point spacing is $\Delta\lesssim 0.25\,\mu$m. This discretization naturally implements the required periodic boundary conditions along $z$ and allows the various terms in the eGPE operator to be computed with spectral accuracy. The DDI term requires special consideration and we discuss this in the next subsection.

Rather than optimise the wavefunction completely to a stationary state we regularly evaluate how the energy per particle changes with uc length and adjust the uc size appropriately. In practice we do this by evaluating the partial derivatives $\left(\frac{\partial\mathcal{E}}{\partial L}\right)_{\psi}$ and $\left(\frac{\partial^{2}\mathcal{E}}{\partial L^{2}}\right)_{\psi}$ using central finite differences and with this information we perform a Newton-Raphson update to adjust the uc length $L$ .

Our algorithm thus progresses by executing a $\psi$-optimization stage followed by a uc update. This repeats until the residuals, given by

	$\displaystyle\mathrm{resid}_{\psi}$	$\displaystyle\equiv\max_{\mathbf{x}}\left|\mathcal{L}_{\mathrm{GP}}\psi-\mu\psi\right|,$		(7)
	$\displaystyle\mathrm{resid}_{L}$	$\displaystyle=\left|\left(\frac{\partial\mathcal{E}}{\partial L}\right)_{\psi}\right|,$		(8)

both decrease to values below the termination criteria.²²2 These residuals are dependent on the choice of units. Here we use harmonic oscillator units defined by the strongest transverse frequency. Note that we evaluate the chemical potential as $\mu\equiv\int_{\mathrm{uc}}d\mathbf{x}\,\psi^{*}\mathcal{L}_{\mathrm{GP}}\psi/nL$. We typically require $\mathrm{resid}_{\psi}\sim 10^{-8}$ and $\mathrm{resid}_{L}\sim 10^{-5}$ for the algorithm to terminate.

The dipolar interactions are conveniently evaluated using the convolution theorem as

$\displaystyle\Phi_{\mathrm{dd}}(\mathbf{x})=\mathcal{F}^{-1}\{\tilde{U}_{\mathrm{dd}}(\mathbf{k})\mathcal{F}\{|\psi(\mathbf{x})|^{2}\}\},$

(9)

where $\mathcal{F}$ and $\mathcal{F}^{-1}$ are the forward and inverse Fourier transforms, respectively. Here we have also introduced the $k$-space interaction kernel

$\displaystyle\tilde{U}_{\mathrm{dd}}(\mathbf{k})=g_{\mathrm{dd}}\biggl{(}3\frac{k_{y}^{2}}{k^{2}}-1\biggr{)},$

(10)

which is the Fourier transform of Eq. (4). This naturally ensures that the periodic repetitions of the density along $z$ are included in the evaluation of $\Phi_{\mathrm{dd}}$ [see Eq. (3)]. However, because the transverse directions also have a finite range ($L_{\rho}$), unphysical periodic copies of the uc density in the transverse plane also contribute to Eq. (9). The effect of these copies decay as $1/L_{\rho}^{3}$, and would require an impractically large transverse spatial grid to reduce their effect to an acceptable level; instead we use a truncated interaction kernel. This involves limiting the spatial extent of the DDI to a defined spatial region. For the infinite tube trap we use the following truncation:

$\displaystyle U_{\mathrm{dd}}^{R}(\mathbf{r})=\begin{cases}U_{\mathrm{dd}}(\mathbf{r}),&\rho<R\\ 0,&\text{otherwise}\end{cases}$

(11)

where $\rho=\sqrt{x^{2}+y^{2}}$ is the radial coordinate. The radial spatial limit ensures that the DDI does not allow (unphysical) transverse copies to interact. To apply this truncated interaction we need to obtain an accurate Fourier transformed form for use in Eq. (9). To do this we express the Fourier transformed kernel as

$\displaystyle\tilde{U}_{\mathrm{dd}}^{R}(\mathbf{k})$

$\displaystyle=\tilde{U}_{\mathrm{dd}}(\mathbf{k})-\tilde{U}_{\mathrm{dd}}^{R^{\prime}}(\mathbf{k}),$

(12)

where ${R^{\prime}}$ denotes the complementary truncated region $\{\rho\geq R\}$. We can evaluate this term as

	$\displaystyle\tilde{U}_{\mathrm{dd}}^{R^{\prime}}(\mathbf{k})=\int_{R}^{\infty}\rho d\rho\int_{-\infty}^{\infty}dz\int_{0}^{2\pi}d\phi\,e^{-i\mathbf{k}\cdot\mathbf{r}}U_{\mathrm{dd}}(\mathbf{r}),$		(13)
	$\displaystyle=3g_{\mathrm{dd}}[-\tfrac{1}{2}l_{0}(k_{\rho}R,|k_{z}|R)+(k_{x}^{2}/k_{\rho}^{2}-\tfrac{1}{2})l_{2}(k_{\rho}R,|k_{z}|R)],$		(14)

where $\mathbf{k}\cdot\mathbf{r}=k_{\rho}\rho\cos(\phi-k_{\phi})+k_{z}z$, and using 6.521(2,4) of [32], for $u>0$, $v>0$, $n\geq 0$:

	$\displaystyle l_{n}(u,v)$	$\displaystyle\equiv v^{2}\int_{1}^{\infty}tdt\,K_{n}(vt)J_{n}(ut),$		(15)
		$\displaystyle=\frac{v^{2}}{u^{2}+v^{2}}[vJ_{n}(u)K_{n+1}(v)-uJ_{n+1}(u)K_{n}(v)].$		(16)

To benchmark this result and demonstrate the usefulness of this cutoff potential we have calculated the dipolar energy per particle,

$\displaystyle\mathcal{E}_{D}=\frac{1}{2nL}\int_{\mathrm{uc}}d\mathbf{x}\,\Phi_{\mathrm{dd}}(\mathbf{x})|\psi_{\mathrm{tr}}(\mathbf{x})|^{2},$

(17)

with the trial wavefunction,

$\displaystyle\psi_{\mathrm{tr}}(\mathbf{x})=\frac{\sqrt{n}}{\sqrt{\pi}l_{x}l_{y}}e^{-(x^{2}/l_{x}^{2}+y^{2}/l_{y}^{2})/2}.$

(18)

We evaluate Eq. (17) numerically, and compare to the exact value

$\displaystyle\mathcal{E}_{D}^{\mathrm{ex}}=\frac{ng_{\mathrm{dd}}}{4\pi}\frac{2l_{x}-l_{y}}{l_{x}l_{y}(l_{x}+l_{y})}.$

(19)

In Fig. 1 we compare the error in calculating the DDI energy with and without a cutoff potential. This shows that in the absence of a cutoff there is a slow decay of the relative error in the energy of the DDI as the size of the grid is increased which demonstrates the inaccuracy that can arise due to improper treatment of the DDI. The relative error decays algebraically $\sim R^{-4}$ when there is no cutoff potential. However, once a cutoff is introduced, the error in this calculation falls off rapidly, converging to machine precision once the state is well represented on the grid.

The singular nature of the DDI potential has limited the development of analytic truncated kernels to two particular cases (see [33]), and our result developed here represents a new contribution. For other specific geometries the truncated kernels can be obtained numerically [34, 35], but these are not suitable for the tube situation we consider here. In our algorithm the numerical grid frequently changes (from the $L$ optimisation). This requires constant recomputing of the truncated kernel, making the analytical expression especially well-suited to our problem.

To quantify the translational symmetry that is broken due to density modulation along $z$, we define the density contrast

$\displaystyle\mathcal{C}=\frac{n_{\mathrm{max}}-n_{\mathrm{min}}}{n_{\mathrm{max}}+n_{\mathrm{min}}},$

(20)

where $n_{\mathrm{max}}$ and $n_{\mathrm{min}}$ are the maximum and minimum of the density $|\psi|^{2}$ on the $z$-axis. For a uniform state, $\mathcal{C}=0$, and for a crystalline state $\mathcal{C}>0$. For $\mathcal{C}=1$ the density goes to zero on the $z$ axis.

Second, we are interested in quantifying the superfluid fraction of the system. Superfluidity of a Bose-Einstein condensate is associated with a broken global $U(1)$ symmetry. Notably, as pointed out by Leggett [36] if the translational invariance of the Hamiltonian is broken by the ground state, then the $T=0$ superfluid faction of a Bose gas can be reduced from unity. Thus as the we expect a reduction in the superfluid as the condensate develops crystalline structure. We can most directly quantify the superfluid fraction by computing the nonclassical translational inertia (see [37, 36, 38]) as

$\displaystyle f_{s}=1-\lim_{v_{z}\to 0}\frac{\langle P_{z}\rangle}{nLmv_{z}},$

(21)

where $\langle P_{z}\rangle=-i\hbar\int_{\mathrm{uc}}d\mathbf{x}\,\psi^{*}\frac{\partial}{\partial z}\psi$ is the expectation of the $z$-component of momentum in a frame moving with uniform velocity $v_{z}$. In Refs. [6, 36] Leggett developed bounds for the superfluid fraction such that $f_{s}^{l}\leq f_{s}\leq f_{s}^{u}$, where

$\displaystyle f_{s}^{u}\equiv\frac{L}{n}\left[\int_{\mathrm{uc}}\frac{dz}{\int d\bm{\rho}\,|\psi|^{2}}\right]^{-1},$

(22)

and,

$\displaystyle f_{s}^{l}\equiv\frac{L}{n}\int d\bm{\rho}\,\left[\int_{\mathrm{uc}}\frac{dz}{|\psi|^{2}}\right]^{-1},$

(23)

are the upper and lower bounds, respectively. These expressions can be directly computed from the ground state solution avoiding the need for additional calculations in a moving frame. While the measures in Eq. (22) and Eq. (23) are bounds of the superfluid fraction, for the infinite tube dipolar gas we have confirmed that $f_{s}$, $f_{s}^{u}$ and, $f_{s}^{l}$ are all in good agreement.³³3In 1D cases [36, 38]) or situations where the wavefunction is separable (e.g. reduced theory presented in Sec. II.6) we have $f_{s}=f_{s}^{u}=f_{s}^{l}$. Notably, for the results in Fig. 2 the maximum difference from the bounds to $f_{s}$ is $\sim 0.7\%$. The moving frame measure is more difficult to apply near the transition⁴⁴4Equation (21) is evaluated using the momentum expectation of the state in a slowly moving frame. For parameters very close to the transition it can be difficult to obtain a modulated solution in the moving frame as the additional kinetic energy can cause it to convert to a uniform to state. and for this reason the superfluid fraction results we present here are evaluated using Eq. (22).

The reduced 3D theory was introduced in Ref. [26], and we briefly review it here as it is used to compare against the full 3D results for the phase diagram. The basis of this theory is to decompose the 3D field as $\psi(\mathbf{x})=\phi(z)\chi_{\mathrm{var}}(\bm{\rho})$ where $\chi_{\mathrm{var}}(\bm{\rho})=\tfrac{1}{\sqrt{\pi}l}{e^{-(\eta x^{2}+y^{2}/\eta)/2l^{2}}}$ is a two-dimensional Gaussian function with variational parameters $\{l,\eta\}$, and $\phi(z)$ describes the axial field with $\int_{\mathrm{uc}}dz\,|\phi|^{2}=nL$ and periodic boundary conditions. The energy per particle of the reduced theory is given by

$\displaystyle\mathcal{E}_{\mathrm{red}}=\mathcal{E}_{\perp}+\int_{\mathrm{uc}}\!\frac{dz}{nL}\,\phi^{*}\!\left(\!-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dz^{2}}+\frac{1}{2}\Phi+\frac{4\gamma_{\mathrm{QF}}|\phi|^{3}}{25\pi^{3/2}l^{3}}\right)\!\phi,$

(24)

where

$\displaystyle\mathcal{E}_{\perp}=\frac{\hbar^{2}}{4ml^{2}}\left(\eta+\frac{1}{\eta}\right)+\frac{ml^{2}}{4}\left(\frac{\omega_{x}^{2}}{\eta}+\omega_{y}^{2}\eta\right),$

(25)

is the single-particle energy of the transverse degrees of freedom. The two-body interactions are described by the effective potential

$\displaystyle\Phi(z)=\mathcal{F}_{z}^{-1}\left\{\tilde{U}(k_{z})\mathcal{F}_{z}\{|\phi|^{2}\}\right\},$

(26)

with $\mathcal{F}_{z}$ being the 1D Fourier transform, and where

$\displaystyle\tilde{U}(k_{z})$

$\displaystyle=\frac{g_{s}}{2\pi l^{2}}+\frac{g_{\mathrm{dd}}}{2\pi l^{2}}\!\left\{\!\frac{3[Qe^{Q}\operatorname{Ei}(-Q)+1]}{1+\eta}-1\!\right\},$

(27)

with $\operatorname{Ei}$ being the exponential integral, and $Q\equiv\tfrac{1}{2}\sqrt{\eta}k_{z}^{2}l^{2}$ (see [27]). To obtain stationary solutions of the reduced theory we vary $\{l,\eta,L\}$ and $\psi(z)$ to find local minima of (24). This theory is rather efficient to solve and was used to construct a phase diagram for the infinite tube dipolar gas in Ref. [26].

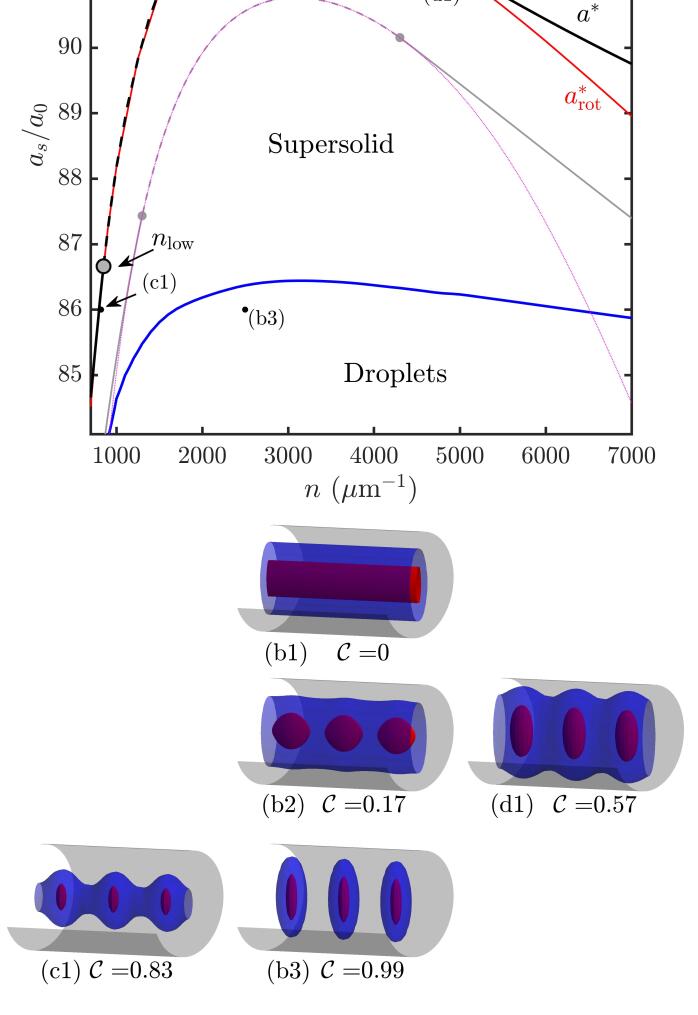
The results presented here are for a Bose gas of ¹⁶⁴Dy atoms with $a_{\mathrm{dd}}=130.8a_{0}$, confined to a radially symmetric trap with $\omega_{x,y}/2\pi=150\,$Hz. This system is similar to that considered for the main results of Ref. [26] calculated using the reduced theory.⁵⁵5For the theory presented here we have used $\mathcal{Q}_{5}$ in the definition of the quantum fluctuation term rather than the quadratic approximation used in Ref. [26]. This gives rise to a small shift in the predictions. Figure 3(a) is the phase diagram obtained by minimising the energy per particle (5) as $a_{s}$ and $n$ are varied, and is the main result of this paper. We identify three different phases using the ground state properties. (i) The uniform Bose-Einstein condensate (BEC) is translationally invariant along $z$, with $\mathcal{C}=0$ and $f_{s}=1$ [see Fig. 3(b1)]; (ii) The supersolid state is a crystalline state with $\mathcal{C}>0$, yet retaining a finite superfluid fraction $f_{s}$ [see Figs. 3(b2), (c1), and (d1)]; (iii) The insulating droplet state is a crystalline state with tightly-bound and separated droplets [see Fig. 3(b3)]. For the insulating droplet state the contrast of the density modulation along $z$ is essentially complete ($\mathcal{C}\approx 1$) and the superfluid fraction is negligible⁶⁶6Here we follow Ref. [26] and set a superfluid fraction of $f_{s}^{\min}=0.1$ to distinguish between the supersolid and insulating droplet states. $f_{s}\approx 0$. We do not concern ourselves with the nature of the transition or crossover from supersolid to insulating droplets. A proper description of this is beyond the eGPE theory, and requires a theory capable of capturing correlations between droplets needed to drive the insulating transition.

We define $a^{*}$ as the value of $a_{s}$ at which the ground state transitions from a uniform BEC to having crystalline order (i.e. $\mathcal{C}=0$ to $\mathcal{C}\neq 0$) for a system with average linear density $n$. Over the range of $n$ values shown in Fig. 3(a) the transition occurs directly from the uniform BEC state into a supersolid state, with the insulating droplet state emerging at lower values of $a_{s}$. We observe that $a^{*}$ initially increases with $n$ as the role of interactions increases relative to kinetic energy, but then $a^{*}$ decreases for $n\gtrsim 2.8\times 10^{3}/\mu$m, as quantum fluctuation effects become stronger.⁷⁷7The quantum fluctuation term acts as a local repulsive interaction, thus at high $n$ the $a_{s}$ value needs to be reduced further for the DDIs to overcome the local repulsive interactions and drive the system to crystallize. Our main interest here is the nature of the BEC to crystalline transition. At each density $n$ we have obtained the crystalline ground state solution at the transition point $a^{*}$, where it is degenerate with the uniform BEC state. The contrast and superfluid fraction of these states are shown in Fig. 4, revealing that for an intermediate density range $n\in[n_{\mathrm{low}},n_{\mathrm{high}}]$ with $n_{\mathrm{low}}\approx 0.8\times 10^{3}/\mu$m and $n_{\mathrm{high}}\approx 4.5\times 10^{3}/\mu$m, the transition is continuous. That is, in this range $\mathcal{C}\to 0$ and $f_{s}\to 1$ as $a_{s}\to a^{*}$ from below. The end points of this continuous transition line are indicated by two circles in Fig. 3(a).

In Fig. 5 we examine the variation of the superfluid fraction and the density contrast of the ground state as a function of $a_{s}$. We present a low density discontinuous case [Fig. 5(a)], an intermediate density continuous case [Fig. 5(b)], and a high density discontinuous case [Fig. 5(c)]. These results also show that in the discontinuous transition the superfluid fraction of the crystalline state is significantly less than unity, even for $a_{s}$ values very close to the transition. In contrast, in the vicinity of the continuous transition the superfluid fraction of the crystalline state tends to be close to unity for an appreciable range of $a_{s}$ values below $a^{*}$.

Since crystalline order causes a reduction in the superfluid fraction we can use either $f_{s}$ or $\mathcal{C}$ to quantify the crystalline transition (e.g. cf. Refs. [25, 26, 39]). The density contrast $\mathcal{C}$ is most frequently used in application to the experimental regime with a cigar shaped harmonic trap. Our results show that immediately below the continuous transition point $\mathcal{C}$ charges more rapidly with $a_{s}$ than $f_{s}$ [see Fig. 5(b)]. This can be understood by a simplified analytic model of the weakly modulated state developed in Ref. [26], which shows that in the vicinity of the continuous transition for small $\mathcal{C}$, the reduction in superfluid fraction is second order in $\mathcal{C}$ [40]

$\displaystyle f_{s}=1-\frac{1}{2}\mathcal{C}^{2}+O(\mathcal{C}^{4}).$

(28)

If the transition is continuous or almost continuous then, near the transition, (weakly) crystalline and uniform states have very similar energy, which makes precisely determining $a^{*}$ challenging. For the results presented in Fig. 4, we have taken cases with $\mathcal{C}<0.1$ to be equivalent to $\mathcal{C}=0$ (i.e. results in the grey shaded region), and identified these as being the continuous transition regime. We find $a^{*}$ to an accuracy of $\sim 10^{-4}\,a_{0}$, which requires resolving a difference in the relative energy per particle of crystalline and uniform states to $\sim 10^{-7}$. In contrast, the difference in the numerically obtained $f_{s}$ from unity at $a^{*}$ is almost too small to notice in Fig. 4, i.e. the scatter in $f_{s}$ is less than 1% [consistent with Eq. (28)].

For comparison, we also indicate the phase transition from the reduced theory in Fig. 3(a). The transition boundary $a^{*}$ predicted by the reduced theory is approximately $1\,a_{0}$ to $2\,a_{0}$ lower than that of the full eGPE calculation. This shift arises from the variational treatment of the transverse degrees of freedom in the reduced theory, and is consistent with other such comparisons of the reduced theory to full 3D calculations (e.g. see the shifts in scattering lengths for the occurrence of rotons noted in Fig. 5 of [27]).

We determined the collective excitations of the uniform BEC state by solving the Bogoliubov-de Gennes equations (see Ref. [27] for details). As the uniform groundstate is translationally invariant, the excitations can be characterized by the $z$-component of momentum ($\hbar k_{z}$), and occur as a set of bands with different transverse excitation. In Fig. 6(a) we show the results for the lowest excitation band for a system with $n=2500/\mu$m and at various $a_{s}$ values. At the highest value shown ($a_{s}=105a_{0}$) the spectrum is a monotonically increasing function of $k_{z}$. As $a_{s}$ is lowered, a local minimum develops at a non-zero wavevector, a roton-like mode which arises in dipolar BECs from the interplay of the DDIs and confinement [41, 42, 43]. The minimum energy of the roton decreases with decreasing $a_{s}$, until the energy softens to zero energy. We identify the value of scattering length when this occurs as $a_{\mathrm{rot}}^{*}$, and the corresponding $k_{z}$ value of the zero-energy mode as the roton wavevector $k_{\mathrm{rot}}$. For $a_{s}<a_{\mathrm{rot}}^{*}$ the roton is dynamically unstable, indicating that the uniform BEC state is no longer the ground state [see Fig. 6(b)]. For the density considered in these results $a_{\mathrm{rot}}^{*}=a^{*}$ [cf. Fig. 5(b)] and the roton softening marks the critical point at which the crystalline order continuously emerges. In Fig. 6(c) we show that the uc length $L$ of the crystalline ground state corresponds to the roton wavelength at the critical point.

We indicate the roton instability as a function of density in the phase diagram, Fig. 3(a). We see that where a continuous transition is found, the roton instability coincides with the transition, i.e. $a^{*}=a_{\mathrm{rot}}^{*}$ for $n\in[n_{\mathrm{low}},n_{\mathrm{high}}]$. Outside of this region $a_{\mathrm{rot}}^{*}<a^{*}$, such that the uniform BEC state is energetically unstable for $a_{s}<a^{*}$, but not dynamically unstable until $a_{s}<a_{\mathrm{rot}}^{*}$.

Ref. [25] considers a finite tube with periodic boundary conditions and a fixed unit cell size, and finds a discontinuous $\sim 10\%$ jump in $f_{s}$ at the crystallization transition. We have performed calculations for those parameters (¹⁶⁶Er Bose gas with $n=3.78\times 10^{3}/\mu$m and $\omega_{x,y}/2\pi=600\,$Hz), but for an infinite tube with the unit cell size chosen to minimize energy. We find that the transition to the crystalline transition is continuous and occurs with $a^{*}=a_{\mathrm{rot}}^{*}$ [similar to Fig. 6(a) and 5(b)]. The fixed system length (e.g., not being an integer multiple of $\lambda_{\mathrm{rot}}$) and the absence of a truncated DDI potential for the calculations in Ref. [25] may have contributed to the prediction of a discontinuous transition.

In Fig. 7 we examine the behavior of the transition for low- and high-density discontinuous cases. Here the energy per particle of the uniform and crystalline states cross [difficult to see in Figs. 7 (a) and (c)]. We are unable to follow the crystalline branch to values of $a_{s}$ much higher than $a^{*}$ because the gradient flow algorithm is an energy minimisation scheme and causes the crystalline state to jump to the uniform branch. In contrast, we are able to solve for the uniform solution for $a_{s}<a^{*}$ using the ansatz $\psi=\sqrt{n}\chi(\bm{\rho})$, which does not allow any modulation to develop along $z$. The uc length comparison in Figs. 7(a) and (c) also shows that the crystalline states have $L>\lambda_{\mathrm{rot}}$ in the region of the discontinuous transition. The high density discontinuous transition occurs in a regime where the quantum fluctuation effects are relatively strong and has been identified as a fluctuation induced first order transition in the finite system studied in Ref. [39].