This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Supplemental Material for
An Eulerian nonlinear elastic model for compressible and fluidic tissue with radially symmetric growth

Chaozhen Wei cwei4@wpi.edu Department of Mathematical Sciences, Worcester Polytechnic Institute, Worcester, MA 10605 USA    Min Wu englier@gmail.com Department of Mathematical Sciences, Worcester Polytechnic Institute, Worcester, MA 10605 USA

I Dynamics with Tissue Rearrangement

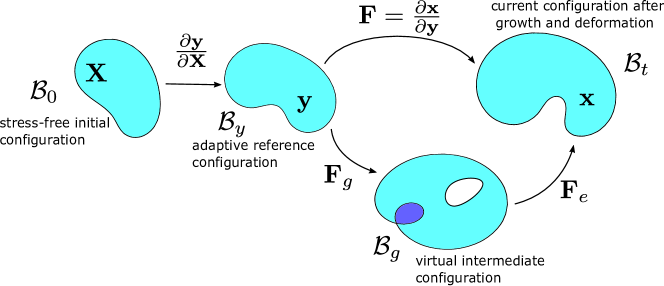
Refer to caption
Figure S1: Decomposition of the geometric deformation gradient into growth stretch tensor and elastic deformation tensor. Loop ℬ0→ℬy→ℬg→ℬt\mathcal{B}_{0}\rightarrow\mathcal{B}_{y}\rightarrow\mathcal{B}_{g}\rightarrow\mathcal{B}_{t}: relaxation of initial configuration to adaptive reference configuration and the decomposition of the geometric deformation with respect to adaptive reference configuration.

We consider that the adaptive reference configuration ℬy\mathcal{B}_{y} relaxes from the initial reference configuration ℬ0\mathcal{B}_{0} to the current deformed configuration ℬt\mathcal{B}_{t}; see Fig. S1. The relaxed reference coordinate is described by the adaptive reference map 𝐲=𝐘​(𝐱,t)∈ℬy\mathbf{y}=\mathbf{Y}(\mathbf{x},t)\in\mathcal{B}_{y}, whose dynamics is given by

d​𝐲d​t=∂𝐘∂t+𝐯⋅∇𝐘=β​(𝐑T​𝐱−𝐲),\frac{d\mathbf{y}}{dt}=\frac{\partial\mathbf{Y}}{\partial t}+\mathbf{v}\cdot\nabla\mathbf{Y}=\beta(\mathbf{R}^{T}\mathbf{x}-\mathbf{y}), (1)

where 𝐲​(𝐱,0)=𝐱\mathbf{y}(\mathbf{x},0)=\mathbf{x}, 𝐑\mathbf{R} is the rotational part of the deformation gradient 𝐅\mathbf{F}, and β\beta is the rate of rearrangement that measures how fast the reference configuration of the tissue adapts to the current configuration. From the polar decomposition of 𝐅=𝐑𝐔\mathbf{F}=\mathbf{R}\mathbf{U}, where 𝐔=𝐅T​𝐅=𝐂\mathbf{U}=\sqrt{\mathbf{F}^{T}\mathbf{F}}=\sqrt{\mathbf{C}} is the symmetric positive-definite stretch tensor in the material coordinate, 𝐑=𝐅𝐔−1\mathbf{R}=\mathbf{F}\mathbf{U}^{-1} can be uniquely defined as the local rotation (orthogonal transformation 𝐑T=𝐑−1\mathbf{R}^{T}=\mathbf{R}^{-1}) that transforms differential elements from the tangent space in the material (curvilinear) coordinate into the tangent space in the current (curvilinear) coordinate. The combination 𝐑T​𝐱\mathbf{R}^{T}{\mathbf{x}} is needed to ensure frame invariance of the tensorial evolution equations below under the rotation 𝐱+=𝐐​(t)​𝐱{\mathbf{x}}^{+}=\mathbf{Q}(t){\mathbf{x}}.

With β≠0\beta\neq 0, the adaptive reference configuration ℬy\mathcal{B}_{y} is a new configuration with respect to which we can define the effective deformation gradient 𝐅=∂𝐱/∂𝐲=∇𝐘−1\mathbf{F}=\partial\mathbf{x}/\partial\mathbf{y}=\nabla\mathbf{Y}^{-1}. The dynamics of 𝐅\mathbf{F} and its determinant JJ is consequently affected by β\beta. Following similar derivation process in main text with the dynamics of adaptive reference map Eq. (1), we can get the dynamics of the relaxed deformation gradient

d​(∇𝐘−1)d​t=∇𝐯​∇𝐘−1−β​∇𝐘−1​(𝐔−𝐈)−β​∇𝐘−1​(𝐱⋅∇𝐑)​∇𝐘−1.\frac{d(\nabla\mathbf{Y}^{-1})}{d{{t}}}=\nabla\mathbf{v}\nabla\mathbf{Y}^{-1}-\beta\nabla\mathbf{Y}^{-1}(\mathbf{U}-\mathbf{I})-\beta\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R})\nabla\mathbf{Y}^{-1}. (2)

Notice that this equation is invariant under the rotation 𝐱+=𝐐​(t)​𝐱{\mathbf{x}}^{+}=\mathbf{Q}(t){\mathbf{x}} because (d​(∇𝐘−1)/d​t−∇𝐯​∇𝐘−1)+=𝐐​(d​(∇𝐘−1)/d​t−∇𝐯​∇𝐘−1)({d(\nabla\mathbf{Y}^{-1})}/{d{{t}}}-\nabla\mathbf{v}\nabla\mathbf{Y}^{-1})^{+}=\mathbf{Q}({d(\nabla\mathbf{Y}^{-1})}/{d{{t}}}-\nabla\mathbf{v}\nabla\mathbf{Y}^{-1}), [∇𝐘−1​(𝐔−𝐈)]+=[∇𝐘−1]+​(𝐔−𝐈)=𝐐​[∇𝐘−1]​(𝐔−𝐈)=𝐐​[∇𝐘−1​(𝐔−𝐈)][\nabla\mathbf{Y}^{-1}(\mathbf{U}-\mathbf{I})]^{+}=[\nabla\mathbf{Y}^{-1}]^{+}(\mathbf{U}-\mathbf{I})=\mathbf{Q}[\nabla\mathbf{Y}^{-1}](\mathbf{U}-\mathbf{I})=\mathbf{Q}[\nabla\mathbf{Y}^{-1}(\mathbf{U}-\mathbf{I})], and [∇𝐘−1​(𝐱⋅∇𝐑)​∇𝐘−1]+=[∇𝐘−1]+​(𝐱+⋅∇𝐱+𝐑+)​[∇𝐘−1]+=𝐐​[∇𝐘−1]​(𝐱⋅∇𝐱𝐑)​[∇𝐘−1][\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R})\nabla\mathbf{Y}^{-1}]^{+}=[\nabla\mathbf{Y}^{-1}]^{+}(\mathbf{x}^{+}\cdot\nabla_{\mathbf{x}^{+}}\mathbf{R}^{+})[\nabla\mathbf{Y}^{-1}]^{+}=\mathbf{Q}[\nabla\mathbf{Y}^{-1}](\mathbf{x}\cdot\nabla_{\mathbf{x}}\mathbf{R})[\nabla\mathbf{Y}^{-1}], where we have omitted the β\beta for simplicity. The first term with β\beta demonstrates the adaption of the deformation gradient weighted by the local Biot strain tensor (𝐔−𝐈)(\mathbf{U}-\mathbf{I}). The second term shows the effect from the rotation ∇𝐑\nabla\mathbf{R} on the dynamics of ∇𝐘−1\nabla\mathbf{Y}^{-1}.

Then the dynamics of relaxed geometric volume variation tracked by the adaptive reference map is J=det(∇𝐘)−1J=\det{(\nabla\mathbf{Y})^{-1}}:

d​Jd​t=J​[∇⋅𝐯+β​Tr⁡(𝐈−𝐔)−β​Tr⁡(∇𝐘−1​(𝐱⋅∇𝐑))].\frac{dJ}{dt}=J\big{[}\nabla\cdot\mathbf{v}+{\beta}\operatorname{Tr}(\mathbf{I}-\mathbf{U})-\beta\operatorname{Tr}(\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R}))\big{]}. (3)

We assume that tissue rearrangement does not interfere the dynamics of tissue density

d​ρd​t=∂ρ∂t+𝐯⋅∇ρ=ρ​(γ−∇⋅𝐯).\frac{d\rho}{dt}=\frac{\partial\rho}{\partial t}+\mathbf{v}\cdot\nabla\rho=\rho(\gamma-\nabla\cdot\mathbf{v}). (4)

Combining the relation ρ​J=ρ0​Jg\rho J=\rho_{0}J_{g} with eqs. 4 and 3, we obtain the dynamics of JgJ_{g} with rearrangement

d​Jgd​t=Jg​[γ+β​Tr⁡(𝐈−𝐔)−β​Tr⁡(∇𝐘−1​(𝐱⋅∇𝐑))].\frac{dJ_{g}}{dt}=J_{g}\big{[}\gamma+{\beta}\operatorname{Tr}(\mathbf{I}-\mathbf{U})-\beta\operatorname{Tr}(\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R}))\big{]}. (5)

Assuming that the growth stretch tensor 𝐅g\mathbf{F}_{g} is still isotropic with tissue rearrangement, the elastic deformation tensor is 𝐅e=Jg−1/d​∇𝐘−1\mathbf{F}_{e}=J_{g}^{-1/d}\nabla\mathbf{Y}^{-1}. Thus, the dynamics of the elastic deformation tensor is

d​𝐅ed​t=(∇𝐯−𝚪i​s​o)​𝐅e−β​[𝐑​(𝐔−𝐈)​𝐑T−1d​Tr⁡(𝐔−𝐈)​𝐈]​𝐅e−β​[∇𝐘−1​(𝐱⋅∇𝐑)−1d​Tr⁡(∇𝐘−1​(𝐱⋅∇𝐑))]​𝐅e.\frac{d\mathbf{F}_{e}}{dt}=(\nabla\mathbf{v}-\boldsymbol{\Gamma}_{iso})\mathbf{F}_{e}-\beta[\mathbf{R}\left(\mathbf{U}-\mathbf{I}\right)\mathbf{R}^{T}-\frac{1}{d}\operatorname{Tr}(\mathbf{U}-\mathbf{I})\mathbf{I}]\mathbf{F}_{e}-\beta[\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R})-\frac{1}{d}\operatorname{Tr}(\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R}))]\mathbf{F}_{e}. (6)

The second term −β​[𝐑​(𝐔−𝐈)​𝐑T−1d​Tr⁡(𝐔−𝐈)​𝐈]-\beta[\mathbf{R}\left(\mathbf{U}-\mathbf{I}\right)\mathbf{R}^{T}-\frac{1}{d}\operatorname{Tr}(\mathbf{U}-\mathbf{I})\mathbf{I}] contributes to an anisotropic effect on the update of 𝐅e\mathbf{F}_{e} where [𝐑​(𝐔−𝐈)​𝐑T−1d​Tr⁡(𝐔−𝐈)​𝐈][\mathbf{R}\left(\mathbf{U}-\mathbf{I}\right)\mathbf{R}^{T}-\frac{1}{d}\operatorname{Tr}(\mathbf{U}-\mathbf{I})\mathbf{I}] is traceless. Then the dynamics of the elastic volume variation Je=det𝐅eJ_{e}=\det\mathbf{F}_{e} is

d​Jed​t=Je​(∇⋅𝐯−γ).\frac{dJ_{e}}{dt}=J_{e}(\nabla\cdot\mathbf{v}-\gamma). (7)

One can check that eqs. 3, 4, 5, 6 and 7 are all invariant under the rotation 𝐱+=𝐐​(t)​𝐱{\mathbf{x}}^{+}=\mathbf{Q}(t){\mathbf{x}}.

Considering the total strain energy E​(t)=∫ΩtJe−1​W​(𝐅e)​𝑑VtE(t)=\int_{\Omega_{t}}J_{e}^{-1}W(\mathbf{F}_{e})dV_{t}, the rate of change of total strain energy is given by the dynamics eqs. 6 and 7

d​Ed​t=\displaystyle\frac{dE}{dt}= ∫Ωt(𝝈:(∇𝐯−𝚪i​s​o)+Je−1Wγ)dVt\displaystyle\int_{\Omega_{t}}\Big{(}\boldsymbol{\sigma}:(\nabla\mathbf{v}-\boldsymbol{\Gamma}_{iso})+J_{e}^{-1}W\gamma\Big{)}dV_{t}
−β​∫Ωt𝝈s:[𝐑​(𝐔−𝐈)​𝐑T−1d​Tr⁡(𝐔−𝐈)​𝐈]​d​Vt\displaystyle-\beta\int_{\Omega_{t}}\boldsymbol{\sigma}_{s}:[\mathbf{R}\left(\mathbf{U}-\mathbf{I}\right)\mathbf{R}^{T}-\frac{1}{d}\operatorname{Tr}(\mathbf{U}-\mathbf{I})\mathbf{I}]dV_{t}
−β​∫Ωt𝝈s:[∇𝐘−1​(𝐱⋅∇𝐑)−1d​Tr⁡(∇𝐘−1​(𝐱⋅∇𝐑))]​d​Vt,\displaystyle-\beta\int_{\Omega_{t}}\boldsymbol{\sigma}_{s}:[\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R})-\frac{1}{d}\operatorname{Tr}(\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R}))]dV_{t}, (8)

where the stress is given by the constitutive law

𝝈\displaystyle\boldsymbol{\sigma} =μ​Je−2+dd​(𝐅e​𝐅eT−I1d​𝐈)+K​(Je−1)​𝐈,\displaystyle=\mu J_{e}^{-\frac{2+d}{d}}\Big{(}\mathbf{F}_{e}\mathbf{F}_{e}^{\text{T}}-\frac{I_{1}}{d}\mathbf{I}\Big{)}+K(J_{e}-1)\mathbf{I},
=μ​Jg​J−2+dd​(∇𝐘−1​∇𝐘−T−I~1d​𝐈)+K​(Jg−1​J−1)​𝐈\displaystyle=\mu J_{g}J^{-\frac{2+d}{d}}\Big{(}\nabla\mathbf{Y}^{-1}\nabla\mathbf{Y}^{-\text{T}}-\frac{\tilde{I}_{1}}{d}\mathbf{I}\Big{)}+K(J_{g}^{-1}J-1)\mathbf{I} (9)

where I~1=Tr⁡(𝐂)\tilde{I}_{1}=\operatorname{Tr}(\mathbf{C}) and I1=Tr⁡(𝐂e)=Tr⁡(𝐅eT​𝐅e)I_{1}=\operatorname{Tr}(\mathbf{C}_{e})=\operatorname{Tr}(\mathbf{F}_{e}^{\text{T}}\mathbf{F}_{e}). The stress can be decomposed as 𝝈=𝝈s+𝝈p\boldsymbol{\sigma}=\boldsymbol{\sigma}_{s}+\boldsymbol{\sigma}_{p}, the sum of the deviatoric part 𝝈s\boldsymbol{\sigma}_{s} (proportional to μ\mu) and the isotropic part 𝝈p\boldsymbol{\sigma}_{p} (proportional to KK). The first integral in eq. 8 represents the energy change due to active growth. The second and the third integrals represent the energy change due to the rearrangement rate β\beta. Notice 𝝈\boldsymbol{\sigma} is replaced by 𝝈s\boldsymbol{\sigma}_{s} since 𝝈p:[𝐑​(𝐔−𝐈)​𝐑T−1d​Tr⁡(𝐔−𝐈)​𝐈]\boldsymbol{\sigma}_{p}:[\mathbf{R}\left(\mathbf{U}-\mathbf{I}\right)\mathbf{R}^{T}-\frac{1}{d}\operatorname{Tr}(\mathbf{U}-\mathbf{I})\mathbf{I}] and 𝝈p:[∇𝐘−1​(𝐱⋅∇𝐑)−1d​Tr⁡(∇𝐘−1​(𝐱⋅∇𝐑))]\boldsymbol{\sigma}_{p}:[\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R})-\frac{1}{d}\operatorname{Tr}(\nabla\mathbf{Y}^{-1}(\mathbf{x}\cdot\nabla\mathbf{R}))] both vanish. Using eq. 9, one can check that 𝝈s:[𝐑​(𝐔−𝐈)​𝐑T−1d​Tr⁡(𝐔−𝐈)​𝐈]\boldsymbol{\sigma}_{s}:[\mathbf{R}\left(\mathbf{U}-\mathbf{I}\right)\mathbf{R}^{T}-\frac{1}{d}\operatorname{Tr}(\mathbf{U}-\mathbf{I})\mathbf{I}] is nonnegative and only vanish when 𝐔=λ​𝐈\mathbf{U}=\lambda\mathbf{I} is isotropic or 𝝈s=𝟎\boldsymbol{\sigma}_{s}=\mathbf{0}. This means that the second integral with β>0\beta>0 dissipates the stored strain energy only when there are both shear stress and shear deformation. Thus, the adaptive reference map results in physically intuitive properties in the dynamics of the total strain energy in terms related to the Biot strain 𝐔−𝐈\mathbf{U}-\mathbf{I}. However, the last term involving 𝐱⋅∇𝐑\mathbf{x}\cdot\nabla\mathbf{R} is not straightforward to interpret geometrically or physically. Thus, we limit our attention to symmetric cases in this work where 𝐱⋅∇𝐑=𝟎\mathbf{x}\cdot\nabla\mathbf{R}=\mathbf{0}.

II Growth of Compressible Tissue in a 2D Disc

We have also studied the growth of tissue in a 2D disc with fixed height (where there is no deformation in the direction of its thickness). As in Sec. 5 in the main text, we first give the analytic equilibrium solutions for the linearized system. Then we show some numerical simulation results for the nonlinear system.

II.1 Mechanical Equilibrium in a 2D Disc

Writing the linearized system in the approximation of small deformation in the polar coordinates (r,θ)(r,\theta), we obtain

{∂u∂t=v−β​u,∂g∂t=γ−β​(∂u∂r+ur),∂σr​r∂r+1r​(σr​r−σθ​θ)=0,σr​r=μ​(∂u∂r−ur)+K​(∂u∂r+ur−g),σθ​θ=μ​(ur−∂u∂r)+K​(∂u∂r+ur−g),\begin{dcases}&\frac{\partial u}{\partial t}=v-\beta u,\\ &\frac{\partial g}{\partial t}=\gamma-\beta\Big{(}\frac{\partial u}{\partial r}+\frac{u}{r}\Big{)},\\ &\frac{\partial\sigma_{rr}}{\partial r}+\frac{1}{r}(\sigma_{rr}-\sigma_{\theta\theta})=0,\\ &\sigma_{rr}=\mu\Big{(}\frac{\partial u}{\partial r}-\frac{u}{r}\Big{)}+K\Big{(}\frac{\partial u}{\partial r}+\frac{u}{r}-g\Big{)},\\ &\sigma_{\theta\theta}=\mu\Big{(}\frac{u}{r}-\frac{\partial u}{\partial r}\Big{)}+K\Big{(}\frac{\partial u}{\partial r}+\frac{u}{r}-g\Big{)},\end{dcases}

subject to deformation-free initial conditions and free moving boundary conditions

{u​(r,0)=0,g​(r,0)=0,v​(0,t)=0,σr​r​(R​(t),t)=0,d​Rd​t=v​(R,t).\begin{dcases}u(r,0)=0,\quad g(r,0)=0,\\ v(0,t)=0,\\ \sigma_{rr}(R(t),t)=0,\quad\frac{dR}{dt}=v(R,t).\end{dcases}

When the growth rate γ\gamma is partially positive and partially negative within the tissue, there exists an equilibrium tissue size Re​qR_{eq} such that

G​(Re​q)=0,whereG​(r)=∫0rγ​(ξ)​ξ​𝑑ξ.G(R_{eq})=0,\quad\text{where}\quad G(r)=\int_{0}^{r}\gamma(\xi)\xi d\xi. (10)

We can also obtain the solutions in mechanical equilibrium:

{v=G​(r)randg=(1+μK)​γ​(r)β,σr​r=−2​μ​G​(r)β​r2,σθ​θ=2​μβ​(G​(r)r2−γ​(r)),Je=1−μK​γ​(r)β.\begin{dcases}&v=\frac{G(r)}{r}\quad\text{and}\quad g=\Big{(}1+\frac{\mu}{K}\Big{)}\frac{\gamma(r)}{\beta},\\ &\sigma_{rr}=-\frac{2\mu G(r)}{\beta r^{2}},\\ &\sigma_{\theta\theta}=\frac{2\mu}{\beta}\Big{(}\frac{G(r)}{r^{2}}-\gamma(r)\Big{)},\\ &J_{e}=1-\frac{\mu}{K}\frac{\gamma(r)}{\beta}.\end{dcases} (11)

Similar as in the 3D case, the stresses can be dissipated with large β/μ\beta/\mu and the variation in JeJ_{e} (and also tissue density ρ=ρ0/Je\rho=\rho_{0}/J_{e}) is modulated by relative compressibility K/μK/\mu and tissue fluidity relative to growth β/γ\beta/\gamma.

II.2 Nonlinear Simulations

We perform simulations for the nonlinear system of tissue in a 2D disc

{∂u∂t+v​∂u∂r=v−β​u,∂Jg∂t+v​∂Jg∂r=Jg​[Γ+β​(2−(∂y∂r)−1−(yr)−1)],∂σr​r∂r+1r​(σr​r−σθ​θ)=0,σr​r=12​μ​Jg​[(yr)2−(∂y∂r)2]+K​(Jg−1​(∂y∂r)−1​(yr)−1−1),σθ​θ=12​μ​Jg​[(∂y∂r)2−(yr)2]+K​(Jg−1​(∂y∂r)−1​(yr)−1−1),\begin{dcases}&\frac{\partial u}{\partial t}+v\frac{\partial u}{\partial r}=v-\beta u,\\ &\frac{\partial J_{g}}{\partial t}+v\frac{\partial J_{g}}{\partial r}=J_{g}\Big{[}\Gamma+\beta\Big{(}2-(\frac{\partial y}{\partial r})^{-1}-(\frac{y}{r})^{-1}\Big{)}\Big{]},\\ &\frac{\partial\sigma_{rr}}{\partial r}+\frac{1}{r}(\sigma_{rr}-\sigma_{\theta\theta})=0,\\ &\sigma_{rr}=\frac{1}{2}\mu J_{g}\Big{[}(\frac{y}{r})^{2}-(\frac{\partial y}{\partial r})^{2}\Big{]}+K\Big{(}J_{g}^{-1}(\frac{\partial y}{\partial r})^{-1}(\frac{y}{r})^{-1}-1\Big{)},\\ &\sigma_{\theta\theta}=\frac{1}{2}\mu J_{g}\Big{[}(\frac{\partial y}{\partial r})^{2}-(\frac{y}{r})^{2}\Big{]}+K\Big{(}J_{g}^{-1}(\frac{\partial y}{\partial r})^{-1}(\frac{y}{r})^{-1}-1\Big{)},\end{dcases} (12)

subject to the deformation-free initial condition and free moving boundary conditions

{y​(r,0)=r,Jg​(r,0)=1,v​(0,t)=0,σr​r​(R,t)=0,d​Rd​t=v​(R,t).\begin{dcases}y(r,0)=r,\quad J_{g}(r,0)=1,\\ v(0,t)=0,\\ \sigma_{rr}(R,t)=0,\quad\frac{dR}{dt}=v(R,t).\end{dcases} (13)
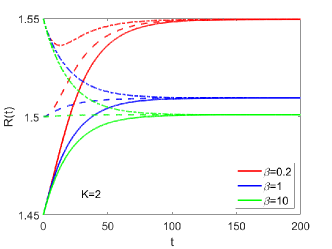
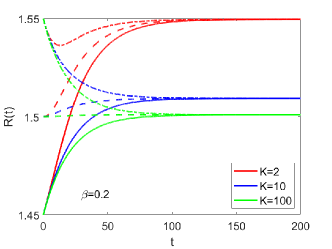
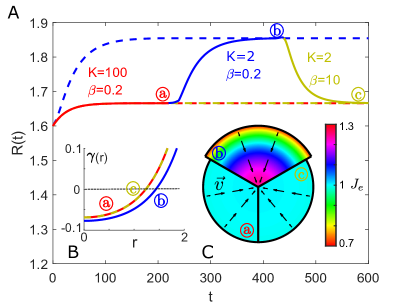
Refer to caption
Figure S2: (A) Evolution of tissue size with dynamical modulation of β\beta and KK (solid line) and with fixed sets of β\beta and KK (dashed lines) for prescribed γ\gamma. a-e indicate the equilibrium states for each set of parameters β\beta and KK. (B) The spatial profile of growth rate γ=0.1​(1−r)\gamma=0.1(1-r), where γ>0\gamma>0 (above dashed line) induces growth and γ<0\gamma<0 (below dashed line) induces death. (C) The distributions of the inverse of cell density JeJ_{e} and the tissue flow velocity vv, at equilibria a-e in (A). The color map shows the values of JeJ_{e}. The arrows indicate the direction and dimensionless magnitude of the tissue velocity.
Refer to caption
(a)
Refer to caption
(b)
Figure S3: Evolution of tissue size R​(t)R(t) with different initial sizes for (a) K=2K=2 and β=0.2,1,10\beta=0.2,1,10 and (b) β=0.2\beta=0.2 and K=2,10,100K=2,10,100. Solid lines starts with initial size R=1.45R=1.45, dash lines with R=1.5R=1.5 and dash-dot lines with R=1.55R=1.55. The equilibrium size is independent on the initial size and only dependent on the tissue properties KK and β\beta.

Nonlinear Effect on Equilibrium Tumor Size. We first simulate the growth of a tissue disc with prescribed growth rate γ=0.1​(1−r)\gamma=0.1(1-r) (Fig. S2 B) and initial radius R0=1.45R_{0}=1.45. The simulation results for the evolution of R​(t)R(t) for different KK and β\beta are shown in Fig. S2 A. The inverse of density Je=ρ0/ρJ_{e}=\rho_{0}/\rho (with ρ0=1\rho_{0}=1) in equilibrium for different KK and β\beta is shown in Fig. S2 C by each sector. The evolution of R​(t)R(t) with different initial sizes is shown in Fig. S3. The equilibrium size is independent on the initial size and only dependent on the tissue properties KK and β\beta.

The equilibrium tissue size Re​qR_{eq} for tissue disc satisfies the condition

G​(Re​q)=∫0Re​qγ​r​𝑑r=−∫0Re​q1Je​(v​∂Je∂r)​r​𝑑r,\displaystyle G(R_{eq})=\int_{0}^{R_{eq}}\gamma rdr=-\int_{0}^{R_{eq}}\frac{1}{J_{e}}\Big{(}v\frac{\partial J_{e}}{\partial r}\Big{)}rdr, (14)

where γ=γ​(r)\gamma=\gamma(r) for the prescribed growth rate and γ=γR​(r)\gamma=\gamma_{R}(r) for the growth rate coupled with chemical growth factor within the tissue disc of size RR. This condition demonstrates the coupling of tissue size growth with tissue mechanics.

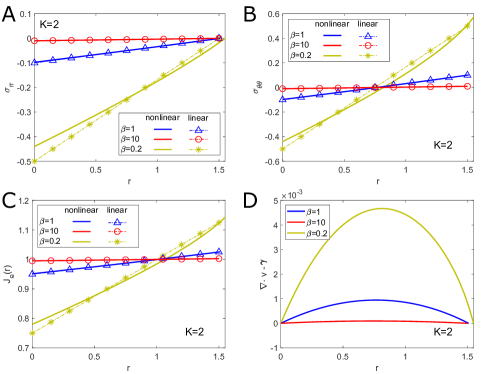
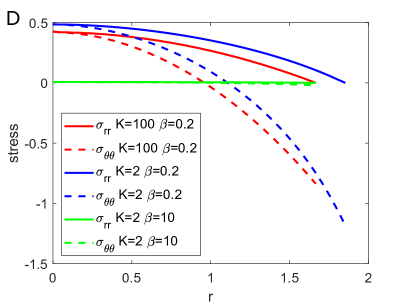
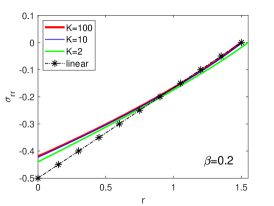
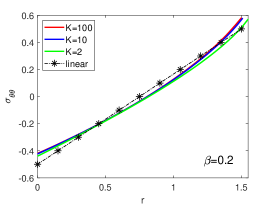
Refer to caption
Figure S4: Effect of tissue rearrangement on the mechanical state of tissue at equilibrium for prescribed γ\gamma. (A and B) Radial and circumferential stresses. (C) The elastic stretch JeJ_{e}. Cells are compressed and concentrated near the center and stretched near the boundary. The nonlinear solutions (solid lines) agrees with the linear solutions (dashed lines with markers) when the tissue rearrangement is much faster than tissue growth (β=1,10\beta=1,10). For slower rearrangement (β=0.2\beta=0.2), the nonlinear solutions start to deviate from linear solutions. (D) Compressibility of tissue flow. For incompressible flow, ∇⋅v−γ=0\nabla\cdot v-\gamma=0.

Regulation of Mechanical Stress and Tissue Density. The mechanical states including stresses σr​r\sigma_{rr}, σθ​θ\sigma_{\theta\theta} and elastic volume variation JeJ_{e} in equilibrium for different β\beta are shown in Fig. S4. They can be dissipated by fast rearrangement (large β\beta), just as in 3D case. In particular, the incompressibility condition ∇⋅𝐯−γ\nabla\cdot\mathbf{v}-\gamma is achieved for β=10\beta=10 (Fig. S4 D), as predicted in linear solutions. The stresses are scarcely altered by the change of KK, as shown in Fig. S5.

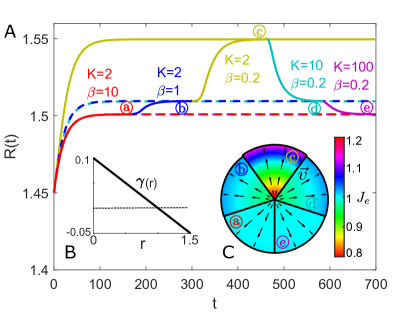
Refer to caption
(a)
Refer to caption
(b)
Figure S5: Effect of incompressibility KK on (a) radial stress σr​r\sigma_{rr} and (b) circumferential stress σθ​θ\sigma_{\theta\theta} with β=0.2\beta=0.2 for prescribed γ\gamma.

Growth Rate Coupled with Chemical Signals. We then simulate the growth of a tissue disc when the growth rate γR​(r)\gamma_{R}(r) is coupled with the concentration of growth factor cR​(r)c_{R}(r)

γR​(r)=cR​(r)​λp−λa,\gamma_{R}(r)=c_{R}(r)\lambda_{p}-\lambda_{a}, (15)

where cR​λpc_{R}\lambda_{p} and λa\lambda_{a} are the local rates of cell proliferation and apoptosis, respectively. The concentration of growth factor within a tissue disc of size R​(t)R(t) follows the reaction-diffusion process

{1λ​∂c​(r)∂t=L2​1r​∂∂r​(r​∂c∂r)−c,for 0<r<R​(t),c​(R​(t),t)=1,∂c∂r​(0,t)=0.\begin{dcases}&\frac{1}{\lambda}\frac{\partial c(r)}{\partial t}=L^{2}\frac{1}{r}\frac{\partial}{\partial r}\Big{(}r\frac{\partial c}{\partial r}\Big{)}-c,\quad\text{for $0<r<R(t)$,}\\ &c(R(t),t)=1,\quad\frac{\partial c}{\partial r}(0,t)=0.\end{dcases} (16)

Assuming λ≫γ\lambda\gg\gamma, we can obtain the quasi-steady-state solution cR​(r)c_{R}(r) of eq. 16 for tissue radius R​(t)R(t) at each time point:

cR​(r)=I0​(r/L)/I0​(R/L),c_{R}(r)=I_{0}(r/L)/I_{0}(R/L), (17)

where I0​(x)I_{0}(x) is the modified Bessel function of first kind. We perform simulation for the growth of a tissue disc with γR\gamma_{R}. The evolution of R​(t)R(t) for different KK and β\beta is shown in Fig. S6 A. The growth rate γR\gamma_{R} in equilibria is shown in Fig. S6 B and the elastic volume variation JeJ_{e} in equilibria is shown in Fig. S6 C. The stresses can be dissipated by large β\beta and can be moderately reduced by large KK, as shown in Fig. S6 D.

Refer to caption
Refer to caption
Figure S6: (A) Evolution of tissue size with dynamical modulation of β\beta and KK (solid line) and with fixed sets of β\beta and KK (dashed lines) for γ\gamma coupled with growth factor. a-c indicate the equilibria for each set of parameters β\beta and KK. (B) The spatial profile of γ\gamma, coupled with the reaction-diffusion process of growth factor (with L=0.5L=0.5, λp=0.2\lambda_{p}=0.2 and λa=0.1\lambda_{a}=0.1). The profiles of γ\gamma for the equilibrium a and c are identical due to the same equilibrium tissue size R​(t)R(t). (C) The inverse of cell density JeJ_{e} and the tissue flow velocity vv, at equilibria a-c in (A). The color map shows the values of JeJ_{e}. The arrows indicate the direction and dimensionless magnitude of the tissue velocity. (D) Modulation of stresses by KK and β\beta.