Supplementary Material of “Valency, charge-transfer, and orbital-dependent correlation in bilayer nickelates Nd₃Ni₂O₇”

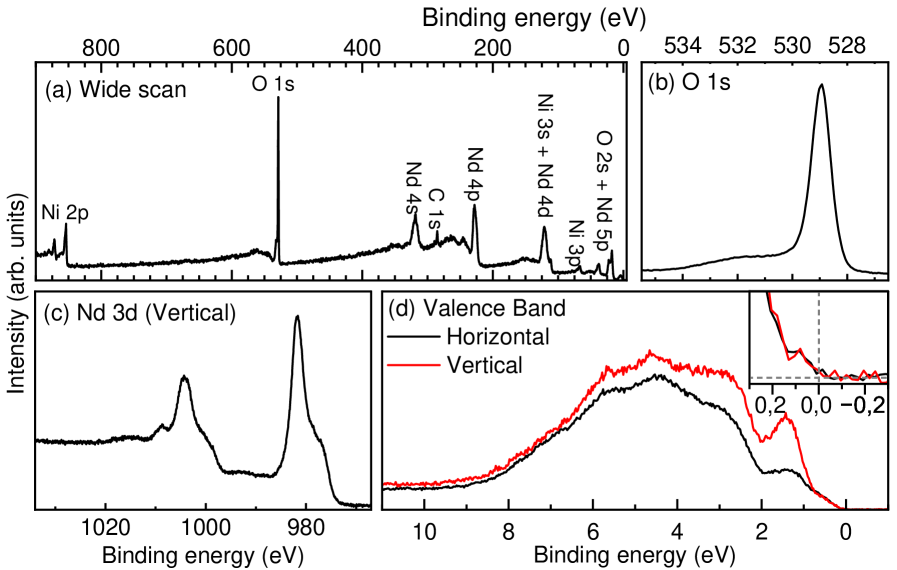
Fig. S2(a) shows the wide survey scan of Nd₃Ni₂O₇. All observed peaks are consistent with the expected composition of the film, except for the C $1s$ from the adsorbed impurities on the untreated surface of the film. The O $1s$, in Fig. S2(b), displays one single sharp peak from the oxide, with only a weak higher energy tail from the surface impurities, indicating that the obtained HAXPES data is representative of the intrinsic Nd₃Ni₂O₇ contributions. The Nd $3d$ core level multiplet structure is consistent with that of Nd₂O₃ Kotani and Ogasawara (1992). Figure S2(d) shows the experimental valence band spectra. Overall, the HAXPES spectra is dominated by the O $2p$ bands through their hybridization with the RE $5p$, which are highly enhanced due to the large photoionization cross-sections Takegami et al. (2019). The stronger polarization dependence for the peak at 1.5 eV indicates its dominant Ni $3d$ character (from the Ni $3d$ $t_{2g}$, as discussed below), while the weaker dependence closer to the Fermi energy is the result of the stronger mixing of the $e_{g}$ states with the O $2p$. At the Fermi energy, a finite but suppressed spectral weight is observed.

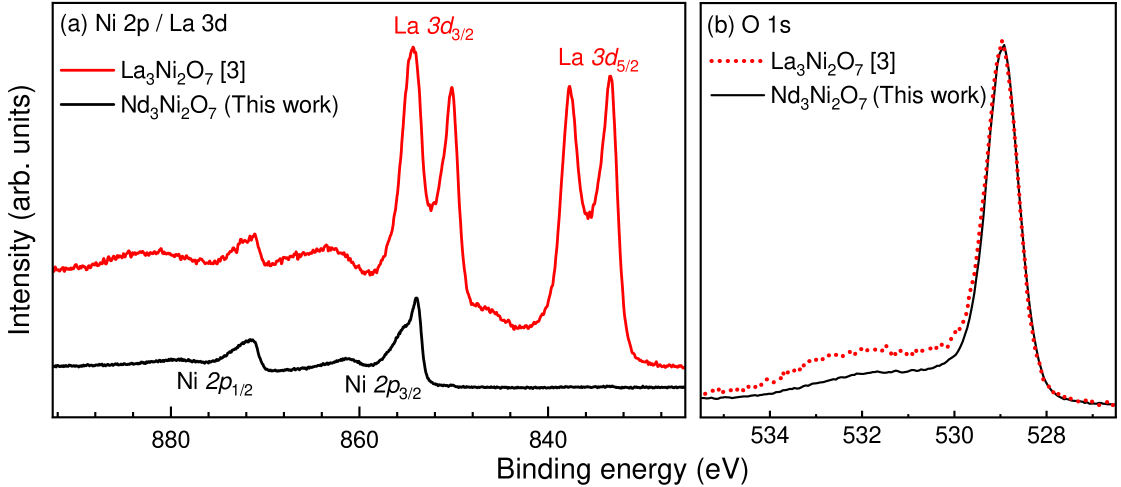
Figure S3(a) shows a comparison of the experimental HAXPES spectra in the vicinity of the Ni 2$p$ core level binding energy for Nd₃Ni₂O₇ and La₃Ni₂O₇ (from Ref. Takegami et al. (2024)). In the presence of La, two sets of double peaks show up in the region due to the La 3$d_{3/2}$ and La 3$d_{5/2}$ contributions, with the La 3$d_{3/2}$ signal overlapping, and largely dominating the Ni 2$p_{3/2}$ region. As a result, any attempt to estimate the Ni 2$p_{3/2}$ spectral shape in La-containing systems such as La₃Ni₂O₇ requires some form of data treatment method. Such procedures are highly sensitive to the assumptions used for the overlapping La 3$d$ complex spectral lineshape and are thus not as reliable as raw experimental spectra.

Figure S3(b) shows a comparison of the O $1s$ spectra from the Nd₃Ni₂O₇ in this study and the polycrystalline La₃Ni₂O₇ from Ref. Takegami et al. (2024). Oxygen deficiencies are usually manifested in the form of an asymmetric shape of the O $1s$ main peak Takegami et al. (2024b). In both cases displayed in Fig. S3(b), the O $1s$ main peaks are sharp and Guassian-like, with La₃Ni₂O₇ displaying a slightly more asymmetric shape at around $529-530$ eV. This suggests a similar, or lower amount of oxygen deficiency in the measured Nd₃Ni₂O₇ compared to the polycrystalline La₃Ni₂O₇ from Ref. Takegami et al. (2024), reported to have $\delta\approx 0.07$.

We calculate the DFT bands using the local density approximation (LDA) for the exchange-correlation potential with the WIEN2K package Blaha et al. (2001). The DFT calculations are performed for La₃Ni₂O₇ (using its crystal structure at ambient pressure Voronin et al. (2001)), a representative compound of the R₃Ni₂O₇ series. Since the La/Nd 5$d$ states are well-separated above the Fermi level in the R₃Ni₂O₇ compounds, their contributions to the spectra and physical quantities discussed in the main text can be safely neglected. Moreover, the hybridization between Ni 3$d$ and Nd 4$f$ orbitals is expected to be substantially weaker than that between Ni 3$d$ and O 2$p$. As a result, the relationship between the Ni 2$p$ core-level spectrum and Ni valency in Fig. 2 of the main text remains unaffected by the presence of Nd 4$f$ states. The calculated DFT bands are subsequently mapped onto a tight-binding (TB) model explicitly including all Ni 3$d$ and O 2$p$ bands, using the wien2wannier and wannier90 packages Mostofi et al. (2014); Kuneš et al. (2010). The Ni 3$d$ electron self-energy is computed using the auxiliary Anderson impurity model (AIM) in the DMFT self-consistent calculations, employing the continuous-time hybridization expansion Monte Carlo method Werner et al. (2006). Spectral functions and hybridization densities $\Delta(\omega)$ on the real-frequency axis are obtained by analytically continuing the self-energy $\Sigma(\omega)$ via the maximum entropy method Jarrell and Gubernatis (1996). The Ni 2$p$ core-level HAXPES spectra are calculated from the AIM, incorporating the DMFT hybridization densities $\Delta(\omega)$, as detailed in Refs. Hariki et al. (2017); Winder et al. (2020); Ghiasi et al. (2019). In this step, the AIM is extended to include the core orbitals and their interactions ($U_{dc}$) with the valence electrons.

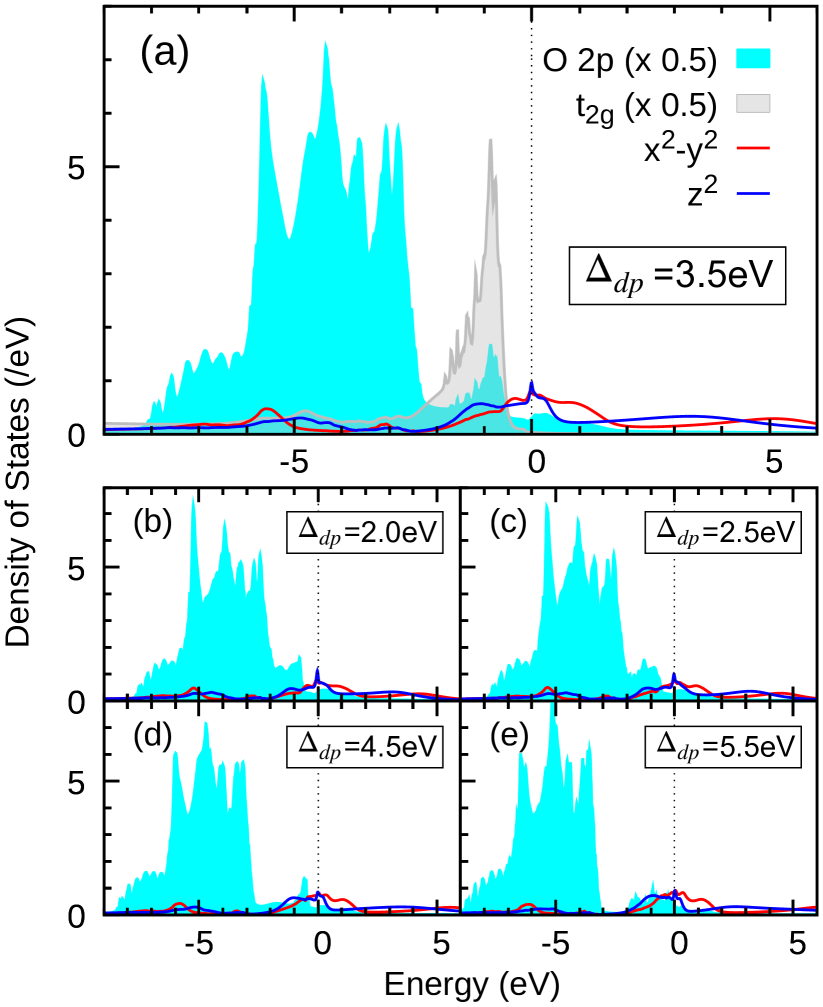
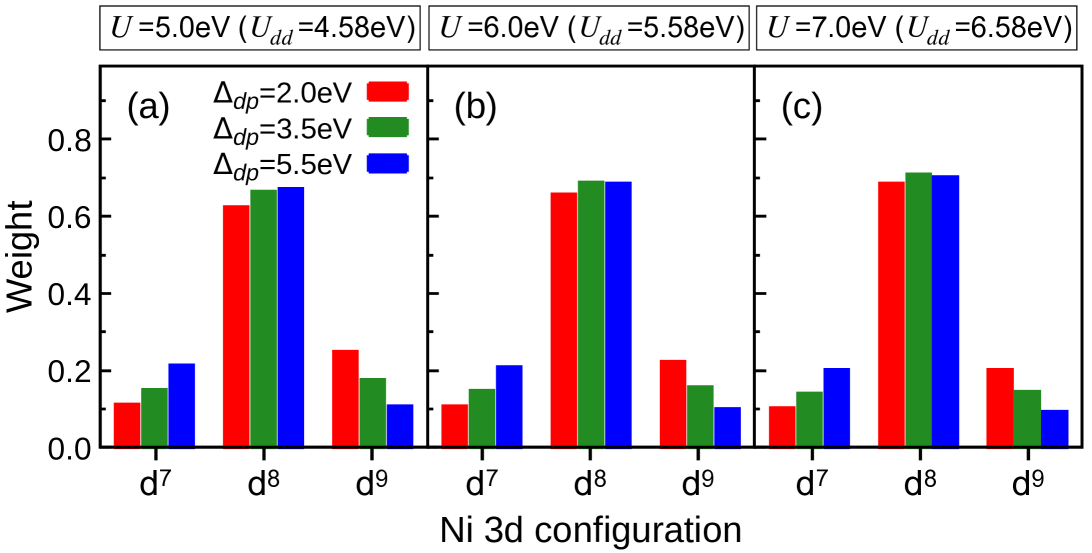
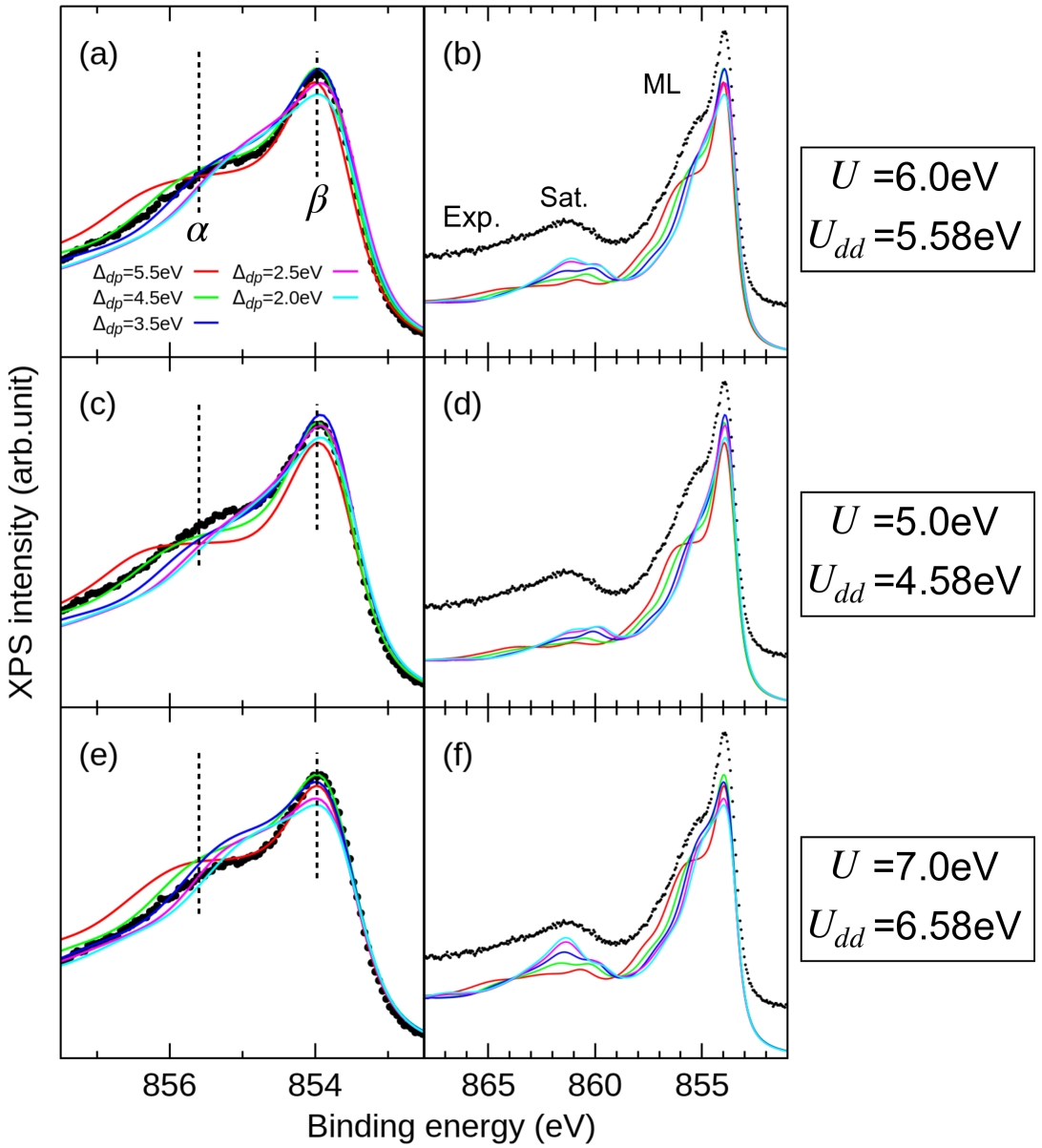
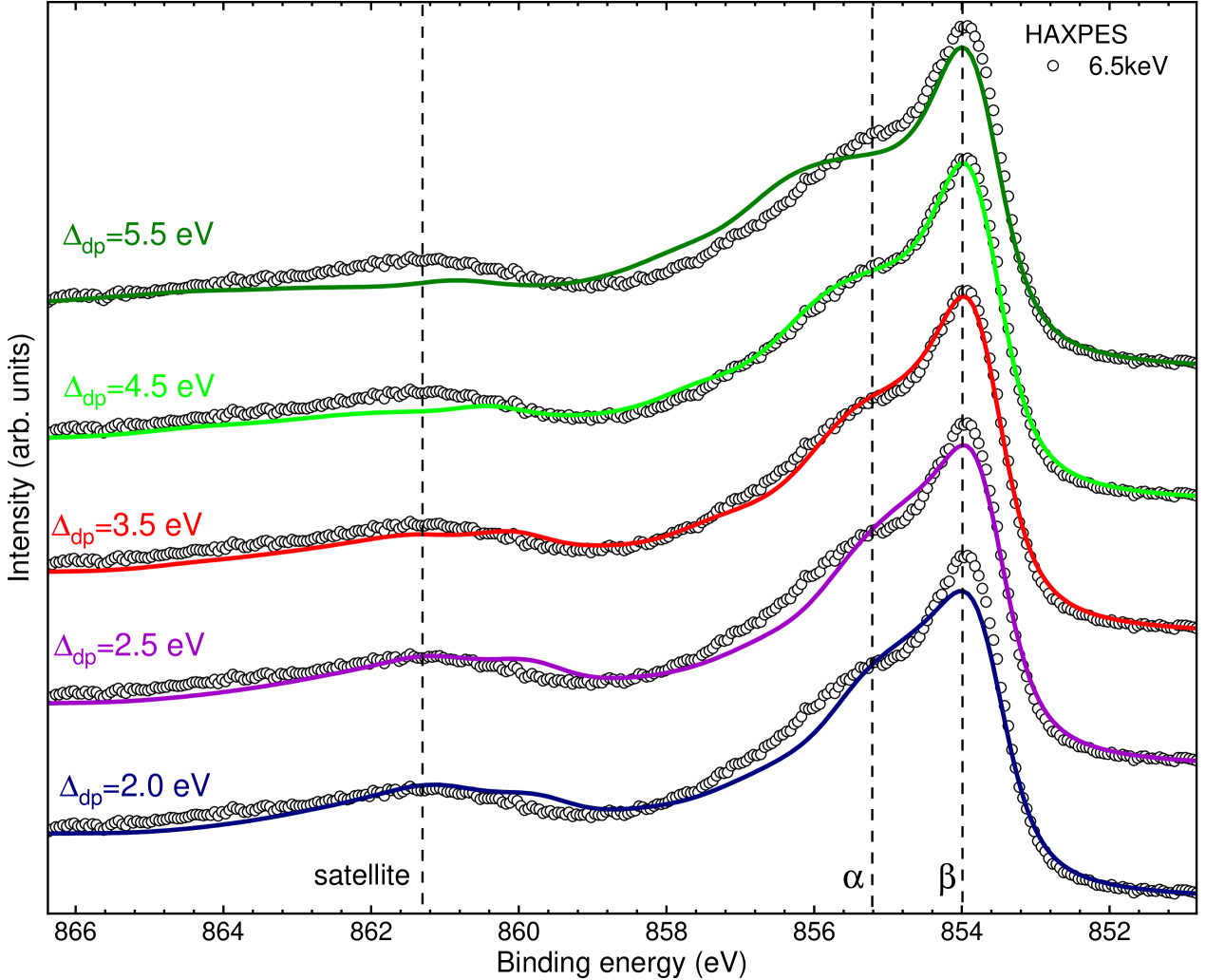
Figure S5 shows the LDA+DMFT valence-band spectral intensities of Nd₃Ni₂O₇ calculated for selected $\Delta_{dp}$ parameters. Besides the Ni $d_{x^{2}-y^{2}}$ (red) and $d_{z^{2}}$ (blue), we find the sizable weights of the O 2$p$ states near the Fermi energy. Note that the spectral intensities of the O 2$p$ states are scaled by a factor of 0.5 in the panels. The bandwidth of the $x^{2}-y^{2}$ state is wider than that of the $z^{2}$ state. The center of the Ni $t_{2g}$ band is approximately 1.5 eV, in good agreement with the experimental VB data mentioned above. In Fig. S6, we present the Ni atomic configuration histograms computed for different Hubbard $U$ parameters. We observe that the histogram depends strongly on the $\Delta_{dp}$ value, but is rather insensitive to changes in the $U$ parameter. This behavior is consistent with the system being of a charge-transfer type system. To further support the choice of the $U$ parameter in the main text, Fig. S7 shows the $U$ dependence of the Ni 2$p$ core-level XPS spectrum for a range of $\Delta_{dp}$ values in the LDA+DMFT AIM result. We find good agreement with the experimental spectrum for both the Ni 2$p_{3/2}$ main line (ML) and the satellite (Sat.) when $U=6.0$ eV is used. In the 2$p$ core-level XPS and XAS simulations, we use a core-hole potential value of $U_{dc}=1.2\times U_{dd}$, a well-established empirical relation for 3$d$ transition metal oxides Hariki et al. (2017).

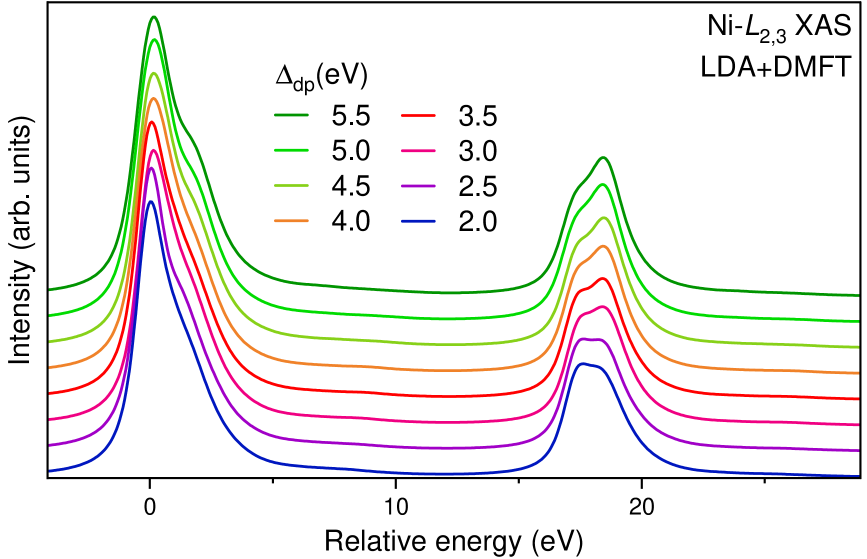
Figure S4 shows the Ni L_2,3 X-ray absorption spectra (XAS) of Nd₃Ni₂O₇ calculated for selected $\Delta_{dp}$ parameters. Both the L₃ and L₂ edges display two distinct features, with the ratio and their energy separation affected by $\Delta_{dp}$. The qualitative trends observed are similar to those experimentally observed in the Nd_n+1Ni_nO_3n+1 series Pan et al. (2022), with a reduction (increase) of the $\Delta_{dp}$ value resulting in a spectra closer to the divalent (trivalent) cases.