Suppression of the near-infrared OH night sky lines with fibre Bragg gratings – first results
Abstract
The background noise between 1 and 1.8 m in ground-based instruments is dominated by atmospheric emission from hydroxyl molecules. We have built and commissioned a new instrument, GNOSIS, which suppresses 103 OH doublets between – m by a factor of with a resolving power of . We present the first results from the commissioning of GNOSIS using the IRIS2 spectrograph at the Anglo-Australian Telescope. We present measurements of sensitivity, background and throughput. The combined throughput of the GNOSIS fore-optics, grating unit and relay optics is per cent, but this could be improved to per cent with a more optimal design. We measure strong suppression of the OH lines, confirming that OH suppression with fibre Bragg gratings will be a powerful technology for low resolution spectroscopy. The integrated OH suppressed background between 1.5 and 1.7 m is reduced by a factor of 9 compared to a control spectrum using the same system without suppression. The potential of low resolution OH suppressed spectroscopy is illustrated with example observations of Seyfert galaxies and a low mass star.
The GNOSIS background is dominated by detector dark current below 1.67 m and by thermal emission above 1.67 m. After subtracting these we detect an unidentified residual interline component of photons s-1 m-2 arcsec-2 m-1, comparable to previous measurements. This component is equally bright in the suppressed and control spectra. We have investigated the possible source of the interline component, but were unable to discriminate between a possible instrumental artifact and intrinsic atmospheric emission. Resolving the source of this emission is crucial for the design of fully optimised OH suppression spectrographs. The next generation OH suppression spectrograph will be focussed on resolving the source of the interline component, taking advantage of better optimisation for a fibre Bragg grating feed incorporating refinements of design based on our findings from GNOSIS. We quantify the necessary improvements for an optimal OH suppressing fibre spectrograph design.
keywords:
infrared:general–instrumentation:miscellaneous–atmospheric effects1 Introduction
Observations at near-infrared wavelengths are severely hindered by the night-sky background. The night-sky surface brightness is AB mag arcsec-2 in the H band, compared to AB mag arcsec-2 in the V band. This results in high Poisson noise in any observation. Compounded with this, the night-sky brightness varies by factors of per cent on the timescale of minutes (Ramsay et al. 1992; Frey et al. 2000), with a further gradual dimming of about a factor of 2 throughout the night (Shimazaki & Laird 1970). This temporal variability results in a high systematic noise when performing sky subtraction, which is not trivial to remove (e.g. Davies 2007; Sharp & Parkinson 2010).
In the J and H bands the dominant sources of background are the Meinel bands of emission lines resulting from the rotational and vibrational de-excitation of OH molecules (Meinel 1950; Dufay 1951). We have reviewed the near-infrared background, and in particular the characteristics of the OH emission line spectrum in an earlier paper (Ellis & Bland-Hawthorn 2008). We note that although they are very bright, the OH lines are intrinsically narrow (FWHM m), and between the OH lines the night-sky background should be very faint, possibly as low as photons s-1 m-2 arcsec-2 m-1 if the background is dominated by zodiacal scattered light, and is likely to be at least as faint as photons s-1 m-2 arcsec-2 m-1 as shown by spectroscopic observations made by Maihara et al. (1993). Thus, if the OH lines can be efficiently filtered from the night-sky spectrum, whilst maintaining good throughput between the lines, it should be possible to achieve a dark background in the NIR, allowing much deeper observations than possible hitherto.
This paper presents the first results from an instrument designed to achieve exactly this efficient filtering of the OH skylines. The filtering is achieved using fibre Bragg gratings (FBGs). FBGs were originally developed for use in telecommunications, and required significant modification to be used for OH suppression (see Bland-Hawthorn et al. 2011 for a comprehensive treatment on the physics of OH suppression with FBGs). Firstly, it was necessary to significantly increase the number of notches in each grating (typically only one notch is used in devices used in telecommunications) and the wavelength range of the devices which were available at the time, a breakthrough which was enabled with the design of aperiodic FBGs (Bland-Hawthorn et al. 2004). Secondly it was required to develop a multi-mode to single-mode fibre converter (Leon-Saval et al. 2005; Noordegraaf et al. 2009), since at the plate-scale of typical telescopes the narrow core of a single mode fibre has too small a field-of-view to collect an adequate amount of light from the seeing disc. Subsequent refinement (Bland-Hawthorn et al. 2008, 2011) has resulted in the latest FBGs being able to suppress 103 notches over a wavelength range of 230 nm, which is achieved using two devices in series.
Ellis & Bland-Hawthorn (2008) presented the potential benefit for astronomy of OH suppression with FBGs and described the expected performance. Ellis & Bland-Hawthorn (2008) point out that a key benefit of OH suppression with FBGs compared to other previously suggested methods of OH suppression (e.g. high dispersion masking, Maihara & Iwamuro 2000) is that the OH light is removed before it enters the spectrograph and in a manner dependent only on wavelength. Hence the interline continuum is not contaminated with scattered OH light within the spectrograph which can otherwise dominate other sources of interline continuum. The testing of this prediction was a central goal of GNOSIS commissioning.
The first on-sky tests of OH suppression with FBGs were performed at the Anglo-Australian Telescope in December 2008. This experiment consisted of two multimode fibres pointed directly at the sky through hole in the AAT dome wall. Both fibres fed a photonic lantern (see § 2), one of which had FBGs inserted, and the other did not, to serve as a control. The results of these tests are described in Bland-Hawthorn et al. (2009, 2011), and demonstrated the clean suppression of the OH lines. However, since each fibre accepted light from a degree patch of sky these tests could not perform observations of individual sources, nor could they measure the interline continuum since every observation included light from many stars and other sources.
We have designed, built and commissioned the first instrument to use FBGs for OH suppression. GNOSIS is an OH suppression unit designed to feed the IRIS2 infrared imaging spectrograph at the AAT (Tinney et al. 2004). The name is an acronym for Gemini Near-infrared OH Suppression IFU System, revealing the intention to install a similar system on the GNIRS spectrograph at Gemini North (Elias et al. 1998, 2006b, 2006a) at a future date. A summary description of the instrument is given in section 2 below. In this paper we concentrate on the performance and results of the OH suppression. We describe the observations in section 3 and we present the results in section 4 giving details of throughput, sensitivity and background. The near-infrared background will be examined in detail in a future paper (Trinh et al., in prep.), examining the various components of the background and their dependence on moonlight, ecliptic latitude, airmass, Galactic latitude etc.; a brief description of the main components will be given here. In section 4.4 we present observations of two Seyfert galaxies and an L/T dwarf illustrative of OH suppression. In section 5 we discuss our results in the context of the benefit of OH suppression to NIR spectroscopy and in the context of lessons for future OH suppressed instruments.
2 GNOSIS
The optical light path for GNOSIS is illustrated in Figure 1. A 7 element lenslet array accepts light from the f/8 Cassegrain focus and feeds this to seven 50m core fibres. The individual lenslets subtend a width (from face to face) of 0.4 arcsec on the sky. Each of the 50m core fibres is capable of carrying modes, but light is injected at less than the full numerical aperture of the fibres (i.e. a slower beam) such that only modes are carried. These fibres are spliced to a photonic lantern (Leon-Saval et al. 2005; Noordegraaf et al. 2009), which converts a multimode fibre (MMF) into a parallel array of single mode fibres (SMFs) via a fibre taper; in the case of GNOSIS into 19 single mode fibres since there are 19 modes per fibre. These single mode fibres are each spliced to two FBGs in series which suppress the 206 brightest OH lines (i.e. 103 closely spaced doublets) between and 1.7 m. These FBGs are then spliced to a reverse photonic lantern converting each of the SMFs back into 7 MMFs. These are connected to a 12m fibre run which leads to IRIS2, located on the dome floor beneath the telescope. The ends of the fibres form a pseudo-slit, the output of which is reimaged via two lenses into IRIS2. A custom slit mask within IRIS2 blocks extraneous light. IRIS2 has a Rockwell Hawaii-1 detector with pixels, a dark current of 0.015 e- s-1 and an effective read noise of e- when using an up-the-ramp non-destructive read-out mode. The point spread function of GNOSIS with IRIS2 was measured to be 2.0 pixels FWHM, which gives a spectral resolving power of . The mean dispersion was measured to be Å pixel-1. A full description of the instrument may be found in a forthcoming paper (Trinh et al. in prep.).
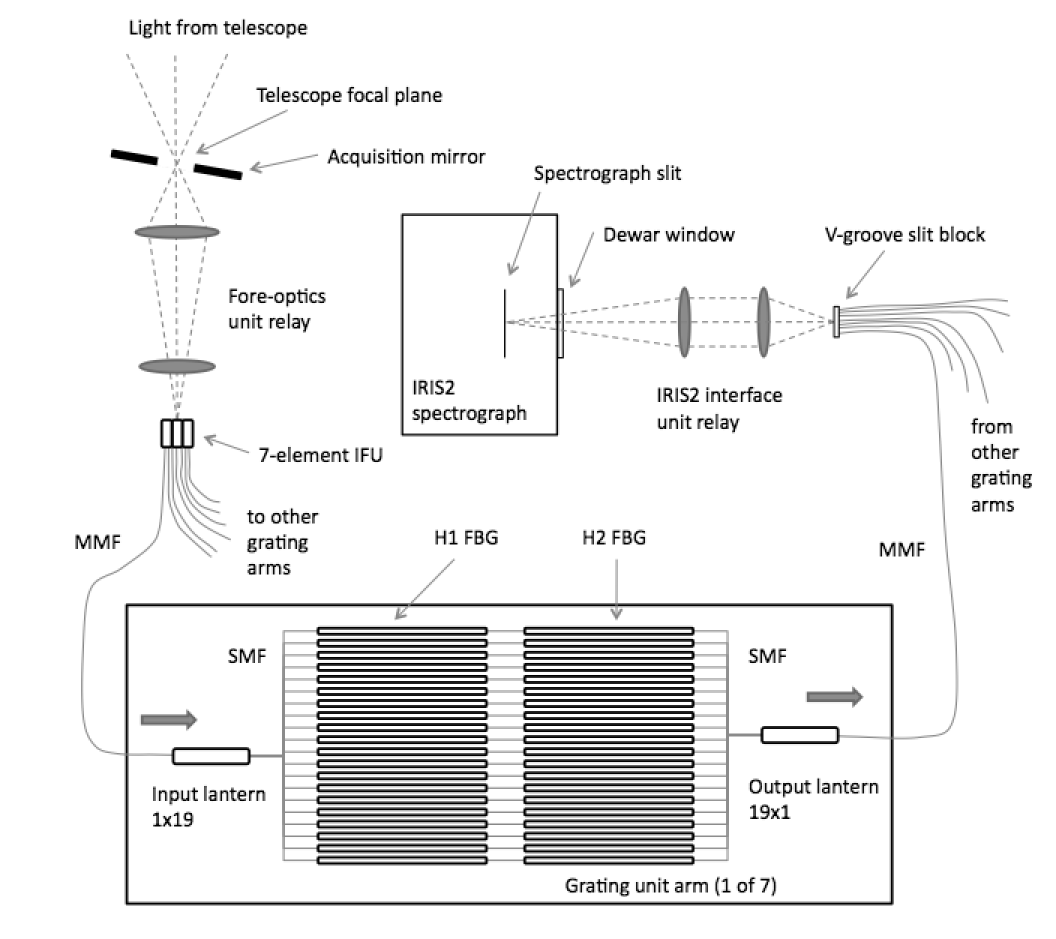
The properties of the GNOSIS system are given in Table 1. These include properties of GNOSIS per se and also those properties of IRIS2 on which GNOSIS observations depend. The observed wavelength range is defined by the spectrograph and the blocking filter, and is larger than the OH suppressed range which is that of the FBGs.
| Total field of view | 0.97 arcsec2 |
|---|---|
| Field of view per IFU element | 0.14 arcsec2 |
| Spectral resolving power | 2350 |
| PSF FWHM | 2 pixels |
| Dispersion | Å pix-1 |
| Observed wavelength range | 1.49 – 1.77m |
| OH suppressed range | 1.47 – 1.7m |
| Read noise (MRM) | e- |
| Dark current | e- s-1 |
3 Observations
GNOSIS was commissioned on five separate observing runs in March, May, July, September and November of 2011. In this paper we present only observations from the September and November commissioning runs, which incorporate the improvements made to the instrument in the previous commissioning runs. The observations presented are listed in Table 2. We present four different experiments: (i) measurement of the instrument throughput from standard star observations, (ii) measurement of the night sky background and (iii) measurement of the instrument sensitivity by observations of a low-surface brightness galaxy, and (iv) observations of Seyfert galaxies illustrating the benefits of OH suppression.
All observations were made using an up-the-ramp read mode to minimise the effect of detector read noise; we have recorded the period and number of reads in Table 2; the final exposure time for an individual frame is . All observations of objects included an equal amount of time spent on sky, and followed an object-sky-sky-object pattern. We give the total number of object frames as “Nods” in Table 2. For observations on 1st – 4th September we disconnected a MMF from the grating unit, to provide a control fibre with no OH suppression, as indicated in the ‘Control’ column of Table 2.
| Object | Date | Period (s) | Reads | Nods | Total exposure (s) | Control | Comments |
|---|---|---|---|---|---|---|---|
| Sky | 1st Sep 2011 | 30 | 61 | 6 | 10800 | Y | |
| Sky | 2nd Sep 2011 | 30 | 61 | 3 | 5400 | Y | |
| HIP 104664 | 3rd Sep 2011 | 5 | 13 | 2 | 120 | Y | A0V standard star, mag |
| HIP 109476 | 5th Sep 2011 | 5 | 13 | 2 | 120 | N | A0V standard star, mag |
| Sky | 3rd Sep 2011 | 30 | 61 | 4 | 7200 | Y | |
| Sky | 4th Sep 2011 | 30 | 61 | 2 | 1800 | Y | |
| HIZOA J0836-43 | 26th Nov 2011 | 15 | 61 | 2 | 1800 | Y | LSBG1, mag arcsec-2 |
| NGC 7674 | 4th Sep 2011 | 15 | 61 | 2 | 1800 | Y | Seyfert galaxy |
| NGC 7714 | 4th Sep 2011 | 15 | 61 | 2 | 1800 | Y | Seyfert galaxy |
| 2MASS 0257-3105 | 27th Nov 2011 | 15 | 61 | 1 | 900 | N | Candidate L7 dwarf |
| 1. Low surface brightness galaxy. | |||||||
3.1 Data reduction
We reduced the data using bespoke code written as a Mathematica notebook, except for the first step of collapsing the data cubes (see § 3.1.1), which was performed using a C program. Since the night sky background is considerably reduced using OH suppression the issue of correctly accounting for the effects of detector noise becomes very important, and we have paid careful attention to this in our data reduction. Our procedure was as follows.
3.1.1 Collapsing the data cubes
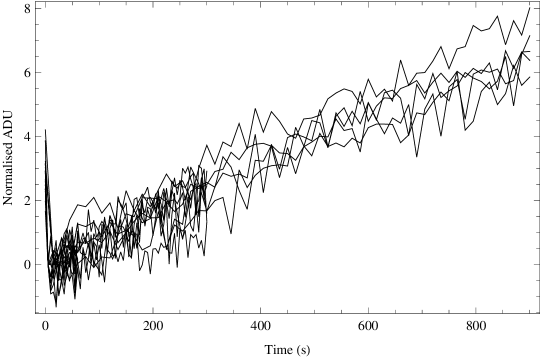
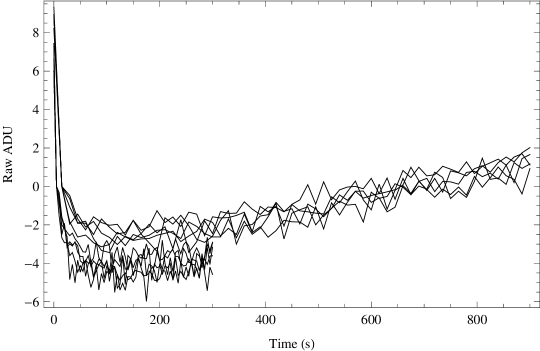
For each frame the detector was used in a multiple-read mode (MRM) using an up-the-ramp sampling, with intervals of either 5, 15 or 30s and either 13 or 61 reads, see Table 2. This means that the detector is re-set, then read non-destructively at a fixed time interval for a specified number of times. This enables non-linearity in the detector response to be removed. Upon investigation we found significant non-linearity in the first few reads. For dark frames with the blank filters in, if one always observes in MRM then the first read after re-set is higher than the second read, and thereafter the counts are linear until about ADU (see Figure 2a). If the MRM exposure follows a double read mode observation (DRM; i.e. only two reads immediately prior to and after the exposure), then the first reads show a decline in the bias levels (see Figure 2b). This effect has been seen by one of us (AJH) in other Hawaii-1 PACE detectors. The largest observed drop in bias levels in the first few reads is ADU, which is insignificant under typical non-OH suppressed observations since the brightness of the night sky swamps such small variations. Thus for normal NIR observations a linear least-squares fit to the reads suffices to recover the incident count rate. However, in the case of OH suppressed observations this is no longer so, since the incident count rate can be very low for pixels between the OH lines. Therefore we have simply dropped the first 5 reads from our data cubes, before performing a linear least squares fit to the remaining data. The slope of this fit is then multiplied by the original number of reads minus one to recover the true incident count rate.
3.1.2 Detector linearity
The detector non-linearity due to the filling of the pixel wells is mitigated by keeping the counts per pixel below 20,000 ADU. Thus in collapsing the data cubes as described above, we use a linear least squares fit. Thereafter we correct for any non-linearity following the procedure given on the IRIS2 web pages (http://www.aao.gov.au/AAO/iris2/iris2_linearity.html).
3.1.3 Background subtraction
The GNOSIS background consists of dark current, instrument thermal background, telescope thermal background, and the night sky background (including OH emission, thermal emission, zodiacal scattered light, moonlight etc.). For our object observations we nod the telescope between object and sky, and thus all the background can be subtracted simultaneously using the sky observations. Pairs of observations are first subtracted, then averaged using the median if there is more than two.
For our sky observations this is not possible. In this case we subtract the dark current and the thermal background separately. The dark current is subtracted using the median of several dark frames of the same read mode and exposure time as the observations.
We have measured the thermal component from “cold frame” observations. A cold frame is an observation for which the GNOSIS fore-optics were removed from the Cassegrain focus and pointed directly into a dewar filled with liquid nitrogen. Thus the cold frame contains the GNOSIS fore-optics and IRIS2 thermal backgrounds and the detector dark current alone. The telescope thermal background should be much lower than the instrument background since the emissivity from the mirror should be less than per cent, and the emissivity from the Cassegrain hole is from a much smaller solid angle.
The average cold frames are shown in Figure 3. The counts have been calibrated to reproduce a K, 100 per cent emissivity black body, i.e. the expected emission from the slit block etc. at the output end of GNOSIS. This calibration provides an independent check of the efficiency of IRIS2 as discussed in section 4.1.
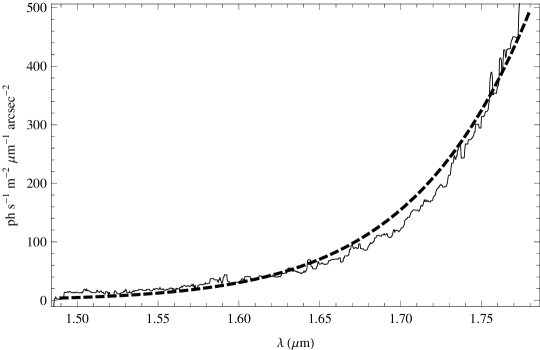
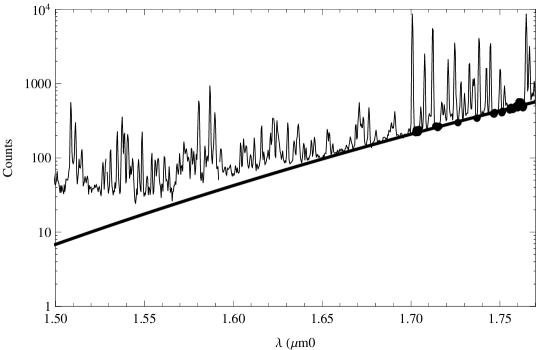
Obtaining cold frames is a significant overhead on observing time since the fore-optics must be removed and then re-fitted and re-aligned during the night when the optics are at the same temperature as for the sky frames. Thus in practice we fit a black-body spectrum to our observations by choosing regions of the continuum between the OH lines with m. The best fitting model is subtracted from observations. We note that thermal emission is only approximately black-body (see Figure. 3). However, a more general function may inadvertently fit and subtract intrinsic features of the sky emission. Since we do not know the exact function of the thermal emission we revert to an approximate, but physically motivated black-body fit. An example black-body fit is shown in Figure 4. This is actually done after the residual background correction step detailed in § 3.1.8 below.
3.1.4 Spectral extraction
Spectroscopic observations of the illuminated dome flat field screen were taken to provide a trace of the spectra across the detector. The centre of each of the 7 spectra is calculated at each spectral pixel. This is done by fitting the sum of seven Gaussians to the pixel counts in the spatial direction at each spectral pixel. The Gaussians for each fibre are assumed to have identical and to be equally spaced. The fit yields the centre of each Gaussian, and this is stored in a look-up table, along with the of the Gaussian fit. The separation between the spectra is 11 pixels, which is times the FWHM of the PSF, and therefore cross-talk between the spectra is negligible.
Object spectra are then extracted following the “Gaussian summation extraction by least squares” method of Sharp & Birchall (2010), i.e. the count for each spectral pixel, is given by,
| (1) |
where the sum ranges over each pixel, , in the spatial direction between the pitch between spectra, is the count at each pixel, is the variance on the count, and is the value of the normalised Gaussian profile at that pixel. This method minimises the contribution due to noise in the extraction.
3.1.5 Fibre-to-fibre variations
We next correct for variations in throughput between fibres. The fibre-to-fibre variation is measured from dispersed images of the illuminated dome flat field screen which are extracted in the same manner as the object spectra. The normalised fibre-to-fibre variation is the ratio of the total flux in each spectrum to the average of the total flux of all seven spectra. The extracted spectra are divided by the normalised variation.
3.1.6 Spectral combination
The seven extracted spectra are combined by taking the sum of each spectral pixel. If a control fibre was used, this is excluded from the combination. This step neglects to take into account differences in the wavelength solution of each spectrum, which are less than 1.5 pixels over most of the detector. We have checked that not correcting for these differences does not introduce spurious signals by repeating the reduction of the sky spectrum for a single fibre only. We find that the single extracted spectrum is consistent with that of the summed spectrum.
3.1.7 Wavelength calibration
The wavelength calibration is achieved using Xe arc lamp spectra. These spectra are extracted and combined as described above. The Xe lines are automatically detected and a cubic polynomial is fit to give the wavelength as a function of spectral pixel number. This solution is then applied to the object spectra. The wavelength calibration is accurate to Å, and is limited by the slight shift in the dispersion solution for each spectrum.
3.1.8 Residual background subtraction
Hawaii-1 detectors are known to suffer from significant inter-quadrant cross-talk (Tinney et al. 2003111See also
http://www.eso.org/gfinger/hawaii_1Kx1K/crosstalk_rock/crosstalk.pdf); if a bright object appears at pixel , then there will also be a faint glow at pixel (where is the modulo operation), and along the entire row . The cross-talk between quadrants does not affect GNOSIS observations, since all seven spectra are located on the lower two quadrants, but the cross talk along rows does.
The cross-talk along a row can be measured in the region of the spectrum at m, since this region ought to be completely dark due to the spectroscopic blocking filter. This measurement may also include other residual background from systematic errors in the previous subtraction, due to changing background levels. We measure the mean count rate at m and subtract it from the spectrum.
3.1.9 Instrument response and telluric correction
The efficiency of the GNOSIS system, including the atmosphere, the telescope and IRIS2, is measured from observations of A0V stars. These observations are reduced as described in the previous steps. We then take a model spectrum of Vega (Castelli & Kurucz 1994) and divide the observations by this to give a relative throughput of the system as a function of wavelength, including telluric features. Note that this will also include the averaged pixel-to-pixel variation in our extracted spectra, and hence includes the detector flat-field response. The relative throughput is normalised between 1.5 and 1.69 m to give the instrument response function. The object spectra are then divided by the instrument response function.
3.1.10 Flux calibration
The observations of the telluric standard stars described in the previous step can also be used to estimate the flux calibration. Since the magnitude of the A0V stars is already known, we can scale the model Vega spectrum to the appropriate brightness before dividing the observed spectrum to yield a flux calibrated correction. This step is not very accurate since scaling the Vega spectrum relies on knowing the aperture losses of the IFU at the time of observation, which in turn depends upon the seeing and acquisition, which are not readily measurable. The flux calibration is discussed further in § 4.1.2.
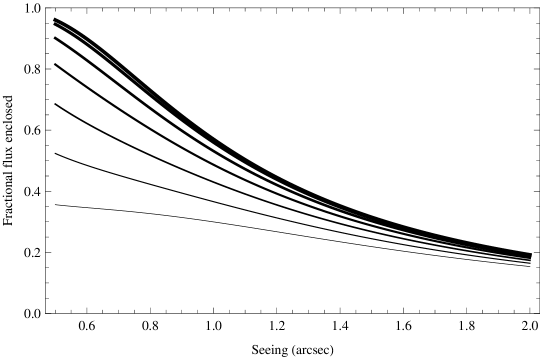
Due to the difficulty of measuring the seeing and the centring of our objects in the IFU we have computed the aperture losses for a seven element hexagonal array, assuming the seeing profile is Gaussian. The results are shown in Figure 5 as a function of seeing for several values of mis-alignment. Assuming that we can accurately align to within one element of the IFU, i.e. the offset is arcsec, and the seeing is 1.2 arcsec (extrapolated from measurements taken with the acquisition camera in the I band during the observations), then the typical aperture loss for a point source is .
4 Results
We now describe the results of the first three experiments, viz. the instrument throughput, the night sky background and the instrument sensitivity.
4.1 Instrument throughput
4.1.1 Laboratory measurements
The throughput of GNOSIS was measured in the laboratory using a super-continuum source and a near-infrared camera (see Trinh et al. in preparation for details). The total end-to-end throughput of GNOSIS is per cent and the throughputs of the individual components are given in Table 3 with the estimated errors.
The throughput of the AAT is approximately for the two reflections off the aluminium coated primary and secondary mirrors, which is estimated from a reflectivity of bare Al, combined with an extra throughput from the accumulation of dirt on the mirrors etc. This extra loss is compatible with that measured in the visible on the AAT.
We have estimated the throughput of IRIS2 in two ways. First we used the IRIS2 imaging exposure calculator to estimate the efficiency of an imaging observation, which for H is per cent. Combined with the throughput of the grism ( per cent) this gives a total efficiency of per cent. Secondly we used the observations of the “cold frames” (see § 3.1.3) compared to a theoretical blackbody spectrum taking into account the area and solid angle of the IRIS2 slit-mask holes and assuming K as recorded, and 100 per cent emissivity, since most of the emission will come from the slit block and other mechanical parts surrounding the fibres due to the oversized slit mask holes. This also yielded an efficiency of 12 per cent.
The end-to-end system throughput is therefore expected to be, per cent, or per cent for a point source including typical aperture losses. We emphasise that this low throughput is not an intrinsic property of OH suppression systems, but is rather a consequence of retro-fitting an OH suppression unit to an existing spectrograph, which already has only 12 per cent throughput. The throughput of GNOSIS itself is 36 per cent and is limited mainly by the photonic lanterns. This will be discussed further in § 5.
4.1.2 Standard star measurements
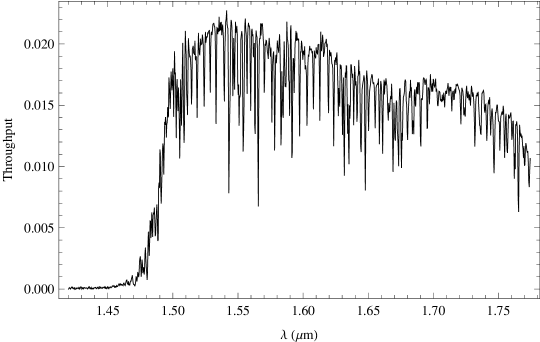
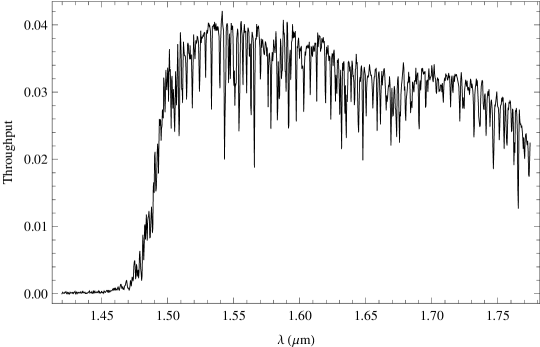
We have also measured the end-to-end throughput as a function of wavelength from our observations of A0V stars. Examples are shown in Figure 6. The notches in the FBGs are visible as the significant narrow dips in the throughput. Note that in this graph the notches have been convolved with the spectrograph point spread function, so they appear shallower than the actual suppression depth. The measurement for HIP 104664 does not include the control fibre. The measured values are very sensitive to seeing and aperture losses as shown in Figure 5, but are within the errors of the anticipated throughput estimate in Table 3. In the case of HIP 109476 the measured throughput would require very low aperture losses due to exceptional seeing, suggesting some of the values in the table may be pessimistic. However, we assume the conservative values in Table 3 for the rest of the paper.
| Element | Throughput | Cumulative throughput |
|---|---|---|
| Primary mirror | ||
| Secondary mirror | ||
| GNOSIS: | ||
| Fore-optics | ||
| IFU | ||
| Grating unit | ||
| Relay-optics | ||
| Total | 0.356 0.05 | |
| Relay alignment | ||
| IRIS2 | ||
| Aperture losses |
4.2 Night sky background
Observations of blank sky were made as targeted observations and as “sky frames” during observations of objects. Figure 7 shows the reduced sky spectra for 7.5 hours of observations on the 1st – 4th of September. These data were all deg from the moon, deg south of the Galactic plane, deg off the ecliptic plane and at an airmass . Therefore the night sky spectra should not be significantly contaminated by moonlight, starlight, or zodiacal scattered light.
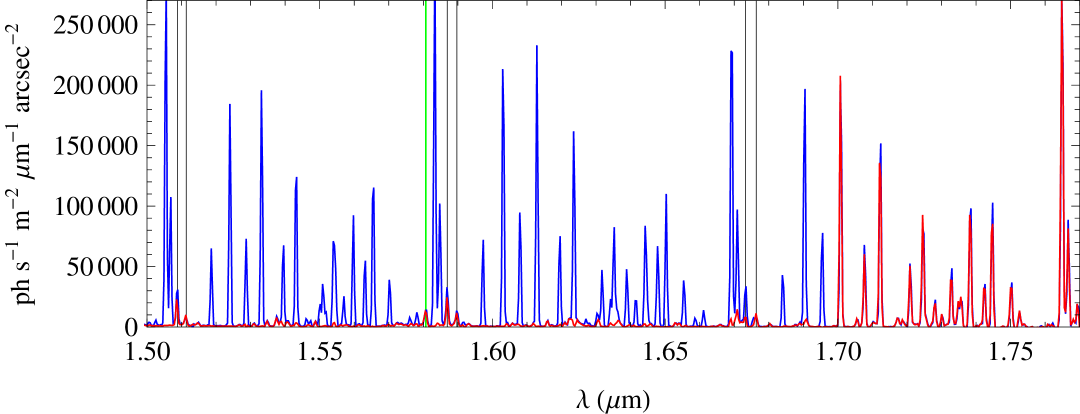
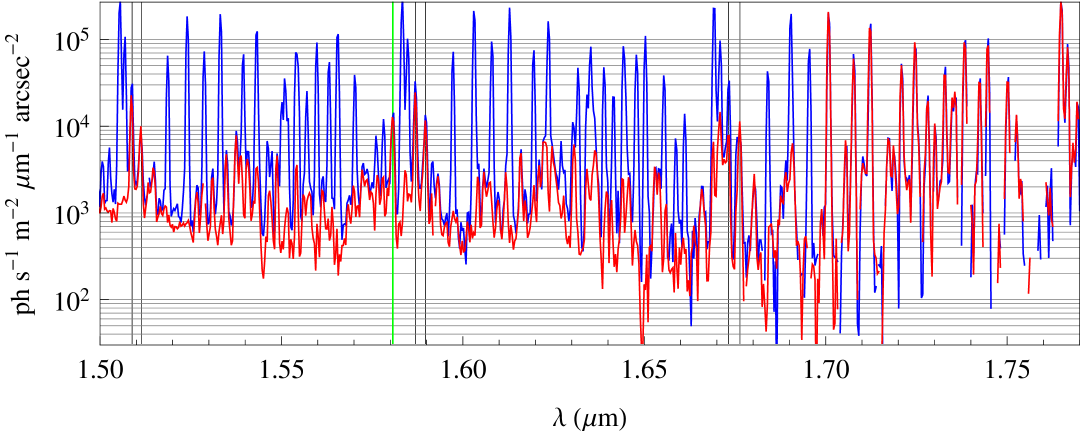
4.2.1 OH suppression
The OH lines between 1.5 – 1.7 m are strongly suppressed. We have measured the suppression factor for 57 doublets; for the remaining 46 doublets we were unable to obtain a good fit to the unsuppressed line due to either line blending, intrinsic faintness or due to the filter cut-off (at m). In most cases the measured strength of the suppressed line is poorly constrained because the flux is so low. Nevertheless, of the 57 doublets 78 per cent meet or exceed the target specifications.
Some quite bright lines are not suppressed by the FBGs. These are marked with black and green vertical lines in Figure 7. The green line is an O2 emission line resulting from the a-X v=0 – 1 vibrational transition (Jeremy Bailey, private communication). This line is very bright in the day time and fades rapidly throughout twilight, but there is faint persistent emission throughout the night. It was not included in our FBG designs.
The lines marked in black are OH lines from the Q1(3.5) and Q1(4.5) rotational lines in the 3–1, 4–2 and 5–3 vibrational transitions. The FBGs have notches of dB for all these lines, printed at the wavelengths given by Rousselot et al. (2000). However, we measure a mean suppression factor of only dB. There may be an issue with the printed notch wavelengths of these particular transitions due to a larger spacing between the individual doublets than for other transitions (Pierre Rousselot, private communication). We show the wavelengths and gap size of the transitions in question as modelled by Rousselot et al. (2000) and as measured by Abrams et al. (1994) in Table 4. The mean wavelengths of the doublets are identical in each case, but the measured gap size is considerably larger; this is not a problem for the Q1(0.5), Q1(1.5) and Q1(2.5) transitions for which the doublets are much more closely spaced ( pm). However for the Q(3.5) and Q(4.5) transitions the doublet spacings derived from the Abrams et al. (1994) measurements are larger than the typical GNOSIS FBG notch widths, i.e. the individual lines fall either side of the notch. These lines account for 37 per cent of the doublets which did not meet the target suppression depth.
| Rousselot | Abrams | |||||||
|---|---|---|---|---|---|---|---|---|
| e | f | mean | e | f | mean | |||
| 3–1 | ||||||||
| Q1(3.5) | 1.50883 | 1.50882 | 1.50883 | 0.000013 | 1.50892 | 1.50874 | 1.50883 | 0.000177 |
| Q1(4.5) | 1.51138 | 1.51136 | 1.51137 | 0.000022 | 1.51153 | 1.51121 | 1.51137 | 0.000317 |
| 4–2 | ||||||||
| Q1(3.5) | 1.58694 | 1.58692 | 1.58693 | 0.000014 | 1.58702 | 1.58693 | 1.58684 | 0.000181 |
| Q1(4.5) | 1.58974 | 1.58972 | 1.58973 | 0.000025 | 1.58989 | 1.58957 | 1.58973 | 0.000326 |
| 5–3 | ||||||||
| Q1(3.5) | 1.67397 | 1.67324 | 1.67367 | 0.00073 | 1.67334 | 1.67316 | 1.67325 | 0.000185 |
| Q1(4.5) | 1.67637 | 1.67634 | 1.67636 | 0.000029 | 1.67652 | 1.67619 | 1.67636 | 0.000333 |
4.2.2 Interline component
We have measured the level of suppression at each pixel by dividing the control spectrum by the suppressed spectrum (after first correcting the control spectrum for the fact that this is from a single fibre compared to six fibres for the suppressed spectrum), this is shown in Figure 8. The mean reduction per pixel between and m is , and the median is . The reduction of the integrated background between and m is .

To compare the interline components in the suppressed and control spectra we first subtract the detector dark current and instrument thermal emission. However, these components are brighter than the interline component we are trying to measure, and the subtraction is inevitably noisy. Figure 9 shows a comparison of the electrons per second per pixel due to dark current, thermal emission and suppressed and unsuppressed OH lines. The statistical fractional error on the suppressed observations is shown in Figure 10, which is calculated from the mean and standard deviation of counts per pixel from15 separate half-hour exposures. The typical error on the interline component is per cent; however there may be unquantified systematic errors on these measurements.
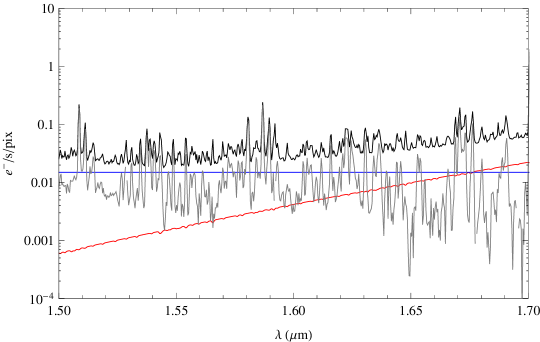
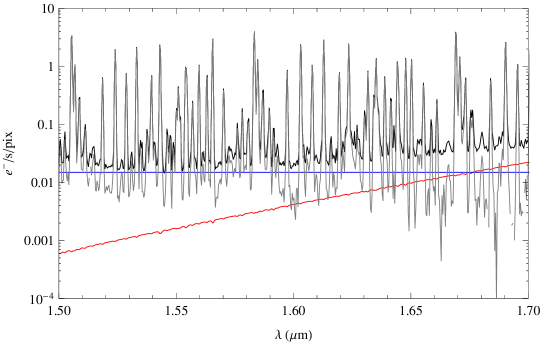
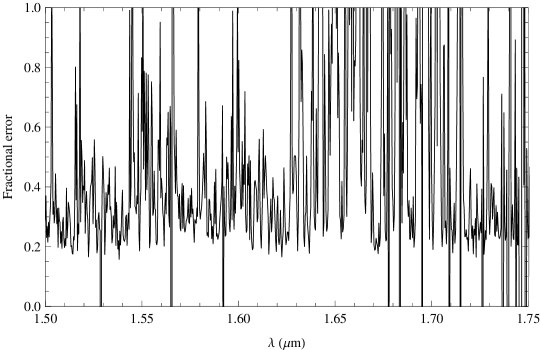
Nevertheless, after dark and thermal subtraction, there is no discernible reduction in the background between the OH lines. This is unexpected; the models of Ellis & Bland-Hawthorn (2008) show that if the background (after dark subtraction) is composed of thermal emission, zodiacal scattered light and OH lines then the interline region should be dominated by light that originates as OH lines that is scattered by the spectrograph. Thus suppressing the OH lines should also suppress this light scattered from the OH lines. The fact that we do not see this suggests four possibilities: (i) there is residual instrumental emission which has not been properly removed in the data reduction, (ii) the IRIS2 spectrograph does not scatter significant amounts of OH light between the lines, (iii) the interline region is dominated by some source that Ellis & Bland-Hawthorn (2008) did not account for, (iv) the FBGs are not suppressing the OH lines as predicted, and hence the reduction is not as predicted.
We have addressed (i), the possibility of residual thermal emission, as fully as possible in our data reduction method (§ 3.1). However we are operating in the regime of very low count rates, such that systematic errors may become significant. The raw ADU per pixel in the interline component region is in a half hour exposure, which corresponds to e- per pixel, of which e- per pixel are due to the sky and the detector dark current contributes e- per pixel . That is we are detecting less that 1 e- per pixel per minute, and we are dominated by detector noise. At this level systematics become very important. For example the effective read noise is e- per pixel which alone gives per cent uncertainty in the interline component measurements. There are systematics in detector linearity such as discussed in section 3.1.1, and there may be other effects such as reciprocity failure (Biesiadzinski et al. 2011) which are very difficult to characterise.
We can discount (ii) since we have measured the scattering of IRIS2, and indeed it was this empirical scattering model from IRIS2 that was used in the models of Ellis & Bland-Hawthorn (2008). There is a small change in the PSF of IRIS2 due to a different slit and a different f-ratio at the input, however this will affect only the Gaussian core of the PSF, and then only slightly, and not at all the Lorentzian wings of the PSF.
Regarding (iii), we have searched for other molecular bands and lines of emission in the H band. We used the SpectralCalc.com facility to compute the emission line intensities from the HITRAN2008 models (Rothman et al. 2009). We included lines from H2O, CO2, O3, N2O, CO, CH4, O2, NO, SO2, NO2, NH3, HNO3, N2, HF, HCl, HBr, HI, ClO, OCS, H2CO, HOCl, HCN, CH3Cl, H2O2, C2H2, C2H6, PH3, COF2, SF6, H2S, HCOOH, HO2 and ClONO2. The relative intensities were taken directly from the atmospheric paths of SpectralCalc.com assuming an observing altitude of 1.2 km, a target height of 600km, standard atmospheric conditions and zenith angle of 0 deg. The resulting emission is shown in Figure 11 where we have normalised the intensity to match roughly the interline component. There are hints that some of the structure in the interline component arises from certain molecular bands. The O2 band at 1.58 m and a CH4 feature at m are most obvious, but there are possibly some other broad features due to CO2, N2O and C2H2. However the relative intensities of these features are not right, and neither is the overall shape of the combined emission from these molecules. Moreover, with the exception of O2 and CH4 there are no features corresponding to the obvious emission lines seen throughout.
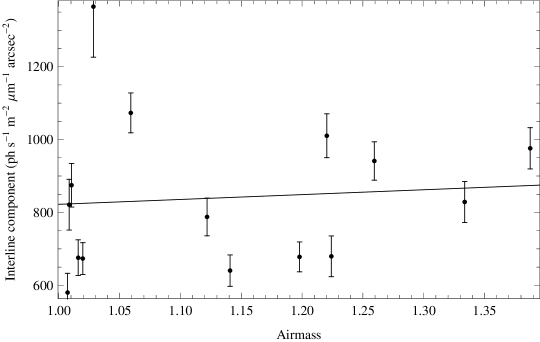
Scattering from aerosols or dust in the upper atmosphere, and certain chemical reactions may also produce a nightglow continuum. For example the continuum produced in the reaction NO O NO h, has been found to correlate well with the optical nightglow (Sternberg & Ingham 1972; Sternberg 1972), and it has been suggested (Content 1996)that this may increase in the NIR and is of the same order as the brightness of the interline component measured by Maihara et al. (1993). We have measured the interline component strength for individual observations as a function of airmass and find no trend, see Figure 12. This suggests that the interline component does not have an atmospheric origin, but we caution that the atmospheric emission could be temporally variable, as for the OH lines, which could mask any dependence on airmass. In summary there are individual features of the interline component due to other atmospheric molecular emission, but as yet we cannot explain the overall structure of the interline emission.
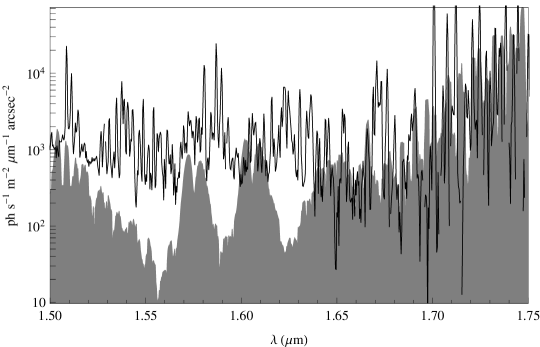
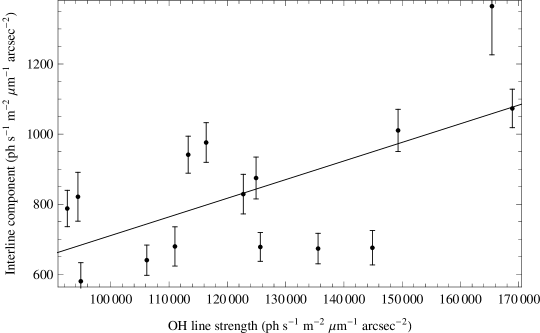
Finally we consider (iv), that there may still be unsuppressed OH emission dominating the interline component (e.g. the Q1(3.5) and Q1(4.5) transitions discussed in § 4.2.1). We have tested this and find a weak correlation between the OH line strength and the interline component strength for individual observations (recall that the OH line strength varies by about 10 per cent on the timescale of minutes Ramsay et al. 1992; Frey et al. 2000 and by a factor of throughout the night Shimazaki & Laird 1970), shown in Figure 13. The r2 goodness of fit is 0.38, with a significance of . Thus the OH line intensity does indeed affect the interline component. Nota bene, this is expected even with OH suppression, and is not an indication that the FBGs are not correctly suppressing the OH lines. Ellis & Bland-Hawthorn (2008) show that at a resolving power of the scattering from residual suppressed OH lines, even though very faint, will still dominate the interline region even after OH suppression. In fact it is the relative weakness of the correlation between interline component and OH line strength that must be explained, especially when coupled with the lack of dependence on airmass in Figure 12. This will at least in part be due to uncertainty in the measurements. The signal to noise on the interline component is poor, and the standard deviation of the residuals to the best fit shown in Figure 13 is 160 photons s-1 m-2 arcsec-2 m-1, which gives an indication as to the error on the interline component measurements. However, the weakness of the correlation may also be further indication that there is still some unidentified source of interline emission.
In summary, we feel confident that we can rule out (ii), i.e. we believe we understand the scattering function, but cannot rule out any of the other options. Instrumental artifacts, unknown atmospheric components and inaccurate modelling of the OH lines may all contribute to the interline component at some level.
4.3 Sensitivity
We have measured the sensitivity of GNOSIS with an observation of a low surface brightness galaxy, which obviates the need to address the problem of aperture losses. The galaxy selected was HIZOA J0836-43 (see Cluver et al. 2010), with an H band surface brightness of 17.3 mag arcsec-2, the details of which were kindly provided by Michelle Cluver. We obtained half an hour exposure on target, the details of which are given in Table 2. The resulting spectrum is shown in Figure 14 along with a spectrum with no sky or dark subtraction.
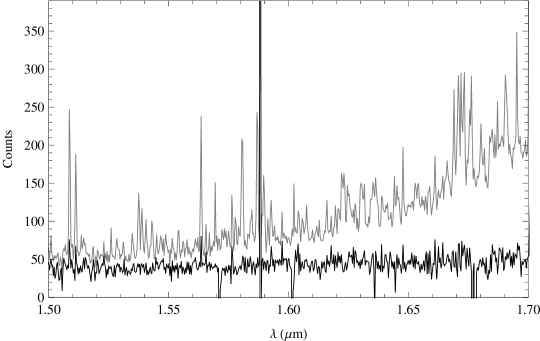
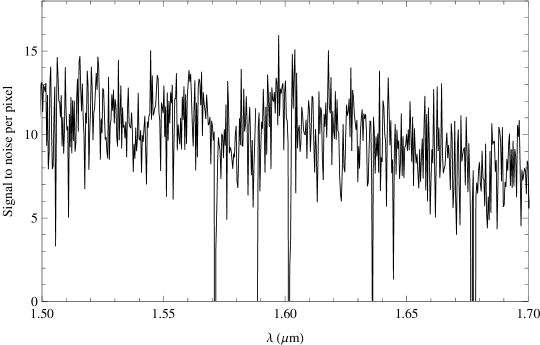
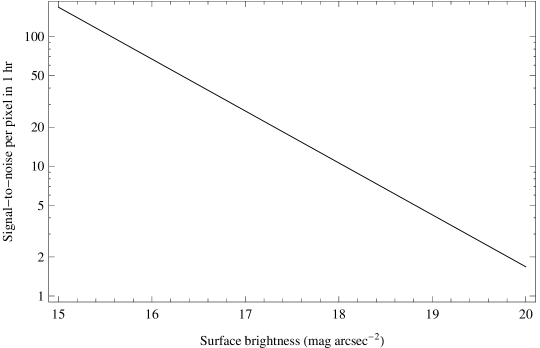
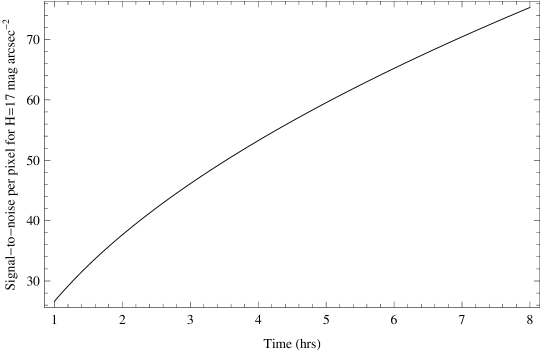
The signal-to-noise per pixel for this observation was calculated by dividing the sky-subtracted spectrum by the square root of the non-subtracted spectrum after first scaling by the detector gain and correcting to the full GNOSIS IFU area (as this spectrum is from only 6 of the 7 IFU elements). The signal-to-noise per pixel is shown in Figure 15. The median signal-to-noise per pixel is 10.1. An identical analysis on the control fibre yields an identical median signal-to-noise. This is because the OH suppression only improves the signal-to-noise near the night sky lines; between the lines the background is the same and these interline pixels dominate the calculation of the average signal-to-noise. The improvement that comes from the OH suppression is counteracted by the loss in throughput from the FBG unit. We note that this is not an inherent problem for OH suppression; improvements in throughput of the FBG unit along with lower thermal and detector backgrounds will improve the signal-to-noise. A better understanding of the interline component discussed in section 4.2.2 may also lead to improvements in the suppression of the interline background as proposed in Ellis & Bland-Hawthorn (2008). We have computed the median signal-to-noise as a function of time and magnitude, which are shown in Figure 16.
4.4 Illustrative observations
We now demonstrate the benefit of OH suppression with three illustrative observations. The first two are of [FeII] emission from the Seyfert galaxies, and allow a comparison of OH suppressed and non-OH suppressed observations. The third is of a candidate L7 dwarf star which is an example of OH suppressed observation of a continuum source. The purpose of these examples is not to show that GNOSIS is competitive with the current generation of NIR spectrographs. The prototype nature of GNOSIS results in a low overall throughput, a large number of pixels per square arcsecond and resultant high detector noise, and an efficiency loss in having to spend half the exposure time on blank sky, and therefore GNOSIS observations do not give any advantage over standard IRIS2 observations. Rather, we wish to show the potential of OH suppression, by means of a comparison of the OH suppressed and control spectra. With improvements to the throughput, the thermal background and the detector dark current similar observations of both emission line and continuum sources will be possible on much fainter objects. We discuss how future instruments can best benefit from the potential of OH suppression and what changes are necessary to do so (§ 5).
We give two examples of [FeII] emission from the Seyfert galaxies NGC 7674 and NGC 7714. In both cases we compare a single OH suppressed fibre to the single control fibre, shown in Figure 17. In the case of NGC 7714 the [FeII] emission falls between the OH lines and is clearly visible in both suppressed and non-suppressed spectra. In the case of NGC 7674 the [FeII] emission falls in a dense region of OH lines, but is still clearly visible in the suppressed spectrum, but less so in the non-suppressed spectrum.
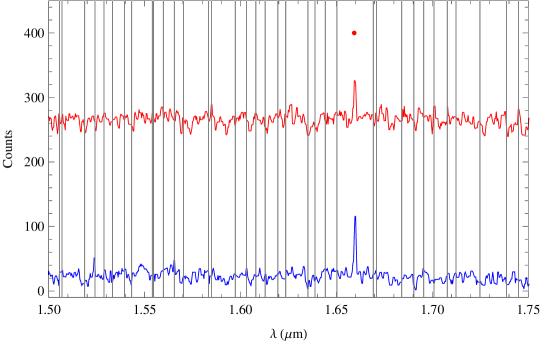
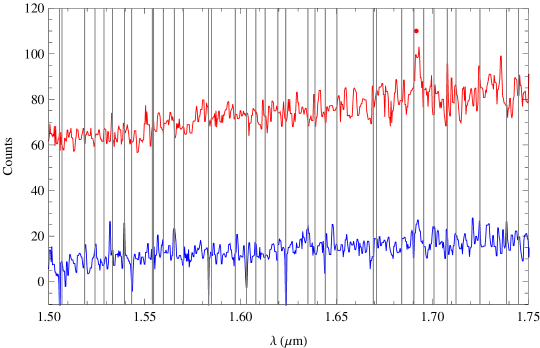
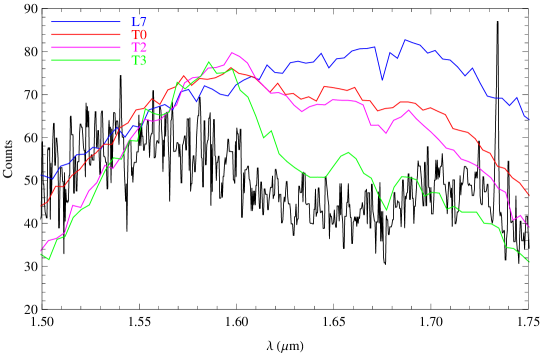
Figure 18 shows a GNOSIS spectrum of a candidate L7 dwarf, 2MASS J0257-3105, which was observed as part of Prof. C. Tinney’s scheduled GNOSIS observing on 27th Nov 2011 (see Table 2). For these observations no control fibre was used, and therefore no comparison of OH suppressed spectra to non-suppressed can be made. However, our experience observing brown dwarfs with IRIS2 tells us that the spectrum is comparable in quality and signal-to-noise to standard long slit IRIS2 spectroscopy. The observations provide an example of the kind of science which may be done with OH suppression on continuum sources. The object was selected as an L7 dwarf from Kirkpatrick et al. (2008). However, a comparison of the H band spectrum with standard spectra from Burgasser et al. (2004) shows that it has stronger CH4 absorption, similar to an early T dwarf. An exact spectral type is difficult to give since none of the standard spectra gives a perfect match.
5 Discussion
We have demonstrated the first instrument to employ OH suppression with fibre Bragg gratings. To test the performance of this new technology we made five key measurements: (i) the overall, and component, instrument throughput, (ii) the instrument sensitivity, (iii) the level of OH suppression, (iv) the interline component, (iv) illustrative observations of Seyfert galaxies. We now discuss the results of these measurements in the context of the continuing development of OH suppressed NIR spectrographs.
(i) The total throughput is per cent but the throughput of IRIS2 is only per cent while that of GNOSIS itself is per cent. The latter can be greatly improved by the following measures. First on a specialised OH suppression spectrograph the need for relay optics could be eliminated by using a fibre vacuum feed through. This would remove at least 4 optical surfaces, greatly improve alignment losses and have the additional benefit of lowering the thermal background. Secondly, an even larger improvement could be made in the photonic lanterns. Recent laboratory tests imply that the efficiency of the photonic lanterns is a function of the input f ratio, and that by feeding the lanterns at a slower speed we could increase the efficiency from 50 per cent to per cent. These tests are preliminary, but indicate that the coupling efficiency of the lanterns may depend on the mode being coupled.
(ii) The sensitivity of GNOSIS+IRIS2 is about that of IRIS2 when used in its standard spectrograph mode with a slit.. That is, in the particular implementation used for GNOSIS, the benefits of OH suppression are offset by lower throughput, higher detector background, higher thermal background and lower observing efficiency. The low throughput has been discussed above and in section 4.1.
The high detector background comes from the fact that a small field of view of 1.2 arcsec is being divided into 7 elements, and the spectra from each of these is being sampled by pixels, thus when extracting the spectra for each spectral pixel there is dark current and read noise from spatial pixels, compared to spatial pixels for the same sky area using IRIS2 (recall that GNOSIS feeds IRIS2 at a slower f-ratio than for long-slit IRIS2 observations). Since the background is dominated by detector dark current this is a significant loss of sensitivity.
The high thermal background results almost entirely from the slit block, and is a significant source of noise at m. GNOSIS observations are also less efficient than IRIS2 observations in that half the time must be spent on sky, whereas with IRIS2 the object can be nodded up and down the slit. Note that these problems are not intrinsic to OH suppression in general, and it is easy to envisage improved instruments that circumvent all these issues.
Using photonic lanterns with a larger number of cores will allow the use of larger diameter fibres and thus increase the field of view per fibre, thereby lessening the effects of detector background. This will require faster spectrograph optics of around .
The low observing efficiency is simply a matter of cost. If two IFUs can be afforded then cross beam switching of observations will ensure that all observing time is spent on target.
Of course there are also many improvements that should be made to the spectrograph itself to improve the overall efficiency. For example newer detectors with lower dark current and higher quantum efficiency, VPH gratings instead of grisms, and fixed format optics will all improve the throughput. These improvements would of course be true of non-OH suppressed spectrographs as well.
(iii) The suppression of the OH lines was a success. The sky spectra and the object spectra show that the OH lines can be cleanly removed whilst maintaining good throughput (in the FBGs themselves) between the lines. The level of suppression is high with per cent of the targeted lines suppressed at the required level. Of the lines which do not meet the required level of suppression 37 per cent are due to residuals from the Q1(3.5) and Q1(4.5) OH lines (§ 4.2.1). Similarly there is an unsuppressed O2 line.
(iv) The expected reduction of the interline component was not observed. This seems to indicate either an unaccounted source of interline emission, inaccuracy of our OH line models or unaccounted-for systematic errors.
Systematic errors are a real possibility since we are operating in a very low-count regime of less that 1 e- per pixel per minute, and we are dominated by detector noise. We have observed (and corrected for) systematic deviations from detector linearity as discussed in section 3.1.1, and have noted that there may still be other effects such as reciprocity failure (Biesiadzinski et al. 2011) which are very difficult to characterise.
We have already noted that specific transitions in the OH energy levels were not properly suppressed, which seems to be due to a larger energy gap between the doublets than predicted in our models. It is possible that other such errors may exist in fainter lines, or that other branches of lines are brighter than supposed, but we are unable to measure this with the current sensitivity. Unsuppressed faint OH lines could masquerade as continuum due to the spectrograph scattering.
On the other hand there could be emission from another source. A thorough search of the emission lines from 33 different molecules in the HITRAN2008 database cannot account for the structure and the faint lines we observe in the interline component except for a couple of individual features from O2 and CH4. Also there is no dependence of the interline component on airmass, as would be expected for an atmospheric source. However, there always remains the possibility that there is another overlooked source or that or relative intensities of the molecular emission needs improving.
To try to distinguish between these two possibilities we looked at the correlation between the interline component and the OH line strength and found that they were only weakly correlated. If true, this suggests that there is indeed an unknown source of interline emission, since otherwise the correlation would be much stronger. However, this interpretation should be treated with much caution due to the large measurement errors and possibly significant systematic errors on the interline measurements.
The absolute level of the interline emission is photons s-1 m-2 arcsec-2 m-1 which is slightly higher than that measured by Maihara et al. (1993), (590 photons s-1 m-2 arcsec-2 m-1) and slightly less than that measured by Cuby et al. (2000) (1200 photons s-1 m-2 arcsec-2 m-1). We again point out that there may be significant systematic error on our measurement due to the low count rates measured. However, the similarity to previous measurements could indicate that we have indeed reached a floor in the interline component which is significantly higher than the zodiacal scattered light background (see Ellis & Bland-Hawthorn 2008).
If the interline emission is the result of unsuppressed OH lines due to inaccuracies in our OH line models, this may be fixed with better models or with wider FBG notches to account such uncertainties. However, as things stand, the lack of a reduction in the interline component suggests that OH suppression will find its niche in low resolution () observations which would normally be insufficient to ‘resolve out’ the OH lines. Indeed OH suppression could be used at low resolutions, , at which conventional observations would be impractical.
(v) The suggested benefit of OH suppression at low resolution is supported by our observations of Seyfert galaxies (§ 4.4). We find that in regions where the OH line density is high, as for NGC 7674, the low resolution of IRIS2 makes it difficult to identify the [FeII] emission in the control spectrum, but that the line is obvious in the suppressed spectrum. Similarly when working between the lines as for NGC 7714, then the benefits of OH suppression are much less apparent since in this case we are limited by the detector dark current in both cases.
We conclude by noting that GNOSIS is the first step toward an OH suppression optimised spectrograph, and not a fully fledged facility instrument. The overall performance of the OH suppression unit itself is good, but can be substantially improved. However there remains uncertainty about the origin of the interline emission, which could higher than predicted either due to some unknown source of emission or because of unaccounted-for systematics in the detector. The next step will be to design and build a spectrograph optimised for a FBG feed, which will avoid the disadvantages that result from retrofitting an OH suppression system to an existing spectrograph. Furthermore, in doing so we can capitalise on the lessons learnt with GNOSIS in terms of detector background, optimal spectral resolution and design.
We present simulations of such a system in Figure LABEL:fig:sims. This simulation is based on the method presented in Ellis & Bland-Hawthorn (2008) with modifications to reflect our experience with GNOSIS. These modifications include an updated OH line spectrum which is an amalgamation of the observations of Abrams et al. (1994) with the models of Rousselot et al. (2000), giving precedence to Abrams et al. (1994) where lines occur in both lists. The thermal background modelling has also been updated to consider the emission and the numerical aperture of each component of the optical train separately. We first use the models to simulate the GNOSIS spectrum and compare these to the observations. We next model PRAXIS, a concept for an optimised OH suppression system. Specifically we assume that we have a corrected FBG design to account for the residual OH lines, that the fibre slit is cooled via a vacuum feed-through, that we have improved spectrograph throughput through the use of VPH gratings, and lower intrinsic detector noise through the use of a Hawaii-2RG 1.7m cut-off detector, and better spatial sampling with 2 pixels per PSF FWHM.
Acknowledgments
We thank Pierre Rousselot and Chris Lidman for illuminating discussions on the OH spectrum. We thank Michelle Cluver for kindly providing the details of HIZOA J0836-43 for observation. We thank the referee for useful comments which have improved this paper. GNOSIS was funded by an ARC LIEF grant LE100100164. This research has benefitted from the SpeX Prism Spectral Libraries, maintained by Adam Burgasser at http://pono.ucsd.edu/adam/browndwarfs/spexprism.
References
- Abrams et al. (1994) Abrams, M. C., Davis, S. P., Rao, M. L. P., Engleman, Jr., R., Brault, J. W. 1994, ApJS, 93, 351
- Biesiadzinski et al. (2011) Biesiadzinski, T., Lorenzon, W., Newman, R., Schubnell, M., Tarlé, G., Weaverdyck, C. 2011, PASP, 123, 958
- Bland-Hawthorn et al. (2008) Bland-Hawthorn, J., Buryak, A., Kolossovski, K. 2008, Journal of the Optical Society of America A, 25, 153
- Bland-Hawthorn et al. (2009) Bland-Hawthorn, J., Ellis, S., Haynes, R., Horton, A. 2009, Anglo-Australian Observatory Newsletter, 115, 15
- Bland-Hawthorn et al. (2004) Bland-Hawthorn, J., Englund, M., Edvell, G. 2004, Optics Express, 12, 5902
- Bland-Hawthorn et al. (2011) Bland-Hawthorn, J., et al. 2011, Nature Communications, 2
- Burgasser et al. (2004) Burgasser, A. J., McElwain, M. W., Kirkpatrick, J. D., Cruz, K. L., Tinney, C. G., Reid, I. N. 2004, AJ, 127, 2856
- Castelli & Kurucz (1994) Castelli, F., Kurucz, R. L. 1994, A&A, 281, 817
- Cluver et al. (2010) Cluver, M. E., Jarrett, T. H., Kraan-Korteweg, R. C., Koribalski, B. S., Appleton, P. N., Melbourne, J., Emonts, B., Woudt, P. A. 2010, ApJ, 725, 1550
- Content (1996) Content, R. 1996, ApJ, 464, 412
- Cuby et al. (2000) Cuby, J., Lidman, C., Moutou, C. 2000, ESO Messenger, 101, 2
- Davies (2007) Davies, R. I. 2007, MNRAS, 375, 1099
- Dufay (1951) Dufay, M. 1951, Publications of the Observatoire Haute-Provence, 2
- Elias et al. (2006a) Elias, J. H., Joyce, R. R., Liang, M., Muller, G. P., Hileman, E. A., George, J. R. 2006a, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 6269, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series
- Elias et al. (2006b) Elias, J. H., Rodgers, B., Joyce, R. R., Lazo, M., Doppmann, G., Winge, C., Rodríguez-Ardila, A. 2006b, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 6269, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series
- Elias et al. (1998) Elias, J. H., et al. 1998, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 3354, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, ed. A. M. Fowler, 555
- Ellis & Bland-Hawthorn (2008) Ellis, S. C., Bland-Hawthorn, J. 2008, MNRAS, 386, 47
- Frey et al. (2000) Frey, H. U., Mende, S. B., Arens, J. F., McCullough, P. R., Swenson, G. R. 2000, Geophysical Research Letters, 27, 41
- Kirkpatrick et al. (2008) Kirkpatrick, J. D., et al. 2008, ApJ, 689, 1295
- Leon-Saval et al. (2005) Leon-Saval, S., Birks, T., Bland-Hawthorn, J., Englund, M. 2005, Optics Letters, 30, 19
- Maihara & Iwamuro (2000) Maihara, T., Iwamuro, F. 2000, in Astronomical Society of the Pacific Conference Series, Vol. 195, Imaging the Universe in Three Dimensions, ed. W. van Breugel J. Bland-Hawthorn, 585
- Maihara et al. (1993) Maihara, T., Iwamuro, F., Yamashita, T., Hall, D. N. B., Cowie, L. L., Tokunaga, A. T., Pickles, A. 1993, PASP, 105, 940
- Meinel (1950) Meinel, I. A. B. 1950, ApJ, 111, 555
- Noordegraaf et al. (2009) Noordegraaf, D., Skovgaard, P. M. W., Nielsen, M. D., Bland-Hawthorn, J. 2009, Optics Express, 17, 1988
- Ramsay et al. (1992) Ramsay, S. K., Mountain, C. M., Geballe, T. R. 1992, MNRAS, 259, 751
- Rothman et al. (2009) Rothman, L. S., et al. 2009, JQSRT, 110, 533
- Rousselot et al. (2000) Rousselot, P., Lidman, C., Cuby, J.-G., Moreels, G., Monnet, G. 2000, A&A, 354, 1134
- Sharp & Birchall (2010) Sharp, R., Birchall, M. N. 2010, PASA, 27, 91
- Sharp & Parkinson (2010) Sharp, R., Parkinson, H. 2010, MNRAS, 408, 2495
- Shimazaki & Laird (1970) Shimazaki, T., Laird, A. 1970, Journal of Geophysical Research, 75, 3221
- Sternberg (1972) Sternberg, J. R. 1972, MNRAS, 159, 21
- Sternberg & Ingham (1972) Sternberg, J. R., Ingham, M. F. 1972, MNRAS, 159, 1
- Tinney et al. (2003) Tinney, C. G., Burgasser, A. J., Kirkpatrick, J. D. 2003, AJ, 126, 975
- Tinney et al. (2004) Tinney, C. G., et al. 2004, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 5492, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, ed. A. F. M. Moorwood & M. Iye, 998–1009