Symmetry-guided inverse design of self-assembling multiscale DNA origami tilings
Abstract
Recent advances enable the creation of nanoscale building blocks with complex geometries and interaction specificities for self-assembly. This nearly boundless design space necessitates design principles for defining the mutual interactions between multiple particle species to target a user-specified complex structure or pattern. In this article, we develop a symmetry-based method to generate the interaction matrices that specify the assembly of two-dimensional tilings which we illustrate using equilateral triangles. By exploiting the allowed 2D symmetries, we develop an algorithmic approach by which any periodic 2D tiling can be generated from an arbitrarily large number of subunit species, notably addressing an unmet challenge of engineering 2D crystals with periodicities that can be arbitrarily larger than subunit size. To demonstrate the utility of our design approach, we encode specific interactions between triangular subunits synthesized by DNA origami and show that we can guide their self-assembly into tilings with a wide variety of symmetries, using up to 12 unique species of triangles. By conjugating specific triangles with gold nanoparticles, we fabricate gold-nanoparticle supercrystals whose lattice parameter spans up to 300 nm. Finally, to generate economical design rules, we compare the design economy of various tilings. In particular, we show that (1) higher symmetries allow assembly of larger unit cells with fewer subunits and (2) linear supercrystals can be designed more economically using linear primitive unit cells. This work provides a simple algorithmic approach to designing periodic assemblies, which may open new doors to the multiscale assembly of superlattices of nanostructured “metatoms” with engineered plasmonic functions.
Self-assembly is a powerful method for building ordered structures using components ranging in size from nanometers to micrometers [1]. Unlike conventional ‘top-down’ manufacturing, in self-assembly, the instructions for building a final material structure are encoded in the geometry and the interaction specificity of the individual building blocks. In the past few decades, various techniques for synthesizing nanoscale building blocks have been developed, such as DNA-grafted colloids [2, 3, 4, 5], DNA origami [6, 7, 8, 9], DNA tiles and bricks [10, 11, 12, 13], and de-novo protein design [14, 15, 16]. This ever-expanding suite of user-prescribed building blocks has enabled the self-assembly of increasingly complex architectures and devices, including crystals [3, 4, 5, 9, 17, 18], fully-addressable structures [8, 19, 11, 10, 13], shells [20, 21, 14], tubules [15, 22, 23, 24], and sheets [25, 26, 27, 28].
One compelling target for self-assembly that has emerged in the past few years is programmable crystalline materials with user-specified unit-cell sizes and symmetries that can be controlled independently of the subunit geometry. In contrast to conventional crystalline materials, in which the lattice parameter is set by the subunit size, such ‘supercrystals’ in principle allow for the precise ordering of molecules or nanoparticles at length scales that can be arbitrarily large in comparison to the building-block dimensions and with symmetries that are decoupled from the subunit shape [29, 19]. This class of materials is particularly useful for a range of applications, including photonic-plasmonic devices that require the periodic positioning of metallic nanostructures, i.e. ‘mesoatoms’ of complex and precisely defined shapes, at the micrometer length scale to carefully tune plasmonic lattice couplings [30, 31, 32, 33]. However, there is no general method for the optimal design of multi-component assembly to produce a given unit-cell dimension and symmetry. Furthermore, there is no general strategy for how to do so in an economical way, that reaches a given complex 2D crystalline target via the minimal number of unique components and interactions, thereby making the designs easier to implement in practice.
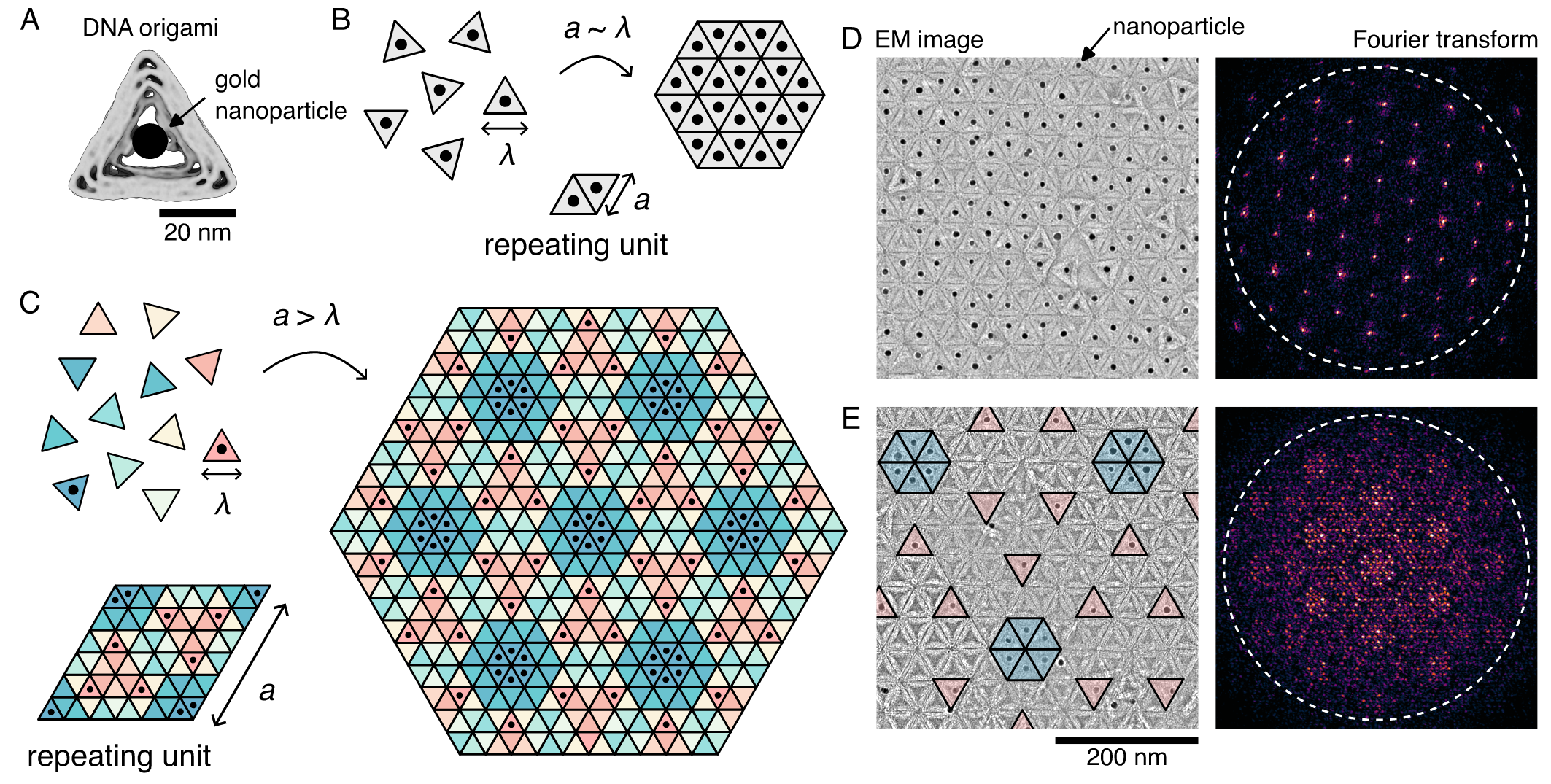
Here, we develop a symmetry-based inverse-design method to generate the interaction matrices that specify the assembly of supercrystals of arbitrarily large complexity. We consider equilateral triangular building blocks with programmable interactions on their edges that assemble into two-dimensional (2D) tilings (Fig. 1A). In a mixture that contains only one unique component, which we refer to as a species, our subunits crystallize into a simple triangular lattice with a lattice parameter, , that is given by the subunit size, (Fig. 1B). By increasing the number of subunit species, we can assemble more complex tilings with arbitrarily large lattice spacings, (Fig. 1C). We develop an inverse design method for selecting the most economical designs by exploiting translational and rotational symmetries. To show that our design scheme works in practice, we synthesize DNA origami subunits with programmable interactions (Fig. 1A). We assemble tilings with up to 12 species, containing as many as 72 triangles in a unit cell, significantly larger than other recent examples reported in the literature [34]. Finally, by conjugating DNA-grafted gold nanoparticles onto a small number of species, we fabricate various gold nanoparticle supercrystals with periodicities reaching hundreds of nanometers (Fig. 1D and E). Fourier transforms of the gold nanoparticles exhibit distinct low-spatial-frequency features, demonstrating order on length scales larger than the gold nanoparticles themselves.
Results
We consider a system of equilateral triangles that bind to one another through their edges. The triangles have three sides whose interactions are programmed independently (Fig. 2A). Note that we limit ourselves to triangles that do not flip in-plane. Under these simple rules, the set of interactions can be represented by a symmetric matrix, in which each element is either filled for favorable interactions or unfilled for unfavorable interactions (Fig. 2B).
Perhaps the most naive and straightforward strategy for generating complex 2D patterns for self-assembly is through direct enumeration of all possible interaction matrices. However, this strategy does not work in practice because only a tiny fraction of the interaction matrices encode for unique periodic tilings. For example, there exist only three tilings using a single species, as compared to the , or 64, possible interaction matrices (see SI Section II A). This problem gets even worse as the number of species, , increases because the number of distinct interaction matrices diverges as , rendering the enumeration untenable for all but the absolute smallest system sizes. For a more detailed discussion, see SI Section II.
.1 Generating tilings using symmetry
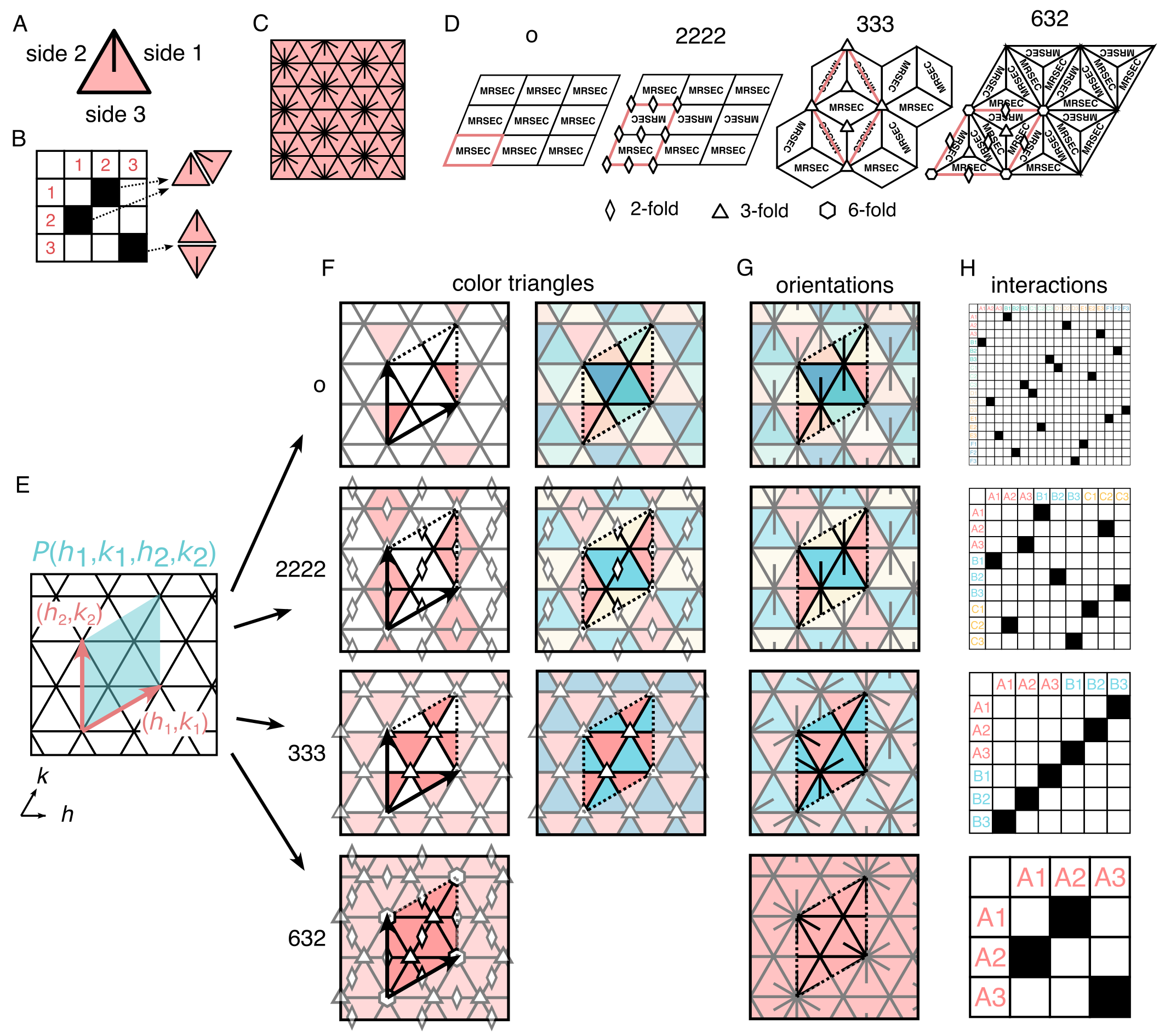
To circumvent the challenges associated with direct enumeration, we develop a symmetry-based design strategy to generate complex interaction matrices. Each planar tiling can be classified by the symmetry operation that leaves it unchanged. Given their translational symmetry, all 2D planar tilings must fall under one of the 17 Wallpaper groups [35, 36]. Here, we use orbifold notation to describe the symmetries of the Wallpaper groups [37]. In our system, the allowed symmetry operations are constrained by the interaction rules and the geometry of the particles. Since we prohibit triangles from flipping in-plane, reflections, and glide reflections are not allowed. Additionally, 90-degree rotational symmetries are prohibited in a system with triangular subunits. Therefore, we find only four of the available Wallpaper groups: o tilings with only translational symmetry, 2222 tilings with four distinct 2-fold rotational symmetries, 333 tilings with three distinct 3-fold rotational symmetries, and 632 tilings with 6, 3, and 2-fold rotational symmetries (Fig. 2D).
Taking advantage of the Wallpaper symmetries, we develop a tractable approach to designing 2D tilings with arbitrarily large complexity. The core idea is to invert the process of generating tilings: Rather than enumerating every possible interaction matrix and then sifting through them to find those that encode 2D tilings, we directly generate tilings using symmetry and then we infer the interaction matrices that encode the assembly of those tilings. We break down our approach into three steps.
First, we generate a parallelogram that tiles the plane and corresponds to the periodicity of the resulting tiling (Fig. 2E). Specifically, we create a coordinate system along two lattice directions with the subunit size being unit length and define a parallelogram using two linearly independent vectors with integer components, and . We call these two vectors the primitive unit vectors, and the corresponding parallelogram, the primitive unit cell (PU cell).
Next, we ‘color’ individual triangles and specify their orientations in each parallelogram while enforcing the symmetry operations prescribed by the Wallpaper groups. The procedure consists of: (1) choosing a blank triangle, (2) coloring it with a new color, (3) coloring all symmetrically invariant triangles with the same color, and (4) repeating this process until every triangle has been colored in (Fig. 2F). We note that because 2-fold symmetries can be placed on either an edge or a vertex, and 3-fold symmetries can be placed on either a vertex or a face, more than one tiling can exist for a given PU cell for 2222 and 333 symmetries (see SI Section III). Then we repeat this procedure to specify the orientations of each of the triangles similarly to how we specified the colors (Fig. 2G). Here, again, an exception exists for tiles with 3-fold symmetry. When the 3-fold symmetry point lies on the face of a triangle, the three edges of the triangle become homologous, and therefore the triangle does not have a deterministic orientation within the tiling.
Finally, we derive the interaction matrix that encodes the tiling deterministically by assigning interactions between unique bond pairs (Fig. 2H). This procedure amounts to setting the interaction matrix equal to the adjacency matrix. Each unique bond pair is recorded as a filled box in the interaction matrix.
This design method allows us to generate 2D tilings with a large number of species using a personal computer. To show the feasibility of our approach, we generate an exhaustive list up to PU cells containing triangles, which consist of 1628 o tilings, 2826 2222 tilings, 52 333 tilings, and 38 632 tilings, totaling 4544 2D tilings. Figures 3 and S15 show some examples of o, 2222, 333, and 632 tilings. Using a typical PC, computing all the associated interaction matrices takes only a few days, whereas direct enumeration would be impossible (see SI Section II B for details) and other modern inverse-design methods, such as SAT-assembly [38, 39], start to become intractable above roughly 100 species [40].
.2 Self-assembly of 2D supercrystals using DNA origami
Inspired by the engineering challenge of assembling programmable 2D arrays of plasmonically functional nanostructures [31, 33], we demonstrate the use of our symmetry-guided design to template the assembly of supercrystals of 10-nm-diameter gold nanoparticles. To demonstrate the principle, we label the centers of specific subsets of triangles, though more sophisticated multispecies labelings can be achieved by exploiting the addressability of DNA origami [41, 8, 19]. Given the symmetry rules of the tiling templates, the supercrystals that one can assemble in this way are required to satisfy a small number of constraints. First, the largest possible lattice parameter of the supercrystal is bounded by the PU cell size, . Second, the symmetry of the supercrystal need not be the same as the symmetry of the underlying tiling. And third, the order of symmetry of the supercrystal, , cannot be smaller than the order of symmetry of the underlying tiling, , where the order of symmetry, , is the size of the PU cell divided by the size of the fundamental domain. For example, a 2222 tiling () can template the assembly of a 632 supercrystal (), but a 632 tiling () cannot template the assembly of a 2222 supercrystal ().
To demonstrate the power of our design approach, we develop a system based on DNA origami to construct 2D tilings from a large number of distinct species, on which supercrystals of gold nanoparticles can be assembled. Specifically, we make triangular subunits that are roughly 50 nm in edge length and encode specific interparticle interactions using DNA hybridization of sticky ends that protrude from the edges of the subunits (Fig. 1A). In this way, we can program the complex interaction matrices that we generate above by exploiting Watson-Crick base pairing. We then assemble DNA origami tilings isothermally at the temperature at which monomers and assemblies coexist, typically around 34 ∘C for the 6-nucleotide sticky ends that we use. Subsequently, we add DNA-grafted gold nanoparticles at a small stoichiometric excess at room temperature to assemble the supercrystals, which we then image using negative-stain transmission electron microscopy (TEM) (Fig. 3A–B). We find that the labeling efficiency of gold nanoparticles is roughly 75% at this stoichiometric ratio.
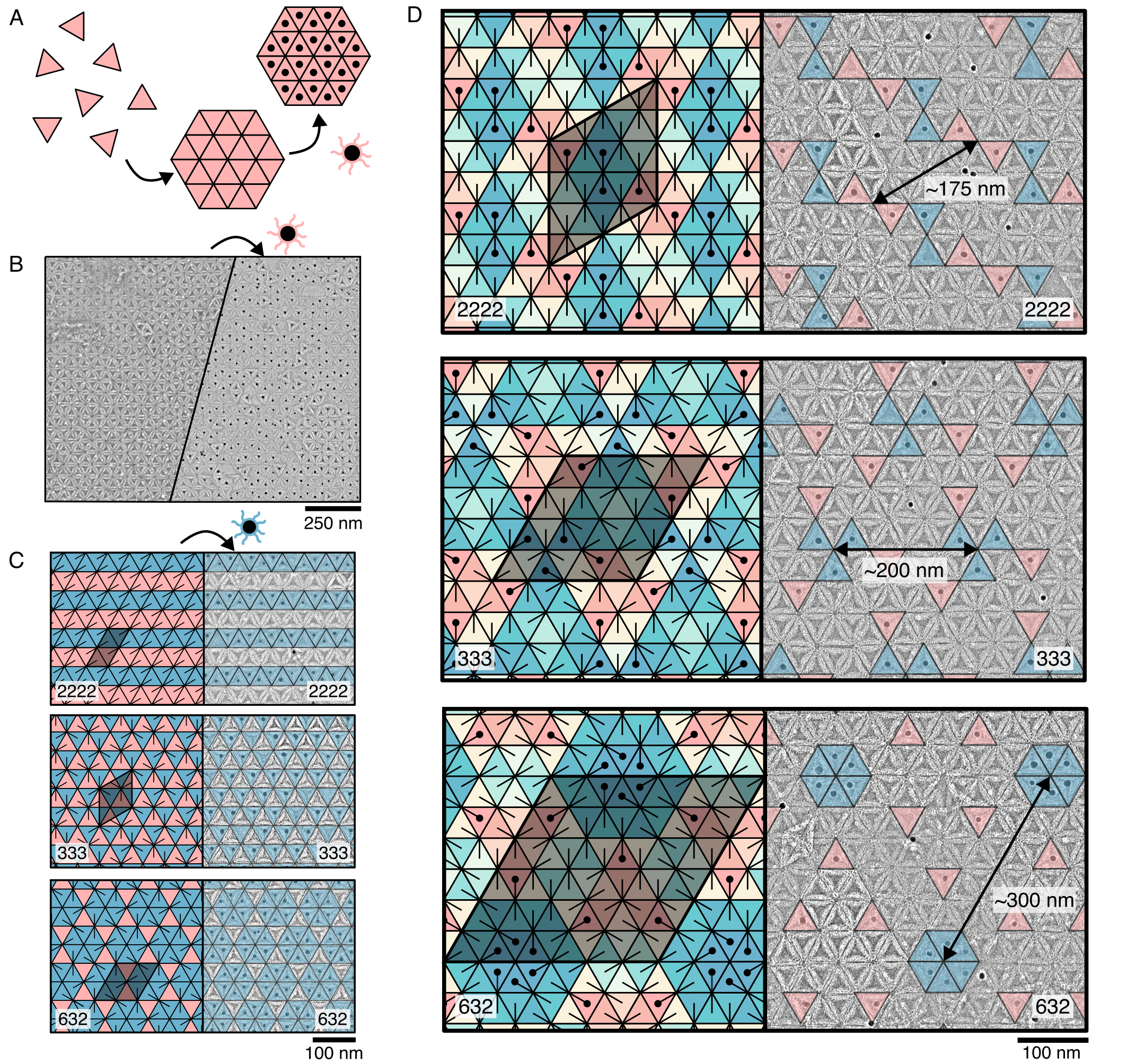
First, we show that micrometer-sized tilings assemble for the simplest interaction matrix possible. We encode all three sides of a single species of triangle to be homologous and self-complementary. We predict that the triangles in the resulting tiling will have no orientational order, and will correspond to the simplest 632 tiling. Under TEM, we observe 2D sheets spanning micrometers in size—containing over 1,000 subunits—that have the anticipated symmetry (Fig. 3B).
We further demonstrate the utility of our approach by making supercrystals from binary tilings of three different symmetries. By using multiple species with specific interactions, we encode more sophisticated patterns with larger PU cells. First, we assemble representative 2222, 333, and 632 tilings from two species of triangles at the stoichiometric ratios of the tilings (1:1 for 2222 and 333; and 1:3 for 632), as shown as red and blue in Fig. 3C, left. The resulting supercrystals, overlayed with false color, are shown in Fig. 3C, right. Interestingly, whereas the 2222 and 632 tilings lead to supercrystals with the same symmetry as the parent tiling, the 333 tiling produces a supercrystal with 632 symmetry. This observation highlights the importance of choosing the position of the gold nanoparticle in determining the symmetry of the supercrystal: labeling the center of a triangle yields 632 crystals whereas labeling the edge of a triangle yields 333 crystals, matching the symmetry of the parent.
Encouraged by the success of our two-species experiments, we assemble more complex supercrystals with larger PU cells, including supercrystals with periodicities comparable to the wavelength of visible light. Figure 3D shows examples of 2222, 333, and 632 tilings assembled from 12 species of triangles (see Fig. S16 for examples of 6-species tilings and SI Section VI for programmed interactions). We label two triangles for all of the 12-species tilings to maintain an appreciable density of gold nanoparticles. In all cases, we find that the supercrystals are consistent with the underlying tilings, have the same symmetries as their parent tilings, and have low defect densities, indicating that the programmed interactions are truly orthogonal. As anticipated, the size of the PU cell increases as the number of species of triangles increases, leading to larger distances between the gold nanoparticles. This is further seen by the increasing complexity and low-spatial-frequency signal from the Fourier transforms of the gold-particle positions (see SI Section VII and Fig. S14 for details). Additionally, we observe that the PU cell size increases with the order of the symmetry of the tiling for a fixed number of species from 175 nm to 200 nm to 300 nm for the 2222, 333, and 632 symmetry tilings, respectively. This final observation hints at the possibility that some tiling patterns might be more useful than others in templating nanoparticle supercrystals.
.3 Economy of design
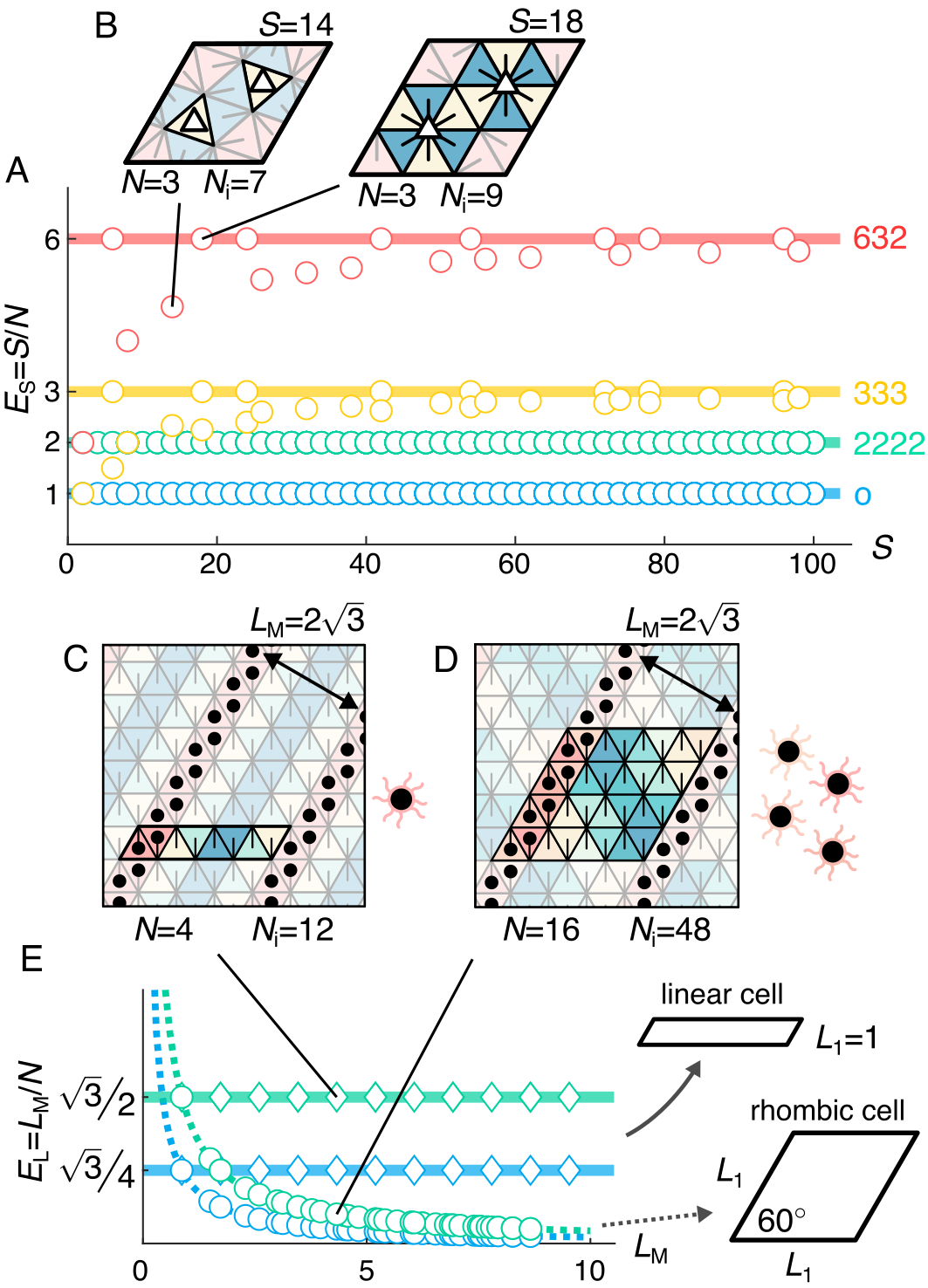
From the perspective of inverse design, we ask the following questions: What is the ‘cost’ of assembling a given tiling, and are some tilings more ‘economical’ than others [42]? In the experiment, it is natural to define the cost as the number of species of triangles that need to be synthesized because each species requires unique DNA staple sequences and must be folded and purified separately. We must also define the ‘value’ of a tiling. Here, we choose the size of the PU cell, , as the value of the tiling, since this parameter controls the spacing of the periodic patterns. Combining these two definitions, the ‘species economy’, , of a tiling can be calculated by taking the ratio of the value to the cost, or .
We find that the species economy has a maximum value that is determined by the order of symmetry of the tilings, (Fig. 4A). We observe that there is an upper limit to the species economy that can be achieved depending on the symmetry of tilings, which is 1, 2, 3, and 6 for o, 2222, 333, and 632 tilings, respectively. For o and 2222, the species economy for all tilings is constant, while for 333 and 632 tilings, some tilings do not reach the maximum species economy.
These observations can be rationalized by considering the fundamental domain of the tilings. The size of the fundamental domain is given by , where for o, 2222, 333, and 632, respectively. As a consequence, the fundamental domain contains all unique triangle species and edges that appear in a tiling. If we simply assume that every unique triangle has to appear in the fundamental domain once, we obtain . Combining this expression with our definition of species economy, we obtain , which places an upper limit on the economy of any given tiling.
The loss of species economy in some 333 and 632 tilings can be attributed to triangles having homologous interactions and, therefore, not maximally exploiting all of the information that can be encoded in every subunit. In Fig. 4B, we show two examples of 632 tilings, one whose species economy is smaller than the order of symmetry and another whose species economy matches the order of symmetry. The major difference between the two tilings is the location of the 3-fold rotational symmetry point; while the tiling with the higher species economy has a 3-fold symmetry point located at the vertex of the tiling, the one with the smaller species economy has a 3-fold symmetry point located in the middle of a triangle. In the lower species economy case, since the 3-fold rotational symmetry is located in the middle of the triangle, the three sides of that triangle must have the same interactions. Therefore, the interactions encoded in that triangle are redundant, decreasing the overall species economy. In general, whenever there is a 3-fold rotational symmetry placed in the middle of the face of a triangle, the triangle has homologous interactions on three sides and results in a loss of species economy. This feature explains why only 333 and 632 tilings encounter this decrease in the species economy since they are the only tilings in which the symmetry points can have the same symmetry as the 3-fold-symmetric triangular subunits.
Instead of focusing on the number of species of triangles, the ‘cost’ could instead be defined as the number of unique interactions, . Indeed, in some systems, the number of unique, orthogonal interactions might be the limiting factor in realizing more and more complex assemblies, such as systems in which the interactions are specified by DNA sequences, magnetic dipoles, or geometric shapes [43, 7, 44, 45]. Surprisingly, within this definition of economy, which we refer to as the interaction economy, , every planar tiling discussed in this paper follows a simple equation:
| (1) |
irrespective of the specific locations of the symmetry points. This relationship can be understood as a consequence of the fact that the number of unique edges contained in the fundamental domain is always . We note that the number of unique species and interactions are just two potential metrics of the ‘cost’, and other strategies for quantifying the information content of complex assemblies might lead to other definitions of economy [46].
.4 Economical design of linear supercrystals
We conclude by considering a specific class of supercrystals, in which the periodic distance between rows of nanoparticles is the only relevant design constraint. Figures 4C and D show two example tilings that yield the same supercrystal, with nanoparticles labeled in lines that are periodic in one of the other two lattice directions. In one case, the tiling requires four unique triangles, one of which is labeled to construct the supercrystal (Fig. 4C). In the other case, it takes 16 unique triangles, of which four are labeled (Fig. 4D). Because we are only concerned with the maximum periodic distance, , defined as the length of the PU cell perpendicular to the short axis, we define another economy, linear size economy, as the number of unique particles it takes to program the maximum periodic distance, or .
We find that the linear size economy of supercrystals depends on a combination of the symmetry group and the aspect ratio of the PU cell, with highly anisotropic PU cells of high order being the most economical. Figure 4E shows the maximum periodic distance of o and 2222 tilings that have linear and rhombic PU cell shapes. Here, we define a linear PU cell to have length and a rhombic PU cell to have , where and are the lengths of short and long edges of the PU cell, respectively. For o and 2222 tilings, the values of can be predicted using a simple geometrical argument. Specifically, for 2222 tilings, the periodicity is given by for linear PU cells and for rhombic PU cells. As before, o tilings are less economical, as the PU cell is half the size of the 2222 PU cell for the same number of subunit species. These results show the importance of the shape of the PU cell for the linear size economy: Tilings with linear PU cells are more economical than rhombic ones.
Discussion and Conclusions
In summary, we developed an inverse design method to create self-assembling tilings and supercrystals of arbitrary size and complexity by exploiting their underlying symmetries. By identifying the right symmetry tilings and the right aspect ratio of the primitive unit cell, our strategy is guaranteed to yield economical, deterministic designs. Here, the two central take-home messages are: (1) Tilings of the highest order symmetry, 632 in our case, yield the largest PU cell for the smallest number of components; and (2) Highly anisotropic PU cells with 2222 symmetry yield the most economical linear supercrystals. Using DNA origami, we demonstrated how our strategy could be used to assemble supercrystalline arrangements of 10-nm-diameter gold nanoparticles with periodicities up to 300 nm, comparable to the wavelength of visible light. We are optimistic that this work will help to pave the way toward making user-defined tilings and crystals of arbitrary complexity, ushering in the possibility of making mesoscopic materials with complex plasmonic and photonic functionality via self-assembly.
Whereas in the main text, our initial definition of economy focused on the economic cost of synthesizing many subunit species, we highlight another cost associated with increasing the assembly complexity: the time to assembly. Specifically, we found that increasing the number of species in a tiling requires increasing the time to assembly. Whereas single-species systems assembled micrometer-sized tilings in less than a day, similarly sized tilings made from 12 species took roughly two weeks to assemble at the same temperature (see Fig. S17). This observation indicates that the growth rate decreases roughly linearly with the number of species, which is consistent with detailed measurements of the growth rate of multi-species tubules using a similar experimental system [23]. Although not explored in this paper, we anticipate that hierarchical or nonequilibrium approaches [8, 47, 19, 48] may help to overcome these kinetic ‘costs’ of multi-species assembly.
Though the general principle of economy introduced in this paper can easily be extended to other conventional tilings and crystal systems, naturally, one may wonder how the system compares to nonconventional ones, such as the crisscross structure [49, 19]. Unlike a typical tiling, where a polygon interacts with other polygons through their edges, the component of crisscross structures are slats which can interact with other slats at designated points along the slat length. A unique feature of the crisscross system is that the number of interaction sites per component is much larger than that achievable in typical tiling systems, allowing for a robust design of the nucleation barrier. To compare the economy of the slate system with that of tilings, we introduce a new metric of economy. Whereas the ‘cost’ of assembly can be defined as the number of particle species as before, we define the new ‘value’ as the area of the PU cell normalized by the representative subunit length. Defining economy as the value over the cost, we observe that the economy of the triangular tiling is much larger than that of the crisscross structures (for details, see SI Section V). This result agrees with the intuition that crisscross systems have increased connectivity between components spanning smaller areas, which leads to a limited economy. Therefore, though the crisscross system is advantageous regarding the suppression of spurious nucleation, it may require more unique components as compared to conventional tiling designs.
Finally, we conclude by highlighting that our symmetry-based inverse design method can be extended to other tilings and is not constrained by the shape of the building block, including both 2D tilings and 3D crystals. In this work, we specifically focused on orientable triangle tilings, in which the corresponding symmetry groups include o, 2222, 333, and 632. However, depending on the specific target structure or application, one may prefer to fabricate 2D supercrystals with different symmetries or even 3D supercrystals. We emphasize that the procedures developed herein can be universally applied to other systems that have translational symmetry. In SI Section IV, we summarize general inverse design strategies that can be applied to translationally symmetric structures and show examples, including square, hexagonal, parallelogram, rhombille, and snub-square tilings. Therefore, the inverse design method we developed can be applied to self-assemble other 2D and 3D supercrystals of arbitrary complexity. In addition, we speculate that the design rules we identified have connections to 2D manifolds, which opens up new design spaces that can be accessed by controlling the dihedral angles between neighboring subunits to create curved structures [50, 51, 23, 21, 42].
Acknowledgements.
TEM images were prepared and imaged at the Brandeis Electron Microscopy facility. This work is supported by the Brandeis University Materials Research Science and Engineering Center, which is funded by the National Science Foundation under award number DMR-2011846. D.H. acknowledges support from the Masason Foundation. We acknowledge Oleg Gang for guidance on conjugating DNA to gold nanoparticles and Ian Murphy for reducing thiolated DNA.References
- Whitesides and Grzybowski [2002] G. M. Whitesides and B. Grzybowski, Self-Assembly at All Scales, Science 295, 2418 (2002).
- Mirkin et al. [1996] C. A. Mirkin, R. L. Letsinger, R. C. Mucic, and J. J. Storhoff, A DNA-based method for rationally assembling nanoparticles into macroscopic materials, Nature 382, 607 (1996).
- Macfarlane et al. [2011] R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz, and C. A. Mirkin, Nanoparticle Superlattice Engineering with DNA, Science 334, 204 (2011).
- Wang et al. [2015] Y. Wang, Y. Wang, X. Zheng, É. Ducrot, J. S. Yodh, M. Weck, and D. J. Pine, Crystallization of DNA-coated colloids, Nature Communications 6, 7253 (2015).
- He et al. [2020] M. He, J. P. Gales, E. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna, and D. J. Pine, Colloidal diamond, Nature 585, 524 (2020).
- Rothemund [2006] P. W. K. Rothemund, Folding DNA to create nanoscale shapes and patterns, Nature 440, 297 (2006).
- Gerling et al. [2015] T. Gerling, K. F. Wagenbauer, A. M. Neuner, and H. Dietz, Dynamic DNA devices and assemblies formed by shape-complementary, non–base pairing 3D components, Science 347, 1446 (2015).
- Tikhomirov et al. [2017a] G. Tikhomirov, P. Petersen, and L. Qian, Fractal assembly of micrometre-scale DNA origami arrays with arbitrary patterns, Nature 552, 67 (2017a).
- Wang et al. [2021] Y. Wang, L. Dai, Z. Ding, M. Ji, J. Liu, H. Xing, X. Liu, Y. Ke, C. Fan, P. Wang, and Y. Tian, DNA origami single crystals with Wulff shapes, Nature Communications 12, 1 (2021).
- Wei et al. [2012] B. Wei, M. Dai, and P. Yin, Complex shapes self-assembled from single-stranded DNA tiles, Nature 485, 623 (2012).
- Ke et al. [2012] Y. Ke, L. L. Ong, W. M. Shih, and P. Yin, Three-Dimensional Structures Self-Assembled from DNA Bricks, Science 338, 1177 (2012).
- Ke et al. [2014] Y. Ke, L. L. Ong, W. Sun, J. Song, M. Dong, W. M. Shih, and P. Yin, DNA brick crystals with prescribed depths, Nature Chemistry 6, 994 (2014).
- Ong et al. [2017] L. L. Ong, N. Hanikel, O. K. Yaghi, C. Grun, M. T. Strauss, P. Bron, J. Lai-Kee-Him, F. Schueder, B. Wang, P. Wang, et al., Programmable self-assembly of three-dimensional nanostructures from 10,000 unique components, Nature 552, 72 (2017).
- Bale et al. [2016] J. B. Bale, S. Gonen, Y. Liu, W. Sheffler, D. Ellis, C. Thomas, D. Cascio, T. O. Yeates, T. Gonen, N. P. King, and D. Baker, Accurate design of megadalton-scale two-component icosahedral protein complexes, Science 353, 389 (2016).
- Shen et al. [2018] H. Shen, J. A. Fallas, E. Lynch, W. Sheffler, B. Parry, N. Jannetty, J. Decarreau, M. Wagenbach, J. J. Vicente, J. Chen, L. Wang, Q. Dowling, G. Oberdorfer, L. Stewart, L. Wordeman, J. De Yoreo, C. Jacobs-Wagner, J. Kollman, and D. Baker, De novo design of self-assembling helical protein filaments, Science 362, 705 (2018).
- Sahtoe et al. [2022] D. D. Sahtoe, F. Praetorius, A. Courbet, Y. Hsia, B. I. M. Wicky, N. I. Edman, L. M. Miller, B. J. R. Timmermans, J. Decarreau, H. M. Morris, A. Kang, A. K. Bera, and D. Baker, Reconfigurable asymmetric protein assemblies through implicit negative design, Science 375, 10.1126/science.abj7662 (2022).
- Hensley et al. [2022] A. Hensley, W. M. Jacobs, and W. B. Rogers, Self-assembly of photonic crystals by controlling the nucleation and growth of dna-coated colloids, Proceedings of the National Academy of Sciences 119, e2114050118 (2022).
- Hensley et al. [2023] A. Hensley, T. E. Videbæk, H. Seyforth, W. M. Jacobs, and W. B. Rogers, Macroscopic photonic single crystals via seeded growth of dna-coated colloids, Nature Communications 14, 4237 (2023).
- Wintersinger et al. [2023] C. M. Wintersinger, D. Minev, A. Ershova, H. M. Sasaki, G. Gowri, J. F. Berengut, F. E. Corea-Dilbert, P. Yin, and W. M. Shih, Multi-micron crisscross structures grown from DNA-origami slats, Nature Nanotechnology 18, 281 (2023).
- Tikhomirov et al. [2018] G. Tikhomirov, P. Petersen, and L. Qian, Triangular DNA Origami Tilings, Journal of the American Chemical Society 140, 17361 (2018).
- Sigl et al. [2021] C. Sigl, E. M. Willner, W. Engelen, J. A. Kretzmann, K. Sachenbacher, A. Liedl, F. Kolbe, F. Wilsch, S. A. Aghvami, U. Protzer, M. F. Hagan, S. Fraden, and H. Dietz, Programmable icosahedral shell system for virus trapping, Nature Materials 20, 1281 (2021).
- Hayakawa et al. [2022] D. Hayakawa, T. E. Videbaek, D. M. Hall, H. Fang, C. Sigl, E. Feigl, H. Dietz, S. Fraden, M. F. Hagan, G. M. Grason, and W. B. Rogers, Geometrically programmed self-limited assembly of tubules using DNA origami colloids, Proceedings of the National Academy of Sciences 119, e2207902119 (2022).
- Videbæk et al. [2023] T. E. Videbæk, D. Hayakawa, G. M. Grason, M. F. Hagan, S. Fraden, and W. B. Rogers, Economical routes to size-specific assembly of self-closing structures, arXiv preprint arXiv:2311.01383 (2023).
- Rothemund et al. [2004a] P. W. K. Rothemund, A. Ekani-Nkodo, N. Papadakis, A. Kumar, D. K. Fygenson, and E. Winfree, Design and Characterization of Programmable DNA Nanotubes, Journal of the American Chemical Society 126, 16344 (2004a).
- Tikhomirov et al. [2017b] G. Tikhomirov, P. Petersen, and L. Qian, Programmable disorder in random DNA tilings, Nature Nanotechnology 12, 251 (2017b).
- Zhang et al. [2013] F. Zhang, Y. Liu, and H. Yan, Complex Archimedean Tiling Self-Assembled from DNA Nanostructures, Journal of the American Chemical Society 135, 7458 (2013).
- Tang et al. [2023] Y. Tang, H. Liu, Q. Wang, X. Qi, L. Yu, P. Šulc, F. Zhang, H. Yan, and S. Jiang, DNA Origami Tessellations, Journal of the American Chemical Society 145, 13858 (2023).
- Rothemund et al. [2004b] P. W. K. Rothemund, N. Papadakis, and E. Winfree, Algorithmic Self-Assembly of DNA Sierpinski Triangles, PLoS Biology 2, e424 (2004b).
- Liu et al. [2016] W. Liu, J. Halverson, Y. Tian, A. V. Tkachenko, and O. Gang, Self-organized architectures from assorted DNA-framed nanoparticles, Nature Chemistry 8, 867 (2016).
- Auguié and Barnes [2008] B. Auguié and W. L. Barnes, Collective Resonances in Gold Nanoparticle Arrays, Physical Review Letters 101, 143902 (2008).
- Kravets et al. [2018] V. G. Kravets, A. V. Kabashin, W. L. Barnes, and A. N. Grigorenko, Plasmonic Surface Lattice Resonances: A Review of Properties and Applications, Chemical Reviews 118, 5912 (2018).
- Bin-Alam et al. [2021] M. S. Bin-Alam, O. Reshef, Y. Mamchur, M. Z. Alam, G. Carlow, J. Upham, B. T. Sullivan, J.-M. Ménard, M. J. Huttunen, R. W. Boyd, and K. Dolgaleva, Ultra-high-Q resonances in plasmonic metasurfaces, Nature Communications 12, 1 (2021).
- Cortés et al. [2022] E. Cortés, F. J. Wendisch, L. Sortino, A. Mancini, S. Ezendam, S. Saris, L. de S. Menezes, A. Tittl, H. Ren, and S. A. Maier, Optical Metasurfaces for Energy Conversion, Chemical Reviews 122, 15082 (2022).
- Kahn et al. [2022] J. S. Kahn, B. Minevich, A. Michelson, H. Emamy, K. Kisslinger, S. Xiang, S. K. Kumar, and O. Gang, Encoding Hierarchical 3D Architecture through Inverse Design of Programmable Bonds, ChemRxiv 10.26434/chemrxiv-2022-xwbst (2022).
- Hahn et al. [1983] T. Hahn, U. Shmueli, and J. W. Arthur, International tables for crystallography, Vol. 1 (Reidel Dordrecht, 1983).
- Conway et al. [2008] J. Conway, H. Burgiel, and C. Goodman-Strauss, The Symmetries of Things, AK Peters/CRC Recreational Mathematics Series (Taylor & Francis, 2008).
- Conway and Huson [2002] J. H. Conway and D. H. Huson, The Orbifold Notation for Two-Dimensional Groups, Structural Chemistry 13, 247 (2002).
- Romano et al. [2020] F. Romano, J. Russo, L. Kroc, and P. Šulc, Designing patchy interactions to self-assemble arbitrary structures, Physical Review Letters 125, 118003 (2020).
- Russo et al. [2022] J. Russo, F. Romano, L. Kroc, F. Sciortino, L. Rovigatti, and P. Šulc, SAT-assembly: A new approach for designing self-assembling systems, Journal of Physics: Condensed Matter 34, 354002 (2022).
- Bohlin et al. [2023] J. Bohlin, A. J. Turberfield, A. A. Louis, and P. Sulc, Designing the self-assembly of arbitrary shapes using minimal complexity building blocks, ACS Nano 17, 5387 (2023).
- Schnitzbauer et al. [2017] J. Schnitzbauer, M. T. Strauss, T. Schlichthaerle, F. Schueder, and R. Jungmann, Super-resolution microscopy with DNA-PAINT, Nature Protocols 12, 1198 (2017).
- Duque et al. [2023] C. M. Duque, D. M. Hall, B. Tyukodi, M. F. Hagan, C. D. Santangelo, and G. M. Grason, Limits of economy and fidelity for programmable assembly of size-controlled triply-periodic polyhedra, arXiv preprint arXiv:2309.04632 (2023).
- Wu et al. [2012] K.-T. Wu, L. Feng, R. Sha, R. Dreyfus, A. Y. Grosberg, N. C. Seeman, and P. M. Chaikin, Polygamous particles, Proceedings of the National Academy of Sciences 109, 18731 (2012).
- Huntley et al. [2016] M. H. Huntley, A. Murugan, and M. P. Brenner, Information capacity of specific interactions, Proceedings of the National Academy of Sciences 113, 5841 (2016).
- Niu et al. [2019] R. Niu, C. X. Du, E. Esposito, J. Ng, M. P. Brenner, P. L. McEuen, and I. Cohen, Magnetic handshake materials as a scale-invariant platform for programmed self-assembly, Proceedings of the National Academy of Sciences 116, 24402 (2019).
- Ahnert et al. [2010] S. E. Ahnert, I. G. Johnston, T. M. A. Fink, J. P. K. Doye, and A. A. Louis, Self-assembly, modularity, and physical complexity, Physical Review E 82, 026117 (2010).
- Jacobs and Frenkel [2015] W. M. Jacobs and D. Frenkel, Self-assembly protocol design for periodic multicomponent structures, Soft Matter 11, 8930 (2015).
- Gartner et al. [2022] F. M. Gartner, I. R. Graf, and E. Frey, The time complexity of self-assembly, Proceedings of the National Academy of Sciences 119, e2116373119 (2022).
- Minev et al. [2021] D. Minev, C. M. Wintersinger, A. Ershova, and W. M. Shih, Robust nucleation control via crisscross polymerization of highly coordinated DNA slats, Nature Communications 12, 1 (2021).
- Caspar and Klug [1962] D. L. D. Caspar and A. Klug, Physical Principles in the Construction of Regular Viruses, Cold Spring Harbor Symposia on Quantitative Biology 27, 1 (1962).
- Tanaka et al. [2023] H. Tanaka, T. Dotera, and S. T. Hyde, Programmable self-assembly of nanoplates into bicontinuous nanostructures, ACS Nano 17, 15371 (2023).