Symmetry, spin-texture, and tunable quantum geometry in a WTe₂ monolayer

Structure and material property/functionality have an intimate relationship. A striking example is monolayer WTe₂ where a structural change from 1T to a distorted 1T’ structure induces a topological phase transition from trivial to $Z_{2}$ topological phase Qian . Recently realized in experiment Tang ; Fei ; Wu , the distorted 1T’-WTe₂ monolayer possesses a large bulk bandgap $\sim 0.055\,{\rm eV}$ Tang , and helical edge modes that mediate robust edge conduction Fei ; Wu characteristic of a robust quantum spin Hall state.

Here we argue that, aside from determining the band topology, the distorted crystal structure of 1T’-WTe₂ (Fig. 1a-c) also enables unusual bulk band quantum geometry and spin physics to be accessed and controlled. By developing a low energy ${\bf k}\cdot{\bf p}$ model from symmetry analysis we find that when an out-of-plane electric field $E_{\perp}$ is applied, spin-degeneracy is lifted (Fig. 1d,e) by inducing both in-plane as well as out-of-plane spin orientations (Fig. 2a,b). While in-plane spin orientations are synonymous with an out-of-plane inversion symmetry (IS) breaking, out-of-plane spin orientations are less common and typically weak Yuan . As we discuss, 1T’-WTe₂ bucks this expectation: even though $E_{\perp}$ is out-of-plane, the non-aligned outer Te atoms (Fig. 1c) enables an in-plane electric dipole to develop and a strong out-of-plane spin orientation to be induced.

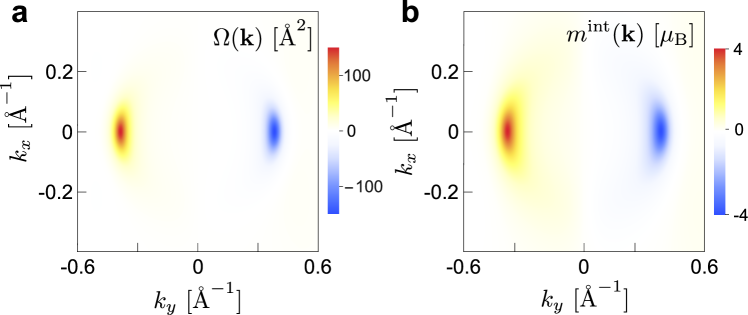
Crucially, applied $E_{\perp}$ induces Berry curvature as well as magnetic moment. Berry curvature value is determined by an interplay between strong atomic (spin-selective) inter-orbital mixing of the 1T’-WTe₂ and $E_{\perp}$ induced terms, and exhibits a characteristic anisotropic distribution; magnetic moment mirrors this behavior (see Fig. A-2). While an electrically tunable Berry curvature can be readily realized in bilayer systems Xiao07 owing to a electric control over layer degree of freedom, electrical tunability in monolayer systems is considerably more difficult. Berry curvature is realizable in 1T’-WTe₂ as a direct result of the asymmetric non-aligned outer Te atoms.

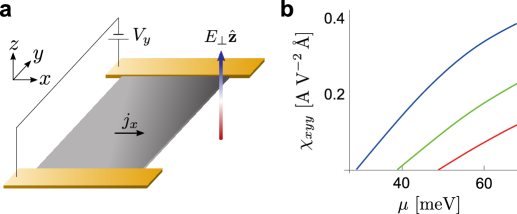
Further, due to the low symmetry of 1T’-WTe₂ distorted crystal structure, induced Berry curvature and magnetic moment also possess an asymmetry characterized by a dipolar distribution in reciprocal space. As a result, shifts in the distribution function (e.g., induced when a dissipative charge current is flowing, ${\bf j}$) enable a net Berry flux, and a net out-of-plane magnetization, $M_{z}$, to develop (Fig. 4). The latter corresponds to a direct (linear) magneto-electric effect $M_{z}=\sum_{i}\tilde{\alpha}_{zi}j_{i}$ ($i=x,y$), where $\tilde{\alpha}_{zi}$ characterizes the strength of the magneto-electric effect; the former mediates a quantum nonlinear anomalous Hall effect Sodemann .

Both these are intimately tied to the low-symmetry of gated 1T’-WTe₂; they do not appear in rotationally symmetric systems. They constitute striking experimental signatures of the tunable quantum geometry (induced Berry curvature and magnetic moment) of 1T’-WTe₂, as well as the direct impact that its distorted structure has on its material response. Using available parameters for 1T’-WTe₂, we anticipate a sizeable $M_{z}$ that can be readily probed for e.g., using Kerr effect microscopy lee2017 . 1T’-WTe₂ provides a compelling venue to manipulate spins and magnetic moments in a tunable two-dimensional material. Out-of-plane spin orientations are particularly useful since they may enable to couple to out-of-plane spins necessary for high-density magnetic applications MacNeil ; Kurebayashi .

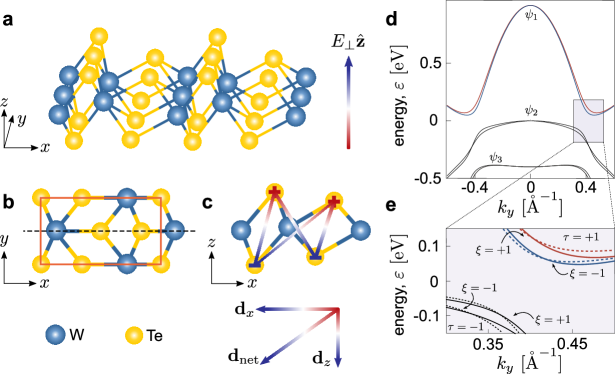
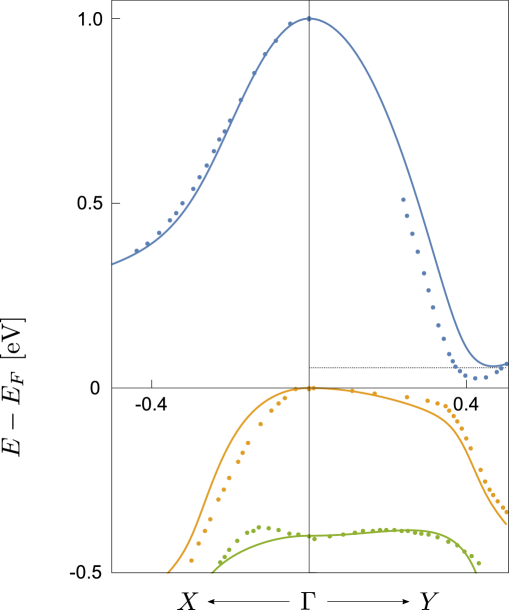
Symmetry analysis and ${\bf k}\cdot{\bf p}$ model — We begin by analyzing the band structure of monolayer 1T’-WTe₂ in the presence of an applied out-of-plane electric field $E_{\perp}$ [Fig. 1(a)]. In doing so, we will employ a ${\bf k}\cdot{\bf p}$ method based on the underlying symmetries of the material: for e.g., mirror symmetry about the $xz$ mirror plane [dashed line in Fig. 1(b)], time-reversal symmetry (TRS), and (broken) inversion symmetry (IS). For completeness, our analysis takes into account the three relevant atomic orbitals ($\psi_{1,2,3}$) and two spin states ($\uparrow,\downarrow$) that contribute to the states near the $\Gamma$ point and the gap opening [Fig. 1(d)], as revealed by ARPES measurements Tang as well as first principles calculations Qian ; Choe ; Lin ; Xu . This produces a six-band ${\bf k}\cdot{\bf p}$ description (SBD), see Appendix Supp , for a detailed account of the symmetry analysis of these orbitals and spin operators and the symmetry allowed terms in the SBD description.

Importantly, while $E_{\perp}=0$ produces a spin-degenerate bandstructure Tang ; Qian ; Choe ; Lin ; Xu , when $E_{\perp}\neq 0$ (e.g., induced by proximal gate) we find the bands become spin-split (Fig. 1d). As shown in Fig. 1d, this is particularly relevant away from the $\Gamma$ point, where the splitting becomes pronounced close to the band gap (gray shaded region, Fig. 1d,e). These are characterized by states $\Psi_{\tau\xi}$ with higher ($\xi=+1$) or lower ($\xi=-1$) energies as shown in Fig. 1e, and $\tau=\pm 1$ correspond to the conduction and valence bands. As we will see, the splitting induced by $E_{\perp}$ drives a range of novel spin behavior.

At low carrier densities typical for 1T’-WTe₂ devices Wu , the electronic and spin behavior is dominated by low-energy excitations around the bandgap in the four bands (Fig. 1e). In order to compactly illustrate the physics, we develop a simple effective four-band model using the basis $\{\psi_{c\uparrow}$, $\psi_{v\uparrow}$, $\psi_{c\downarrow}$, $\psi_{v\downarrow}\}$ in the regime around the gap opening (see gray region). This is obtained by performing a Löwdin partitioning (see Supp ) of the bands in Fig. 1d and can be expressed as $h^{\rm eff}({\bf k})=h_{0}({\bf k})+h_{1}({\bf k})$. Here $h_{0}({\bf k})$ describes the electronic behavior in pristine 1T’-WTe₂ ($E_{\perp}=0$):

where $\bar{\epsilon}_{{\bf k}}=(\epsilon_{c{\bf k}}+\epsilon_{v{\bf k}})/2$, $m_{{\bf k}}=(\epsilon_{c{\bf k}}-\epsilon_{v{\bf k}})/2$, $v_{{\bf k}}^{\pm}=\pm v_{x}k_{x}+iv_{y}k_{y}$ represents the strong spin selective atomic orbital coupling (sharing the same spin), while $\epsilon_{c{\bf k}}$ and $\epsilon_{v{\bf k}}$ are diagonal parts for the conduction and valence bands, capturing their energy offsets and effective masses Supp . We note that $h_{0}({\bf k})$ is simply a tilted Bernevig-Hughes-Zhang (BHZ) hamiltonian Bernevig that describes the spin-degenerate bands in pristine 1T’-WTe₂; here the tilt arises from large effective mass differences between the conduction and valence bands (see Table. A-III Supp ).

On the other hand, $h_{1}({\bf k})=h_{Z}({\bf k})+h_{R}({\bf k})$ captures the electric field-induced spin-orbit coupling that are allowed by symmetry

where we have grouped the electric field-induced spin-orbit coupling terms into $h_{Z}({\bf k})$ and $h_{R}({\bf k})$ in order to highlight the out-of-plane and in-plane spin orientations they induce respectively (see Fig. 2). Here $\alpha_{{\bf k}}^{\pm}=\pm i\alpha_{x}k_{x}+\alpha_{y}k_{y}$, $\delta_{x,z}$ are $k$-independent coupling terms, and $\lambda k_{y}$ is a $k$-dependent that can induce out-of-plane spin orientation. We note, parenthetically, that the spin-orbit coupling terms in $h_{Z}$ have sometimes been referred to as “Zeeman-like” see e.g., Ref. Yuan ; Xu so as highlight the out-of-plane spin orientation it induces; in the following, we will not use this terminology, but instead focus on their physical manifestation: its spin orientation. We emphasize that both $h_{Z}({\bf k})$ and $h_{R}({\bf k})$ in this work physically originate from IS breaking induced by the application of the electric field, see next section for detailed discussion.

In writing Eq. (6) we have kept all symmetry allowed terms up to the linear order in $k$ as allowed by symmetry. We remark that the magnitudes of each of the symmetry allowed terms can be determined from experimental or first principle calculation results (see Appendix Supp for a discussion). However, before we move to specific values, we first discuss the physical origin of the coupling terms, and some possible interplays brought by these couplings.

Physical origin of out-of-plane and in-plane spin orientations — For physical clarity, we will denote $h_{R}({\bf k})$ and $h_{Z}({\bf k})$ as spin-orbit coupling induced by out-of-plane and in-plane IS breaking, respectively. In a general sense, $h_{R}({\bf k})$ [or $h_{Z}({\bf k})$] always couple states with opposite spins [the same spin]. As a result, these terms split the spin degeneracy and re-orient the spins of the eigenstate $\Psi_{\tau\xi}$: $h_{R}$ terms create in-plane spin orientations (Fig. 2a) whereas $h_{Z}$ terms align spins out-of-plane (Fig. 2b). Here spin orientations are plotted only for the right valley ($k_{y}>0$). For $k_{y}<0$, spin textures are flipped.

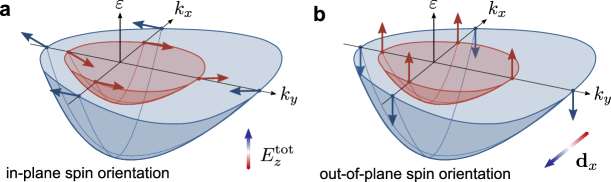
Their physical origins are also distinct. When a charge neutral monolayer 1T’-WTe₂ is placed under $E_{\perp}$, the top layer and the bottom layer Te atoms experience a charge redistribution becoming oppositely charged. This charge redistribution counteracts $E_{\perp}$ forming an out-of-plane dipole moment, $d_{z}$ (see Fig. 1c). Crucially, because the Te atoms are not perfectly aligned, this charge redistribution also creates an in-plane electric dipole moment along the $x$-direction, $d_{x}$, yielding a net induced electric dipole, ${\bf d}_{\rm net}$, that is canted (see Fig. 1c).

As a result, $E_{\perp}$ induces IS breaking in both $z$- and $x$-directions developing a nonzero $\partial_{z}\phi({\bf r})$ and $\partial_{x}\phi({\bf r})$; here $\phi({\bf r})$ is the local electro-static potential induced by $E_{\perp}$. Since spin-orbit coupling arises as matrix elements of the microscopic spin-orbit interaction: ${\hat{H}}_{\rm so}({\bf k})\sim({\bf k}+{\hat{{\bf p}}}/m_{0})\cdot{\bf s}\times\nabla\phi({\bf r})$ ¹¹1see e.g., Eq. (16.1) of Ref. Bir , or Eq. (2.4) of Ref. WinklerBook , we find that spin-orbit coupling terms $\delta_{x}$ and $\alpha_{{\bf k}}^{\pm}$ come from the total out-of-plane electric field $-\partial_{z}\phi({\bf r})$; this constrains the terms ${\bf k}+{\hat{{\bf p}}}/m_{0}$ and ${\bf s}$ in ${\hat{H}}_{\rm so}({\bf k})$ to be in-plane only. However, the charge re-distribution also enables an in-plane $\partial_{x}\phi({\bf r})$ to develop. This in-plane electric field picks out ${\bf s}$ in ${\hat{H}}_{\rm so}({\bf k})$ as the out-of-plane component $s_{z}$, and ${\bf k}+{\hat{{\bf p}}}/m_{0}$ as the $y$-component. As a result of the in-plane $\partial_{x}\phi({\bf r})$, $h_{Z}$ terms $\lambda k_{y}$ and $\delta_{z}$ in Eq. 6 manifest. The distorted structure of 1T’-WTe₂ enables ${\bf d}_{\rm net}$ that is generically canted with finite $h_{Z}$ and $h_{R}$ terms that co-exist. In contrast, since $\lambda k_{y}$ and $\delta_{z}$ result from the in-plane electric field $\partial_{x}\phi({\bf r})$, the non-distorted transition metal dichalcogenide monolayers whose atoms at top and bottom layers are aligned (e.g., MoS₂) do not possess an external $E_{\perp}$-induced out-of-plane spin orientations near the $\Gamma$ point (up to linear in $k$).

As a further illustration of the role that low symmetry plays in 1T’-WTe₂, we can also compare the spin-orbit coupling terms in $h_{R}({\bf k})$ allowed in 1T’-WTe₂ [induced by out-of-plane IS breaking], with that of HgTe quantum wells recently discussed in the literature Tarasenko ; Rothe . For 1T’-WTe₂, all terms in $h_{R}({\bf k})$ are allowable when an out-of-plane electric field is applied because of its very low symmetry, and that fact that angular momentum in the $z$-direction is not a good quantum number. In contrast, HgTe quantum wells possess a $D_{2d}$ symmetry, $[h_{R}({\bf k})]_{24,(42)}$ is missing because its 2nd and 4th basis functions are heavy hole bands with $j_{z}=\pm 3/2$ and the coupling between them is at least of $k^{3}$ order. Only $i\delta_{x}$ and $[h_{R}({\bf k})]_{13,(31)}$ can appear, corresponding to the existence of bulk inversion asymmetry Tarasenko and structural inversion asymmetry Rothe , respectively.

Interplay between Berry curvature and the two types of spin-orbit couplings — Pristine 1T’-WTe₂ possesses both IS and TRS ensuring that Berry curvature (and orbital magnetic moment) vanish exactly. As we now discuss, in 1T’-WTe₂ with $E_{\perp}\neq 0$, $h_{Z}$ [Eq. (6)] presents an opportunity to break in-plane IS turning on a finite Berry curvature distribution. For clarity, we will first focus on the case when $\lambda$ and $\alpha_{x,y}$ are non-zero, while setting the $k$-independent terms $\delta_{x,z}=0$, and then analyse the case when $\delta_{x,z}\neq 0$ later in the text.

To proceed, we first note that for pristine 1T’-WTe₂ (when $E_{\perp}=0$), the hamiltonian $h^{\rm eff}=h_{0}({\bf k})$ in Eq. (5) possesses spin degenerate states $\Psi_{\tau\xi}$, with $\xi=\pm 1$ corresponding to $\uparrow,\downarrow$ states, and spin-degenerate energy $\varepsilon_{\tau\xi}({\bf k})=\bar{\epsilon}_{{\bf k}}+\tau\Delta_{{\bf k}}$ where $\Delta_{{\bf k}}^{2}=(v_{x}k_{x})^{2}+(v_{y}k_{y})^{2}+m_{{\bf k}}^{2}$ is the energy difference between the conduction and valence bands. In the absence of $v_{x,y}$, conduction ($\psi_{\tau=+1,\xi}$) and valence ($\psi_{\tau=-1,\xi}$) bands touch, and exhibit a gapless spectrum along $\Gamma$-$Y$ Muechler . However, large spin-selective atomic orbital coupling $v_{x,y}$ in 1T’-WTe₂ creates strong inter-orbital mixing (between $\psi_{c,v}$) giving a large QSH gap $\sim 0.055\,{\rm eV}$ Tang .

Even though the external $E_{\perp}$ induced spin orbit coupling [Eq. (6)] is small as compared with the intrinsic spin-selective atomic orbital coupling, $\alpha_{\pm},\lambda\ll v_{\pm}$, nevertheless, when an external electric field $E_{\perp}\neq 0$ is applied, IS is immediately broken. Specifically, we emphasize that it is in-plane IS breaking that enables a finite Berry curvature, $\Omega_{\tau\xi}({\bf k})$, distribution to develop. As a result, we find that $\lambda$ encoding in-plane IS breaking (arising from $d_{x}$, Fig. 1c) turns on $\Omega_{\tau\xi}({\bf k})$. In contrast, while $\alpha_{x,y}$ is also induced by $E_{\perp}\neq 0$ (and can also spin-split $\psi_{c,v}$ bands) it corresponds to an out-of-plane IS breaking, and does not lead to $\Omega_{\tau\xi}({\bf k})$.

To see this explicitly, we first consider the case $\alpha\ll\lambda$ where out-of-plane IS breaking is much weaker than in-plane IS breaking. In this case, $\lambda$ dominates $h_{1}({\bf k})$ and we can take $\alpha\to 0$. Therefore, $h^{\rm eff}({\bf k})=h_{0}({\bf k})+h_{1}({\bf k})$ produces a $\Psi_{\tau\xi}$ bandstructure with a lifted spin-degeneracy (Fig. 1e) and energies $\varepsilon_{\tau\xi}({\bf k})=\bar{\epsilon}_{{\bf k}}+\tau\Delta_{{\bf k}}+\xi|\lambda k_{y}|$. We note that since both $\lambda$ as well as spin-selective atomic orbital coupling $v_{x,y}$ do not mix spins, $\Psi_{\tau\xi}$ possess spins that purely point out of plane (Fig. 2b). Using this, we find a Berry curvature distribution $\Omega_{\tau\xi}({\bf k})=\boldsymbol{\nabla}_{{\bf k}}\times\langle\Psi_{\tau\xi}({\bf k})|i\boldsymbol{\nabla}_{{\bf k}}|\Psi_{\tau\xi}({\bf k})\rangle$ as

Strikingly, $\Omega_{\tau\xi}^{(0)}({\bf k})$ in Eq. (7) does not depend on $\lambda$ even though finite $\lambda$ was required to break in-plane IS. Instead, $\Omega_{\tau\xi}^{(0)}({\bf k})$ is solely determined by the spin-selective atomic orbital coupling $v_{x,y}$, and the band parameters in pristine 1T’-WTe₂.

This decoupling behavior between IS breaking strength and the value of $\Omega_{\tau\xi}$ persists even in the presence of finite out-of-plane IS breaking characterized by the ratios $\lambda/\alpha$. To see this, we note that when $\alpha$ is finite, $h_{1}({\bf k})$ starts to hybridize $\Psi_{\tau\xi}$ with different spins (in the same $\tau$ band). Since the intrinsic Berry curvature $\Omega_{\tau\xi}^{(0)}({\bf k})$ for spin up and spin down states are opposite in sign, when the $\xi$ states couple (via $\alpha$) the Berry curvature drops. Along the high symmetry line $k_{x}=0$ about which the Berry curvature is even due to the TRS and mirror symmetry in the $y$-direction, the Berry curvature for the spin split bands near band edge can be expressed as Supp

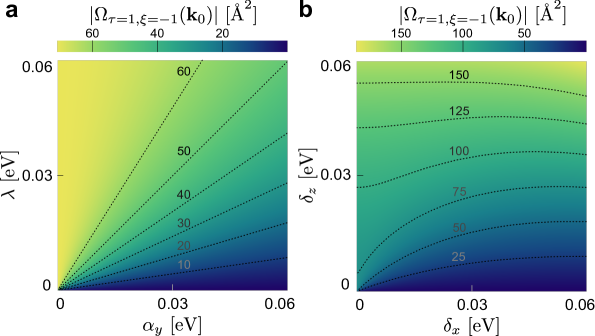
clearly displaying how $\Omega_{\tau\xi}(k_{x}=0,k_{y})$ tends to the value expected in $\Omega_{\tau\xi}^{(0)}$ for $\lambda\gg\alpha$. In Fig. 3a, we plot the peak value of Berry curvature $\Omega_{\tau=1,\xi=-1}$ reproduced in a numerical evaluation of the SBD description. This verifies our above analysis that the value of $\Omega_{\tau\xi}$ is bounded by the intrinsic (depends only on $v_{x,y}$) $\Omega_{\tau\xi}^{(0)}$, and is tuned only by the ratios $\lambda/\alpha$, which makes equi-Berry-curvature contours to be straight lines (see Fig. 3a).

We now consider the case of $\delta_{x,z}\neq 0$, while setting $k$-dependent terms $\alpha,\lambda=0$. By numerically evaluating peak Berry curvature $\Omega_{\tau=1,\xi=-1}({\bf k}_{0})$ (see Fig. 3b), we find that the peak Berry curvature $\Omega_{\tau=1,\xi=-1}({\bf k}_{0})$ develops a more complicated behavior. In particular, $\Omega_{\tau=1,\xi=-1}({\bf k}_{0})$ is no longer bounded by the intrinsic value $\Omega_{\tau\xi}^{(0)}$, and increases with $\delta_{z}$ without saturation. However, similar to the previous case, out-of-plane IS breaking $\delta_{x}$ alone is not able to induce a nonzero Berry curvature since it corresponds to an out-of-plane IS breaking. Large Berry curvature only appears when $\delta_{z}$ is significant.

In the above, we concentrated on unveiling the (Berry curvature) features that the various symmetry allowed spin-orbit coupling terms possess. These features can in turn help to diagnose which of the (a priori symmetry-allowed) spin-orbit coupling terms dominate. We illustrate this by comparing with recent first principles calculations as well as a recent experiment Xu . In Ref. Xu , the Berry curvature of monolayer 1T’-WTe₂ was investigated at different perpendicular electric fields, from 0 to around 1 V nm^-1 using both first principles and a photocurrent measurement. In particular, their first principles results revealed the $E_{\perp}$ induced spin-splitting in the bandstructure that vanished at larger $k_{y}$ away from the band edge, and a peak Berry curvature that increased with $E_{\perp}$. This observation means that $k$-dependent spin-orbit couplings may play only a minimal role. Further both the experiment and the first principles calculations found large Berry curvature at band edge even at small electric field shows that $\delta_{z}>\delta_{x}$ (see Fig. 3). Strikingly, these values of Berry curvature are close to the large intrinsic values expected from $v_{x,y}$ and $m_{{\bf k}}$. Together with Fig. 3b this indicates that the in-plane IS breaking and $h_{Z}$ terms dominates, overwhelming the $h_{R}$ terms. As a result, in what follows we will use the k-independent $\delta_{z}$ spin-orbit coupling term to describe the $E_{\perp}$ induced spin texture.

Current induced magnetization — Another closely related quantity, the (intrinsic) orbital magnetic moment $m_{n}^{\rm int}({\bf k})$, also appears when in-plane IS is broken by $E_{\perp}\hat{{\bf z}}$:

where we have written $n=\{\tau\xi\}$ as a short-hand, and $H$ is the hamiltonian. The orbital magnetic moment comes from the self-rotation of a Bloch electron wave packet around its center of mass, and is an intrinsic property of the Bloch band Xiao , and its distribution in momentum space mimics that of the Berry curvature distribution (see Appendix Supp ).

The low-symmetry of 1T’-WTe₂ enables an asymmetric distribution of of $\Omega_{n}({\bf k})$ and $m_{n}({\bf k})$ (see Fig. 4 a,b). This affords the opportunity to realize Berry phase effects not normally achievable in their rotational symmetric cousins. A striking example is the (linear) magneto-electric effect (ME) $M_{z}=\sum_{i}\alpha_{zi}E_{i}$ ($i=x,y$), where the flow of an in-plane current induces an out-of-plane magnetization. While typically found in multi-ferroic materials Eerenstein where TRS and IS are explicitly broken, ME effects can arise in metals with sufficiently low symmetry (broken IS as well as broken rotational symmetry) and where the dissipation of a charge current breaks TRS Levitov . ²²2 We can see these from the symmetry analysis as follows: (a) in a time-reversal symmetric system $M_{z}=\sum_{i}\alpha_{zi}E_{i}$, then under the symmetry operation $t\to-t$ we have $M_{z}\to-M_{z}$, ${\bf E}\to{\bf E}$, and $M_{z}=\sum_{i}\alpha_{zi}E_{i}\to-M_{z}=\sum_{i}\alpha_{zi}E_{i}$ which leads to $\alpha_{zx}=\alpha_{zy}=0$; (b) if a system has a rotational symmetry, then under the rotation by angle $\theta$ we have $M_{z}\to M_{z}$, $E_{x}\to E_{x}\cos\theta-E_{y}\sin\theta$, $E_{y}\to E\sin\theta+E_{y}\cos\theta$, and $M_{z}=\alpha_{zx}E_{x}+\alpha_{zy}E_{y}\to M_{z}=(\alpha_{zx}E_{x}+\alpha_{zy}E_{y})\cos\theta+(\alpha_{zy}E_{x}-\alpha_{zx}E_{y})\sin\theta$ which leads to $\theta=2n\pi$ ($n=0,1,2,\dots$), i. e., rotational symmetry is not allowed for non-zero $\alpha_{zx}$ and $\alpha_{zy}$; (c) if a system is centrosymmetric, then under the operation $(x,y)\to(-x,-y)$ we have $M_{z}\to M_{z}$, ${\bf E}\to-{\bf E}$, and $M_{z}=\sum_{i}\alpha_{zi}E_{i}\to M_{z}=-\sum_{i}\alpha_{zi}E_{i}$ which also requires $\alpha_{zx}=\alpha_{zy}=0$. . This is termed the kinetic ME effect Levitov ; Sahin .

Indeed, the low-symmetry of 1T’-WTe₂ (with $E_{\perp}\neq 0$) where only a mirror symmetry in the $y$-direction remains is the largest symmetry group that hosts the kinetic ME Levitov ; Sodemann . This makes 1T’-WTe₂ a natural venue to control ME.

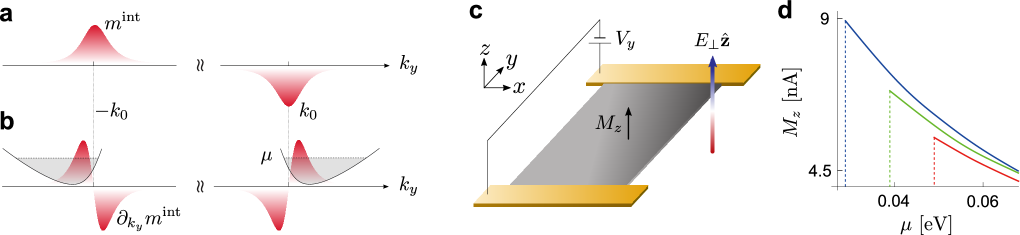
To illustrate the kinetic ME effect in 1T’-WTe₂, we first note that the magnetic moment is asymmetric, displaying a dipolar distribution (see Fig. 4a,b). This can be seen explicitly by considering $\partial_{k_{y}}m$ and noting that it is displaced in relation to the bottom of the band, Fig. 4b. As a result, when an in-plane electric field shifts the distribution function, a uniform out-of-plane magnetization $M_{z}$ develops:

where $D_{ii}$ is the Drude weight along $i$ direction, $f_{n{\bf k}}^{(0)}$ is the equilibrium distribution function, $m_{n}^{\rm tot}({\bf k})=m_{n}^{\rm int}({\bf k})+(ge/2m_{0})\langle u_{{\bf k}}|s_{z}|u_{{\bf k}}\rangle$ is the intrinsic contribution to the magnetic moment in a particular band, containing both orbital and spin contributions with $s_{z}=\hbar\sigma_{z}/2$. For 1T’-WTe₂ monolayer, we estimate $g\sim 5$ Wu ; Fei .

Importantly, Eq. (10) reflects the symmetry of the crystal. For example, magnetic moment distribution has equal magnitudes but opposite signs in the two electron pockets in the conduction band. As a result, $\tilde{\alpha}_{zx}=0$ vanishes as expected from symmetry, see above. In contrast, when in-plane electric field is applied along $y$, a non-zero $M_{z}$ is generated (i.e. $\tilde{\alpha}_{zy}\neq 0$).

Using Eq. (10), we obtain a finite out-of-plane magnetization $M_{z}$ in Fig. 4d when current is driven along the $y$ direction. In doing so, we used $f_{n{\bf k}}^{(0)}=\Theta(\varepsilon_{n{\bf k}}-\mu)$ with $\mu$ the chemical potential, and computed the Drude weight in the usual fashion. Further, to capture the full reciprocal space distribution of the magnetic moment (including regions away from the gap opening), we used the SBD description to compute the magnetic moment distribution. Here we have concentrated on small chemical potentials so that only moments in the lowest conduction band (blue band in Fig. 1e) contribute. Since $m_{n}^{\rm int}({\bf k})$ is an odd function of $k_{y}$ when TRS is present, the filled bands do not contribute to ME. This reflects the fact that kinetic ME arises from a dissipative process. As a result, when the chemical potential is in the gap, $\tilde{\alpha}_{zy}=0$. However, once the system is doped into the conduction band, a non-zero ME develops, see Fig. 4d. Similar analysis also applies to the Berry curvature $\Omega_{\tau\xi}$ (which exhibits a dipolar distribution), and leads to a non-linear Hall effect without applied magnetic field (see Ref. Sodemann as well as the Appendix Supp for an explicit discussion for this system).

Summary – 1T’-WTe₂ with an applied out-of-plane electric field $E_{\perp}$, provides a new and compelling venue to control bulk band quantum geometry. In particular, its bands exhibit a tunable Berry curvature and magnetic moment with switch-like behavior. Crucially, the low symmetry of its crystal structure enable effects not normally found in its rotationally symmetric cousins. These include striking Berry phase effects such as a current induced magnetization (ME), and a quantum non-linear Hall effect. These are particularly sensitive to orientation of in-plane electric field and the crystallographic directions. Indeed, $M_{z}$ is strongest when current runs along the $y$-direction; this sensitivity can be verified through measurements in a single 1T’-WTe₂ sample, for e.g., using a Corbino disc geometry. Perhaps most exciting, however, is how IS broken 1T’-WTe₂ enables direct and electric-field tunable access to out-of-plane magnetic degrees of freedom. Given its two-dimensional nature, 1T’-WTe₂ can be stacked with other two-dimensional materials, providing a key magneto-electric component in creating magnetic van der Waals heterostructures.

Acknowledgements - We gratefully acknowledge useful conversations with Valla Fatemi, Qiong Ma, Su-Yang Xu, and Dima Pesin. This work was supported by the Singapore National Research Foundation (NRF) under NRF fellowship award NRF-NRFF2016-05 and a Nanyang Technological University Start-up grant (NTU-SUG).