Symplectic homology product via Legendrian surgery
Abstract
This research announcement continues the study of the symplectic homology of Weinstein manifolds undertaken in [2] where the symplectic homology, as a vector space, was expressed in terms of the Legendrian homology algebra of the attaching spheres of critical handles. Here we express the product and -operator of symplectic homology in that context.
1 Introduction
Weinstein manifolds are symplectic counterparts of affine (Stein) complex manifolds. They are exact symplectic manifolds which admit symplectic handle decompositions with isotropic core disks. In particular the index of any handle is at most half of the dimension of the manifold. We refer the reader to [2, 15, 10] for precise definitions. Middle dimensional handles are called critical and handles below middle dimension subcritical. Given a Weinstein manifold , its symplectic homology is a symplectic invariant which was first defined by A. Floer and H. Hofer in [11]. It vanishes if is subcritical, see [3]. A general Weinstein manifold is obtained by attaching critical handles to a subcritical manifold along a collection of Legendrian spheres in the contact manifold which is the ideal boundary of . In [2], was expressed in terms of the Legendrian homology algebra of .
Symplectic homology comes with TQFT-like operations which on the homology level are all expressed in terms of a (pair-of-pants) product and a BV-operator, see [14, 12]. In this paper we express the product and the BV-operator in terms of the Legendrian homology algebra of and some additional operations on it. The BV-operator is determined by the algebra itself, whereas the expression of the product involves a duality operation which can be identified with the first term in the extension of Legendrian homology algebra to Legendrian rational symplectic field theory (SFT).
The paper is organized as follows. In Section 2 we introduce algebraic constructions which we later apply to Legendrian homology algebras. In Section 3 we express the Legendrian homology algebra results from [2] in the terminology of Section 2 and also include a discussion on the construction of a version of rational SFT in the Legendrian setting (completion of this construction is work in progress). In Section 4 we present the symplectic homology product and the BV-operator in terms of Legendrian homology algebra and a duality operator and in Section 5 we use the result to compute the symplectic homology, with product and BV-operator, of cotangent bundles of spheres. While proofs are mostly omitted, we note that the proofs of the algebraic results from Section 2 are fairly straightforward.
The authors thank M. Abouzaid, S. Ganatra, E. Getzler, L. Ng, and P. Seidel for inspiring discussions, and Y. Lekili for correcting a sign error in (2.4).
2 Algebraic preliminaries
In this section we describe a number of constructions in a purely algebraic setting. The constructions will be applied in geometrically relevant situations in Sections 3 and 4.
2.1 A tensor algebra and associated objects
We associate to a differential graded algebra over a field a pair of dual -modules and a corresponding tensor algebra. We also discuss cyclic versions of these objects, which are vector spaces over .
2.1.A The algebra
Let be an algebra over a field of characteristic generated by idempotents , where , where is the Kronecker delta. We define a graded module over , which is generated by a countable set decomposed as a disjoint union . The degree of an element will be denoted by . The decomposition of induces a decomposition , where is generated by . When applied on the left, the element , , acts as the identity on and as the -map on , . Similarly, when applied on the right, the element acts as the identity on and as on , .
We define an extension of the module as follows. The module is generated by , where and , where , for and , . We define
where denotes the -dimensional module freely generated by the set and where denotes with grading shifted up by . The module inherits a decomposition from , where
Here the idempotents act as before on as a subset of , and as follows on the new generators: and , .
We will use the following notation. If then denotes the element in that corresponds to . Furthermore, if and are either or and if is an ordered pair of elements in then is composable if .
Let
| (2.1) |
be the tensor algebra over generated by with its natural grading. Then is generated additively by composable monomials , , , where we say that is composable provided is composable for . (Here, as often in the following, we will suppress the tensor sign in the notation for tensor products). The decomposition of induces a corresponding decomposition of , , where is generated by composable monomials with for some and for some .
We will assume that the algebra has a differential of degree which leaves the subspaces , invariant (i.e., , satisfies the Leibniz rule, and ). We will usually write for the homology algebra .
2.1.B The -module and the -complex
Define
| (2.2) |
Then is a graded left-right module over the differential graded algebra which is additively generated by composable monomials , where , , , and , . We say that a composable monomial is cyclically composable if the pair is composable. Let be the submodule generated (over ) by cyclically composable monomials and define as the quotient space of in which monomials which differ by graded cyclic permutation are identified. If then we write for its equivalence class in , i.e. if denotes the natural projection then .
The differential induces a differential as follows. If , , and , then
| (2.3) |
Here
| (2.4) |
where the -module homomorphism is defined by
| (2.5) |
and , for .
Lemma 2.1.
The map is a differential (i.e. ) which leaves invariant and descends to a differential , still denoted , in such a way that the natural projection is a chain map.
We write and , respectively, for the homologies and . Note that is a left-right module over , while is just a -vector space.
Remark 2.2.
We can write
(i.e. is the submodule of generated by and its complement). Let be the projection and let . The second summand can be viewed as a non-commutative version of the “Lie algebra of vector fields” on the space . Indeed, we can identify the cyclic monomial , , , with the vector field . The differential can be naturally viewed as a vector field on , and hence an element of , given by . For any its differential is just the Lie bracket of vector fields, or equivalently the Lie derivative .
This interpretation corresponds to the “satellite philosophy” from [9]. Another interpretation was pointed out to the authors by M. Abouzaid: is isomorphic to the Hochschild homology .
2.1.C The extended tensor algebra and the space
Recall that the module is generated over by a set and that the module is generated over as a left-right module by , where and . Let denote the -vector space dual to . Then is the direct product of the 1-dimensional -vector spaces which are generated by elements of , where and . Furthermore, we have
In , the idempotent , , acts from the left as the identity on and as on , , and acts from the right as the identity on and as on , . Fix an integer (it will correspond to half the dimension of the Liouville domain in Section 3). We endow with a grading defined as follows:
| (2.6) | |||
| (2.7) |
Define
| (2.8) |
We define the tensor algebra
| (2.9) |
as a certain completion of the free associative algebra generated by . Its elements are infinite series in the -variables with polynomial coefficients in the -variables (compare to the above definitions of as an infinite sum and as an infinite product). For simplicity of notation and since all completions we consider below are of the same type as that of (2.9), we will, as in that equation, suppress completions from notation and use the direct sum symbol in decompositions. Consider the extension of obtained by adding multiplicative generators and of degrees
which satisfy the following relations:
and
The algebra can be decomposed according to tensor type: , where is the -subspace generated by monomials with factors from and from . We decompose further: , where is the subspace spanned by all monomials of total -degree and total -degree . In particular, , , and . We also write , , , , and .
For , let
In analogy with the definition of in Section 2.1.B, we define . Further, define as the quotient of obtained by dividing by the following graded cyclic permutation rule: if and if then , and we identify with , where
We will often think of cyclic monomials as written on a circle with the first letter at . This allows us to speak about generators in a cyclic monomial as ordered in the (counter) clockwise direction staring from some fixed generator in the monomial. In this language, the above permutations correspond to rotations of the circle.
The vector space inherits the decomposition by tensor type:
If the monomials and differ by a graded cyclic permutation, i.e. if , then, for , and . We thus define and , and note that this definition does not depend on choice of representative .
A monomial is balanced if and . The subspace of generated by balanced monomials will be denoted by . It contains balanced versions and of and , respectively. More precisely,
2.1.D The operator
Consider a monomial and fix a factor in . Then for monomials . Define
where the sum is taken over all factors in . It is straightforward to check that this gives a well defined operation and by definition . In particular, if then satisfies
where is the operator defined in (2.5) above. Furthermore,
2.1.E Symmetry breaking and contraction operations
We next effectively break the cyclic symmetry of . An excited monomial is a cyclic monomial with one of its factors from distinguished. We call the distinguished factor of an excited monomial the excited generator of . The -vector space generated by excited monomials from will be denoted by . Note that inherits decompositions from , , etc. We set . Define the excitation operator to be the linear map which maps a monomial the sum of all its excitations.
Note that contain excited versions and of and , respectively, which are isomorphic to their non-excited counterparts. (In the context of we think of and as generated by monomials in and without excited generator.)
We will use the following notation to identify excited generators in monomials: we underline the excited generator in a monomial in and write e.g. , , and .
We next define a product on . Consider two excited cyclic monomials . Fix a factor from and a factor from . Write and , where is the sign which arises from cyclically rotating so that is its last factor and where is the sign which arises from cyclically rotating so that is its first factor. Define the contraction operation ,
| (2.10) |
where the sum is taken over all pairs of factors from and from , and where
If and then we define, for , the partial contraction as follows:
where the sum is taken over all from and where is the factor from in counting counter-clockwise from the unique factor from . Similarly, if and then we define, for the partial contraction :
where the sum is taken over all from and where is the -th factor from in counting clockwise from the unique factor from .
Remark 2.3.
Let then . Further if then , and if then .
Define the bracket or commutator as
| (2.11) |
Lemma 2.4.
The bracket satisfies the graded Jacobi identity:
Let
We associate with a multi-linear operation defined by
| (2.12) |
Note that if then , that if exactly one of the arguments lies in then the image lies in , and that the operation vanishes on -tuples with more than component in .
Similarly, defines a multi-linear operation ,
| (2.13) |
if then , if exactly one of the arguments lies in then the image lies in , and the operation vanishes on -tuples with more than one component in .
In the special case , we associate with two more operations,
| (2.14) |
and
| (2.15) |
where
Similarly, induces an operation ,
| (2.16) |
We observe that and .
2.1.F The Hamiltonian
We define special elements which derive from the differential on and which, in the spirit of SFT, see [9], are called Hamiltonians.
Definition 2.5.
We use the Hamiltonian to define a differential on . First define the exterior differential as follows. Consider the map which acts as the algebra differential on generators of from , which maps all other generators to , and which satisfies the graded Leibniz rule. Then preserves , descends to where it preserves . It then induces a map as follows. The map is already determined on and if is a monomial in , where then . Then and we observe that satisfies the following master equation
| (2.17) |
Since , and (2.17) can be rewritten in Maurer-Cartan form:
| (2.18) |
Decomposing , (2.17) is equivalent to the following sequence of identities for the -components of :
| (2.19) |
The first identity in this sequence is
| (2.20) |
Definition 2.6.
The differential interacts with the bracket in the following way.
Lemma 2.7.
For ,
In particular, the operation descends to the homology .
We observe that leaves , , , and invariant. For simple notation we write for the restriction of to any one of these subspaces. Consider the isomorphisms and ,
| (2.21) |
Lemma 2.8.
The maps and are chain isomorphisms.
The following result is a consequence of Lemma 2.7.
2.2 Products
We introduce product operations on and .
2.2.A The product on
Proposition 2.10.
The operation descends to an associative product on the homology which satisfies the following graded commutativity relation for the grading shifted by :
The homology class of the cycle is the unit for this product on . In fact, is a unit for already on the chain level, before passing to homology.
Consider the second and third identities satisfied by the Hamiltonian :
| (2.22) | ||||
| (2.23) |
Here (2.22) is the chain map equation for , and (2.23) shows that this product is associative on the homology level. Indeed,
The unit property can be checked directly if one observes that the sum of all terms in with excited generator from and which contain at least one -factor, is
Hence, taking into account that we have for any
To verify the commutativity relation, let be a -cycle in . Applying the -operator to the equation gives and thus, on the level of homology, and we calculate
2.2.B The product on
If there exists an element
such that satisfies the master equation
| (2.24) |
then we say that is compatible with and we call the full (rational) Hamiltonian. As we shall see later, when is a Legendrian homology algebra then we can always find compatible with using a relative SFT formalism associated with parallel copies of the Legendrian submanifold in the spirit of [5].
Assume now that , and in particular , which satisfies (2.24) exists and is given. Then we define the operation ,
Note that if then .
Theorem 2.11.
-
1.
The operation descends to an operation on the homology where it can be expressed by the following three equivalent expressions:
Equivalently, the following diagram commutes on the homology level,
where
for and .
-
2.
The operation is associative and graded commutative on homology, i.e. if then
The above result is a consequence of the master equation (2.24) which in particular implies the identities
| (2.25) | ||||
| (2.26) |
A straightforward calculation shows that . By (2.25), , by (2.22), , and therefore is a cycle in . Similarly, is a cycle and (2.26) implies that their homology classes coincide. This shows that the product descends to homology and implies the first equation of part 1 of the theorem. The alternative expressions for in part 1 are immediate from the definitions of the operations , , and .
2pt
\pinlabel at -30 460
\pinlabel at 90 460
\pinlabel at 208 460
\pinlabel at 316 460
\pinlabel at 428 460
\pinlabel at 550 460
\pinlabel at -30 300
\pinlabel at 72 300
\pinlabel at 175 300
\pinlabel at 264 300
\pinlabel at 360 300
\pinlabel at 450 300
\pinlabel at 550 300
\pinlabel at 170 120
\pinlabel at 400 120
\endlabellist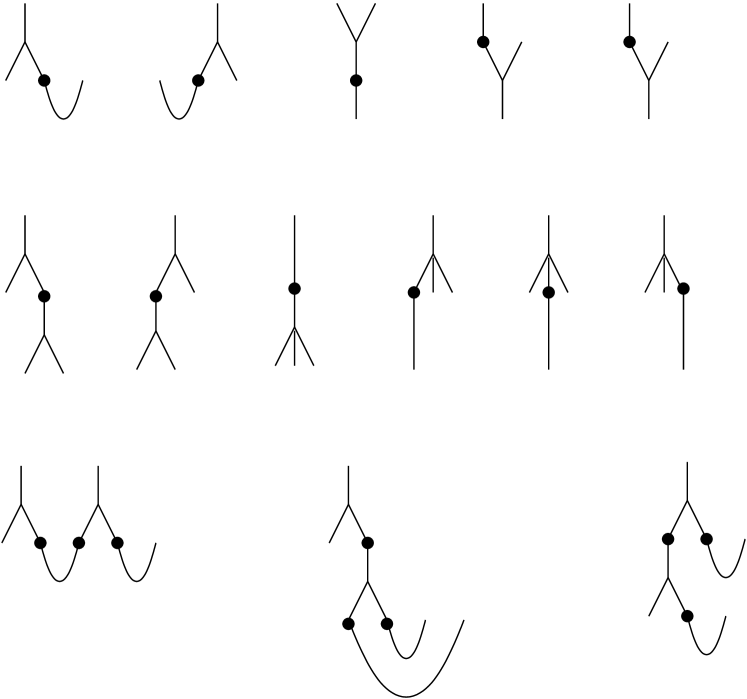
To verify the commutativity we observe that given a cycle , using the homological identity , we calculate
Finally, the proof of associativity is pictorially illustrated on Figure 1.
The products on and on are related via the chain map in the following way.
Proposition 2.12.
The map induced by on homology is a homomorphism of rings . Moreover, if there is a unit for on , i.e. , for all , then is injective.
Indeed, if then, taking into account that , we calculate
To verify the injectivity of we use one of equivalent definitions of from Theorem 2.11, part 1:
and hence, implies
Using the isomorphism , defined above we transport the product to . Given , we define
| (2.27) |
Note that the homomorphism shifts the grading by , and hence the commutation equation for translates to the equation
Let us also point out that the degree of the product is equal to .
3 Legendrian algebra constructions
In this section we first reformulate the main result relating Legendrian homology algebra and symplectic homology [2, Corollary 5.7] in the terminology of Section 2, and second give a brief sketch of the geometry that enters the construction of the full rational Hamiltonian in the framework of Legendrian SFT with focus on the parts of it that enter the expression of the product.
3.1 The complex expressed as
Let be a Liouville domain with contact boundary and let be a union of Legendrian spheres. Let be the set of Reeb chords of and consider the decomposition , where a chord in starts on and ends on . Let be the graded module generated by the set with decomposition , where is generated by . Then the Legendrian homology algebra is the tensor algebra associated to as in (2.1) and the differential gives a differential graded algebra , see [2, Section 4.1]. Let be the chain complex defined in (2.2). The following result is a consequence of [2, Remark 7.4].
Lemma 3.1.
The chain complex is canonically isomorphic to the chain complex defined in [2, Section 4.5].
In [2, Corollary 5.7] it was shown that if (e.g. if is a subcritical Weinstein manifold) and if is obtained from by attaching Lagrangian -handles along , then there is a quasi-isomorphism
| (3.1) |
where denotes a chain complex with homology equal to .
3.2 Legendrian rational SFT
The differential in the Legendrian algebra is defined by counting elements of moduli spaces of rigid holomorphic disks in , with boundary on , and with exactly one positive and several negative punctures, see e.g. [2, Section 4.1]. The formalism of Legendrian rational SFT comes from algebraic structures associated with holomorphic disks with an arbitrary number of positive and negative punctures. As is well known, in order to construct such a theory one needs to handle boundary cusp-degenerations of holomorphic disks. The problem of boundary cusp-degeneration can be solved by incorporating string topology operations into the SFT formalism. The corresponding theory has not yet been constructed in sufficient generality for it to be applicable in the setting of this paper. (See, however [13] for the case of -dimensional Legendrian knots in ).
However, the algebraic formalism described in Section 2 requires a different version of the full rational Hamiltonian , in the spirit of [5]. It arises naturally when one considers moduli spaces of holomorphic disks with boundaries on multiple parallel copies of .
Let us first consider the term . This is the only term besides which is needed for defining the product on , see Figure 3. We recall here that for any is determined by the differential on the Legendrian algebra .
For each fix a point . Let , where and , , be an excited cyclic monomial. We associate to it a moduli space . Here the moduli space consists of holomorphic disks anchored in , see [2, Section 2.2],
where
is a set of cyclically ordered boundary punctures on , with the following properties:
-
()
at the puncture , is asymptotic to the chord at ;
-
()
if then at the puncture is asymptotic to the chord at ;
-
if then, extends continuously over , and .
The moduli space consists of holomorphic disks connected by Morse flow lines. To define it, choose auxiliary Morse functions , , each with exactly two critical points. For define the auxiliary moduli space of pairs of holomorphic disks anchored in ,
where
are sets of cyclically ordered boundary punctures on , with the following properties. At , satisfies condition if or condition if . At , satisfies condition . At the puncture , , extends continuously and the following condition holds:
-
The points and lie in the same component and there exists a trajectory of which starts at and ends at , where is the auxiliary Morse function on . Here the gradient is taken with respect to the metric induced by the symplectic form and the almost complex structure.
Finally, define
Given , let if or . Define , . Then we have the dimension formula
In particular in terms of the grading on , for the balanced monomial we have
Define as , where
| (3.2) |
where the sum is taken over all balanced monomials which additively generate and for which . Here is the algebraic number of -dimensional components of the moduli space . As will be briefly discussed below, the above definition of can generalized to more than two positive punctures and as a consequence we get the following result.
Proposition 3.2.
There exists an element , with trivial component in , such that complements to the full rational SFT Hamiltonian (i.e. if then ).
Here the components , , of the full rational Hamiltonian satisfies the relation , , and are defined through a construction which generalizes that used in the definition of above. These higher order components of the Hamiltonian are not needed for the definition of the product (but some of them are needed for proving its properties) and will not be defined in this paper. We give however a brief description: is defined using moduli spaces of so-called generalized holomorphic disks. Generalized holomorphic disks are combined objects consisting of holomorphic disks with boundary on one copy of connected by gradient flow trees associated to auxiliary Morse functions on , an example is depicted in Figure 2, see [7] for similar considerations. The elements of the moduli space defined above are examples of generalized holomorphic disks where the gradient flow tree consists of only one gradient trajectory. A more general configuration is shown in Figure 2. More precisely, if is a monomial in , where and where , , then we consider the moduli space of generalized holomorphic disks with asymptotic data according to , i.e. positive punctures at if , negative punctures at if , auxiliary negative punctures at the Reeb chords in the monomials , and these punctures appearing along the boundary of the disk in the cyclic order given by . The dimension of is given by
In particular for we have
and is defined as
where the sum ranges over all with .
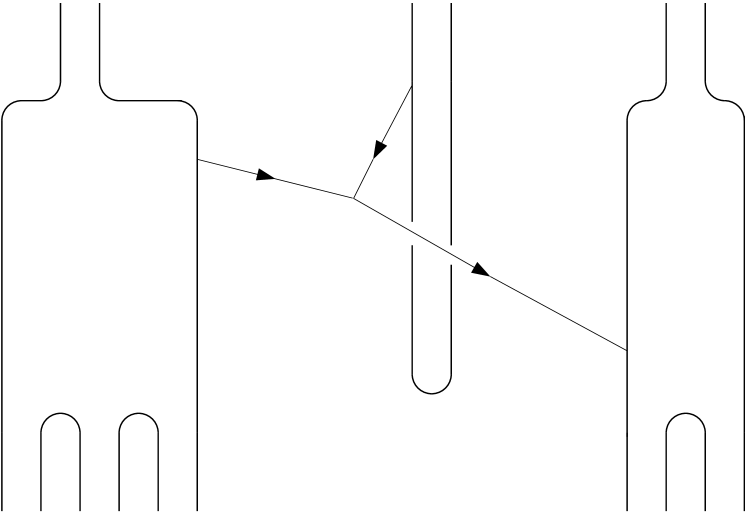
Remark 3.3.
In this geometric context, the excitation operator has the following meaning. Given a generalized holomorphic disk with boundary in the ordered union of (symplectizations of) parallel copies of a Legendrian manifold we always insist that the boundary arcs of the disk between punctures corresponding to generators from be mapped to different copies of . We also require that when going around the boundary of the disk in the counter-clockwise direction we jump at every such puncture except one to a higher copy of in terms of the natural ordering corresponding to the direction of the Reeb vector field. The unique puncture where we jump down corresponds to the excited generator of the monomial corresponding to the boundary punctures. Here the moduli spaces corresponding to different assignment of the distinguished “jump-down” punctures are canonically diffeomorphic, and the operator just associates with this universal moduli space the moduli spaces corresponding to all possible assignments of the “jump-down” vertex.
Remark 3.4.
The geometric motivation for the “gluing sign” in the equations , is as follows. The algebraic variables and , has two dual geometric meanings as follows: when is glued to , corresponds to a positive puncture at a short Reeb chord between copies of at the minimum of the Morse function and corresponds to a negative puncture at this chord, when is glued to , corresponds to a negative puncture at the maximum of and to a positive puncture at this maximum. In a coherent orientation scheme there is a sign difference (a factor ) between the gluings at these two types of punctures.
4 The product and the BV-operator via Legendrian algebra
Let , , and be as above. Let and . Then (3.1) gives a quasi-isomorphism . In this section we present the operations on which correspond to the product and the BV-operator on under .
4.1 The product
Let be the full rational Hamiltonian determined by , see (3.2). Then Proposition 3.2 implies that satisfies (2.25). Hence, according to Theorem 2.11 and (2.27), there exists a product of degree which is associative and commutative on homology and which is defined by conjugating one of the following homotopically equivalent formulas for the product on with :
| (4.1) |
see Figure 3.
Theorem 4.1.
If (e.g. if is subcritical) then, under the map on homology induced by the quasi-isomorphism , see (3.1), the pair of pants product on corresponds to the product on .
2pt
\pinlabel at 31 114
\pinlabel at 140 114
\pinlabel at 88 35
\pinlabel at 340 130
\pinlabel at 340 50
\pinlabelin at 672 190
\pinlabelout at 713 57
\pinlabelin at 515 80
\endlabellist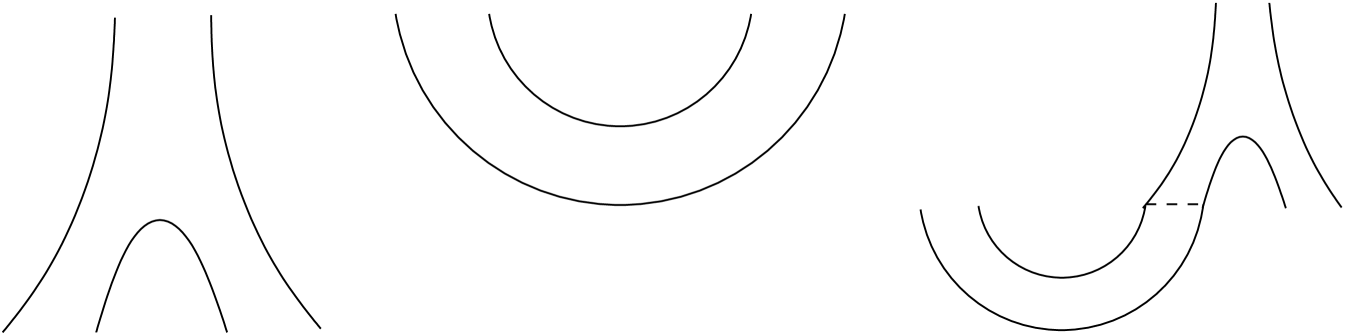
4.2 The BV-operator
Let and consider the linear map of degree defined as follows on monomials , , :
Proposition 4.2.
The map is a chain map and if then, under the map on homology induced by the quasi-isomorphism , see (3.1), the BV-operator on corresponds to the operator on .
5 Example:
In this section we compute the symplectic homology with product and BV-operator for cotangent bundles of spheres presented as the result of attaching a Lagrangian -handle to the Legendrian unknot in the boundary of the ball.
Consider the Legendrian unknot in with coordinates and contact form . Figure 4 shows the projection of the Legendrian unknot for to the -plane.
2pt
\pinlabel at 125 218
\pinlabel at 595 123
\endlabellist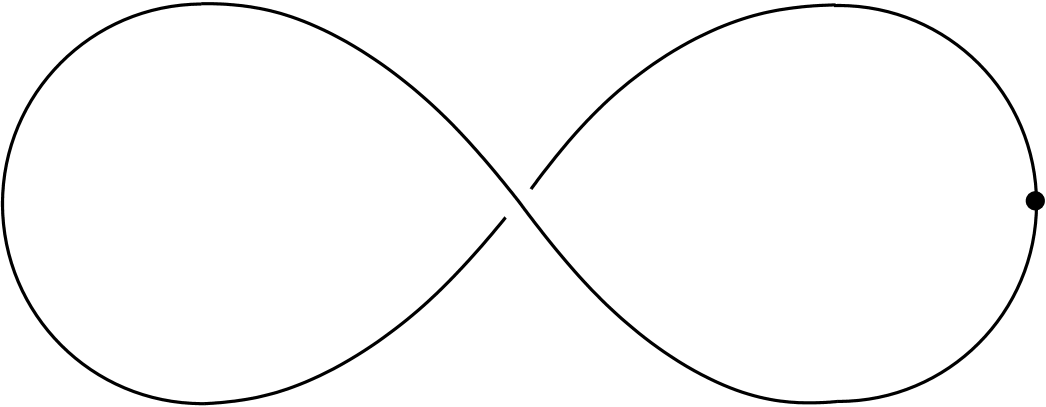
To define the Legendrian unknot of dimension consider the -dimensional unknot with Reeb chord over and symmetric with respect to the rotation by a half turn around the axis. Include into the -subspace of and take the -dimensional unknot as the orbit of under the action by given by for . For simplicity, we let denote the Legendrian unknot in for any .
Consider and include it into a Darboux chart in the boundary of the -ball . Then attaching a Lagrangian -handle to along gives a symplectic manifold which is symplectomorphic to the cotangent bundle of the -sphere. As explained in [2], in order to determine it suffices to study Reeb chords and holomorphic disks that are contained in the Darboux chart. The unknot has only one Reeb chord which we denote and .
The moduli space of holomorphic disks with positive puncture at and a marked point on the boundary evaluates with degree to . To see this, note that for , holomorphic disks that are rigid up to translation correspond to polygons with boundary on the knot diagram and with convex corners, where at positive punctures the boundary orientation goes from the lower to the upper strand and vice versa at negative punctures. There are thus two disks with evaluation maps that give a degree map since we use the null-cobordant spin structure on the circle to orient moduli spaces. For we note that we may take the almost complex structure to be invariant with respect to the action and it follows that the moduli space of holomorphic disks with positive puncture at is diffeomorphic to and that, when equipped with a marked point on the boundary, it evaluates with degree .
The above description of moduli spaces implies in particular that the differential on is trivial, i. e., . Consequently, the differential on satisfies
where
| (5.1) |
Thus and (recall the chain isomorphism , see (2.21)) are generated by the cycles listed in Tables 1 and 2 when is even and odd, respectively.
| degree | degree | ||
|---|---|---|---|
| degree | degree | ||
|---|---|---|---|
In order to compute the product we need to determine and . Consider first (see Definition 2.5):
| (5.2) |
see Remark 5.2 for a discussion of the sign in this formula.
Remark 5.1.
In our description of in terms of generalized holomorphic disks, the disks which give rise to (5.2) are degenerate. The first two terms comes from the trivial strip of with an unconstrained Morse puncture lying in one of the two boundary components. The last term comes from the -family of three-punctured constant disks lying in with one puncture constrained to lie in and remaining two punctures unconstrained.
Next, consider . Since the evaluation map from the moduli space of holomorphic disks with positive puncture at into has degree there is algebraically disk which satisfies a point constraint at and we conclude from the description of generalized holomorphic disks that
| (5.3) |
see Remark 5.2 for a discussion of the sign in this formula.
Remark 5.2.
Orientations of moduli spaces are fixed by orienting capping operators at Reeb chords, see [8] for details. The overall sign in (5.2) is independent of the choice of capping operator for since variables associated to appears quadratically in , the overall signs in (5.2) changes with the orientation data at , and the overall sign in (5.3) changes, independently, with the orientations of capping operators at both and . It follows that we can choose any sign combination in the two equations and in particular the one under consideration.
To compute acting on we use the components of in which the puncture at the second leg is excited. We will denote the sum of these by . The relevant parts of the Hamiltonian are thus, see (5.3) and (5.2), (recall gradings: , , , and )
and we get
Using (4.1) for the tensor of the product then gives the following expression for the product, with : If is odd then
and if is even then for
We conclude from this calculation that the commutative product which corresponds to the pair of pants product on has unit represented by the class and multiplication according to the above formulas after substituting with everywhere.
To finish the example we determine also the operator which corresponds to the -operator on . If is odd then
and if is even then
References
- [1] M. Abouzaid, P. Seidel, An open-string analogue of Viterbo functoriality, Geom. Topol., 14 (2010), no. 2, 627–718.
- [2] F. Bourgeois, T. Ekholm, Y. Eliashberg, Effect of Legendrian surgery, arXiv:0911.0026
- [3] K. Cieliebak, Handle attaching in symplectic homology and the Chord Conjecture, J. Eur. Math. Soc. (JEMS) 4 (2002), 115–142.
- [4] K. Cieliebak, T. Ekholm, J. Latschev, Compactness for holomorphic curves with switching Lagrangian boundary conditions, J. Symplectic Geom., 8 (2010), no. 3, 267–298.
- [5] T. Ekholm, Rational symplectic field theory over for exact Lagrangian cobordisms, J. Eur. Math. Soc., 10 (2008), no. 3, 641–704.
- [6] T. Ekholm, Rational SFT, linearized Legendrian contact homology, and Lagrangian Floer cohomology, arXiv:0902.4317.
- [7] T. Ekholm, J. Etnyre, J. Sabloff, A duality exact sequence for Legendrian contact homology, Duke Math. J., 150 (2009), no. 1, 1–75.
- [8] T. Ekholm, J. Etnyre, M. Sullivan, Orientations in Legendrian contact homology and exact Lagrangian immersions, Internat. J. Math. 16 (2005), no. 5, 453–532.
- [9] Y. Eliashberg, A. Givental and H. Hofer, Introduction to Symplectic Field Theory, GAFA, Special volume GAFA-2000, 560–673.
- [10] Y. Eliashberg, M. Gromov, Convex symplectic manifolds, in “Several complex variables and complex geometry, Part 2” (Santa Cruz, CA, 1989), 135–162, Proc. Sympos. Pure Math. 52, Part 2, Amer. Math. Soc., Providence, RI, 1991.
- [11] A. Floer, H. Hofer, Symplectic homology. I. Open sets in , Math. Z. 215 (1994), no. 1, 37–88.
- [12] E. Getzler, Batalin-Vilkovisky algebras and 2d Topological Field Theories, Commun. Math. Phys, 159(1994), 265–285.
- [13] L. Ng, Rational Symplectic Field Theory for Legendrian knots, arXiv:0806.4598.
- [14] P. Seidel, A biased survey of symplectic cohomology. In Current Developments in Mathematics (Harvard, 2006), Intl. Press, 2008, 211–253.
- [15] A. Weinstein, Contact surgery and symplectic handlebodies, Hokkaido Math. J., 20(1991), 241–251.