Synthetic photonic lattice for single-shot reconstruction of frequency combs
Abstract
We formulate theoretically and demonstrate experimentally an all-optical method for reconstruction of the amplitude, phase and coherence of frequency combs from a single-shot measurement of the spectral intensity. Our approach exploits synthetic frequency lattices with pump-induced spectral short- and long-range couplings between different signal components across a broad bandwidth of of hundreds GHz in a single nonlinear fiber. When combined with ultra-fast signal conversion techniques, this approach has the potential to provide real-time measurement of pulse-to-pulse variations in the spectral phase and coherence properties of exotic light sources.
I Introduction
The concept of synthetic frequency lattice in photonics Yuan et al. (2018); Ozawa and Price (2019), where dynamic modulation induces cross-talks between discrete spectral lines to produce lattice-like behavior Bell et al. (2017); Dutt et al. (2020), is stimulating rapidly growing research in recent years. The development of synthetic lattices not only provides a new means for the reshaping of discrete spectral lines, but also enables tailored transformations of optical spectra underpinned by the remarkable capability of inducing multiple arbitrary short- and long-range couplings in frequency domain Bell et al. (2017), beyond the physical constraints of spatial lattices Szameit et al. (2009). So far, synthetic lattices were extensively investigated in their capacity for creating multiple artificial dimensions Yuan, Shi, and Fan (2016); Ozawa et al. (2016); Lustig et al. (2019); Maczewsky et al. (2020); Wang et al. (2020), yet their other potential applications remain largely undeveloped. This motivates our current research on employing the fundamental advances of synthetic lattices to the practically important task of fast and efficient characterisation of frequency combs.
The full characterization of ultra-short optical signals, including both their phase and coherence properties, is crucial for the development and understanding of novel engineered light sources, such as optical frequency combs Walmsley and Dorrer (2009); Kippenberg, Holzwarth, and Diddams (2011); Schmeissner et al. (2014), frequency encoded quantum states Kues et al. (2017), and optical soliton molecules Herink et al. (2017). Furthermore, full optical signal characterization is important for the communication of timing information over fiber networks Foreman et al. (2007) and wavelength division multiplexing transmission formats where the relative phases between individual carriers are important Ellis and Gunning (2005). The most commonly used methods for measuring optical pulses, frequency-resolved optical gating (FROG) Scott et al. (2007) and Spectral Phase Interferometry for Direct Electric-field Reconstruction (SPIDER) Walmsley and Dorrer (2009); Dorrer and Kang (2003), require complex multimode optical setups in order to reconstruct the amplitude and degree of coherence.
Techniques with the capability to recover spectral phase information with just a single spatial mode are being actively developed. This includes ultra-fast signal conversion methods like stretch transform spectroscopy Solli, Chou, and Jalali (2008), which could allow real time measurement of pulse to pulse variations in the spectral phase profile, without a need to use an interferometric setup Xu et al. (2016). The technique of electro-optic spectral shear interferometry (EOSI) Wong and Walmsley (1994); Dorrer and Kang (2003); Bromage et al. (2006) can also be implemented for determining the spectral phase and amplitude of frequency combs using a single mode setup, by employing an electro-optic modulator (EOM) Supradeepa et al. (2010). The electro-optic phase modulation enables particularly effective characterization of weak coherent frequency combs, even in quantum regime at the single- and few-photon levels Kues et al. (2017); Imany et al. (2018a). However, EOSI necessarily requires a sequence of different EOM shears to be applied to the signal to fully determine its state, which significantly limits the data acquisition speed. Furthermore, the temporal resolution of EOSI is limited by the free spectral range of the EOM, while the steady growth of telecommunication bandwidth calls for fast and efficient methods of optical spectral characterisation.
Here we propose and experimentally demonstrate that specially designed synthetic lattices can facilitate a new method for recovering the full spectral amplitude, phase and coherence information of an optical frequency comb from a single-shot measurement of the spectral intensities after an input signal is transformed in a nonlinear fiber. This is mediated by a co-propagating pump, which is tailored to realize an effective synthetic lattice for the signal through the energy-conserving process of four-wave mixing Bragg scattering (FWM-BS) Bell et al. (2017). The presented method can be much faster than FROG, SPIDER or EOM based approaches, since it only needs a single measurement and minimal post-processing, while allowing for a significantly larger free spectral range compared to the EOM approach.
In the following, we first introduce the concept and theory of the reconstruction with a synthetic frequency lattice in Sec. II. Then, we describe the experimental setup and demonstrate the reconstruction of signals with two and four spectral lines in Sec. III. Finally, we present conclusions and outlook in Sec. IV.
II Concept of reconstruction with synthetic frequency lattice
We propose to use a synthetic frequency lattice to transform input signals into a form where a single-shot spectral intensity measurement at the output would allow full reconstruction of the input spectral phase and coherence. In a synthetic lattice, discrete frequency components effectively become lattice sites, where light can couple or hop to nearest-neighbor or farther frequencies corresponding to the short- and long-range couplings on a lattice. Such frequency lattices allow complex spectral manipulation of light within a single spatial mode of an optical fiber or waveguide Yuan, Shi, and Fan (2016); Bell et al. (2017); Bersch, Onishchukov, and Peschel (2009).
We build on the recently developed approaches based on spatial lattices Minardi et al. (2012); Minardi (2015); Titchener, Solntsev, and Sukhorukov (2016); Oren et al. (2017); Titchener et al. (2018); Wang et al. (2019), and reveal that light propagation and reshaping in nonlinearly induced synthetic lattices can be utilized to allow full reconstruction of an input signal from a simple spectral intensity measurement at the output. Specifically, the spectral amplitude, phase and relative coherence of the signal can be recovered. The system is all-optical, with the synthetic lattice induced through optical nonlinearity and controlled via a pump, which can be altered quickly to provide different functionalities. Furthermore, manipulation of light within the spectral dimensions, without resorting to spatial multiplexing, makes such devices very compact.
We consider an input signal which spectrum consists of a number of discrete frequency components separated by a constant spectral spacing , as shown in Fig. 1. After propagating through the synthetic lattice, which introduces coupling between the frequency lines, the input signal is spread across an increased number of synthetic lattice sites. In the regime of coherent frequency conversion, the output spectral intensity pattern is dependent on the relative phases and coherence of the input signal. Importantly, we find that, for certain parameters of the synthetic lattice, it is sufficient to measure just the output spectral intensities in order to perform robust reconstruction of the input spectrum and phase. The propagation of a fully coherent signal through the synthetic lattice, which can be induced experimentally in an optical fiber as we discuss in the following Sec. III, can be described by coupled-mode equations Bell et al. (2017) for a set of complex amplitudes at frequency components ,
| (1) |
where is the -th order coupling coefficient, is the effective nonlinearity, and are the complex amplitudes of the envelope of pump spectral components. We determine the lattice dispersion in the framework of Eq. (1) by considering the plane-wave solutions in the form , where is the wavenumber, and find the propagation constant as:
| (2) |
The output state after propagation through the fiber length is related to the input state via a linear transformation which can be expressed through the transfer matrix ,
| (3) |
We obtain the transfer matrix elements by performing a Fourier transform of Eq. (1) as
| (4) |
In general, noise and fluctuations may affect the coherence of comb spectrum. Such partially coherent signals can be characterized by the mutual coherence or complex visibility Mandel and Wolf (1995) between different pairs of spectral lines,
| (5) |
where are the fluctuating complex field amplitudes of the spectral comb lines and angled brackets denote averaging. It is established Mandel and Wolf (1995) that any partially coherent field can be represented as an incoherent mixture of coherent fields indexed by , such that
| (6) |
We substitute Eq. (3) into Eq. (6) and obtain
| (7) |
The output comb intensities, which can be directly measured by a spectrometer, are then found as
| (8) |
Therefore the input complex visibility can be retrieved by inverting Eq. (8) to find in terms of the output spectral intensities . Considering the input signal to consist of spectral lines, and the output spread out to lines, we require that the number of measurements is equal to or larger than the number of unknowns, . The robustness of the inversion process can be characterized by the “condition number”, , where is the instrument matrix that directly links the observable () and the reconstructed quantities () and denotes the norm of a matrix. The condition number quantifies the amplification of the measurement errors and noise of the output intensities in the process of reconstruction of the input complex visibility function Press et al. (2007); Minardi (2015); Titchener et al. (2018); Wang et al. (2018). A high condition number implies that small errors in the measurement data would be highly amplified after the inversion, making the result of reconstruction unreliable. Thus for an accurate reconstruction, we require a low condition number. As we discuss in the following, robust reconstruction, associated with a small condition number close to a theoretical optimum, requires specially tailored simultaneous short- and long-range couplings in the synthetic frequency lattice. We note that the reconstruction procedure is also possible in the presence of absorption, which effect can be incorporated in the coupled-mode Eq. (1), while the general approach formulated in Eqs. (3),(5)-(8) remains the same.
III Experimental comb reconstruction via the synthetic lattice in an optical fiber
We realize the synthetic frequency lattice through the process of four-wave mixing Bragg scattering (FWM-BS) in a nonlinear fiber Bell et al. (2017), see Fig. 2(a). Here, the lattice sites are represented by discrete signal frequency channels, which are coupled together by nonlinear frequency conversion. In this system, controllable coupling is made possible by shaping the spectrum of the optical pump. A broad phase-matched bandwidth for FWM-BS is achieved by placing the signal and pump spectra on either side of the zero-dispersion wavelength. One of the unique features of this approach is that it allows long-range coupling, which enables efficient reconstruction of complex input signal states by measuring the output spectra.
We experimentally demonstrate the reconstruction of a signal consisting of up to four frequency channels, but in principle the method is applicable to more complicated signals. We choose a pump spectrum consisting of different frequency components around nm wavelength, separated by GHz [Fig. 2(b)]. By having three equally spaced pump spectral lines with , the signal can be up- or down-shifted by or via the FWM-BS. This realizes a synthetic lattice with first and second order coupling coefficients . The corresponding lattice dispersion is presented in Fig. 2(c), with the contributions of the first and second order coupling shown individually as dashed lines.
We first numerically investigate the inversion problem for the case where the input signal is limited to two input synthetic lattice sites. We study the effect of varying the coupling rates and , while assuming that other couplings are zero (), and the normalized fiber length is held constant at . For each set of values of and we calculated the transfer function according to Eq. (4) and the corresponding condition number. The plot of the condition number vs. the coupling rates is shown in Fig. 2(d), indicating that inversion will be practical given and are chosen in an optimal region. Importantly, both short- and long-range couplings need to be present simultaneously, with .
Next, we experimentally measure the transfer function of the nonlinear fiber system for a range of different coupling rates. This measurement fully incorporates the effect of losses both on the pump and signal, which enables reconstruction under realistic experimental conditions. We vary the power of the three equal-amplitude pump spectral lines to simultaneously control the first- and second-order coupling rates with , as indicated by the dashed line in Fig. 2(d). The transfer function of the system for a given set of pump powers was determined by performing measurements for a set of four different input signals. We used the basis set , , and , where and correspond to the wavelengths of nm and nm, respectively. The output states resulting from the input basis state are shown in Fig. 2(e), where the x-axis indicates the pump power. We use the experimentally determined transfer function to calculate the condition number of the inverse problem as a function of pump power, see Fig. 2(f). We also solved the inverse problem using the data from the basis state as the input, then calculated the fidelity of the reconstructed state with the input. This fidelity is shown by the right hand y-axis on Fig. 2(f). The decrease in fidelity with increasing pump power indicates that the assumption that the fiber system preforms linear transformation on the input signal breaks down, as other effects begin to emerge at higher pump powers. We use Fig. 2(f) to determine the pump power which minimizes the condition number and maximizes the fidelity in order to allow the most accurate reconstruction of arbitrary input states.
A pump power of was chosen to enable the optimal reconstruction accuracy of input signals. We then tested our reconstruction method experimentally by coupling a sequence of random input signals into the fiber. The general form of the input signals was , where and are randomly chosen, and implemented using a waveshaper. Then the output spectra at the end of the fiber are measured and used to reconstruct the input signal. An example of the real and imaginary parts of a reconstructed input complex visibility function is shown in Figs. 3(a) and 3(b), respectively. The reconstructions were carried out for many random input signals parametrized by and as shown in Fig. 3(c). We observe that the reconstructed signals’ fidelity to the input that the waveshaper was configured to produce is typically above .
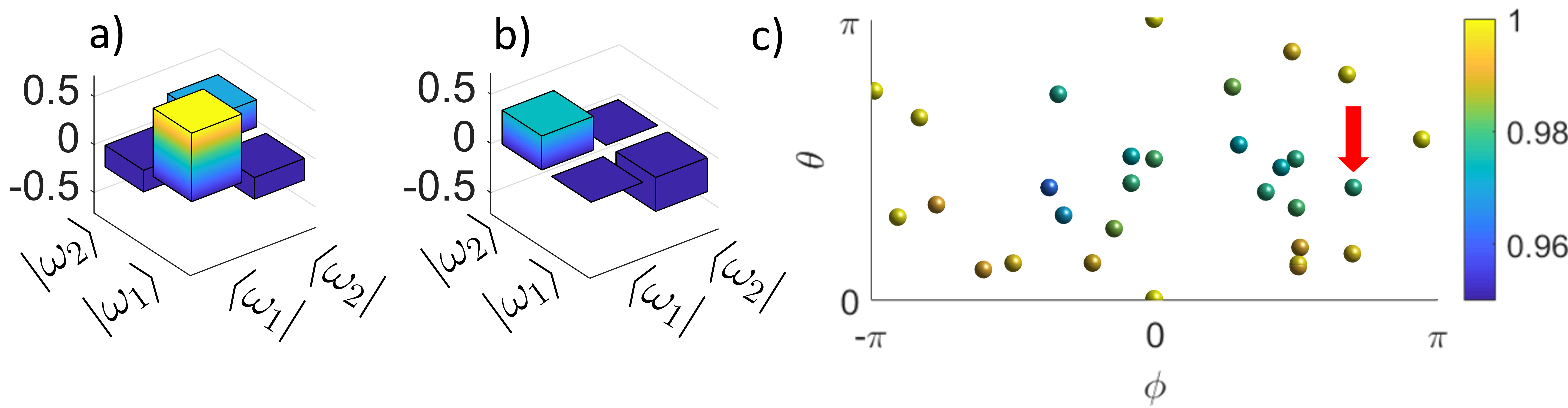
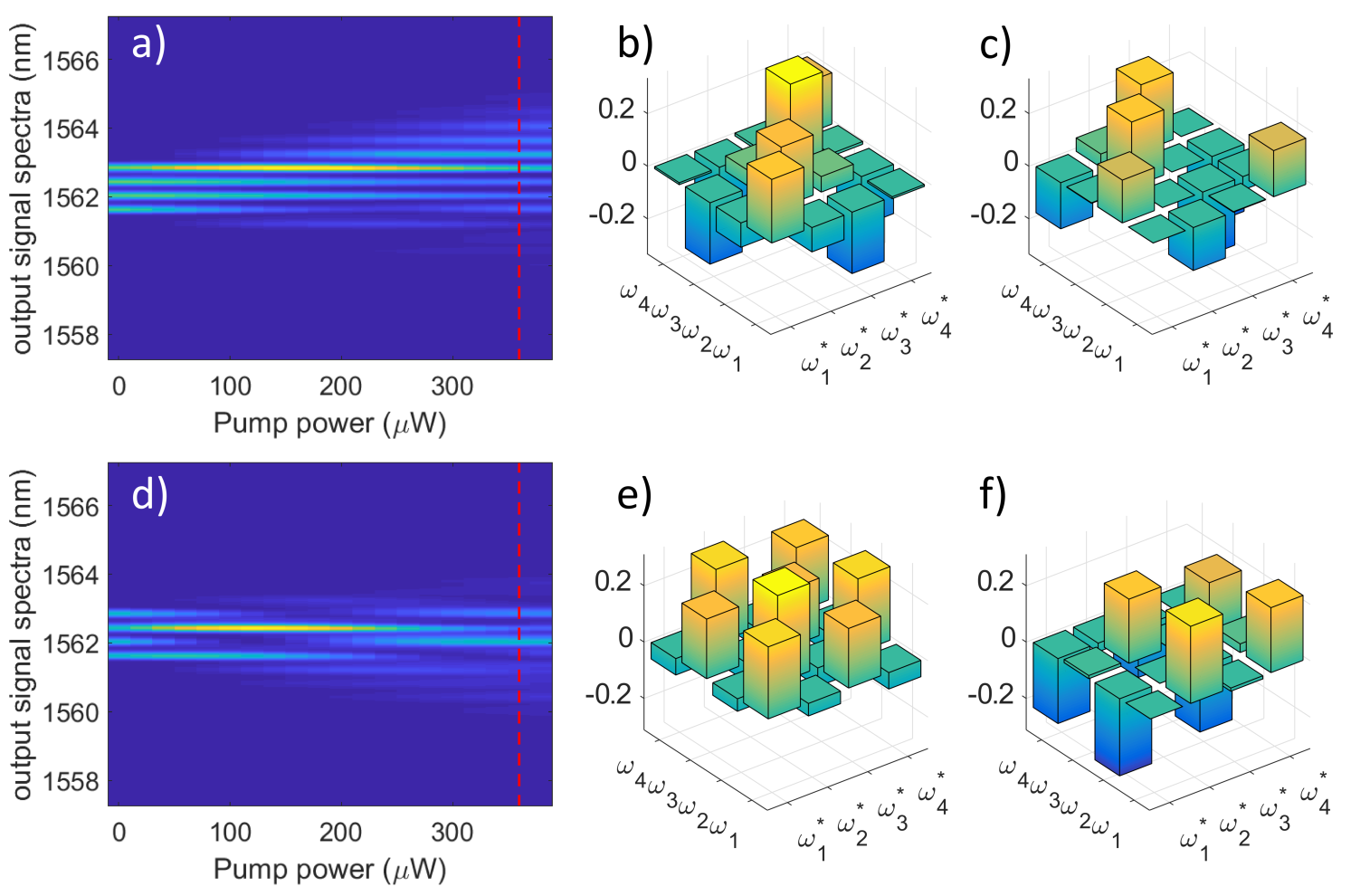
We also demonstrate the reconstruction of more complex input signals. As an example, we consider an input consisting of four lattice sites centered at frequencies nm, nm, nm, and nm, which we denote by the kets , , , and , respectively. First the transfer function of the fiber and pump system was determined by measuring the output spectra of a set of 16 basis states. Then this was used to reconstruct a number of random input states. The output spectra as a function of pump power of two representative input states are shown in Figs. 4(a) and 4(d). The pump power providing optimum condition number of 24.7 for inversion was determined to be , as indicated by the dashed vertical lines in Figs. 4(a) and 4(d). The real and imaginary parts of the reconstructed complex visibility functions are shown in Figs. 4(b,c) and 4(e,f). We obtain a high fidelity of the reconstructed states to the input at and , respectively.
IV Conclusion and outlook
In conclusion, we have experimentally investigated the use of synthetic lattices for single-shot reconstruction of frequency combs. We have shown that the full complex visibility of input spectral comb signals can be reconstructed just by measuring its output spectra after propagating through a synthetic lattice with specially optimized short- and long-range couplings. This technique is naturally suited to characterizing input signals consisting of a number of evenly spaced narrow frequency components. Furthermore, there appears an interesting potential to extend the approach for characterizing non-equidistant spectra by using more complex pump profiles to induce couplings with incommensurate frequency spacings.
The developed single-shot nonlinear-optical frequency comb characterisation is also well-suited for weak non-classical light, since the nonlinear process of FWM-BS does not introduce quantum noise. Recently, there has been significant progress in quantum optics in the spectral domain Reimer et al. (2016); Kues et al. (2017). Frequency domain Hong-Ou-Mandel interference has proven stable and practical to implement Kobayashi et al. (2016); Imany et al. (2018b), and frequency-encoded photonic states are now poised to enable scalable quantum information processing Lukens and Lougovski (2017); Lu et al. (2018a, b). Having access to fast and simple means to perform a full tomographic characterization of a quantum state in the frequency domain would be indispensable. We anticipate a potential in applying our approach based on synthetic frequency lattices in the quantum regime, where the measurement of output multi-photon correlations between different combinations of the spectral lines can enable full reconstruction of the input quantum density matrix based on the mathematical formalism developed in the spatial domain Titchener, Solntsev, and Sukhorukov (2016); Oren et al. (2017); Titchener et al. (2018); Wang et al. (2019), bringing the benefits of simplicity and speed of all-optical realization.
ACKNOWLEDGMENTS
We acknowledge support by the Australian Research Council (ARC): Discovery Project (DP160100619, DE180100070, and DP190100277); Centre of Excellence CUDOS (CE110001018); Laureate Fellowship (FL120100029).
References
- Yuan et al. (2018) L. Q. Yuan, Q. Lin, M. Xiao, and S. H. Fan, “Synthetic dimension in photonics,” Optica 5, 1396–1405 (2018).
- Ozawa and Price (2019) T. Ozawa and H. M. Price, “Topological quantum matter in synthetic dimensions,” Nat. Rev. Phys. 1, 349–357 (2019).
- Bell et al. (2017) B. A. Bell, K. Wang, A. S. Solntsev, D. N. Neshev, A. A. Sukhorukov, and B. J. Eggleton, “Spectral photonic lattices with complex long-range coupling,” Optica 4, 1433–1436 (2017).
- Dutt et al. (2020) A. Dutt, Q. Lin, L. Q. Yuan, M. Minkov, M. Xiao, and S. H. Fan, “A single photonic cavity with two independent physical synthetic dimensions,” Science 367, 59–89 (2020).
- Szameit et al. (2009) A. Szameit, R. Keil, F. Dreisow, M. Heinrich, T. Pertsch, S. Nolte, and A. Tunnermann, “Observation of discrete solitons in lattices with second-order interaction,” Opt. Lett. 34, 2838–2840 (2009).
- Yuan, Shi, and Fan (2016) L. Q. Yuan, Y. Shi, and S. H. Fan, “Photonic gauge potential in a system with a synthetic frequency dimension,” Opt. Lett. 41, 741–744 (2016).
- Ozawa et al. (2016) T. Ozawa, H. M. Price, N. Goldman, O. Zilberberg, and I. Carusotto, “Synthetic dimensions in integrated photonics: From optical isolation to four-dimensional quantum Hall physics,” Phys. Rev. A 93, 043827 (2016).
- Lustig et al. (2019) E. Lustig, S. Weimann, Y. Plotnik, Y. Lumer, M. A. Bandres, A. Szameit, and M. Segev, “Photonic topological insulator in synthetic dimensions,” Nature 567, 356–371 (2019).
- Maczewsky et al. (2020) L. J. Maczewsky, K. Wang, A. A. Dovgiy, A. E. Miroshnichenko, A. Moroz, M. Ehrhardt, M. Heinrich, D. N. Christodoulides, A. Szameit, and A. A. Sukhorukov, “Synthesizing multi-dimensional excitation dynamics and localization transition in one-dimensional lattices,” Nat. Photon. 14, 76–81 (2020).
- Wang et al. (2020) K. Wang, B. Bell, A. S. Solntsev, D. N. Neshev, B. J. Eggleton, and A. A. Sukhorukov, “Multidimensional synthetic chiral-tube lattices via nonlinear frequency conversion,” arXiv 2002.08591 (2020).
- Walmsley and Dorrer (2009) I. A. Walmsley and C. Dorrer, “Characterization of ultrashort electromagnetic pulses,” Adv. Opt. Photon. 1, 308–437 (2009).
- Kippenberg, Holzwarth, and Diddams (2011) T. J. Kippenberg, R. Holzwarth, and S. A. Diddams, “Microresonator-based optical frequency combs,” Science 332, 555–559 (2011).
- Schmeissner et al. (2014) R. Schmeissner, J. Roslund, C. Fabre, and N. Treps, “Spectral noise correlations of an ultrafast frequency comb,” Phys. Rev. Lett. 113, 263906 (2014).
- Kues et al. (2017) M. Kues, C. Reimer, P. Roztocki, L. R. Cortes, S. Sciara, B. Wetzel, Y. B. Zhang, A. Cino, S. T. Chu, B. E. Little, D. J. Moss, L. Caspani, J. Azana, and R. Morandotti, “On-chip generation of high-dimensional entangled quantum states and their coherent control,” Nature 546, 622–631 (2017).
- Herink et al. (2017) G. Herink, F. Kurtz, B. Jalali, D. R. Solli, and C. Ropers, “Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules,” Science 356, 50–53 (2017).
- Foreman et al. (2007) S. M. Foreman, K. W. Holman, D. D. Hudson, D. J. Jones, and J. Ye, “Remote transfer of ultrastable frequency references via fiber networks,” Rev. Sci. Instrum. 78, 021101 (2007).
- Ellis and Gunning (2005) A. D. Ellis and F. C. G. Gunning, “Spectral density enhancement using coherent wdm,” IEEE Photonics Technol. Lett. 17, 504–506 (2005).
- Scott et al. (2007) R. P. Scott, N. K. Fontaine, J. Cao, K. Okamoto, B. H. Kolner, J. P. Heritage, and S. J. Ben Yoo, “High-fidelity line-by-line optical waveform generation and complete characterization using frog,” Opt. Express 15, 9977–9988 (2007).
- Dorrer and Kang (2003) C. Dorrer and I. Kang, “Highly sensitive direct characterization of femtosecond pulses by electro-optic spectral shearing interferometry,” Opt. Lett. 28, 477–479 (2003).
- Solli, Chou, and Jalali (2008) D. R. Solli, J. Chou, and B. Jalali, “Amplified wavelength-time transformation for real-time spectroscopy,” Nat. Photon. 2, 48–51 (2008).
- Xu et al. (2016) Y. Q. Xu, X. M. Wei, Z. B. Ren, K. K. Y. Wong, and K. K. Tsia, “Ultrafast measurements of optical spectral coherence by single-shot time-stretch interferometry,” Sci. Rep. 6, 27937 (2016).
- Wong and Walmsley (1994) V. Wong and I. A. Walmsley, “Analysis of ultrashort pulse-shape measurement using linear interferometers,” Opt. Lett. 19, 287–289 (1994).
- Bromage et al. (2006) J. Bromage, C. Dorrer, I. A. Begishev, N. G. Usechak, and J. D. Zuegel, “Highly sensitive, single-shot characterization for pulse widths from 0.4 to 85 ps using electro-optic shearing interferometry,” Opt. Lett. 31, 3523–3525 (2006).
- Supradeepa et al. (2010) V. R. Supradeepa, C. M. Long, D. E. Leaird, and A. M. Weiner, “Self-referenced characterization of optical frequency combs and arbitrary waveforms using a simple, linear, zero-delay implementation of spectral shearing interferometry,” Opt. Express 18, 18171–18179 (2010).
- Imany et al. (2018a) P. Imany, O. D. Odele, J. A. Jaramillo-Villegas, D. E. Leaird, and A. M. Weiner, “Characterization of coherent quantum frequency combs using electro-optic phase modulation,” Phys. Rev. A 97, 013813 (2018a).
- Bersch, Onishchukov, and Peschel (2009) C. Bersch, G. Onishchukov, and U. Peschel, “Experimental observation of spectral Bloch oscillations,” Opt. Lett. 34, 2372–2374 (2009).
- Minardi et al. (2012) S. Minardi, F. Dreisow, M. Grafe, S. Nolte, and T. Pertsch, “Three-dimensional photonic component for multichannel coherence measurements,” Opt. Lett. 37, 3030–3032 (2012).
- Minardi (2015) S. Minardi, “Nonlocality of coupling and the retrieval of field correlations with arrays of waveguides,” Phys. Rev. A 92, 013804 (2015).
- Titchener, Solntsev, and Sukhorukov (2016) J. G. Titchener, A. S. Solntsev, and A. A. Sukhorukov, “Two-photon tomography using on-chip quantum walks,” Opt. Lett. 41, 4079–4082 (2016).
- Oren et al. (2017) D. Oren, M. Mutzafi, Y. C. Eldar, and M. Segev, “Quantum state tomography with a single measurement setup,” Optica 4, 993–999 (2017).
- Titchener et al. (2018) J. G. Titchener, M. Grafe, R. Heilmann, A. S. Solntsev, A. Szameit, and A. A. Sukhorukov, “Scalable on-chip quantum state tomography,” npj Quant. Inform. 4, 19 (2018).
- Wang et al. (2019) K. Wang, S. V. Suchkov, J. G. Titchener, A. Szameit, and A. A. Sukhorukov, “Inline detection and reconstruction of multiphoton quantum states,” Optica 6, 41–44 (2019).
- Mandel and Wolf (1995) L. Mandel and E. Wolf, Optical Coherence and Quantum Optics (Cambridge University Press, New York, 1995).
- Press et al. (2007) W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes: The Art of Scientific Computing, 3rd ed. (Cambridge University Press, Cambridge, 2007).
- Wang et al. (2018) K. Wang, J. G. Titchener, S. S. Kruk, L. Xu, H. P. Chung, M. Parry, I. I. Kravchenko, Y. H. Chen, A. S. Solntsev, Y. S. Kivshar, D. N. Neshev, and A. A. Sukhorukov, “Quantum metasurface for multiphoton interference and state reconstruction,” Science 361, 1104–1107 (2018).
- Reimer et al. (2016) C. Reimer, M. Kues, P. Roztocki, B. Wetzel, F. Grazioso, B. E. Little, S. T. Chu, T. Johnston, Y. Bromberg, L. Caspani, D. J. Moss, and R. Morandotti, “Generation of multiphoton entangled quantum states by means of integrated frequency combs,” Science 351, 1176–1180 (2016).
- Kobayashi et al. (2016) T. Kobayashi, R. Ikuta, S. Yasui, S. Miki, T. Yamashita, H. Terai, T. Yamamoto, M. Koashi, and N. Imoto, “Frequency-domain Hong-Ou-Mandel interference,” Nat. Photon. 10, 441–445 (2016).
- Imany et al. (2018b) P. Imany, O. D. Odele, M. S. Alshaykh, H. H. Lu, D. E. Leaird, and A. M. Weiner, “Frequency-domain Hong-Ou-Mandel interference with linear optics,” Opt. Lett. 43, 2760–2763 (2018b).
- Lukens and Lougovski (2017) J. M. Lukens and P. Lougovski, “Frequency-encoded photonic qubits for scalable quantum information processing,” Optica 4, 8–16 (2017).
- Lu et al. (2018a) H. H. Lu, J. M. Lukens, N. A. Peters, O. D. Odele, D. E. Leaird, A. M. Weiner, and P. Lougovski, “Electro-optic frequency beam splitters and tritters for high-fidelity photonic quantum information processing,” Phys. Rev. Lett. 120, 030502 (2018a).
- Lu et al. (2018b) H. H. Lu, J. M. Lukens, N. A. Peters, B. P. Williams, A. M. Weiner, and P. Lougovski, “Quantum interference and correlation control of frequency-bin qubits,” Optica 5, 1455–1460 (2018b).