Systematic analysis of strange single heavy baryons $\Xi_{c}$ and $\Xi_{b}$

The relativistic quark model is based on the hypothesis that baryons may be approximately described in terms of center-of-mass (CM) frame valence-quark configurations, the dynamics of which are governed by a Hamiltonian with a one-gluon exchange dominant component at short distances and with a confinement implemented by a flavor-independent Lorentz-scalar interaction art4 . For a three-quark system the Hamiltonian reads,

where $\tilde{H}^{conf}_{ij}$, $\tilde{H}^{so}_{ij}$ and $\tilde{H}^{hyp}_{ij}$ are the confinement, spin-orbit and hyperfine interactions, respectively. The confinement item includes one-gluon exchange potentials and the linear confined potentials. Due to the relativistic effect, the interactions should be modified with CM momentum-dependent factors. It is worth noting that the forms of the interactions in this paper have been rearranged for ease of use art116 ; art93 . The interactions are decomposed as follows:

with

The modified terms in Eqs. (4), (7), (8), (9) and (10) read,

where $E_{i}=\sqrt{m^{2}_{i}+p^{2}_{ij}}$ is the relativistic kinetic energy, and $p_{ij}$ is the momentum magnitude of either of the quarks in the CM frame of the $ij$ quark subsystem art93 .

$\tilde{G}_{ij}(r_{ij})$ and $\tilde{S}_{ij}(r_{ij})$ are obtained by the smearing transformations of the one-gluon exchange potential $G(r)=-\frac{4\alpha_{s}(r)}{3r}$ and linear confinement potential $S(r)=br+c$, respectively,

with

Here $\alpha_{k}$ and $\gamma_{k}$ are constants. $\textbf{F}_{i}\cdot\textbf{F}_{j}$ stands for the inner product of the color matrices of quarks $i$ and $j$. F includes 8 components (the so-called Gell-mann matrices), which can be written as

with $n=1,\cdot\cdot\cdot,8$. All of the parameters in these formulas are taken from reference art4 , except that $b$ and $c$ are revised to be 0.14 GeV² and -0.198 GeV, respectively.

To represent the internal motion of quarks in a few-body system, one commonly introduces the Jacobi coordinates. As shown in Fig.1, there are totally three channels of Jacobi coordinates for the three-body system. The corresponding Jacobi coordinates are defined as

where $i$, $j$, $k$ = 1, 2, 3(or replace their positions in turn). $\textbf{r}_{i}$ and $m_{i}$ denote the position vector and the mass of the $i$th quark, respectively.

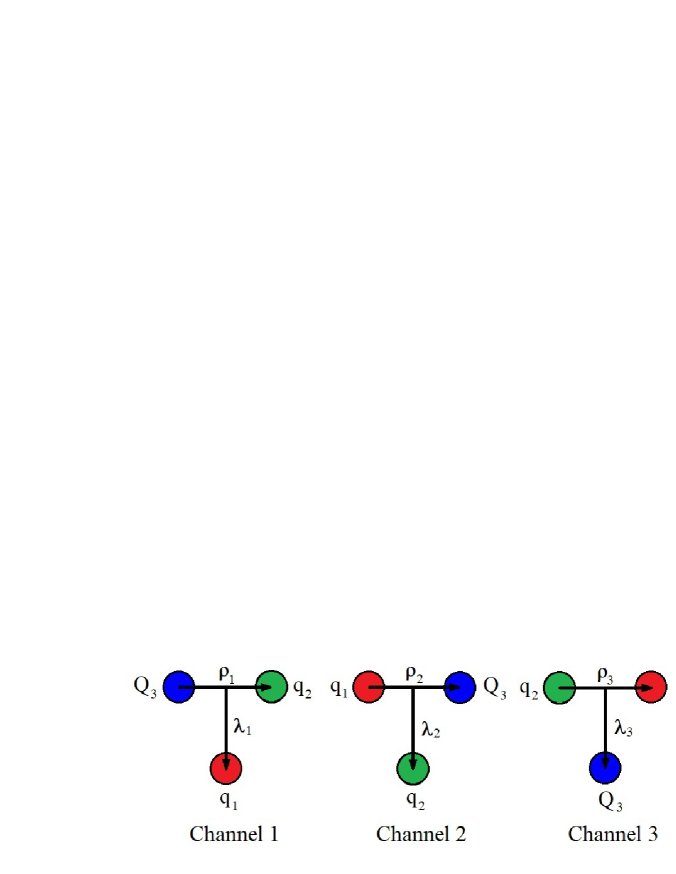
We perform the calculations based on the channel 3. In this case, the 3rd quark is just the heavy quark, which is consistent with the heavy quark limit art118 ; art117 . What is more, $\textbf{\emph{l}}_{\rho 3}$ (denoted in short as $\textbf{\emph{l}}_{\rho}$) is clearly defined as the orbital angular momentum between the light quarks, and $\textbf{\emph{l}}_{\lambda 3}$ (denoted in short as $\textbf{\emph{l}}_{\lambda}$) represents the one between the heavy quark and the light-quark pair.

In the heavy quark limit, the heavy quark within the heavy baryon system is decoupled from the two light quarks. With the requirement of the flavor SU(3) subgroups for the light quarks, the baryons belong to either a sextet $(6_{F})$ of flavor symmetric states $\Xi_{Q}^{{}^{\prime}}$, or an antitriplet $(\bar{3}_{F})$ of the flavor antisymmetric states $\Xi_{Q}$. The flavor wave functions of strange single heavy baryons are written as,

Here $q$ denotes up or down quark, and $Q$ is charm or bottom quark. $q_{s}$ is strange quark. For a quantum state with specified angular momenta in this work, the spatial wave function is combined with the spin function as follow.

with $\textbf{L}=\textbf{\emph{l}}_{\rho}+\textbf{\emph{l}}_{\lambda}$, $\textbf{s}=\textbf{s}_{1}+\textbf{s}_{2}$, $\textbf{j}=\textbf{L}+\textbf{s}$, $\textbf{J}=\textbf{j}+\textbf{s}_{3}$. $l_{\rho}$, $l_{\lambda}$, $L$, $s$, $j$, $J$ and $M_{J}$ are the quantum numbers which characterize a given quantum state in theory. This scheme $|l_{\rho}\ l_{\lambda}\ L\ s\ j\ J\ M_{J}\rangle$ ($j$-$s$ coupling) is also commonly used to analyze the strong decay of heavy baryons art48 .

In calculations, the spatial wave function $|l_{\rho}\ m_{\rho}\rangle\otimes|l_{\lambda}\ m_{\lambda}\rangle$ in formula (24) should be expanded in a set of basis functions. Naturally, one of the candidates is the simple harmonic oscillator(SHO) basis for its good orthogonality. However, the completeness of the SHO is not rigorous in calculations because a truncated set has to be used art91 ; art4 . Compared to the SHO basis functions, the advantage of the Gaussian basis functions is that they can form an approximately complete set in a finite coordinate space.

Following formula (24), the spatial wave function is expanded in terms of a set of Gaussian basis functions,

where the Gaussian basis function $|nlm\rangle^{G}$ is commonly written in position space as

or in momentum space as

with

$r_{1}$, $a$, and $n_{max}$ are the Gaussian size parameters in the geometric progression for numerical calculations, and the final results are stable and independent of these parameters within an approximately complete set in a sufficiently large space.

The Gaussian basis functions are non-orthogonal, which leads to a generalized matrix eigenvalue problem,

with

where $\kappa=1,\ 2,\ ...,\ \kappa_{max}$, $\kappa_{max}=n_{max}\times n_{max}$ and $c_{\kappa}=c_{n_{\rho}n_{\lambda}}$. $H$ and $E$ denote the Hamiltonian and the eigenvalue, respectively.

In the calculation of Hamiltonian matrix elements of three-body systems, particularly when complicated interactions are employed, integrations over all of the radial and angular coordinates become laborious even with the Gaussian basis functions. This process can be simplified by introducing the ISG basis functions art92 .

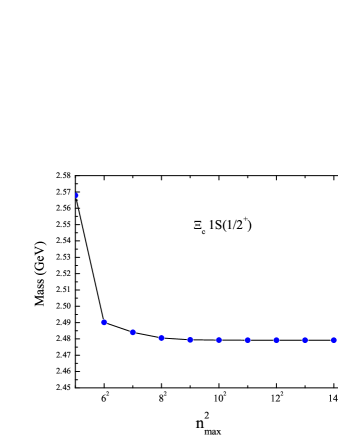
To obtain stable numerical solutions, the Gaussian size parameters set $\{n_{max},\ r_{1},\ r_{n_{max}}\}$ should be optimized. For the Gaussian functions which are a set of non-orthogonal bases in a finite coordinate space, the number of the bases should be in a reasonable range. As shown in Fig.2, the numerical stability is achieved when the dimension parameter $n_{max}$ falls in the range of $9\sim 14$, with $r_{1}=0.18$GeV^-1 and $r_{n_{max}}=15$GeV^-1. $n_{max}=10$ is finally adopted in this work, with which both the computation efficiency and accuracy are actually satisfied.

$nL(J^{P})$ is commonly used to describe a baryon state. If angular momentum $L\neq 0$, there exist several $|l_{\rho}l_{\lambda}LsjJM_{J}\rangle$ states under the condition $\textbf{L}=\textbf{\emph{l}}_{\rho}+\textbf{\emph{l}}_{\lambda}$. They may be divided into the following three modes: (1) The $\rho$-mode with $l_{\rho}\neq 0$ and $l_{\lambda}=0$; (2) The $\lambda$-mode with $l_{\rho}=0$ and $l_{\lambda}\neq 0$; (3) The $\lambda$-$\rho$ mixing mode with $l_{\rho}\neq 0$ and $l_{\lambda}\neq 0$.

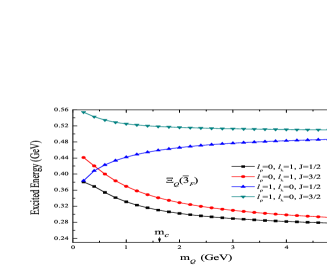
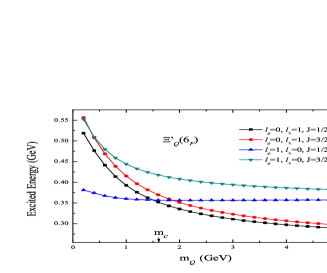
As an example, the excitation energies of the $1P(\frac{1}{2}^{-},\frac{3}{2}^{-})_{j=1}$ states of $\bar{3}_{F}$ as functions of $m_{Q}$ are investigated, where the dependence of excitation energies on $m_{Q}$ of the $\lambda$-mode is compared with that of the $\rho$-mode. As shown in Fig.3, the $\lambda$-mode and the $\rho$-mode are clearly separated when $m_{Q}$ increases from 1.0 GeV to 5.0 GeV. In the case of $6_{F}$, we come to the same conclusion when $m_{Q}>1.5$GeV as shown in Fig.4. Besides of $p$-wave states, the same feature is also shown in higher angular excited states actually. This conclusion has been obtained in reference art28 . Thus, we investigate the mass spectrum in the $\lambda$-mode.

In this subsection, the root mean square radii, radial probability density distributions and the mass spectra of strange single heavy baryons are presented. For convenience, the relevant experimental data are given together. The detailed results are listed in Tables I-VI (see the appendix). There are a total of four families, namely $\Xi_{c}$, $\Xi_{c}^{{}^{\prime}}$, $\Xi_{b}$ and $\Xi_{b}^{{}^{\prime}}$. The mass spectra of excited states with quantum numbers up to $n=4$ and $L=4$ are displayed. There have been a lot of other theoretical works on this subject art23 ; art70 ; art411 ; art12 ; art318 . Among them, Ebert $et\ al.$ have studied the heavy baryon spectra with a quark potential model in the heavy quark-light diquark picture art1 . As an important reference, their numerical results are also placed in the tables.

Through the analysis of these calculated results, some general features of the mass spectra are summarized as follows: First, $\Xi_{Q}$ is lower than $\Xi_{Q}^{{}^{\prime}}$ in energy. This feature has been recognized in light baryons where the highly orbitally excited states have an antisymmetric structure which minimizes the energy art122 ; Second, the mass splitting of spin-doublet states becomes smaller with increasing $L$. For example, Table I shows the mass differences of the spin-doublets of $1P$-, $1D$-, $1F$-, and $1G$-wave are 30 MeV, 13 MeV, 5 MeV, and 1 MeV, respectively; Thirdly, for the same $L$, the mass splitting hardly changes with the increase of $j$. For example, Tables II and III show the mass differences of $1D$ doublets with $j=1,2,3$ are 10 MeV, 10 MeV and 13 MeV, respectively; The last, the mass difference between the two adjacent radial excited states gradually decreases with increasing $n$, which is clearly different from that given by Ebert $et\ al.$.

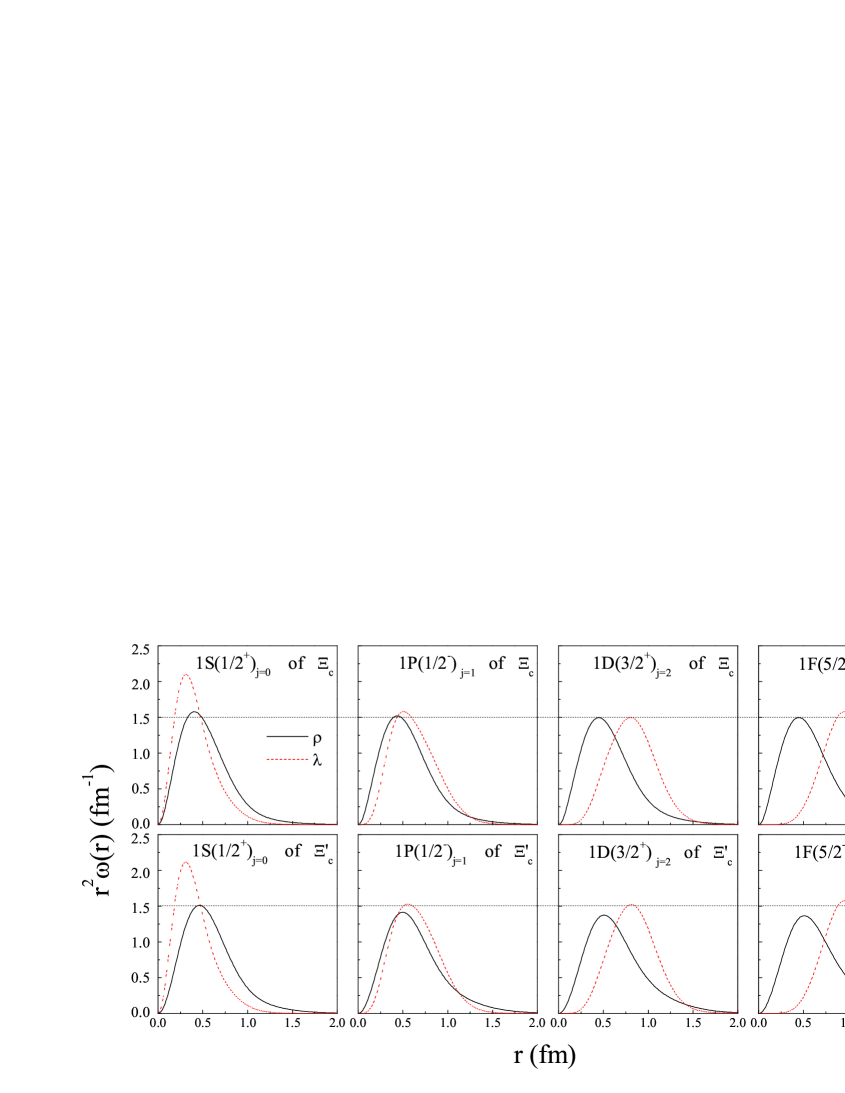
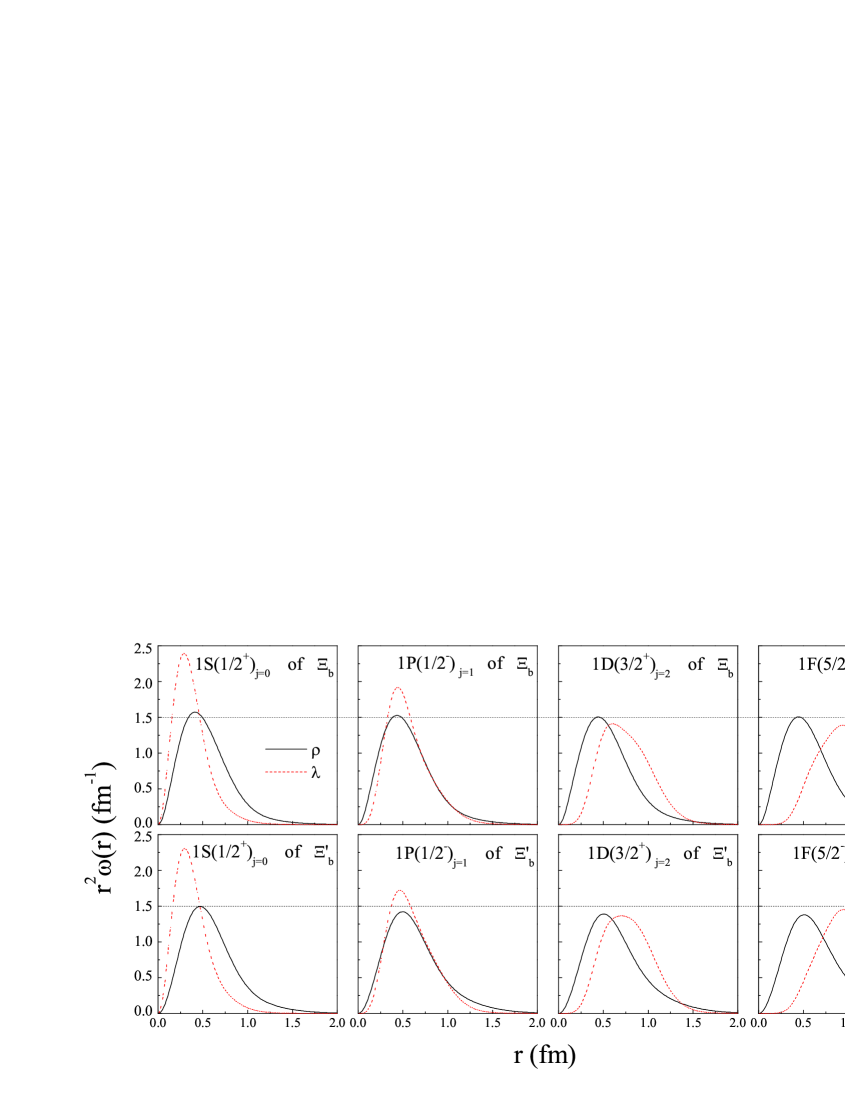
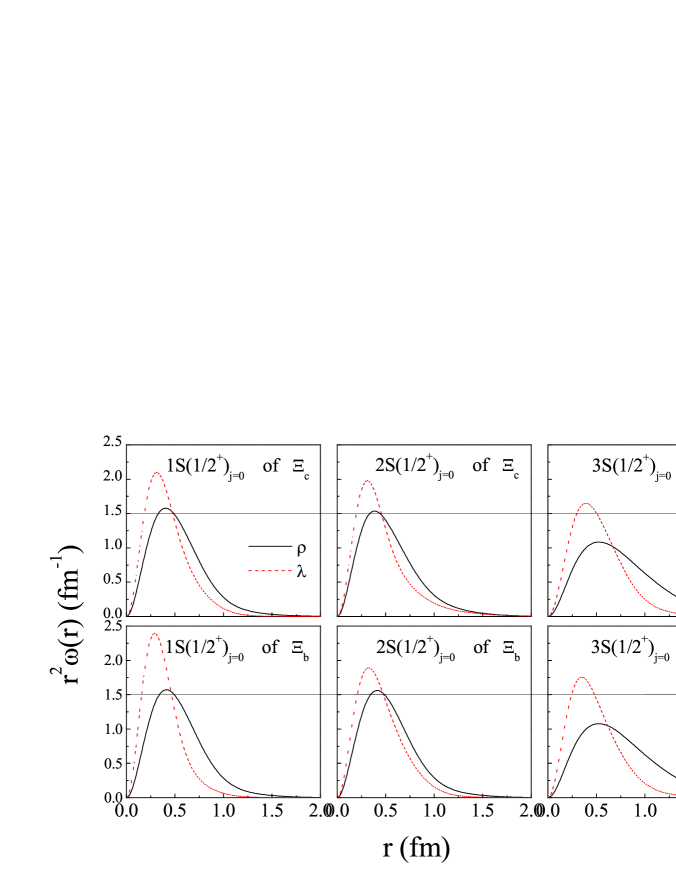
On the other hand, the calculated root mean square radii and radial probability density distributions carry important information. For a three-quark system, the radial probability densities $\omega(r_{\rho})$ and $\omega(r_{\lambda})$ can be defined as follows,

where $\Omega_{\rho}$ and $\Omega_{\lambda}$ are the solid angles spanned by vectors $\textbf{r}_{\rho}$ and $\textbf{r}_{\lambda}$, respectively. From Figs.5-7 and tables I-VI, one can find some interesting properties.

(1) For the same $n$ states, when $L$ changes from 1 to 4, their $\langle r_{\rho}^{2}\rangle^{1/2}$ values increase small. But their $\langle r_{\lambda}^{2}\rangle^{1/2}$ values become larger gradually. The similar phenomenon can be seen in Figs.5 and 6, where the radial probability of $r_{\rho}^{2}\omega(r_{\rho})$ changes a little with different $L$ values. However, the peak of the $r_{\lambda}^{2}\omega(r_{\lambda})$ significantly shifts outward with increasing $L$.

(2) For the same $L$ states, $\langle r_{\rho}^{2}\rangle^{1/2}$ and $\langle r_{\lambda}^{2}\rangle^{1/2}$ generally become larger with increasing $n$. And the peaks of their probability densities are generally shifted outward, as shown in Fig.7.

(3) The shapes of the eight black (solid) lines in Fig.5 are almost as same as those in Fig.6. And the values of $\langle r_{\rho}^{2}\rangle^{1/2}$ for the same state are almost the same for $\Xi_{c}$($\Xi_{c}^{{}^{\prime}}$) and $\Xi_{b}$($\Xi_{b}^{{}^{\prime}}$) families. This reflects the fact that the configurations of the two light quarks in $\Xi_{c}$($\Xi_{c}^{{}^{\prime}}$) and $\Xi_{b}$($\Xi_{b}^{{}^{\prime}}$) baryons are similar to each other.

(4) As shown in tables I-VI, the root mean square radii of those baryons which have been experimentally well established are generally less than 0.8 fm.

When the root mean square radius becomes larger, the radial probability distribution of the wave function appears more outwardly extended, and the baryons become even looser. Generally speaking, the root mean square radius of a compact baryon might be within a threshold, which is of help to estimate the upper limit of the mass spectrum and constrain the number of members for each heavy baryon family.

Regge trajectories is an effective method to discribe the hadron mass spectrumart503 ; art504 ; art501 ; art502 ; art505 . In 2011, Ebert $et\ al.$ constructed the heavy baryon Regge trajectories in both the $(J,M^{2})$ and the $(n,M^{2})$ planes art1 .

In this subsection, we investigate the Regge trajectories in the $(J,M^{2})$ plane based on our calculated mass spectra. The states in a baryon family can be classified according to the following parities and angular momenta: (1) Natural $P=(-1)^{J+1/2}$ and unnatural $P=(-1)^{J-1/2}$ parities (written in short as $NP$ and $UP$, respectively)art124 ; (2) $J=j+1/2$ and $J=j-1/2$ (written in short as $NJ$ and $UJ$). Thus, the states in the $\Xi_{c}$ or $\Xi_{b}$ family are divided into two groups, and the states in the $\Xi_{c}^{{}^{\prime}}$ or $\Xi_{b}^{{}^{\prime}}$ family are divided into six groups. In this paper, we use the following definition for the $(J,M^{2})$ Regge trajectories,

where $\alpha$ and $\beta$ are the slope and intercept. In Figs. 7 and 8, we plot the Regge trajectories in the $(J,M^{2})$ plane. The three lines in each figure correspond to the radial quantum number $n$= 1, 2, 3, respectively. The fitted slopes and intercepts of the Regge trajectories are given in Tables VII and VIII.

It is shown that the linear trajectories appear clearly in the $(J,M^{2})$ plane. All the data points fall on the trajectory lines. This indicates that the Regge trajectory has a strong universality and our theoretical calculations are reliable. These trajectories are almost parallel, but not equidistant, which is an apparent difference between our mass spectra and those in reference art1 .

In this paper, we do not show the Regge trajectories in the $(n,M^{2})$ plane. In fact, the linear trajectories in the $(n,M^{2})$ plane can not be constructed from our predicted masses. As will be mentioned in subsection 3.5, if the observation of heavy baryons in forthcoming experiments touched the $3S$ sub shell, it would be a chance to check the $(n,M^{2})$ Regge trajectories, and then we can determine whether a single heavy baryons is a three-quark system or a quark-diquark system.

For the well determined $\Xi_{c}$ ($\Xi^{{}^{\prime}}_{c}$) baryons in the PDG, we can assign them to the corresponding positions nicely as follows, $\Xi_{c}^{+}$ and $\Xi_{c}^{0}$ $\leftrightarrow$ $\Xi_{c}$ $1S(\frac{1}{2}^{+})$, $\Xi_{c}^{{}^{\prime}+,0}$ $\leftrightarrow$ $\Xi_{c}$ $1S(\frac{1}{2}^{+})$, $\Xi_{c}(2645)^{+,0}$ $\leftrightarrow$ $\Xi_{c}^{{}^{\prime}}$ $1S(\frac{3}{2}^{+})$, $\Xi_{c}(2790)^{+,0}$ and $\Xi_{c}(2815)^{+,0}$ $\leftrightarrow$ $\Xi_{c}$ $1P(\frac{1}{2}^{-},\frac{3}{2}^{-})$ as shown in Tables I and II. The measured masses can be well reproduced in our calculations and the deviation is usually less than 14 MeV. Additionally, it needs to be noted that $\Xi_{c}(2645)$ in the PDG should be labelled with $\Xi_{c}^{{}^{\prime}}(2645)$.

$\Xi_{c}(2970)$, earlier known as $\Xi_{c}(2980)$, was first observed by the Belle art30 in 2006. Now the quantum numbers of $\Xi_{c}(2970)$ are determined as $\frac{1}{2}^{+}$ in the latest PDG. In our calculations, the only candidate is the $2S(\frac{1}{2}^{+})$ of $\Xi_{c}$ as shown in Tables I. And the predicted mass is 15 MeV less than the experimental data. At last, $\Xi_{c}$(3055) and $\Xi_{c}$(3080) were observed by the BABAR art31 and the Belle art89 ; art30 ; art601 . As shown in the PDG, their spin and parity values have not yet been clear so far. According to the measured masses, $\Xi_{c}$(3055) and $\Xi_{c}$(3080) are likely to be the $1D$ doublet ($\frac{3}{2}^{+}$, $\frac{5}{2}^{+}$) of $\Xi_{c}$ in Table I or the $2S$ doublet ($\frac{1}{2}^{+}$, $\frac{3}{2}^{+}$) of $\Xi_{c}^{{}^{\prime}}$ in Table II. Considering the system with a smaller root mean square radius (especially for $\langle r_{\lambda}^{2}\rangle^{1/2}$) is more stable, the $2S$ doublet states should then be the ideal candidates.

Outside of the PDG data, the Belle and the LHCb observed four charm-strange baryons, namely $\Xi_{c}(2930)$ art120 , $\Xi_{c}(2923)$, $\Xi_{c}(2939)$, and $\Xi_{c}(2964)$ art125 , whose masses are very close to each other. By the predicted masses in Tables I and II, the above four baryons can be assigned to be the first orbital ($1P$) excitation of $\Xi_{c}^{{}^{\prime}}$ or the first radial (2S) excitation of $\Xi_{c}$. At present, we can not determine their quantum numbers accurately.

The $\Xi_{c}$(3123) was observed by the BABAR Collaboration art31 . However, it has not yet appeared in the PDG art2 so far. In our calculations, the predicted masses of the $\Xi_{c}$ $3S(\frac{1}{2}^{+})$ and $\Xi_{c}^{{}^{\prime}}$ $2S(\frac{3}{2}^{+})$ are 3155 MeV and 3095 MeV, respectively, which are relatively closer to the measured value of the $\Xi_{c}$(3123) than those of other states. Because the $\Xi_{c}^{{}^{\prime}}$ $2S(\frac{3}{2}^{+})$ has been considered as the candidate of the $\Xi_{c}(3080)$, the $\Xi_{c}$(3123) is likely to be the $\Xi_{c}$ $3S(\frac{1}{2}^{+})$ state. Of course, whether $\Xi_{c}$(3123) exists remains to be tested.

The calculated mass spectra of $\Xi_{b}$ and $\Xi^{{}^{\prime}}_{b}$ families are listed in Tables IV-VI where a total of six bottom-strange baryons with determined quantum numbers in the PDG have been assigned to the possible states, such as $\Xi_{b}^{-,0}$ $\leftrightarrow$ $\Xi_{b}$ $1S(\frac{1}{2}^{+})$, $\Xi_{b}^{{}^{\prime}}(5935)^{-}$ $\leftrightarrow$ $\Xi_{b}^{{}^{\prime}}$ $1S(\frac{1}{2}^{+})$, $\Xi_{b}(5945)^{0}$ and $\Xi_{b}(5955)^{-}$ $\leftrightarrow$ $\Xi_{b}^{{}^{\prime}}$ $1S(\frac{3}{2}^{+})$.

In 2021, AMS collaboration determined the $\Xi_{b}(6100)$ with the quantum numbers $J^{P}=\frac{3}{2}^{-}$ by measuring the typical decay chain of $\Xi_{b}(6100)^{-}\rightarrow\Xi_{b}^{*0}\pi^{-}\rightarrow\Xi_{b}^{-}\pi^{+}\pi^{-}$ art90 . Very recently, the values of $J^{P}=\frac{3}{2}^{-}$ of $\Xi_{b}(6100)$ were written into the PDG data. Table IV shows the mass of the $\Xi_{b}(6100)$ is very close to that of the $\Xi_{b}$ $1P(\frac{3}{2}^{-})$ state. So, the $\Xi_{b}(6100)$ is most likely to be the $1P(\frac{3}{2}^{-})$ state of $\Xi_{b}$. From Tables IV and V, we find the experimental data can be well reproduced by our theoretical calculations. In addition, it should be pointed out $\Xi_{b}(5945)^{0}$ and $\Xi_{b}(5955)^{-}$ in the PDG ought to be labelled with $\Xi_{b}^{{}^{\prime}}(5945)^{0}$ and $\Xi_{b}^{{}^{\prime}}(5955)^{-}$.

The last two $\Xi_{b}$ baryons in the PDG, $\Xi_{b}(6227)^{-}$ and $\Xi_{b}(6227)^{0}$, were reported by the LHCb Collaboration in 2018 art130 . But their spin and parity values are still not confirmed. In Tables IV and V, there are six states (one $2S$ state of $\Xi_{b}$ and five $1P$ states of $\Xi_{b}^{{}^{\prime}}$) whose masses range from 6224 MeV to 6243 MeV. Each of them could be considered as a possible assignment to the $\Xi_{b}(6227)$.

In 2021, two bottom-strange baryons $\Xi_{b}(6327)$ and $\Xi_{b}(6333)$ were reported by the LHCb Collaboration. Very recently, the LHCb implied in experiment that they should belong to the $\Xi_{b}$ 1D($\frac{3}{2}^{+}$, $\frac{5}{2}^{+}$) doublet art126 . In Table IV, one can see the predicted masses of the 1D doublet ($\frac{3}{2}^{+}$, $\frac{5}{2}^{+}$) of $\Xi_{b}$ indeed match with the experimental data of the $\Xi_{b}(6327)$ and $\Xi_{b}(6333)$.

The shell structure of the mass spectra are presented in Figs.10 and 11, where only the states with their root mean square radii less than 1 fm are collected. In this two figures, the well established baryons in experiment are labeled next to the corresponding states, and the recently observed baryons in experiment are arranged in their possible positions preliminarily according to the discussions in subsection 3.4.

From these two figures, we could get a bird’s-eye view of the mass spectra. Firstly, the baryon spectra of the $\Xi_{c}$ ($\Xi_{c}^{{}^{\prime}}$) and $\Xi_{b}$ ($\Xi_{b}^{{}^{\prime}}$) almost have the same shell structure. Secondly, the baryons with lighter masses were discovered earlier in experiment. Thirdly, there is a serious energy degeneracy in the $P$, $D$ and $F$ states for the $\Xi_{c}^{{}^{\prime}}$ ($\Xi_{b}^{{}^{\prime}}$) family. And the calculated masses for the $2S$ states of $\Xi_{c}$ ($\Xi_{b}$) family are very close to those of the $1P$ states of the $\Xi_{c}^{{}^{\prime}}$ ($\Xi_{b}^{{}^{\prime}}$) family. This makes these states hard to be identified in experiment.

At last, the states which are possibly observed in experiment can be predicted. For the $\Xi_{c}$ family, the $1D$ doublets and the $3S(1/2)^{+}$ are likely to be experimentally observed first. In the $\Xi_{c}^{{}^{\prime}}$ family, the $3S$ doublets might be the next ones to be observed. However, the predicted mass range of $3S$ doublet states overlaps heavily with that of the $1D$ states. As to the $\Xi_{b}$ family, we find the $1P(1/2)^{-}$ state should have been discovered earlier in experiment and the predicted mass is $6084$ MeV. The possibly observed states in the $\Xi_{b}^{{}^{\prime}}$ family should be the $1P$ states where experimental observations will encounter the difficulty of the energy degeneracy.