Tangential Navier-Stokes equations on evolving surfaces: Analysis and simulations††thanks: This work was partially supported by US National Science Foundation (NSF) through grants DMS-1953535 and DMS-2011444.
Abstract
The paper considers a system of equations that models a lateral flow of a Boussinesq–Scriven fluid on a passively evolving surface embedded in . For the resulting Navier-Stokes type system, posed on a smooth closed time-dependent surface, we introduce a weak formulation in terms of functional spaces on a space-time manifold defined by the surface evolution. The weak formulation is shown to be well-posed for any finite final time and without smallness conditions on data. We further extend an unfitted finite element method, known as TraceFEM, to compute solutions to the fluid system. Convergence of the method is demonstrated numerically. In another series of experiments we visualize lateral flows induced by smooth deformations of a material surface.
1 Introduction
There is extensive literature on analysis and numerical simulation of the incompressible Navier-Stokes equations, a fundamental model of fluid mechanics. While the overwhelming majority of papers in this field treats these equations in Euclidean domains, there also is literature on analysis of the incompressible Navier-Stokes equations on surfaces, or more general on Riemannian manifolds. Building on a fundamental observation made by Arnold [2] that relates equations of incompressible fluid to finding geodesics on the group of all volume preserving diffeomorphisms, local existence and uniqueness results for Navier-Stokes equations on compact oriented Riemannian manifolds were proved in the seminal paper [11]. This work has been followed by many other studies, cf. [44, 42] and the overview in [8]. Very recent activity in the field includes the work [33, 40], in which local-in-time-well-posedness in the framework of maximal regularity is established. All these papers restrict to stationary surfaces or manifolds.
In recent years there has been a growing interest in fluid equations on evolving surfaces [47, 20, 16, 24, 38], motivated in particular by applications to modeling of biological membranes, e.g. [39, 34, 4, 45]. In [6] one finds an overview and comparison of different modeling approaches for evolving viscous fluid layers that result in the surface Navier-Stokes equations. We are not aware of any literature presenting well-posedness analysis of this system on evolving surfaces. Furthermore, only very few papers address numerical treatment of such equations. In [36, 37] computational results are presented, based on a surface vorticity-stream function formulation of the Navier-Stokes equations. The surface motion is prescribed and the evolving SFEM of Dziuk-Elliott [9, 10] is applied to the partial differential equations for the scalar vorticity and stream function unknowns. The authors of [26] consider another discretization approach that is based on the techniques developed in [38]. These papers focus on modeling and illustration of certain interesting flow phenomena but not on the performance of the numerical methods. Several recent papers [17, 5, 14, 19] present error analysis of finite element discretization methods for vector valued PDEs on stationary surfaces. We are not aware of any paper with a systematic numerical study or an error analysis of a discretization method for vector valued PDEs on evolving surfaces. We conclude that in the field of incompressible Navier-Stokes equations on time-dependent surfaces basic problems related to well-posedness of the systems, development and analysis of numerical methods remain open. This paper addresses two of these problems: well-posedness and numerical method development.
It is shown in [6] that several different modeling approaches all yield the same tangential surface Navier-Stokes equations (TSNSE). These equations govern the evolution of tangential velocity and surface pressure if the normal velocity of the surface is prescribed. The main topic of the present paper is the analysis of a variational formulation of the TSNSE. In particular, a well-posedness result for this formulation is proved. To the best of our knowledge, this is the first well-posedness result for evolving surface Navier-Stokes equations. The paper also touches on the development of a new discretization method for the TSNSE. This method combines an implicit time stepping scheme with a TraceFEM [27, 30] for discretization in space. We explain this method, validate its optimal second order convergence for a test problem with a known solution and apply it to the simulation of a lateral flow induced by deformations of a sphere. Error analysis of this method is not addressed in this paper and left for future research.
The remainder of the paper is organized as follows. In section 2 we recall the surface Navier-Stokes equations known from the literature. In particular, the tangential surface Navier-Stokes equations are described. Appropriate function spaces for a variational formulation of the TSNSE are introduced in section 3. Relevant properties of these spaces are derived. The main results of this paper are given in section 4. We introduce and analyze two variational formulations of the TSNE: The first one is for the tangential velocity only, which is solenoidal by construction of the solution space. Then we introduce the pressure and study a mixed variational problem. For both formulations well-posedness results are derived. In section 5 we explain a discretization method. Finally, section 6 collects and discusses results of numerical experiments.
2 Surface Navier–Stokes equations
We first introduce necessary notations of surface quantities and tangential differential operators. For a closed smooth surface embedded in , the outward pointing normal vector is denoted by , and the normal projector on the tangential space at is . Let be the Weingarten mapping (second fundamental form) and twice the mean curvature. For a scalar function or a vector field their smooth extensions to a neighborhood of are denoted by and , respectively. Surface gradients and covariant derivatives on can be defined through derivatives in as , , and . These definitions are independent of a particular smooth extension of and off . The surface rate-of-strain tensor [13] is given by , the surface divergence and operators for a vector field are and . For a tensor field , is defined row-wise and is a third-order tensor such that .
We now let be a material surface embedded in as defined in [13, 25], with a density distribution . By , , we denote a velocity field of the density flow on , i.e. is the velocity of a material point . The derivative of a surface quantity along the corresponding trajectories of material points is called the material derivative. Assuming the surface evolution is such that the space-time manifold
is smooth, the material derivative can be defined as
| (2.1) |
where is a smooth extension of into a spatial neighborhood of . Note that is a tangential derivative for , and hence it depends only on the surface values of on . For a vector field on , one defines componentwise.
The conservation of mass and linear momentum for a thin material layer represented by together with the Boussinesq–Scriven constitutive relation for the surface stress tensor and an inextensibility condition leads to the surface Navier-Stokes equations:
| (2.2) |
where is the surface fluid pressure and stands for the viscosity coefficient. Equations (2.2) model the evolution of an inextensible viscous fluidic material surface with acting area force , cf. [20, 16] for derivations of this model and [6] for a literature overview and alternative forms of this system. The pure geometrical evolution of is defined by its normal velocity that is given by the normal component of the material velocity,
| (2.3) |
If is given or defined through other unknowns, then (2.2)–(2.3) form a closed system of six equations for six unknowns , , , and , subject to suitable initial conditions.
2.1 Tangential surface Navier-Stokes equations
We now introduce a major simplification by assuming that the geometric evolution of is known. We make this more precise below and derive equations governing the unknown lateral motions of the surface fluid. To this end, consider a smooth velocity field in that passively advects the embedded surface given by
| (2.4) |
where the trajectories are the unique solutions of the Cauchy problem
| (2.5) |
for all on an initial smooth connected surface embedded in . We now assume that the normal material motion of is completely determined by the ambient flow and the lateral material motion is free, i.e., for the given the relation
| (2.6) |
holds for the normal component111For velocity fields defined on we use a splitting into tangential and normal components , with . , while the tangential component of the surface fluid flow is unknown and depends on only implicitly through the variation of and conservation laws represented by equations (2.2). The resulting system can be seen as an idealized model for the motion of a fluid layer embedded in bulk fluid, where one neglects friction forces between the surface and bulk fluids as well as any effect of the layer on the bulk flow. In such a physical setting, (2.6) means non-penetration of the bulk fluid through the material layer.
Material trajectories of points on the surface are defined by the flow field , rather than . We are also interested in a derivative determined by the variation of a quantity along the so-called normal trajectories defined below.
Definition 1.
Let , be the flow map of the pure geometric (normal) evolution of the surface, i.e., for , the normal trajectory solves
| (2.7) |
Eq. (2.7) defines a bijection between and for every with inverse mapping . The Lagrangian derivative for the flow map is denoted by :
| (2.8) |
We call the normal time derivative of .
It is clear from (2.8) that this normal time derivative is an intrinsic surface quantity. Similar to the material derivative in (2.1), it can be expressed in terms of bulk derivatives if one assumes a smooth extension of from to its neighborhood:
| (2.9) |
for . Comparing the material and normal time derivatives of a flow field on the surface we find the equality
With the splitting we get
| (2.10) |
Noting that and (cf. (2.16) in [16]), we rewrite as
We also have the relation . Using these results and letting in (2.10) one obtains
| (2.11) |
where we also used . To derive an equation for the unknown tangential velocity , we apply the projection to the first equation in (2.2). For we have the result (2.11). Note that the term is known and can be treated as a source term. For a stationary surface () the normal time derivative is just the usual time derivative, . The term is the analog of the quadratic term in Navier-Stokes equations. Using and , the second equation in (2.2) yields . We are not interested in variable density case and let . Summarizing, from the surface Navier-Stokes equations (2.2) we get the following reduced system for and which we call the tangential surface Navier-Stokes equations (TSNSE):
| (2.12) |
with right-hand sides known in terms of geometric quantities, and the tangential component of the external area force :
| (2.13) |
In the remainder of this paper we study this TSNSE. Note that these equations have a structure similar to the standard incompressible Navier-Stokes equations in Euclidean domains. Important differences are that TSNSE is formulated on a space-time manifold that does not have an evident tensor product structure and, related to this, a normal time derivative instead of the standard time derivative is used and an additional term occurs. After some preliminary results in the next section, we introduce a well-posed weak formulation of the TSNSE in section 4.
Remark 2.1.
If one does not assume a given normal velocity , an equation for can be derived from (2.2), cf. [16]. The surface Navier-Stokes equations (2.2) are then rewritten as a coupled system for , and , that consists of TSNSE (2.12) and the coupled equation
| (2.14) |
A challenging problem, not addressed in this paper, is the well-posedness of the surface Navier-Stokes equations (2.2), i.e., of the coupled system (2.12)–(2.14). For studying this problem, results on well-posedness of only the TSNSE (2.12) may be useful.
3 Preliminaries
In this section we introduce several function spaces and derive relevant properties of these spaces. We will use these spaces to formulate a well-posed weak formulation of the TSNSE (2.12). At this point, we make our assumptions on and its evolution more precise. We introduce the following smoothness assumptions:
| (3.1) |
Then the ODE system (2.5) has a unique solution for any , which defines a one-to-one mapping for all (Theorems II.1.1, V.3.1 and remark to Theorem V.2.1 in [15]). Moreover, this mapping is (Corollary V.4.1 [15]) with
Therefore, is a manifold as the image of under a smooth mapping.
We need a globally -smooth extension of the spatial normal , that can be constructed as follows. Let be the signed distance function to . On a tubular neighborhood of , with diameter sufficiently small, we have , cf. [10, Lemma 2.8]. We extend this function to be from and zero outside . Thus we have and is a signed distance function in a neighborhood of . Let be the flow map for the velocity field . The mapping is and is regular [15]. Define the level set function and the neighborhood of . Then we have and for it holds , and iff . Set for . Clearly on and , and by a standard procedure we can extend it to . To simplify the notation, this extension is denoted by . For such an extended vector field we have that holds. Arguing in the same way as above, we conclude that for the normal flow mapping from definition 1 we have
| (3.2) |
Note that and , i.e., and are closed manifolds.
We need function spaces suitable for a weak formulation of the TSNSE. For this we make use of a general framework of evolving spaces presented in [1]. In section 3.2 we introduce specific evolving Hilbert spaces, based on a Piola pushforward mapping. Based on results from [1] several properties of these spaces are derived. In section 3.4 an evolving space of functions for which suitable weak “material” derivatives exist is introduced. Here we deviate from [1] in the sense that this “material” derivative is not based on the pushforward map but on the normal time derivative defined above.
3.1 Surface Piola transform
To define evolving Hilbert spaces based on standard Bochner spaces, we need a suitable pushforward map. In the context of this paper it is natural to use a surface Piola transform as pushforward map, since this transform conserves the solenoidal property of a tangential vector field.
To define a surface variant of the Piola transform based on the normal flow map , we need some further notation. Below we always take and . Since for each the map is a -diffeomorphism, the differential , is invertible. Define , . Denote by and the matrices of linear mappings given by and , respectively. Note that and hold. For these mappings the following useful identities hold:
| (3.3) |
We need the Piola transform for arbitrary, not necessarily tangential vectors. For this it is convenient to define an invertible operator such that and . We use the operator
| (3.4) |
For it holds . The matrices of and in the standard basis are also denoted by and , respectively. Note that holds. We define the surface Piola transform by
| (3.5) |
This operator maps tangential vectors on to tangential vectors on and for tangential vectors it satisfies a.e. on iff a.e. on , cf. [41].
We need some regularity properties of , and , , which are collected in the following lemma. For a function the maximum norm is and similarly for vector and matrix valued functions as well as for such functions on .
Lemma 2.
It holds that , and, in particular,
| (3.6) |
Proof.
From (3.2) we know that is in and hence . Moreover, is -smooth, so is a smooth mapping with matrix representation
| (3.7) |
Hence, and hold. Combining this with , (3.4) and the property that is closed, implies the bound in (3.6) for , and . The mapping is one-to-one. By the inverse mapping theorem the inverse is and for its differential we have . The matrix of the smooth mapping is
This and imply the desired bound for , and . ∎
3.2 Evolving Hilbert spaces
For constructing suitable evolving Hilbert spaces, we first define tangential velocity spaces on . The notation and is used for the canonical inner product and norm in . We need the Sobolev spaces of order one
with the inner product , and its closed subspace of divergence free tangential fields,
The space is defined as closure of a space of smooth div-free tangential fields in the norm:
The space of smooth functions is dense not only in but also in . Indeed, for any tangential velocity field on the smooth surface we have a Helmholz decomposition with some and a harmonic field [35]. For we have and the result follows from the density of -smooth functions in . Therefore, endowed with canonical scalar products, the spaces form a Gelfand triple . We also have that the dense embedding is compact. Here and later always denotes a dual of a Hilbert space , and we adopt the common notation for .
For the space we define a pushforward map , based on the Piola transform, by
| (3.8) |
The inverse map (pullback) is given by , . Since , the restriction of to is a pushforward map from to . Because is based on the Piola transform and thus conserves the solenoidal property, we also have that is a pushforward map from to , and from to . For this pushforward map we have for :
The result (3.6) implies that the norms , , , are uniformly bounded in and thus
holds with some independent of . With similar arguments one easily shows that holds for all , with independent of and . These bounds remain obviously true if , and the corresponding norms are replaced by , and the corresponding norms. Using (3.6) one shows that the maps and are continuous. These properties imply that , , and are “compatible pairs” in the sense of Definition 2.4 in [1]. This compatibility structure induces natural properties of the evolving spaces defined as follows:
where is the dual of . We shall also need the spaces , , , which are defined analogously, and the spaces of smooth space-time functions
| (3.9) |
Note that functions in have zero traces on . With a slight abuse of notation we identify with .
In [1] it is shown that if is a Gelfand triple, with a compact embedding , and both and are compatible pairs, then the -spaces inherit certain properties of the standard Bochner spaces. In particular, cf. Section 2 in [1], the spaces and with
are separable Hilbert spaces, homeomorphic to and respectively. Furthermore, the embedding is dense and compact, the dual space is isometrically isomorphic to , and
is a Gelfand triple. The space is dense in and so is dense also in . By the same arguments is also a Hilbert space with inner product . The subspace of smooth functions
| (3.10) |
is dense in and holds. Note that is a closed subspace of and that functions in are solenoidal and functions in are not necessarily solenoidal.
3.3 Some uniform inequalities
We need to establish several basic inequalities on with constants uniformly bounded in .
We first consider a Korn inequality. Recall that the estimate
| (3.11) |
holds with a constant that depends on smoothness properties of , cf. [16]. In the next lemma we show that the constant can be taken such that holds.
Lemma 3.
The constant in (3.11) can be chosen finite and independent of .
Proof.
The following inf-sup estimate holds [16]:
| (3.13) |
with . A uniformity result for this inf-sup constant is derived in the following lemma.
Lemma 4.
The constant in (3.13) can be taken such that holds.
Proof.
We use a similar approach as in the proof of the previous lemma, and derive an estimate on by pulling forward the result on . We use the pullforward that is based on the Piola transform and satisfies , , . Take and with . Define and . Note that with a constant uniformly bounded in (compatibility property). We have
Using this and the result (3.13) for we get:
which yields a -independent strictly positive lower bound for in (3.13). ∎
We now derive a uniform interpolation estimate.
Lemma 5.
The interpolation inequality (Ladyzhenskaya’s inequality)
| (3.14) |
holds with a constant independent of .
Proof.
For consider the Helmholtz decomposition (see e.g. [35])
| (3.15) |
Lemma 6.
For as in (3.15) we have and , , with a constant finite and independent of .
Proof.
Due to the orthogonality of the Helmholtz decomposition we have . Also note that , , , . Furthermore on we have the norm equivalence . A -dependence in the constants in this norm equivalence enters only through the Gaussian curvature of , cf. [35, Theorem 3.2]. Due to the smoothness property the Gaussian curvature is uniformly bounded on and thus the constants in this norm equivalence can be taken independent of . Using these results we get
and by similar arguments with a constant uniformly bounded in . ∎
3.4 Solution space
In this section we introduce a subspace of consisting of functions for which a suitable weak normal time derivative exists. This space will be the solution space in the weak formulation of TSNSE.
We recall the Leibniz rule
Thus for velocity fields we get
| (3.16) |
This implies the integration by parts identity
| (3.17) |
Based on this we define for the normal time derivative as the functional :
| (3.18) |
Note that functions in are not necessarily solenoidal, cf. (3.10). Restricting now to , assume is such that
is bounded. Since is dense in , can then be extended to a bounded linear functional on . We use and introduce the space
This space is used as solution space in the weak formulation of TSNSE below. In the remainder of this section we derive certain useful properties of this space. For this it will be helpful to introduce in addition to the Lagrangian derivatives (material derivative) and (normal time derivative) one other Lagrangian derivative, which is based on the pushforward operator :
| (3.19) |
The reason that we introduce the derivative is, that it is the same as the one used in the general framework in [1] and we can use results derived in that paper. Note that the derivative is defined for tangential flow fields and based on the Piola transform implying
| (3.20) |
We now derive relations between the derivatives and .
Lemma 7.
For the following holds:
| (3.21) | ||||
| (3.22) |
Proof.
From (3.21) we obtain the identity
with . Based on this, we define for as the functional
| (3.23) |
with defined in (3.18). The density of in and of in allows us to define as an element of and , respectively. The following result holds:
| (3.24) |
Implication “” in (3.24) is trivial since . To see “”, consider any and together with its Helmholtz decomposition , cf. (3.15). Thanks to Lemma 6 we get , and . Since we have
| (3.25) |
while for the other component we get employing (3.20)
| (3.26) |
We thus conclude for all and . The result in (3.24) follows from the density of in .
We are now ready to prove the following result.
Lemma 8.
The space is a Hilbert space and is dense in . For any and , is well-defined as an element of and it holds
Proof.
The idea of the proof is to relate the space to the space , with , and to show that the latter is homeomorphic to a standard Bochner space for . Lemma 2 ensures and thus from (3.23) we obtain
Therefore, is a linear bounded functional on iff has this property. We conclude iff . Moreover, the above inequalities, definition of the -norm, -norm and yield
with constants and independent of and so algebraically and topologically. Thus, it is sufficient to check the claims of the lemma for . For the latter we apply results from [1], more specifically, Corollary 2.32 ( is a Hilbert space), Lemma 2.35 (continuous embedding ) and Lemma 2.38 (density of smooth functions). For these results to hold one has to verify Assumption 2.31 [1], which requires the mapping to be a homeomorphism between and , the standard Bochner space
It remains to check this homeomorphism property. We already derived the norm equivalence , cf. Section 3.2. To relate the norms and we consider the following equalities for , , and :
| (3.27) |
Note that for all and from Lemma 2 it follows that . Hence it holds
From this, equality (3.27) and (3.24) one obtains after simple calculations,
The reverse estimate follows from the identity
by similar arguments (in particular the analogue result to (3.24) holds for the time derivative on ). Therefore we proved and hence and are homeomorphic. ∎
4 Well-posed weak formulation
In this section we introduce and analyze a weak formulation of TSNSE (2.12). We restrict our arguments to the solenoidal case . The extension of the analysis to the case is discussed in section 4.3. In the weak formulation we take a solution space with only solenoidal vector fields, and thus the pressure term vanishes. The existence of a corresponding unique pressure solution is shown in section 4.1.
We introduce the notation
| (4.1) |
and consider the following weak formulation of TSNSE (2.12) with : For given , with , , find such that and
| (4.2) |
One easily checks that any smooth solution of (2.12) satisfies (4.2).
For the analysis of the weak formulation (4.2) we apply an established approach, e.g. [43]. Compared to the analysis of the non-stationary Navier-Stokes equations in Euclidean domains the main differences are that we use evolving spaces as introduced above instead of the standard Bochner ones, we have a normal time derivative in place of the usual , and an additional curvature-dependent term . We show the existence of a Galerkin solution, derive a-priori bounds and based on this show existence of a solution . We then show uniqueness of the solution with the help of Ladyzhenskaya’s inequality.
Faedo–Galerkin approximation
The space has a countable basis , which is pushed forward to a countable basis of by letting . Consider
| (4.3) |
We determine the unknown functions from (4.3) by considering the system of ODEs
| (4.4) |
Here is the -orthogonal projection of on .
A priori bounds
Assume as in (4.3) satisfies (4.4). Multiplying (4.4) by and summing over , we get, using ,
| (4.5) |
and applying integration by parts (3.17) we have
| (4.6) |
From this we obtain for ,
| (4.7) |
Here and in the remainder we write to denote with some constant which may depend on the final time , the maximum normal velocity and on smoothness properties of the space-time manifold, quantified by . Note that . The Gronwall lemma and (4.7) yield the a priori bound,
| (4.8) |
Existence of solution
Consider the ODEs system (4.4). Due to Lemma 7 we have , with . Thus (4.4) results in the following system for :
| (4.10) |
for . From the fact that the pushforward map is one-to-one and linear for every , and are linear independent we infer that are linear independent for every and thus the matrix is invertible for . Moreover, (3.6) and the definition of implies . Since any eigenvalue of , denoted by , continuously depends on matrix coefficients, the bound for each implies uniformly on . The uniform lower bound for the eigenvalues and the symmetry of ensures . Multiplying both sides of (4.10) with , one verifies that the Picard-Lindelöf theorem applies. Hence a unique solution , , exists for a maximal interval , . If , then , which contradicts the established bound (4.8) with replaced by . Hence, a unique solution exists for .
From the a priori bounds (4.8), (4.9) it follows that there is a subsequence of of that is weak-star convergent in and weakly convergent in to . Due to the compactness of this sequence also strongly converges in . Now note that, with , as above, functions , , , with , are dense in . We multiply (4.4) with such a function , integrate over and apply partial integration (3.17), which yields
| (4.11) | |||
| (4.12) | |||
| (4.13) |
Due to the strong convergence in we can pass to the limit in the two terms in (4.11) and the first term in (4.13). Since is a functional on for any , we can pass to the limit in the first term in (4.12). Using the strong convergence in we can also pass to the limit in the second term in (4.12), cf. [43, Lemma 3.2]. By definition of we have strongly in . Thus we get, cf. (4.1),
| (4.14) |
We restrict to with and build linear combinations of (4.14) to arrive at
| (4.15) |
for all . We estimate the nonlinear term with the help of uniform Ladyzhenskaya inequality and (4.8), (4.9):
| (4.16) |
Using the above estimate and obvious continuity estimates for other terms on the right hand side in (4.15) together with a density argument we conclude that
| (4.17) |
hence and furthermore satisfies (4.2).
To check that holds, we apply standard arguments. Using continuity of for ([1, Theorem2.40]) and density of smooth functions in it follows that the partial integration rule (3.17) can be generalized to . Test (4.2) with , with , applying partial integration and comparing the result with (4.14) we obtain . Since is dense in we conclude that holds.
Uniqueness of solution
We prove uniqueness of the solution using essentially the same arguments as in Euclidean space. For the sake of presentation below, we use to denote duality pairing between and and introduce the notation for -level bilinear forms, cf. (4.1):
Note that holds. A solution of (4.2) satisfies
| (4.18) |
The Leibniz rule (3.16) extends to (cf. [1, Lemma 3.4]) yielding
Let , be solutions of (4.2) with . Letting and using we compute, with ,
We have . For the other terms on the right hand side above we use (3.14) and the Korn inequality (3.11) to estimate
with a suitable constant independent of and of . Thus we get
Now, implies that is bounded and so the Gronwall inequality together with yields for and thus the uniqueness result holds.
Summarizing we proved the following main well-posedness result.
Theorem 9.
The weak formulation (4.2) of the TSNSE has a unique solution . The solution satisfies
| (4.19) |
4.1 Surface pressure
For , (3.18) defines as a functional on . The density of in and the density of in is used to define the bounded linear functionals and , respectively. The following equivalence holds:
| (4.20) |
Implication “” in (4.20) is trivial since . The “” implication follows from (3.24) and Lemma 7.
Below we introduce a weak formulation of TSNSE on the velocity space
with a pressure unknown . One checks that is a Hilbert space by the same arguments as for . Consider the following mixed formulation of TSNSE, which relates to the well-posed weak formulation (4.2): For given , with , , find and , with a.e. , such that and
| (4.21) |
for all , .
Theorem 10.
Proof.
Let be the solution of (4.2). Define
Using (4.20) and straightforward estimates we obtain .222To see , one uses the same arguments as in (4.16). We use the standard argument (e.g. Remark I.1.9 in [43]) that for every estimate (3.13) implies that has a closed range in and so
Note that is an element of for a.e. and, since is the solution of (4.2), for all . Hence, which means
We take such that holds. To see that is measurable, we note the following. Let , with be the solution of the Laplace-Beltrami equation on . We then have . From and we conclude that is measurable. From (4.21) we get, with notation as in (4.1),
Using the uniform inf-sup estimate, cf. Lemma 4, we get
with a constant independent of . Hence, holds. The estimate for velocity in (4.22) is the same as in Theorem 4.19. Note that holds, cf. (4.8). Using this and the velocity estimate we obtain the bound for the pressure in (4.22). Uniqueness of follows by restricting to in (4.21) and using the fact that (4.2) has a unique solution. Uniqueness of is easily derived using the inf-sup property. ∎
4.2 Energy balance
Multiplying (2.12) by , integrating over and using (3.16), we obtain, for a smooth solution, the energy balance of the system at any ,
| (4.23) |
Next we comment on the contribution of the third term in (4.23), which appears if the surface is both evolving and non-flat. First we note that on and . Since we get . This implies that the symmetric matrix has real eigenvalues with the eigenvalue corresponding to vectors normal to . Take a fixed point on the surface with . Denote by and the two principle curvatures of . For the eigenvalue of we have . Therefore iff holds, and it is indefinite otherwise. In the latter case increase or decrease of kinetic energy due to this term depends on the alignment of the flow with the principle directions and the sign of .
4.3 Non-solonoidal solution
The tangential surface Navier–Stokes system (2.12) admits non-solonoidal solutions with , where , for , is defined by the surface geometry and evolution. We outline how the analysis for the solonoidal case presented above can be extended to such a problem. We assume that is sufficiently regular. Let be the unique solution of the Laplace-Beltrami equation , , and define . Then solves (2.12) iff and solve the system
| (4.24) |
with
The two additional terms and in the momentum equation in (4.24) are linear with respect to the unknown velocity field and can be treated very similar to the zero order term . The necessary regularity of can be established using the smoothness of and . We skip working out further details.
5 Discretization method
As discussed in the introduction, only very few papers are available in which finite element discretization methods for vector- or tensor valued surface PDEs, such as the surface Navier-Stokes equations, on evolving surfaces are treated. In this section we present a discretization method for the TSNSE (2.12). The method is based on a combination of an implicit time stepping scheme with a TraceFEM for discretization in space. The general idea behind TraceFEM is to use standard time-independent (bulk) finite element spaces to approximate surface quantities. The method is based on tangential calculus in the ambient space . For scalar PDEs on evolving surfaces, a space–time variant of TraceFEM is treated in [31]. A finite difference (FD) in time – FEM in space variant for PDEs on time-dependent surfaces is treated in [23] (scalar problems) and in time-dependent volumetric domains in [22] (scalar equations) and [46] (Stokes problem). Compared to the space–time variant the FD–FEM approach is more flexible in terms of implementation and the choice of elements. Below we explain this FD–FEM approach applied to the TSNSE. We start with the numerical treatment of the system’s evolution in time.
5.1 Time-stepping scheme
Consider uniformly distributed time nodes , , with the time step . We assume that the time step is sufficiently small such that
| (5.1) |
with a neighborhood of where a smooth extension of surface quantities on is well defined. Assuming a smooth extension , we rewrite the normal time derivative used in (2.12) in terms of standard time and space derivatives:
| (5.2) |
On the time derivative term is approximated by
Note that due to (5.1) is defined on . The normal surface velocity is known, so a natural linearization of the nonlinear term in (5.2) is given by
The finite difference approximations above need extensions of quantities defined on to . It is natural to consider a normal extension, which can be characterized as follows. Let in , where is the signed distance function for , and a function defined on . The normal extension of is such that on and
| (5.3) |
For practical purposes, can be a smooth level set function for rather than a signed distance. In this case, the vector field is normal on but defines quasi-normal directions in a neighborhood. Extension of the velocity field along quasi-normal directions is equally admissible. We assume that at an extension on solving (5.3) is given. We use the notation and for an approximation of and , respectively. Based on the approximations above and (5.3) consider the following time discretization method for (2.12). Given , for , find , defined on and tangential to , i.e. , and defined on such that:
| (5.4) | ||||
| (5.5) |
with , , , . Geometric information in (5.4) is taken for , i.e. , . For space discretization, the stationary linearized surface PDE in (5.4) can be treated using a variational approach known from the literature [16, 18], in which the tangential constraint for the solution is relaxed using a penalty approach. This technique is now outlined. We set , and introduce the following bilinear forms on , with arguments , vector functions on that are not necessarily tangential:
| (5.6) | ||||
| (5.7) |
where is a penalty parameter. We introduce two Hilbert spaces
with the norm . A variational formulation corresponding to (5.4) is as follows: Find , such that
| (5.8) |
with . This variational formulation is consistent in the sense that if is a strong solution of (5.4) then solves (5.8). Using the Korn type inequality (3.11) and an inf-sup property of it can be shown that for sufficiently small and sufficiently large (but independent of ) the problem (5.8) is well-posed and its unique solution satisfies , cf. [16] for a precise analysis. Therefore, for such and eq. (5.8) is a well-posed weak formulation of (5.4). For a finite element method introduced later it is important that the space admits vector functions not necessarily tangential to . The solution of (5.8) is defined only on and we do not specify an extension as in (5.5), yet. Such an extension will be determined in the finite element method, as explained in the next section.
Remark 5.1.
In the practical implementation of a finite element method for (5.8) the surface will be approximated by a piecewise planar surface and the corresponding projection operator has discontinuities across boundaries between different planar segments of this approximate surface. This causes difficulties for the terms in the bilinear forms , where derivatives of are involved. These can be avoided by eliminating these derivatives as follows. For we have , which elimates derivatives of . For the bilinear form we can use the relation and thus .
5.2 Finite element method
We now explain the spatial discretization of (5.8). Consider a fixed polygonal domain that strictly contains for all . Let be a family of shape-regular consistent triangulations of the bulk domain , with . Corresponding to the bulk triangulation we define a standard finite element space of piecewise polynomial continuous functions of a fixed degree :
| (5.9) |
The bulk velocity and pressure finite element spaces are standard Taylor–Hood spaces:
For efficiency reasons, we use an extension not in the given ( and -independent) neighborhood of but in a narrow band around . This -dependent narrow band consists of all tetrahedra within a distance from the surface, with
| (5.10) |
and , an mesh-independent parameter. More precisely, we define the mesh-dependent narrow band
We also need a subdomain of only consisting of tetrahedra intersected by ,
In a time step from to , the surface may move up to distance in normal direction, which is thus the maximum distance from to . Therefore, in (5.10) can be taken sufficiently large, but independent of , such that
| (5.11) |
This condition is the discrete analog of (5.1) and it is essential for the well-posedness of the finite element problem at time step .
Next we define finite element spaces for velocity and pressure as restrictions to the narrow band of the time-independent bulk spaces and :
| (5.12) |
Denote by the Lagrange interpolation of . Our finite element formulation is based on formulation (5.8). Recall that in (5.8) we do not require to be tangential to . The tangential condition is weakly enforced by the penalty term in (5.6) with penalty parameter . Such a penalty approach is often used in finite element methods for vector values surface PDEs [14, 18, 29, 32]. In the discretization in addition to this penalty term we include two volume terms with integrals over and . The discrete problem is as follows: For given and find , , satisfying
| (5.13) | ||||
for . The term , with a parameter , is included for two reasons. Firstly, this term is often used in TraceFEM to improve the conditioning of the resulting stiffness matrix, cf. e.g. [7]. Secondly, this volume term weakly enforces the extension condition (5.5) with replaced by . In particular, at time a well-conditioned algebraic system is solved for all discrete velocity degrees of freedom in the neighborhood ; we refer to [23] for a stability and convergence analysis of such an extension procedure for a scalar surface equation. The volume term in the pressure equation is added for the purpose of numerical stabilization of pressure [28]. The formulation (5.13) is consistent in the sense that the equations hold if the solution of (5.4), extended along normal directions, is substituted instead of and . Penalty and stabilization parameters are set following the error analysis in [28]:
In practice, , , is replaced by a sufficiently accurate approximation in such a way that integrals over can be computed accurately and efficiently. Other geometric quantities, i.e. , and , are also replaced by sufficiently accurate approximations. The derivatives of projected fields, i.e. and , are handled as discussed in Remark 5.1. For the surface Stokes problem discretized by the trace –, , elements, the introduced geometric error is analyzed in [17]. Below we will use the lowest order trace Taylor-Hood pair –. An approximation that is piece-wise planar with respect to leads to an geometric error. This geometric error order is suboptimal given the interpolation order of the Taylor–Hood pair –. This suboptimality can be overcome by the isoparametric TraceFEM [12]. For numerical results in this paper we use the following less efficient but simpler approach. For the geometry approximation (only) we construct a piece-wise planar with respect to a local refinement of each tetrahedron from . The number of local refinement levels is chosen sufficiently large to restore the optimal convergence. Note that this local refinement only influences the surface approximation and not the finite element spaces used.
6 Numerical examples
For discretization, an initial triangulation was build by dividing into cubes and further splitting each cube into 6 tetrahedra with . Further, the mesh is refined in a sufficiently large neighborhood of a surface so that tetrahedra cut by belong to the same refinement level for all . denotes the level of refinement and . The trace – Taylor–Hood finite element method with BDF2 time stepping, as described in the previous section, is applied.
6.1 Convergence for a smooth solution
To verify the implementation and to check the convergence order of the discrete solution, we set up an experiment with a known tangential flow along an expanding/contracting sphere. In this example the total area of is not preserved, but it allows to prescribe a flow analytically and calculate and .
The surface is given by its distance function
| (6.1) |
We consider . The surface normal velocity is then , with We choose .
The exact solution is given by
| (6.2) |
and right hand sides and are computed accordingly from (6.1)–(6.2). For numerical integration, exact solutions and right hand sides are extended along normal directions to .
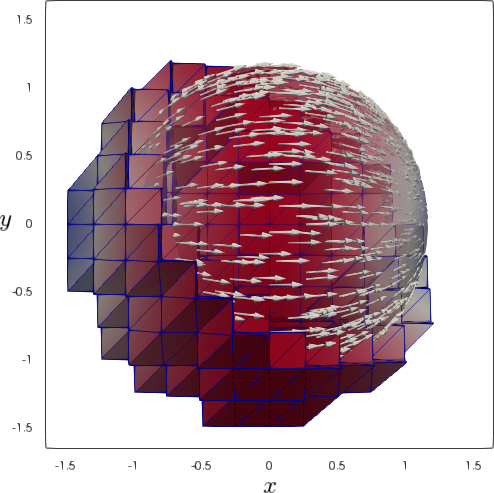
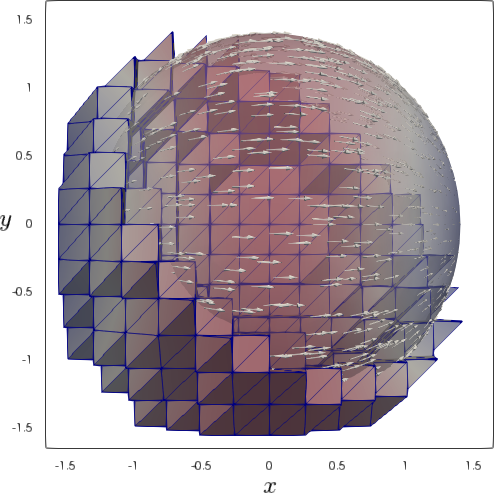
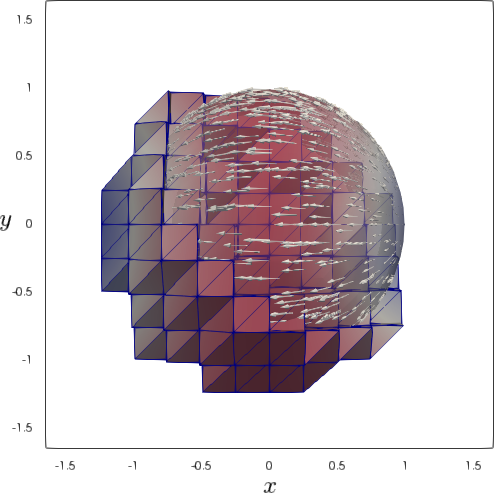
| Mesh level | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| Averaged # d.o.f. |
| Order | Order | Order | |||
The numerical solution was computed on four consecutive meshes with refinement levels and a time step on level 2; is halved in each spatial refinement, and for parameter in (5.10) we set . A mesh in together with the embedded and computed solution are illustrated in Figure 1. In Table 1 we show the mesh parameter and the resulting (averaged over all time steps) number of active degrees of freedom (# d.o.f.). We see that a mesh refinement leads to approximately four times more degrees of freedom. Table 1 further reports the velocity and pressure errors measured in (approximate) and norms. These norms were computed using a quadrature rule for time integration. Results demonstrate the expected 2nd order convergence in the “natural” norms and a higher order for the velocity error in the norm. These orders are optimal for the – elements used.
6.2 Tangential flow on a deforming sphere
In this numerical example we consider a deforming unit sphere and compute the induced tangential flow, i.e., the numerical solution of the TSNSE (2.12). Denote by the reference sphere of radius with the center in the origin . Consider spherical coordinates and denote by , the spherical harmonic of degree and order . Assume that are normalized, i.e. . For the evolving surface we consider as ansatz
| (6.3) |
with suitably chosen coefficients . The function describes the radial deformation. We assume small oscillations, . Under this assumption, an accurate approximation of the normal velocity is given by , with
| (6.4) |
We want the surface to be inextensible, i.e., . Appropriate coefficients such that we have inextensibility can be determined as follows. Application of the surface Reynolds transport formula and integration by parts gives for the variation of surface area:
| (6.5) |
For the doubled mean curvature we have, cf. [21],
Using , , and , we compute for the area variation:
| (6.6) |
Based on this formula we set , , and for other coefficients. For this choice of coefficients one easily verifies . The TSNSE equations (2.12) are then solved with the right hand side given by (2.13) with computed from (6.4). The initial velocity is zero.
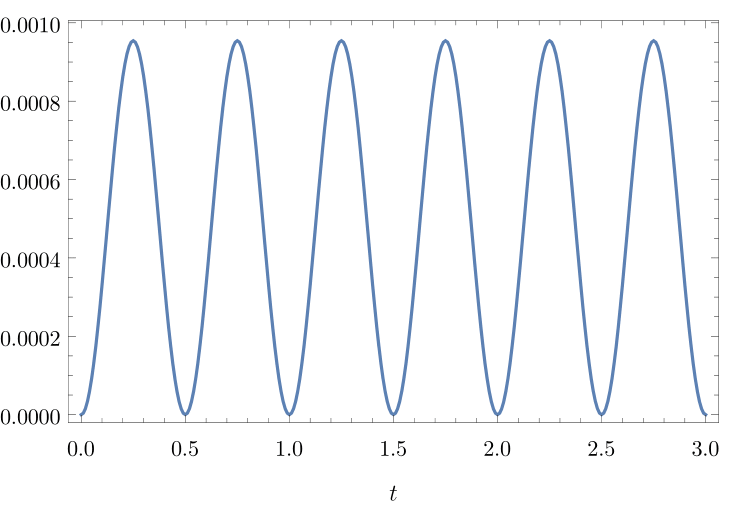
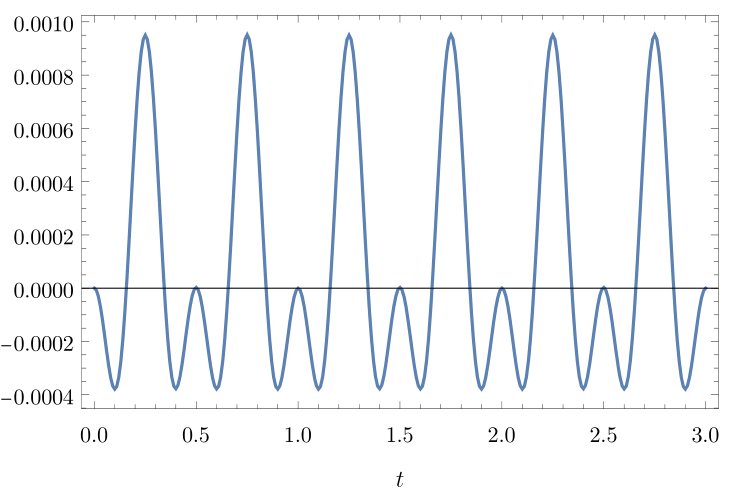
In the first numerical example we let , , , and include and , two zonal spherical harmonics of degree 2 and 3. The relative variation of the surface area in the left plot in Figure 2 shows less than of surface variation, which is due to approximation errors and finite (rather than infinitesimal) deformations. The latter causes an approximation error in (6.4).
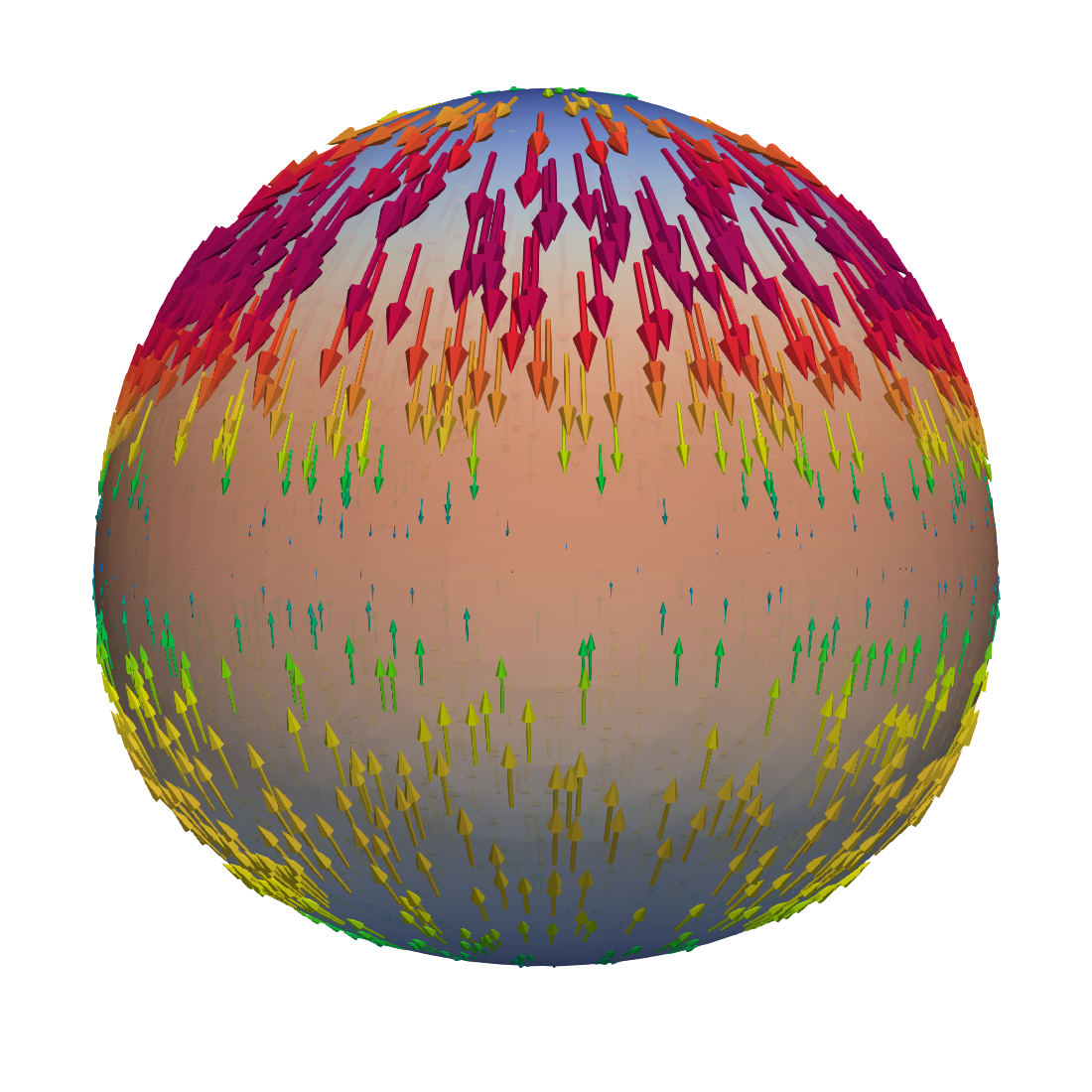
The velocity field induced by these axisymmetric deformations of the sphere is visualized in Figure 3. We see that the velocity pattern is dominated by a sink-and-source flow driven by the term on the right-hand side of the divergence condition in (2.12).


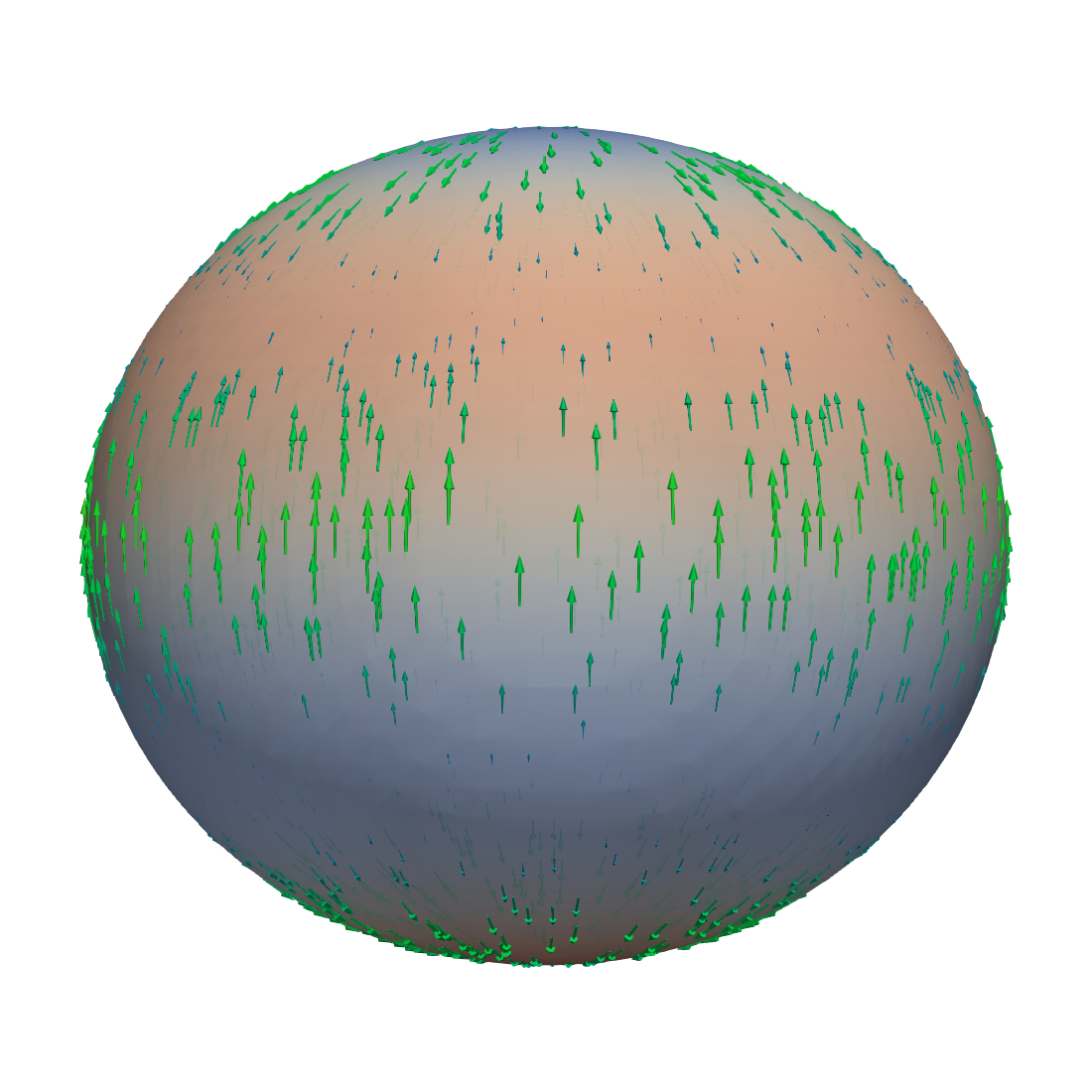
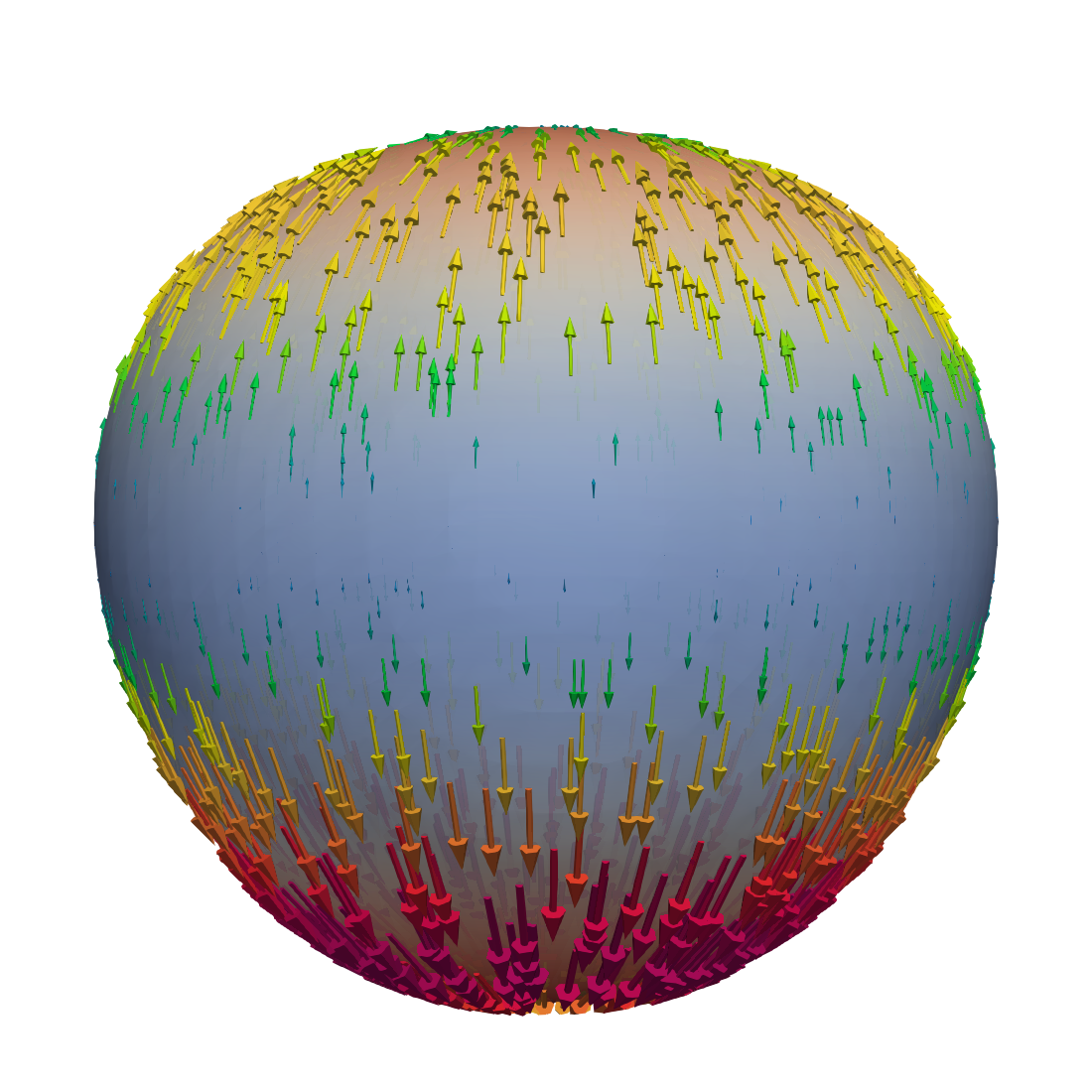
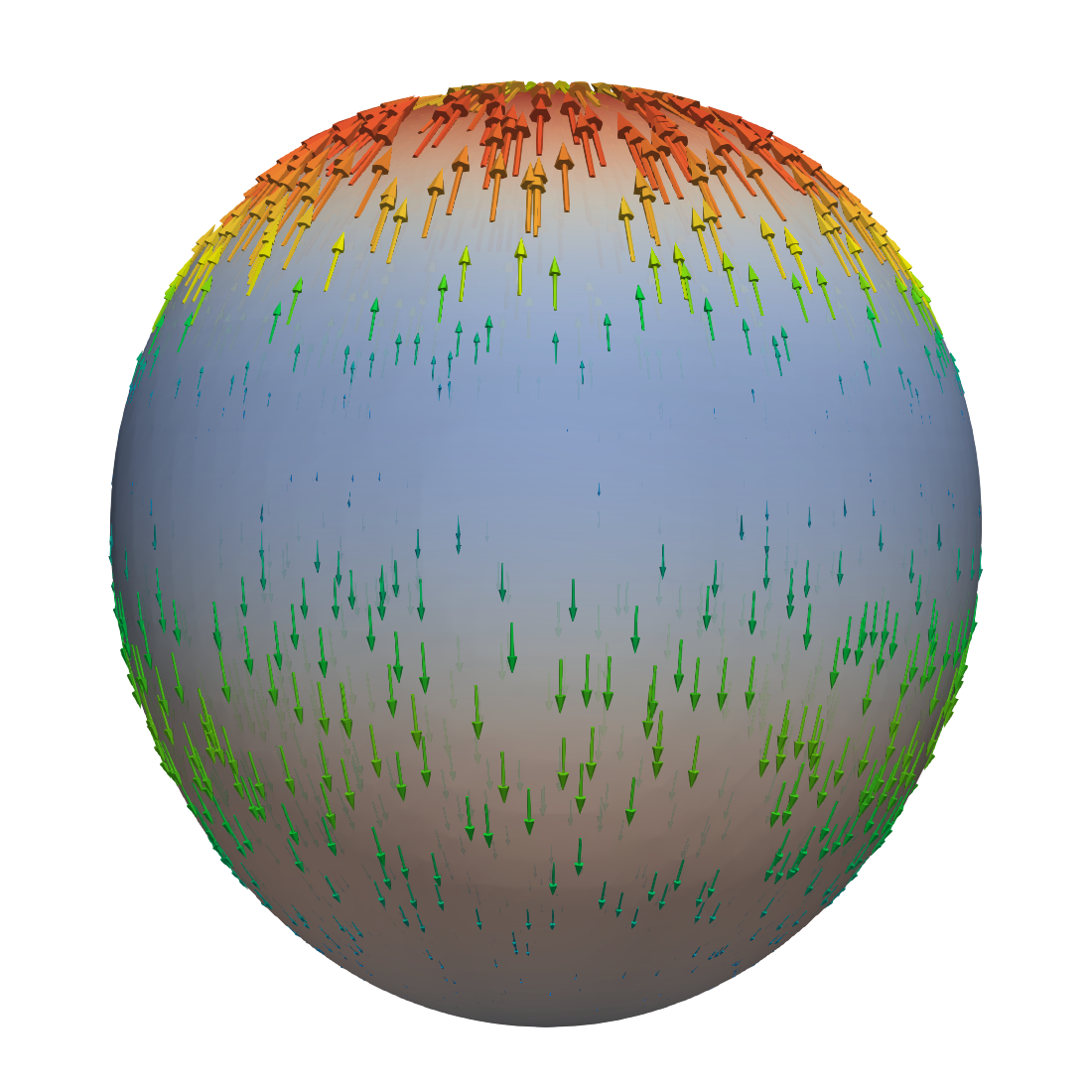
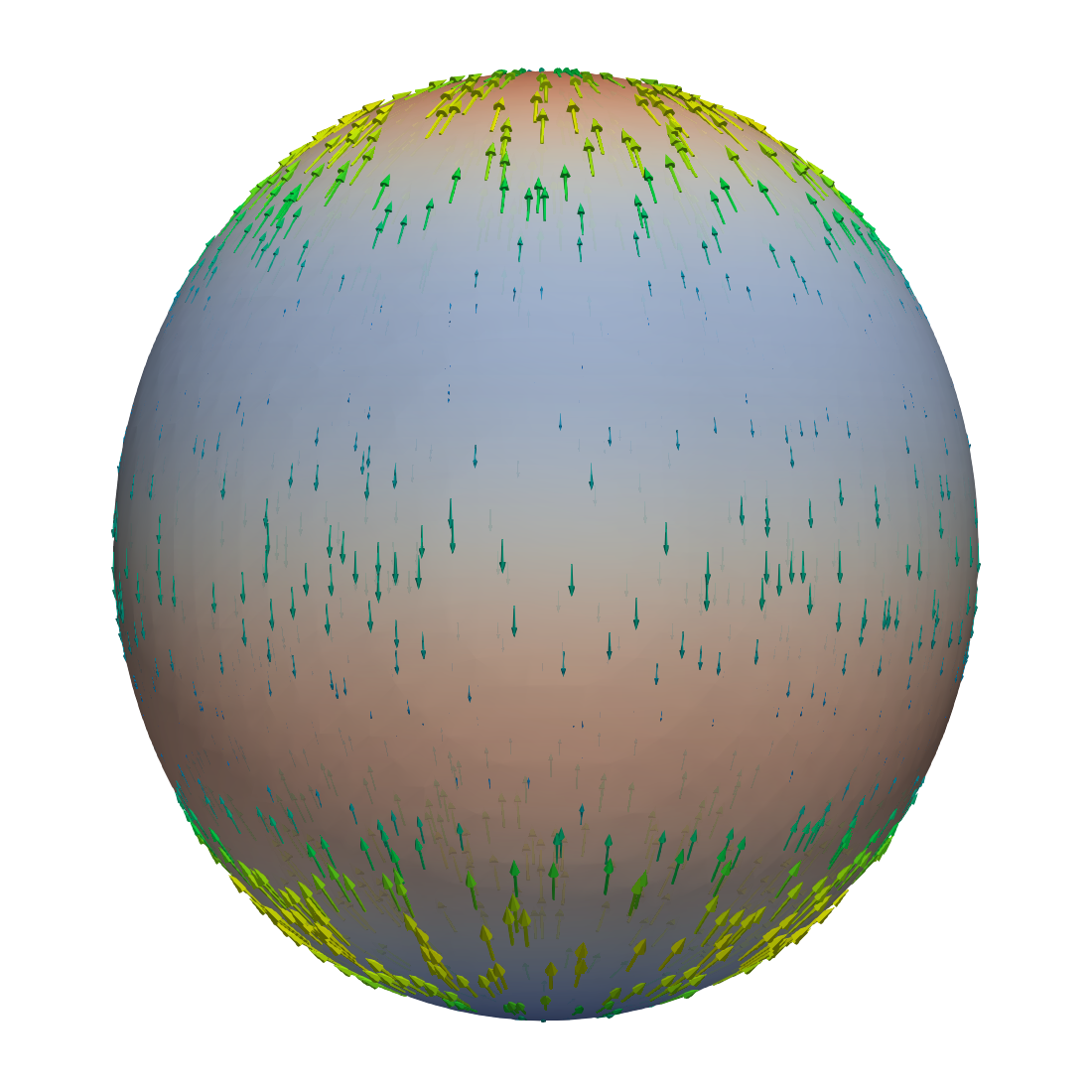

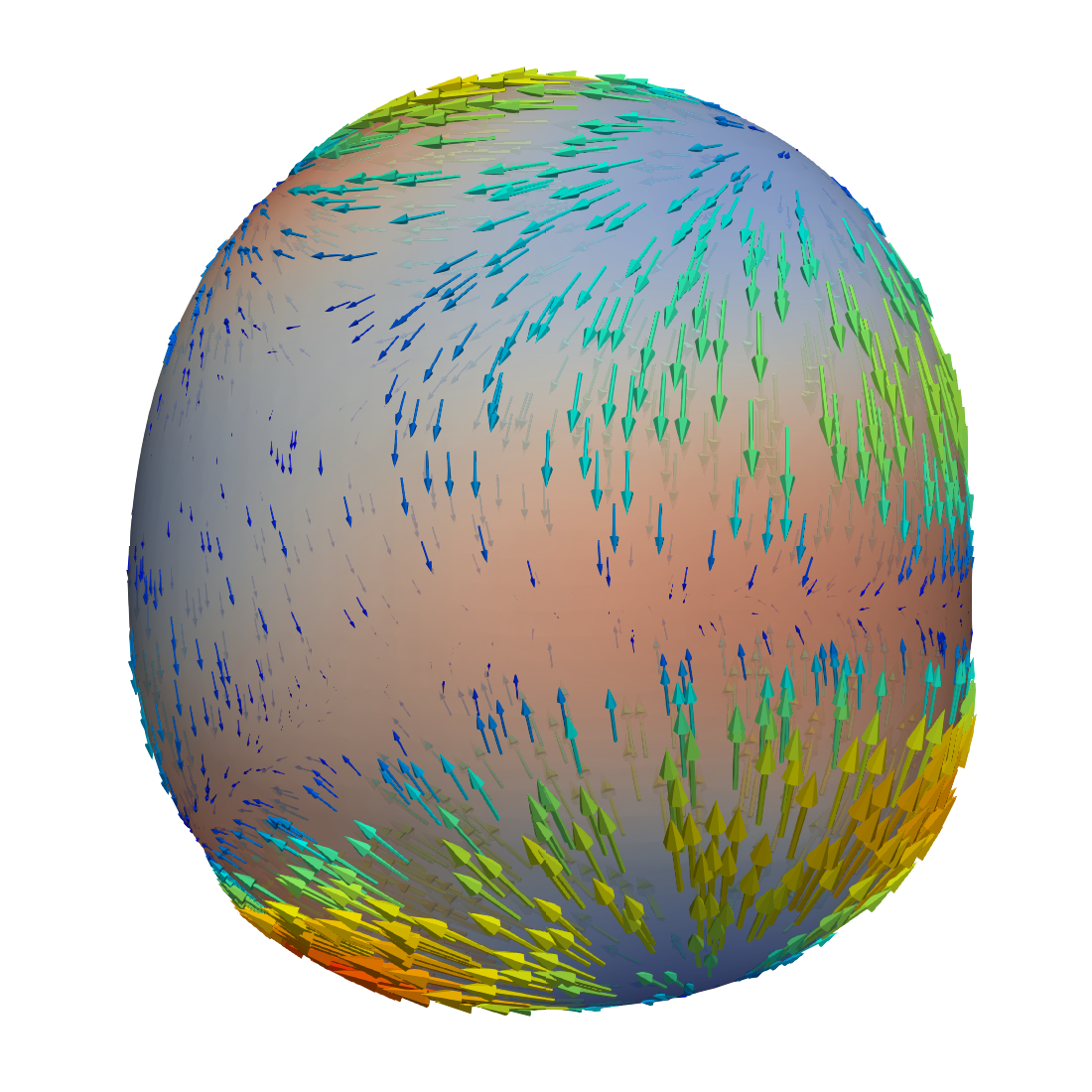
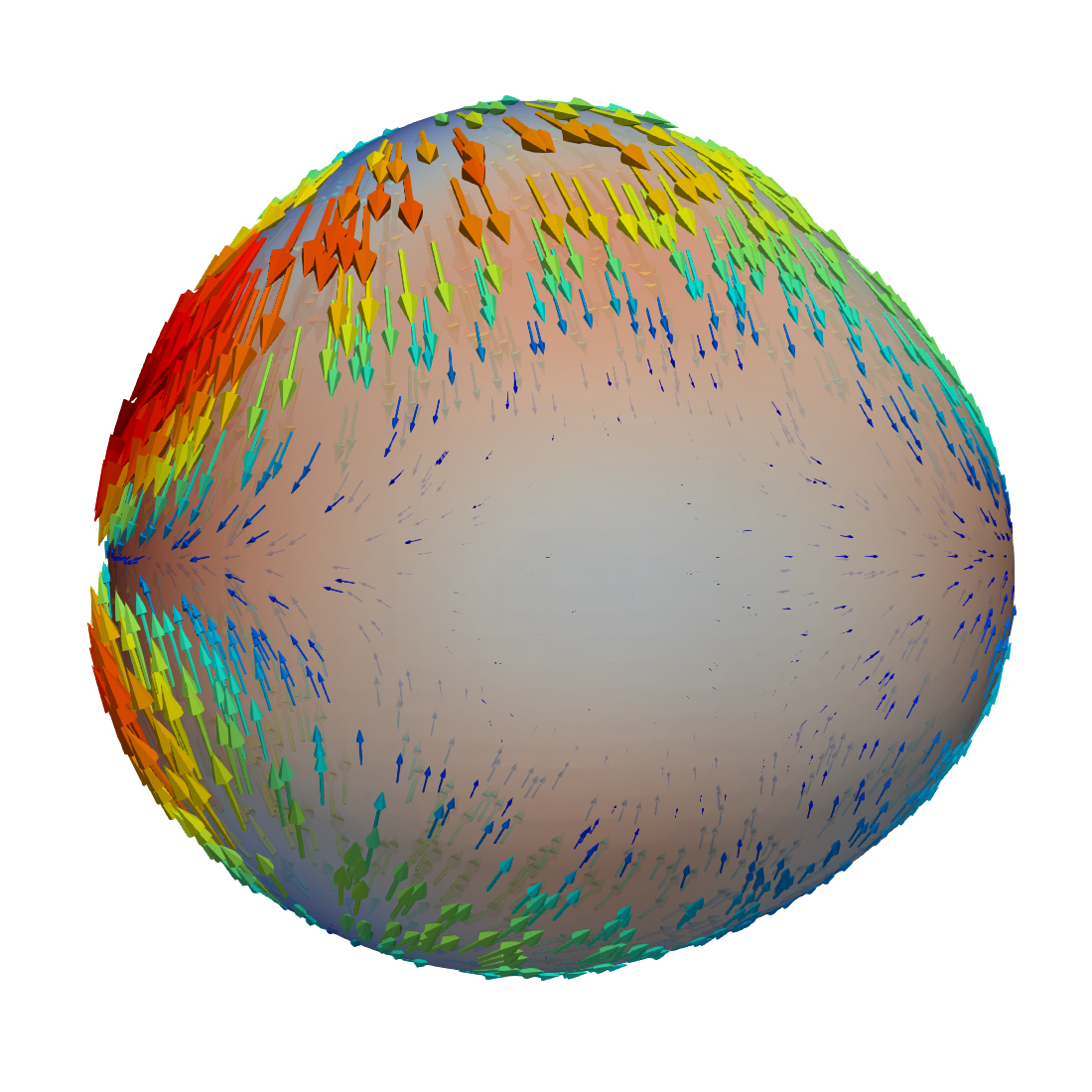

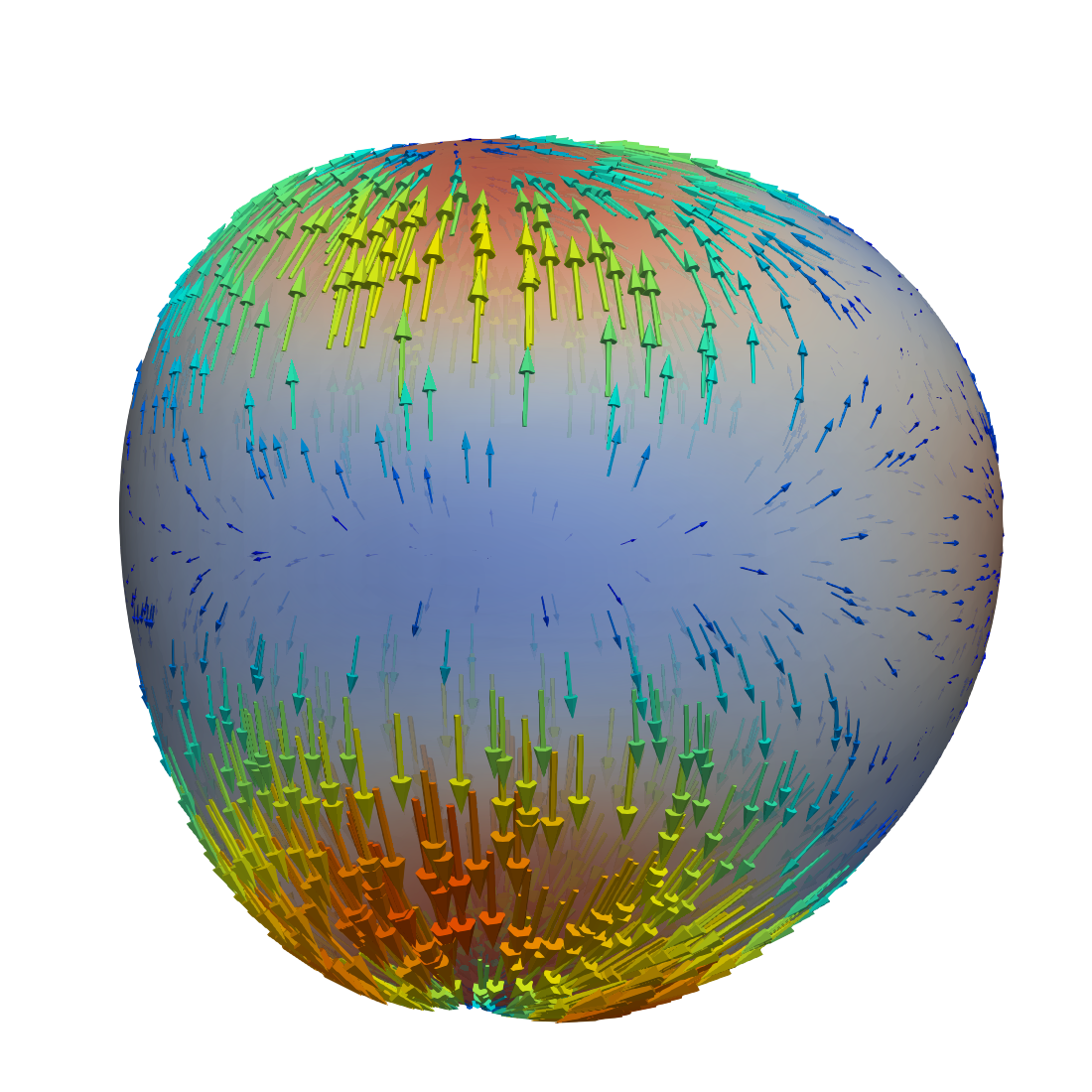

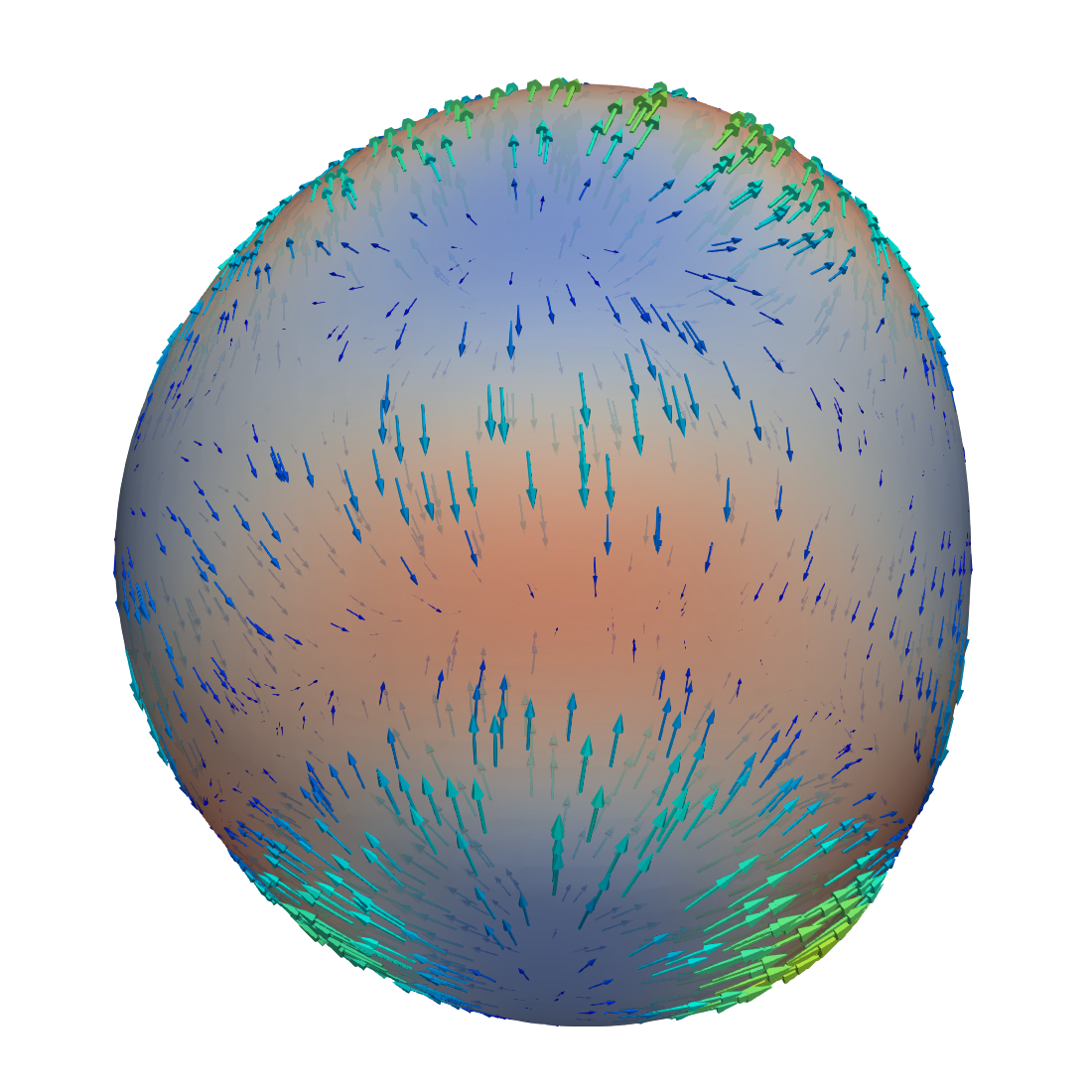
We repeat the experiment, but decrease the viscosity to and add two more spherical harmonics, the sectorial harmonic and the tesseral one, to make the deformation asymmetric. The radial displacement in this experiment is then given by
Again, the coefficients are such that according to equation (6.6). The resulting velocity field is visualized in Figure 4. The velocity pattern is still dominated by the sink-and-source flow. Note that in both cases there are no outer forces and the flow is completely “geometry driven”.
References
- [1] A. Alphonse, C. M. Elliott, and B. Stinner, An abstract framework for parabolic PDEs on evolving spaces, Port. Math., (2015), pp. 1–46.
- [2] V. Arnold, Sur la géométrie différentielle des groupes de lie de dimension infinie et ses applications à l’hydrodynamique des fluides parfaits, in Annales de l’institut Fourier, vol. 16, 1966, pp. 319–361.
- [3] T. Aubin, Nonlinear analysis on manifolds. Monge-Ampere equations, Springer, Berlin, 1982.
- [4] J. W. Barrett, H. Garcke, and R. Nürnberg, Numerical computations of the dynamics of fluidic membranes and vesicles, Physical review E, 92 (2015), p. 052704.
- [5] A. Bonito, A. Demlow, and M. Licht, A divergence-conforming finite element method for the surface Stokes equation, SIAM Journal on Numerical Analysis, 58 (2020), pp. 2764–2798.
- [6] P. Brandner, A. Reusken, and P. Schwering, On derivations of evolving surface Navier-Stokes equations, arXiv preprint arXiv:2110.14262, (2021).
- [7] E. Burman, P. Hansbo, M. G. Larson, and A. Massing, Cut finite element methods for partial differential equations on embedded manifolds of arbitrary codimensions, ESAIM: Mathematical Modelling and Numerical Analysis, 52 (2018), pp. 2247–2282.
- [8] C. Chan, M. Czubak, and M. Disconzi, The formulation of the Navier-Stokes equations on Riemannian manifolds, J. Geom. Phys., 121 (2017), pp. 335–346.
- [9] G. Dziuk and C. Elliott, Finite elements on evolving surfaces, IMA J. Numer. Anal., 27 (2007), pp. 262–292.
- [10] G. Dziuk and C. M. Elliott, Finite element methods for surface PDEs, Acta Numerica, 22 (2013), pp. 289–396.
- [11] D. G. Ebin and J. Marsden, Groups of diffeomorphisms and the motion of an incompressible fluid, Annals of Mathematics, 92 (1970), pp. 102–163.
- [12] J. Grande, C. Lehrenfeld, and A. Reusken, Analysis of a high-order trace finite element method for PDEs on level set surfaces, SIAM Journal on Numerical Analysis, 56 (2018), pp. 228–255.
- [13] M. E. Gurtin and A. I. Murdoch, A continuum theory of elastic material surfaces, Archive for Rational Mechanics and Analysis, 57 (1975), pp. 291–323.
- [14] P. Hansbo, M. G. Larson, and K. Larsson, Analysis of finite element methods for vector Laplacians on surfaces, IMA J. Numer. Anal., (2019).
- [15] P. Hartman, Ordinary Differential Equations, vol. 590, John Wiley and Sons, 1964.
- [16] T. Jankuhn, M. A. Olshanskii, and A. Reusken, Incompressible fluid problems on embedded surfaces: Modeling and variational formulations, Interfaces and Free Boundaries, 20 (2018), pp. 353–377.
- [17] T. Jankuhn, M. A. Olshanskii, A. Reusken, and A. Zhiliakov, Error analysis of higher order trace finite element methods for the surface Stokes equations, Journal of Numerical Mathematics, 29 (2021), pp. 245–267.
- [18] T. Jankuhn and A. Reusken, Higher order trace finite element methods for the surface Stokes equation, Preprint arXiv:1909.08327, (2019).
- [19] , Trace finite element methods for surface vector-Laplace equations, IMA Journal of Numerical Analysis, 41 (2020), pp. 48–83.
- [20] H. Koba, C. Liu, and Y. Giga, Energetic variational approaches for incompressible fluid systems on an evolving surface, Quarterly of Applied Mathematics, (2016).
- [21] H. Lamb, Hydrodynamics, University Press, 1924.
- [22] C. Lehrenfeld and M. Olshanskii, An Eulerian finite element method for PDEs in time-dependent domains, ESAIM: M2AN, 53 (2019), pp. 585–614.
- [23] C. Lehrenfeld, M. A. Olshanskii, and X. Xu, A stabilized trace finite element method for partial differential equations on evolving surfaces, SIAM Journal on Numerical Analysis, 56 (2018), pp. 1643–1672.
- [24] T.-H. Miura, On singular limit equations for incompressible fluids in moving thin domains, Quart. Appl. Math., 76 (2018), pp. 215–251.
- [25] A. Murdoch and H. Cohen, Symmetry considerations for material surfaces, Archive for Rational Mechanics and Analysis, 72 (1979), pp. 61–98.
- [26] I. Nitschke, S. Reuther, and A. Voigt, Hydrodynamic interactions in polar liquid crystals on evolving surfaces, Phys. Rev. Fluids, 4 (2019), p. 044002.
- [27] M. Olshanskii, A. Reusken, and J. Grande, A finite element method for elliptic equations on surfaces, SIAM J. Numer. Anal., 47 (2009), pp. 3339–3358.
- [28] M. Olshanskii, A. Reusken, and A. Zhiliakov, Inf-sup stability of the trace P2-P1 Taylor–Hood elements for surface PDEs, Mathematics of Computation, 90 (2021), pp. 1527–1555.
- [29] M. A. Olshanskii, A. Quaini, A. Reusken, and V. Yushutin, A finite element method for the surface Stokes problem, SIAM Journal on Scientific Computing, 40 (2018), pp. A2492–A2518.
- [30] M. A. Olshanskii and A. Reusken, Trace finite element methods for PDEs on surfaces, in Geometrically Unfitted Finite Element Methods and Applications, S. P. A. Bordas, E. Burman, M. G. Larson, and M. A. Olshanskii, eds., Cham, 2017, Springer International Publishing, pp. 211–258.
- [31] M. A. Olshanskii, A. Reusken, and X. Xu, An Eulerian space–time finite element method for diffusion problems on evolving surfaces, SIAM Journal on Numerical Analysis, 52 (2014), pp. 1354–1377.
- [32] M. A. Olshanskii and V. Yushutin, A penalty finite element method for a fluid system posed on embedded surface, Journal of Mathematical Fluid Mechanics, 21 (2019), p. 14.
- [33] J. Prüss, G. Simonett, and M. Wilke, On the Navier-Stokes equations on surfaces, J. Evol. Equ., 21 (2021), pp. 3153–3179.
- [34] P. Rangamani, A. Agrawal, K. K. Mandadapu, G. Oster, and D. J. Steigmann, Interaction between surface shape and intra-surface viscous flow on lipid membranes, Biomechanics and modeling in mechanobiology, (2013), pp. 1–13.
- [35] A. Reusken, Stream function formulation of surface Stokes equations, IMA Journal of Numerical Analysis, 40 (2020), pp. 109–139.
- [36] S. Reuther and A. Voigt, The interplay of curvature and vortices in flow on curved surfaces, Multiscale Modeling & Simulation, 13 (2015), pp. 632–643.
- [37] , Erratum: The interplay of curvature and vortices in flow on curved surfaces, Multiscale Modeling & Simulation, 16 (2018), pp. 1448–1453.
- [38] , Solving the incompressible surface Navier–Stokes equation by surface finite elements, Physics of Fluids, 30 (2018), p. 012107.
- [39] P. Saffman and M. Delbrück, Brownian motion in biological membranes, Proceedings of the National Academy of Sciences, 72 (1975), pp. 3111–3113.
- [40] G. Simonett and M. Wilke, -calculus for the surface Stokes operator and applications, arXiv preprint arXiv:2111.12586, (2021).
- [41] P. Steinmann, On boundary potential energies in deformational and configurational mechanics, Journal of the Mechanics and Physics of Solids, 56 (2008), pp. 772–800.
- [42] M. E. Taylor, Analysis on Morrey spaces and applications to Navier-Stokes and other evolution equations, Communications in Partial Differential Equations, 17 (1992), pp. 1407–1456.
- [43] R. Temam, Navier–Stokes equations, theory and numerical analysis, North-Holland, Amsterdam, 1977.
- [44] , Infinite-dimensional dynamical systems in mechanics and physics, Springer, New York, 1988.
- [45] A. Torres-Sánchez, D. Millán, and M. Arroyo, Modelling fluid deformable surfaces with an emphasis on biological interfaces, Journal of Fluid Mechanics, 872 (2019), pp. 218–271.
- [46] H. von Wahl, T. Richter, and C. Lehrenfeld, An unfitted Eulerian finite element method for the time-dependent Stokes problem on moving domains, IMA Journal of Numerical Analysis, (2021).
- [47] A. Yavari, A. Ozakin, and S. Sadik, Nonlinear elasticity in a deforming ambient space, J. Nonlinear Sci., 26 (2016), pp. 1651–1692.